Fully alternating, triaxial electric or magnetic fields offer new routes to fluid vorticity

Abstract

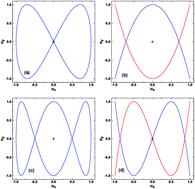
Noncontact methods of generating strong fluid vorticity are important to problems involving heat and mass transfer, fluid mixing, active wetting, and droplet transport. Furthermore, because zero or even negative shear viscosities can be induced, vorticity can greatly extend the control range of the smart fluids used in magnetorheological devices. In recent work we have shown that a particular class of ac/ac/dc triaxial fields (symmetry-breaking rational fields) can create strong vorticity in magnetic particle suspensions and have presented a theory of the vorticity that is based on the symmetry of the 2-d Lissajous trajectories of the field and its converse. In this paper we demonstrate that there are three countably infinite sets of fully alternating ac/ac/ac triaxial fields whose frequencies form rational triads that have the symmetry required to drive fluid vorticity. The symmetry of the 3-d Lissajous trajectories of the field and its converse can be derived and from this the direction of the vorticity axis can be predicted, as can the dependence of the sign of the vorticity on the phase relations between the three field components. Experimental results are presented that validate the symmetry theory. These discoveries significantly broaden the class of triaxial fields that can be exploited to produce strong noncontact flow.