Crossover between entropic and interfacial elasticity and osmotic pressure in uniform disordered emulsions
Abstract
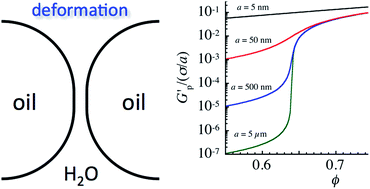
We develop a simple predictive model of the osmotic pressure Π and linear shear elastic modulus G′p of uniform disordered emulsions that includes energetic contributions from entropy and interfacial deformation. This model yields a smooth crossover between an entropically dominated G′p ∼ kBT/a3 for droplet volume fractions ϕ below a jamming threshold for spheres, ϕc, and an interfacially dominated G′p ∼ σ/a for ϕ above ϕc, where a and σ are the undeformed radius and interfacial tension, respectively, of a droplet and T is the temperature. We show that this model reduces to the known ϕ-dependent jamming behavior G′p(ϕ) ∼ (σ/a)ϕ(ϕ − ϕc) as T → 0 for ϕ > ϕc of disordered uniform emulsions, and it also produces the known divergence for disordered hard spheres G′p(ϕ) ∼ (kBT/a3)ϕ/(ϕc − ϕ) for ϕ < ϕc when σ → ∞. We compare predictions of this model to data for disordered uniform microscale emulsion droplets, corrected for electrostatic repulsions. The smooth crossover captures the observed trends in G′p and Π below ϕc better than existing analytic models of disordered emulsions, which do not make predictions below ϕc. Moreover, the model predicts that entropic contributions to the shear modulus can become more significant for nanoemulsions as compared to microscale emulsions.

 Please wait while we load your content...
Please wait while we load your content...