Breakdown of continuum elasticity in amorphous solids
Abstract
We show numerically that the response of simple amorphous solids (elastic networks and particle packings) to a local force dipole is characterized by a lengthscale 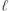 c that diverges as unjamming is approached as
c that diverges as unjamming is approached as 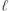 c ∼ (z − 2d)−1/2, where z ≥ 2d is the mean coordination, and d is the spatial dimension, at odds with previous numerical claims. We also show how the magnitude of the lengthscale
c ∼ (z − 2d)−1/2, where z ≥ 2d is the mean coordination, and d is the spatial dimension, at odds with previous numerical claims. We also show how the magnitude of the lengthscale 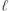 c is amplified by the presence of internal stresses in the disordered solid. Our data suggests a divergence of
c is amplified by the presence of internal stresses in the disordered solid. Our data suggests a divergence of 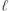 c ∼ (pc − p)−1/4 with proximity to a critical internal stress pc at which soft elastic modes become unstable.
c ∼ (pc − p)−1/4 with proximity to a critical internal stress pc at which soft elastic modes become unstable.


 Please wait while we load your content...
Please wait while we load your content...