Semi-flexible polymer chains in quasi-one-dimensional confinement: a Monte Carlo study on the square lattice

Abstract

Single semi-flexible polymer chains are modeled as self-avoiding walks (SAWs) on the square lattice with every 90° kink requiring an energy ε_b. While for ε_b = 0 this is the ordinary SAW, varying the parameter q_b = exp(−ε_b/k_BT) allows the variation of the effective persistence length _p over about two decades. Using the pruned-enriched Rosenbluth method (PERM), chain lengths up to about N = 10⁵ steps can be studied. 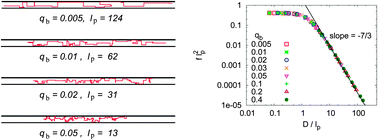In previous work it has already been shown that for contour lengths L = N_b (the bond length _b is the lattice spacing) of order _p a smooth crossover from rods to two-dimensional self-avoiding walks occurs, with radii R ∝ _p^1/4L^3/4, the Gaussian regime predicted by the Kratky–Porod model for worm-like chains being completely absent. In the present study, confinement of such chains in strips of width D is considered, varying D from 4 to 320 lattice spacings. It is shown that for narrow strips (D < _p) the effective persistence length of the chains (in the direction parallel to the confining boundaries) scales like _p²/D, and R_‖ ∝ L (with a pre-factor of order unity). For very wide strips, D ≫ _p, the two-dimensional SAW behavior prevails for chain lengths up to L_cross ∝ _p(D/_p)^4/3, while for L ≫ L_cross the chain is a string of blobs of diameter D, i.e. R_‖ ∝ L(_p/D)^1/3. In the regime D < _p, the chain is a sequence of straight sequences with length of the order _p²/D parallel to the boundary, separated by sequences with length < D perpendicular to the boundary; thus Odijk's deflection length plays no role for discrete bond angles.