Theoretical analysis of growth or swelling wrinkles on constrained soft slabs

Abstract

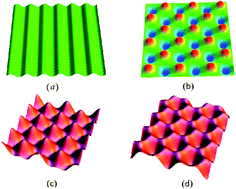
Growth or swelling of soft slabs attached to a rigid substrate generates large compressive stresses at their surfaces. When the stresses exceed a critical value, the smooth surface becomes unstable. For an in-plane isotropic material, a nonlinear three dimensional analysis is employed to ascertain the energy in the buckled state for different modes: stripes, squares and hexagons. When increasing the growth control parameter, we show that hexagonal patterns with a dimple at the center minimize the elastic energy and will be the dominant mode if the mode with minimal energy is the most likely to be observed. The growth of an anisotropic material reinforced by fibers is also considered. The results provide a way to understand surface wrinkling patterns induced by equi-biaxial growth or swelling of elastic layers, with possible applications for micro-patterns fabrication through an appropriate fiber arrangement.