On the meaning of the diffusion layer thickness for slow electrode reactions

Abstract

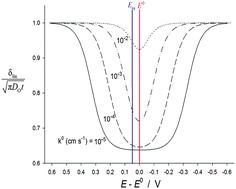
A key concept underpinning electrochemical science is that of the diffusion layer – the zone of depletion around an electrode accompanying electrolysis. The size of this zone can be found either from the simulated or measured concentration profiles (yielding the ‘true’ diffusion layer thickness) or, in the case of the Nernst (‘linear’) diffusion layer by extrapolating the concentration gradient at the electrode surface to the distance at which the concentration takes its bulk value. The latter concept is very well developed in the case of fast (so-called reversible) electrode processes, however the study of the linear diffusion layer has received scant attention in the case of slow charge transfer processes, despite its study being of great interest in the analysis of the influence of different experimental variables which determine the electrochemical response. Analytical explicit solutions for the concentration profiles, surface concentrations and real and linear diffusion layers corresponding to the application of a potential step to a slow charge transfer process are presented. From these expressions the dependence of the diffusion layer thickness on the potential, pulse time, heterogeneous rate constant and ratio of bulk concentrations of electroactive species and of diffusion coefficients is quantified. A profound influence of the reversibility degree of the charge transfer on the diffusion layer thickness is clear, showing that for non-reversible processes the real and linear diffusion layers reveal a minimum thickness which coincides with the equilibrium potential of the redox couple in the former case and with the reversible half-wave potential in the latter one.