Mechanics of a liquid drop deposited on a solid substrate

Abstract

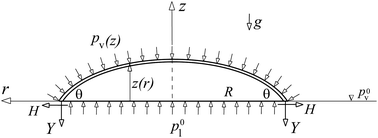
New derivations of Young–Laplace's and Young's equations for a liquid drop deposited on a smooth solid substrate are presented, based on an integral form of equilibrium conditions applied to appropriately selected finite portions of the drop. A simple proof for the gravity independence of the contact angle is constructed and compared with a commonly utilized but more involved proof based on the energy minimization. It is demonstrated that the vertical component of the adhesive force along a triple contact line does not depend on the specific weight of the liquid, provided that the line tension along a triple contact is ignored. The uplifting of the surface of the substrate due to vertical force is calculated by using a linear elasticity theory. The resulting singularity in the vertical displacement and the discontinuity in the radial displacement along a triple contact line are eliminated by incorporating in the analysis the effective width of the triple contact region. It is shown that the radial displacement vanishes on the surface of the substrate outside its contact with a deposited drop.