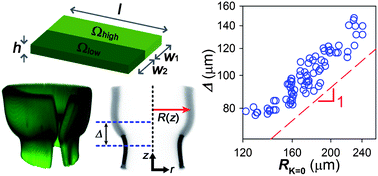
The process by which spatial variations in growth transform two-dimensional elastic membranes into three-dimensional shapes is both a fundamentally interesting mechanism of shape selection and a powerful tool for the preparation of responsive materials. From the perspective of lithographic patterning of thin gel sheets, it is most straightforward to prepare materials consisting of discrete regions with different degrees of swelling. However, the sharp variations in swelling at the boundaries between such regions make it impossible for the sheet to adopt a configuration that is free of in-plane stresses everywhere. Thus, the deformation of such materials is not well understood. Here, we consider the geometrically simple case of a photo-crosslinkable poly(N-isopropylacrylamide) copolymer patterned into thin rectangular strips divided into one high- and one low-swelling region. When swelled in an aqueous medium at 22 °C, the sheet rolls into a three-dimensional shape consisting of two nearly cylindrical regions connected by a transitional neck. Heating to 50 °C leads to fully reversible de-swelling back to a flat configuration. We propose a scaling argument based on a balance between stretching and bending energies that relates the curvature of the 3D shape to the width and thickness of the strip, find good agreement with experimental data and numerical simulations, and further demonstrate how this simple geometry provides a powerful route for the fabrication of self-folding stimuli-responsive micro-devices.