Geometry optimization using tuned and balanced redistributed charge schemes for combined quantum mechanical and molecular mechanical calculations†
Abstract
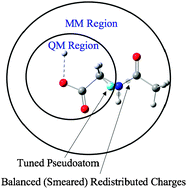
We performed geometry optimizations using the tuned and balanced redistributed charge algorithms to treat the QM–MM boundary in combined quantum mechanical and molecular mechanical (QM/MM) methods. In the tuned and balanced redistributed charge (TBRC) scheme, the QM boundary atom is terminated by a tuned F link atom, and the charge of the MM boundary atom is properly adjusted to conserve the total charge of the entire QM/MM system; then the adjusted MM boundary charge is moved evenly to the midpoints of the bonds between the MM boundary atom and its neighboring MM atoms. In the tuned and balanced redistributed charge-2 (TBRC2) scheme, the adjusted MM boundary charge is moved evenly to all MM atoms that are attached to the MM boundary atom. A new option, namely charge smearing, has been added to the TBRC scheme, yielding the tuned and balanced smeared redistributed charge (TBSRC) scheme. In the new scheme, the redistributed charges near the QM–MM boundary are smeared to make the electrostatic interactions between the QM region and the redistributed charges more realistic. The TBRC2 scheme and new TBSRC scheme have been tested for various kinds of bonds at a QM–MM boundary, including C–C, C–N, C–O, O–C, N–C, C–S, S–S, S–C, C–Si, and O–N bonds. Charge smearing is necessary if the redistributed charges are close to the QM region, as in the TBSRC scheme, but not if the redistributed charge is farther from the QM region, as in the TBRC2 scheme. We found that QM/MM results using either the TBRC2 scheme or the TBSRC scheme agree well with full QM results; the mean unsigned error (MUE) of the QM/MM deprotonation energy is 1.6 kcal/mol in both cases, and the MUE of QM/MM optimized bond lengths over the three bonds closest to the QM–MM boundary, with errors averaged over the protonated forms and unprotonated forms, is 0.015 Å for TBRC2 and 0.021 Å for TBSRC. The improvements in the new scheme are essential for QM–MM boundaries that pass through a polar bond, but even for boundaries that pass through C–C bonds, the improvement can be quite significant.
- This article is part of the themed collection: Multiscale modelling

 Please wait while we load your content...
Please wait while we load your content...