Stern–Brocot trees in the periodicity of mixed-mode oscillations

Abstract

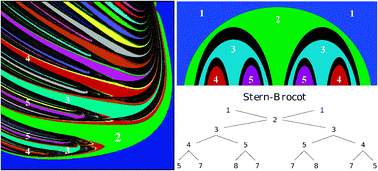
We investigate the distribution of mixed-mode oscillations in the control parameter space for two paradigmatic chemical models: a three-variable fourteen-parameter model of the Belousov–Zhabotinsky reaction and a three-variable four-parameter autocatalator. For both systems, several high-resolution phase diagrams show that the number of spikes of their mixed-mode oscillations emerges consistently organized in a surprising and unexpected symmetrical way, forming Stern–Brocot trees. The Stern–Brocot tree is more general and contains the Farey tree as a subtree. We conjecture the Stern–Brocot hierarchical organization to be the archetypal skeleton underlying several systems displaying mixed-mode oscillations.