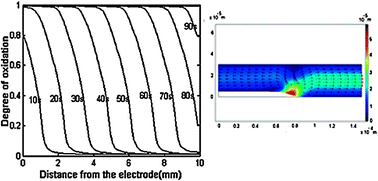
We present a theoretical description of the propagation of composition waves along a strip of electrochemically-active conducting polymer, upon electrochemical stimulation. We develop an efficient solution of the electro-neutral Nernst–Plank equations in 2-D for electromigration and diffusional transport in the solution based on an extension of the methods of Scharfetter and Gummel [D. L. Scharfetter and H. K. Gummel, IEEE Trans. Electron Devices, 1969, ED16, 64–77.] and of Cohen and Cooley [H. Cohen and J. W. Cooley, Biophys. J., 1965, 5, 145–162.], and demonstrate important effects of the geometry of the cell. Under some circumstances, waves reflecting back from the end of the strip are predicted. We then demonstrate theoretically how such waves, associated as they are with expansion of the polymer, could be employed to enhance mixing or induce pumping in microfluidic systems.
You have access to this article
 Please wait while we load your content...
Something went wrong. Try again?
Please wait while we load your content...
Something went wrong. Try again?

 Please wait while we load your content...
Please wait while we load your content...