Phase behaviour of quasi-block copolymers: A DFT-based Monte-Carlo study

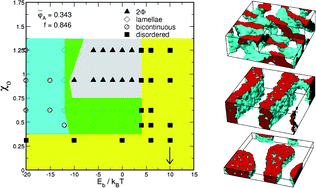
We develop a mesoscopic density functional theory (DFT)-based Monte-Carlo approach for studying the phase behaviour of multi-component systems comprised of irreversibly bonded, conventional macromolecules and supramolecular entities. The latter can reversibly associate with each other and the conventional components to “living”, equilibrium polymers. The computational approach can be applied to a broad class of supramolecular systems and we focus here on quasi-block copolymer systems that contain conventional, “dead” AB-copolymers with a supramolecular B-terminus and supramolecular B-units. The simulations show that, by properly selecting the architecture of the “dead” copolymers and by varying the supramolecular association constant and the incompatibility between the segment species, A and B, one obtains a variety of different microphase-separated morphologies and macrophase separations. Two representative phase diagrams are reported as a function of the association constant, E_b, and the Flory–Huggins parameter, χ, quantifying the repulsion between A and B segments. The simulation results are qualitatively rationalised by considering the dependence of the stoichiometry on the system's parameters, and fractionation effects between coexisting phases are illustrated.