Interstitial fractionalization and spherical crystallography

Abstract

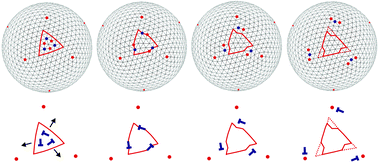
Finding the ground states of identical particles packed on spheres has relevance for stabilizing emulsions and has a venerable history in the literature of theoretical physics and mathematics. Theory and experiment have confirmed that defects such as disclinations and dislocations are an intrinsic part of the ground state. Here we discuss the remarkable behavior of vacancies and interstitials in spherical crystals. The strain fields of isolated disclinations forced in by the spherical topology literally rip interstitials and vacancies apart, typically into dislocation fragments that combine with the disclinations to create small grain-boundary scars. The fractionalization is often into three charge-neutral dislocations, although dislocation pairs can be created as well. We use a powerful, freely-available computer program to explore interstitial fractionalization in some detail, for a variety of power-law pair potentials. We investigate the dependence on initial conditions and the final state energies, and compare the position dependence of interstitial energies with the predictions of continuum elastic theory on the sphere. The theory predicts that, before fragmentation, interstitials are repelled and vacancies are attracted from 5-fold disclinations. We also use vacancies and interstitials to study low-energy states in the vicinity of “magic numbers” that accommodate regular icosadeltahedral tessellations.