Physical properties of soft repulsive particle fluids

Abstract

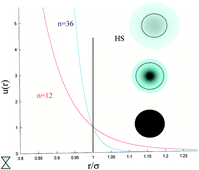
Molecular dynamics computer simulation has been applied to inverse power or soft-sphere fluids, in which the particles interact through the soft-sphere pair potential, ϕ(r) = ε(σ/r)ⁿ, where n measures the steepness or stiffness of the potential, and ε and σ are a characteristic energy and distance, respectively. The focus of the study is on very soft particles with n values down to 4 considered, at densities up to and along the fluid–solid co-existence density. It is shown that in the soft-particle limit the local structure is dominated by the lengthscale associated with the average nearest neighbour distance of a random structure, which is ∝ρ^−1/3 and increasingly only very weakly dependent on n. This scaling is also manifest in the behaviour of the average energy per particle with density. The self-diffusion coefficient and shear viscosity are computed along the fluid–solid co-existence line as a function of n, for the first time. The product Dη_s steadily increases with softness for n < 10, whereas the modified Stokes–Einstein relationship of Zwanzig, Dη_s/ρ^1/3, where ρ is the number density, is within statistics constant over the same softness range. This is consistent with our observation that the static properties are determined by a characteristic lengthscale (i.e., l) which is ∝ρ^−1/3 in the soft-particle limit. The high frequency elastic moduli of these fluids are examined, which reveals that the mechanical properties become more ‘rubbery’ as the particles get softer.