Time-dependent orientation distribution function calculated from time-correlation functions by use of information theory

Abstract

The information-theory method of Berne and coworkers for the orientational distribution function 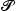(Ω, t) has been extended by adding 〈P₂[cos θ(t)]〉 to the quantities assumed to be known. The original theory and its extension have been applied to the case of rotational diffusion where 〈P₁[cos θ(t)]〉, 〈P₂[cos θ(t)]〉 and 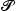(Ω, t) are analytically related. The accuracy of the 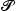(Ω, t) deduced by the two information methods is discussed. In addition, 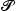(Ω, t) has been evaluated using the information theory method for the computer simulated results obtained by Berne for CO using a modified Stockmayer potential, for Gordon's results for liquid methane and for experimental dielectric data for two supercooled o-terphenyl solutions.