Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermally induced breakup of metallic nanowires: experiment and theory
Martin
Schnedlitz
a,
Maximilian
Lasserus
a,
Daniel
Knez
b,
Andreas W.
Hauser
 *a,
Ferdinand
Hofer
b and
Wolfgang E.
Ernst
*a,
Ferdinand
Hofer
b and
Wolfgang E.
Ernst
 *a
*a
aInstitute of Experimental Physics, Graz University of Technology, Petersgasse 16, A-8010 Graz, Austria. E-mail: andreas.w.hauser@gmail.com; wolfgang.ernst@tugraz.at; Fax: +43 (316) 873-108140; Tel: +43 (316) 873-8157 Tel: +43 (316) 873-8140
bInstitute for Electron Microscopy and Nanoanalysis & Graz Centre for Electron Microscopy, Graz University of Technology, Steyrergasse 17, A-8010 Graz, Austria
First published on 10th March 2017
Abstract
We present time-resolved transmission electron microscopy studies of the degradation of Au, Ag, Cu and Ni nanowires deposited on a heated support. The wires are grown under fully inert conditions in superfluid helium droplets and deposited onto amorphous carbon. The inherent stability of these pristine metal nanowires with diameters below 10 nm is investigated in the absence of any stabilizers, templates or solvents. The phenomenon of Rayleigh-breakup, a consequence of diffusion processes along the wire surfaces, is analysed in situ via scans over time and support temperature. Our experimental efforts are combined with simulations based on a novel model featuring a cellular automaton to emulate surface diffusion. Based on this model, correlations between the material parameters and actual breakup behaviour are studied.
1 Introduction
Recently, wire-shaped nanostructures have attracted attention due to their potential usage in circuits and nanodevices,1,2 biosensors,3–5 waveguides,6 membranes,7 transparent electrodes8 or antennae for photochemistry applications.9 At diameters in the range of a few nanometres a whole series of unusual properties emerge: ferromagnetism,10 negative magnetoresistance11 or quantum conductance have been reported,12 making the smallest nanowires potential components particularly interesting for miniature electronic circuits.13In a recent publication we studied the Rayleigh breakup of Ag nanowires,14 exploiting superfluid He nanodroplets (HeN) as nanolabs for the production of one-dimensional metallic structures.15,16 The doping of HeN with particles is well established in spectroscopy,17–19 and has recently been adapted for the controlled production and structure preserving soft deposition of metal clusters.20–24 For the creation of metallic nanowires we take advantage of a vortex formation, a quantum effect25,26 occurring for larger droplets with diameters of a few μm. As was originally observed in bulk superfluid helium (He II),27–29 these vortices attract dopants immersed in the helium due to a pressure gradient around the vortex core,30,31 causing a preference for one-dimensional growth which leads to the formation of nanowires.32–35
The experimentally challenging technique offers the benefit of complete inertness during wire production, deposition and measurement. Typically, nanowires in the sub 10 nm diameter range are stabilized by templates,36–38 which introduce a large bias in stability measurements.
When comparing the structures obtained for different metals after deposition on amorphous carbon via transmission electron microscopy (TEM), it became obvious that silver behaved significantly differently from the other elements. Whereas continuous wires could be observed for Au, Cu and Ni under standard conditions, the typical outcome for silver deposition would be an accumulation of segmented chains of silver clusters. This phenomenon was originally thought to be a consequence of the formation within the He droplets before deposition. However, a detailed study of the wire structures as a function of the substrate temperature revealed that this segmentation was caused by Rayleigh breakup, a temperature-dependent outcome of surface diffusion processes along the wires.14 This behaviour is well captured by an adaptation of Rayleigh's original model for the breakup of a fluid jet39 performed by Nichols and Mullins.40–42 While this has been postulated earlier by Gordon et al.,33,43 it could only be proven by a series of TEM images taken at increasing substrate temperatures. The study revealed that silver nanowires are particularly sensitive to heating with breakup temperatures as low as 263 K.
The current article aims to deepen our understanding of this diffusion process with regard to material-specific constants. In order to do this, we perform a combined approach involving theory and experiment.
On the experimental side, we broaden our spectrum of material investigation by detailed, temperature-programmed diffusion studies, originally only performed for Ag, now also for the elements Au, Ni and Cu. These metals have been chosen in order to cover a wide stability range. In addition to previous studies, the current experimental setup combines a very efficient and reproducible method for the production of metallic nanowires with a novel method for highly resolved in situ measurements of surface diffusion processes in ultrathin nanowires. This unique combination of apparatus and analysis tools offers the first in situ observations of the very nature of the formation and surface diffusion of metallic clusters.
On the theoretical side, we present a novel approach of describing the experimentally observed Rayleigh breakup phenomenon. Following ref. 44, we previously applied a two-dimensional computational method based on the Mullins equation,45 which states a relation between the flux of surface atoms and the gradient of the local surface curvature. With this method we could predict the location and the order (with respect to time evolution) of future breakups for initial structures of the arbitrary shape.14 Despite its success, this approach suffers from severe limitations, both in terms of computational efficiency as well as in its ability to grasp the real-world process of material redistribution: the actual motion of atoms in the diffusion process is represented by an artificial force acting on the contour line of the metallic structure. Therefore, we replaced the contour-line method by a cellular automaton (CA) ansatz on a three-dimensional grid. This new method, which is discussed in greater detail in the theory section of this article, together with additional data from the experiment, allows us to address several new questions regarding surface diffusion on metallic nanostructures:
(1) The higher computational efficiency allows the simulation of larger nanostructures and takes their actual height on the substrate into consideration.
(2) Material properties such as bond lengths and the binding energy enter the simulations. This way, metal-specific behaviour can be simulated and concrete changes of the structure can be reproduced in the time- and temperature domain.
(3) The broader choice of metals allows for a first analysis of trends in the periodic system and of tentative correlations between the breakup behaviour and the related material properties.
Our article is structured as follows: first, we give a brief overview of our experimental setup in Section 2. We discuss the He-droplet-mediated creation of metallic nanowires and their follow-up measurement. In Section 3 we provide details of the computational approach. A comparison of the simulated results and experimental nature is given in Section 4. Correlations between the actual behaviour of various metals and their corresponding atomic properties or material constants are analysed.
2 Experimental
A detailed description of the used helium droplet apparatus can be found in ref. 46. In short, gaseous helium (grade 6 He ≡ 99.9999% pure He) is cooled down to 5.4 K using a closed-cycle refrigerator (Sumitomo, RDK-408D2) and expanded with a stagnation pressure of 20 bar into a high vacuum chamber through a 5 μm nozzle. The stagnation pressure was kept constant at 20 bar for all experiments discussed in this work. Those settings correspond to![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) ≈ 1.7 × 1010 atoms per He droplet.17 The beam of HeN droplets is collimated with a 0.4 mm skimmer and is directed into a separate chamber (with a base pressure of ≈10−7 mbar). In this chamber the collimated beam passes through pickup cells, providing the desired partial pressure to dope the droplets with metal atoms of highest purity. The pickup cells consist of resistively heated alumina ovens of 2.3 cm length. The doping process triggers an evaporation of weakly bound He atoms, due to the release of the binding energy of the dopants, which can be monitored when measuring the difference in partial pressure of He via a residual gas analyzer (Balzers QMA 200/QME 200), mounted off the beam axis. The formation process of nanowires takes place during the flight time in which the doped droplets entered the measurement chamber (a base pressure of ≈6 × 10−10 mbar).35 In this chamber the nanowires are deposited either on a heatable TEM grid (DENSsolutions Nano-Chip XT carbon) or on an amorphous carbon TEM grid (Ted Pella, Inc., Prod. No. 01824), which can be cooled using liquid N2. The two different types of grids and TEMs are used to analyse both room-temperature-stable and -unstable nanowires. A differential pumping stage is mounted between the measurement chamber and the chamber with the evaporating cells.
≈ 1.7 × 1010 atoms per He droplet.17 The beam of HeN droplets is collimated with a 0.4 mm skimmer and is directed into a separate chamber (with a base pressure of ≈10−7 mbar). In this chamber the collimated beam passes through pickup cells, providing the desired partial pressure to dope the droplets with metal atoms of highest purity. The pickup cells consist of resistively heated alumina ovens of 2.3 cm length. The doping process triggers an evaporation of weakly bound He atoms, due to the release of the binding energy of the dopants, which can be monitored when measuring the difference in partial pressure of He via a residual gas analyzer (Balzers QMA 200/QME 200), mounted off the beam axis. The formation process of nanowires takes place during the flight time in which the doped droplets entered the measurement chamber (a base pressure of ≈6 × 10−10 mbar).35 In this chamber the nanowires are deposited either on a heatable TEM grid (DENSsolutions Nano-Chip XT carbon) or on an amorphous carbon TEM grid (Ted Pella, Inc., Prod. No. 01824), which can be cooled using liquid N2. The two different types of grids and TEMs are used to analyse both room-temperature-stable and -unstable nanowires. A differential pumping stage is mounted between the measurement chamber and the chamber with the evaporating cells.
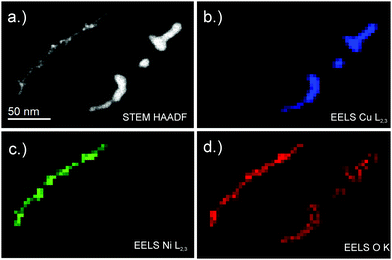
To investigate the temperature dependent diffusion processes for room-temperature-stable metal nanowires, scanning transmission electron microscope (STEM) high-angle annular dark-field (HAADF) images are recorded using a probe-corrected FEI Titan3 G2 60-300. The microscope is equipped with a Gatan Quantum energy filter for electron energy loss spectroscopy (EELS) and a four-quadrant energy-dispersive X-ray spectroscopy (EDX) detector (FEI Super-X), for the determination of material compositions. The temperature of the heatable carbon grid can be controlled from room temperature up to ≈1300 °C with heating rates of 200 °C ms−1. Since some nanowires show breakups below ambient temperature conditions14 the second substrate holder is cooled to liquid nitrogen (N2,liq) temperature. After the deposition of nanowires the cooled substrates are detached from the sample holder and immersed in N2,liq within ≈5 s. During this time the sample holder is flooded with dry nitrogen to prevent contact with ambient air. Afterwards the sample is analysed in a N2,liq environment via a FEI Tecnai 12 TEM, equipped with a Bio Scan Camera (Gatan, Model 792), where it is possible to manipulate the substrate temperature from 77 K to 363 K via the cryo-TEM holder (Gatan model No. 613).
The advantage over previous measurements is the possibility of in situ recording of breakup events as a function of the substrate temperature. To observe temperature dependent breakup events, recordings are taken during the heat-up process using a small temperature ramp of 2 K min−1 and at constant substrate temperatures. For each of the Au, Ag, Ni and Cu wires, one particular segment of the observable area was kept constant for a continuous observation throughout the whole heating time.
In the literature, experiments were described on nanowires made from e.g. Ag,47 Cu,48,49 Au,50,51 Sn52 and Pt,53 all with diameters above 20 nm. Breakup temperatures well below the bulk melting temperature were reported in all cases, but still far above room temperature. Only for Ag nanofractals, with initial branch diameters of ≈16 nm, structural changes near room temperature were observed.54,55 We note that a breakup of Ag nanowires, due to surface effects, has also been observed by Gordon et al. in bulk He II.32,43
3 Theory
In our previous work14 we based our simulations on the Mullins equation which was originally introduced to simulate the thermal grooving at metallic grain boundaries.45 The gradient of the chemical potential for a given surface atom can be related to the gradient of the local surface curvature; from this, a force on the respective surface element can be derived.44 However, this approach has several flaws such as the need for an extremely fine discretization of time in the numerical evaluation, and the tendency to numerical instabilities at breakup events, which correspond to local constrictions of contour lines during time propagation. Without going into details, these instabilities evolved from inhomogeneous point distributions in the discretisation of a contour line after a breakup, and had to be repaired by a costly increase of the point density. Besides, after breakup, each isolated fragment had to be propagated separately in time.14Our novel ansatz is fundamentally different from this previous approach and much closer to the actual physical process of particle migration. We employ a cellular automaton (CA), which uses the information obtained from the TEM data to create a three dimensional reconstruction of the nanowires in the form of a three-dimensional logical grid.
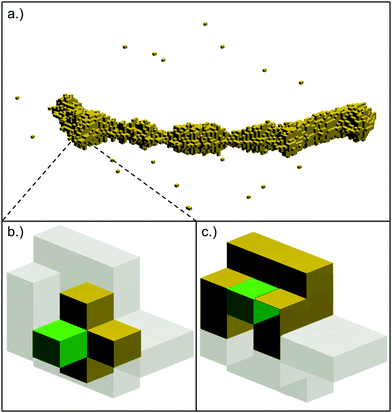
Given a change in the detected intensity with the material thickness, and assuming a circular cross section for each nanostructure, we can translate image contrast data into a three-dimensional object. As TEM intensity information is provided in the form of a two-dimensional matrix, the wires are created layer by layer, starting with a lower threshold I0 for the central layer, and counting only those pixels with intensities above I0. For the next layers this threshold is continuously increased, which adds additional voxels above the starting layer and results in a three-dimensional reconstruction of the total structure.
Each element of the grid represents a ‘voxel’, whose size is given by the pixel size of the TEM image. Following the basic idea of a CA, such a voxel is either filled with material or remains empty. For our data set, one voxel measures (0.95 nm)3, which corresponds to approximately 40 atoms per filled voxel.
The dynamics of the CA is defined by the choice of update rules which apply to all cells or voxels of the system. These updates are executed simultaneously for all cells in each time step.56 A simulation of the thermally induced surface diffusion process can now be obtained by choosing update rules which describe a particle hopping on the grid. This process depends on the local environment of a voxel, but must also account for the stochastic character of a temperature-driven particle migration. This can be achieved by employing an ansatz from reaction kinematics, the Eyring equation,57 defining jumping rates via
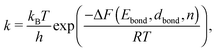 | (1) |
As k is strongly dependent on the temperature, the reaction rate will drastically increase as soon as the thermal energy is high enough to overcome the energy barrier ΔE and detach one voxel from its neighbour cells. After detaching, the voxel is free to change its position within its nearest neighbourhood. The number of nearest and next nearest neighbours determines, together with the probabilities derived for possible migrations, to which position the voxel will most likely be transferred. With the ongoing simulation time, this algorithm leads to preferably spherical structures, where the number of nearest neighbours in total reaches a maximum. Note that this model does not take any substrate interaction into account due to the extremely low wetting behaviour on the chosen substrate. This is particularly obvious for the interaction of gold and carbon in comparison to the intermetallic bond energy (EAu–C = 0.03 eV per atom,59EAu–Au = 3.81 eV per atom58). For a two-dimensional study of surface diffusion including the interaction with various substrates we refer to the work of Solov'yov et al. on Ag nanoparticles.60 Diffusion time is not directly linked to the in situ observed diffusion process. Therefore, a fit between the observed time dependent TEM surface diffusion process at constant temperature and the stepwise iteration process is necessary for realistic predictions of the behaviour over time. The simple linear dependence of the pre-exponential factor in eqn (1) is derived from statistical mechanics under the assumption of a single degree of freedom being responsible for reaction barrier transmission. The fact that not every attempt in this degree of motion leads to a successful hopping is usually taken into consideration by a proportionality constant κ referred to as the transmission coefficient. Although not in the atomic picture, we can follow this nomenclature for our discussion of voxel migration and include all unknown scaling factors which occur in the coarse-grained model into this constant κ. With F = E − TS we can rewrite eqn (1) as
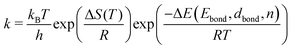 | (2) |
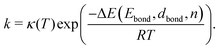 | (3) |
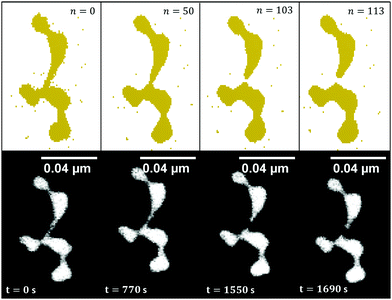
Fig. 1 displays graphically the situation of a selected surface voxel and its initial neighbourhood. In this setup, the energy can be minimized by moving the green voxel in a way which maximizes its number of neighbour voxels. The stochastic character of the process of breaking and forming bonds enters viaeqn (1), which yields the probabilities for hopping events.
4 Results and discussion
4.1 Nanowire growth, deposition and stability measurements
HeN droplets are used to create monometallic nanowires with diameters below 10 nm and lengths of several 100 nm. With increasing sample temperature a smoothing of the wire surface sets in. Also, the diameters of the nanowires start to decrease at constriction spots. A further increase of the temperature then leads to a breakup at these constriction spots.With our technique we were able to perform in situ observations of the very nature of this thermally induced breakup down to wire diameters of 1 nm covering a total observation area of (3 mm)2.
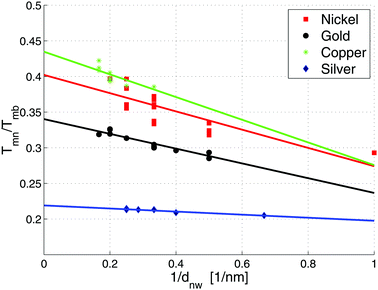
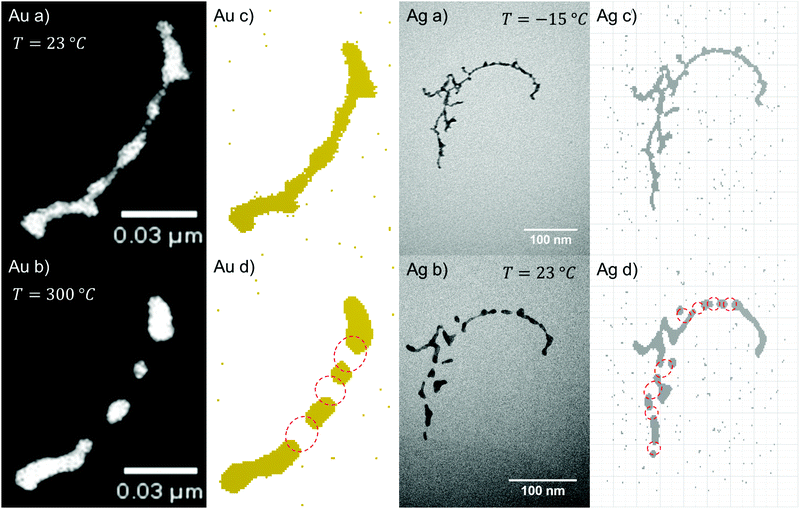
Particularly interesting is the finding that the breakup temperatures are far below the corresponding bulk melting temperatures. Therefore, a special cryo-TEM experiment for silver nanowires had to be designed, which showed that breakup starts at temperatures as low as ≈258 K (−15 °C).14 In the current extended study, all metals are analysed with respect to different diameters of the initially stable nanowires. The measurement confirmed the known relation between the breakup temperature of nanowires and their corresponding bulk melting temperature given by58
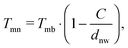 | (4) |
When heating above the breakup-temperature, a fragmentation takes place as it is predicted by the CA simulations. The resulting nanostructures show elliptical or spherical shapes. Details of this process and a comparison with our simulations are given below.
4.2 Surface diffusion in theory and experiment
The principle of surface diffusion is illustrated in Fig. 4(c) and (d), where the voxels tend to leave the initially constricted points, which results in a patternization of the nanowire. The migration is initiated by the energy gain when moving into an energetically more preferable position, where the sum of the number of all the nearest neighbours of all voxels is larger than in the initial configuration of the wire, which corresponds in other words to the minimization of surface energy in the macroscopic picture.The following features and their temperature dependence are well predicted by our simulations for all materials tested:
˙ Smoothing of the surface of the wires as a result of the induced surface diffusion.
˙ Rayleigh breakup and fragmentation of the nanowire.
˙ Contraction of nanostructures by minimization of the number of surface atoms
˙ The exact breakup points and the final shape of the wires
Our CA ansatz further allows the prediction of the breakup-sequence of constriction points. We note that the diffusion process is simulated in three dimensions, although measurement is limited to a “projected”, two-dimensional view. The dynamics during the simulations matches the structural changes observed in the TEM nicely. The agreement between simulations and measured structures after heating can be seen in Fig. 4. Even for very complex forms we are able to accurately predict the exact surface diffusion process. However, a correction factor has to be introduced to the Eyring equation in the case of the more reactive metals Cu and Ni, which accounts for the formation of an oxide layer on the surface of those clusters. This oxide layer is assumed to quench particle migration, leading to an inhibited or delayed breakup.
For the case of gold nanowires we also present a more detailed study of time dependence which includes a fit of the transmission coefficient κ(T). Its deviation is based on a series of TEM images taken at a constant substrate temperature of 150 °C. The surface diffusion of gold nanowires in real time is studied and compared to the structure evolution simulated with the CA. A selection of nanoparticles and their corresponding constriction points in time are used to perform a linear fit of the real time evolution as a function of the number of update cycles. For this particular combination of materials (Au nanowires on a non-wetting support) and the given temperature we find that 1500 real time seconds of TEM observation correspond to 100 iteration steps. One example of a Rayleigh breakup as a function of time and iteration step is presented in Fig. 5.
4.3 Material trends
To determine a material trend of the breakup of nanowires the diameter dependent breakup temperature Tmn is measured and fitted according to eqn (4). Good agreement between the cellular automaton simulation and the observed surface diffusion process is obtained when dealing with noble metals like Au and Ag.For the non-noble metals like Ni and Cu an oxide layer covering the metal cluster is observed (see Fig. 3) which results in a higher breakup temperature as the oxide has to evaporate before the diffusion process can continue. As a result, larger deviations from the linear behaviour are observed.
Cu shows a particularly interesting behaviour, as the surface diffusion for pure Cu takes place at room temperature. However, the exposure to oxygen at least during the transfer process of the specimen stops the diffusion process, which is continued at much higher temperatures after the oxygen layer is evaporated inside the TEM.
5 Conclusions
The temperature-dependent break-up process of Cu, Ni, Au and Ag nanowires is analysed at 1 nm spatial resolution. A new ansatz for modelling the dynamic behaviour of nanosolids is implemented. It is based on a cellular automaton, which is able to predict the thermal diffusion process at the nanoscale (see Fig. 4) and may also be suitable for the application to related phenomena such as alloying processes. We find that the breakup temperature for nanowires is significantly smaller in comparison to the corresponding bulk melting temperature. In addition, a 1/dnw dependence for the reduced breakup temperature Tnm/Tbm is found and the effect of an oxide layer on the stability is studied. The oxide layer leads to an inhibited particle diffusion, which slows the process down continuously and eventually increases the observed breakup temperature. It is possible to simulate the temperature dependent behaviour even for complex structures. An extension of the cellular automaton approach is currently planned which also includes substrate interactions.Acknowledgements
The authors enjoyed fruitful discussions with Markus Koch and Alexander Volk. This research has been supported by the Austrian Science Fund (FWF) under Grant FWF-E-P22962, by the European Commission and the Styrian Government within the ERDF program as well as by the European Union within the 7th Framework Programme (FP7/2007-2013) under Grant Agreement No. 312483 (ESTEEM2). The authors gratefully acknowledge support from NAWI Graz.References
- Z. K. Tang, L. Zhang, N. Wang, X. X. Zhang, G. H. Wen, G. D. Li, J. N. Wang, C. T. Chan and P. Sheng, Science, 2001, 292, 2462–2465 CrossRef CAS PubMed
.
- Y. Huang, X. Duan, Y. Cui and C. M. Lieber, Nano Lett., 2002, 2, 101–104 CrossRef CAS
.
- J.-H. Ahn, S.-J. Choi, J.-W. Han, T. J. Park, S. Y. Lee and Y.-K. Choi, Nano Lett., 2010, 10, 2934–2938 CrossRef CAS PubMed
.
- J. C. Claussen, A. D. Franklin, A. ul Haque, D. M. Porterfield and T. S. Fisher, ACS Nano, 2009, 3, 37–44 CrossRef CAS PubMed
.
- Q. Wang, F. Min and J. Zhu, Mater. Lett., 2013, 91, 9–11 CrossRef CAS
.
- Y. Yin, Y. Sun, M. Yu, X. Liu, T. Jiang, B. Yang, D. Liu, S. Liu and W. Cao, Sci. Rep., 2015, 5, 8152 CrossRef CAS PubMed
.
- P. Kohli, C. C. Harrell, Z. Cao, R. Gasparac, W. Tan and C. R. Martin, Science, 2004, 305, 984–986 CrossRef CAS PubMed
.
- B. Sciacca, J. van de Groep, A. Polman and E. C. Garnett, Adv. Mater., 2016, 28, 905–909 CrossRef CAS PubMed
.
- Y. Su, C. Liu, S. Brittman, J. Tang, A. Fu, N. Kornienko, Q. Kong and P. Yang, Nat. Nano, 2016, 11, 609–612 CrossRef CAS PubMed
.
- G. Zhu, S. Zhang, Z. Xu, J. Ma and X. Shen, J. Am. Chem. Soc., 2011, 133, 15605–15612 CrossRef CAS PubMed
.
- K. Yu. Arutyunov, Phys. C, 2008, 468, 272–275 CrossRef CAS
.
- M. Dreher, F. Pauly, J. Heurich, J. C. Cuevas, E. Scheer and P. Nielaba, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075435 CrossRef
.
- C. M. Lieber, MRS Bull., 2003, 28, 486–491 CrossRef CAS
.
- A. Volk, D. Knez, P. Thaler, A. W. Hauser, W. Grogger, F. Hofer and W. E. Ernst, Phys. Chem. Chem. Phys., 2015, 17, 24570–24575 RSC
.
- E. Latimer, D. Spence, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Nano Lett., 2014, 14, 2902–2906 CrossRef CAS PubMed
.
- P. Thaler, A. Volk, F. Lackner, J. Steurer, D. Knez, W. Grogger, F. Hofer and W. E. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155442 CrossRef
.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed
.
-
C. Callegari and W. E. Ernst, in Handbook of High Resolution Spectroscopy, ed. F. Merkt and M. Quack, John Wiley & Sons, Chichester, 2011 Search PubMed
.
- J. Tiggesbäumker and F. Stienkemeier, Phys. Chem. Chem. Phys., 2007, 9, 4748–4770 RSC
.
- V. Mozhayskiy, M. N. Slipchenko, V. K. Adamchuk and A. F. Vilesov, J. Chem. Phys., 2007, 127, 094701 CrossRef PubMed
.
- E. Loginov, L. F. Gomez and A. F. Vilesov, J. Phys. Chem. A, 2011, 115, 7199–7204 CrossRef CAS PubMed
.
- A. Volk, P. Thaler, M. Koch, E. Fisslthaler, W. Grogger and W. E. Ernst, J. Chem. Phys., 2013, 138, 214312 CrossRef PubMed
.
- P. Thaler, A. Volk, M. Ratschek, M. Koch and W. E. Ernst, J. Chem. Phys., 2014, 140, 044326 CrossRef PubMed
.
- M. P. de Lara-Castells, N. F. Aguirre, H. Stoll, A. O. Mitrushchenkov, D. Mateo and M. Pi, J. Chem. Phys., 2015, 142, 131101 Search PubMed
.
-
R. P. Feynman, in Progress in Low Temperature Physics, ed. C. J. Gorter, North-Holland, Amsterdam, 1955, pp. 17–53 Search PubMed
.
-
L. Onsager, Proc. Int. Conf. Theor. Phys., Science Council of Japan, Tokyo, 1953, pp. 877–880 Search PubMed
.
- G. P. Bewley, D. P. Lathrop and K. R. Sreenivasan, Nature, 2006, 441, 588 CrossRef CAS PubMed
.
- E. J. Yarmchuk, M. J. V. Gordon and R. E. Packard, Phys. Rev. Lett., 1979, 43, 214–217 CrossRef CAS
.
- G. A. Williams and R. E. Packard, Phys. Rev. Lett., 1974, 33, 280–283 CrossRef CAS
.
-
R. J. Donelly, Quantized Vortices in Helium II, Cambridge University Press, Cambridge, 1991 Search PubMed
.
- Y. A. Sergeev and C. F. Barenghi, J. Low Temp. Phys., 2009, 157, 429–475 CrossRef CAS
.
- E. B. Gordon, A. V. Karabulin, A. A. Morozov, V. I. Matyushenko, V. D. Sizov and I. I. Khodos, J. Phys. Chem. Lett., 2014, 5, 1072–1076 CrossRef CAS PubMed
.
- E. Gordon, A. Karabulin, V. Matyushenko, V. Sizov and I. Khodos, Phys. Chem. Chem. Phys., 2014, 16, 25229–25233 RSC
.
- P. Moroshkin, V. Lebedev, B. Grobety, C. Neururer, E. B. Gordon and A. Weis, EPL, 2010, 90, 34002 CrossRef
.
- A. Volk, P. Thaler, D. Knez, A. W. Hauser, J. Steurer, W. Grogger, F. Hofer and W. E. Ernst, Phys. Chem. Chem. Phys., 2016, 18, 1451–1459 RSC
.
- B. H. Hong, S. C. Bae, C.-W. Lee, S. Jeong and K. S. Kim, Science, 2001, 294, 348–351 CrossRef CAS PubMed
.
- M. Malisauskas, R. Meskys and L. A. Morozova-Roche, Biotechnol. Prog., 2008, 24, 1166–1170 CrossRef CAS PubMed
.
- D. M. Eisele, H. von Berlepsch, C. Böttcher, K. J. Stevenson, D. A. Vanden Bout, S. Kirstein and J. P. Rabe, J. Am. Chem. Soc., 2010, 132, 2104–2105 CrossRef CAS PubMed
.
- J. W. S. Rayleigh, Proc. London Math. Soc., 1878, 10, 4–13 CrossRef
.
- F. A. Nichols and W. W. Mullins, Trans. Metall. Soc. AIME, 1965, 233, 1840–1848 CAS
.
- F. A. Nichols and W. W. Mullins, J. Appl. Phys., 1965, 36, 1826–1835 CrossRef
.
- F. A. Nichols, J. Mater. Sci., 1976, 11, 1077–1082 CrossRef
.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko and I. I. Khodos, J. Phys. Chem. A, 2015, 119, 2490–2501 CrossRef CAS PubMed
.
- R. Thouy, N. Olivi-Tran and R. Jullien, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 5321–5327 CrossRef CAS
.
- W. W. Mullins, J. Appl. Phys., 1957, 28, 333–339 CrossRef CAS
.
- P. Thaler, A. Volk, D. Knez, F. Lackner, G. Haberfehlner, J. Steurer, M. Schnedlitz and W. E. Ernst, J. Chem. Phys., 2015, 143, 134201 CrossRef PubMed
.
- E. Marzbanrad, G. Rivers, P. Peng, B. Zhao and N. Y. Zhou, Phys. Chem. Chem. Phys., 2015, 17, 315–324 RSC
.
- M. E. Toimil Molares, A. G. Balogh, T. W. Cornelius, R. Neumann and C. Trautmann, Appl. Phys. Lett., 2004, 85, 5337–5339 CrossRef CAS
.
- H. Li, J. M. Biser, J. T. Perkins, S. Dutta, R. P. Vinci and H. M. Chan, J. Appl. Phys., 2008, 103, 024315 CrossRef
.
- S. Karim, M. E. Toimil-Molares, A. G. Balogh, W. Ensinger, T. W. Cornelius, E. U. Khan and R. Neumann, Nanotechnology, 2006, 17, 5954–5959 CrossRef CAS
.
- S. Karim, M. E. Toimil-Molares, W. Ensinger, A. G. Balogh, T. W. Cornelius, E. U. Khan and R. Neumann, J. Phys. D: Appl. Phys., 2007, 40, 3767–3770 CrossRef CAS
.
- H. S. Shin, J. Yu and J. Y. Song, Appl. Phys. Lett., 2007, 91, 173106 CrossRef
.
- M. Rauber, F. Muench, M. E. Toimil-Molares and W. Ensinger, Nanotechnology, 2012, 23, 475710 CrossRef CAS PubMed
.
- C. Bréchignac, Ph. Cahuzac, F. Carlier, C. Colliex, J. Leroux, A. Masson, B. Yoon and U. Landman, Phys. Rev. Lett., 2002, 88, 196103 CrossRef PubMed
.
- A. Lando, N. Kébaïli, Ph. Cahuzac, A. Masson and C. Bréchignac, Phys. Rev. Lett., 2006, 97, 133402 CrossRef CAS PubMed
.
- To avoid an impossible double occupation of a given voxel the jumps of all movable voxels are tabulated at each timestep and a random permutation is applied before migration takes place. The latter is executed stepwise in the randomized order.
- H. Eyring, J. Chem. Phys., 1934, 3, 107–115 CrossRef
.
-
C. Kittel, Introduction to Solid State Physics, John Wiley and Sons Ltd, 8 Rev edn, 2004 Search PubMed
.
- G. Giovannetti, P. A. Khomyakov, G. Brocks, V. M. Karpan, J. van den Brink and P. J. Kelly, Phys. Rev. Lett., 2008, 101, 026803 CrossRef CAS PubMed
.
- I. A. Solov'yov, A. V. Yakubovich, P. V. Nikolaev, I. Volkovets and A. V. Solov'yov, J. Comput. Chem., 2012, 33, 2412–2439 CrossRef PubMed
.
| This journal is © the Owner Societies 2017 |