Open Access Article
Open Access ArticleReal-time capture of nuclear motions influencing photoinduced electron transfer†
Pyosang
Kim
 *ab,
Subhangi
Roy
c,
Andrew J. S.
Valentine
d,
Xiaolin
Liu
*ab,
Subhangi
Roy
c,
Andrew J. S.
Valentine
d,
Xiaolin
Liu
 d,
Sarah
Kromer
d,
Sarah
Kromer
 c,
Tae Wu
Kim
a,
Xiaosong
Li
c,
Tae Wu
Kim
a,
Xiaosong
Li
 *d,
Felix N.
Castellano
*d,
Felix N.
Castellano
 *c and
Lin X.
Chen
*c and
Lin X.
Chen
 *ab
*ab
aChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, IL 60439, USA. E-mail: kimp@anl.gov; lchen@anl.gov
bChemistry Department, Northwestern University, Evanston, IL 60208, USA
cChemistry Department, North Carolina State University, Raleigh, NC 27695-8204, USA. E-mail: fncastel@ncsu.edu
dChemistry Department, University of Washington, Seattle, WA 98195, USA. E-mail: xsli@uw.edu
First published on 22nd August 2024
Abstract
Although vibronic coupling phenomena have been recognized in the excite state dynamics of transition metal complexes, its impact on photoinduced electron transfer (PET) remains largely unexplored. This study investigates coherent wavepacket (CWP) dynamics during PET processes in a covalently linked electron donor–acceptor complex featuring a cyclometalated Pt(II) dimer as the donor and naphthalene diimide (NDI) as the acceptors. Upon photoexciting the Pt(II) dimer electron donor, ultrafast broadband transient absorption spectroscopy revealed direct modulation of NDI radical anion formation through certain CWP motions and correlated temporal evolutions of the amplitudes for these CWPs with the NDI radical anion formation. These results provide clear evidence that the CWP motions are the vibronic coherences coupled to the PET reaction coordinates. Normal mode analysis identified that the CWP motions originate from vibrational modes associated with the dihedral angles and bond lengths between the planes of the cyclometalating ligand and the NDI, the key modes altering their π-interaction, consequently influencing PET dynamics. The findings highlight the pivotal role of vibrations in shaping the favorable trajectories for the efficient PET processes.
Introduction
Natural photosynthetic reaction centers set examples for nearly 100% quantum efficiency in photoinduced charge separation, driving biochemical reactions responsible for storing the energy necessary to sustain life on Earth.1 The detection of coherent wavepacket (CWP) motions within the reaction centers stimulated investigations on the role of nuclear motions in achieving highly efficient charge separation.2–4 Subsequent studies have identified the CWP motion as an electronic–vibrational (vibronic) coherence that persists over the timescale of the photoinduced charge separation.5–7 It was proposed that the vibronic resonance across the exciton and charge transfer state could harness electronic coherence as a robust function in the primary electron transfer processes even in the fluctuating environmental conditions within the protein matrix.8–10 Vibronic coherence has also garnered significant attention for its potential role in photoinduced electron transfer (PET), a fundamental process in artificial solar energy conversion systems.11–13 For instance, a 100 fs PET process in a blend of poly(3-hexylthiophene) (P3HT) and fullerene coincided with the emergence of CWP motions attributed to the vibrations of fullerene, highlighting the interplay of electron and vibrational motions during the primary charge separation.14 Furthermore, it was experimentally demonstrated that the vibronic coherence directly influences the photocurrent generation in other organic heterojunctions solar cells.15 These observations suggest that the vibronic coherence between the electron donor and acceptor could play a pivot role in facilitating efficient PET dynamics in artificial systems.The aforementioned studies demonstrating the role of vibronic coherence in PET processes has inspired the present study on an electron donor–acceptor system featuring a transition metal complex (TMC) as the donor. The light absorption process directly gives rise to a charge transfer (CT) state in the TMCs, either from metals to ligands or vice versa. The CT transition functions as a driving force, initiating the primary ET reactions in many applications for solar energy conversion, photocatalysis, and optoelectronics.16–19 Recent advances in ultrafast optical and X-ray spectroscopies have revealed that the CT excitation results in significant structural rearrangements, accompanied by CWP motions associated with the structural changes in the vibronic manifold of the CT excited states.20–32 Furthermore, the CWP motions evolve along the excited state trajectories to the final states during intersystem crossing and spin-crossover dynamics, shedding light on the possibility of the vibronic coherence between different spin states.29,30,33–36 These examples imply that the CWP motions following the CT transition in the TMCs can exert a significant impact on subsequent PET toward the electron acceptor.
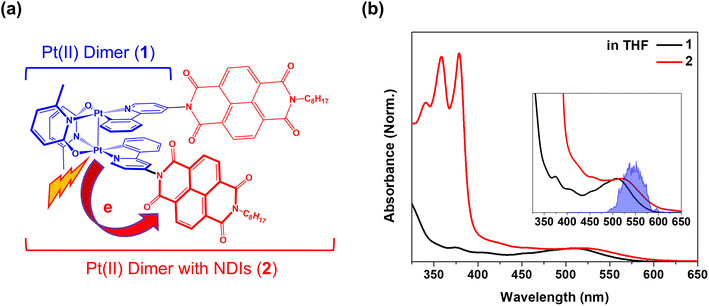
To investigate the effects of CWP motion in PET reactions, we designed an electron donor–acceptor system (2) with a cyclometalated Pt(II) dimer (1) as the donor and naphthalene diimide (NDI) as the acceptor (Fig. 1a). As shown in previous studies, a metal–metal-to-ligand charge transfer (MMLCT, dσ* → π*) transition in Pt(II) dimer directly induces ∼0.2 Å or larger Pt–Pt distance contraction as the electron density from an antibonding orbital is depleted.29,32,37 Meanwhile, a significant amplitude of CWP motions associated with Pt–Pt stretching vibration can be launched in the MMLCT excited state, as evidenced by ultrafast optical transient absorption and X-ray solution scattering experiments.29,32,36 In this study, using ultrafast broadband transient absorption (BBTA) spectroscopy with 20 fs (FWHM) pump pulses, we track the CWP motions during the PET from Pt(II) dimer to NDI to identify the key reaction coordinates in 2. The results unveil the clear evidence for the certain CWP motions to directly modulate the NDI radical anion formation dynamics and to influence the PET trajectories across the MMLCT and charge-separated (CS) states.
Results and discussion
Excited state and PET kinetics
Pt(II) dimer (1) exhibits the typical electronic transitions of a cyclometalated Pt(II) dimer as reported in previous studies, featuring (1) ligand-centered (LC) transitions below 350 nm, (2) a mixture of LC and metal-to-ligand charge transfer (MLCT) transitions between 350–450 nm and (3) the MMLCT transition above 450 nm (Fig. 1b, S5–S7 and Table S1†).37,38 The electron donor–acceptor complex (2) also displays the MMLCT band above 450 nm, while a strong π–π* transition of the NDI electron acceptors appears with a clear vibronic feature below 400 nm in the steady-state absorption spectrum (Fig. 1b, S5–S7 and Table S1†).39 We investigated the PET reaction dynamics from Pt(II) dimer to NDI upon MMLCT excitation using BBTA spectroscopy with 20 fs pump pulses centered at 550 nm (see the inset in Fig. 1b). As a reference, the BBTA signals of 1 display rise dynamics across the entire probe spectral range within the first 2–3 picosecond (ps) time delay window (Fig. 2a). After the first few ps, the TA signal amplitudes persist without significant changes up to 150 ps (Fig. S8†). Global fitting, performed with the Glotaran program40 using a sequential kinetic model, reveals two time constants for the early rise kinetics: 364 fs and 1.76 ps. The analysis of evolution-associated difference spectra (EADS) for each time component demonstrates that these rise kinetics are attributed to the decay kinetics of the stimulated emission (SE) signal (Fig. 2c). The broad SE signal centered around 650 nm first emerges, which subsequently redshifts to 700 nm with a time constant of 364 fs and then is completely quenched with a time constant of 1.76 ps. Since the SE signal stems from the singlet MMLCT state, the time constant of 1.76 ps is attributed to intersystem crossing (ISC) from the singlet to the triplet MMLCT state. After undergoing vibrational cooling within 71 ps,38 the 3MMLCT state persists longer than 150 ps time window, which is consistent with the 3MMLCT lifetime of 341 ns obtained from the previous nanosecond TA measurement on the same Pt(II) dimer.37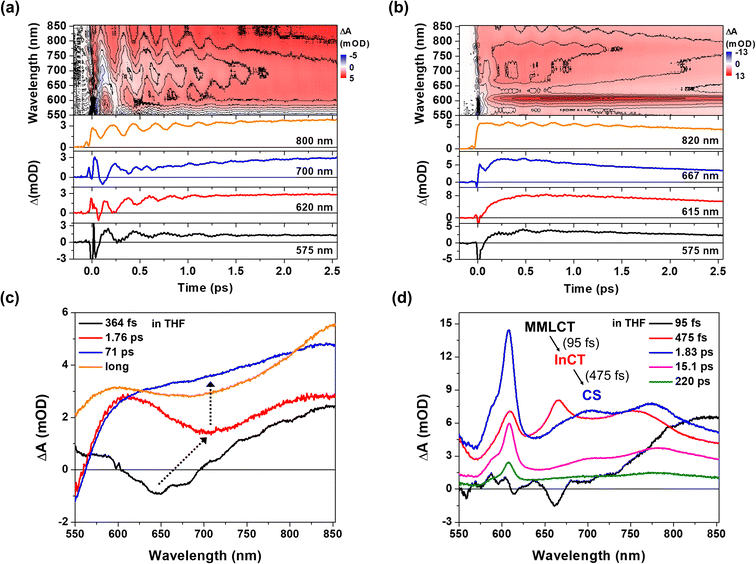 | ||
| Fig. 2 (a and b) 2D contour plots of BBTA spectra and kinetic profiles at specific probe wavelengths for 1 (a) and 2 (b). All measurements were carried out in THF solvent. (c and d) Evolution associated difference spectra (EADS) for 1 (c) and 2 (d), obtained by global kinetic analysis on the BBTA data scanned up to 150 ps (Fig. S8†). Black arrows highlight the temporal evolution of stimulated emission (SE) signal. The BBTA data up to 70 fs were truncated for the global fitting in order to avoid the contribution of coherent spike and cross-phase modulation signal around time zero. | ||
The BBTA signals of 2 exhibit distinctly different early TA kinetics (Fig. 2b) under the same experimental conditions compared as those of 1. The formation of NDI radical anion dominates the temporal and spectral behaviors of 2 due to the PET from Pt(II) dimer to NDI. Using the global fitting of the sequential kinetic model, analysis of EADS demonstrates that the NDI anion spectrum rises with two time constants: 95 fs and 475 fs (Fig. 2d). Based on the computations of time-dependent density functional theory (TD-DFT) and natural transition orbital (NTO) (Fig. S5–7 and Table S1†), we assigned the initial excited state corresponding to the 1MMLCT state featured by the black EADS. Despite cross-phase modulation in the first ∼100 fs after the excitation, the black EADS indicates the significant quenching of the SE signal around 650 nm due to the PET on the similar time scale. The black EADS evolves to the red EADS with a 95 fs time constant, and then to the blue EADS with a 475 fs time constant. Notably, the red EADS differs significantly from the blue EADS with characteristic NDI radical anion bands at 608, 700, and 775 nm.39 Instead, the red EADS shows a broader absorption band at 608 nm and two blue-shifted bands at 667 and 750 nm. This distinction indicates that the charge separation (blue EADS) occurs through an intermediate CT (InCT) state formed between the Pt(II) dimer and NDIs (shown by the red EADS) following the MMLCT excitation. After the completion of the charge separation, the spectrum of the NDI anion decays over time without significant changes in its spectral features (Fig. 2d and S8†). The multiple time constants found in the decay kinetics (1.83, 15.1, and 220 ps) suggests that different relaxation processes could be present, such as vibrational relaxation or ISC during a charge recombination (CR) to the ground-state. Although a detailed investigation of these dynamics could provide insight into the mechanism of CR, the current study focuses on the forward PET processes (Pt(II) dimer → NDI) which can be tracked by the CWP behaviors to deduce their roles in the PET processes.
CWP motions
The CWP motions in both 1 and 2 launched by the 20 fs pump pulses were detected as oscillatory signals across the probe range overlaid with the population evolution signals (Fig. 3a and b). Fast Fourier transformation (FFT) of the beating signals after the removing the population evolution in the TA signal uncovers the frequencies of the CWP motions for 1 and 2 below 1000 cm−1, as shown in Fig. 3c and d. (Note: the THF solvent vibration at 912 cm−1 is induced by an impulsive stimulated Raman scattering (ISRS) process41). Previous ultrafast TA studies on cyclometalated Pt(II) dimers, combined with normal mode analysis, showed a frequency upshift in the CWP motion associated with the Pt–Pt stretching vibration from ∼110 cm−1 for the ground-state to ∼150 cm−1 for the MMLCT excited-state as the result of the Pt–Pt distance shortening or effective bond order increase.29,30,36 Particularly, fs X-ray solution scattering study directly observed a contraction of Pt–Pt distance by ∼0.2 Å in the MMLCT excited-state, accompanied by the Pt–Pt stretching CWP motion with the 150 cm−1 frequency.32 In the current investigation, the CWPs of 1 and 2 also exhibit significant FFT amplitudes at ∼110 and ∼150 cm−1 (Fig. 3c and d), which are similar to the aforementioned frequencies of Pt–Pt stretching vibrations in the ground- and MMLCT excited-states, respectively.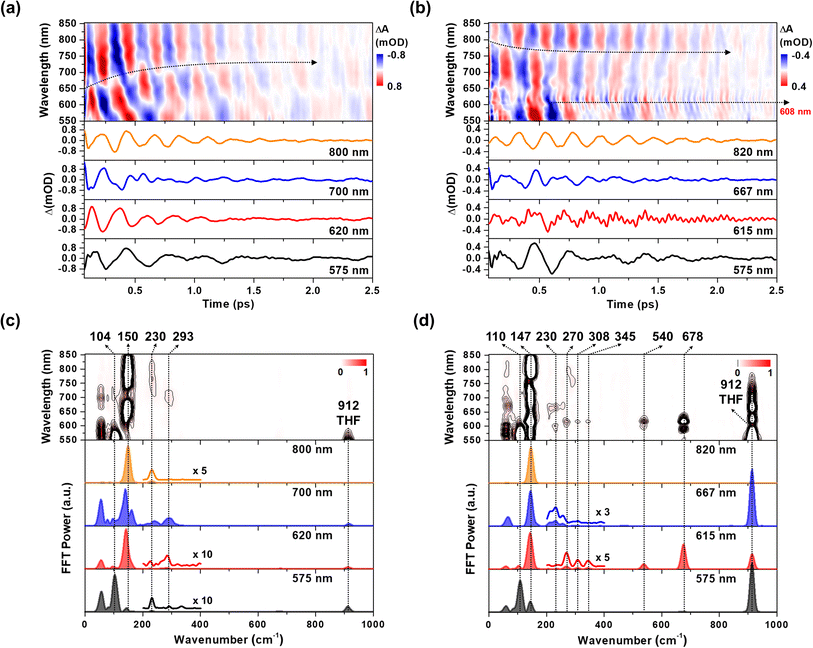 | ||
| Fig. 3 (a and b) Wavelength-resolved residual map (top) and beating signals (bottom) at specific wavelengths for 1 (a) and 2 (b). The oscillatory residuals were extracted by a global kinetic analysis on the BBTA kinetic traces. We performed inverse Fourier filtering on the CWP modes in 0–800 cm−1 in order to visualize the temporal dynamics of the CWP motions obscured by strong THF solvent vibration at 912 cm−1. The raw data are provided in Fig. S9† (c and d) wavelength-resolved FFT map (top) and spectra (bottom) at specific probe wavelengths for 1 (c) and 2 (d). The FFT was carried out for the residuals within the time range of 0.07–2.5 ps to avoid the contribution of cross-phase modulation around time zero. | ||
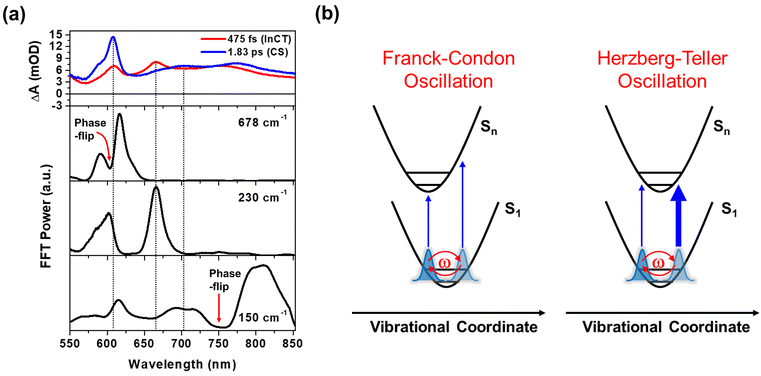
Our fs-BBTA spectroscopy provides a broad probe spectral range of 550–850 nm, allowing us to precisely map out a phase-flip position associated with the Pt–Pt stretching CWP motion and its temporal evolution (black dotted arrows in Fig. 3a and b). Since the phase flip occurs around the energy minimum of the potential energy surface (PES), its spectral position provides the assignments of the electronic state where the CWP motions take place.30,42–46 Specifically, the phase flip in the ground-state CWP would occur around the ground-state bleaching (GSB) maximum, while that in the excited-state CWP arises near the SE or excited-state absorption (ESA) maximum.
The ∼110 cm−1 CWP motions in 1 and 2 commonly display the strong FFT amplitudes exclusively around the GSB region of 550–600 nm, supporting that the CWPs are prepared in the ground-state PES via the ISRS process.47 It is highly likely that the phase-flip for this ground-state CWP is located around the absorption maximum (520 nm), which falls beyond the probe range of BBTA spectroscopy. An interference between the ∼110 and ∼150 cm−1 CWP motions is observed around the GSB region (∼600 nm) due to the overlap of these oscillations. This interference is distinct from the phase flip that arises from the ∼150 cm−1 excited state CWP observed beyond the GSB region.
In Fig. 3a, the wavelength-resolved residual map for 1 reveal that the phase flip emerges first around 650 nm and then redshifts to ∼700 nm, which is consistent with the redshift of the SE maximum from 650 to 700 nm with the time constant of 364 fs (Fig. 2c). The temporal evolution of the phase flip demonstrates that the 150 cm−1 CWP motion directly modulates the SE spectral shape and amplitude along the probe wavelength axis (also see Fig. S10†). In addition, the CWP undergoes a damping with a time constant of ∼610 fs (Fig. S11 and Table S2†). These results confirm that the 150 cm−1 Pt–Pt stretching CWP launched by the 1MMLCT excitation decays in the PES of the 1MMLCT excited state during the ISC to the 3MMLCT state. In contrast, the phase flip for the 150 cm−1 CWP motions in 2 disappears at the SE peak of 650 nm in <300 fs, while a new phase flip emerges at 800 nm in early time and blueshifts to 750 nm. Moreover, the 150 cm−1 CWP motions of 2 display an initial amplitude growth within ∼100 fs, similar to the TA rise time of ∼100 fs associated with forming the InCT state in the PET process (Fig. S11 and Table S2†). These features differentiate the origin of the 150 cm−1 CWPs for 2 from that for 1. The decay and rise of the phase flip at ∼650 and ∼800 nm demonstrate that the PET reaction quenches the SE signal of the 1MMLCT excited-state and concomitantly enhances the ESA signals of the InCT and CS states. In addition, the damping time of ∼1 ps indicates that the Pt–Pt stretching CWP sustains its phase during the PET reaction (Fig. S11 and Table S2†). Therefore, the 150 cm−1 CWP motion observed in 2 is attributed to the nuclear motion associated with the Pt–Pt stretching vibration in the InCT and CS states.
In Fig. 3c and d, FFT analysis also reveals other CWP motions in 200–700 cm−1 frequency range. The weak FFT amplitudes were observed at 230 and 293 cm−1 in 1, which were not clearly detected in previous work.29 The 230 and 293 cm−1 modes largely appear beyond the onset of the absorption spectra at ∼600 nm and thus can be reasonably assigned to the CWPs in the 1MMLCT excited-state. The 230 cm−1 CWP motion is also observed in 2, while its spectral amplitude distribution is distinct. The mode is predominantly detected around 608 and 667 nm, which are near the peaks of InCT state represented by red EADS (Fig. 2d). 2 also shows new CWP motions with the frequencies of 270, 308, 345, 540 and 678 cm−1 around 608 nm peak of NDI anion. Interestingly, the wavelength-resolved residual map displays the beating patterns of these modes (dominantly 678 cm−1 frequency) with the phase flip around 608 nm (black dotted arrow in Fig. 3b). Additionally, the amplitude of the 678 cm−1 beating signal gradually increases over a period of ∼0.8 ps, as shown in the oscillation at 615 nm (Fig. 3b).
Franck–Condon vs. Herzberg–Teller type CWP oscillations
The FFT amplitude spectra plotted as a function of probe wavelength provide further characterization of the CWP motions in 2 (Fig. 4a and S12†). The FFT amplitude of the 678 cm−1 mode is predominantly present around the NDI radical anion band at 608 nm. Similar behavior is observed in the FFT amplitudes of 270, 308, 345, and 540 cm−1 CWPs (Fig. S12†). The spectra show a distinct valley at 608 nm due to the phase flip of the CWP motion, which is consistent with the wavelength resolved residual map (black dotted arrow at 608 nm in Fig. 3b). These CWP motions are attributed to Franck–Condon type oscillations. As illustrated in Fig. 4b, the periodic propagation of the CWP motions along its vibrational coordinates leads to spectral modulations of the NDI radical anion due to the displacement between the PESs of the lowest (S1) and higher excited states (Sn) in the ESA region. Specifically, the 678 cm−1 CWP motion causes the peak of NDI radical anion band to oscillate between wavelengths larger (∼615 nm) and smaller (∼595 nm) than 608 nm with its vibrational frequency. Although we do not directly excite NDI, the phase flip at the peak of the NDI radical anion absorption strongly indicates that the CWP in 2 originates from the nuclear motions associated with the CS active vibration pertaining to the NDI core.48 However, the PET time scales of ∼100 and ∼500 fs are not sufficiently short to impulsively generate 50 fs period of 678 cm−1 CWP mode in the CS state. This result suggests a different mechanism for the formation of 678 cm−1 CWP motion in the CS state of 2.The FFT amplitude for the 230 cm−1 CWP displays two bands with peaks around 608 and 667 nm. Importantly, these peaks match well with the characteristic bands at 608 and 667 nm of the red EADS corresponding to the InCT state of the PET reaction (Fig. 4a). This feature indicates that the 230 cm−1 CWP motion only modulates the amplitudes of both ∼608 and 667 nm bands without the spectral shifts, in contrast to the 678 cm−1 motion. Such CWP motions can be interpreted as Herzberg–Teller type oscillation, as illustrated in Fig. 4b.49–52 In this case, the CWP motion cannot modulate the TA spectral shape and amplitude because the displacement between the two PESs is negligible or zero; therefore, the transition energies on both sides of the PES are identical. When the nuclear motions, however, can differentiate the oscillator strength on the right and left sides of the PES, it can be possible to probe the intensity modulation while maintaining the spectral shape. This phenomenon occurs through a vibronic coupling that allows the intensity borrowing from one electronic state to another at a specific molecular structure compared to the opposite structure.49–53 Thus, the Herzberg–Teller type beating pattern provides the strong evidence for non-Condon effect of 230 cm−1 CWP motion. Given that the transition strengths at ∼608 and 667 nm are proportional to the population of the InCT state in the PET processes, it can be suggested that there is the vibronic coupling between the 1MMLCT and InCT states along the 230 cm−1 vibrational coordinates.
The Pt–Pt stretching vibration (150 cm−1 mode) exhibits FFT amplitude spectra characterized by a sharp peak at ∼608 nm and a broad peak at ∼700 nm (Fig. 4a). These features match the NDI anion bands in the CS state (blue EADS in Fig. 2d). Notably, the oscillation residual map reveals the absence of phase flips associated with the 150 cm−1 oscillation at ∼608 nm and ∼700 nm (Fig. 3b). The presence of a phase flip near 750 nm (black dotted arrow in Fig. 3b and red arrow in Fig. 4a) complicates the assignment of the origin of the 150 cm−1 CWP. Nevertheless, the FFT spectral features at ∼608 and 700 nm strongly suggests the non-Condon effect in the 150 cm−1 vibration, leading to alternation in the intensity of the NDI radical anion spectrum. In contrast to the 230 cm−1 CWP motion, the 150 cm−1 CWP only affects the TA spectra associated with the CS state (∼608 and 700 nm at the blue EADS). Thus, the non-Condon effect for the 150 cm−1 Pt–Pt stretching CWP motion implies that the vibronic coupling between the InCT and CS states occurs along the 150 cm−1 vibrational coordinate.
Solvent-polarity dependence of PET and CWP dynamics
To verify the correlations of the PET kinetics and the CWP evolution, we also investigated the solvent dependence of the PET and CWP dynamics (Fig. S13 and 14†). It is well-known from Marcus theory that the solvent reorganization energy in the ET processes changes with its dielectric constant, and thus the PET rate.54 Generally, the polar solvent stabilizes the charged species (radical cations and anions, i.e., CS state) and thus increases the driving force of the PET reaction. We anticipated that a polar solvent would enhance the PET rate and affect the damping or rise time of the CWP motions. This approach allows us to identify the CWP motions associated with the PET reaction coordinates.55–57 As shown in Fig. 5c, the rise kinetics of NDI anion peak at ∼608 nm become faster as the polarity increases; toluene (dielectric constant ε ≈ 2.38) < THF (ε ≈ 7.58) < acetonitrile (MeCN, ε ≈ 37.5). The global kinetic analysis further reveals the solvent polarity dependency of the PET processes (Fig. 2d, 5a and b): (1) the time scale of ∼100 fs corresponding to the formation of the InCT state (the red EADS) remain almost unchanged across different solvent polarities. (2) the transition from the InCT to the CS state (the blue EADS) becomes faster with increasing polarity, toluene (952 fs) > THF (475 fs) > MeCN (224 fs). (3) the CR processes also occur faster in higher polarity solvents.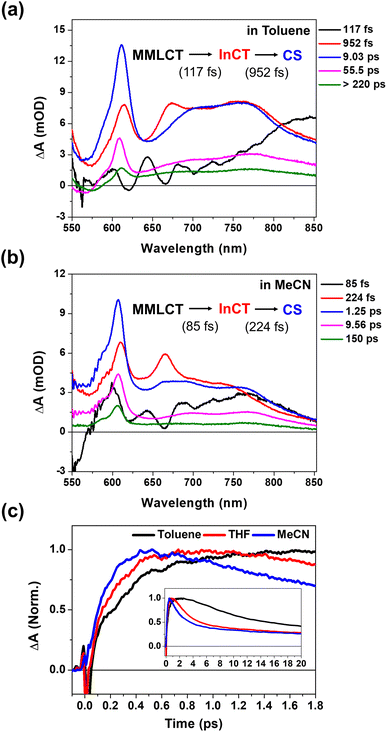 | ||
| Fig. 5 (a and b) EADS for 2 in toluene and acetonitrile (MeCN), obtained by global kinetic analysis on the BBTA data scanned up to 150 ps (Fig. S13†). (c) Early TA kinetic traces observed at the NDI anion peaks at ∼608 nm in toluene, THF and MeCN. Inset shows the kinetic traces up to 20 ps. | ||
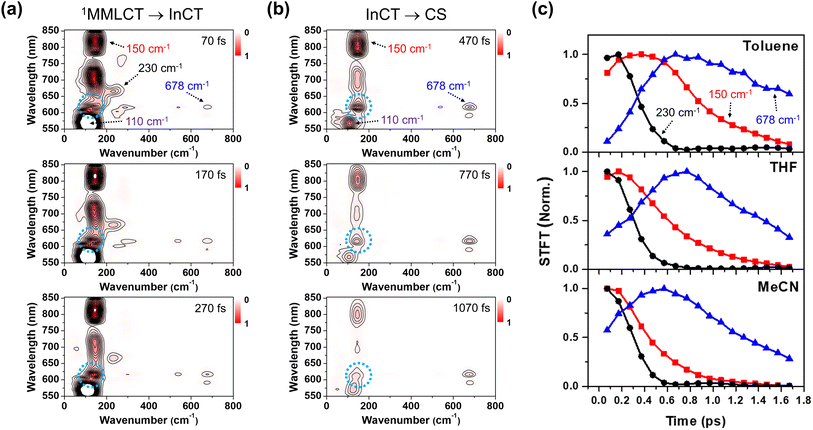
Using the short-time Fourier transformation (STFT) method, we analyze the temporal evolution of the CWP motions and their correlation with the PET kinetics observed in different solvents (Fig. 6, S16 and S17†). The STFT analysis captures the time evolution of the amplitude of the frequency content extracted from the oscillatory signals, and provides information about the dephasing dynamics of CWP motions (see the details in Fig. S15†). As shown in the wavelength-resolved STFT maps (Fig. 6a and b), the ∼100 cm−1 ground state wavepacket dephases only around the GSB region (550–600 nm). It is because this CWP doesn't undergo any electronic transition and vibrational relaxation in the ground state PES. Therefore, we exclude the ground-state wavepacket contribution on the excited state CWP dynamics beyond the ground state absorption.
The amplitude of the 230 cm−1 mode significantly decreases during the PET from the 1MMLCT to InCT and almost completely vanishes within 0.6 ps. Additionally, its dephasing dynamics appear to be nearly independent of solvent polarity. The 150 cm−1 mode exhibits a noticeable dependence on solvent polarity. The time point at which the amplitude reaches half of its maximum value becomes smaller with increasing solvent polarity, ranging from ∼0.9 ps in toluene, ∼0.6 ps in THF to ∼0.4 ps in MeCN. This trend illustrates that the 150 cm−1 CWP undergoes faster dephasing dynamics in higher polar solvents. Furthermore, the STFT maps show that the amplitude of the ∼150 cm−1 CWP around 608 nm (blue dotted circle in Fig. 6a and b) increases during the PET process from 1MMLCT to InCT and becomes evident during the PET process from InCT to CS. This feature indicates that the non-Condon effect for the 150 cm−1 mode is delayed in time and affects the CS spectra later. This emergence suggests that the 150 cm−1 CWP induces the vibronic coupling between the InCT and CS states. Most interestingly, the 678 cm−1 CWP clearly show a distinct trend from the others, with its amplitude rise during the PET processes. As the solvent polarity increases, the STFT amplitude reaches its maximum faster at earlier delay times, ∼0.8 ps in THF to ∼0.6 ps in MeCN. The onset of the amplitude decay for the 678 cm−1 mode also varies with the solvent polarity, which can be interpreted as the consequence of the polar solvents accelerating both CS and CR processes. This finding demonstrates that the rise dynamics of this mode become faster as the polarity increases, which is consistent with the faster rise of NDI anion in MeCN solvent (Fig. 5c). Although the STFT amplitude at early time is the lowest in toluene, the time point at the maximum value remains similar to THF, followed by slower dephasing. This result indicates that the 678 cm−1 CWP in toluene begins the damping concurrently with the rise dynamics during the PET processes, distinct from those observed in other solvents. The 270, 308, 345 and 540 cm−1 CWPs do not show the polarity dependence (Fig. S17†).
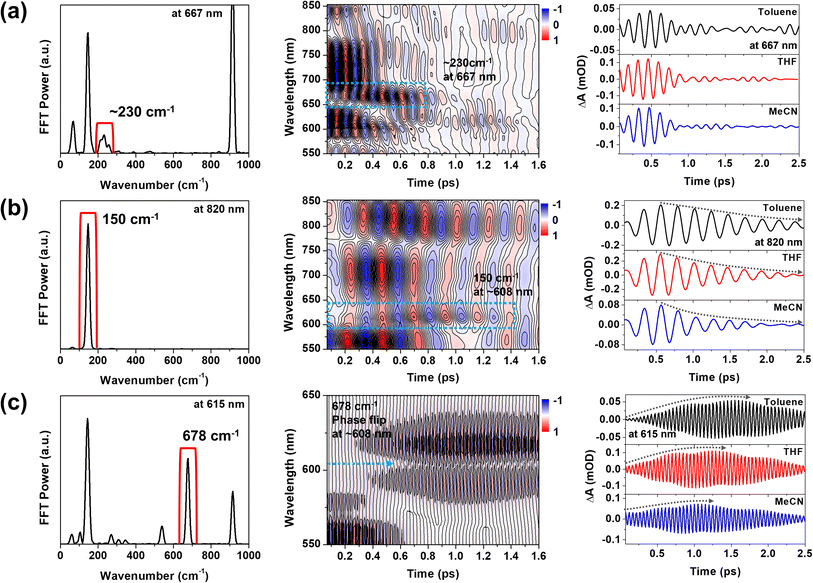
To support the STFT analysis, we performed a Fourier filtering analysis using a super-Gaussian window.45 We selectively filtered out the 230, 150 and 678 cm−1 FFT bands and then conducted inverse Fourier transformation to retrieve the filtered frequency domain data back to the time domain one. As shown in Fig. 7, the 230 cm−1 CWP motion doesn't exhibit the solvent-polarity dependence. However, the damping of the 150 cm−1 CWP motion significantly accelerates in polar solvent, and the rise dynamics of the 678 cm−1 CWP also become faster in polar solvent. Although narrow filters require careful use due to potential artefacts, these results are consistent with STFT analysis. Notably, the beating maps for 230 and 150 cm−1 CWPs reveal the changes in the beating patterns around 667 and 608 nm during the PET processes (blue dotted boxes in Fig. 7a and b). These features indicate that the 230 and 150 cm−1 CWP motions propagate along the PET reaction coordinates, modulating the transition strengths of TA spectra associated with InCT and CS states, respectively. These results support the non-Condon effects of these CWP motions. Specifically, the non-Condon effect of the 230 cm−1 CWP indicates the vibronic coupling between the 1MMLCT and InCT along the 230 cm−1 vibrational coordinate. This coupling might explain why the dephasing dynamics of the 230 cm−1 CWP are independent of the solvent polarity, which is similar to the trend in the PET rate change from the 1MMLCT to InCT across different solvent polarities. For the 150 cm−1 CWP motion, the non-Condon effect suggests the vibronic coupling between the InCT and CS along this vibrational coordinate, strongly supported by the solvent-polarity dependence of its dephasing dynamics.
Compared to the damping dynamics of 230 and 150 cm−1 CWPs, the 678 cm−1 CWP dynamics clearly exhibit an intensity growth during the PET processes in both STFT and Fourier filtering analyses. Since the amplitude rise dynamics depend on the PET rate varied by solvent polarity, we rule out the possibility that this CWP is a spectator mode orthogonal to the PET reaction coordinate and, thus, not active in the reaction. As mentioned in the previous section, the impulsive generation via the PET processes is also excluded because the PET time scales of ∼100 and 224–950 fs are much longer than the vibrational period of 678 cm−1 CWP (∼50 fs). Hence, the 678 cm−1 CWP transfer strongly suggests the vibronic mechanism for the entire PET processes, 1MMLCT → InCT → CS, which will be discussed below.
Key PET reaction coordinates
To gain insight into how the molecular vibrations of 150, 230, and 678 cm−1 modes contribute to the PET reactions, we conducted calculations involving optimized structures and normal modes in both ground- and CS states (Fig. 8a and S18–23†). Based on the knowledge of which the 150 cm−1 CWP motion originates from the Pt–Pt stretching vibration, our initial focus is on examining the relevant normal modes in the ground- and CS states. Similar to 1, the Pt–Pt stretching vibration in 2 exhibits an upshift in frequency from 113 cm−1 in the ground- to 148 cm−1 in CS state. It is because the one electron transferred to the NDI comes from a dσ* antibonding orbital, leading to Pt–Pt bond contraction. Notably, the nuclear motion triggers an out-of-plane (OOP) motion of 2-phenylpyridine (ppy) ligands (left in Fig. 8a and S19†), which arises due to the short distance (∼3.6 Å) between these ligands. More interestingly, the induced OOP motion concurrently leads to a dihedral angle (DA) change between the ppy ligand and the NDI moiety, resulting in ∼5° alteration (Fig. S21†). The DA alteration can potentially increase the overlap of π orbitals between the ppy and NDI, thereby accelerating the transfer of electrons from ppy to NDI. Such a torsional motion has been noted to enhance π-interactions, leading to rapid intramolecular CT in copolymers and covalent organic frameworks built from donor–bridge–acceptor configurations.58–60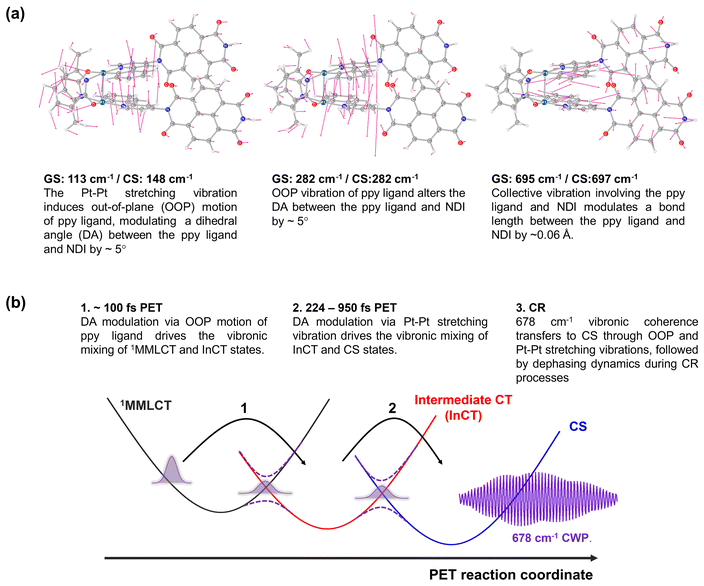 | ||
| Fig. 8 (a) Calculated normal modes in the ground-state, assigned to 150, 230 and 678 cm−1 CWP motions. (b) Illustration of PET reaction trajectories. | ||
Based on the Pt–Pt stretching motion, we searched for an OOP vibration within the 200–300 cm−1 frequency range, potentially corresponding to the 230 cm−1 mode. The calculated OOP vibrational mode has a frequency around 282 cm−1 in both the ground- and CS states, displaying an alteration of the DA by ∼5° (middle in Fig. 8a, S19 and S22†). The OOP motion is also observable around a similar frequency in the normal mode analysis for 1 (Fig. S20†), consistent with the CWP motion observation at ∼230 cm−1 in 1 and 2 (Fig. 3c and d). An intriguing collective vibration involving both the ppy ligand and NDI core was calculated around 687 cm−1 in both ground and CS states (right in Fig. 8a). This nuclear motion alters ∼0.06 Å in the bond distance between the ppy and NDI constituents (Fig. S23†). Therefore, the molecular vibrations of 150, 230 and 678 cm−1 frequencies are expected to be PET active due to the alternation of DA and bond length between the ppy and NDI moieties.
Based on the analyses of CWP motions and their corresponding normal modes, the PET reaction mechanism for 2 can be proposed, as illustrated in Fig. 8b. In the initial PET process (∼100 fs), the 1MMLCT and InCT states are vibronically coupled via the 230 cm−1 OOP vibration initiated by the MMLCT excitation. This vibration leads to an enhancement in π-interaction between the ppy and NDI moieties through the modulation in the DA configuration. Even though the 230 cm−1 mode completely decoheres in the InCT state, the π-interaction keeps being boosted through the vibration of the Pt–Pt stretching mode (150 cm−1), which also alters in the DA configuration. Consequently, the vibronic couplings driven by the OOP and Pt–Pt stretching vibrations render the efficient PET pathway through the multiple PESs. More importantly, the PET pathway is accompanied by coherence transfer of the 678 cm−1 CWP to the CS state. The DA modulations enable vibronic wavefunction delocalization across the multiple PESs, leading to the transfer of the 678 cm−1 CWP along the entire PET processes. Along this line, the vibronic couplings driven by the OOP and Pt–Pt stretching vibrations may engender multiple conical intersections (CIs) through the PET trajectories (Fig. 8b). The CI is a crossing region where two adiabatic PESs are degenerate at a particular geometry. In this vicinity, strong vibronic mixing of the electronic and nuclear degrees of freedom dominates, leading to the breakdown of the Born–Oppenheimer approximation and enabling nonadiabatic transitions from the higher to lower surfaces.61–63 Such vibronic coupling significantly influences the CWP dynamics at the CI, facilitating its passage through the CI and subsequent population in the final state.64,65 In 2, the DA modulations enhance the nonadiabatic couplings at the CIs, conserving the 678 cm−1 wavepacket phase and leading to efficient coherence transfer to the CS state. In other words, the 678 cm−1 CWP in 2 passes through the two CIs in the crossing regions between the PESs of the MMLCT, InCT and CS states, followed by dephasing processes during the CR processes. In this context, the observation of non-Condon effects can imply that the 230 and 150 cm−1 vibrations are the coupling modes to form the CIs. In addition, it is conceivable that the InCT state represents a vibronic CT state delocalized between the ppy and NDI, vibronically bridging the 1MMLCT and CS states during the PET processes. The strong dependence of the TA kinetics for the InCT state on the solvent polarity also supports this interpretation. Furthermore, the calculated collective motion involving the ppy and NDI entities may signify a distinct intramolecular vibration associated with the vibronic CT.
Conclusions
In summary, we experimentally detected that MMLCT excitation of Pt(II) dimer launches certain CWP motions (150, 230 and 678 cm−1) which directly alter the formation and evolution of the NDI radical anion during PET. The temporal correlation between the CWP and the PET dynamics revealed these modes as key reaction coordinates for the PET processes. Based on normal mode analysis, these findings strongly suggest that the CWP motions are coupled to the PET reaction coordinates by modulating the energies associated with vibronic states to be delocalized between the ligand and NDI. As a result, we also discovered the dynamic interplay of these vibronic motions enables the 678 cm−1 vibronic coherence to survive the entire PET processes, even in ∼1 ps CS in toluene. Our findings demonstrate new possibility to leverage the vibronic effect to determine the most desirable trajectory for an efficient PET reaction. The vibrational motions coupled to the CT transition of TMCs will offer an ideal avenue for harnessing the vibration-assisted coherent ET in artificial solar energy conversion systems.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
PK: performed the ultrafast BBTA experiments and analysis, as well as wrote the manuscript. PK, XL, FNC and LXC: conceptualized and supervised the project and reviewed and edited the manuscript. SR and SK: performed the synthesis and characterization, wrote the synthetic methodology. AJSV and XL: performed the computations, wrote the computational methodology. PK and TWK: built up the ultrafast BBTA spectroscopic technique.Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. K., S. R., A. J. S. V, X. L., S. K., T. W. K., X. L., F. N. C and L. X. C. as well as computational work are supported in part by the Ultrafast Initiative of the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, through Argonne National Laboratory under Contract No. DE-AC02-06CH11357. The development of computational method for simulating excited state dynamics is supported by the National Science Foundation (CHE-1856210 to X. L). The synthesis and initial spectroscopic characterization were supported by the National Science Foundation (CHE-2247821 to L. X. C and CHE-2247822 to F. N. C).References
- G. R. Fleming and R. v. Grondelle, Phys. Today, 1994, 47, 48–55 CrossRef CAS.
- M. H. Vos, F. Rappaport, J.-C. Lambry, J. Breton and J.-L. Martin, Nature, 1993, 363, 320–325 CrossRef CAS.
- K. Ando and H. Sumi, J. Phys. Chem. B, 1998, 102, 10991–11000 CrossRef CAS.
- V. I. Novoderezhkin, A. G. Yakovlev, R. van Grondelle and V. A. Shuvalov, J. Phys. Chem. B, 2004, 108, 7445–7457 CrossRef CAS.
- E. Romero, R. Augulis, V. I. Novoderezhkin, M. Ferretti, J. Thieme, D. Zigmantas and R. van Grondelle, Nat. Phys., 2014, 10, 676–682 Search PubMed.
- F. D. Fuller, J. Pan, A. Gelzinis, V. Butkus, S. S. Senlik, D. E. Wilcox, C. F. Yocum, L. Valkunas, D. Abramavicius and J. P. Ogilvie, Nat. Chem., 2014, 6, 706–711 CrossRef CAS PubMed.
- F. Ma, E. Romero, M. R. Jones, V. I. Novoderezhkin and R. van Grondelle, J. Phys. Chem. Lett., 2018, 9, 1827–1832 CrossRef CAS PubMed.
- V. I. Novoderezhkin, E. Romero and R. van Grondelle, Phys. Chem. Chem. Phys., 2015, 17, 30828–30841 RSC.
- E. Romero, V. I. Novoderezhkin and R. van Grondelle, Nature, 2017, 543, 355–365 CrossRef CAS PubMed.
- A. Sahu, J. S. Kurian and V. Tiwari, J. Chem. Phys., 2020, 153, 224114 CrossRef CAS PubMed.
- J.-L. Brédas, E. H. Sargent and G. D. Scholes, Nat. Mater., 2017, 16, 35–44 CrossRef.
- G. D. Scholes, G. R. Fleming, L. X. Chen, A. Aspuru-Guzik, A. Buchleitner, D. F. Coker, G. S. Engel, R. van Grondelle, A. Ishizaki, D. M. Jonas, J. S. Lundeen, J. K. McCusker, S. Mukamel, J. P. Ogilvie, A. Olaya-Castro, M. A. Ratner, F. C. Spano, K. B. Whaley and X. Zhu, Nature, 2017, 543, 647–656 CrossRef CAS.
- S. Rafiq and G. D. Scholes, J. Am. Chem. Soc., 2019, 141, 708–722 CrossRef PubMed.
- S. M. Falke, C. A. Rozzi, D. Brida, M. Maiuri, M. Amato, E. Sommer, A. De Sio, A. Rubio, G. Cerullo, E. Molinari and C. Lienau, Science, 2014, 344, 1001–1005 CrossRef CAS PubMed.
- Q. Bian, F. Ma, S. Chen, Q. Wei, X. Su, I. A. Buyanova, W. M. Chen, C. S. Ponseca, M. Linares, K. J. Karki, A. Yartsev and O. Inganäs, Nat. Commun., 2020, 11, 617 CrossRef CAS PubMed.
- D. M. Schultz and T. P. Yoon, Science, 2014, 343, 1239176 CrossRef PubMed.
- O. S. Wenger, J. Am. Chem. Soc., 2018, 140, 13522–13533 CrossRef CAS.
- J. Twilton, C. Le, P. Zhang, M. H. Shaw, R. W. Evans and D. W. C. MacMillan, Nat. Rev. Chem, 2017, 1, 0052 CrossRef CAS.
- V. W.-W. Yam, V. K.-M. Au and S. Y.-L. Leung, Chem. Rev., 2015, 115, 7589–7728 CrossRef CAS PubMed.
- M. Iwamura, S. Takeuchi and T. Tahara, Acc. Chem. Res., 2015, 48, 782–791 CrossRef CAS PubMed.
- T. Katayama, T. Northey, W. Gawelda, C. J. Milne, G. Vankó, F. A. Lima, R. Bohinc, Z. Németh, S. Nozawa, T. Sato, D. Khakhulin, J. Szlachetko, T. Togashi, S. Owada, S.-i. Adachi, C. Bressler, M. Yabashi and T. J. Penfold, Nat. Commun., 2019, 10, 3606 CrossRef.
- G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633 CrossRef PubMed.
- F. Hainer, N. Alagna, A. Reddy Marri, T. J. Penfold, P. C. Gros, S. Haacke and T. Buckup, J. Phys. Chem. Lett., 2021, 12, 8560–8565 CrossRef CAS PubMed.
- H. T. Lemke, K. S. Kjær, R. Hartsock, T. B. van Driel, M. Chollet, J. M. Glownia, S. Song, D. Zhu, E. Pace, S. F. Matar, M. M. Nielsen, M. Benfatto, K. J. Gaffney, E. Collet and M. Cammarata, Nat. Commun., 2017, 8, 15342 CrossRef CAS PubMed.
- K. Kunnus, M. Vacher, T. C. B. Harlang, K. S. Kjær, K. Haldrup, E. Biasin, T. B. van Driel, M. Pápai, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, E. Källman, M. Delcey, R. W. Hartsock, M. E. Reinhard, S. Koroidov, M. G. Laursen, F. B. Hansen, P. Vester, M. Christensen, L. Sandberg, Z. Németh, D. S. Szemes, É. Bajnóczi, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, H. T. Lemke, S. E. Canton, K. B. Møller, M. M. Nielsen, G. Vankó, K. Wärnmark, V. Sundström, P. Persson, M. Lundberg, J. Uhlig and K. J. Gaffney, Nat. Commun., 2020, 11, 634 CrossRef CAS PubMed.
- S. Cho, M. W. Mara, X. Wang, J. V. Lockard, A. A. Rachford, F. N. Castellano and L. X. Chen, J. Phys. Chem. A, 2011, 115, 3990–3996 CrossRef CAS.
- P. Kim, M. S. Kelley, A. Chakraborty, N. L. Wong, R. P. Van Duyne, G. C. Schatz, F. N. Castellano and L. X. Chen, J. Phys. Chem. C, 2018, 122, 14195–14204 CrossRef CAS.
- L. Mewes, R. A. Ingle, S. Megow, H. Böhnke, E. Baranoff, F. Temps and M. Chergui, Inorg. Chem., 2020, 59, 14643–14653 CrossRef CAS PubMed.
- P. Kim, A. J. S. Valentine, S. Roy, A. W. Mills, A. Chakraborty, F. N. Castellano, X. Li and L. X. Chen, J. Phys. Chem. Lett., 2021, 12, 6794–6803 CrossRef CAS PubMed.
- P. Kim, A. J. S. Valentine, S. Roy, A. W. Mills, F. N. Castellano, X. Li and L. X. Chen, Faraday Discuss., 2022, 237, 259–273 RSC.
- T. W. Kim, P. Kim, A. W. Mills, A. Chakraborty, S. Kromer, A. J. S. Valentine, F. N. Castellano, X. Li and L. X. Chen, J. Phys. Chem. C, 2022, 126, 11487–11497 CrossRef CAS.
- D. Leshchev, A. J. S. Valentine, P. Kim, A. W. Mills, S. Roy, A. Chakraborty, E. Biasin, K. Haldrup, D. J. Hsu, M. S. Kirschner, D. Rimmerman, M. Chollet, J. M. Glownia, T. B. van Driel, F. N. Castellano, X. Li and L. X. Chen, Angew. Chem., Int. Ed., 2023, 62, e202304615 CrossRef CAS.
- B. C. Paulus, S. L. Adelman, L. L. Jamula and J. K. McCusker, Nature, 2020, 582, 214–218 CrossRef CAS.
- J. D. Gaynor, J. Sandwisch and M. Khalil, Nat. Commun., 2019, 10, 5621 CrossRef CAS PubMed.
- R. Monni, G. Capano, G. Auböck, H. B. Gray, A. Vlček, I. Tavernelli and M. Chergui, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6396 CrossRef CAS.
- S. Rafiq, N. P. Weingartz, S. Kromer, F. N. Castellano and L. X. Chen, Nature, 2023, 620, 776–781 CrossRef CAS.
- A. Chakraborty, J. E. Yarnell, R. D. Sommer, S. Roy and F. N. Castellano, Inorg. Chem., 2018, 57, 1298–1310 CrossRef CAS PubMed.
- S. E. Brown-Xu, M. S. J. Kelley, K. A. Fransted, A. Chakraborty, G. C. Schatz, F. N. Castellano and L. X. Chen, J. Phys. Chem. A, 2016, 120, 543–550 CrossRef CAS.
- S. V. Bhosale, C. H. Jani and S. J. Langford, Chem. Soc. Rev., 2008, 37, 331–342 RSC.
- J. J. Snellenburg, S. P. Laptenok, R. Seger, K. M. Mullen and I. H. M. van Stokkum, J. Stat. Software, 2012, 49, 1–22 Search PubMed.
- L. Dhar, J. A. Rogers and K. A. Nelson, Chem. Rev., 1994, 94, 157–193 CrossRef CAS.
- S. D. McClure, D. B. Turner, P. C. Arpin, T. Mirkovic and G. D. Scholes, J. Phys. Chem. B, 2014, 118, 1296–1308 CrossRef CAS.
- S. Rafiq and G. D. Scholes, J. Phys. Chem. A, 2016, 120, 6792–6799 CrossRef.
- R. Xian, G. Corthey, D. M. Rogers, C. A. Morrison, V. I. Prokhorenko, S. A. Hayes and R. J. D. Miller, Nat. Chem., 2017, 9, 516–522 CrossRef CAS.
- C. Fitzpatrick, J. H. Odhner and R. J. Levis, J. Phys. Chem. A, 2020, 124, 6856–6866 CrossRef CAS PubMed.
- V. K. Jaiswal, P. Kabaciński, B. E. Nogueira de Faria, M. Gentile, A. M. de Paula, R. Borrego-Varillas, A. Nenov, I. Conti, G. Cerullo and M. Garavelli, J. Am. Chem. Soc., 2022, 144, 12884–12892 CrossRef CAS PubMed.
- W. T. Pollard, S. Y. Lee and R. A. Mathies, J. Chem. Phys., 1990, 92, 4012–4029 CrossRef CAS.
- A. Aster, A.-B. Bornhof, N. Sakai, S. Matile and E. Vauthey, J. Phys. Chem. Lett., 2021, 12, 1052–1057 CrossRef CAS PubMed.
- H. Kano, T. Saito and T. Kobayashi, J. Phys. Chem. A, 2002, 106, 3445–3453 CrossRef CAS.
- Y. Yoneda, H. Sotome, R. Mathew, Y. A. Lakshmanna and H. Miyasaka, J. Phys. Chem. A, 2020, 124, 265–271 CrossRef CAS.
- H. Kuramochi, G. Aoyama, H. Okajima, A. Sakamoto, S. Kanegawa, O. Sato, S. Takeuchi and T. Tahara, Angew. Chem., Int. Ed., 2020, 59, 15865–15869 CrossRef CAS PubMed.
- S. H. Sohn, W. Heo, C. Lee, J. Kim and T. Joo, J. Phys. Chem. A, 2019, 123, 6904–6910 CrossRef CAS PubMed.
- L. A. Bizimana, W. P. Carbery, T. A. Gellen and D. B. Turner, J. Chem. Phys., 2017, 146, 084311 CrossRef PubMed.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- S. Rafiq, B. Fu, B. Kudisch and G. D. Scholes, Nat. Chem., 2021, 13, 70–76 CrossRef CAS.
- Y. Yoneda, B. Kudisch, S. Rafiq, M. Maiuri, Y. Nagasawa, G. D. Scholes and H. Miyasaka, J. Am. Chem. Soc., 2021, 143, 14511–14522 CrossRef CAS PubMed.
- S. Rafiq and G. D. Scholes, Chem. Phys. Lett., 2017, 683, 500–506 CrossRef CAS.
- I. Hwang, S. Beaupré, M. Leclerc and G. D. Scholes, Chem. Sci., 2012, 3, 2270–2277 RSC.
- P. Roy, A. Jha, V. B. Yasarapudi, T. Ram, B. Puttaraju, S. Patil and J. Dasgupta, Nat. Commun., 2017, 8, 1716 CrossRef.
- T. W. Kim, S. Jun, Y. Ha, R. K. Yadav, A. Kumar, C.-Y. Yoo, I. Oh, H.-K. Lim, J. W. Shin, R. Ryoo, H. Kim, J. Kim, J.-O. Baeg and H. Ihee, Nat. Commun., 2019, 10, 1873 CrossRef.
- G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS PubMed.
- W. Domcke and D. R. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325–352 CrossRef CAS PubMed.
- Y. Boeije and M. Olivucci, Chem. Soc. Rev., 2023, 52, 2643–2687 RSC.
- A. Kühl and W. Domcke, J. Chem. Phys., 2002, 116, 263–274 CrossRef.
- D. Egorova and W. Domcke, J. Photochem. Photobiol., A, 2004, 166, 19–31 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc01876a |
| This journal is © The Royal Society of Chemistry 2024 |