DOI:
10.1039/D4MA00167B
(Paper)
Mater. Adv., 2024,
5, 3998-4005
Theoretical insights into the lattice thermal conductivity and thermal expansion of CoNiFe medium-entropy alloys†
Received
19th February 2024
, Accepted 18th March 2024
First published on 21st March 2024
Abstract
Medium-entropy alloys (MEAs) have important potential applications in aerospace as well as nuclear energy due to their excellent mechanical and thermodynamic properties. In this paper, we calculate the lattice thermal conductivity of CoNiFe MEA using the equilibrium molecular dynamics method. We investigate the impact of the elemental concentration in MEAs (Co1.5NiFe, CoNi1.5Fe, and CoNiFe1.5) on their lattice thermal conductivity. Increasing the Co and Fe concentration will slightly decrease the lattice thermal conductivity. On the other hand, by increasing the Ni concentration, its lattice thermal conductivity increases up to 17%. Such anomalous lattice thermal conductivity enhancement is explained by an increase in the mode participation rate and acoustic phonon lifetime. Moreover, the impacts of tensile strain and temperature on lattice thermal conductivity are explored. This study contributes to the understanding of the thermal behavior of MEAs and promotes the development of MEAs in the field of thermal science.
1. Introduction
Medium-entropy alloys (MEAs)1–3 have been attracting the attention of researchers due to their excellent mechanical properties,4–8 especially the alloy systems based on Al and the fourth row elements Fe, Co, Ni, Cr, Cu, Mn and Ti, and Pd.9–15 For example, Lang et al.14 studied and compared the formation and evolution of irradiation-induced defects in CoNiFe alloys and pure Ni using molecular dynamics (MD) simulations. They found that the defect recombination rate of ternary CoNiFe MEA was higher than that of pure Ni, which was mainly due to the decrease in the energy dissipated by atomic displacements during cascade collisions with the increase of chemical disorder.
Recently, the thermodynamic properties of high-entropy alloys have also attracted extensive research attention, particularly their thermal conductivity.16–25 For example, Farias et al.17 calculated the lattice thermal conductivity of random solid solution Cantor alloys using the Green–Kubo method in the temperature range from 0 K to 300 K. The thermal conductivity at 300 K was found to be within 21% of the experimental results.18 Chou et al.19 studied the thermal conductivity of AlxCoCrFeNi (0 ≤ x ≤ 2), which is significantly lower than that of the pure metal. Jin et al.20 synthesized a series of nickel-based face-centered cubic (FCC) isotropic alloys and investigated their thermal conductivity. The thermal conductivity of the alloys is lower than that of the pure metal, primarily due to the high resistivity that inhibits electronic thermal conductivity. Lee et al.23 investigated how the ratio between the thermal conductivity and yield strength of FCC CoNiFeCrMn can be controlled by varying the number of principal elements (NPE) and temperature. CoNiFe MEA exhibited the lowest thermal conductivity and the highest yield strength in solid solutions ranging from Ni to ternary alloys. However, the temperature dependence of the lattice thermal conductivity of CoNiFe is still not clear.24,25 In addition, Jin et al.26 reviewed the contribution of lattice thermal conductivity to the total thermal conductivity in different multi-principal alloys to illustrate that lattice thermal conductivity is a transport property well-worth investigating. However, the associated data of CoNiFe have not been reported. Therefore, it is necessary to directly calculate the lattice thermal conductivity of CoNiFe.
In this paper, we investigated the lattice thermal conductivity of CoNiFe MEA using the equilibrium molecular dynamics (EMD) method. The impacts of various factors on the lattice thermal conductivity, including supercell size, elemental concentration dependence, tensile strain, and temperature, were explored. The underlying mechanisms were revealed through phonon localization theory and phonon lifetimes. In addition, we explored the coefficient of thermal expansion of different MEAs. This study can help researchers to better understand the thermodynamic properties of MEAs.
2. Method
The primitive unit cell of CoNiFe MEA used in this paper is shown in Fig. 1(a). It is a face-centered cubic (FCC) structure and contains 144 atoms with a lattice constant of 3.66 Å. We characterize the chemical order of all atomic pairs by calculating the Warren–Cowley parameters (WCPs) in the first-nearest-neighboring shell,27| | 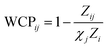 | (1) |
where Zij is the number of atoms i in the first nearest neighbors of atom j, Zi is the total number of atoms in the first nearest neighbors of atom j, and χj is the atomic ratio of atom j in the MEA. When WCPij = 0 the atom i and atom j are randomly distributed. The WCP of the initial structures of CoNiFe is shown in Fig. 1(b). The WCP are all 0, indicating that each element is randomly distributed. The primitive unit cell is replicated to calculate lattice thermal conductivity, and the supercell contains (N × N × N) unit cells. We use LAMMPS packages28 to perform MD calculations. The modified embedded atom method (MEAM) potential15 is used to describe the interaction between atoms. Cui et al.29 have proved the accuracy of the potential in terms of CoCrFeMnNi. The periodic boundaries are used in all directions, and the timestep is 1 fs. The system is fully relaxed by first being placed in the isothermal–isobaric (NPT) ensemble for 1 ns and then in the canonical (NVT) ensemble for 1 ns. Finally, the system is placed in the microcanonical (NVE) ensemble to calculate heat current.
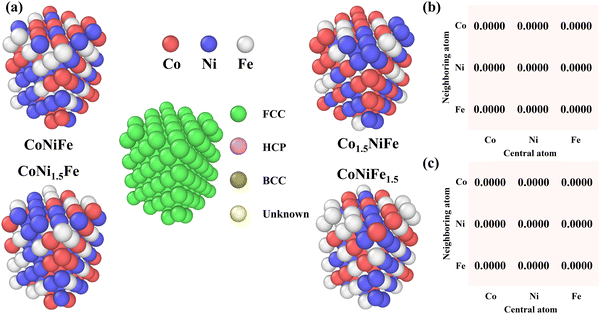 |
| | Fig. 1 (a) The primitive unit cell of the equiatomic MEA (CoNiFe) and three non-equiatomic MEAs (Co1.5NiFe, CoNi1.5Fe, and CoNiFe1.5) and their phase structure. (b) The WCP of equiatomic MEA. (c) The WCP of three non-equiatomic MEAs. | |
We use EMD simulations to calculate the lattice thermal conductivity based on the integration of the heat current autocorrelation function (HCACF) using the Green–Kubo formula (GKF),30,31
| | 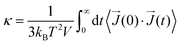 | (2) |
where
V is the volume,
kB is the Boltzmann constant,
T is the temperature,
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif)
(
t) is the heat current and the angular bracket denotes an ensemble average. In principle, there is no computational error in the EMD method,
32 but due to the computational time constraints, computational errors are introduced.
33 Researchers have proposed First Dip (FD)
34 and First Avalanche (FA)
33 methods to determine the cutoff time. It has been shown that the cutoff time determined by the FA method is more accurate;
35 therefore, in this paper, the FA method is adopted.
3. Results and discussion
3.1 Effect of elemental concentration on lattice thermal conductivity
We first consider the finite size effects present in the EMD calculations, the details of which are given in the ESI.† As shown in the ESI,† Fig. S2, when N ≥ 3, the thermal conductivity converges to 5.05 ± 0.20 W m−1 K−1, which agrees well with the range of lattice thermal conductivity (1.95 to 7.83 W m−1 K−1) reported in previous experiments.23,24 This consistency also demonstrates the robustness of the interatomic potential. The applications of MEAs in aerospace and nuclear energy require them to have high thermal conductivity. Therefore, in this section, we investigate the feasibility of enhancing the lattice thermal conductivity by adjusting elemental concentrations. We increase the concentration of one element in the MEA from 33.3% to 42.9%, respectively, and reconstruct three non-equiatomic MEAs (Co1.5NiFe, CoNi1.5Fe, and CoNiFe1.5). The WCPs of the initial structures of three non-equiatomic MEAs are shown in Fig. 1(c). The atomic configurations after EMD calculation are also characterized by WCPs. The WCPs of all atomic pairs in different MEAs are shown in the ESI,† Fig. S3. The results indicate that each element is still uniformly distributed. The lattice thermal conductivity at 300 K of these three alloys is shown in Fig. 2. With increasing the Ni concentration from 33.3% (CoNiFe) to 42.9% (CoNi1.5Fe), the lattice thermal conductivity increases by 17%. Usually, the lattice thermal conductivity increases when the concentration of light element increases;36,37 however, Co (58.93), Ni (58.69), and Fe (55.85) are comparable in atomic mass. Therefore, it is worth studying the underlying mechanisms of the increased lattice thermal conductivity with increasing Ni concentration.
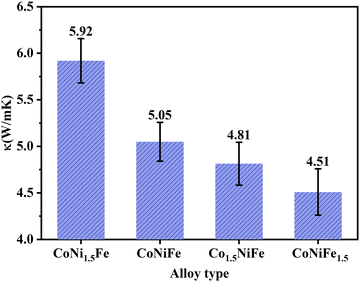 |
| | Fig. 2 The lattice thermal conductivity of different MEAs. | |
We use phonon localization theory to explain the variation of lattice thermal conductivity. We first calculate the mode participation rate (MPR) in four MEAs. The MPR can be used to determine the delocalized characteristic (i.e., MPR > 0.4) and localized characteristic (i.e., MPR < 0.4) of phonon modes. The localized mode leads to a decrease in the lattice thermal conductivity. The MPR is calculated as follows:38
| | 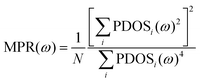 | (3) |
where
N is the number of atoms; the phonon density of states (PDOS) can be calculated by the Fourier transform of the velocity autocorrelation,
39| | 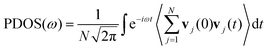 | (4) |
where
ω is the phonon frequency, and
v is the velocity vector. We calculate the MPR in the four MEAs (three non-equiatomic and one equiatomic MEAs) as shown in
Fig. 3. The MPRs of the four MEAs show a large variation in the range of 12–17 THz, with CoNi
1.5Fe having the largest MPR, suggesting that the anomalous lattice thermal conductivity is affected by the MPR.
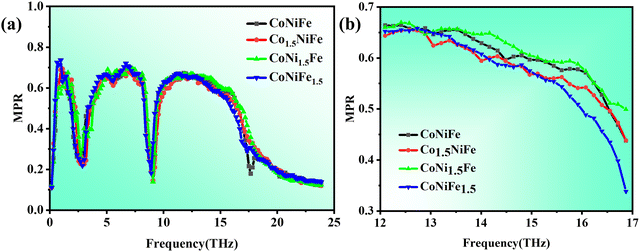 |
| | Fig. 3 The mode participation rates (MPR) of different MEAs in the range of (a) 0–25 THz and (b) 12–17 THz. | |
Next, we calculate the phonon-weighted mode participation rate (WPR), which removes the effect of frequency,40 so that the average WPR can be calculated to assess the overall effect of MPR on lattice thermal conductivity. The WPR can be calculated from the PDOS,
| |  | (5) |
where ℏ is the reduced Planck constant. We study the difference in WPR after increasing the element concentration with the WPR of the equiatomic MEA as a reference.
Fig. 4 shows the difference in WPR between the non-equiatomic and equiatomic MEAs, with CoNi
1.5Fe having the largest WPR, which can explain the increased lattice thermal conductivity.
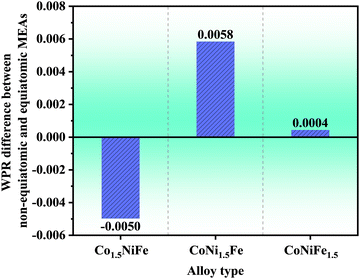 |
| | Fig. 4 The difference in average phonon-weighted mode participation rates (WPR) between non-equiatomic and equiatomic MEAs. | |
The lattice thermal conductivity is mainly due to heat transfer from lattice vibrations, on which the phonon lifetime has an important effect. Therefore, to further explain the anomalous lattice thermal conductivity, we perform a double exponential fit to the normalized HCACF with two-time constants.41,42 The existence of two phases of HCACF decay is due to the different optical and acoustic phonon lifetimes, originally proposed by Che et al.41 The fitted equations are as follows:
| | | HCACF = A1e−t/τ1 + A2e−t/τ2 | (6) |
where
A1 and
A2 are fitting parameters, and
τ1 and
τ2 are the phonon lifetimes of optical and acoustic phonons. The results of HCACF fitting with four MEAs are shown in the ESI,
† Fig. S4. The phonon lifetimes of different MEAs are shown in
Table 1. The optical phonon lifetimes are almost the same. For most bulk materials, acoustic phonons have the dominant contribution to lattice thermal conductivity. However, the acoustic phonon lifetimes show large differences, and the increase of Ni concentration extends the acoustic phonon lifetime from 1.151 ps to 1.273 ps, which suggests that the anomalous lattice thermal conductivity is affected by both the MPR and the acoustic phonon lifetime. The inconsistency between the WPR and the lattice thermal conductivity changes for the four MEAs is because the lattice thermal conductivity is not only affected by the WPR, but also affected by the atomic mass, phonon lifetime,
etc. For Co
1.5NiFe and CoNiFe
1.5, the atomic mass of Co is larger than that of Fe, and the WPR of Co
1.5NiFe is also larger than that of CoNiFe
1.5. However, the acoustic phonon lifetime of Co
1.5NiFe is short, which ultimately leads to the lower lattice thermal conductivity of Co
1.5NiFe.
Table 1 The phonon lifetime of different MEAs
| Alloy type |
Optical phonon lifetime (ps) |
Acoustic phonon lifetimes (ps) |
| CoNiFe |
0.036 |
1.151 |
| Co1.5NiFe |
0.036 |
1.181 |
| CoNi1.5Fe |
0.039 |
1.273 |
| CoNiFe1.5 |
0.036 |
1.028 |
3.2 Effect of tensile strain and temperature on lattice thermal conductivity
MEAs are generally used in extreme environments, such as those where tensile strain exists; so it is of great engineering importance to study the effect of tensile strain on lattice thermal conductivity. We first calculate the stress–strain relationship of the four MEAs by stretching the four alloys along the x direction, and the stress–strain curves are shown in Fig. 5(a). When the strain reaches about 13%, the alloy is fractured. Therefore, we calculate the effect of tensile strain on lattice thermal conductivity before the alloys are fractured. We first stretch the alloy in the x-direction to a specified strain. Then, the system is placed in the NVT ensemble for 1 ns. Finally, the system is placed in the NVE ensemble to calculate heat current. The heat current autocorrelation calculations are performed 10 times with an autocorrelation time of 100 ps. The lattice thermal conductivity is then calculated using eqn (2). The relationship of lattice thermal conductivity with strain for four different MEAs is shown in Fig. 5(b). The lattice thermal conductivity of all four alloys decreases with increasing strain. For example, for CoNiFe MEA, the lattice thermal conductivity decreases from 5.05 W m−1 K−1 at 0 strain to 2.65 W m−1 K−1 at 10% strain. This is because the phonon group velocity and phonon lifetime decrease with increasing tensile strain.43,44 In addition, the CoNi1.5Fe MEA still has the highest lattice thermal conductivity.
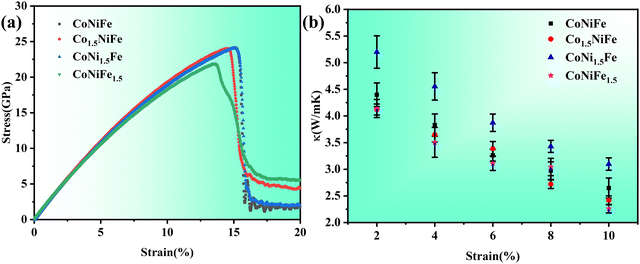 |
| | Fig. 5 (a) The stress–strain curves of four different MEAs. (b) The relationship of lattice thermal conductivity with strain for four different MEAs. | |
In addition, it is of great engineering importance to study the effect of temperature on the lattice thermal conductivity. Bag et al.24 and Lee et al.23 calculated the lattice thermal conductivity of CoNiFe at 0–300 K and 300–600 K, respectively. Their results exhibited the opposite trends: the lattice thermal conductivity at 0–300 K decreased with temperature24 whereas at 300–600 K, it increased with temperature.23 It is well known that the lattice thermal conductivity decreases as the anharmonic effect is enhanced with increasing temperature.45,46 Therefore, we focus on the lattice thermal conductivity at high temperatures. The system is fully relaxed at the desired temperature (300–1500 K) in the NPT ensemble for 1 ns and then follow the method of calculating the lattice thermal conductivity. The lattice thermal conductivity of CoNiFe in the temperature range of 300–1500 K is shown in Fig. 6. The lattice thermal conductivity decreases with increasing temperature and shows an approximately linear relationship with the inverse of temperature. At high temperatures, the lattice thermal conductivity is slightly lower than the T−1 dependence curve. This is attributed to the enhancement of the phonon–phonon anharmonic effect, which suppresses the thermal conduction. In addition, thermal expansion and phonon-granular scattering may also lead to such discrepancy.
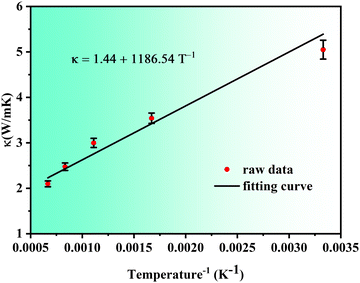 |
| | Fig. 6 The lattice thermal conductivity of CoNiFe MEA from 300 K (0.0033 K−1) to 1500 K (0.00067 K−1). | |
3.3 Thermal expansion properties of different medium-entropy alloys
MEAs contain varieties of components with different coefficients of thermal expansion, which may cause thermal stresses during solidification and processing, thus affecting the strength.47,48 Therefore, it is important to calculate the coefficient of thermal expansion. We calculate the coefficients of thermal expansion of equiatomic and non-equiatomic MEAs at 400–1500 K as shown in Fig. 7, and the details of the calculations are given in the ESI.† The calculated results of CoNiFe are in good agreement with the experimental results of Laplanche et al.49 In addition, we find that Ni concentration has the least effect on the coefficient of thermal expansion. This is because only Ni has an FCC structure among the three elements and increasing the Ni concentration has a smaller effect on the MEA structure. Co and Fe concentrations have opposite effects on the coefficient of thermal expansion, which increases by increasing Fe concentration and decreases by increasing Co concentration. For example, increasing Co concentration can reduce the coefficient of thermal expansion from 1.178 × 10−5 K−1 (CoNiFe) to 1.159 × 10−5 K−1 at 300 K (Co1.5NiFe). This suggests that the elemental structure can significantly impact the thermal expansion of an alloy when it deviates from the alloy structure.
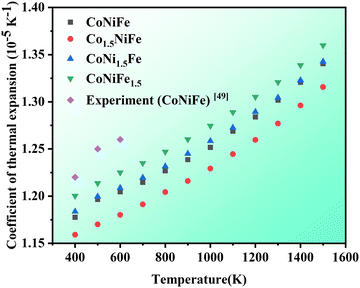 |
| | Fig. 7 The coefficient of thermal expansion for different MEAs. | |
4. Conclusions
In summary, we used the EMD method to calculate the lattice thermal conductivity of CoNiFe MEA. First, we investigated the finite-size effect on the lattice thermal conductivity, which reached a stable value as the supercell increased. Then, the feasibility of adjusting the elemental concentration (CoNiFe, Co1.5NiFe, CoNi1.5Fe, and CoNiFe1.5) to enhance the lattice thermal conductivity was investigated. Since Co, Ni, and Fe have comparable atomic masses, they should have the same effect on the lattice thermal conductivity; however, by increasing the Ni concentration (CoNiFe to CoNi1.5Fe), the lattice thermal conductivity increased by 17%. We found that increasing Ni concentration increases the MPR at 12–17 THz. Besides, increasing Ni concentration increases the acoustic phonon lifetime, while the optical phonon lifetime was similar. These results indicated that the MPR and acoustic phonon lifetime can be altered by adjusting the elemental concentration, thereby affecting the lattice thermal conductivity of MEAs. Therefore, we can increase or decrease the lattice thermal conductivity of MEAs by adjusting the elemental concentrations. Moreover, the lattice thermal conductivity decreased with increasing tensile strain and CoNi1.5Fe remains the largest. Next, the effect of temperature on the lattice thermal conductivity was explored. The lattice thermal conductivity gradually decreased with increasing temperature from 300 to 1500 K and has an approximately linear distribution with the inverse of temperature, which indicated that anharmonicity has a strong effect. Finally, the coefficients of thermal expansion for the different MEAs were calculated. The result of CoNiFe was in good agreement with the experimental report. In addition, we found that increasing Co concentration can reduce the coefficient of thermal expansion (from 1.178 × 10−5 K−1 to 1.159 × 10−5 K−1 at 300 K). This study is useful for advancing the application of medium-entropy alloys in thermal sciences.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
J. Zhang gratefully acknowledges the financial support from the China Scholarship Council (no. 202206120136). The contributions of S. Chen in this paper are sponsored by the National Natural Science Foundation of China (Grant no. 52301017), and the Shanghai Pujiang Program (Grant no. 22PJ1403700). This work is also supported by the A*STAR Computational Resource Centre, and the Shanghai Technical Service Center of Science and Engineering Computing, Shanghai University, through the use of its high-performance computing facilities.
References
- P. K. Huang, J. W. Yeh, T. T. Shun and S. K. Chen, Multi-principal-element alloys with improved oxidation and wear resistance for thermal spray coating, Adv. Eng. Mater., 2004, 6, 74–78, DOI:10.1002/adem.200300507
 .
.
- J. W. Yeh, S. K. Chen, J. W. Gan, S. J. Lin, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang, Formation of simple crystal structures in Cu-Co-Ni-Cr-Al-Fe-Ti-V alloys with multiprincipal metallic elements, Metall. Mater. Trans. A, 2004, 35, 2533–2536, DOI:10.1007/s11661-006-0234-4
 .
.
- J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang, Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes, Adv. Eng. Mater., 2004, 6, 299–303, DOI:10.1002/adem.200300567
 .
.
-
Y. Zhang, High-Entropy Materials: Advances and Applications, CRC Press, 1st edn, 2023 DOI:10.1201/9781003319986
 .
.
- C. H. Chan, Q. X. Huo, A. Kumar, Y. H. Shi, H. H. Hong, Y. T. Du, S. Ren, K. P. Wong and C. T. Yip, Heterogeneity and Memory Effect in the Sluggish Dynamics of Vacancy Defects in Colloidal Disordered Crystals and Their Implications to High-Entropy Alloys, Adv. Sci., 2022, 9, 2205522, DOI:10.1002/advs.202205522
 .
.
- J. Y. Zhang, X. Wang, X. N. Li, Y. H. Zheng, R. W. Liu, J. H. Luan, Z. B. Jiao, C. Dong and P. K. Liaw, Native Oxidation and Complex Magnetic Anisotropy-Dominated Soft Magnetic CoCrFeNi-Based High-Entropy Alloy Thin Films, Adv. Sci., 2022, 9, 2203139, DOI:10.1002/advs.202203139
 .
.
- Y. F. Jia, S. W. Wu, Y. K. Mu, L. Xu, C. Ren, K. Sun, J. Yi, Y. D. Jia, W. T. Yan and G. Wang, Efficient Coarse-Grained Superplasticity of a Gigapascal Lightweight Refractory Medium Entropy Alloy, Adv. Sci., 2023, 10, 2207535, DOI:10.1002/advs.202207535
 .
.
- K. Huang, J. Y. Xia, Y. Lu, B. W. Zhang, W. C. Shi, X. Cao, X. Y. Zhang, L. M. Woods, C. C. Han, C. J. Chen, T. Wang, J. S. Wu and Y. Z. Huang, Self-Reconstructed Spinel Surface Structure Enabling the Long-Term Stable Hydrogen Evolution Reaction/Oxygen Evolution Reaction Efficiency of FeCoNiRu High-Entropy Alloyed Electrocatalyst, Adv. Sci., 2023, 10, 2300094, DOI:10.1002/advs.202300094
 .
.
- S. Chen, Z. H. Aitken, S. Pattamatta, Z. Wu, Z. G. Yu, D. J. Srolovitz, P. K. Liaw and Y. W. Zhang, Simultaneously Enhancing the Ultimate Strength and Ductility of High-Entropy Alloys via Short-Range Ordering, Nat. Commun., 2021, 12, 4953, DOI:10.1038/s41467-021-25264-5
 .
.
- Z. R. Pei, K. A. Rozman, O. N. Dogan, Y. H. Wen, N. Gao, E. A. Holm, J. A. Hawk, D. E. Alman and M. C. Gao, Machine-Learning Microstructure for Inverse Material Design, Adv. Sci., 2021, 8, 2101207, DOI:10.1002/advs.202101207
 .
.
- L. Y. Liu, Y. Zhang, J. H. Han, X. Y. Wang, W. Q. Jiang, C. T. Liu, Z. W. Zhang and P. K. Liaw, Nanoprecipitate-Strengthened High-Entropy Alloys, Adv. Sci., 2021, 8, 2100870, DOI:10.1002/advs.202100870
 .
.
- C. M. Clausen, T. A. A. Batchelor, J. K. Pedersen and J. Rossmeisl, What Atomic Positions Determines Reactivity of a Surface? Long-Range, Directional Ligand Effects in Metallic Alloys, Adv. Sci., 2021, 8, 2003357, DOI:10.1002/advs.202003357
 .
.
- R. Li, X. J. Liu, W. H. Liu, Z. B. Li, K. C. Chan and Z. P. Lu, Design of Hierarchical
Porosity Via Manipulating Chemical and Microstructural Complexities in High-Entropy Alloys for Efficient Water Electrolysis, Adv. Sci., 2022, 9, 2105808, DOI:10.1002/advs.202105808
 .
.
- L. Lang, H. Q. Deng, J. Y. Tao, T. F. Yang, Y. P. Lin and W. Y. Hu, Comparison of formation and evolution of radiation-induced defects in pure Ni and Ni–Co–Fe medium-entropy alloy, Chin. Phys. B, 2022, 31, 126102, DOI:10.1088/1674-1056/ac891e
 .
.
- B. T. Yang, J. F. Fang, C. Y. Xu, H. Cao, R. X. Zhang, B. Zhao, M. Q. Huang, X. Y. Wang, H. L. Lv and R. C. Che, One-Dimensional Magnetic FeCoNi Alloy Toward Low-Frequency Electromagnetic Wave Absorption, Nano-Micro Lett., 2022, 14, 170, DOI:10.1007/s40820-022-00920-7
 .
.
- J. Y. Yang, W. J. Ren, X. G. Zhao, T. Kikuchi, P. Miao, K. Nakajima, B. Li and Z. D. Zhang, Mictomagnetism and suppressed thermal conduction of the prototype high-entropy alloy CrMnFeCoNi, J. Mater. Sci. Technol., 2022, 99, 55–60, DOI:10.1016/j.jmst.2021.04.077
 .
.
- M. Farias, H. Hu, S. S. Zhang, J. Z. Li and B. Xu, A molecular dynamics study of atomic diffusion effects on thermomechanical properties applying laser additive alloying process for the Cantor high entropy alloy, J. Manuf. Process., 2023, 91, 149–166, DOI:10.1016/j.jmapro.2023.02.016
 .
.
- J. Yang, W. Ren, X. Zhao, T. Kikuchi, P. Miao, K. Nakajima, B. Li and Z. Zhang, Mictomagnetism and suppressed thermal conduction of the prototype high-entropy alloy CrMnFeCoNi, J. Mater. Sci. Technol., 2022, 99, 55–60, DOI:10.1016/j.jmst.2021.04.077
 .
.
- H. P. Chou, Y. S. Chang, S. K. Chen and J. W. Ye, Microstructure, thermophysical and electrical properties in AlxCoCrFeNi (0 ≤ x ≤ 2) high-entropy alloys, Mater. Sci. Eng. B, 2009, 163, 184–189, DOI:10.1016/j.mseb.2009.05.024
 .
.
- K. Jin, B. C. Sales, G. M. Stocks, G. D. Samolyuk, M. Daene, W. J. Weber, Y. Zhang and H. Bei, Tailoring the physical properties of Ni-based single-phase equiatomic alloys by modifying the chemical complexity, Sci. Rep., 2016, 6, 20159, DOI:10.1038/srep20159
 .
.
- L. N. Zhao, Y. Chang, S. Qiu, H. S. Liu, J. J. Zhao and J. F. Gao, High Mechanical Energy Storage Capacity of Ultranarrow Carbon Nanowires Bundles by Machine Learning Driving Predictions, Adv. Energy Sustainability Res., 2023, 4, 2300112, DOI:10.1002/aesr.202300112
 .
.
- A. Zhang, S. Qiu, L. Zhao, H. Liu, J. Zhao and J. Gao, Robust Type-II Band Alignment and Stacking-Controlling Second Harmonic Generation in GaN/ZnO vdW Heterostructure, Laser Photonics Rev., 2024, 18, 2300742, DOI:10.1002/lpor.202300742
 .
.
- J. I. Lee, H. S. Oh and E. S. Park, Manipulation of σy/κ ratio in single phase FCC solid-solutions, Appl. Phys. Lett., 2016, 109, 061906, DOI:10.1063/1.4960809
 .
.
- P. Bag, Y. C. Su, Y. K. Kuo, Y. C. Lai and S. K. Wu, Physical properties of face-centered cubic structured high-entropy alloys: Effects of NiCo, NiFe, and NiCoFe alloying with Mn, Cr, and Pd, Phys. Rev. Mater., 2021, 5, 085003, DOI:10.1103/PhysRevMaterials.5.085003
 .
.
- X. Zheng, D. G. Cahill, P. Krasnochtchekov, R. S. Averback and J. C. Zhao, High-throughput thermal conductivity measurements of nickel solid solutions and the applicability of the Wiedemann–Franz law, Acta Mater., 2007, 55, 5177–5185, DOI:10.1016/j.actamat.2007.05.037
 .
.
- K. Jin and H. B. Bei, Single-Phase Concentrated Solid-Solution Alloys: Bridging Intrinsic Transport Properties and Irradiation Resistance, Front. Mater., 2018, 5, 26, DOI:10.3389/fmats.2018.00026
 .
.
- J. M. Cowley, X-Ray Measurement of Order in Single Crystals of Cu3Au, J. Appl. Phys., 1950, 21, 24–30, DOI:10.1063/1.1699415
 .
.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19, DOI:10.1006/jcph.1995.1039
 .
.
- Y. Cui, Z. T. Chen, S. J. Gu, W. Z. Yang and Y. Ju, Investigating size dependence in nanovoid-embedded high-entropy-alloy films under biaxial tension, Arch. Appl. Mech., 2023, 93, 335–353, DOI:10.1007/s00419-021-02100-2
 .
.
- M. S. Green, Markoff Random Processes and the Statistical Mechanics of Time-Dependent Phenomena. II. Irreversible Processes in Fluids, J. Chem. Phys., 1954, 22, 398–413, DOI:10.1063/1.1740082
 .
.
- R. Kubo, Statistical-Mechanical Theory of Irreversible Processes. I. General Theory and Simple Applications to Magnetic and Conduction Problems, J. Phys. Soc. Jpn, 1957, 12, 570–586, DOI:10.1143/JPSJ.12.570
 .
.
- R. Kubo, M. Yokota and S. Nakajima, Statistical-Mechanical Theory of Irreversible Processes. II. Response to Thermal Disturbance, J. Phys. Soc. Jpn., 1957, 12, 1203–1211, DOI:10.1143/JPSJ.12.1203
 .
.
- J. Chen, G. Zhang and B. W. Li, How to improve the accuracy of equilibrium molecular dynamics for computation of thermal conductivity?, Phys. Lett. A, 2010, 374, 2392–2396, DOI:10.1016/j.physleta.2010.03.067
 .
.
- J. Li, L. Porter and S. Yip, Atomistic modeling of finite-temperature properties of crystalline β-SiC: II. Thermal conductivity and effects of point defects, J. Nucl. Mater., 1998, 255, 139–152, DOI:10.1016/S0022-3115(98)00034-8
 .
.
- A. J. H. McGaughey and M. Kaviany, Phonon Transport in Molecular Dynamics Simulations: Formulation and Thermal Conductivity Prediction, Adv. Heat Transfer, 2006, 39, 169–255, DOI:10.1016/S0065-2717(06)39002-8
 .
.
- G. A. Slack, Nonmetallic crystals with high thermal conductivity, J. Phys. Chem. Solids, 1973, 34, 321–335, DOI:10.1016/0022-3697(73)90092-9
 .
.
- G. A. Slack, The Thermal Conductivity of Nonmetallic Crystals, Solid State Phys., 1979, 34, 1–71, DOI:10.1016/S0081-1947(08)60359-8
 .
.
- G. C. Loh, E. H. T. Teo and B. K. Tay, Phonon localization around vacancies in graphene nanoribbons, Diam. Relat. Mater., 2012, 23, 88–92, DOI:10.1016/j.diamond.2012.01.006
 .
.
- J. M. Dickey and A. Paskin, Computer Simulation of the Lattice Dynamics of Solids, Phys. Rev., 1969, 188, 1407–1418, DOI:10.1103/PhysRev.188.1407
 .
.
- T. Tohei, A. Kuwabara, F. Oba and I. Tanaka, Debye temperature and stiffness of carbon and boron nitride polymorphs from first principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 064304, DOI:10.1103/PhysRevB.73.064304
 .
.
- J. W. Che, T. Cagin, W. Q. Deng and W. A. Goddard, Thermal conductivity of diamond and related materials from molecular dynamics simulations, J. Chem. Phys., 2000, 113, 6888–6900, DOI:10.1063/1.1310223
 .
.
- A. J. H. McGaughey and M. Kaviany, Thermal conductivity decomposition and analysis using molecular dynamics simulations. Part I. Lennard-Jones argon, Int. J. Heat Mass Transfer, 2004, 47, 1783–1798, DOI:10.1016/j.ijheatmasstransfer.2003.11.002
 .
.
- K. P. Yuan, X. L. Zhang, L. Li and D. W. Tang, Effects of tensile strain and finite size on thermal conductivity in monolayer WSe2, Phys. Chem. Chem. Phys., 2019, 21, 468–477, 10.1039/C8CP06414H
 .
.
- N. Wei, L. Q. Xu, H. Q. Wang and J. C. Zheng, Strain engineering of thermal conductivity in graphene sheets and nanoribbons: a demonstration of magic flexibility, Nanotechnology, 2011, 22, 105705, DOI:10.1088/0957-4484/22/10/105705
 .
.
- X. L. Yang, J. Tiwari and T. L. Feng, Reduced anharmonic phonon scattering cross-section slows the decrease of thermal conductivity with temperature, Mater. Today Phys., 2022, 24, 100689, DOI:10.1016/j.mtphys.2022.100689
 .
.
- X. Y. Zhu and C. Shao, Effect of anharmonicity on the thermal conductivity of amorphous silica, Phys. Rev. B, 2022, 106, 014305, DOI:10.1103/PhysRevB.106.014305
 .
.
-
K. K. Chawla, Composite Materials: Science and Engineering, Springer, New York, 1998 DOI:10.1007/978-0-387-74365-3
 .
.
- J. Bonneville, G. Laplanche, A. Joulain, V. Gauthier-Brunet and S. Dubois, Al-matrix composite materials reinforced by Al-Cu-Fe particles, J. Phys.: Conf. Ser., 2010, 240, 012013, DOI:10.1088/1742-6596/240/1/012013
 .
.
- G. Laplanche, P. Gadaud, C. Barsch, K. Demtroder, C. Reinhart, J. Schreuer and E. P. George, Elastic moduli and thermal expansion coefficients of medium-entropy subsystems of the CrMnFeCoNi high-entropy alloy, J. Alloys Compd., 2018, 746, 244–255, DOI:10.1016/j.jallcom.2018.02.251
 .
.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Haochun
Zhang
*a,
Jie
Xiong
ab,
Haochun
Zhang
*a,
Jie
Xiong
 cd,
Shuai
Chen
cd,
Shuai
Chen
 *cd and
Gang
Zhang
*cd and
Gang
Zhang
 *b
*b
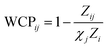
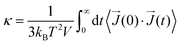
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) (t) is the heat current and the angular bracket denotes an ensemble average. In principle, there is no computational error in the EMD method,32 but due to the computational time constraints, computational errors are introduced.33 Researchers have proposed First Dip (FD)34 and First Avalanche (FA)33 methods to determine the cutoff time. It has been shown that the cutoff time determined by the FA method is more accurate;35 therefore, in this paper, the FA method is adopted.
(t) is the heat current and the angular bracket denotes an ensemble average. In principle, there is no computational error in the EMD method,32 but due to the computational time constraints, computational errors are introduced.33 Researchers have proposed First Dip (FD)34 and First Avalanche (FA)33 methods to determine the cutoff time. It has been shown that the cutoff time determined by the FA method is more accurate;35 therefore, in this paper, the FA method is adopted.
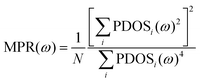
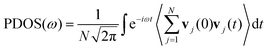





.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.



