Substrate effect on charging of electrified graphene/water interfaces

Abstract

Graphene, a transparent two-dimensional (2D) conductive electrode, has brought extensive new perspectives and prospects to electrochemical systems, such as chemical sensors, energy storage, and energy conversion devices. In many of these applications, graphene, supported on a substrate, is in contact with an aqueous solution. An increasing number of studies indicate that the substrate, rather than graphene, determines the organization of water in contact with graphene, i.e., the electric double layer (EDL) structure near the electrified graphene, and the wetting behavior of the graphene: the graphene sheet is transparent in terms of its supporting substrate. By applying surface-specific heterodyne-detected sum-frequency generation (HD-SFG) spectroscopy to the silicon dioxide (SiO₂)-supported graphene electrode/aqueous electrolyte interface and comparing the data with those for the calcium fluoride (CaF₂)-supported graphene [Y. Wang et al., Angew. Chem., Int. Ed., 2023, 62, e202216604], we discuss the impact of the different substrates on the charging of both the graphene and the substrate upon applying potentials. The SiO₂-supported graphene shows pseudocapacitive behavior, consistent with the CaF₂-supported graphene case, although the surface charges on SiO₂ and CaF₂ differ substantially. The SiO₂ surface is already negatively charged at +0.57 V (vs. Pd/H₂), and the negative surface charge is doubled when negative potentials are applied, in contrast with the CaF₂ case, where the positive charge is reduced when negative potentials are applied. Interestingly, the charging of the graphene sheet is almost identical between the negatively charged SiO₂ surface and positively charged CaF₂ surface, demonstrating that the graphene charging is decoupled from the charging of the substrates.

---

Introduction

Graphene, an atom-thin transparent electrode with high conductivity, ultra-high chemical stability, unparalleled breaking strength, and large surface area, has brought exclusive new perspectives and prospects to electrochemical systems, spanning from chemical and biological sensors^1,2 to energy storage, conversion technologies,^3,4 and neuromorphic iontronics.^5–7 In these applications, graphene is usually supported on a transparent substrate, such as calcium fluoride (CaF₂) and silicon dioxide (SiO₂).^8–10 Molecular details of the substrate-supported graphene electrode/aqueous electrolyte interface under potentiostatically controlled conditions are essential and an indispensable prerequisite to comprehending the mechanisms of those systems, in particular the local electric field across the electrode and the electrical double layer (EDL). The local electric field significantly impacts the physicochemical properties of the interface. For instance, the local electric field can modify the electrode–electrolyte interactions to alter reaction kinetics and electron transfer^11–17 and is closely linked with charge storage at the electrode/aqueous electrolyte interface.^18,19 As such, knowledge of the local electric field at the graphene electrode/aqueous electrolyte interface is essential for its rational applications in electrochemical systems.

An increasing number of studies have indicated that the graphene sheet cannot shield the substrate's surface charge from the aqueous electrolyte, known as the “wetting translucency”.^20–22 As a result, the substrate's surface charges greatly contribute to the local electric field and strongly affect the organization of water and electrolyte ions in the EDL.^10,20,23 We have recently shown that water dissociation caused by the applied potentials on the graphene electrode changes the local pH near the CaF₂-supported graphene electrode.¹⁰ Aqueous proton permeation through the monolayer graphene electrode^24–27 induces the chemical reaction at the CaF₂ surface, altering the surface charge of the CaF₂ substrate.^10,20,23 A question arising here is whether such a chemical reaction-induced surface charge variation is a universal observation for substrate-supported graphene electrodes.

Here, we probe the charging of the SiO₂ supported-graphene electrode/aqueous electrolyte interface under potentiostatically controlled conditions using heterodyne-detected sum-frequency generation (HD-SFG) spectroscopy employing the interfacial water signal (χ⁽²⁾). HD-SFG spectroscopy is a surface-specific technique that selectively probes molecular vibrations from molecules at the interface. Signals from the bulk are naturally excluded due to the selection rule.^28,29 Importantly, the complex χ⁽²⁾ signal of the interfacial water provides insights not only into the molecular structure and orientation of the interfacial water,^30,31 but also the charges at the interface.^32,33 By this, we are able to directly probe the charging of the interface under potentiostatically controlled conditions. In addition to the HD-SFG measurements, we independently characterized the charges of the graphene electrode using Raman spectroscopy. Combining Raman with HD-SFG lets us fully map the charges of the SiO₂-supported graphene electrode/aqueous electrolyte interface and distinguish the different contributions from the graphene electrode and its supporting substrate to the local electric field. Furthermore, by comparing the data collected at the SiO₂- and CaF₂-supported graphene electrode surfaces, we unveil the impact of the different substrates on the charging of the graphene and the substrate upon applying the electrochemical potentials. Our approach allows us to obtain molecular details of the graphene electrode/aqueous electrolyte interface, including the reorganization of interfacial water molecules and charges of the interface, which are relevant for various technological applications of graphene such as water desalination, chemosensing, biosensing, energy storage and conversion, and neuromorphic iontronics.

Results and discussion

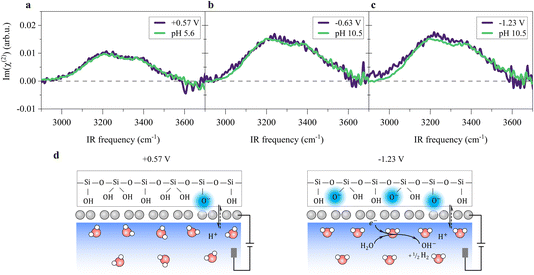
To probe the ordered water molecules near the SiO₂-supported graphene electrode/aqueous electrolyte interface, we measured the Im(χ⁽²⁾) spectra of the interfacial water in the O–H stretching mode frequency region (2900–3700 cm⁻¹). A schematic diagram of the electrochemical HD-SFG setup is depicted in Fig. 1a. Further details regarding the sample preparation and electrochemical HD-SFG measurements can be found in ref. 9, 10, 23 and 34 and are recalled in the Experimental section and the ESI.† We used 10 mM NaClO₄ as the electrolyte. The data at different potentials (vs. Pd/H₂ reference electrode) are displayed in Fig. 1b. At +0.57 V, the Im(χ⁽²⁾) spectrum exhibits a positive band spanning from 2950 cm⁻¹ to 3550 cm⁻¹. This band is assigned to the O–H stretching mode of water molecules hydrogen-bonded (H-bonded) to the other water molecules,^29,35 and the positive sign of this band indicates that the H-bonded O–H group points up towards the graphene electrode (away from the bulk solution).^31,36 This H-bonded O–H band is insensitive to the variation of the applied potential in the range of +0.57 V to −0.03 V and rapidly increases when decreasing the potential from −0.03 V to −0.63 V. The increase in the band suggests an enhanced alignment of the H-bonded O–H group pointing up towards the graphene electrode. Further decreasing the potential from −0.63 V to −1.23 V, the Im(χ⁽²⁾) spectra are again insensitive to the applied potentials.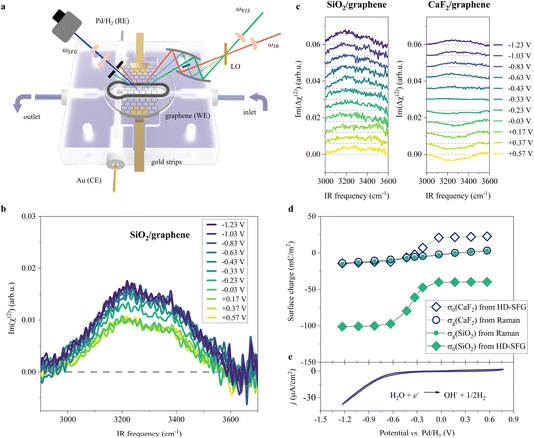

Fig. 1 O–H stretching spectra at the SiO₂-supported graphene/water interface measured by HD-SFG, at different electrochemical potentials vs. Pd/H₂. (a) Schematic diagram of the electrochemical flowing liquid cell for Raman and HD-SFG measurements. SiO₂-supported graphene, Pd/H₂, and Au wire were used as the working electrode (WE), reference electrode (RE), and counter electrode (CE), respectively. The inlet of the flow cell is connected to a variable flow syringe pump to exchange the solution. (b) O–H stretching Im(χ⁽²⁾) spectra at various applied potentials for the SiO₂-supported graphene electrode. The dashed line indicates the zero line. (c) The differential Im(Δχ⁽²⁾) spectra obtained from taking the difference between χ⁽²⁾ spectra recorded at 10 mM and 100 mM NaClO₄ aqueous solutions for the (left panel) SiO₂- and (right panel) CaF₂-supported graphene electrode. The Im(Δχ⁽²⁾) spectra for the CaF₂-supported graphene electrode are adapted from ref. 10. The data are offset for clarity. (d) σ₀ and σ_g as a function of the applied potentials for the SiO₂- and CaF₂-supported graphene electrodes. σ₀ was inferred from the Δχ⁽²⁾ spectra while σ_g was inferred from the Raman G-band frequency shift of the graphene electrode. (e) Cyclic voltammogram (CV) of the SiO₂-supported graphene electrode. The scan rate is 50 mV s⁻¹. The CV curve shows two typical features: the HER region (below −0.23 V where the current density is above 1 μA cm⁻², H₂O + e⁻ → ½H₂ + OH⁻)^48,49 and the double-layer capacitive region (above −0.23 V). We used 10 mM NaClO₄ aqueous solution for the experiments shown in (b) and (e).

Such a nonlinear change in the water orientations may arise from the nonlinear change in the net surface charges (σ₀) at the graphene electrode/aqueous electrolyte interface. To examine this hypothesis, we measured the χ⁽²⁾ spectra at two different electrolyte concentrations (c₁ = 10 mM and c₂ = 100 mM), and then extracted σ₀ from the differential spectra Δχ⁽²⁾(σ₀,V) = χ⁽²⁾(σ₀(V),c₁) − χ⁽²⁾(σ₀(V),c₂). The surface charge can be obtained in the following manner. At the charged interfaces, observed χ⁽²⁾ is given as the sum of the Stern layer contribution (χ⁽²⁾_s-term) and the diffuse layer contribution (χ⁽³⁾-term) within the Gouy–Chapman theory:^33,37,38

χ⁽²⁾(σ₀,c) = χ⁽²⁾_s + χ⁽³⁾ϕ₀(σ₀,c)κ(c)/(κ(c) − iΔk_z), (1)

where χ⁽³⁾ primarily represents the third-order nonlinear susceptibility originating from bulk water,³³ϕ₀ is the electrostatic potential, κ the inverse of Debye screening length, and Δk_z the phase-mismatch of the SF, visible, and IR beams in the depth direction. Assuming that the χ⁽²⁾_s-term is insensitive to the ion concentrations (10–100 mM), one can omit the χ⁽²⁾-term and then connect the differential spectra Δχ⁽²⁾ with σ₀ through the χ⁽³⁾-term via:^10,32Even though the exact origin of χ⁽³⁾ has been argued to be a second-order optical process,³⁹ its lineshape has been found to be constant regardless of the surface potential^33,40,41 and can be measured directly.^23,32,33 As such, σ₀ can then be obtained from the comparison of the experimentally obtained left side and the computed right side of eqn (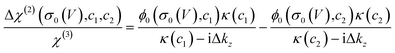2).

The obtained Im(Δχ⁽²⁾) spectra at various potentials for the SiO₂-supported graphene electrode are shown in Fig. 1c. The signs of the H-bonded O–H band in the Im(Δχ⁽²⁾) spectra are positive irrespective of applied potential, manifesting that the net surface charge (σ₀) of the whole SiO₂-supported graphene electrode is negative. Since the bare SiO₂–water interface is intrinsically negatively charged,^40–42 the result implies the transparency of the graphene in terms of the substrate–water interaction.^10,20,43 The Im(Δχ⁽²⁾) spectra monotonically increase with lowering the potentials, indicating a negatively charged surface and an increase in the negative surface charge density, respectively. The corresponding σ₀ extracted from the Δχ⁽²⁾ spectra using eqn (2) is shown in Fig. 1d. Consistent with the nonlinear change in the Im(χ⁽²⁾) spectra, σ₀ varies in a very nonlinear fashion with the applied potential. It rapidly increases from −40 mC m⁻² to −101 mC m⁻² when decreasing the applied potential from −0.03 V to −0.63 V, and is insensitive to the applied potentials in the ranges of +0.57 V to −0.03 V and −0.63 V to −1.23 V. The nonlinear change in σ₀ explains the nonlinear change in the Im(χ⁽²⁾) spectra upon the variation of the applied potentials and suggests the nonlinear variation of the local electric field at the graphene electrode/aqueous electrolyte interface.

Is such a variation of the surface charge upon the applied potential universal for different substrates? To address this question, we compared the current data for the SiO₂-supported graphene electrode with the data for the CaF₂-supported graphene electrode.¹⁰ Because the SiO₂ surface is negatively charged at pH ∼ 6, while the CaF₂ surface is positively charged^10,44 giving that the isoelectric points of SiO₂ and CaF₂ are in the pH range of 2–3 (ref. 45) and 9–10 (ref. 46 and 47) respectively, the comparison of the SiO₂ and CaF₂ samples provides a unified view of the impact of the substrate on the graphene electrode/aqueous electrolyte interface. The variations of the Im(Δχ⁽²⁾) spectra and the extracted σ₀ are displayed in Fig. 1c and d, respectively. Both cases show the nonlinear changes in σ₀ at ∼−0.33 V vs. Pd/H₂, while the values of σ₀ are largely different. This difference reflects the intrinsically different surface charge of the SiO₂ and CaF₂ substrates upon applying potentials on the graphene electrode. Nevertheless, the trend in the surface charge variation is not different.

To further look deeply at the charge of the graphene sheet supported by these two different substrates, we measured the Raman G-band of the graphene electrodes at different applied potentials, from which we estimated the charges (σ_g) of the graphene sheets (for details, see Section S1 in the ESI†).^50,51 The data is plotted in Fig. 1d. Consistent with previous studies,^50,52σ_g varies linearly vs. the applied potentials, decreasing from +3 mC m⁻² to −16 mC m⁻² when changing the potential from +0.57 V to −1.23 V for the SiO₂-supported graphene electrode. Importantly, we observed the same change in σ_g with potential within the experimental error, irrespective of different substrates, despite σ₀ differing significantly for these two different substrates. This clearly demonstrates that the charges on the graphene sheets upon applying potentials are decoupled from the charges on the substrates. This is reasonable because the impact of the substrate's charges on σ_g is small, less than 1 mC m⁻² even if considering the biggest substrate's charge of 100 mC m⁻² according to self-consistent theory (for details, see Section S2 in the ESI†).^53,54

By using the analogy of the CaF₂ and SiO₂ substrates,¹⁰ the electrified graphene leads to the hydrogen evolution reaction (HER), altering the local pH near the graphene electrode. To see how the applied potential alters the local pH and the role of the substrate of the graphene electrode, we plotted the comparison of the local pH near the CaF₂-supported graphene and SiO₂-supported graphene (for details, see Section S3 in the ESI†). The data is shown in Fig. 2. The local pH vs. applied potential is identical within the experimental error, manifesting that the local pH created by the electrified graphene electrodes is independent of its supporting substrate. Not only the surface charge on the graphene electrode but also the local pH created by the electrified graphene electrode are not affected by its supporting substrate. Notably, the same local pH change explains the same nonlinear change trend in σ₀ for the SiO₂- and CaF₂-supported graphene electrode (Fig. 1d). It also verifies that the different Im(Δχ⁽²⁾) spectra and σ₀ (Fig. 1c and d) for the SiO₂- and CaF₂-supported graphene electrodes simply arise from the different isoelectric points of the SiO₂ and CaF₂ substrates.

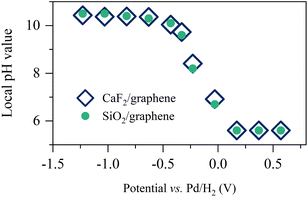Fig. 2 Pseudocapacitive pH changes near the graphene electrode. Inferred local pH value as a function of the applied potentials for the SiO₂- and CaF₂-supported graphene electrodes. The data for the CaF₂-supported graphene electrode is adapted from ref. 10.

A remaining question is which type of interfacial acid–base equilibrium occurs at the electrified SiO₂-supported graphene interface. At +0.57 V, the solution has the original solution pH of ∼5.6, and the SiO₂ surface is negatively charged (composed of ≡SiO⁻, ≡SiOH and ≡Si(OH)₂ groups,^42,55 where ≡ indicates a surface-bound state). Changing the potential to below −0.23 V, HER occurs (Fig. 1e), raising the local pH at the graphene/aqueous electrolyte interface.^10,56 The elevated local pH induces the dissociation of water (I) trapped between the graphene and the SiO₂ substrate. Subsequent proton permeation through the graphene (II)^24–27 to the bulk water leaves OH⁻ causing the deprotonation of the SiO₂ (ref. 27 and 57) and then the increase in σ₀(III). The increase in σ₀ leads to the enhanced alignment of the H-bonded O–H group pointing up towards the graphene electrode.

H₂O ⇌ OH⁻ + H⁺, (I)

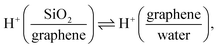≡Si(OH)₂ + OH⁻ ⇌ ≡Si(OH)O⁻ + H₂O. (III)

The exact deprotonation process of the SiO₂ substrate depends on the solution pH and the silanol surface groups on its surface. It is generally accepted that the SiO₂ surface has two distinct types of silanol surface groups with pK_a values of ∼4.5 (≡SiOH) and ∼8.5 (Si(OH)₂) respectively.^27,42,57 We note that the bimodal pK_a has been debated, recently. For example, Gibbs-Davis et al.⁵⁸ argued that there could be three types of silanol surface groups, while Tahara et al.⁴⁰ argued only one. To further understand the interfacial acid–base equilibria of the SiO₂ in the presence of the monolayer graphene electrode, we measured the Im(χ⁽²⁾) spectra at the SiO₂-supported graphene/aqueous electrolyte interface under different pH conditions. The H-bonded O–H peak area as a function of the solution pH exhibits two inflection points, indicating two interfacial acid–base equilibria with two pK_a values of ∼4.3 and ∼9.0 respectively (for details, see Section S3 in the ESI†), which are consistent with the generally accepted bimodal acidity behavior. Those results indicate that the presence of the monolayer graphene electrode hardly affects the interfacial acid–base equilibria of the SiO₂ substrate, which is also consistent with previous second-harmonic generation (SHG) measurements.²⁷

The potential-induced deprotonation of SiO₂ arises from the HER-induced local pH increase, which starts from an initial pH of ∼5.6. From the above analysis, we can conclude that the potential-induced deprotonation of SiO₂ corresponds to the equilibrium (III) with the pK_a value of ∼9.0. In any case, the deprotonation of SiO₂ explains the increase in σ₀ and the H-bonded O–H band upon the decrease in the potential. Variation of the Im(χ⁽²⁾) spectra upon applying potentials can be reproduced by changing the solution pH (Fig. 3a–c), further supporting this explanation. The reorganization of the interfacial water at the SiO₂-supported graphene electrode surface is consistent with previous observations at the bare SiO₂–water interface.^40,41,59 Those results verify that the local electric field at the SiO₂-supported graphene surface is governed by the HER-induced local pH change and subsequently charging of the SiO₂ through interfacial acid–base equilibria. We note that the potentials at which we observe HER-induced local pH changes lie in the capacitive region of the cyclic voltammogram (Fig. 1e, below −0.23 V where the current density is around 1 μA cm⁻²), constituting an electrochemical mechanism that appears to be capacitive but actually originates from charge transfer processes across the electrode/electrolyte interface. Thus, this reflects the pseudocapacitive effect.^10,14 A molecular picture of the pseudocapacitive behaviors at the SiO₂-supported graphene/aqueous electrolyte interface is schematically depicted in Fig. 3d.

Fig. 3 Molecular structure of interfacial water and surface charging at the SiO₂-supported graphene electrode/aqueous electrolyte interface. (a–c) Comparison of the O–H stretching Im(χ⁽²⁾) spectra measured by changing the applied potentials on the graphene electrode and by changing the solution pH. We used 10 mM NaClO₄. (d) Molecular pictures of the pseudocapacitive pH change and interfacial water organization at various indicated potentials at the SiO₂-supported graphene/aqueous electrolyte interface.

Remarkably, the alignment of interfacial water saturates at increasingly low potentials below −0.63 V (Fig. 1b and 3a–c). The saturation of the water alignment suggests a saturation of the local pH increase (Fig. 2). Such saturation has also been observed at the CaF₂-supported graphene electrode/aqueous electrolyte interface and was attributed to the limited amount of water trapped between the graphene and the CaF₂ substrate. For CaF₂, dissociation of the trapped water molecules is necessary to increase the local pH.¹⁰ This is, however, unlike the case at the SiO₂-supported graphene electrode/aqueous electrolyte interface because the charging of SiO₂ does not require the consumption of the trapped water molecules (I–III). Rather, we attribute the saturation of local pH increase to the slow HER kinetics. The local pH results from the balance/competition of proton consumption by HER and proton supply by diffusion from the bulk solution. In the potential range from −0.03 V to −0.63 V, the HER rate controls the local pH.¹⁰ Towards more negative potential below −0.63 V, the local pH is elevated to ∼10.5 (Fig. 2), giving rise to a large proton concentration gradient of ∼5 pH units across the interface and in turn a fast bulk supply of proton. The catalytic activity of graphene for HER is very weak, manifesting as ultra-slow HER kinetics (for details, see Section S4 in the ESI†).⁶⁰ As a result, the proton diffusion limits the increase in the local pH at potentials below −0.63 V. Notably, the saturation of interfacial acid–base equilibrium might also play a role in the saturation of water alignment. The deprotonation of SiO₂ saturating at pH above 11.0 indicates the surface charges on the SiO₂ saturates (Fig. S2†). The highest local pH induced by negative electrochemical potentials is ∼10.5. We attribute the saturation of water alignment to saturation of the surface charge density on SiO₂ and/or the diffusion-limit local pH increase. The observation that for both CaF₂ and SiO₂ substrates we infer the same limiting interfacial pH of ∼10.5 at negative potential points to the dominance of diffusion limitations in determining the local pH increase. This is also consistent with the Tafel plot (see Section S4 in the ESI†).

Conclusions

Employing surface-specific HD-SFG spectroscopy, we obtained molecular-level insights into the charging and reorganization of interfacial water at the SiO₂-supported graphene electrode/aqueous electrolyte interface under potentiostatically controlled conditions. Similar to the CaF₂-supported graphene electrode surface, our results show that reorganization of the interfacial water on the SiO₂-supported graphene electrode is not due to charging of the graphene electrode but due to the local pH change-induced pseudocapacitive charging of the SiO₂ substrate, although the potential-induced reorganization of interfacial water on the two electrodes is different. Within experimental uncertainty, the pH changes near the graphene electrodes are identical. The difference arises from the different charging of the CaF₂ and SiO₂ substrates with potentials as the isoelectric points of the two substrates are different. From comparing the data collected at the SiO₂- and CaF₂-supported graphene electrode surfaces, we demonstrate that the charging of the substrate relies on its isoelectric point and dominantly determines and affects the charging of the graphene electrode/aqueous electrolyte interface. In contrast, independent Raman measurements show that the charging of the graphene electrode is hardly affected by its substrate. Our work unveils the impact of the different substrates on the charging of graphene and its supporting substrate upon applying electrochemical potentials. The pseudocapacitive response of interfacial water and surface charges uncovered here complements our molecular-level understanding of the graphene electrode/aqueous electrolyte interface, relevant for various technological applications of graphene such as water desalination, chemosensing, biosensing, energy storage and conversion, and neuromorphic iontronics. The extension of the work to the SiO₂-supported graphene electrode demonstrates that HD-SFG spectroscopy is an ideal tool for probing molecular details at the buried graphene electrode/aqueous electrolyte interface. Finally, our work also demonstrates that interfacial water can be a sensitive probe of the electrochemical process at the electrode surface in aqueous systems.

Experimental

Chemicals

The sodium hydroxide (NaOH), hydrochloride (HCl), ammonium persulfate ((NH₄)₂S₂O₈), concentrated sulfuric acid (H₂SO₄), 30 wt% hydrogen peroxide solution (H₂O₂), cellulose acetate butyrate (CAB), ethyl acetate, ethanol, and acetone (>99%, analytical grade) were purchased from Sigma-Aldrich, and used without further purification. Sodium perchlorate (NaClO₄, metals basis, 99.99%) was obtained from Merck and used as a supporting electrolyte in our electrochemical experiment with a concentration of 10 mM or 100 mM. Deionized water (pH ∼ 5.6) was provided by a Milli-Q system (resistivity ≥ 18.2 MΩ cm and TOC ≤ 4 ppb). CVD-grown monolayer graphene on a copper foil was purchased from Grolltex Inc.

SiO₂ substrate preparation

The SiO₂ windows (25 mm diameter with a thickness of 2 mm, PI-KEM Ltd.) were cleaned with acetone, ethanol, and deionized water sequentially in an ultrasonic environment for five minutes. Subsequently, the SiO₂ windows were immersed in piranha solution for 10 minutes to clean the surface. After that, two 100 nm-thick gold strips were thermally evaporated onto the SiO₂ window with a shadow mask. The gold strips enable us to measure the conductance of the graphene electrode and manipulate electrochemical potentials between the graphene and a reference electrode. Besides, the gold strips also serve as the reference sample to generate a stable and precise reference phase.

Graphene electrode preparation

We use CVD-grown monolayer graphene on copper foil to prepare the SiO₂-supported graphene electrode by means of the polymer-assisted wet transfer technique.⁶¹ In brief, the copper foil was spin-coated with CAB (30 mg mL⁻¹, dissolved in ethyl acetate) at 1000 rpm for 10 seconds, followed by 4000 rpm for 60 seconds, and then baked at 180 °C for 3 minutes. After cooling down to room temperature, the copper foil/CAB was placed into an HCl/H₂O₂/H₂O mixture solution (volume ratio, 1 : 1 : 10) for 60 seconds to remove the graphene layer grown on the backside of the copper foil. After being rinsed with deionized water, the copper foil on the film was then etched away in a 0.1 M ammonium persulfate aqueous solution. Subsequently, the obtained CAB–graphene films were rinsed in deionized water several times to remove residual chemical species, and then were transferred onto the SiO₂ substrate. Two gold strips were pre-deposited onto the SiO₂ substrate before the transfer, and the CAB–graphene film was put in contact with the gold strips for electrical connection. The samples were dried for more than 12 hours at 110 °C in a vacuum (∼1 mbar) to remove residual water. Finally, the CAB layer on graphene was dissolved in acetone. This method allows us to obtain complete large-area monolayer graphene electrodes up to a centimeter scale.¹⁰ Such a large-area graphene electrode is useful for HD-SFG measurements because the laser spot size is usually hundreds of micrometers.

Spectro-electrochemical cell

We used a homemade electrochemical flowing cell for the electrochemical HD-SFG and Raman measurements. A schematic diagram of the electrochemical flowing cell is depicted in Fig. 1a. The cell mainly consists of two rectangular polytetrafluoroethylenes (PTFE) parts, the top clamp part, and the bottom flowing channel (12 × 3 × 3 mm³) part. The top clamp has an opening of ∼16 mm in diameter for the light beam paths. The bottom part has four round holes on the four side walls. Two for inlets and outlets of electrolyte solution (10 mM and 100 mM NaClO₄) while another two for insertion of the RE and the CE. The monolayer graphene electrode on a SiO₂ substrate and an O-ring were then sandwiched between the top and the bottom PTFE parts. The O-ring was used to create a seal between the electrolyte solution and the graphene electrode to avoid contact between the solution and the two gold strips. The base and clamp parts were cleaned with piranha solution before use. We used a three-electrode setup for the potential control. In this setup, the graphene electrode serves as the WE. As the CE and RE, gold wire and hydrogen-loaded palladium wire (Pd/H₂) wires were used. These three electrodes were connected to an electrochemical workstation (Metrohm Autolab PGSTAT302).

Raman measurements

The Raman spectra were recorded with a WITec confocal Raman spectrometer (alpha 300 R, ×10 objective) with 600 grooves per mm grating, 532 nm laser, 2 mW power, and 10 s integration time.

HD-SFG measurements

HD-SFG measurements were performed on a non-collinear beam geometry with a Ti:sapphire regenerative amplifier laser system (Spitfire Ace, Spectra-Physics, centered at 800 nm, ∼40 fs pulse duration, 5 mJ pulse energy, 1 kHz repetition rate). A part of the output was directed to a grating-cylindrical lens pulse shaper to produce a narrowband visible pulse (10 μJ pulse energy, FWHM = ∼10 cm⁻¹), while the other part was used to generate a broadband infrared (IR) pulse (3.5 μJ pulse energy, FWHM = ∼530 cm⁻¹) through an optical parametric amplifier (Light Conversion TOPAS-C) with a silver gallium disulfide (AgGaS₂) crystal. The IR and visible beams were firstly focused into 200 nm-thick ZnO on a 1 mm-thick CaF₂ window to generate a local oscillator (LO) signal similar to ref. 62. Then these beams were re-focused by a two off-axis parabolic mirrors pair and overlapped spatially and temporally at the graphene/water interface. A fused silica glass plate with a 1.5 mm thickness was placed in the optical path for the LO signal between the two off-axis parabolic mirrors, allowing the phase modulation for the LO signal. The SFG signal from the sample interfered with the SFG signal from the LO, generating the SFG interferogram, which was then dispersed in a spectrometer (Shamrock 303i, Andor Technology) and detected by an EMCCD camera (Newton, Andor Technology). HD-SFG spectra were measured in an N₂ atmosphere to avoid spectral distortion due to water vapor. To avoid erroneous measurements due to the height change of the sample surface upon flowing electrolyte solutions, we used a height displacement sensor (CL-3000, Keyence). Each spectrum was acquired with an exposure time of 10 seconds and measured more than ten times on average. IR, visible, and LO beams were re-focused onto the graphene/water interface at the angles of incidence of 33°, 39°, and 37.6°, respectively. The measurements were performed at the ssp polarization combination, where ssp denotes s-polarized SFG, s-polarized visible, and p-polarized IR beams.

The complex-valued spectra of second-order nonlinear susceptibility (χ⁽²⁾) of the graphene/water interface samples were obtained via the Fourier analysis of the interferogram and normalization with that of the SiO₂/gold interface. The interferogram of the SiO₂/gold interface was collected at the gold strip region of the sample immediately before the sample measurement to ensure a precise and stable reference phase. The phase of the gold thin film is determined by measuring the O–H stretching Im(χ⁽²⁾) spectrum of the SiO₂-supported graphene/D₂O interface via normalization of the signal with that of SiO₂/gold. As D₂O does not have any vibrational response in this region, and its χ⁽²⁾ response arises solely from the interface,⁶³ we can determine the phase of gold based on the fact that the Im(χ⁽²⁾) spectrum of the SiO₂-supported graphene/D₂O interface shows a flat zero line.

Author contributions

Y. W. prepared and characterized the samples for Raman and electrochemical measurements. Y. W. performed the HD-SFG measurements and data analysis. Y. W., Y. N., and M. B. wrote and modified the manuscript. All authors discussed the results.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful for the financial support from the MaxWater Initiative of the Max Planck Society. Y. W. thanks the support from the China Scholarship Council. We thank Florian Gericke, Marc-Jan van Zadel, and the technical workshop at the Max Planck Institute for Polymer Research for excellent technical support. Open Access funding provided by the Max Planck Society.

Notes and references

1. Y. Liu, X. Dong and P. Chen, Chem. Soc. Rev., 2012, 41, 2283–2307.
2. F. Yavari and N. Koratkar, J. Phys. Chem. Lett., 2012, 3, 1746–1753.
3. A. Ambrosi, C. K. Chua, A. Bonanni and M. Pumera, Chem. Rev., 2014, 114, 7150–7188.
4. A. Ambrosi, C. K. Chua, N. M. Latiff, A. H. Loo, C. H. A. Wong, A. Y. S. Eng, A. Bonanni and M. Pumera, Chem. Soc. Rev., 2016, 45, 2458–2493.
5. T. F. Schranghamer, A. Oberoi and S. Das, Nat. Commun., 2020, 11, 5474.
6. H. Tian, W. Mi, X.-F. Wang, H. Zhao, Q.-Y. Xie, C. Li, Y.-X. Li, Y. Yang and T.-L. Ren, Nano Lett., 2015, 15, 8013–8019.
7. B. Liu, Z. Liu, I.-S. Chiu, M. Di, Y. Wu, J.-C. Wang, T.-H. Hou and C.-S. Lai, ACS Appl. Mater. Interfaces, 2018, 10, 20237–20243.
8. Y. Ohno, K. Maehashi, Y. Yamashiro and K. Matsumoto, Nano Lett., 2009, 9, 3318–3322.
9. A. Montenegro, C. Dutta, M. Mammetkuliev, H. Shi, B. Hou, D. Bhattacharyya, B. Zhao, S. B. Cronin and A. V. Benderskii, Nature, 2021, 594, 62–65.
10. Y. Wang, T. Seki, X. Liu, X. Yu, C.-C. Yu, K. F. Domke, J. Hunger, M. T. M. Koper, Y. Chen, Y. Nagata and M. Bonn, Angew. Chem., Int. Ed., 2023, 62, e202216604.
11. I. Ledezma-Yanez, W. D. Z. Wallace, P. Sebastián-Pascual, V. Climent, J. M. Feliu and M. T. Koper, Nat. Energy, 2017, 2, 17031.
12. Y.-H. Wang, S. Zheng, W.-M. Yang, R.-Y. Zhou, Q.-F. He, P. Radjenovic, J.-C. Dong, S. Li, J. Zheng, Z.-L. Yang, G. Attard, F. Pan, Z.-Q. Tian and J.-F. Li, Nature, 2021, 600, 81–85.
13. T. Cheng, L. Wang, B. V. Merinov and W. A. Goddard, J. Am. Chem. Soc., 2018, 140, 7787–7790.
14. S. Fleischmann, J. B. Mitchell, R. Wang, C. Zhan, D. Jiang, V. Presser and V. Augustyn, Chem. Rev., 2020, 120, 6738–6782.
15. C. Chen, Y. Wen, X. Hu, X. Ji, M. Yan, L. Mai, P. Hu, B. Shan and Y. Huang, Nat. Commun., 2015, 6, 6929.
16. J. B. Mitchell, W. C. Lo, A. Genc, J. LeBeau and V. Augustyn, Chem. Mater., 2017, 29, 3928–3937.
17. P. Xu, A. D. von Rueden, R. Schimmenti, M. Mavrikakis and J. Suntivich, Nat. Mater., 2023, 22, 503–510.
18. J. Chmiola, Science, 2006, 313, 1760–1763.
19. S. Boyd, K. Ganeshan, W.-Y. Tsai, T. Wu, S. Saeed, D. Jiang, N. Balke, A. C. T. van Duin and V. Augustyn, Nat. Mater., 2021, 20, 1689–1694.
20. D. Kim, E. Kim, S. Park, S. Kim, B. K. Min, H. J. Yoon, K. Kwak and M. Cho, Chem, 2021, 7, 1602–1614.
21. W. Kong, H. Li, K. Qiao, Y. Kim, K. Lee, Y. Nie, D. Lee, T. Osadchy, R. J. Molnar, D. K. Gaskill, R. L. Myers-Ward, K. M. Daniels, Y. Zhang, S. Sundram, Y. Yu, S. Bae, S. Rajan, Y. Shao-Horn, K. Cho, A. Ougazzaden, J. C. Grossman and J. Kim, Nat. Mater., 2018, 17, 999–1004.
22. B. Gaire, S. Singla and A. Dhinojwala, Nanoscale, 2021, 13, 8098–8106.
23. Y. Wang, T. Seki, X. Yu, C.-C. Yu, K.-Y. Chiang, K. F. Domke, J. Hunger, Y. Chen, Y. Nagata and M. Bonn, Nature, 2023, 615, E1–E2.
24. S. Hu, M. Lozada-Hidalgo, F. C. Wang, A. Mishchenko, F. Schedin, R. R. Nair, E. W. Hill, D. W. Boukhvalov, M. I. Katsnelson, R. A. W. Dryfe, I. V. Grigorieva, H. A. Wu and A. K. Geim, Nature, 2014, 516, 227–230.
25. S. Bukola, Y. Liang, C. Korzeniewski, J. Harris and S. Creager, J. Am. Chem. Soc., 2018, 140, 1743–1752.
26. J. Xu, H. Jiang, Y. Shen, X.-Z. Li, E. G. Wang and S. Meng, Nat. Commun., 2019, 10, 3971.
27. J. L. Achtyl, R. R. Unocic, L. Xu, Y. Cai, M. Raju, W. Zhang, R. L. Sacci, I. V. Vlassiouk, P. F. Fulvio, P. Ganesh, D. J. Wesolowski, S. Dai, A. C. T. van Duin, M. Neurock and F. M. Geiger, Nat. Commun., 2015, 6, 6539.
28. Y. R. Shen and V. Ostroverkhov, Chem. Rev., 2006, 106, 1140–1154.
29. M. Bonn, Y. Nagata and E. H. G. Backus, Angew. Chem., Int. Ed., 2015, 54, 5560–5576.
30. N. Ji, V. Ostroverkhov, C. S. Tian and Y. R. Shen, Phys. Rev. Lett., 2008, 100, 096102.
31. S. Yamaguchi and T. Tahara, J. Chem. Phys., 2008, 129, 101102.
32. T. Seki, X. Yu, P. Zhang, C.-C. Yu, K. Liu, L. Gunkel, R. Dong, Y. Nagata, X. Feng and M. Bonn, Chem, 2021, 7, 2758–2770.
33. Y.-C. Wen, S. Zha, X. Liu, S. Yang, P. Guo, G. Shi, H. Fang, Y. R. Shen and C. Tian, Phys. Rev. Lett., 2016, 116, 016101.
34. L. B. Dreier, Z. Liu, A. Narita, M.-J. van Zadel, K. Müllen, K.-J. Tielrooij, E. H. G. Backus and M. Bonn, J. Phys. Chem. C, 2019, 123, 24031–24038.
35. S. Nihonyanagi, J. A. Mondal, S. Yamaguchi and T. Tahara, Annu. Rev. Phys. Chem., 2013, 64, 579–603.
36. T. Ohto, H. Tada and Y. Nagata, Phys. Chem. Chem. Phys., 2018, 20, 12979–12985.
37. S. K. Reddy, R. Thiraux, B. A. Wellen Rudd, L. Lin, T. Adel, T. Joutsuka, F. M. Geiger, H. C. Allen, A. Morita and F. Paesani, Chem, 2018, 4, 1629–1644.
38. P. E. Ohno, H. Wang and F. M. Geiger, Nat. Commun., 2017, 8, 1032.
39. S. Pezzotti, D. R. Galimberti, Y. R. Shen and M.-P. Gaigeot, Phys. Chem. Chem. Phys., 2018, 20, 5190–5199.
40. F. Wei, S. Urashima, S. Nihonyanagi and T. Tahara, J. Am. Chem. Soc., 2023, 145, 8833–8846.
41. B. Rehl, E. Ma, S. Parshotam, E. L. DeWalt-Kerian, T. Liu, F. M. Geiger and J. M. Gibbs, J. Am. Chem. Soc., 2022, 144, 16338–16349.
42. C. T. Konek, M. J. Musorrafiti, H. A. Al-Abadleh, P. A. Bertin, S. T. Nguyen and F. M. Geiger, J. Am. Chem. Soc., 2004, 126, 11754–11755.
43. C.-J. Shih, M. S. Strano and D. Blankschtein, Nat. Mater., 2013, 12, 866–869.
44. K. A. Becraft and G. L. Richmond, Langmuir, 2001, 17, 7721–7724.
45. W. Stumm and J. J. Morgan, Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters, John Wiley & Sons, 2012.
46. J. D. Miller and J. B. Hiskey, J. Colloid Interface Sci., 1972, 41, 567–573.
47. S. Assemi, J. Nalaskowski, J. D. Miller and W. P. Johnson, Langmuir, 2006, 22, 1403–1405.
48. I. T. McCrum and M. Koper, Nat. Energy, 2020, 5, 891–899.
49. V. Grozovski, S. Vesztergom, G. G. Láng and P. Broekmann, J. Electrochem. Soc., 2017, 164, E3171.
50. G. Froehlicher and S. Berciaud, Phys. Rev. B, 2015, 91, 205413.
51. S. Das Sarma, S. Adam, E. H. Hwang and E. Rossi, Rev. Mod. Phys., 2011, 83, 407–470.
52. J. Yan, Y. Zhang, P. Kim and A. Pinczuk, Phys. Rev. Lett., 2007, 98, 166802.
53. J. Xia, F. Chen, J. Li and N. Tao, Nat. Nanotechnol., 2009, 4, 505–509.
54. S. Adam, E. H. Hwang, V. M. Galitski and S. D. Sarma, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18392–18397.
55. S. Kim, M.-J. Stébé, J.-L. Blin and A. Pasc, J. Mater. Chem. B, 2014, 2, 7910–7917.
56. M. C. O. Monteiro and M. T. M. Koper, Curr. Opin. Electrochem., 2021, 25, 100649.
57. S. Ong, X. Zhao and K. B. Eisenthal, Chem. Phys. Lett., 1992, 191, 327–335.
58. A. M. Darlington and J. M. Gibbs-Davis, J. Phys. Chem. C, 2015, 119, 16560–16567.
59. A. Myalitsin, S. Urashima, S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Phys. Chem. C, 2016, 120, 9357–9363.
60. Y. Ito, W. Cong, T. Fujita, Z. Tang and M. Chen, Angew. Chem., Int. Ed., 2015, 54, 2131–2136.
61. T. Hallam, N. C. Berner, C. Yim and G. S. Duesberg, Adv. Mater. Interfaces, 2014, 1, 1400115.
62. H. Vanselous and P. B. Petersen, J. Phys. Chem. C, 2016, 120, 8175–8184.
63. A. Adhikari, J. Chem. Phys., 2015, 143, 124707.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00107e

---