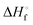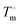Influence of solute association on the phase behavior of 12-hydroxystearic acid/n-alkane solutions†
Tzu-Yu
Lai‡
a,
Fardin
Khabaz
 ab and
Kevin A.
Cavicchi
ab and
Kevin A.
Cavicchi
 *a
*a
aSchool of Polymer Science and Polymer Engineering, University of Akron, Akron, OH 44325, USA. E-mail: kac58@uakron.edu
bDepartment of Chemical, Biomolecular, and Corrosion Engineering, University of Akron, Akron, OH 44325, USA
First published on 28th February 2023
Abstract
The phase behavior of 12-hydroxystearic acid (12-HSA) in even-numbered alkanes ranging from octane (C8) to hexatriacontane (C36) was measured by visual observation of liquid + solid to liquid and liquid–liquid to liquid cloud points and liquid + solid to liquid + liquid transitions. In general solid phases were stabilized to low concentration and higher temperature with increasing alkane length. Liquid–liquid immiscibility was observed in larger alkanes starting with octadecane. The liquidus lines of shorter alkanes (octane to hexadecane) showing only liquid to liquid + solid transitions were fit with an attenuated associated solution model based on the Flory–Huggins lattice model assuming that 12-HSA forms a carboxylic acid dimer over all concentrations investigated. The fit results show that 12-HSA forms associated structures with degrees of association ranging from 3.7–4.5 dimers in the neat 12-HSA. At low concentrations, the 12-HSA is dissociated into dimers, however the free energy cost of dissociation stabilizes the solid phase giving a sharp knee at low concentrations. The role of 12-HSA association in its phase behavior and gelation behavior are discussed. More broadly, the importance of solute association in small molecule organogelators and its potential as a molecular design parameter similar to other component thermodynamic parameters, such as melting temperature and heat of fusion, is discussed.
Introduction
Molecular organogelators are small molecules that gel or immobilize an organic fluid by their self-assembly into structure spanning, solid networks, at low concentrations. This field has grown rapidly in the past three decades producing a wide-range of chemically distinct organogelators.1–5 A large class of organogelators are molecular crystals that that gel a solution through nucleation and growth with preferential growth along a particular crystal axis to form three dimensional self-assembled fibrillar networks (SAFiNs).6,7 The reversible nature of the non-covalent interactions governing the SAFiN formation allows for stimuli-responsive properties, such as the sol–gel transition. While thermally responsive gels dominate, there are also examples of pH, light, anion/chemical, and mechano-responsive gels.8 This broad combination of chemical motifs and stimuli has led to their application as rheological modifiers, structure directing agents, and sensors in a range of fields including plastics processing, separations, drug delivery, cosmetics, and remediation of crude oil spills.9–13A long-standing challenge in the field of molecular organogels is the difficulty in predicting whether a molecule will gel a particular solvent.14 This is most vexing in systems where seemingly minor structural variations made in either the solvent or the organogelator lead to large variations in the gel properties.15–17 These cases highlight the complex interdependence of the solvent–solvent, solvent–organogelator, and organogelator–organogelator interactions on the structure of the organogelator, where it is difficult to independently tune these interactions and it therefore is an active area of study.3,18 For example, there has been good success in correlating solvent parameters to gelation ability,19–22 most notably with Hansen solubility parameters to map gelation spheres.23–28
Another avenue of study of the structure–property relationships of organogelators is the measurement of the phase behavior of different organogelator solutions.29 For thermally-responsive organogels that form through the nucleation and growth of organogel fibers, strong correlations have been observed among the gel properties (e.g. gel transition temperature, minimum gelation concentration), the phase behavior (e.g. solubility or liquidus curve, miscibility gap), and the processing conditions (e.g. cooling rate and extent of undercooling/supersaturation).30–40 In particular, conditions that produce sufficient undercooling30 (or supersaturation36) at low organogelator concentration and direct liquid to liquid + solid phase transitions tend to favor gelation for “good” organogelators. Understanding the thermodynamics governing the phase behavior of an organogel provides a means to link the physical properties of the solution and the gel performance.
The focus of this paper is the solution phase behavior of R-12-hydroxystearic acid (12-HSA, Fig. 1) in a series of n-alkanes and the relationship to its gelation behavior. 12-HSA is known as an excellent organogelator that has a propensity to form fibrillar networks.41–50 It is also an inexpensive, bio-derived material produced from the hydrogenation of rincinoleic acid from castor oil.51 It has been used as an organogelator in a number of fields, such as food science,52 cosmetics,53 drug delivery,54,55 and oil spill remediation.56 An interesting property of 12-HSA solutions is the formation of aggregated or associated structures in the sol state, which has been observed in both experiment and simulation. The fitting of carbon NMR data of 12-HSA solutions in benzene by Sakurai et al. showed an equilibrium between monomer, dimer, and tetramer in the solution state.48 Simulation of 12-HSA has shown that stable cyclic structures are formed from the dimerization of the acid head group and cyclization of six hydroxyl groups.57,58 12-HSA solutions should be associating solutions where the degree of association of 12-HSA with temperature and concentration influences the phase behavior and therefore should be a key factor in its gelation ability.59,60 There have been numerous reports focusing on the influence of solvent–organogelator interactions in 12-HSA systems and the ability of polar solvent to disrupt organogelator–oganogelator interaction is recognized.61–63 However, to our knowledge, besides the work of Sakurai et al., there are no direct investigations of the role solution state gelator–gelator interactions play in the solution phase behavior and gelation ability of 12-HSA.
As a model system, the phase behavior of 12-HSA in n-alkanes ranging from octane to hexatriacontane was investigated. Two reasons this system was chosen were, first, aliphatic alkanes do not have any functional groups that strongly compete with the hydrogen bonding in 12-HSA to limit concentration and solvent dependent solvent–gelator interactions. Second, the solubility parameter of n-alkanes varies over a small range, increasing at low carbon lengths and leveling off at higher carbon lengths, while the molar volume systematically increases (Fig. S1, ESI†). Consequently, this system is an excellent choice for isolating the effect of gelator–gelator interactions on the phase behavior of 12-HSA solutions.
The structure of this paper is as follows. First, the measurements of the phase behavior and the construction of phase diagrams are presented. Second, the liquidus lines are fit using an attenuated associating solution model that allows the variation of the associated structure of 12-HSA vs. concentration in solution to be assessed. A significant finding is that gelator association is a relevant factor at low concentrations where 12-HSA is used as an organogelator. Third, the role of gelator–gelator association in 12-HSA solutions is more broadly discussed based on the associated solution model.
Experimental section
Materials
Octane (>98% Alfa Aesar), decane (>99% TCI), dodecane (>99% TCI), hexadecane (>98% TCI), tetradecane (>99% TCI), hexadecane (≥98.5% Fisher Scientific), octadecane (99% Alfa Aesar), eicosane (>98% TCI), docosane (99% Acros), tetracosane (99% Aldrich), octacosane (99% Aldrich), dotriacontane (97% Aldrich), and hextriacontane (98% Aldrich) were used without further purification. 12-Hydroxystearic acid (12-HSA) with purity above 80.0% was purchased from TCI and further purified through repeated process of recrystallization by slowly cooling in hexane/ethyl acetate (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v
1 v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) cosolvent.41,64 Stearic acid (>98% TCI) was also used as received. Solution samples were prepared by weighing out appropriate amounts of 12-HSA or stearic acid and solvent. The volume fractions of samples were calculated by converting the mass of each component to its volume using component volume = (mass)(molar volume)/(molar mass) where the molar volume was calculated using group contribution method.65
v) cosolvent.41,64 Stearic acid (>98% TCI) was also used as received. Solution samples were prepared by weighing out appropriate amounts of 12-HSA or stearic acid and solvent. The volume fractions of samples were calculated by converting the mass of each component to its volume using component volume = (mass)(molar volume)/(molar mass) where the molar volume was calculated using group contribution method.65
Differential scanning calorimetry (DSC)
DSC measurements were made using a DSC 8500 (PerkinElmer) under nitrogen atmosphere. Samples (∼2–6 mg) were prepared and sealed in hermetic pans (DSC Consumables, Inc). Samples were initially cooled to 20 °C for 2 min then heated at a rate of 2 °C min−1 to 100 °C. The molar heat of fusion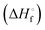 of pure 12-HSA was determined calorimetrically by peak integration on cooling at 5 °C min−1. Melting points were taken from the endpoint of the melting endotherm.
of pure 12-HSA was determined calorimetrically by peak integration on cooling at 5 °C min−1. Melting points were taken from the endpoint of the melting endotherm.
Tube inversion
Tube inversion measurements were used to measure the sol–gel transition temperature where the sample no longer was able to support its own weight when inverted.66 Additionally, the solubility was measured by recording the temperature at which the sol sample became optically clear. In the case of liquid–liquid phase separation, the cloud point (Tcp) was determined as the temperature at which the sample became optically clear. To prepare samples for measurement, ca. 1.5 g of 12-HSA and solvent were loaded in 8 mL vials. Solutions were heated to 130 °C to form transparent and homogeneous solution, which were then air-cooled down to ambient temperature at the workbench.The as-prepared samples were heated using a hot plate equipped with an aluminum heating block which can hold up to 40 samples at a time. Temperature ramps were started from 25 °C, at steps of 1 °C with annealing for 20 min after each temperature change. After annealing, sample vials were tilted to a 90° angle. The temperature at which flow behavior was first observed was recorded at Tgel. Two phenomena occurred above Tgel. Either the sample gradually turned optically transparent from the dissolution of the 12-HSA crystals or the sample underwent a transition to a liquid–liquid phase separated structure with droplets of one phase in the matrix of the second phase, followed by a transition to an optically transparent solution. The temperature where the solution turned homogeneously transparent was recorded as the cloud point, Tcp. The temperature where liquid–liquid phase separated was first observed was recorded as TL–L. Each sample was tested through three heating ramps and the average values for each sample are presented. Identical sample preparation methods and tube inversed measurements were applied to solutions of stearic acid (SA) in dodecane.
Cloud point apparatus
An OptiMelt MPA100 (Stanford Research System) was used to measure the melting point of the samples where a sharp increase in the optical transparency was recorded. To prepare samples a hot, transparent solution was transferred into a capillary tube and air-cooled down to the room temperature. In the instrument, samples were heated at a rate of 2 °C min−1 from ambient temperature to 120 °C.Results and discussion
Phase diagrams of 12-HSA/alkane solutions
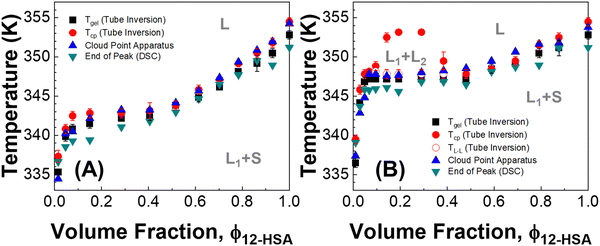
Three methods were used to determine the phase diagrams of 12-HSA in different n-alkanes, visual observations during tube inversion measurements, automated cloud point measurements, and differential scanning calorimetry (DSC). Fig. 2 displays the transitions temperatures recorded as function of volume fraction of 12-HSA in two solutions, 12-HSA/decane and 12-HSA/octadecane. Tgel was measured by tube inversion as the temperature at which the sample exhibited flow when tilted 90° from vertical. Technically, gels are only formed at low concentration of 12-HSA where the sample is primarily composed of the solvent. Rather than try to differentiate the samples based on this criterion Tgel is used to delineate the rheological observation of the transition where the self-supporting solid structure of the 12-HSA disappears. Tcp is the cloud point temperature above which the sample was homogeneous and optically transparent as determined either by visual inspection or by the cloud point apparatus. Tm is the endpoint of the endothermic melting peak measured by DSC, corresponding to the dissolution of the 12-HSA crystals. TL–L is the temperature above which only a two-phase liquid was observed by visual inspection. In decane, these measurements gave qualitatively similar curves, corresponding to the liquidus line separating the one phase liquid from the two phase solid + liquid regions. While there is some spread in the temperatures among the different curves it is only ca. 3–6 °C, with the largest spread at small 12-HSA volume fractions. The Tgel curve is generally lower than the others, which is to be expected as the mechanical failure of the sample would occur during partial dissolution of the 12-HSA. The Tcp agree well with that gathered from the cloud point apparatus (raw data in Fig. S2, ESI†) and visual inspection.In the 12-HSA/octadecane system a liquid–liquid miscibility gap is observed as an additional feature. The cloud-point measurement of the miscibility gap is only observed with the visual cloud point measurement. In the cloud point apparatus, the detected cloud point corresponds to the melting of the solid 12-HSA. Under the miscibility gap, the transition temperature for 12-HSA is roughly invariant as would be expected for a monotectic phase diagram. As the visual results obtained during tube inversion measurements are consistent with these other measurements and offer measurements of both dissolution and liquid–liquid phase separation in a single experiment, this method was used as the primary route to determine the phase diagrams in the other 12-HSA/n-alkane systems.
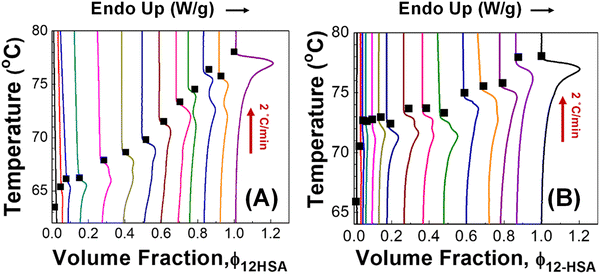
The DSC heating traces of samples prepared in decane and octadecane are shown in Fig. 3. In decane, multiple endothermic peaks are observed above a volume fraction of ϕ12-HSA = 0.14. The most likely origin for this phenomenon is a solid–solid transition Previously, transition between different 12-HSA polymorphs were observed by Takeno and co-workers is a study of the phase behavior of 12-HSA in phenyl methyl silicone.67 Using small angle X-ray scattering and polarized optical microscopy, three crystal forms were identified (form I, form II, and form III). An enantiotropic Gibbs free energy profile was proposed where form I is thermodynamically stable at low temperature (<ca. 70 °C) and form II is stable at higher temperature (>ca. 70 °C). Form III was proposed to be unstable at any temperature. The energy barrier between form III and form I was smaller than the energy barrier between form I and form II, which may explain its metastable formation. Similar behavior was observed in 12-HSA/ionic liquid solutions where the same three crystal forms was observed and the solid–solid transition between form I and form II was observed at 70–75 °C.68
Similar DSC behavior to the 12-HSA/decane solution is observed in the 12-HSA/octadecane DSCs. It appears that the solid–solid transition temperature is below the monotectic temperature (Tmt ≈ 75 °C). Therefore, there should be an additional peak in the DSC trace at compositions to the right of the monotectic point due to melting at the monotectic temperature and the liquidus temperature.69–71 Based on the composition where single melting peaks first appear on moving from high to low composition, the low temperature stable phase of 12-HSA appears to be stable below 66 °C in decane and 72 °C in octadecane. One source for this temperature difference is kinetic hindrance in the solid–solid transition as measured by DSC.72 Therefore, the lower solubility of 12-HSA in octadecane compared to decane may result in higher kinetic hindrance and a higher observed solid–solid transition temperature. For example, in stearic acid, which is structurally similar to 12-HSA, similar solid–solid transition temperature was measured in decane, methanol, and butanone by solubility measurements, but a higher transition temperature was measured by DSC in decane.73,74
The exact origin of these solid–solid transitions is not clear. As detailed in a recent review by Guenet, solid–solid transitions can be categorized into two main types.7 In the first case, the solid–solid transition occurs due to the formation of an alloy or a molecular compound below the peritectic temperature. In the absence of a solid solution phase containing both the solvent and solute at higher composition, this would result in an invariant melting temperature with solute composition. If this occurred in the phase diagrams shown in Fig. 3, they would be consistent with the formation of an incongruently melting compound where at solute concentrations below the stoichiometric composition of the compound this crystal melts to form a solid phase plus a liquid phase rather than melting directly to the liquid in the case a congruently melting compound. In the second case, there is a metatectic transition where the solid undergoes a solid–solid phase transition at the metatectic temperature. This would also give an invariant solid–solid transition temperature, however the likely presence of a solid-solution at higher solute concentration would give a solidus line below the liquidus resulting in the melting temperature increasing with solute composition and three melting endotherms could be detected on heating. At low temperatures below the peritectic and metatectic temperatures, and therefore low solute concentration, the liquid would directly solidify into the molecular compound or second solid phase, different from the bulk crystal stable just below the neat compound's melting temperature.
More detailed DSC, optical microscopy and potentially scattering measurements would be needed to investigate the solid–solid phase transitions more fully to delineate between the type of solid–solid transition and determine the solidus line.75,76 The thermodynamic modeling in the next section assumes a simpler system where the solid–solid transitions are not considered. The implications of this approximation on the fitting results are discussed.
Fig. 4 displays the liquidus lines and miscibility gaps measured by visual inspection of 12-HSA in alkanes ranging from octane to hexatriacontane. A variation is observed in the positions of the miscibility gap and liquidus line with the length of the alkanes (carbon number, n). The plateau temperature at intermediate concentration moves up with an increasing length of the alkane. At octadecane, a miscibility gap appears, with a composition invariant melting temperature beneath it. This miscibility gap grows as the length of the alkane increases. As the solubility parameter difference between the alkanes and 12-HSA (δ12-HSA = 18.1 MPa1/2)61 decreases with increasing alkane length (see Fig. S1, ESI†), the increasing liquid–liquid immiscibility is likely driven by the lower entropy of mixing with increasing alkane length, such as is observed in polymer solutions. Interestingly the miscibility gap is asymmetric with its maximum at ϕ12-HSA < 0.5. This is similar to what is observed in polymer solutions and associated solutions where the molar volume of the solute is greater than the solvent.77 However, it is difficult to fit the binodal line defining the miscibility gap analytically. Therefore more quantitative investigation of the phase behavior focuses on the solutions in hexadecane and shorter alkanes that do not show liquid–liquid phase separation above the liquidus line.
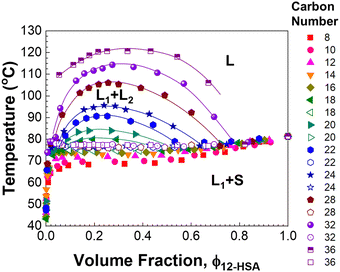 | ||
| Fig. 4 Phase diagram of 12-HSA/n-alkanes mixtures (n = 8–36) measured by tube inversion. Solid symbols indicate the phase transition from two components (solid–liquid or liquid–liquid) to one component, and open symbols indicate the solid–liquid to liquid–liquid phase transition. The solid lines on the binodal are guides to the eye. The 12-HSA/dodecane data was previously reported in ref. 29. Adapted with permission from ref. 29. Copyright 2018 American Chemical Society. | ||
Solution model fitting of the liquidus line
An approach to further investigate the solution state structure of 12-HSA is to fit the liquidus lines to a thermodynamic solution model. The liquidus line separates the pure liquid phases from the mixed liquid and solid phases. At the temperatures and compositions on the liquidus line the chemical potential of 12-HSA is equal in the liquid and solid phase. Assuming that 12-HSA forms pure crystals in the solid-state (i.e. no solid solution phase), the enthalpy and entropy of fusion are not temperature dependent, the interfacial tension between the liquid and solid phases is small, the crystals are large, and the crystals form the same polymorph as the neat 12-HSA, the chemical potential of the liquid at composition ϕ12-HSA, μ12-HSA(l) is equal to the chemical potential of the pure solid, , taken as the standard state of the solid. The difference in the chemical potential between the 12-HSA in the liquid at composition, ϕ12-HSA, μ12-HSA(l), and the neat 12-HSA liquid,
, taken as the standard state of the solid. The difference in the chemical potential between the 12-HSA in the liquid at composition, ϕ12-HSA, μ12-HSA(l), and the neat 12-HSA liquid,  , taken as the standard state, is,
, taken as the standard state, is,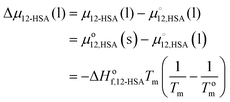 | (1) |
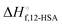 is the heat of fusion of the neat 12-HSA, Tm is the melting point of 12-HSA at composition ϕ12-HSA, and
is the heat of fusion of the neat 12-HSA, Tm is the melting point of 12-HSA at composition ϕ12-HSA, and 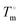 is the melting point of the neat 12-HSA.78
is the melting point of the neat 12-HSA.78
This chemical potential difference, Δμ12-HSA(l), may also be found from the free energy of mixing of the one-phase liquid. As it is assumed that the 12-HSA molecules can associate through the hydrogen bonding of carboxylic acid groups to form dimers and the alcohol units to form cyclic structures an associating solution model should be used for the free energy of mixing. The lattice model used for an associating solution was first derived by Flory for treating a polymer solution with a molecular weight dispersity79 and was applied to alcohol–hydrocarbon mixtures.80 More recently, this model was applied to the solubility of asphaltenes in oil, which has some similarity to 12-HSA/alkane systems, motivating the use of this model.77,81–83 While the main equations are discussed below, the full derivation of this model following previous references is given in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77,79–81,84 For solutions where 12-HSA forms associated aggregates in a non-associating solvent, Δμ12-HSA(l) is given by,
77,79–81,84 For solutions where 12-HSA forms associated aggregates in a non-associating solvent, Δμ12-HSA(l) is given by,
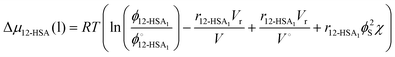 | (2) |
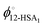 is the volume fraction of 12-HSA monomer in the neat 12-HSA liquid, r12-HSA1 is the ratio of the molar volume of the 12-HSA monomer, V12-HSA1 to a reference lattice cell volume, Vr, V is the volume of 1 true mole of solution, V° is the molar volume of the neat 12-HSA liquid, ϕs is the volume fraction of the solvent, and χ is the Flory–Huggins interaction parameter. To compare eqn (1) and (2), the standard state,
is the volume fraction of 12-HSA monomer in the neat 12-HSA liquid, r12-HSA1 is the ratio of the molar volume of the 12-HSA monomer, V12-HSA1 to a reference lattice cell volume, Vr, V is the volume of 1 true mole of solution, V° is the molar volume of the neat 12-HSA liquid, ϕs is the volume fraction of the solvent, and χ is the Flory–Huggins interaction parameter. To compare eqn (1) and (2), the standard state,  , is the pure 12-HSA liquid. 12-HSA is a supramolecular polymer with a molecular weight distribution with an average degree of association. On mixing with the solvent, the degree of association of 12-HSA will shift with temperature and composition to minimize the free energy. The first three terms in the parentheses on the right-hand side of eqn (2) describe the partial molar entropy of mixing and the partial molar free energy change from breaking the hydrogen bonds. It should be noted that the composition is expressed in terms of the monomer volume fraction rather than the 12-HSA volume fraction. This simplification is allowed from the results of Prigogine where the chemical potential of component A (μA) is equal to the chemical potential of its monomer (μAi).85 The last term on the right hand side describes the non-specific enthalpic interactions between the liquid 12-HSA and solvent using the standard χ parameter from the Flory–Huggins model given by,
, is the pure 12-HSA liquid. 12-HSA is a supramolecular polymer with a molecular weight distribution with an average degree of association. On mixing with the solvent, the degree of association of 12-HSA will shift with temperature and composition to minimize the free energy. The first three terms in the parentheses on the right-hand side of eqn (2) describe the partial molar entropy of mixing and the partial molar free energy change from breaking the hydrogen bonds. It should be noted that the composition is expressed in terms of the monomer volume fraction rather than the 12-HSA volume fraction. This simplification is allowed from the results of Prigogine where the chemical potential of component A (μA) is equal to the chemical potential of its monomer (μAi).85 The last term on the right hand side describes the non-specific enthalpic interactions between the liquid 12-HSA and solvent using the standard χ parameter from the Flory–Huggins model given by,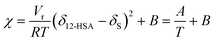 | (3) |
Combining eqn (1) and (2) and rearranging gives an equation for the liquidus line as,
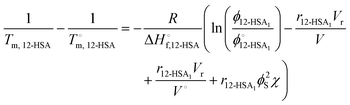 | (4) |
To fit the experimental liquidus lines a specific association model is needed for the variation of ϕ12-HSA1vs. ϕS and the value of 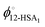 . A standard model is a continuous association model where the association of a monomer A with an aggregate of degree of polymerization i is described as an equilibrium reaction,77
. A standard model is a continuous association model where the association of a monomer A with an aggregate of degree of polymerization i is described as an equilibrium reaction,77
| CAi + CA1⇌CAi+1 | (5) |
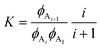 | (6) |
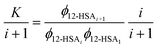 | (7) |
This equation gives a general equation for ϕ12-HSAi in terms of the equilibrium constant and 12-HSA monomer concentration as,
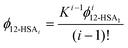 | (8) |
The overall volume fraction of 12-HSA is,
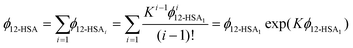 | (9) |
Eqn (9) allows the second and third terms in the parentheses on the right-hand side of eqn (4) to be written in terms of K, ϕ12-HSA1, and 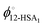 as,
as,
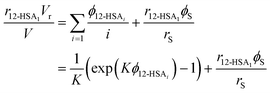 | (10) |
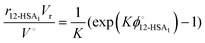 | (11) |
Substituting eqn (10) and (11) into eqn (4) gives,
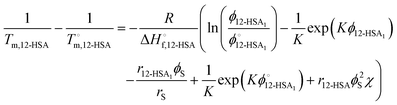 | (12) |
 | (13) |
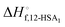 was also calculated using the moles of 12-HSA dimer
was also calculated using the moles of 12-HSA dimer 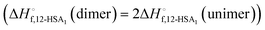 . This is driven by literature reports that the equilibrium constant for carboxylic acid dimers (e.g. 3200 L mol−1 acetic acid in hexane at 25 °C)87 is much greater than that of alcohol dimers (12.5 L mol−1 for 1-hexanol in alkane at 25 °C).88 Therefore, by assuming that 12-HSA forms dimers over the entire concentration range, the attenuation model captures the variation in alcohol association with concentration. This assumption was tested by measuring the liquidus line of stearic acid in dodecane and fitting Tmvs. the volume fraction of stearic acid assuming the stearic acid was a dimer over the entire concentration range with B as the only fitting parameter. The stearic acid fitting is shown in the ESI† (Fig. S3). A reasonable fit is obtained with B = 0. The fit overpredicts the melting point at the lowest concentration by ca. 5 K. We believe this is mostly due to the uncertainty in the solubility limit at this low temperature, rather than a low equilibrium constant for dimerization. The fitting constants are listed in Table 1. The fits for the 12-HSA data are shown in Fig. 5A (ϕ12-HSAvs. Tm) and Fig. 5B (ln
. This is driven by literature reports that the equilibrium constant for carboxylic acid dimers (e.g. 3200 L mol−1 acetic acid in hexane at 25 °C)87 is much greater than that of alcohol dimers (12.5 L mol−1 for 1-hexanol in alkane at 25 °C).88 Therefore, by assuming that 12-HSA forms dimers over the entire concentration range, the attenuation model captures the variation in alcohol association with concentration. This assumption was tested by measuring the liquidus line of stearic acid in dodecane and fitting Tmvs. the volume fraction of stearic acid assuming the stearic acid was a dimer over the entire concentration range with B as the only fitting parameter. The stearic acid fitting is shown in the ESI† (Fig. S3). A reasonable fit is obtained with B = 0. The fit overpredicts the melting point at the lowest concentration by ca. 5 K. We believe this is mostly due to the uncertainty in the solubility limit at this low temperature, rather than a low equilibrium constant for dimerization. The fitting constants are listed in Table 1. The fits for the 12-HSA data are shown in Fig. 5A (ϕ12-HSAvs. Tm) and Fig. 5B (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ12-HSAvs. 1/Tm), K and B are plotted in Fig. 5C. The number average degree of association of the 12-HSA dimers is given by,77
ϕ12-HSAvs. 1/Tm), K and B are plotted in Fig. 5C. The number average degree of association of the 12-HSA dimers is given by,77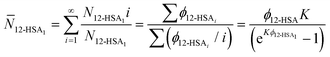 | (14) |
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 12-HSA1vs. ϕ12-HSA is plotted in Fig. 5D.
12-HSA1vs. ϕ12-HSA is plotted in Fig. 5D.
| Compound | δ (MPa1/2) | V (cm3 mol−1) | (kJ mol−1) | (K) | M (g mol−1) |
|---|---|---|---|---|---|
| a Previously reported values for all compounds except tetradecane, which was calculated by the group contribution method using the values of Fedors.61,65 b Calculated by group contribution methods using the values of Fedors.65 c Previously reported values measured by DSC on heating for moles of molecules (i.e. unimers).35 d Measured by visual cloud point measurement. | |||||
| Octane | 15.5 | 163.6 | — | — | 114.23 |
| Decane | 15.7 | 195.8 | — | — | 142.28 |
| Dodecane | 16.0 | 228.0 | — | — | 170.33 |
| Tetradecane | 16.2 | 260.2 | — | — | 198.39 |
| Hexadecane | 16.3 | 292.4 | — | — | 226.44 |
| 12-HSA | 18.1 | 312.5 | 50.45 | 354.5 | 300.48 |
| Stearic acid | 17.5 | 319.6 | 64.28 | 344.2 | 284.48 |
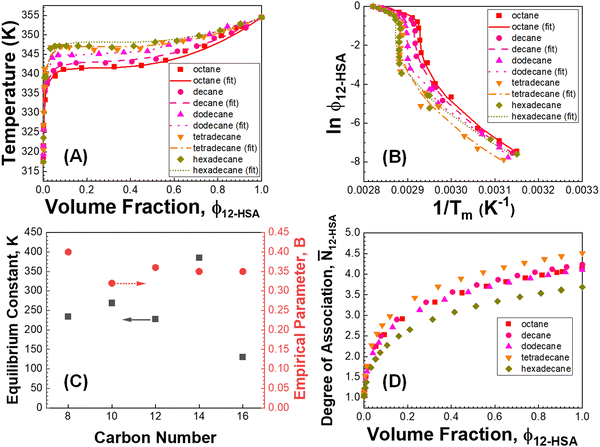 | ||
| Fig. 5 (A and B) Fitting results of 12-HSA alkane solutions. (C) Fitting parameters vs. the number of backbone carbons in each alkane. (D) The degree of association of 12-HSA dimers vs. 12-HSA volume fraction in different alkanes. The 12-HSA/dodecane data in (A) was previously reported in ref. 29. Adapted with permission from ref. 29. Copyright 2018 American Chemical Society. | ||
The fits of the liquidus line are best for the shorter alkanes (octane, decane and dodecane). In tetradecane and hexadecane the liquidus line has a sinusoidal shape at intermediate concentration that is not captured as well with this fitting model. As the molar volume of the solvent increases, its contribution to the entropy of mixing decreases, which magnifies the contributions of the 12-HSA to liquidus line. Therefore, the model is most challenged in these larger alkanes. More exact models could be used, for example using separate equilibrium constants for the carboxylic acid dimer, alcohol dimer and cyclic alcohol polymer.88 However, the increased number of fitting constants makes it more difficult to find a unique local minima and are best applied when associated structures and equilibrium constants can be independently measured, such as by FTIR spectroscopy.88 Three other simplifying assumptions of these fit are, first, the temperature dependence of K is not accounted for and therefore the fits give an average K over the temperature range. Second, the polymorph formation at low concentration is ignored. A lower value of  , a higher value of
, a higher value of 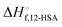 , and potentially an additional interaction parameter is needed in this region where the lower melting point, higher heat of fusion polymorph is stable. The model assuming one solid polymorph is formed therefore likely underpredicts the liquidus line at lower 12-HSA concentration. It is possible that the molecular compound formation is more favorable in longer alkanes giving rise to more fitting error. Third, solid solution formation at high 12-HSA concentration would result in a solidus line below the liquidus line. This would introduce additional terms into eqn (13) due to the free energy of mixing in the solid solution that depend on the composition of the solidus line at the same temperature as the liquidus line and potentially a second interaction parameter between the liquid and solid phases.89,90 As the solidus line is likely much steeper than the liquidus line, it would have a smaller composition variation, so that it could potentially be approximated as an additional constant term in eqn (13), which would be similar to allowing
, and potentially an additional interaction parameter is needed in this region where the lower melting point, higher heat of fusion polymorph is stable. The model assuming one solid polymorph is formed therefore likely underpredicts the liquidus line at lower 12-HSA concentration. It is possible that the molecular compound formation is more favorable in longer alkanes giving rise to more fitting error. Third, solid solution formation at high 12-HSA concentration would result in a solidus line below the liquidus line. This would introduce additional terms into eqn (13) due to the free energy of mixing in the solid solution that depend on the composition of the solidus line at the same temperature as the liquidus line and potentially a second interaction parameter between the liquid and solid phases.89,90 As the solidus line is likely much steeper than the liquidus line, it would have a smaller composition variation, so that it could potentially be approximated as an additional constant term in eqn (13), which would be similar to allowing 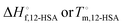 to be used as a fitting term. The value of the lattice model is in finding reasonable agreement to the data to allow interpretation of the different component contributions to the phase behavior, where gross disagreement with the experimental and fit curves indicate more complexity and the need for less simplifying assumptions and a more complex model. The good agreement of the fits with the data, especially in shorter alkanes, show that the model is adequate description of the solution behavior.
to be used as a fitting term. The value of the lattice model is in finding reasonable agreement to the data to allow interpretation of the different component contributions to the phase behavior, where gross disagreement with the experimental and fit curves indicate more complexity and the need for less simplifying assumptions and a more complex model. The good agreement of the fits with the data, especially in shorter alkanes, show that the model is adequate description of the solution behavior.
Examining the plots in Fig. 5D, the average degree of association at ϕ12-HSA = 1 ranges from 3.7–4.5, with excellent agreement between octane (4.1) decane (4.2) and dodecane (4.1) with more variation in tetradecane (4.5) and hexadecane (3.7) in-line with fitting results. This an excellent order of magnitude agreement with the previous work of Gordon et al. showing 12-HSA dimers forms six-member rings,57 and the work of Sakurai that fit the association of 12-HSA in benzene to a monomer, dimer, tetramer model.91 In addition, the previous fitting of alcohol alkane solutions showed a degree of association ranging from 3–5 with lower degree of association for secondary alcohols compared to primary alcohols.88 At lower concentrations of 12-HSA in the concentration range where gelation is typically studied the alcohol groups are not strongly associated, but the 12-HSA still primarily exist as carboxylic acid dimers based on the fitting model. An important feature of the association model is that the dissociation of the alcohol groups at low concentrations contributes to a higher entropy of mixing and stabilizes the liquid, there is also the free-energy cost of dissociation, which favors crystallization. This is the topic of the next section.
Role of self-association in 12-HSA solution phase behavior
The influence of the self-association of the 12-HSA is visualized in Fig. 6A by plotting the predicted Tmvs. ϕ12-HSA using eqn (13) for the 12-HSA/octane solution for B = 0.4 and K = 234 (original fit), 10 and 0.01 and the case where K = 0.01 and the 12-HSA monomer is assumed to a single 12-HSA molecule (i.e. 12-HSA unimer) with half the molar volume and half the heat of fusion of the 12-HSA dimer. In Fig. 6B, ϕ12-HSA1vs. ϕ12-HSA is plotted. In the case of K = 0.01, ϕ12-HSA1 = ϕ12-HSA over the entire concentration range. Going from the 12-HSA unimer to the dimer at K = 0.01 to higher values of K, the liquidus line shows a more persistent plateau at lower concentrations with a sharper knee where the melting point drops off at low concentrations. Therefore, it is clear that even though the degree of association is low at low concentrations solute association still significantly influences the phase behavior. This also can be seen by examining eqn (13) where K and are found in two concentration independent terms in the denominator (second and third terms). These terms are both negative and therefore act to increase Tm. They have a similar effect of a high bulk melting temperature,
are found in two concentration independent terms in the denominator (second and third terms). These terms are both negative and therefore act to increase Tm. They have a similar effect of a high bulk melting temperature,  , which also is in a concentration independent term in the denominator.
, which also is in a concentration independent term in the denominator.
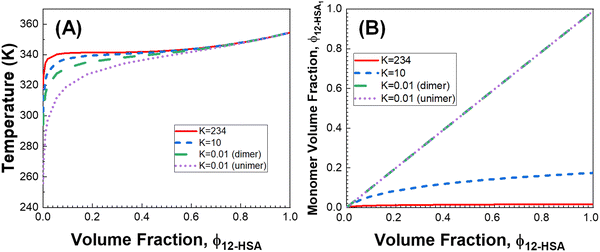 | ||
Fig. 6 (A) Predicted liquidus lines for 12-HSA in octane at K = 234, 10, and 0.01 for 12-HSA dimers and K = 0.01 for a 12-HSA unimer using eqn (13) with B = 0.4, 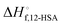 = 1 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 00 00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 J mol−1 (dimer) and 50 900 J mol−1 (dimer) and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 J mol−1 (unimer), V12-HSA = 625 cm3 mol−1 (dimer) and 312.5 cm3 mol−1 (unimer), Vs = 163.6 cm3 mol−1, Vr = 163.6 cm3 mol−1. (B) Monomer volume fraction (ϕ12-HSA1) vs. 12-HSA volume fraction for the predicted liquidus lines shown in (A). 450 J mol−1 (unimer), V12-HSA = 625 cm3 mol−1 (dimer) and 312.5 cm3 mol−1 (unimer), Vs = 163.6 cm3 mol−1, Vr = 163.6 cm3 mol−1. (B) Monomer volume fraction (ϕ12-HSA1) vs. 12-HSA volume fraction for the predicted liquidus lines shown in (A). | ||
A likely key to the ability of 12-HSA to efficiently gel a wide-range of solvents is the balance achieved in its physical properties. While stronger directional interactions would raise Tm and stabilize the solid phase, this would also likely increase K, which increases the possibility of liquid–liquid phase separation as larger associated structures would persist to lower concentration. Liquid–liquid phase separation is typically not advantageous for gelation, as it forms dispersed organogelator rich phases, that lowers the concentration of the fine structure spanning organogelator fibers form from the liquid to liquid + solid phase transition.29 Similarly, the size limiting effect of the cyclization of the hydroxyl groups also provides a significant free energy penalty from the disassociation of a large number of alcohol bonds, which stabilizes the liquidus line to lower concentrations, while not producing supramolecular polymers with a significantly large degree of association,92 which could also drive liquid–liquid phase separation from the large effective molar volume of the supramolecular species.
This associated solution phase behavior also provides a rationale for why solvent–gelator interactions are able to influence the gelation behavior of 12-HSA. For example, Gao et al. examined the gelation behavior of 12-HSA in a number of different classes of solvents (e.g. alkanes, ketones, alcohols).61 It was observed that in solvents with higher Hansen hydrogen bonding solubility parameters (δh) higher critical gelation concentrations were observed (i.e. the concentrations below which gels would not form on cooling a heated solution to room temperature). In addition, a shift from clear gels, to opaque gels to no gelation was observed with increasing δh. In these systems at low concentrations, as the temperature is lowered association becomes more favorable, however cross-association between the 12-HSA and solvent in hydrogen-bonding systems may compatibilize the solution and make crystallization less favorable. At the same time this may result in larger χ parameters and larger associated solvent molecules, that could drive liquid–liquid phase separation resulting in cloudy gels. A second example is the comparison of the gelation behavior of 12-HSA in alcohols and the corresponding diols.16 While 12-HSA is not able to gel the alcohols, the diols could be gelled. This may be due to the diols forming larger associated aggregates, which stabilize the liquidus line providing more favorable conditions for gelation. While this discussion is speculative, it motivates revisiting these systems and investigating their phase behavior to understand the role of solvent and solute association on the phase diagrams and gelation behavior. In addition, while the solution solute structure strongly influences the phase behavior, it is only facet of the gelation behavior, which also includes the solid-state structure of the organogelator, and its ability to crystallize quickly in one-dimension to form fibrillar networks. Therefore, it would also be useful to study the interplay between the liquid-state and solid-state structure of the organogelator. For example, are the preference between different polymorphs related to the degree of association in the solution?
Conclusions
It has been demonstrated that the phase behavior of 12-hydroxystearic acid (12-HSA)/alkane solutions may be interpreted by using an associated solution model. The liquidus lines in shorter alkanes (octane to hexadecane with even number of carbons) were fit to an attenuated solute association model with only two fitting parameters that give results consistent with the association of 12-HSA dimers into cyclic aggregates through alcohol hydrogen bonding at high 12-HSA concentration. At low 12-HSA concentration, 12-HSA dimers are primarily formed, but the influence of the high concentration associated aggregates is present at low concentration through the free energy cost of dissociating the alcohol groups. Therefore, the monomer concentration of 12-HSA dimers in the neat 12-HSA plays a similar role to the melting temperature in setting the liquidus line. As many different small molecule organogelators use hydrogen bonding groups to drive gelation, solute association offers additional design parameters, such as the neat monomer concentration or the association mechanism, to tune the phase behavior similar to other solute parameters, such as the melting point, heat of fusion and solubility parameter. As the design of organogelator has always been limited by some measure of empirical, trial-and-error variations in structure, it would therefore be extremely useful to revisit some widely used organogelator systems to see the extent that solute association models can be used to interpret differences in the structure–property relationships with systematic variation of the molecular structure.Author contributions
Conceptualization T-YL, KAC; data curation T-YL; formal analysis T-YL, KAC, FK; funding acquisition KAC; investigation T-YL; methodology T-YZL, KAC; project administration KAC; resources KAC, software T-YL, KAC, FK; supervision KAC; validation T-YL, KAC; visualization T-YL, KAC; writing – original draft T-YL, KAC; writing – review & editing T-YL, KAC, FK.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Acknowledgement is made to the donors of the American Chemical Society Petroleum Research Fund for partial support of this research.References
- R. G. Weiss, J. Am. Chem. Soc., 2014, 136, 7519–7530 CrossRef CAS PubMed.
- P. Terech and R. G. Weiss, Chem. Rev., 1997, 97, 3133–3159 CrossRef CAS PubMed.
- E. R. Draper and D. J. Adams, Chem, 2017, 3, 390–410 CAS.
- P. R. A. Chivers and D. K. Smith, Nat. Rev. Mater., 2019, 4, 463–478 CrossRef CAS.
- R. G. Weiss, Molecular Gels: Structure and Dynamics, The Royal Society of Chemistry, 2018 Search PubMed.
- R. G. Weiss and P. Terech, Molecular Gels: Materials with Self-Assembled Fibrillar Networks, Springer, Dordrecht, Netherlands, 2006 Search PubMed.
- J.-M. Guenet, Gels, 2021, 7, 65 CrossRef CAS PubMed.
- M. D. Segarra-Maset, V. J. Nebot, J. F. Miravet and B. Escuder, Chem. Soc. Rev., 2013, 42, 7086–7098 RSC.
- P. Kirilov, S. Rum, E. Gilbert, L. Roussel, D. Salmon, R. Abdayem, C. Serre, C. Villa, M. Haftek, F. Falson and F. Pirot, Int. J. Cosmet. Sci., 2014, 36, 336–346 CrossRef CAS PubMed.
- K. J. Skilling, F. Citossi, T. D. Bradshaw, M. Ashford, B. Kellam and M. Marlow, Soft Matter, 2014, 10, 237–256 RSC.
- D. B. Amabilino and J. Puigmarti-Luis, Soft Matter, 2010, 6, 1605–1612 RSC.
- A. Singh, F. I. Auzanneau and M. A. Rogers, Food Res. Int., 2017, 97, 307–317 CrossRef CAS PubMed.
- N. M. Sangeetha and U. Maitra, Chem. Soc. Rev., 2005, 34, 821–836 RSC.
- M. de Loos, B. L. Feringa and J. H. van Esch, Eur. J. Org. Chem., 2005, 3615–3631 CrossRef CAS.
- S. Abraham, Y. Lan, R. S. H. Lam, D. A. S. Grahame, J. J. H. Kim, R. G. Weiss and M. A. Rogers, Langmuir, 2012, 28, 4955–4964 CrossRef CAS PubMed.
- Y. Lan and M. A. Rogers, CrystEngComm, 2015, 17, 8031–8038 RSC.
- M. Suzuki, M. Yumoto, M. Kimura, H. Shirai and K. Hanabusa, Chem. – Eur. J., 2003, 9, 348–354 CrossRef CAS PubMed.
- J.-M. Guenet, Organogels: Thermodynamics, structure, solvent role, and properties, Springer, 2016 Search PubMed.
- G. Zhu and J. S. Dordick, Chem. Mater., 2006, 18, 5988–5995 CrossRef CAS.
- W. Edwards, C. A. Lagadec and D. K. Smith, Soft Matter, 2011, 7, 110–117 RSC.
- M. Bielejewski, A. Łapiński, R. Luboradzki and J. Tritt-Goc, Langmuir, 2009, 25, 8274–8279 CrossRef CAS PubMed.
- J. Makarević, M. Jokić, B. Perić, V. Tomišić, B. Kojić-Prodić and M. Žinić, Chem. – Eur. J., 2001, 7, 3328–3341 CrossRef.
- C. Liu, M. Corradini and M. A. Rogers, Colloid Polym. Sci., 2015, 293, 975–983 CrossRef CAS.
- J. Gao, S. Wu and M. A. Rogers, J. Mater. Chem., 2012, 22, 12651–12658 RSC.
- J. Bonnet, G. Suissa, M. Raynal and L. Bouteiller, Soft Matter, 2014, 10, 3154–3160 RSC.
- M. A. Rogers and A. G. Marangoni, Langmuir, 2016, 32, 12833–12841 CrossRef CAS PubMed.
- M. Raynal and L. Bouteiller, Chem. Commun., 2011, 47, 8271–8273 RSC.
- Y. Lan, M. G. Corradini, X. Liu, T. E. May, F. Borondics, R. G. Weiss and M. A. Rogers, Langmuir, 2014, 30, 14128–14142 CrossRef CAS PubMed.
- K. A. Cavicchi, M. Pantoja and T.-Y. Lai, ACS Symp. Ser., 2018, 1296, 246–265 CrossRef CAS.
- A. R. Hirst, I. A. Coates, T. R. Boucheteau, J. F. Miravet, B. Escuder, V. Castelletto, I. W. Hamley and D. K. Smith, J. Am. Chem. Soc., 2008, 130, 9113–9121 CrossRef CAS PubMed.
- C. Lagadec and D. K. Smith, Chem. Commun., 2011, 47, 340–342 RSC.
- E. A. Wilder, C. K. Hall, S. A. Khan and R. J. Spontak, Langmuir, 2003, 19, 6004–6013 CrossRef CAS.
- X. Huang, P. Terech, S. R. Raghavan and R. G. Weiss, J. Am. Chem. Soc., 2005, 127, 4336–4344 CrossRef CAS PubMed.
- M. Lescanne, A. Colin, O. Mondain-Monval, F. Fages and J. L. Pozzo, Langmuir, 2003, 19, 2013–2020 CrossRef CAS.
- J. F. Toro-Vazquez, J. Morales-Rueda, A. Torres-Martínez, M. A. Charó-Alonso, V. A. Mallia and R. G. Weiss, Langmuir, 2013, 29, 7642–7654 CrossRef CAS PubMed.
- R. Wang, X.-Y. Liu, J. Xiong and J. Li, J. Phys. Chem. B, 2006, 110, 7275–7280 CrossRef CAS PubMed.
- R. J. Twieg, T. P. Russell, R. Siemens and J. F. Rabolt, Macromolecules, 1985, 18, 1361–1362 CrossRef CAS.
- E. Christ, C. Blanc, A. Al Ouahabi, D. Maurin, R. Le Parc, J.-L. Bantignies, J.-M. Guenet, D. Collin and P. J. Mésini, Langmuir, 2016, 32, 4975–4982 CrossRef CAS PubMed.
- E. Christ, D. Collin, J.-P. Lamps and P. J. Mésini, Phys. Chem. Chem. Phys., 2018, 20, 9644–9650 RSC.
- L. Feng and K. A. Cavicchi, Soft Matter, 2012, 8, 6483–6492 RSC.
- V. A. Mallia, M. George, D. L. Blair and R. G. Weiss, Langmuir, 2009, 25, 8615–8625 CrossRef CAS PubMed.
- N. M. Sangeetha and U. Maitra, Chem. Soc. Rev., 2005, 34, 821–836 RSC.
- Y. Lan, M. G. Corradini, R. G. Weiss, S. R. Raghavan and M. A. Rogers, Chem. Soc. Rev., 2015, 44, 6035–6058 RSC.
- V. A. Mallia and R. G. Weiss, Soft Matter, 2015, 11, 5010–5022 RSC.
- D. A. S. Grahame, C. Olauson, R. S. H. Lam, T. Pedersen, F. Borondics, S. Abraham, R. G. Weiss and M. A. Rogers, Soft Matter, 2011, 7, 7359–7365 RSC.
- T. Taro and K. Hideko, Bull. Chem. Soc. Jpn., 1969, 42, 3422–3424 CrossRef.
- T. Tachibana and K. Hori, J. Colloid Interface Sci., 1977, 61, 398–400 CrossRef CAS.
- T. Sakurai, Y. Masuda, H. Sato, A. Yamagishi, H. Kawaji, T. Atake and K. Hori, Bull. Chem. Soc. Jpn., 2010, 83, 145–150 CrossRef CAS.
- V. A. Mallia and R. G. Weiss, in Gels and Other Soft Amorphous Solids, American Chemical Society, 2018, vol. 1296, ch. 12, pp. 227–243 Search PubMed.
- M. A. Rogers, S. Abraham, F. Bodondics and R. G. Weiss, Cryst. Growth Des., 2012, 12, 5497–5504 CrossRef CAS.
- H. Mutlu and M. A. R. Meier, Eur. J. Lipid Sci. Technol., 2010, 112, 10–30 CrossRef CAS.
- A. K. Zetzl, A. G. Marangoni and S. Barbut, Food Funct., 2012, 3, 327–337 RSC.
- P. Kirilov, S. Rum, E. Gilbert, L. Roussel, D. Salmon, R. Abdayem, C. Serre, C. Villa, M. Haftek and F. Falson, Int. J. Cosmet. Sci., 2014, 36, 336–346 CrossRef CAS PubMed.
- C. L. Esposito, V. Tardif, M. Sarrazin, P. Kirilov and V. G. Roullin, Mater. Sci. Eng., C, 2020, 114, 110999 CrossRef CAS PubMed.
- B. Martin, G. Garrait, E. Beyssac, D. Goudouneche, E. Perez and S. Franceschi, Pharm. Res., 2020, 37, 92 CrossRef CAS PubMed.
- P. Lee and M. A. Rogers, Langmuir, 2013, 29, 5617–5621 CrossRef CAS PubMed.
- R. Gordon, S. T. Stober and C. F. Abrams, J. Phys. Chem. B, 2017, 121, 9223–9233 CrossRef CAS PubMed.
- R. Gordon, S. T. Stober and C. F. Abrams, J. Phys. Chem. B, 2019, 123, 534–541 CrossRef CAS PubMed.
- K. Marsh and F. Kohler, J. Mol. Liq., 1985, 30, 13–55 CrossRef CAS.
- A. Apelblat, J. Mol. Liq., 2006, 128, 1–31 CrossRef CAS.
- J. Gao, S. Wu and M. A. Rogers, J. Mater. Chem., 2012, 22, 12651–12658 RSC.
- V. A. Mallia and R. G. Weiss, J. Phys. Org. Chem., 2014, 27, 310–315 CrossRef CAS.
- A. Bui and N. Virgilio, Ind. Eng. Chem. Res., 2013, 52, 14185–14191 CrossRef CAS.
- P. Fei, S. J. Wood, Y. Chen and K. A. Cavicchi, Langmuir, 2015, 31, 492–498 CrossRef CAS PubMed.
- C. M. Hansen, Hansen's solubility Parameters: A Users Handbook, CRC Press, Boca Raton, FL, 2007 Search PubMed.
- S. R. Raghavan and B. H. Cipriano, in Molecular Gels: Materials with Self-Assembled Fibrillar Networks, ed. R. G. Weiss and P. Terech, Springer Netherlands, Dordrecht, 2006, pp. 241–252 Search PubMed.
- H. Takeno, M. Yanagita, Y. Motegi and S. Kondo, Colloid Polym. Sci., 2015, 293, 199–207 CrossRef CAS.
- H. Takeno and M. Kozuka, Adv. Mater. Sci. Eng., 2017, 2017, 4762379 Search PubMed.
- J.-M. Guenet, Thermochim. Acta, 1996, 284, 67–83 CrossRef CAS.
- Y. K. Lin, G. Chen, J. Yang and X. L. Wang, Desalination, 2009, 236, 8–15 CrossRef CAS.
- L. Rycerz, J. Therm. Anal. Calorim., 2013, 113, 231–238 CrossRef CAS.
- D. Giron, J. Therm. Anal. Calorim., 2001, 64, 37–60 CrossRef CAS.
- K. Sato, K. Suzuki, M. Okada and N. Garti, J. Cryst. Growth, 1985, 72, 699–704 CrossRef CAS.
- E. Moreno, R. Cordobilla, T. Calvet, M. A. Cuevas-Diarte, G. Gbabode, P. Negrier, D. Mondieig and H. A. J. Oonk, New J. Chem., 2007, 31, 947–957 RSC.
- M. C. Costa, M. P. Rolemberg, A. J. A. Meirelles, J. A. P. Coutinho and M. A. Krähenbühl, Thermochim. Acta, 2009, 496, 30–37 CrossRef CAS.
- J. M. Guenet, B. Demé, O. Gavat, E. Moulin and N. Giuseppone, Soft Matter, 2022, 18, 2851–2857 RSC.
- P. Painter, B. Veytsman and J. Youtcheff, Energy Fuels, 2014, 28, 2472–2480 CrossRef CAS.
- R. Koningsveld, W. H. Stockmayer and E. Nies, Polymer Phase Diagrams, Oxford University Press, New York, 2001 Search PubMed.
- P. J. Flory, J. Chem. Phys., 1944, 12, 425–438 CrossRef CAS.
- C. B. Kretschmer and R. Wiebe, J. Chem. Phys., 1954, 22, 1697–1701 CrossRef CAS.
- P. Painter, B. Veytsman and J. Youtcheff, Energy Fuels, 2015, 29, 2120–2133 CrossRef CAS.
- P. Painter, B. Veytsman and J. Youtcheff, Energy Fuels, 2015, 29, 7048–7057 CrossRef CAS.
- P. Painter, B. Veytsman and J. Youtcheff, Energy Fuels, 2015, 29, 2951–2961 CrossRef CAS.
- J. William and E. Acree, Thermodynamic Properties of Nonelectrolyte Solutions, Academic Press, Orlando, FL, 1984 Search PubMed.
- I. Prigogine, A. Bellemans and M. Mathot, The Molecular Theory of Solutions, Interscience Publishers, Inc., New York NY, 1957 Search PubMed.
- A. F. M. Barton, Chem. Rev., 1975, 75, 731–753 CrossRef CAS.
- Y. Fujii, H. Yamada and M. Mizuta, J. Phys. Chem., 1988, 92, 6768–6772 CrossRef CAS.
- N. Asprion, H. Hasse and G. Maurer, Fluid Phase Equilib., 2001, 186, 1–25 CrossRef CAS.
- K. Nakasone, K. Shiokawa, Y. Urabe and N. Nemoto, J. Phys. Chem. B, 2000, 104, 7483–7489 CrossRef CAS.
- R. A. Matkar and T. Kyu, J. Phys. Chem. B, 2006, 110, 12728–12732 CrossRef CAS PubMed.
- T. Sakurai, Y. Masuda, H. Sato, A. Yamagishi, H. Kawaji, T. Atake and K. Hori, Bull. Chem. Soc. Jpn., 2010, 83, 145–150 CrossRef CAS.
- D. Zhao and J. S. Moore, Org. Biomol. Chem., 2003, 1, 3471–3491 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Document containing molar volume and solubility parameters of alkanes, example cloud-point measurements, stearic acid/dodecane phase behavior, and derivation of the attenuated associated solution model. Matlab files for curve fitting. Excel file of raw data for curve fitting. See DOI: https://doi.org/10.1039/d3sm00013c |
| ‡ Current address: 3M Company, St. Paul, MN 55144, USA. |
| This journal is © The Royal Society of Chemistry 2023 |