Engineering magic number Au₁₉ and Au₂₀ cage structures using electron withdrawing atoms

Abstract

Gold cages are a subset of gold nanoparticles and these structures are of major interest due to their favourable physiochemical properties. In order for these structures to be useful in applications, they must be chemically stable. The objective of this research is to transform non-magic number cage structures into magic number cage structures by the addition of electron-withdrawing groups on the cages. The electronic properties for Au₁₉X and Au₂₀X₂ (X = F, Cl, Br, I) are calculated and observed. It is expected that the electron-withdrawing groups will remove the electron density from the gold cages and leave them positively charged. We first optimize the geometries of the initial gold cages and verify the structures are a local minima. From there, we attach our halogens to the gold cages and optimize the structures to determine the NICS values and HOMO–LUMO gaps. NICS values were found to be more negative when a more electronegative halogen was used. Calculations have found that Au₁₉F and Au₂₀F₂ have the most negative NICS values, indicating greater spherical aromaticity. Iodine, being the least electronegative atom, had the most positive NICS value and smallest HOMO–LUMO gap. All calculations are compared to the magic cluster Au₁₈ which satisfies Hirsh's 2(N + 1)² rule for n = 2.

---

Introduction

Small gold nanostructures are of considerable interest in the fields of nanoscience and nanotechnology. Viewed as elementary building blocks for the construction of nanoarchitectures, these species have become optimal candidates in a broad range of applications including electrochemistry,¹ quantum electronics,² and heterogeneous catalysis.³ With diameters ranging from sub-nanometer to approximately 2 nm,^4,5 they exhibit novel properties resulting from unique atomic packing and strong quantum effects that differ significantly from gold nanostructures in the 5–100 nm range, and from bulk gold.⁶ Their properties can be fine-tuned by altering characteristics such as the size, shape, and composition of the nanostructure.^7–10

Compact gold nanostructures can be qualitatively described by the jellium model.¹¹ The discrete orbitals are labeled 1S, 1P, 1D + 2S, 1F + 2P… and have stable configurations of valence electrons (2, 8, 20, 40…) that differs from the atomic series (2, 10, 18, 36…).^12–15 In gold nanostructures, each gold atom contributes one 6s valence electron that moves freely throughout the structure¹⁶ and it has been shown that compact gold structures with 2, 8, 20, and 40 gold atoms have special electronic and chemical stability.^13,17,18 In particular, it is well-established that the minimum energy Au₂₀ structure is the (compact) tetrahedron, Au₂₀(T_d).¹⁸ We obtained initial Au₁₉ and Au₁₈ compact structures by removing one and two corner gold atoms from Au₂₀(T_d).

For cage structures, only the highest angular momentum is relevant. The discrete orbitals are labeled 1S, 1P, 1D, 1F… and have stable configuration of valence electrons (2, 8, 18, 32…) and it has been shown that cage structures with 18 and 32 gold atoms have special electronic and chemical stability.¹⁷ Of relevance to our paper, there is strong experimental evidence of (anionic) gold cage structures with 16, 17, and 18 atoms in the gas phase.¹⁹ Also of relevance is a computational study which showed that, for Au₁₈, the compact truncated tetrahedral structure transitioned to a cage structure during soft-landing onto a TiO₂(110) surface.²⁰

Although used frequently in current scientific literature, aromaticity is a concept with no single, universally accepted definition despite dedicated research into the topic spanning over centuries.^21,22 Previously, aromatic compounds were largely defined as planar ring systems that satisfied the 4n + 2π electron rule.²³ In this work, aromaticity is defined as electron delocalization in a closed circuit in either two or three dimensions and is associated with extra stability within three-dimensional molecules.²⁴ Experimentally, electronic ring currents in aromatic species are measured through nuclear magnetic resonance (NMR).^25–27 A long-standing and widely accepted method for measuring aromaticity theoretically is the nucleus-independent chemical shift (NICS)²⁸ due to its simplicity, efficiency, and easy computability. Specifically, ¹H NMR chemical shifts are commonly used for characterizing aromatic (and anti-aromatic) compounds,²⁹ and this method proves useful for three-dimensional structures as long as the chemical shift is calculated at the center of the cage.³⁰ These isotropic NICS values correspond to the negative of the magnetic shielding computed at the center of the cage and substantially negative isotropic NICS values signify the presence of induced ring currents which corresponds to high aromaticity. NICS values therefore serve as a means to quantify the electronic and chemical stability of small spherical gold cage structures. While the correlation between electronic ring currents and stability in aromatic compounds has been questioned regarding organic^27,31–33 and inorganic^34–36 species, this work focuses on the relationship between NICS values and the stability of spherical gold clusters ranging in size from 18–20 atoms.

To overcome their high surface energy and prevent agglomeration, nanostructures should be stabilized via electrostatic and/or steric means. Electrostatic stabilization is achieved through the adsorption of ions to the nanostructure surface and results in the repulsion of individual particles.³⁷ Steric stabilization is achieved by encompassing the metal core in layers of materials that are sterically bulky, thus providing a barrier which prevents close contact of the metal cores.³⁷ An added benefit to these stabilization methods is that the number of valence electrons in the nanocluster can be adjusted by selecting the appropriate ligand resulting in tremendous control of the physiochemical properties of the nanocluster.³⁸ It has been shown that, for charged and neutral clusters, the relative stability among 3D isomers can change as a result of the ligand stabilization effect.^39–43 Although thiols are the most popular and well-studied ligand for gold clusters,¹ other common ligands include amines,⁴⁴ arynes,⁴⁵ phosphines,⁴⁶ and halides.^47,48 In this paper, motivated by studies which use electron withdrawing substituents to alter the stability of organic molecules,^49,50 we use halides to stabilize small spherical gold cage structures.

Chemical hardness, a measure of the resistance to change or deformation, is another property with an expected relation to structural stability.^51–53 It is equal to the difference between the ionization potential and the electron affinity. It has been shown that the negative energy value of the HOMO is approximately equal to the ionization potential, and the negative energy value of the LUMO is approximately equal to the electron affinity.^54,55 Therefore, chemical hardness can be associated with the gap between these two frontier orbitals, and it is expected that the larger the HOMO–LUMO gap the more stable the nanocluster.

Here we report increased stability achieved for local minima Au₁₉ and Au₂₀ cage structures through the adsorption of halogens (X = F, Cl, Br, I) on the cage. In Au₁₉X and Au₂₀X₂, the gold cage has a formal valence electron count of 18 and we show these halogenated species exhibit stability analogous to Au₁₈, a magic number cage structure that satisfies Hirsch's 2(N + 1)² rule for n = 2. Specifically, we show that Au₁₉X and Au₂₀X₂ have more negative isotropic NICS values and more positive HOMO–LUMO gaps than their unhalogenated counterparts. We also show that, when the electronegativity of the ligand increases (from iodide to fluoride), the stability of the ligated cage structure increases.

All gold local minima isomers presented in this work were adapted from Trombach et al.⁵⁶ who constructed the spherical gold cages using standard algorithms employed for the construction of fullerenes.^57–59 Bulusu et al.¹⁹ were successful in identifying and analyzing golden cages via photoelectron spectroscopy.

Methodology

Geometries for the six Au₁₈, Au₁₉, and Au₂₀ cage isomers, as well as the Au₁₈, Au₁₉, and Au₂₀ compact structures, were initially optimized via the CP2K software package⁶⁰ using density functional theory (DFT) with the Perdew–Burke–Ernzerhof (PBE) exchange correlation functional⁶¹ and the double-zeta valence polarized (DZVP) basis set. To include relativistic effects, which are large for gold, we used the Geodecker–Teter–Hutter (GTH) pseudopotential,⁶² and dispersion corrections were included via the Grimme D3 approach.⁶³ The Mulliken charge⁶⁴ of each gold atom was calculated to aid in the placement of the ligands. Each charged and ligated cage was also optimized under identical conditions prior to the subsequent steps. CP2K was also used to calculate the structural energies and HOMO–LUMO gap (in eV) of all bare and ligated species. While DFT is known to underestimate HOMO–LUMO gaps, we can confidently compare the computed HOMO–LUMO gaps to one another. Next using the Gaussian 16 software package⁶⁵ with the PBE functional and the triple-zeta valence polarized (TZVP) basis set, normal mode calculations were performed on all bare and ligated cages to ensure the optimized structures were local minima via the absence of imaginary vibrational frequencies. To account for relativistic effects in Gaussian, the Def2TZVP basis set was selected as it makes use of the Stuttgart Dresden core potentials for elements heavier than Krypton. We then computed the isotropic NICS value (in ppm) for each gold cage structure. All structures were visualized with the aid of Chemcraft software.⁶⁶

Results and discussion

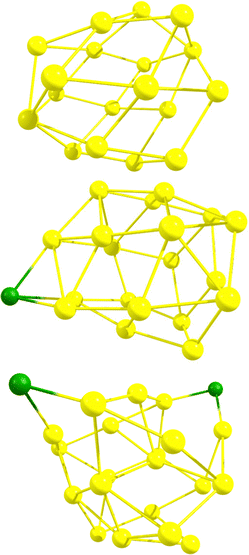
Initially, DFT calculations were performed for six neutral Au₁₈ cage isomers (number in parenthesis denotes the number of different isomers for that particular symmetry group):⁵⁶ C₂–Au₁₈ (2), D₂–Au₁₈, D_3d–Au₁₈, D_3h–Au₁₈, and D₃–Au₁₈. Visuals of each optimized structure are located in Fig. S1 of the ESI.† After confirming the isomers were local minima, the Au₁₈ cage structures were determined to have an average energy equal to that of the neutral Au₁₈ compact cluster, as oultined in Table S1 of the ESI.† Next, HOMO–LUMO gaps and isotropic NICS values of the six neutral Au₁₈ cage isomers were computed and are compiled in Table S2 of the ESI† along with the XYZ coordinates. Since Au₁₈ is a closed–shell cage structure with high stability, it was previously found, and confirmed in our calculations, to have a large negative NICS value, averaged at −52.20 ppm. The average HOMO–LUMO gap for the six Au₁₈ isomers was determined to be 1.13 eV. Next, DFT calculations were performed for six Au₁₉ cage isomers:⁵⁶ C₂–Au₁₉ (3), C_s–Au₁₉ (2), and C_3v–Au₁₉, each first with a neutral charge and then with +1 charge. Visuals of each optimized neutral structure are located in Fig. S1 of the ESI.† After confirming the neutral isomers were local minima, the Au₁₉ cage structures were determined to be higher in energy by an average of 0.46 eV compared to the neutral Au₁₉ compact cluster, as oultined in Table S1 of the ESI.† Next, the HOMO–LUMO gaps and isotropic NICS values for the six Au₁₉ cage isomers were computed and are compiled in Tables S2 and S3 of the ESI† along with the XYZ coordinates. In contrast to Au₁₈, Au₁₉ (which is an open–shell system) exhibits less spherical aromaticity and stability, observed through the average NICS value of +12.93 ppm and an average HOMO–LUMO gap of 1.05 eV. The Au₁₉⁺ cage structure (which is isoelectronic to Au₁₈) has an average NICS value of −49.56 ppm and an average HOMO–LUMO gap of 1.19 eV. Finally, DFT calculations were performed for six Au₂₀ cage isomers:⁵⁶ C₂–Au₂₀, D₂–Au₂₀ (2), C₁–Au₂₀, C_s–Au₂₀, and D_2d–Au₂₀, each with a neutral, +1, and +2 charge. Visuals of each optimized neutral structure are located in Fig. S1 of the ESI.† After confirming the neutral isomers were local minima, the Au₂₀ cage structures were determined to be higher in energy by an average of 0.99 eV compared to the neutral Au₂₀ compact cluster, as oultined in Table S1 of the ESI.† This was expected as the literature states the minimum energy Au₂₀ structure is the (compact) tetrahedron. Next, the HOMO–LUMO gaps and isotropic NICS values for the six Au₂₀ cage isomers were computed and are compiled in Tables S2 and S3 of the ESI† along with the XYZ coordinates. The neutral Au₂₀ structure exhibits an average NICS value of +2.61 ppm and an average HOMO–LUMO gap of 0.66 eV. For Au₂₀⁺, a significant increase in stability is observed as the average NICS value decreases to −20.58 ppm and the average HOMO–LUMO gap value increases to 0.71 eV. The Au₂₀²⁺ cage structure (which is isoelectronic to Au₁₈) displays greater aromaticity and stability with an average NICS value of −38.18 ppm and an average HOMO–LUMO gap of 1.06 eV.

For the cationic structures, Au₁₉⁺ and Au₂₀²⁺, electronic stabilization is achieved through the adsorption of halogen anions (X = F⁻, Cl⁻, Br⁻, I⁻) on the cage. The location of each halogen was decided through analysis of the Mulliken charges for the gold atoms in the bare structures. Specifically, halogen atoms were placed at the most positive gold atoms for each gold cage. Visuals of isomer 1 optimized halogenated structures for Au₁₉X and Au₂₀X₂ are located in Fig. S2 of the ESI.† For comparison, the optimized Au₁₈, Au₁₉Cl, and Au₂₀Cl₂ structures are displayed in Fig. 1. The HOMO–LUMO gaps and isotropic NICS values for each of the six isomers for Au₁₉X and Au₂₀X₂ are compiled in Table S4 of the ESI† along with the XYZ coordinates. The average isotropic NICS values and HOMO–LUMO gaps for Au₁₉X and Au₂₀X₂ are displayed in Fig. 2 and given in Table S5 of the ESI.† While all are 18 electron species, each Au₁₉ halogenated structure has greater spherical aromaticity and a larger HOMO–LUMO gap than its Au₂₀ halogenated counterpart. In comparison to the closed–shell Au₁₈ cage structures, with an average NICS value of −52.20 ppm, the average NICS values for the Au₁₉X species are −43.44, −41.46, −40.01, and −38.33 ppm for Au₁₉F, Au₁₉Cl, Au₁₉Br, and Au₁₉I, respectively. The average NICS values for the Au₂₀X₂ species are −31.82, −26.53, −26.43, and −25.79 ppm for Au₂₀F₂, Au₂₀Cl₂, Au₂₀Br₂, and Au₂₀I₂, respectively. For Au₁₉X and Au₂₀X₂, we observe that, as the halogen becomes more electronegative, the spherical aromaticity of the cage structure increases. When cross-referencing the NICS values with the HOMO–LUMO gaps for Au₁₈, Au₁₉X, and Au₂₀X₂, it is observed that the species with more negative NICS values have larger HOMO–LUMO gaps. For instance, Au₁₈ with a NICS value of −52.20 ppm has a HOMO–LUMO gap of 1.13 eV, Au₁₉F with a NICS value of −43.44 ppm has a HOMO–LUMO gap of 1.10 eV, and Au₂₀I₂ with a NICS value of −25.79 ppm has a HOMO–LUMO gap of 0.86 eV. As stated previously, high spherical aromaticities and large HOMO–LUMO gaps are known characteristics of stable gold cage structures.

Fig. 1 From top to bottom: Au₁₈, Au₁₉Cl, and Au₂₀Cl₂ cage structures.

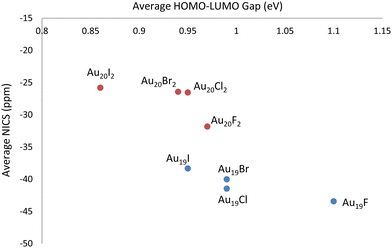Fig. 2 Average (over structural isomers) spherical aromaticity and chemical hardness trends for the halogenated Au₁₉X and Au₂₀X₂ cage structures.

Conclusions

We have shown that high spherical aromaticity can be achieved for structures engineered to have a closed–shell “magic number” of electrons. Specifically, we have shown, using nucleus-independent chemical shifts, that Au₁₉X and Au₂₀X₂ cage structures have spherical aromaticity comparable to the well-known Au₁₈ cage structure and that their corresponding HOMO–LUMO gaps reflect their position in the stability ranking. Electrostatic stabilization was achieved through the adsorption of halogen anions (X = F⁻, Cl⁻, Br⁻, I⁻) on the Au₁₉⁺ and Au₂₀²⁺ cage surface. The trend observed amongst the Au₁₉X and Au₂₀X₂ species is that as the halide becomes more electronegative in going from iodide to fluoride, the spherical aromaticity of the cage structure increases. These results support the broader finding that control over the stability of small gold nanostructures is possible using ligands to fine-tune their electronic properties. As noted above, there is strong experimental evidence of an Au₁₇⁻ cage structure in the gas phase and the formation of an Au₁₈ cage structure on a metal oxide surface. We therefore believe that our electronically equivalent Au₁₉X and Au₂₀X₂ cage structures are experimentally accessible.

Author contributions

All authors have given approval to the final version of the manuscript. Initial calculations were undertaken by HMG. Subsequent calculations were undertaken by HMG and JRC under the supervision of IPH.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge support from NSERC, SOSCIP, Compute Canada, and Wilfrid Laurier University.

References

1. M.-C. Daniel and D. Astruc, Gold Nanoparticles: Assembly, Supramolecular Chemistry, Quantum-Size-Related Properties, and Applications toward Biology, Catalysis, and Nanotechnology, Chem. Rev., 2004, 104, 293–346.
2. S. Chen, R. S. Ingram, M. J. Hostetler, J. J. Pietron, R. W. Murray, T. G. Schaaff, J. T. Khoury, M. M. Alvarez and R. L. Whetten, Gold Nanoelectrodes of Varied Size: Transition to Molecule-Like Charging, Science, 1998, 280, 2098–2101.
3. G. Li and R. Jin, Atomically Precise Gold Nanoclusters as New Model Catalysts, Acc. Chem. Res., 2013, 46, 1749–1758.
4. H. Qian, M. Zhu, Z. Wu and R. Jin, Quantum Sized Gold Nanoclusters with Atomic Precision, Acc. Chem. Res., 2012, 45, 1470–1479.
5. R. Jin, Atomically Precise Metal Nanoclusters: Stable Sizes and Optical Properties, Nanoscale, 2015, 7, 1549–1565.
6. D. Mollenhauer and N. Gaston, Phosphine Passivated Gold Clusters: How Charge Transfer Affects Electronic Structure and Stability, Phys. Chem. Chem. Phys., 2016, 18, 29686–29697.
7. A. W. Castleman and S. N. Khanna, Clusters, Superatoms, and Building Blocks of New Materials, J. Phys. Chem., 2009, 113, 2664–2675.
8. M. V. Kovalenko, L. Manna, A. Cabot, Z. Hens, D. V. Talapin, C. R. Kagan, X. V. I. Klimov, A. L. Rogach, P. Reiss, D. J. Milliron, P. Guyot-sionnnest, G. Konstantatos, W. J. Parak, T. Hyeon, B. A. Korgel, C. B. Murray and W. Heiss, Prospects of Nanoscience with Nanocrystals, Nanotechnol. Focus, 2015, 9, 1012–1057.
9. Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Shape-Controlled Synthesis of Metal Nanocrystals: Simple Chemistry Meets Complex Physics?, Angew. Chem., Int. Ed., 2009, 48, 60–103.
10. R. Fournier, Theoretical Study of the Structure of Silver Clusters, J. Chem. Phys., 2001, 115, 2165–2177.
11. W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Electronic Shell Structure and Abundances of Sodium Clusters, Phys. Rev. Lett., 1984, 52, 2141–2143.
12. W. A. De Heer, The Physics of Simple Metal Clusters: Experimental Aspects and Simple Models, Rev. Mod. Phys., 1993, 65, 611–676.
13. Z. Luo and A. W. Castleman, Special and General Superatoms, Acc. Chem. Res., 2014, 47, 2931–2940.
14. Z. Luo, A. W. Castleman and S. N. Khanna, Reactivity of Metal Clusters, Chem. Rev., 2016, 116, 14456–14492.
15. P. Jena and Q. Sun, Super Atomic Clusters: Design Rules and Potential for Building Blocks of Materials, Chem. Rev., 2018, 118, 5755–5870.
16. M. Faraday and On New, Compounds of Carbon and Hydrogen, and on Certain Other Products Obtained during the Decomposition of Oil by Heat, Philos. Trans. R. Soc. London, 1825, 115, 440–466.
17. H. Häkkinen, Atomic and Electronic Structure of Gold Clusters: Understanding Flakes, Cages and Superatoms from Simple Concepts, Chem. Soc. Rev., 2008, 37, 1847–1859.
18. J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Au₂₀: A Tetrahedral Cluster, Science, 2003, 299, 864–867.
19. S. Bulusu, X. Li, L. Wang and X. C. Zeng, Evidence of Hollow Golden Cages, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8326–8330.
20. L. Li, H. Li and X. C. Zeng, Structure Transition of Au₁₈ from Pyramidal to a Hollow-Cage during Soft-Landing onto a TiO₂(110) Surface, Chem. Commun., 2015, 51, 9535–9538.
21. B. J. R. Cuyacot and C. Foroutan-Nejad, [{Th(C₈H₈)Cl₂}₃]₂—Is Stable But Not Aromatic, Nature, 2022, 603, E18–E20.
22. A. Stanger, What is… Aromaticity: A Critique of the Concept of Aromaticity—Can It Really Be Defined?, Chem. Commun., 2009, 1939–1947.
23. E. Hückel, Quantentheoretische Beiträge zum Problem der Aromatischen und Ungesättigten Verbindungen. III. [Quantum Theoretical Contributions to the Problem of Aromatic and Unsaturated Compounds. III], Z. Phys., 1932, 76, 628–648.
24. P. von Ragué Schleyer, Introduction: Aromaticity, Chem. Rev., 2001, 101, 1115–1118.
25. R. H. Mitchell, Measuring Aromaticity by NMR, Chem. Rev., 2001, 101, 1301–1315.
26. R. Islas, T. Heine and G. Merino, The Induced Magnetic Field, Acc. Chem. Res., 2012, 45, 215–228.
27. J. A. N. F. Gomes and R. B. Mallion, Aromaticity and Ring Currents, Chem. Rev., 2001, 101, 1349–1383.
28. P. Von Rague, C. Maerker, A. Dransfeld, H. Jiao, N. J. R. V. E. Hommes, D. Erlangen and R. V. February, Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe, J. Am. Chem. Soc., 1996, 118, 6317–6318.
29. L. M. Elvidge and J. A. Jackman, Studies of Aromaticity by Nuclear Magnetic Resonance Spectroscopy. Part I. 2-Pyridones and Related Systems, J. Chem. Soc., 1961, 859–866.
30. M. Bühl and A. Hirsch, Spherical Aromaticity of Fullerenes, Chem. Rev., 2001, 101, 1153–1183.
31. Z. Badri and C. Foroutan-Nejad, Unification of Ground-State Aromaticity Criteria – Structure, Electron Delocalization, and Energy – In Light of the Quantum Chemical Topology, Phys. Chem. Chem. Phys., 2016, 18, 11693–11699.
32. L. Zhao, R. Grande-Aztatzi, C. Foroutan-Nejad, J. M. Ugalde and G. Frenking, Aromaticity, the Hückel 4n + 2 Rule and Magnetic Current, ChemistrySelect, 2017, 2, 863–870.
33. R. Gershoni-poranne and A. Stanger, Magnetic Criteria of Aromaticity, Chem. Soc. Rev., 2015, 6597–6615.
34. Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-nejad and K. Ruud, All-Metal Aromaticity: Revisiting the Ring Current Model among Transition Metal Clusters, J. Chem. Theory Comput., 2013, 9, 4789–4796.
35. C. Foroutan-Nejad, S. Shahbazian, F. Feixas, P. Rashidi-Ranjbar and M. Solà, A Dissected Ring Current Model for Assessing Magnetic Aromaticity: A General Approach for both Organic and Inorganic Rings, J. Comput. Chem., 2011, 32, 2422–2431.
36. J. O. C. Jiménez-Halla, E. Matito, J. Robles and M. Solà, Nucleus-Independent Chemical Shift (NICS) Profiles in a Series of Monocyclic Planar Inorganic Compounds, J. Organomet. Chem., 2006, 691, 4359–4366.
37. L. Guerrini, R. A. Alvarez-Puebla and N. Pazos-Perez, Surface Modifications of Nanoparticles for Stability in Biological Fluids, Materials, 2018, 11, 1–28.
38. T. Omoda, S. Takano and T. Tsukuda, Toward Controlling the Electronic Structures of Chemically Modified Superatoms of Gold and Silver, Small, 2020, 2001439, 1–18.
39. G. Shafai, S. Hong, M. Bertino and T. S. Rahman, Effect of Ligands on the Geometric and Electronic Structure of Au₁₃ Clusters, J. Phys. Chem. C, 2009, 113, 12072–12078.
40. K. Spivey, J. I. Williams and L. Wang, Structures of Undecagold Clusters: Ligand Effect, Chem. Phys. Lett., 2006, 432, 163–166.
41. I. L. Garzon, C. Rovira, K. Michaelian, M. R. Beltran, P. Ordejon, J. Junquera, D. Sanchez-Portal, E. Artacho and J. M. Soler, Do Thiols Merely Passivate Gold Nanoclusters?, Phys. Rev. Lett., 2000, 85, 5250–5251.
42. G. Periyasamy and F. Remacle, Ligand and Solvation Effects on the Electronic Properties of Au₅₅ Clusters: A Density Functional Theory Study, Nano Lett., 2009, 9, 3007–3011.
43. N. T. Wilson and R. L. Johnston, Passivated Clusters: A Theoretical Investigation of the Effect of Surface Ligation on Cluster Geometry, Phys. Chem. Chem. Phys., 2002, 4, 4168–4171.
44. D. V. Leff, L. Brandt and J. R. Heath, Synthesis and Characterization of Hydrophobic, Organically-Soluble Gold Nanocrystals Functionalized with Primary Amines, Langmuir, 1996, 12, 4723–4730.
45. P. Maity, H. Tsunoyama, M. Yamauchi, S. Xie and T. Tsukuda, Organogold Clusters Protected by Phenylacetylene, J. Am. Chem. Soc., 2011, 133, 20123–20125.
46. J. Kilmartin, R. Sarip, R. Grau-Crespo, D. Di Tommaso, G. Hogarth, C. Prestipino and G. Sankar, Following the Creation of Active Gold Nanocatalysts from Phosphine-Stabilized Molecular Clusters, ACS Catal., 2012, 2, 957–963.
47. P. Pyykko, Theoretical Chemistry of Gold. II, Inorg. Chim. Acta, 2005, 358, 4113–4130.
48. G. M. Berry, M. E. Bothwell, B. G. Bravo, G. J. Cali, J. E. Harris, T. Mebrahtu, S. L. Michelhaugh, J. F. Rodriguez and M. P. Soriaga, Spectroscopic and Electrochemical Studies of Iodine Coordinated to Noble-Metal Electrode Surfaces, Langmuir, 1989, 5, 707–713.
49. P. von Ragué Schleyer and L. Nyulászi, Hyperconjugative π-Aromaticity: How To Make Cyclopentadiene Aromatic, J. Am. Chem. Soc., 1999, 121, 6872–6875.
50. I. Fernández, J. I. Wu and P. von Ragué Schleyer, Substituent Effects on “Hyperconjugative” Aromaticity and Antiaromaticity in Planar Cyclopolyenes, Org. Lett., 2013, 15, 2990–2993.
51. R. G. Pearson, Hard and Soft Acids and Bases, J. Am. Chem. Soc., 1963, 85, 3533–3539.
52. R. G. Parr and K. Chattara, Pratim, Principle of Maximum Hardness, J. Am. Chem. Soc., 1991, 113, 1854–1855.
53. R. G. Pearson, Chemical Hardness, 1997.
54. R. G. Parr and R. G. Pearson, Absolute Hardness: Companion Parameter to Absolute Electronegativity, J. Am. Chem. Soc., 1983, 105, 7512–7516.
55. R. G. Pearson, Chemical Hardness and Density Functional Theory, J. Chem. Sci., 2005, 117, 369–377.
56. L. Trombach, S. Rampino, L. S. Wang and P. Schwerdtfeger, Hollow Gold Cages and Their Topological Relationship to Dual Fullerenes, Chem. – Eur. J., 2016, 22, 8823–8834.
57. P. Schwerdtfeger, L. N. Wirz and J. Avery, The Topology of Fullerenes, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 96–145.
58. P. Schwerdtfeger, L. Wirz and J. Avery, Program Fullerene: A Software Package for Constructing and Analyzing Structures of Regular Fullerenes, J. Comput. Chem., 2013, 34, 1508–1526.
59. L. N. Wirz, R. Tonner, J. Avery and P. Schwerdtfeger, Structure and Properties of the Nonface-Spiral Fullerenes T-C₃₈₀, D₃-C₃₈₄, D₃-C₄₄₀, and D₃-C₆₇₂ and Their Halma and Leapfrog Transforms, J. Chem. Inf. Model, 2014, 54, 121–130.
60. J. Hutter, M. Iannuzzi, F. Schiffmann and J. Vandevondele, CP2K: Atomistic Simulations of Condensed Matter Systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
61. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
62. S. Goedecker, M. Teter and J. Hutter, Separable Dual-Space Gaussian Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
63. S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787–1799.
64. R. S. Mulliken, Electronic structures of Molecules XI. Electroaffinity, Molecular Orbitals and Dipole Moments, J. Chem. Phys., 1935, 3, 573–585.
65. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ort and D. J. Fox, Gaussian 09 Revision A.02, 2016.
66. G. A. Andrienko, Chemcraft Molecular Visualization Software V1.8, 2023.

---

Footnote

† Electronic supplementary information (ESI) available: NICS values and HOMO–LUMO gaps for all structural isomers. See DOI: https://doi.org/10.1039/d3cp00651d

---