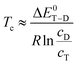Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Raising the benchmark potential of a simple alcohol-ketone intermolecular balance†
Charlotte
Zimmermann
 ,
Arved C.
Dorst
,
Arved C.
Dorst
 and
Martin A.
Suhm
and
Martin A.
Suhm
 *
*
Institute of Physical Chemistry, Georg-August-University Göttingen, Tammannstr. 6, 37077, Göttingen, Germany. E-mail: msuhm@gwdg.de
First published on 29th November 2022
Abstract
2-Butanone offers two hydrogen bond docking variants to a solvating methanol which are cleanly separated by supersonic jet infrared absorption spectroscopy in the OH-stretching range, resolving earlier action spectroscopy indeterminacies for this elementary case of an intermolecular alcohol-ketone balance. The solvent preference for the shorter chain side is unambiguously derived from the spectra of homologous compounds. It is analysed in terms of competing steric and dispersion interactions and the resulting energy differences across a low interconversion barrier. Fortuitous cancellations are discussed and quantitative energy deficiencies of the employed DFT approaches are suggested. Some benchmarkable experimental observations: at low temperature, a single methanol molecule prefers the methyl-sided oxygen lone pair of 2-butanone over the ethyl-sided lone pair by 1–2 kJ mol−1, the trans butane backbone is conserved in both low-lying isomers, the OH-stretching fundamentals differ by 47(2) cm−1.
1 Introduction
The hydrogen bond topology around C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups is diverse1,2 and highly relevant for the solvation of biomolecular model systems.3 Towards a reliable theoretical description of this solvation process, it is important to quantitatively model the first solvation step.4 It is essential to understand any potential error compensation between different intermolecular interactions5 which may break down when the system size is increased. Such competing intermolecular forces include London dispersion6 and it is attractive to study small systems with a controlled balance between hydrogen bonding and London dispersion.
O groups is diverse1,2 and highly relevant for the solvation of biomolecular model systems.3 Towards a reliable theoretical description of this solvation process, it is important to quantitatively model the first solvation step.4 It is essential to understand any potential error compensation between different intermolecular interactions5 which may break down when the system size is increased. Such competing intermolecular forces include London dispersion6 and it is attractive to study small systems with a controlled balance between hydrogen bonding and London dispersion.
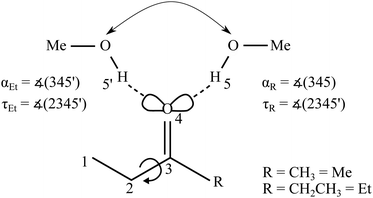
Unsymmetrically substituted ketones offer the possibility to investigate whether a protic solvent molecule prefers one substitution side or the other (see Fig. 1), a situation which has been termed an intermolecular balance or scale.7 This preference may either result from a symmetry breaking of the lone electron pairs at the oxygen themselves, due to induction effects along the chemical bonds, or – more likely – from the different repulsive and attractive environment of the two non-equivalent docking half-spaces. Therefore, such unsymmetric ketones provide a unique opportunity to probe the interplay of intermolecular interactions on a very subtle level, if the two docking isomers can be spectroscopically distinguished, e.g. by vibrational spectroscopy of the protic stretching mode of the solvent. This is only feasible at low temperatures and to avoid interference from the environment it should be attempted in vacuum, by studying isolated 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes of one ketone molecule and one solvent molecule.8 The standard way to prepare such complexes is supersonic jet expansion,9,10 but this is a non-equilibrium method which may freeze competing conformations rather than equilibrating them in the course of collisional cooling across the isomerisation barrier. Therefore, such an experiment only reflects the docking preference near a conformational freezing temperature7Tc, below which the barrier becomes unsurmountable on the time scale of the adiabatic jet expansion. Annealing processes like in weakly interacting matrix isolation are not possible.11 Softer degrees of freedom like rotation, intermolecular vibration or translation may however be further cooled, simplifying the spectra. Excitation in stiff vibrations is depopulated inefficiently, but this is of minor concern if the initial temperature of the molecules is sufficiently low.
1 complexes of one ketone molecule and one solvent molecule.8 The standard way to prepare such complexes is supersonic jet expansion,9,10 but this is a non-equilibrium method which may freeze competing conformations rather than equilibrating them in the course of collisional cooling across the isomerisation barrier. Therefore, such an experiment only reflects the docking preference near a conformational freezing temperature7Tc, below which the barrier becomes unsurmountable on the time scale of the adiabatic jet expansion. Annealing processes like in weakly interacting matrix isolation are not possible.11 Softer degrees of freedom like rotation, intermolecular vibration or translation may however be further cooled, simplifying the spectra. Excitation in stiff vibrations is depopulated inefficiently, but this is of minor concern if the initial temperature of the molecules is sufficiently low.
Therefore, one can idealise the outcome of a diluted supersonic co-expansion of a ketone with a protic solvent as the preparation of a single 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex for symmetric ketones and of two 1
1 complex for symmetric ketones and of two 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex isomers (see Fig. 1) for an unsymmetric ketone,8,12 the ratio of which depends on their energy difference and the barrier separating them. This isomerisation barrier is fairly transmissible for simple ketones. It involves a range of path options for the solvent over the top of the keto group or leaving the ketone plane, and none of these paths requires an intermediate breaking of the hydrogen bond.
1 complex isomers (see Fig. 1) for an unsymmetric ketone,8,12 the ratio of which depends on their energy difference and the barrier separating them. This isomerisation barrier is fairly transmissible for simple ketones. It involves a range of path options for the solvent over the top of the keto group or leaving the ketone plane, and none of these paths requires an intermediate breaking of the hydrogen bond.
Without a detailed simulation of the cooling process, it is difficult to predict the kinetic hindrance of the barrier, but based on several examples where such bistable complexes with low intermolecular barrier have been investigated in mild carrier gas expansions through room temperature slit nozzles, the conformational freezing temperature has been bracketed between about 20 K and 100 K for very low barriers,4,13 between 30 K and 150 K across barriers typical for ketone lone pair switching,12 or more generously between 20 K and 200 K.7 This uncertainty does not allow to extract very quantitative information about the energy difference between the docking isomers, but decisions about the energy sequence can usually be made, even for fairly small differences on the order of 1 kJ mol−1 or less. Gross errors in the size of the barrier can also be uncovered, if the spectral intensity information is reliable. Energy differences of more than 3 kJ mol−1 can usually be safely ruled out if both isomers are clearly observed and if there is no reason for an untypically high interconversion barrier and thus conformational freezing temperature.
The driving energy difference may be affected by different amounts of zero-point vibrational energy (ZPVE) in the isomers, but this effect is usually minimised for ketones, where the local hydrogen bond environment is almost the same on both sides. However, such a theory-favourable cancellation always needs to be checked. If it works, energy decomposition models14–16 can be directly interrogated to explain the energy imbalance in terms of London dispersion and other contributions, although one should always keep in mind that there is more than one way to decompose the observable total interaction energy into components. Error cancellation also helps in comparing observed (anharmonic) spectral shifts between isomers to the usual harmonic predictions, but again, one cannot expect perfect performance and must rely on trends across several systems. Deficiencies in the typically used DFT approaches8,12 can be further uncovered by single point energy calculations at higher levels of electronic structure theory.
Given all these caveats, it makes sense to investigate the simplest realistic model systems for ketone intermolecular balances in particular detail, to better understand the larger systems which start to be dominated by London dispersion interaction.17 The simplest unsymmetric ketone which comes to mind is 2-butanone or methyl ethyl ketone (MEK). 2-Butanone is favourable because it is predominantly monoconformational, disregarding a slight symmetry breaking into a pair of rapidly interconverting enantiomeric conformations.18–20 Its 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with the simplest alcohol methanol has been studied experimentally before,21 but possibly due to the action character of the employed IR-VUV double resonance technique, only a broad (109 cm−1 FWHM) OH-stretching band was observed, likely spanning the two docking sides of interest. This was attributed by the authors to fluxionality of the observed species, which were theoretically characterised at DFT level without including dispersion corrections. As we had not observed such broad bands in related systems8,12 and found dispersion correction to be essential, we decided to reinvestigate this model system using linear FTIR spectroscopy in supersonic jets.22
1 complex with the simplest alcohol methanol has been studied experimentally before,21 but possibly due to the action character of the employed IR-VUV double resonance technique, only a broad (109 cm−1 FWHM) OH-stretching band was observed, likely spanning the two docking sides of interest. This was attributed by the authors to fluxionality of the observed species, which were theoretically characterised at DFT level without including dispersion corrections. As we had not observed such broad bands in related systems8,12 and found dispersion correction to be essential, we decided to reinvestigate this model system using linear FTIR spectroscopy in supersonic jets.22
In this work, we show by comparison to homologous systems that the two docking sides of 2-butanone for methanol are separable and assignable by infrared spectroscopy. We investigate different theoretical approaches with respect to their quantitative deficiencies and error cancellations in describing the experimental findings. Thus, we endow this attractive model system21 with further theory benchmarking potential.
2 Materials and methods
2.1 Experimental methods
Gaseous mixtures of 2-butanone (Sigma-Aldrich, ≥99%) or 3-pentanone (Sigma-Aldrich, ≥99%) with methanol (Roth, >99.9%) were prepared in a large excess of helium (Linde, 99.996%) in a 67 L reservoir at typically 0.75 bar stagnation pressure and expanded over six magnetic valves through a pre-expansion chamber and a 600 mm × 0.2 mm slit nozzle into vacuum. Large (24 m3) buffer volumes and continuous pumping at 500 to 2500 m3 h−1 kept the background pressure sufficiently low while the expansion was probed at a resolution of 2 cm−1 using a Bruker 66v/S FTIR spectrometer, a 150 W tungsten lamp, CaF2 optics and a liquid nitrogen cooled InSb detector. Detailed descriptions of the setup can be found elsewhere.22Spectra of the OH/CH stretching region were co-averaged over 125 to 550 pulses to obtain sufficient signal-to-noise ratios. Cluster size and composition estimates were obtained by concentration variation through temperature control of liquid samples in the gas flow. The abundance of homodimers and oligomers was minimised by methanol dilution to the extent which was achievable with the liquid saturator supply. Towards docking ratio estimates, experimental band integral ratios were determined using a modified automated statistical evaluation.23,24 Integration windows between 4 and 12 cm−1 around the band maxima were statistically varied and synthetic noise appropriate for the instrument characteristics was added. Where band overlap with methanol dimer25 was an issue, dimer-subtracted spectra were also explored. For raw data, see https://doi.org/10.25625/2HXYTM.
2.2 Theoretical methods
The dispersion-corrected B3LYP26–28 hybrid functional is primarily used for band assignment purposes and sometimes compared to a functional (X3LYP) used in the VUV study21 and claimed to be particularly suitable for intermolecular interactions. In the spirit of a benchmark experiment, the exploration of other functionals is invited to minimise some of the deficiencies which are identified in this work. For the GGA functional BP86,26,29 some results are given in the ESI.† For manual structure searches, a def2-TZVP basis set30 was employed and the D3 dispersion correction31 with Becke–Johnson damping32–35 was used with its three body term. CREST36 structure screenings complemented the manual search. Re-optimisations were performed with the extended B3LYP-functional X3LYP37 with D3 correction,38 and for comparison to the VUV study21 also without dispersion correction. Electronic energy differences were recalculated at single-point DLPNO-CCSD(T) level39–41 for some DFT-optimised structures.Most calculations were carried out using ORCA version 4.2.1,42 relaxed torsional scans of monomer and complex structures along with reaction path optimisations using Turbomole.43,44 Transition state structures were searched with the Turbomole tool Woelfling43,44 and re-optimised with ORCA.42 More information on the computational details can be found in Table S1 of the ESI.† Due to the non-uniform cooling of different degrees of freedom during a supersonic jet expansion (10–20 K for rotation, 50–200 K for soft vibration, barrier-dependent for conformation) and the similarity of the interconverting species, partition functions were assumed to cancel between the different isomers and an effective Boltzmann conformational freezing temperature Tc was extracted from the predicted energy difference and the experimental population ratio. This serves to judge whether the predicted energy difference is realistic. Previous studies of ketone balances8,12 have suggested small net ZPVE corrections between the isomers, due to the strong similarity of the local hydrogen bond environment for the two oxygen lone electron pairs. Therefore, ZPVE correction was limited to the harmonic approximation and can even be neglected in several cases. A similar argument applies to IR OH-stretching downshift differences between isomers, where anharmonic effects are expected to cancel better than for the absolute shifts from the monomer to the complex, and much better than for absolute OH-stretching wavenumbers.
3 Results and discussion
3.1 Experimental assignment
To emphasise the benchmark experiment character of this study, the two docking isomers of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
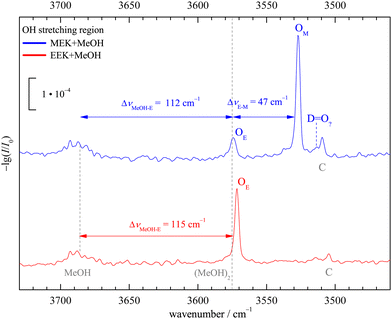
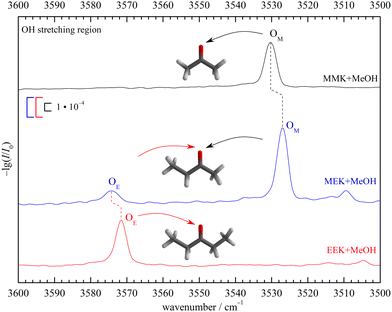
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of 2-butanone (methyl ethyl ketone, from now on MEK) with methanol (MeOH) shall be assigned purely experimentally. This is achieved by reference to the homologs 3-pentanone (ethyl ethyl ketone, from now on EEK) and acetone (methyl methyl ketone, from now on MMK), as shown in Fig. 2 in the IR spectral range where the hydrogen-bonded methanol OH-stretching fundamental is expected. At sufficient dilution, there is a single dominant peak for MMK (OM) and EEK (OE), as expected from the symmetry of the ketones and the dominance of a zig-zag or all-trans conformation of its alkyl backbone. For MEK, there are two peaks which are only slightly shifted from the symmetric MMK and EEK counterparts. OM is significantly stronger than OE, showing that MeOH prefers to dock on the methyl side, because the IR band strengths are unlikely to change much with alkyl substitution.8 The subtle spectral substitution shifts (dashed lines) can be rationalised in terms of the inductive effect of ethyl compared to methyl groups, which increases the hydrogen bond acceptor quality of the ketone and leads to a downshift of the coordinating OH vibration. In the following, this straightforward experimental assignment is further rationalised and analysed using quantum mechanical calculations, starting with DFT results.
1 complex of 2-butanone (methyl ethyl ketone, from now on MEK) with methanol (MeOH) shall be assigned purely experimentally. This is achieved by reference to the homologs 3-pentanone (ethyl ethyl ketone, from now on EEK) and acetone (methyl methyl ketone, from now on MMK), as shown in Fig. 2 in the IR spectral range where the hydrogen-bonded methanol OH-stretching fundamental is expected. At sufficient dilution, there is a single dominant peak for MMK (OM) and EEK (OE), as expected from the symmetry of the ketones and the dominance of a zig-zag or all-trans conformation of its alkyl backbone. For MEK, there are two peaks which are only slightly shifted from the symmetric MMK and EEK counterparts. OM is significantly stronger than OE, showing that MeOH prefers to dock on the methyl side, because the IR band strengths are unlikely to change much with alkyl substitution.8 The subtle spectral substitution shifts (dashed lines) can be rationalised in terms of the inductive effect of ethyl compared to methyl groups, which increases the hydrogen bond acceptor quality of the ketone and leads to a downshift of the coordinating OH vibration. In the following, this straightforward experimental assignment is further rationalised and analysed using quantum mechanical calculations, starting with DFT results.
 | ||
| Fig. 2 Jet FTIR OH-stretching spectra of MEK, EEK and MMK45 (scaled intensity) co-expanded with MeOH. Dashed lines connect analogous docking sites and lead to an unambiguous experimental assignment and preference for methyl side oxygen docking (OM) over ethyl side docking (OE) of MeOH to MEK. See Fig. S7 in the ESI† for more details. | ||
3.2 DFT results
The B3LYP-D3 optimised ketone MeOH complex structures can be characterised by the hydrogen bond angle α and the dihedral angle τ (see Fig. 1). The angle 0 ≤ α ≤ 180° (see however ref. 46) between the hydrogen bonded H and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group describes the deviation from the sp2-like preference of 120°. τ represents the inclination of the alcoholic proton relative to the ketone plane (out-of-plane twist) and encodes the docking preference for unsymmetric ketones with the limiting values of 0° and 180°. This preference is sensitive to local hydrogen bonding and repulsion of the OH group, but also to distant attractive methyl group interactions with the ketone substituents. The resulting complex geometry affects the OH-stretching wavenumber of the hydrogen bonded OH. For MMK and EEK complexes the two docking variants are either identical or enantiomeric and thus give rise to a single signal.
O group describes the deviation from the sp2-like preference of 120°. τ represents the inclination of the alcoholic proton relative to the ketone plane (out-of-plane twist) and encodes the docking preference for unsymmetric ketones with the limiting values of 0° and 180°. This preference is sensitive to local hydrogen bonding and repulsion of the OH group, but also to distant attractive methyl group interactions with the ketone substituents. The resulting complex geometry affects the OH-stretching wavenumber of the hydrogen bonded OH. For MMK and EEK complexes the two docking variants are either identical or enantiomeric and thus give rise to a single signal.
However, the ethyl groups in MEK and EEK induce further isomerism, which is not very competitive in the monomers but may gain importance in the complexes.47,48 Besides the preferred synclinal (s) orientation close to the ketone plane, a pair of anticlinal (ac) orientations rotated by about ±127° out of the ketone plane and, induced by the neighbouring keto group, another pair of clinal (c49) orientations rotated by about ±90° is predicted for MEK and EEK monomers, connected by low torsional barriers and uphill by more than 5 kJ mol−1 from the syn form (see Fig. S1–S3 and Table S2 in the ESI†). These predictions are in qualitative agreement with previous spectroscopic and computational evidence.18,19,50
Turning to the complexes with methanol, two distinguishable and almost isoenergetic isomers with s and c conformation on the docking side of MeOH are predicted for EEK (see Fig. 3). The solvent thus brings the c arrangement almost down to s, whereas the ac conformation is not predicted to be favourable. A somewhat less pronounced energy lowering of c towards s is predicted when MeOH docks on the ethyl or E side of MEK, but methyl side docking (M) is more attractive than either sE or cE in this case (see Fig. 3) and separated by an out-of-plane barrier typical for ketones8,12 (for more details see ESI,† Fig. S5 and S6). The common energy lowering of cE towards sE for MEK and EEK is likely connected to London dispersion interaction of the lateral ethyl group with the alcohol in combination with a relaxed steric repulsion between the alkyl and the OH groups. The ZPVE changes significantly between the two variants so that theory should not be fully trusted on their energy sequence. On the other hand, the shallow barrier predicted between the competing structures (see Fig. 3) should allow the less favourable structure to relax into the more favourable isomer. Because they are expected to differ spectroscopically (vide infra), experiment provides a way to decide between the close competition in a kind of secondary intermolecular balance, now more strongly affected by zero point motion.
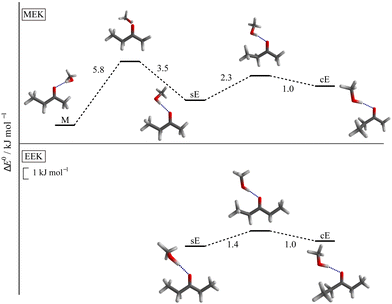 | ||
| Fig. 3 Most stable conformers for MEK (upper panel) and EEK (lower panel) solvated by MeOH and the relevant transition states for the interconversion, calculated at B3LYP-D3(BJ,ABC)/def2-TZVP level. The syn-ethyl- or sE-sided and clinal-ethyl- or cE-sided structure motifs are predicted for both ketones. For the methyl- or M-sided MEK complex only the most stable syn-conformation is shown (see also ESI† Fig. S4 and Table S4). | ||
While X3LYP-D3 calculations are consistent with the B3LYP-D3 findings (see Table S4 in the ESI†), leaving away the D3 correction (as was done in ref. 21) strongly raises the cE energy for EEK and MEK, qualitatively confirming the role of dispersion in stabilising cE. Interestingly, the energy difference between sE and M, i.e. the primary intermolecular energy balance, is hardly affected by the D3 correction. This is a case of fortuitous error cancellation between hydrogen bond, repulsion and different dispersion interactions, when methanol coordinates methyl ethyl ketone. It is also a consequence of the rather small size of the investigated ketone balance.
When the distant, non-solvated ethyl group of the ketone is rotated, the energetics is similar to that of the monomers, i.e. the syn form is without serious competition. Therefore, this distant syn conformation is always implied in the following (as in Fig. 3).
The predicted harmonic OH-stretching wavenumber of the isomers is strongly influenced by the hydrogen bond angle α. If it is close to 120° as in M and cE, the OH stretch has a low wavenumber, even lower for cE than for M. The sE conformation pushes the OH group further away (α > 130°, see Table S3 in the ESI†) and this leads to a predicted blueshift, which aids in the spectral assignment (see Fig. 2). The experimental quantification of isomers profits from robust IR absorption cross-section ratio predictions. As shown in Table S6 in the ESI,† their functional dependence is moderate in the harmonic approximation, as in other ketone balances.8,12
3.3 Comparison to experimental results
In Fig. 4 the OH-stretching region of MeOH expanded with MEK (top, blue) or EEK (bottom, red) is shown. The monomer signal (MeOH) with its rotational-tunneling substructure and traces of the downshifted donor mode51 of the homodimer (MeOH)2 at 3575 cm−1 are marked with black vertical dashed lines. The main signals OM (only MEK) and OE (both ketones, for MEK overlapping with methanol dimer traces25) are caused by the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes and have been assigned in Fig. 2. They fit the ketone balance trend of the sterically less hindered side exhibiting a lower OH-stretching wavenumber8,12 and the theoretical harmonic wavenumber splittings (51–52 cm−1, see Tables S5 and S8 in the ESI†) match the experimental one (47 cm−1) quite well due to cancelling anharmonicity contributions, if the sE conformation is assumed. Assignment to the theoretically competing cE conformation would instead invoke an inverted splitting of – (16–17) cm−1 which can be safely ruled out for OE relative to OM. At best, cE could be responsible for the weak D
1 complexes and have been assigned in Fig. 2. They fit the ketone balance trend of the sterically less hindered side exhibiting a lower OH-stretching wavenumber8,12 and the theoretical harmonic wavenumber splittings (51–52 cm−1, see Tables S5 and S8 in the ESI†) match the experimental one (47 cm−1) quite well due to cancelling anharmonicity contributions, if the sE conformation is assumed. Assignment to the theoretically competing cE conformation would instead invoke an inverted splitting of – (16–17) cm−1 which can be safely ruled out for OE relative to OM. At best, cE could be responsible for the weak D![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O? signal. All these conclusions can be drawn directly from experimental intensities, as the expected visibility of the conformers is similar (see Table S6 in the ESI†) and the methanol dimer contribution is minor (as evidenced in the EEK trace and Fig. S9 and S14 in the ESI†). By either subtracting an upper bound of the methanol dimer contribution or else not subtracting any methanol dimer signal contribution at all, one can bracket the possible influence of methanol dimer on the conformational signal ratio. A wider perspective of the experimental spectra is given in Fig. S8 (ESI†).
O? signal. All these conclusions can be drawn directly from experimental intensities, as the expected visibility of the conformers is similar (see Table S6 in the ESI†) and the methanol dimer contribution is minor (as evidenced in the EEK trace and Fig. S9 and S14 in the ESI†). By either subtracting an upper bound of the methanol dimer contribution or else not subtracting any methanol dimer signal contribution at all, one can bracket the possible influence of methanol dimer on the conformational signal ratio. A wider perspective of the experimental spectra is given in Fig. S8 (ESI†).
Together with the low interconversion barrier between cE and sE, this spectral sensitivity allows for a rigorous experimental constraint which is currently not easy to reproduce robustly by theory. In the complex of MeOH with MEK, the sE arrangement is definitely more stable than the cE arrangement. Because the two significantly differ in their harmonic ZPVE (cE generating more ZPVE when embedding the MeOH unit), this is not a benchmark for electronic structure theory only. It requires a reliable ZPVE prediction for the complexes to match experiment for the right reason. The M-sE balance itself is much less sensitive to such ZPVE issues and can thus be used to test electronic structure predictions more or less directly, as in previous cases.8,12 The C signals at lower wavenumber common to both ketone methanol expansions can be attributed to a trimeric or higher complex species, as shown by concentration and stagnation pressure variation for the EEK (see Fig. S15 and S16 in the ESI†) and MEK case (see Fig. S10–S13 in ESI†) and in analogous cases.52 For the small MEK signal D![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O?, a decision between a trimeric complex and a 1
O?, a decision between a trimeric complex and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 isomer is less clear, but in the analogous EEK case, trimeric contributions in that region can also be identified (see Fig. S16 in the ESI†) and suggest that relaxation of cE is nearly quantitative in the presence of MeOH, if it forms at all in the supersonic jet expansion. Once more, this indicates a sensitive benchmarking potential for combined electronic structure and nuclear zero point motion theory. If cE is predicted below sE in the MeOH complex of MEK at some level of computation, this is in stark contrast to experiment. As shown in Table S4 in the ESI,† all explored DFT-D3 calculations make this prediction at the bare electronic structure level, but the problem is resolved by adding harmonic ZPVE. Interestingly, it is also resolved by removing the D3 correction, so that the experiment is sensitive to overestimated D3 corrections. Because the D3 correction affects the cE–sE energy difference by as much as 2 kJ mol−1, the sensitivity is moderate.
1 isomer is less clear, but in the analogous EEK case, trimeric contributions in that region can also be identified (see Fig. S16 in the ESI†) and suggest that relaxation of cE is nearly quantitative in the presence of MeOH, if it forms at all in the supersonic jet expansion. Once more, this indicates a sensitive benchmarking potential for combined electronic structure and nuclear zero point motion theory. If cE is predicted below sE in the MeOH complex of MEK at some level of computation, this is in stark contrast to experiment. As shown in Table S4 in the ESI,† all explored DFT-D3 calculations make this prediction at the bare electronic structure level, but the problem is resolved by adding harmonic ZPVE. Interestingly, it is also resolved by removing the D3 correction, so that the experiment is sensitive to overestimated D3 corrections. Because the D3 correction affects the cE–sE energy difference by as much as 2 kJ mol−1, the sensitivity is moderate.
In Fig. 5 the downshifts relative to the MeOH monomer fundamental from experiment are plotted against harmonic def2-TZVP DFT predictions. Consistent with the known systematic overestimation of hydrogen bond-induced harmonic downshifts by most DFT methods, all data points stay below the ideal diagonal line. The discrepancy depends on the employed functional. Note that inclusion of anharmonicity likely increases that discrepancy further,53 suggesting that it is an intrinsic deficiency of the functionals. This intrinsic deficiency is not only hidden by the neglect of anharmonicity, but also by the neglect of London dispersion correction (vide infra).
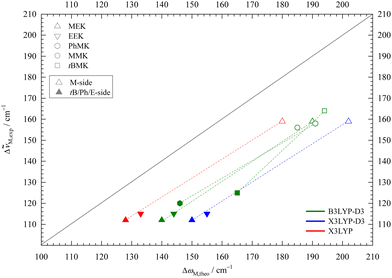 | ||
Fig. 5 Experimental (anharmonic) downshift Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) M,exp of MeOH in 1 M,exp of MeOH in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes with EEK and MEK plotted against the harmonically calculated downshifts ΔωM,theo for three different DFT/def2-TZVP variations. For comparison, published B3LYP-D3 values for acetophenone,8 pinacolone,12 acetone45 are included. Harmonic DFT overestimates wavenumber shifts uniformly, more so for X3LYP-D3 and less for bare X3LYP (even less for bare B3LYP, not shown). 1 complexes with EEK and MEK plotted against the harmonically calculated downshifts ΔωM,theo for three different DFT/def2-TZVP variations. For comparison, published B3LYP-D3 values for acetophenone,8 pinacolone,12 acetone45 are included. Harmonic DFT overestimates wavenumber shifts uniformly, more so for X3LYP-D3 and less for bare X3LYP (even less for bare B3LYP, not shown). | ||
Data from previously published MeOH complexes of MEK analogues are included in Fig. 5 at the B3LYP-D3 level. The M-sided isomers (empty symbols) for MEK, acetophenone,8 pinacolone,12 and MMK45 cluster together, as expected when the molecular variation is on the distant end. Solvation on the non-M side (filled symbols) leads to larger variation, but the difference between sE for MEK, EEK and acetophenone is still small. The main outlier is the bulky pinacolone (tBMK), but that was shown to be partly remedied by using a def2-QZVP basis set.12 Besides that outlier, the slope of the isomer-connecting lines remains similar, underscoring the observation that isomer splittings are predicted more reliably than monomer-referenced downshifts by harmonic DFT.
The trend for X3LYP-D3 is very similar, but with a larger shift from the diagonal, in line with intermolecular deficits noted before.38 Leaving away the dispersion correction brings the data points closer to the diagonal. Together with the insensitivity of the M-sE splitting to dispersion correction and the experimental elusiveness of the dispersion-favoured cE structure, this might encourage the empirical use of raw hybrid functionals, as done in the literature for X3LYP.21 However, it appears unlikely that this will give a systematic improvement beyond the present system, where dispersion forces are minimised due to the small size of the ketone and the alcohol. Even for the present system, dispersion correction during structure optimisation typically leads to lower DLPNO-CCSD(T) final energies than without correction (vide infra), indicating that the structures are improved by the D3 term.
Finally, the experimentally determined abundance ratio of the isomeric species in the MEK and EEK complexes with MeOH can be compared to the predicted energy difference at different theory levels. For this purpose, a concentration ratio of the dominant to the trace species cD/cT is obtained from the corresponding experimental absorption integral ratios, using B3LYP-D3 computed cross sections (the other explored functionals give very similar results). The upper and lower bounds of the absorption integral ratio are obtained with a Monte Carlo program23,54 and if there is no assignable signal (cE case), a lower bound is obtained from noise analysis (see Table 1). A 95% confidence interval is targeted and where MeOH dimer overlaps with the sE signal, the combined uncertainty of raw and difference spectra analysis is used for a conservative estimate.
| Ketone | D (ominant) | T (race) | I D/IT | c D/cT | 100xT |
|---|---|---|---|---|---|
| MEK | M | sE | 3.8–6.6 | 3.4–5.9 | 15–23 |
| sE | cE | >5.2 | >5.9 | <14 | |
| EEK | sE | cE | >7.6 | >9.3 | <10 |
The ranges and bounds in the cD/cT column of Table 1 are thus essentially pure experimental concentration ratios, which refer to the actual region probed in the expansion. They will be slightly different in other expansion regions or for other carrier gases or nozzle geometries, where conformational relaxation may be more or less efficient. Besides indicating that a cE species fraction of 10–15% among all E docking conformations should be visible in the spectra, the analysis shows that the sE species contributes about 20% to the isomer distribution under the employed experimental conditions. These fractions or the corresponding docking ratios cD/cT (Table 1) can now be converted to a conformational freezing temperature Tc under the assumption that theory predicts the correct energy difference between the trace and dominant isomer ΔE0T−D within the simplified Boltzmann analysis,7 with the universal gas constant R:
For the harmonically ZPVE-corrected B3LYP-D3 energy difference of 2.27 kJ mol−1 between the sE and M conformations of the MEK complex (Table S4 in the ESI†), the concentration ratio range extracted from Table 1 yields a Tc range of 154–223 K. This is somewhat above the expected value for a ketone balance and points at an overestimated sE-M energy splitting. The values for the X3LYP (with or without D3 correction) and in particular the BP86 functional are worse, partly even exceeding the nozzle temperature and therefore being unphysical (see Table S9 in the ESI† for details). With respect to the conformational freezing of the cE structure relative to sE, the lower bounds for effective temperatures are much lower and none of the functionals can be ruled out in the sense of predicting a visible cE signal for the MEK complex. For the EEK complex (see Table S10 in the ESI†), the Tc upper bounds are so low that either the computed energy splitting is underestimated or there is some hidden spectral contribution of cE.
When replacing the DFT electronic energy by DLPNO-CCSD(T)39 single point energies, the situation changes somewhat. The sE-M energy gap for MEK + MeOH decreases by more than 1 kJ mol−1 (see ESI,† Table S7) and leads to a more reasonable conformational freezing temperature of 70–100 K for the B3LYP-D3 optimised structure. Structure optimisation with the other functionals yields similar results, with the BP86-D3 structure giving the highest freezing temperatures. LED analysis14,15 confirms that the contribution of dispersion energy to the sE-M balance remains small. The effects on the more dispersion-driven cE conformation are less systematic across MEK and EEK and shall not be discussed in detail, as long as no homologous system is found which makes the cE docking conformation experimentally available.
In summary, DFT seems to overestimate the imbalance between methyl- and ethyl-sided docking of MeOH on MEK by about 1 kJ mol−1, but DLPNO-CCSD(T) electronic energies cure the deficiency and bring the energy prediction in agreement with experiment. The spectral pattern is described very well at DFT level, if systematic offsets are subtracted. It would be interesting to verify the infrared spectroscopy evidence by structural spectroscopy methods and to find a solvent which tips the ethyl side balance from syn to clinal, something which methanol falls short to realise, although the computations indicate a close competition.
3.4 Revisiting the IR + VUV results
The previous IR + VUV double resonance study on supersonic expansions of MEK with MeOH identified mono- and oligosolvate complexes and compared them to computations on X3LYP/6-31++G(d,p) level without dispersion correction.21 Here, we only comment on the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, which does not necessarily require size-selective methods55 to be analysed. As discussed above, the omission of dispersion correction was not critical due to the small, partially cancelling dispersion contributions. Therefore, the predictions are in good agreement with our experimental and computational findings (if a label switch between isomers IA and IB in the main text of ref. 21 is assumed). However, this should not be generalised to larger ketones.8,12
1 complex, which does not necessarily require size-selective methods55 to be analysed. As discussed above, the omission of dispersion correction was not critical due to the small, partially cancelling dispersion contributions. Therefore, the predictions are in good agreement with our experimental and computational findings (if a label switch between isomers IA and IB in the main text of ref. 21 is assumed). However, this should not be generalised to larger ketones.8,12
On the experimental side, the IR + VUV photoionisation vibrational spectrum looks very different. The spectrum is detected on the mass of the positively charged 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. Instead of two narrow, well separated signals of different intensity reflecting the intermolecular balance of the methanol between the two ketone lone electron pairs (Fig. 2), a broad transition with a FWHM (full width half maximum) of about 109 cm−1 with a proposed average band position near 3525 cm−1 was observed. This position is close to the 3527 cm−1 for the dominant OM peak in Fig. 4, but the about 20 times broader band also encompasses the OE signal in the FTIR spectrum as well as substantially lower wavenumbers. There could be many explanations for the broad intensity distribution, all related to the action spectroscopy nature of the VUV experiment. Possibilities include a strong dependence of ionisation on thermal excitation, multiphoton excitation or a fragmentation effect from larger clusters. The latter is particularly likely for the low wavenumber part, where there is also a sign change of the IR + VUV signal. The proposal that dimers between MEK and MeOH do “not adopt a well-defined hydrogen bonding motif”21 but instead dynamically switch over a barrier of about 5 kJ mol−1 cannot be confirmed in the present work and was also not observed in homologous complexes.8,12
1 complex. Instead of two narrow, well separated signals of different intensity reflecting the intermolecular balance of the methanol between the two ketone lone electron pairs (Fig. 2), a broad transition with a FWHM (full width half maximum) of about 109 cm−1 with a proposed average band position near 3525 cm−1 was observed. This position is close to the 3527 cm−1 for the dominant OM peak in Fig. 4, but the about 20 times broader band also encompasses the OE signal in the FTIR spectrum as well as substantially lower wavenumbers. There could be many explanations for the broad intensity distribution, all related to the action spectroscopy nature of the VUV experiment. Possibilities include a strong dependence of ionisation on thermal excitation, multiphoton excitation or a fragmentation effect from larger clusters. The latter is particularly likely for the low wavenumber part, where there is also a sign change of the IR + VUV signal. The proposal that dimers between MEK and MeOH do “not adopt a well-defined hydrogen bonding motif”21 but instead dynamically switch over a barrier of about 5 kJ mol−1 cannot be confirmed in the present work and was also not observed in homologous complexes.8,12
4 Conclusion
If a methanol molecule docks on the oxygen atom of methyl ethyl ketone, it has an energetic preference for the methyl side, which is overestimated by DFT functionals such as B3LYP-D3. Agreement with experiment can be achieved by replacing the electronic energy with CCSD(T) predictions, whereas the spectral splitting between the docking isomers is already well reproduced at DFT level. When the methanol chooses the less favourable ethyl side, it almost manages to tilt the ethyl group out of the ketone plane to maximise London dispersion, but this adaptive structure is not observed in experiment, likely because there is a low barrier towards the undistorted ketone backbone and because the adaption creates extra zero point vibrational energy. Finding an alcohol or phenol56 which brings the adaptive structure below the undistorted one is an interesting challenge, as is structural spectroscopy of this elementary intermolecular ketone balance. These conclusions were enabled by linear absorption infrared spectroscopy and chemical substitution, whereas VUV-detected IR spectroscopy reveals a broad vibrational signature which washes out the isomerism of the ketone solvation. In the context of the HyDRA challenge,57 the complex of 2-butanone with water, for which the triple M,sE,cE-isomerism has already been theoretically discussed,48 is also of interest.Author contributions
Conceptualisation, methodology, funding acquisition, supervision M. A. S.; experimental investigation, C. Z. and A. C. D.; formal analysis, C. Z. and M. A. S.; visualisation, data curation, writing original draft preparation, C. Z.; writing – review and editing, M. A. S., C. Z. and A. C. D.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge computer time on the local chemistry cluster 405832858/INST 186/1294-1 FUGG as well as on the GWDG computer cluster. Valuable support from our mechanical and electronic workshops is much appreciated. This study was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) with grant number 271107160/SPP1807.Notes and references
- J. P. M. Lommerse, S. L. Price and R. Taylor, J. Comput. Chem., 1997, 18, 757–774 CrossRef CAS.
- P. Murray-Rust and J. P. Glusker, J. Am. Chem. Soc., 1984, 106, 1018–1025 CrossRef CAS.
- M. Fioroni, M. D. Diaz, K. Burger and S. Berger, J. Am. Chem. Soc., 2002, 124, 7737–7744 CrossRef CAS.
- H. C. Gottschalk, A. Poblotzki, M. Fatima, D. A. Obenchain, C. Pérez, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, M. Krasowska, L. C. Kröger, K. Leonhard, M. Mogren Al-Mogren, H. Mouhib, F. Neese, M. N. Pereira, M. Prakash, I. S. Ulusoy, R. A. Mata, M. A. Suhm and M. Schnell, J. Chem. Phys., 2020, 152, 164303 CrossRef CAS PubMed.
- P. Hobza and R. Zahradnik, Chem. Rev., 1988, 88, 871–897 CrossRef CAS.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef CAS PubMed.
- A. Poblotzki, H. C. Gottschalk and M. A. Suhm, J. Phys. Chem. Lett., 2017, 8, 5656–5665 CrossRef CAS.
- C. Zimmermann, H. C. Gottschalk and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 2870–2877 RSC.
- J. B. Paul, C. P. Collier, R. J. Saykally, J. J. Scherer and A. O’Keefe, J. Phys. Chem. A, 1997, 101, 5211–5214 CrossRef CAS.
- D. J. Nesbitt, Annu. Rev. Phys. Chem., 1994, 45, 367–399 CrossRef CAS.
- D. Mihrin, A. Voute, P. W. Jakobsen, K. L. Feilberg and R. Wugt Larsen, J. Chem. Phys., 2022, 156, 084305 CrossRef CAS PubMed.
- C. Zimmermann, T. L. Fischer and M. A. Suhm, Molecules, 2020, 25, 5095 CrossRef CAS PubMed.
- H. C. Gottschalk, A. Poblotzki, M. A. Suhm, M. M. Al-Mogren, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, L. C. Kröger, K. Leonhard, H. Mouhib, F. Neese, M. N. Pereira, I. S. Ulusoy, A. Wuttke and R. A. Mata, J. Chem. Phys., 2018, 148, 014301 CrossRef.
- A. Altun, F. Neese and G. Bistoni, Beilstein J. Org. Chem., 2018, 14, 919–929 CrossRef CAS PubMed.
- W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778–4792 CrossRef CAS PubMed.
- A. D. Boese and G. Jansen, J. Chem. Phys., 2019, 150, 154101 CrossRef PubMed.
- C. Zimmermann, M. Lange and M. A. Suhm, Molecules, 2021, 26, 4883 CrossRef CAS PubMed.
- J. R. Durig, F. S. Feng, A. Wang and H. V. Phan, Can. J. Chem., 1991, 69, 1827–1844 CrossRef CAS.
- A. Sharma, V. P. Gupta and A. Virdi, Indian J. Pure Appl. Phys., 2002, 40, 246–251 CAS.
- M. M. Abe, K. Kuchitsu and T. Shimanouchi, J. Mol. Struct., 1969, 4, 245–253 CrossRef CAS.
- J.-W. Shin and E. R. Bernstein, J. Chem. Phys., 2017, 147, 124311 CrossRef.
- M. A. Suhm and F. Kollipost, Phys. Chem. Chem. Phys., 2013, 15, 10702–10721 RSC.
- G. Karir, N. O. B. Lüttschwager and M. A. Suhm, Phys. Chem. Chem. Phys., 2019, 21, 7831–7840 RSC.
- N. O. B. Lüttschwager, J. Open Source Software, 2021, 6, 3526 CrossRef.
- R. W. Larsen, P. Zielke and M. A. Suhm, J. Chem. Phys., 2007, 126, 194307 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- X. Xu and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2673–2677 CrossRef CAS PubMed.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- TURBOMOLE V7.3 2018, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com Search PubMed.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CAS.
- F. Kollipost, A. V. Domanskaya and M. A. Suhm, J. Chem. Phys. A, 2015, 119, 2225–2232 CrossRef CAS PubMed.
- V. Madhurima, Indian J. Pure Appl. Phys., 2004, 43, 550–555 Search PubMed.
- U. W. Suter, J. Am. Chem. Soc., 1979, 101, 6481–6496 CrossRef CAS.
- M. Śmiechowski, Chem. Phys. Lett., 2009, 480, 178–184 CrossRef.
- G. P. Moss, Pure Appl. Chem., 1996, 68, 2193–2222 CAS.
- G. Crowder and Q. Lin, Vib. Spectrosc., 1997, 14, 287–297 CrossRef CAS.
- F. Kollipost, J. Andersen, D. W. Mahler, J. Heimdal, M. Heger, M. A. Suhm and R. Wugt Larsen, J. Chem. Phys., 2014, 141, 174314 CrossRef CAS PubMed.
- E. M. Brás, T. L. Fischer and M. A. Suhm, Angew. Chem., Int. Ed., 2021, 60, 19013–19017 CrossRef PubMed.
- F. Kollipost, K. Papendorf, Y.-F. Lee, Y.-P. Lee and M. A. Suhm, Phys. Chem. Chem. Phys., 2014, 16, 15948–15956 RSC.
- N. O. B. Lüttschwager, NoisySignalIntegration.jl: A tool to determine uncertainty in numeric integrals of noisy x-y data, 2021, Available from GitHub.com: https://github.com/nluetts/NoisySignalIntegration.jl.
- H. Fricke, K. Schwing, A. Gerlach, C. Unterberg and M. Gerhards, Phys. Chem. Chem. Phys., 2010, 12, 3511–3521 RSC.
- T. Ebata, A. Fujii and N. Mikami, Int. Rev. Phys. Chem., 1998, 17, 331–361 Search PubMed.
- T. L. Fischer, M. Bödecker, A. Zehnacker-Rentien, R. A. Mata and M. A. Suhm, Phys. Chem. Chem. Phys., 2022, 24, 11442–11454 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Keywords, structures, energies, spectral details, experimental concentration series. See DOI: https://doi.org/10.1039/d2cp05141a |
| This journal is © the Owner Societies 2023 |