Contact electrification through interfacial charge transfer: a mechanistic viewpoint on solid–liquid interfaces

Abstract

Contact electrification (triboelectrification) has been a long-standing phenomenon for 2600 years. The scientific understanding of contact electrification (triboelectrification) remains un-unified as the term itself implies complex phenomena involving mechanical contact/sliding of two materials involving many physico-chemical processes. Recent experimental evidence suggests that electron transfer occurs in contact electrification between solids and liquids besides the traditional belief of ion adsorption. Here, we have illustrated the Density Functional Theory (DFT) formalism based on a first-principles theory coupled with temperature-dependent ab initio molecular dynamics to describe the phenomenon of interfacial charge transfer. The model captures charge transfer dynamics upon adsorption of different ions and molecules on AlN (001), GaN (001), and Si (001) surfaces, which reveals the influence of interfacial charge transfer and can predict charge transfer differences between materials. We have depicted the substantial difference in charge transfer between fluids and solids when different ions (ions that contribute to physiological pH variations in aqueous solutions, e.g., HCl for acidic pH, and NaOH for alkaline pH) are adsorbed on the surfaces. Moreover, a clear picture has been provided based on the electron localization function as conclusive evidence of contact electrification, which may shed light on solid–liquid interfaces.

---

Introduction

The scientific understanding of contact electrification (CE) (triboelectrification) remains un-unified as the term itself implies complex phenomena involving mechanical contact/sliding of two materials involving many physico-chemical processes.¹ The most prominent factor in deciphering the contact electrification is the interfacial charge transfer between the two materials upon contact. Encompassing the experimental illustrations by Wang et al., the proposed phenomena can only be understood through experimentation.¹ But, due to advanced theoretical presumptions, one can predict the tribology of the materials, which will be beneficial for many sectors, including modern industries, transportation, and power generation industries.²

The fundamental aspect of triboelectrification (TE) encompasses the interfacial charge transfer and tunneling phenomena. Due to physical and mechanical friction, the charges produced can help deliver the electrons in all the states, e.g., gas, liquid, and solid states. It has thus baffled many researchers who have found it cumbersome to propose a unified model to understand a wide variety of materials. Wang's group, on the other hand, has now well clarified the phenomenon as a result of the development of triboelectric nanogenerators (TENGs).³ Following the finding of TENGs, the mechanism of electron transfer, ion transfer, and material species transfer⁴ has gained prominence.

The triboelectric effect is well understood in the case of adsorbed water on surfaces where H⁺ and OH⁻ ions may transfer charges to the surface of the materials.⁵ However, this principle of charge transfer by liquid to solid contact remains controversial but not in the case between solids. The researchers' primary difficulty in studying the impact of ions on the surface of the materials is therefore the solid–liquid interface.⁶ CE between two metals or between metals and semiconductors, on the other hand, is induced by electron transfer, which has previously been thoroughly studied. The difficulty in depicting the exact phenomena in the solid–liquid interface remains a mystery due to the fluidity and dispersibility of liquids, and adsorption of molecules and ions on the surface.⁷

In retrospect, numerous theories have been proposed that electrification or charge transfer is based on physiochemical reactions, phenomenological factors that can be established empirically, such as the wettability of materials by water and relative humidity, and ion adsorption.⁸ The effect on the interfacial transfer between charges of electrified solid and fluid interfaces indicates how much energy transformation and storage systems such as batteries, fuel cells, and electrolyzers function/work. Intercalation, which is a key process in Li-ion and Na-ion batteries, depends on the rate at which an ion is transferred from a liquid to a solid phase and is determined not only by the bulk electrode (or electrolyte) properties but also by the properties of the interface itself.

Research on solid–solid CE has used a variety of processes and phenomena, such as electron transfer,^9,10 ion transport,¹¹ and materials transfer,¹² to describe various forms of triboelectricity (interfacial charge transfer for a wide variety of materials¹³). In relation to liquid and solid CE, it has become a very common phenomenon in our daily lives; for instance, the charging moving water inside a pipe and is now considered as the primary factor for many innovations and physical–chemical phenomena, such as liquid–solid triboelectric nanogenerators (TENGs),¹⁴ electric double-layer (EDL),¹⁵ and hydrophobic and hydrophilic surfaces. Information about liquid–solid CE, however, is exceedingly restricted and due to the profound lack of interpretation of EDL formation as a result of interfacial charge transfer^16–19 as for many decades, the answer remains uncertain on the identity of charge carriers (electrons and ions) in solid–solid CE. Recently, Wang et al. described the charge carriers that have been identified as solid–solid CE electrons based on photoexcitation and temperature-dependent effects on charged surfaces, without the involvement of an ion transfer mechanism.²⁰

For liquid–solid CE, ions are normally supposed to be transferred without exhaustive analysis specifically since ions, such as H⁺ and OH⁻, are also available in solvents (water). The essence of EDL implies the ionization or disassociation of surface groups as well as the adsorption or attachment of ions from the liquid to the solid surface, which induces the charging in the liquids of the separated surfaces. From this point of view, charge carriers are generally considered to be ions in the liquid–solid CE, and the transfer of electrons is not really envisaged. For the general explanation of CE, Wang et al. suggested an “electron-cloud potential-well” model where electron transfer in CE happens due to forced mechanical activity or touch, for induction of an electron-cloud overlap.²¹ Due to liquid pressure, electrons interact with atoms on a solid surface in a liquid interface, resulting in overlapping of the electron cloud. There is still debate on the identity of charge carriers in the liquid–solid CE, which is a basic topic in both CE and physical chemistry.²² Declining studies on surface charge at various temperatures are also being utilized to differentiate between the electron transfer and the solid–liquid contact ion transfer. This is because electrons are removed easily by thermionic emissions from the solid surface, while ions are normally attached to the solid surface atoms especially when the temperature is not too strong and are much harder to remove from the surface in comparison to electrons.²³

Sun et al. have shown that the water droplets tend to be charged positively with a positive solid surface, while the negative charging of a solid-state/surface induces a negative charge on the water droplets.²⁴ Nie et al. suggested that at the liquid–solid interface, the interfacial charge transfer was modulated by the physiological pH of the solvent medium through CE induced electron and ion transfer at the interface.²⁵ The aqueous solutions on the solid interface vary considerably depending on the form and concentration of ions. The increased CE charge level in the ion level increases due to an improvement in the ion transfer process in CE, while the reduction in CE charges in the free ion screen effect can be attributed to an increase in the concentration of ions.

Wang et al.¹ also showed that the solid surface acquires the charges of a molecule by chemical interactions at a liquid–solid interface since molecules are initially adsorbed on a virgin surface, which is not charged. They also suggested that the electron domination of CE occurs at an early stage of the object's exposure to the solution. To illustrate the aforementioned mechanism, herein, we systematically depicted the DFT adsorption mechanism of ions (Cl, H, OH, H₂O, Na, HCl, NaOH, NaCl, H₂, and O) on various solid interfaces/surfaces such as aluminum nitride (001), gallium nitride (001) and silicon (001) surfaces. The employed DFT approach enables us to understand the un-unified mechanism of solid–liquid interfacial charge transfer. Theoretical depictions include binding energies, density of states, electron localization function, and charge transfer. The findings in this paper present evidence for electron transfer (interfacial charge transfer) between solids and liquids, and they have an effect on the conventional interpretation of electric double layers in chemistry.

Computational methods

To ascertain the aforementioned experimentation and theories, theoretical calculations were employed based on the DFT formalism (first-principles theory). All calculations were performed using the Vienna Ab Initio Simulation Package (VASP)²⁶ software. A projected augmented wave (PAW) potential was utilized to represent the ion–electron interaction and an energy cutoff of 520 eV was employed for the plane-wave basis set. The generalized gradient approximation within the Perdew–Burke–Ernzerhof functional (GGA-PBE)²⁷ was used for the exchange-correlation potential. We considered the DFT-D3 dispersion correction method of Grimme to treat the long-range vdW forces.²⁸ The Brillouin zone integration is considered using 9 × 9 × 1 k-point meshes in the Monkhorst–Pack scheme. We utilize a (3 × 3 × 1) supercell for the Si (001) (32 atoms) surface, and a (1 × 1 × 3) supercell for both AlN (001) (32 atoms) and GaN (001) (32 atoms) surfaces with different molecules and ions adsorbed on the considered surfaces. To prevent the physical interaction between the periodic images, we have taken more than 20 Å in the perpendicular direction to the surface of the considered systems. The relaxation of structural parameters, e.g., lattice constant and atomic positions, was optimized until the magnitude of the Hellmann–Feynman force is less than 10⁻² eV Å⁻¹ and the energy convergence criterion between two electronic steps is taken to be 10⁻⁶ eV. The electron localization function of pristine as well as adsorbed surfaces has been analyzed using Vaspkit,²⁹ Vesta³⁰ and XCrysden³¹ (Fig. 1). We have also calculated and depicted the synergy between binding energies, surface charge density, and work function. Moreover, temperature-dependent ab initio molecular dynamics simulation has been performed for all the surfaces with the aforementioned ions to observe the effects of charge transfer at solid–liquid interfaces.³²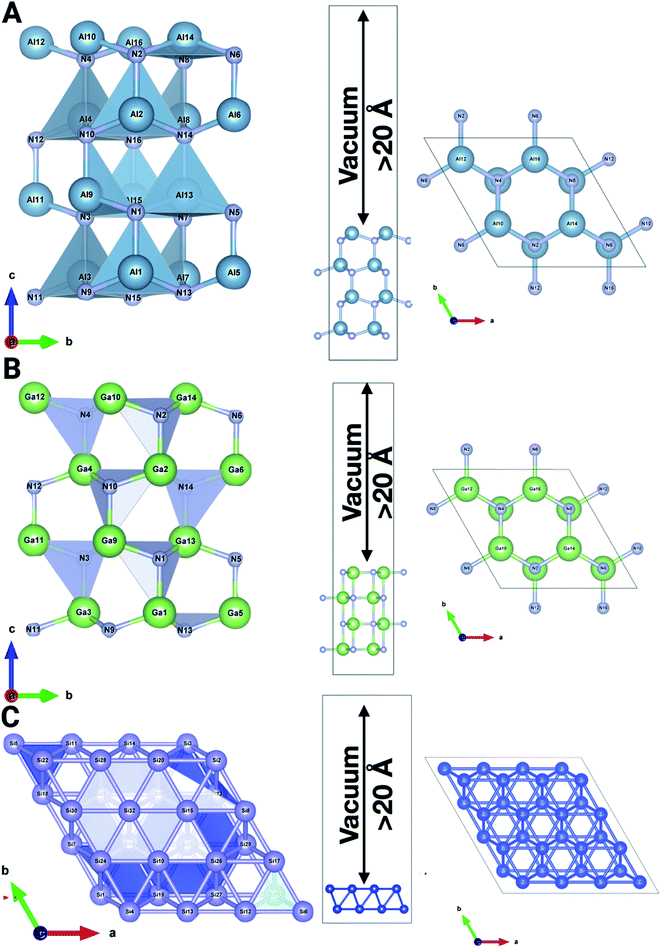

Fig. 1 The system comprising a (3 × 3 × 1) supercell for the Si (001) surface, and a (1 × 1 × 3) supercell for AlN (001) and GaN (001) pristine surfaces with a vacuum of >20 Å.

Molecular dynamics simulations were performed using the LAMMPS package.³³ The initial system has 6 × 6.5 × 10 nm for AlN, 6.5 × 6.5 × 10 nm for GaN, and 6 × 7 × 10 nm for Si in the x, y, and z axes, respectively. Periodic boundary conditions were applied in all directions. In the z-direction, the box is large enough to avoid interactions between mirror particles. The simulation box contains 6000 water molecules. AlN, GaN, and Si are held fixed in space. Water interactions were modeled by SPC/E.³⁴ The Lennard-Jones interaction parameters can be found in Table 1. Lorentz–Berthelot mixing rules were employed for the nonbonded interactions. The long-range electrostatic interactions were calculated using the particle–particle particle–mesh method, and the LJ cutoff distance was set to 1.2 nm. The SHAKE algorithm was used to keep the water molecules rigid.

Table 1 LJ parameters and atomic charges employed in this work

	ε LJ (Kcal mol^−1)	σ LJ (Å)	Charge
O	0.1553	3.166	−0.8476
H	0	0	+0.4238
Na	0.0347	2.580	+1
Cl	0.3825	3.850	−1
Si	0.4690	4.194	0
Al	0.505	4.008	+0.32
Ga	0.415	3.905	+3
N	0.069	3.26	−0.32 (AlN)/−3 (GaN)

---

Each system was equilibrated in a constant number of particles, volume, and temperature (NVT) ensemble for 1 ns at 300 K. The Nosé–Hoover thermostat^35,36 was used with a time constant of 0.1 ps. This was followed by another 1 ns simulation in NVT for data acquisition. The time step was set to 0.5 fs.

Results and discussion

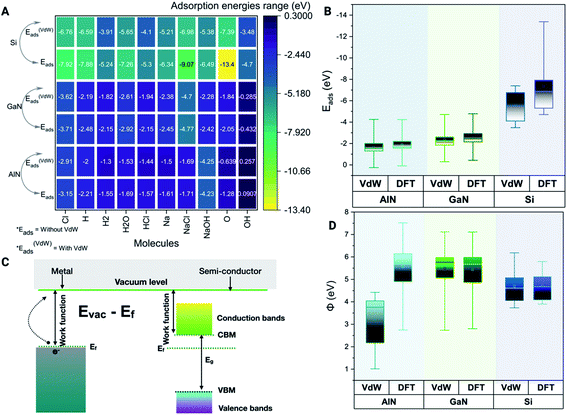
Physiological pH modulates the binding energies based on the adsorption of ions on different surfaces

The binding energy E_b is used to calculate the quantitative adsorption energy of molecules on different surfaces given by eqn (1)

E_b = E_{surface+molecules/ions} − E_{pristine_surface} − E_{molecules/ions} (1)

where E_{surface+molecules/ions} depict the pristine surface's total energy with an adsorbed molecule/ion, while the energies of the corresponding isolated pristine surfaces and isolated molecules/ions, respectively, are given by E_{pristine_surface} and E_{molecules/ions}. According to the above formula, the negative adsorption/binding energy (E_b) means exothermic adsorption. Fig. 2A depicts the binding energies for the ions and molecules on different surfaces from −13.4 eV to +0.09 eV. As stated, the binding energies of both the ions and molecules are higher in the case of Si (001) surfaces in comparison to GaN (001) and AlN (001) surfaces. The binding stability increases in the order AlN < GaN < Si. Moreover, the OH ion tends to be in the range of positive binding energy in the case of AlN but not with the other two surfaces. The most effective binding energy has been contributed by the singlet O atom on the Si surface followed by NaCl > Cl > H > H₂O > NaOH > Na. The overall analysis also deciphers the adsorption or binding mechanisms in which the Si (001) surface tends to have higher adsorption energies followed by GaN and AlN. Also, there has been a very small intrinsic effect of vdW forces on the adsorption energies as shown in Fig. 2B. The larger the molecule, the higher the contribution to the adsorption potential of van der Waals forces. When atoms and molecules do not naturally attract one other, electrostatic attraction between otherwise non-attracting atoms and molecules is generally influenced by van der Waals' forces which are generally weak forces. Similar observations were made from the adsorption potentials where vdW forces have relatively weaker adsorption energies. The aforementioned analysis depicted the contribution of ions and molecules on the different surfaces and their binding strength. In other words, the primary focus of our research was based on pH modulation based on ionic concentrations. Because H₂O has an amphoteric nature, i.e., it contains H atoms which are donatable as H⁺ ions and lone-pair electrons which can embrace H⁺ ions, it behaves as an acid as well as a base. Similarly, HCl is classified as an acid (it donates H⁺ ions to the solvent (water) when dissolved) and NaOH as a base (it dissociates into Na⁺ and OH⁻ ions). Out of all the depicted binding energies, apart from the singlet oxygen ion, NaCl which is a salt formed by the reaction of NaOH + HCl = NaCl + H₂O strongly binds to all the surfaces forming a covalent bond which is described in further sections. The binding strength of acids and bases on all the surfaces can be depicted through the analysis of NaCl which is a combination of a strong acid (HCl) and base (NaOH).

Fig. 2 (A) Heat map depicting the binding energies of the molecules and ions adsorbed on the surface of AlN (001), GaN (001), and Si (001) with and without the effect of vdW forces. (B) Box plot illustrating the overall effect with and without vdW forces (DFT) on binding or adsorption energies. (C) Schematic of the work function Φ in the case of (A) metals and (B) semiconductors. (D) Box plot depicting the work function relation (eV). All the box plots are depicted with 25% to 75% percentile and minimum and maximum points with median energies (eV).

Modulation of work function and surface reactions in the presence of ions and molecules

The minimum energy required to remove an electron from a solid surface is defined as the work function. According to this description, the work function is determined using eqn (2),

Φ = E_∞ − E_F (2)

where E_∞ denotes the electrostatic potential of electrons far from the surface and E_F depicts the electrostatic potential of electrons at the Fermi level, respectively. We have calculated the vacuum potential using p4vasp and Vaspkit using the planar average of the potential, and Fermi levels were taken from the OUTCAR files obtained from VASP optimization calculations. Fig. 2C shows a schematic energy diagram of a metal. The valence bands are filled with electrons up to the Fermi energy (E_F). The energy difference between the Fermi energy and vacuum level corresponds to the work function (Φ). The surface state can be modulated by using small amounts of contaminants or states/reactions that can significantly impact the surface work function. For instance, modulations based on surface conditions in the order of 1 eV are common in metals and semiconductors. These variations are induced by electrical surface dipoles, which modify the energy required for an electron to escape the sample. The work function sensitivity to chemical surface changes provides valuable information about the state of a specified surface. In a nondegenerate semiconductor, the fermi frequency is found inside the bandgap (one with a moderate doping level). This implies that the modulation of work function can be attributed to the ionization energy (energy gap between the valence band maximum (VBM) and vacuum). Since electronic states do not exist inside the bandgap in a semiconductor, the Fermi stage becomes a theoretical framework (Fig. 2C). This entails analyzing the Fermi distribution, a mathematical process that allows for the probability of an electron being in a certain electronic state. In our case, the work functions obtained upon adsorption of ions and molecules calculated with and without vdW forces are depicted in Fig. 2D. The synergy between work function and binding energies clearly entails the relationship that higher the work function, the tendency of binding energies is higher as the amount of energy required to extract an electron from the surface is high. The highest obtained work function for the ions and molecules in AlN and GaN (001) surfaces tends to be more as compared to Si (001) surfaces. Among all the adsorbents, NaOH and NaCl tend to be chemically bonded to all three surfaces, and thus the higher work function. If any adsorbent is chemically bonded to the surfaces, then the removal of electrons from the states of the molecules requires more energy than physically adsorbed molecules.

Ab initio temperature-based simulations

We have also verified the effect of temperature, i.e., at 0 K and 300 K, on the adsorption of ions and molecules on AlN, GaN, and Si surfaces. The total energy of the complex system was evaluated through the canonical (NVT) ensemble where the no. of atoms, volume, and temperature were kept constant and the total energy of the system was allowed to vary during the course of the simulation. We have used the Nosé–Hoover thermostat which is otherwise known as the extended Lagrangian which produces a canonical ensemble due to heat exchange between the fictitious degree of freedom and the real system. The ab initio dynamics gave us insight into how the fluctuations and the energies differ when these three surfaces were bound to ions and molecules at different temperatures. The AlN surface tends to have higher stability (lowest energy) followed by GaN > Si surfaces. The total energy fluctuations were observed at 300 K rather than at 0 K with all the surfaces considered for simulations (Fig. 3 A–C).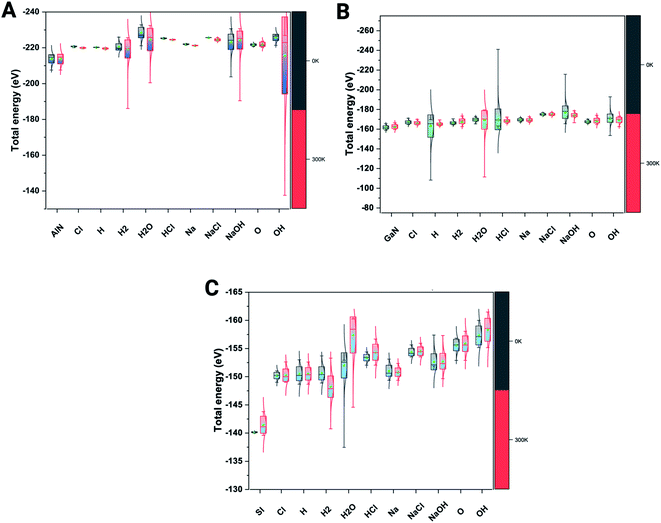

Fig. 3 Complex total energies (eV) are illustrated through the box plots at the given 0 K and 300 K temperatures for three systems. (A) AlN, (001), (B) GaN (001) and (C) Si(001).

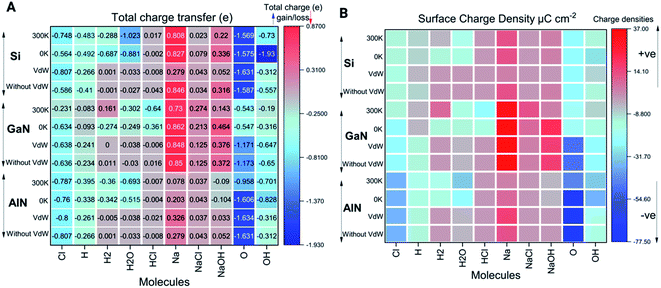
Charge transfer and electron localization function

As shown in Fig. 4A, the electron/charge transfer between the adsorbed ions and molecules on the surfaces has been elucidated to better understand the binding strength of the ions based on temperature-dependent simulations (0 K and 300 K). Furthermore, we have also considered the total charge transfer between molecules and the surfaces during the relaxations induced by vdW forces and without vdW forces as well. The charge transfer among the different ions and molecules can thus indicate the strength of both physical and chemical bonding to the surfaces. Out of all the molecules and ions, the singlet O atom tends to behave as an acceptor while Na behaves as a donor in all the cases. Molecules such as NaOH, H₂, H₂O, HCl, and NaCl and some of the ions such as H, Na, O, Cl and OH have the tendency of losing electrons or gaining electrons based on the electronegativity of the elements. From Fig. 4, H₂, H₂O and HCl molecules behave as electron acceptors while other molecules such as NaCl and NaOH transfer electrons to the surface. Apart from this, each ion (i.e. Cl, H, O, and OH) gained electrons from the surface because these elements have higher electronegativity except Na ions. The detailed values of charge transfer are presented in Fig. 4A.

Fig. 4 (A) Charge transfer between the adsorbed ions/molecules on the three different 001 surfaces (AlN, GaN and Si) analyzed through Bader charge analysis during the relaxation of the complex system with and without vdW forces and at 0 K and 300 K. (B) Surface charge density of the complex system for the ions/molecules during the relaxation of the complex system with and without vdW forces and at 0 K and 300 K.

It can be noted that charge transfer variability has been observed in all three cases at both 0 K and 300 K in terms of charge accumulation and donation to the nearby surfaces (Fig. 4A and ESI† data file). The ions or molecules that have significantly more binding energies tend to transfer electrons/charges to the surfaces, causing them to be chemically or physically adsorbed on the surfaces. Higher the electron density near the adsorbate, more likely the formation of covalent bonds between the adsorbate and adsorbent. Similarly, we have also calculated the surface charge density presented in Fig. 4B and given by the following equation (eqn (3)),

σ = q/A (3)

where q = charge and A = surface area. As per the definition, surface charge density (σ) is the quantity of charge per unit area, measured in coulombs per square meter (C m⁻²), at any point on a surface charge distribution on a two-dimensional surface. Charge density can be either positive or negative since electric charge can be either positive or negative. The charge density often depends on the electric charge accumulated on two-dimensional surfaces. In light of the calculations performed at varying temperatures, the surface charge density of Cl, H₂O, O, and OH atoms has mostly been accumulated on AlN/GaN, AlN, AlN/GaN/Si, and AlN/GaN/Si surfaces, respectively. All the other molecules and ions have a tendency to be physisorbed on the surfaces, i.e., move away from the surfaces, which is further illustrated by the Electron Localization Function (ELF).

The electron localization function (ELF) calculates the probability of finding an electron in the neighborhood space of a reference electron positioned at a given point and with the same spin. Physically, this calculates the degree of the reference electron's spatial localization and offers a mechanism for mapping electron pair likelihood in a multi-electron system. In this work, the adsorption of ions and molecules on different surfaces at 0 K and 300 K (AlN, GaN, and Si) has been analyzed and is depicted in Fig. 5, respectively. We have also shown the electron localization function of the relaxed complex structures in ESI Fig. S1.† ELF is a medium for describing chemical bonding, and the Lewis illustration can be said to reflect the chemical bonding organization in direct space. It appears to have a more complex relationship to the physical principle of localized and indigent (delocalized) electrons (orbital picture). The integrated electron density of an ELF basin (electronic basin population) does not seem to be related to the energetics of the bonding. The electronic basin population, on the other hand, characterizes the spatial arrangement of the bonding in terms of ELF and electron density. From the analysis, it can be depicted that, at 0 K, most of the molecules and ions are in a physisorption state rather than a chemisorption state. In consideration of the surfaces, we now delve into the nature of the bonding of molecules and ions on each surface. At 0 K, the AlN surface tends to form covalent bonds with O and NaOH, while at 300 K, it forms covalent bonds with Cl, NaCl, Na, OH, O, and OH, which means that the temperature has a substantial effect on different physisorption and chemisorption states. Similarly, in the case of GaN, NaCl, O, and Na form covalent bonds with the surface, while at 300 K, Cl, Na, NaCl, NaOH, O, and OH form covalent bonds. In the case of the Si surface, most of the molecules and ions form covalent bonds with the surface Si atoms except H₂, HCl, and NaCl at 0 K, and H₂ and NaCl at 300 K. Furthermore, this phenomenon of bonding patterns has been reflected previously with total charge transfer and surface charge density calculations.

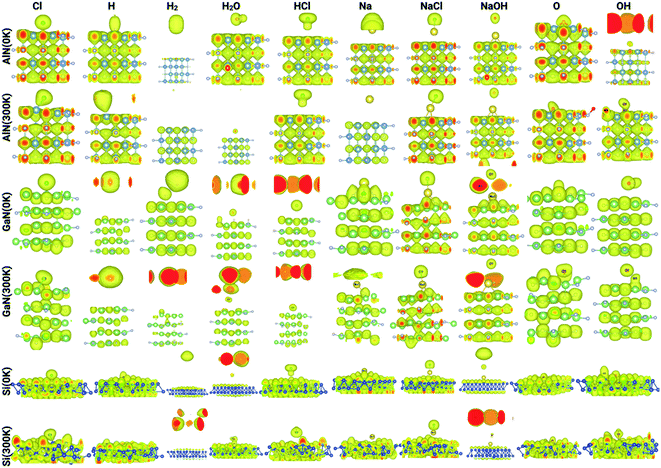Fig. 5 Electron localization function of the complex systems analyzed through Vesta for different ions/molecules adsorbed on the surface of AlN, GaN, and Si at 0 K and 300 K.

Classical dynamics to interpret the adsorption of ions/molecules at the interfacial surfaces

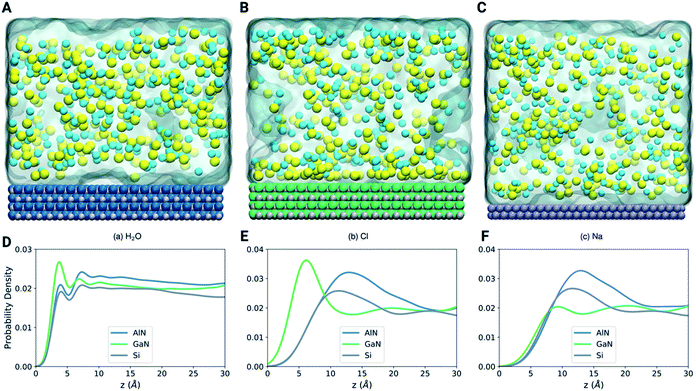
To further illustrate the mechanism of binding of different molecules and ions, we have performed LAMMPS based classical molecular dynamics simulations as shown in Fig. 6A–C (see the methods section). The density profiles in Fig. 6D–F show that the first layer of water is more pronounced at the GaN interface (Fig. 6A). On the other hand, the position of the first layer is similar for the three systems. Fig. 6E shows that the Cl atoms are highly attracted towards the GaN surface in comparison to the AlN and Si surfaces. This highly concentrated layer of Cl atoms in the GaN interface can be clearly visualized in the snapshot of the final configuration (Fig. 6B). On the other hand, both the snapshots of AlN and Si systems show that the Cl atoms are randomly distributed. Fig. 6F shows that there is no noticeable preference of Na atoms for any of the three materials. This analysis can direct us towards understanding the behavior of ion and molecule distribution and their binding mechanism on the different surfaces in a confined environment (in this case the solvent environment).

Fig. 6 LAMMPS based classical molecular dynamics simulations comprising three systems, (A) AlN, (B) GaN and (C) Si surfaces, embedded in a solvent box with different ions and molecules. (D–F) Density profiles of the three complex systems depicting the probability density of H₂O, Cl and Na.

Projected density of states (PDOS) analysis

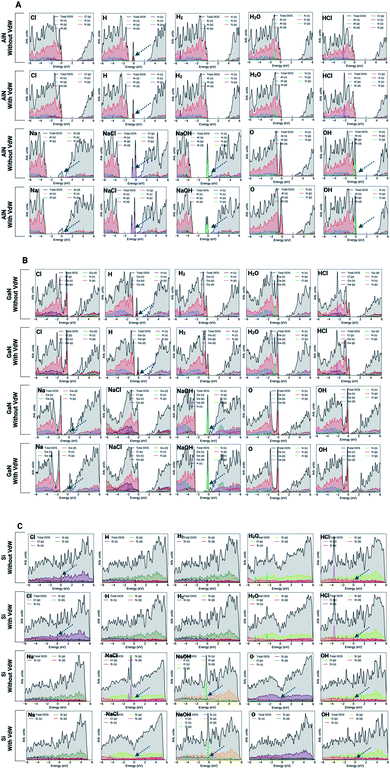
In order to gain a better understanding of the adsorption and binding process, the projected density of states (PDOS) was examined in both cases (with and without vdW forces). The electronic density of states of a system specifies the number of electronic states occupied by the unit at every level of energy. The DOS is directly related to the system's dispersion relationships. Strong energy-specific DOS necessitates the occupation of further states. ESI Fig. S2 and S3† present the PDOS for the pristine surfaces with and without the vdW interactions. As presented in Fig. 7A and B, it is evident that AlN and GaN surfaces show semiconducting behavior while the Si surface shows metallic behavior (Fig. 7C). To better explore the electronic properties of these surfaces along with molecules and ions adsorbed on the surfaces, the PDOS analysis gave us insights into the electronic state contribution of these ions/molecules at the Fermi level. In the case of the AlN surface, no evident electronic states were found near the Fermi level for Cl, H₂, H₂O, and HCl atoms both with and without vdW forces, while the electronic orbitals of N atoms are strongly hybridized with the O orbital and new electronic states appear near the Fermi level. It means that it enhances the conductivity of the AlN surface. But major contributions from NaCl (Cl_(p)), NaOH (O_(p)) and OH (O_(p)) ions at the AlN surface were evident. In the aforementioned molecules and ions, the electronic contributions at the Fermi levels were evident (peak at the Fermi level, which suggests charge transfer from molecules to the surface). Overall, the presence of a finite number of molecular states below/near the Fermi level suggests charge transfer from all these molecules to the surface, and stronger hybridization of molecular states indicates the greater chemical nature of bonds. In particular, at the AlN surface, the valence band states were entirely dominated by the ions or molecules taken into consideration, while in the conduction bands, there are no significant contributions from the molecules. In the case of the GaN (001) surface, the peaks were evident at the Fermi level for NaOH molecules. We also observed a typical metallic behavior of the Na ion upon adsorption on the surface of GaN. Both with and without vdW interactions, the Na ion showed metallic behavior upon adsorption as it formed a covalent bond with the N atom of the GaN surface with and without vdW interactions (Fig. S1†). It was also seen that the GaN surface has been affected by the adsorption of the H atom because the electronic states of the H atom are strongly hybridized with N atomic orbitals. It is evidence of significant charge transfer between the surface and ions. Apart from this, the other ions/molecules also have significant contributions to increasing/decreasing the spacing between the valence band maximum and conduction band minimum which is confirmed by the significant charge transfer between the surface and adsorbed ions/molecules (see Fig. 4 and 7B).

Fig. 7 Projected density of states of the complex systems (A) AlN, (B) GaN and (C) Si comprehending the electronic states with and without vdW forces for different ions/molecules. The Fermi level is at 0. The arrows indicate that there is electronic state contribution at the Fermi level.

In the case of the Si (001) surface, the major electronic state contributions at the Fermi level were from HCl, NaCl, NaOH, and OH molecules. The singlet ions except for Cl showed no major contributions at the Fermi level. It can be depicted from the analysis that the Si surface has a tendency to adsorb or bind to molecules rather than singlet ions. One peculiar observation we have made in the case of the singlet O ion which has the highest binding affinity among all the molecules or ions is that without the effect of vdW forces, the O ion has a higher binding affinity and has major electronic states at the Fermi level, while with vdW forces, the contribution from the O ion was not evident or significant. There was also a substantial two-fold decrease in the binding (adsorption) energy as well. Si–O bonds are usually ∼50% ionic and 50% covalent. With the introduction of vdW forces, the O atoms were covalently bonded to three Si atoms as per our calculations, and without vdW forces, the O atom formed covalent bonds with two Si atoms. Silicon also has a normal valence of 4, while for oxygen it is 6. Applying the octet rule where each atom wants a complete set of 8 shared electrons in the outer shell, Si can bond with 4 oxygen atoms and oxygen can bond with 2 silicon atoms. So, Si surrounds itself with 4 oxygens to fill its octet and oxygen surrounds itself with 2 silicons to complete its octet. In the case without vdW forces, the oxygen atom bonds with 3 silicon atoms but then the added silicon atoms will have unused valences which are, in the case of the calculations without vdW forces, what significantly increase the adsorption energy and thus, we see the electronic state contributions at the Fermi level.

Conclusion

Theoretical calculations using combinatorial DFT and classical molecular dynamics simulation approaches have been systematically investigated on three different surfaces upon the adsorption of different ions and molecules. The basic understanding of this work could be attributed to the effect of physiological pH (i.e., HCl being acidic, NaOH being basic and NaCl being neutral) that can modulate the interfacial charge transfer mechanisms. In other words, contact electrification which has been shown experimentally explicitly by Wang et al. has nearly contributed to the physical meaning of the term using this approach. Unlike previous studies based only upon the adsorption energy of different molecules and gases on solid surfaces, we have explored the atomic scale analysis using a first principles theory based on the DFT formalism. The analysis revealed some intriguing factors such as that the relation of the work function with binding energies does correlate with the fundamental aspects of physics. However, in some cases, e.g., NaCl and NaOH, there seems to be the involvement of coordination chemistry that drives the interfacial charge transfer. Nevertheless, a paradigm shift in the field of electricity generation and storage has contributed to many advancements in the practical world. It is thus an effort to understand some of the basic concepts, and more interestingly theoretical concepts such as the DFT formalism can be applied to replicate the practicality observed in day-to-day life.

Data availability

The calculated energies, charge transfer, complex energies and surface charge densities have been listed in the ESI† data file.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge financial support from the Swedish Research Council (Grant no. VR-2016-06014 and VR-2020-04410) and J. Gust. Richert stiftelse, Sweden (2021-00665). SNIC and HPC2N are acknowledged for providing computing facilities. MK was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brazil (CAPES) – Finance Code 001 – and in part by CNPq (Grant No. 201097/2020-6).

References

1. Z. L. Wang and A. C. Wang, Mater. Today, 2019, 30, 34–51.
2. P. E. Shaw, Nature, 1926, 118, 659–660.
3. Z. L. Wang, ACS Nano, 2013, 7, 9533–9557.
4. F.-R. Fan, Z.-Q. Tian and Z. Lin Wang, Nano Energy, 2012, 1, 328–334.
5. C. Liu and A. J. Bard, Chem. Phys. Lett., 2009, 480, 145–156.
6. J. Lowell, J. Phys. D: Appl. Phys., 1977, 10, L233–L235.
7. W. R. Harper, Contact and Frictional Electrification, Clarendon Press, 1967.
8. A. Schella, S. Herminghaus and M. Schröter, Soft Matter, 2017, 13, 394–401.
9. H. W. Gibson, J. Am. Chem. Soc., 1975, 97, 3832–3833.
10. M. Sakaguchi, M. Makino, T. Ohura and T. Iwata, J. Electrost., 2014, 72, 412–416.
11. L. S. McCarty and G. M. Whitesides, Angew. Chem., Int. Ed., 2008, 47, 2188–2207.
12. A. Šutka, K. Mālnieks, L. Lapčinskis, P. Kaufelde, A. Linarts, A. Bērziņa, R. Zābels, V. Jurķāns, I. Gorņevs, J. Blūms and M. Knite, Energy Environ. Sci., 2019, 12, 2417–2421.
13. R. K. Pandey, H. Kakehashi, H. Nakanishi and S. Soh, J. Phys. Chem. C, 2018, 122, 16154–16160.
14. H. Cho, J. Chung, G. Shin, J.-Y. Sim, D. S. Kim, S. Lee and W. Hwang, Nano Energy, 2019, 56, 56–64.
15. M. A. Brown, A. Goel and Z. Abbas, Angew. Chem., Int. Ed., 2016, 55, 3790–3794.
16. S. Sang, Q. Wu and K. Huang, Colloids Surf., A, 2008, 320, 43–48.
17. R. Hunter and H. J. Wright, J. Colloid Interface Sci., 1971, 37, 564–580.
18. V. N. Paunov, B. P. Binks and N. P. Ashby, Langmuir, 2002, 18, 6946–6955.
19. F.-R. C. Chang and G. Sposito, J. Colloid Interface Sci., 1994, 163, 19–27.
20. S. Lin, L. Xu, A. Chi Wang and Z. L. Wang, Nat. Commun., 2020, 11, 399.
21. S. Lin, L. Xu, C. Xu, X. Chen, A. C. Wang, B. Zhang, P. Lin, Y. Yang, H. Zhao and Z. L. Wang, Adv. Mater., 2019, 31, 1808197.
22. S. Lin, L. Xu, L. Zhu, X. Chen and Z. L. Wang, Adv. Mater., 2019, 31, 1901418.
23. C. Xu, Y. Zi, A. C. Wang, H. Zou, Y. Dai, X. He, P. Wang, Y.-C. Wang, P. Feng, D. Li and Z. L. Wang, Adv. Mater., 2018, 30, 1706790.
24. Y. Sun, X. Huang and S. Soh, Angew. Chem., 2016, 55, 9956–9960.
25. J. Nie, Z. Ren, L. Xu, S. Lin, F. Zhan, X. Chen and Z. L. Wang, Adv. Mater., 2020, 32, e1905696.
26. J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
28. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
29. V. Wang, N. Xu, J. C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2019, 267, 108033.
30. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
31. A. Kokalj, J. Mol. Graphics Modell., 1999, 17, 176–179.
32. D. Marx and J. Hutter, Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge University Press, Cambridge, 2009,  DOI:10.1017/CBO9780511609633.
33. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
34. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
35. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
36. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00467k

---