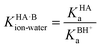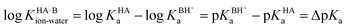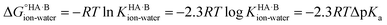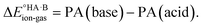Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of solvation in proton transfer reactions: implications for predicting salt/co-crystal formation using the ΔpKa rule†
Aurora J.
Cruz-Cabeza
 *ab,
Matteo
Lusi
*ab,
Matteo
Lusi
 c,
Helen P.
Wheatcroft
b and
Andrew D.
Bond
c,
Helen P.
Wheatcroft
b and
Andrew D.
Bond
 d
d
aDepartment of Chemical Engineering, School of Engineering, University of Manchester, UK. E-mail: aurora.cruzcabeza@manchester.ac.uk
bChemical Development, Pharmaceutical Technology & Development, AstraZeneca, Macclesfield, UK
cDepartment of Chemical Sciences, Bernal Institute, University of Limerick, Limerick, Ireland
dYusuf Hamied Department of Chemistry, University of Cambridge, Cambridge, UK
First published on 21st April 2022
Abstract
The ΔpKa rule is commonly applied by chemists and crystal engineers as a guideline for the rational design of molecular salts and co-crystals. For multi-component crystals containing acid and base constituents, empirical evidence has shown that ΔpKa > 4 almost always leads to salts, ΔpKa < −1 almost always leads to co-crystals and ΔpKa between −1 and 4 can be either. This paper reviews the theoretical background of the ΔpKa rule and highlights the crucial role of solvation in determining the outcome of the potential proton transfer from acid to base. New data on the frequency of the occurrence of co-crystals and salts in multi-component crystal structures containing acid and base constituents show that the relationship between ΔpKa and the frequency of salt/co-crystal formation is influenced by the composition of the crystal. For unsolvated co-crystals/salts, containing only the principal acid and base components, the point of 50% probability for salt/co-crystal formation occurs at ΔpKa ≈ 1.4, while for hydrates of co-crystals and salts, this point is shifted to ΔpKa ≈ −0.5. For acid–base crystals with the possibility for two proton transfers, the overall frequency of occurrence of any salt (monovalent or divalent) versus a co-crystal is comparable to that of the whole data set, but the point of 50% probability for observing a monovalent salt vs. a divalent salt lies at ΔpKa,II ≈ −4.5. Hence, where two proton transfers are possible, the balance is between co-crystals and divalent salts, with monovalent salts being far less common. Finally, the overall role played by the “crystal” solvation is illustrated by the fact that acid–base complexes in the intermediate region of ΔpKa tip towards salt formation if ancillary hydrogen bonds can exist. Thus, the solvation strength of the lattice plays a key role in the stabilisation of the ions.
Introduction
Proton transfer reactions between an acid and a base are responsible for many natural phenomena, from the existence of salts to the zwitterionic nature of common amino acids in environments amenable to life, or the interactions between proteins and substrates. From a chemical point of view, acid–base equilibria can easily be studied. In particular, the activity (or concentration) of ionised species can be measured in solution and acid dissociation constants (Ka) calculated and reported, typically in the form of pKa values. Moreover, robust computational models have been developed to predict aqueous pKa values from the molecular structure.1–3Proton transfer is also common in the solid state, as demonstrated by the large number of molecular salts4 and zwitterionic crystal structures reported in the Cambridge Structural Database (CSD).5 In molecular crystals, proton transfer reactions generally lie fully to one side of the chemical equation, yielding either a co-crystal where no proton transfer occurs or a salt where a proton is transferred from an acid to a base. Exceptions include dynamic systems, such as solid-state proton conductors,6 or cases in which protons appear to be located part way between the acid and the base.7 The characterisation of such systems can be complicated by the inherent difficulties associated with locating H atoms using X-ray diffraction data, and in some cases the extent of proton transfer may be temperature dependent.8,9 Because of this, complementary characterisation techniques, such as XPS,10–12 solid-state NMR13 or neutron diffraction14,15 (amongst others16), often need to be used to locate precisely the position of the acid H atoms. There are also cases where both ionised and non-ionised species of an acid or base are present in the same crystal.17
The ionisation of active pharmaceutical ingredients (APIs) into salts plays a crucial role in the formulation of medicines.4,18 Salts are often more soluble than their corresponding non-ionised forms, thereby affording drugs with improved pharmacokinetics.19 In recent years, co-crystals have been shown to be a viable alternative to salts since they can also improve the solubility of APIs20 whilst offering other advantages, such as being less prone to hydration.21 Co-crystals are often designed using crystal engineering concepts,22–25 whereby suitable co-crystal formers are selected based on their potential to form strong molecule-to-molecule interactions (synthons), typically based on hydrogen bonds.26–28 Very often, the targeted interactions involve an acid and a base. Indeed, hydrogen bonds are particularly strong, and therefore most attractive for crystal engineering strategies, for acid–base pairs with ΔpKa ≈ 0, where ΔpKa = pKa(protonated base) − pKa(acid).29,30 However, such strategies may be compromised by proton transfer in the solid state, thereby yielding a salt rather than the intended co-crystal product.
As a rule of thumb, salt formation in a molecular crystal is typically considered to be likely if the ΔpKa for the constituent acid and base is larger than 3. In 2005, Bhogala et al.31 noted that negative values of ΔpKa always lead to the formation of co-crystals. This so-called “ΔpKa rule” has been commonly used for the rational design of salts and co-crystals, supported by the free availability of experimental and calculated pKa data. In 2012, Cruz-Cabeza revised the rule on the basis of a survey of ca. 6500 crystal structures and pKa values calculated for the molecular components.32 It was found that ΔpKa > 4 almost always leads to salts, ΔpKa < −1 almost always leads to co-crystals and ΔpKa between −1 and 4 can be either. The intermediate region of ΔpKa accommodates what Childs has referred to as the salt/co-crystal continuum.33
Given the enduring popularity of the ΔpKa rule amongst chemists and crystal engineers,34–36 this paper sets out to review the theoretical basis of the rule, highlighting (in particular) the role of solvation for determining the outcome of proton transfer reactions in the solid state. When applying the ΔpKa rule to predict salt/co-crystal formation, a key question is how the crystal lattice influences proton transfer, particularly in the intermediate region close to ΔpKa ≈ 0. Some new data extracted from an extensive set of crystal structures demonstrates how the ΔpKa rule might be fine-tuned for specific classes of crystals, such as crystalline hydrates. Analysis of those structures also reveals the important role played by ancillary hydrogen-bonds in stabilising ionisation in the solid-state.
Methods
pKa and ΔpKa calculations
pKa values were calculated using ChemAxon’s Marvin software suite (version 21.13),37 either through the visualiser or via the command line executable for the bulk processing of many compounds. The calculator returns pKa values for both acids and protonated bases (depicted in the visualiser in red and blue, respectively). The ΔpKa for an acid–base pair was then calculated by subtracting the pKa values of the strongest acid and strongest base, where ΔpKa = pKa(BH+) − pKa(A). For systems where a second proton transfer is possible, a second value of ΔpKa, denoted ΔpKa,II, was also calculated. For this calculation, the stoichiometry of the system was accounted for when considering the second-strongest acid and base. For example, the first ΔpKa uses the lowest pKa(A) and the highest pKa(BH+) in the crystal structure (i.e. the strongest acid and strongest base) and the second ΔpKa,II would use the second lowest pKa(A) and the second highest pKa(BH+). Depending on the crystal composition and stoichiometry, the second base could be the same as the first for a H2A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B system with a 1
B system with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry (resulting in {A2−}{BH+}2) or it could be the second strongest basic functional group in the base for a system with a 1
2 stoichiometry (resulting in {A2−}{BH+}2) or it could be the second strongest basic functional group in the base for a system with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry (resulting in {A2−}{BH22+}). The ΔpKa values were obtained from the calculated pKa values using a simple Python script. Finally, it was recorded whether the acid–base pair for each ΔpKa calculation was located within the same molecule or in different molecules. This differentiates ΔpKa values for intermolecular proton transfer (salt formation) from ΔpKa,self values for intramolecular proton transfer (zwitterion formation).
1 stoichiometry (resulting in {A2−}{BH22+}). The ΔpKa values were obtained from the calculated pKa values using a simple Python script. Finally, it was recorded whether the acid–base pair for each ΔpKa calculation was located within the same molecule or in different molecules. This differentiates ΔpKa values for intermolecular proton transfer (salt formation) from ΔpKa,self values for intramolecular proton transfer (zwitterion formation).
Energy calculations
Energy calculations were performed with Gaussian 16 (ref. 38) using the B97d level of theory and the 6-31+G(d,p) basis sets.39 For the calculation of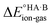 , ions, as well as neutral species, were optimised separately and the term
, ions, as well as neutral species, were optimised separately and the term 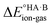 was calculated as the difference between the electronic energy of the ions minus the electronic energy of the neutral species. Implicit solvation models (SMD)40 for toluene, 2-heptanone and water were also used for some calculations. For the calculation of the potential energy for proton transfer in acid–base pairs, molecular models were generated manually using Avogadro41,42 and initially optimised using the MMFF94s forcefield.43 The resulting model for the acid–base dimer was then optimised in the gas phase using Gaussian. In all cases, the acid and base were oriented to form an A–H⋯B hydrogen bond. The resulting geometry (containing neutral species in all cases) was then used to run constrained optimisations in various media (gas phase, toluene, 2-heptanone and water). Here, the distance between the acid proton and the acceptor atom of the base was constrained progressively in the range of −0.8 to +2.4 Å in steps of 0.1 Å. Energies are reported relative to the best non-ionised gas-phase geometry in each case.
was calculated as the difference between the electronic energy of the ions minus the electronic energy of the neutral species. Implicit solvation models (SMD)40 for toluene, 2-heptanone and water were also used for some calculations. For the calculation of the potential energy for proton transfer in acid–base pairs, molecular models were generated manually using Avogadro41,42 and initially optimised using the MMFF94s forcefield.43 The resulting model for the acid–base dimer was then optimised in the gas phase using Gaussian. In all cases, the acid and base were oriented to form an A–H⋯B hydrogen bond. The resulting geometry (containing neutral species in all cases) was then used to run constrained optimisations in various media (gas phase, toluene, 2-heptanone and water). Here, the distance between the acid proton and the acceptor atom of the base was constrained progressively in the range of −0.8 to +2.4 Å in steps of 0.1 Å. Energies are reported relative to the best non-ionised gas-phase geometry in each case.
Datasets of crystal structures
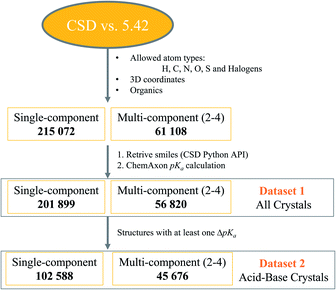
Crystal structure datasets were built following the steps depicted in Fig. 1. The CSD version 5.42 (ref. 44) was first filtered for structures containing any combination of the atom types H, C, O, S and halogens, and with determined 3D coordinates. Only organic structures were thus retrieved. This yielded over 215k structures of single-component crystals and over 61k structures of multi-component crystals.The CSD Python API interface was then used to generate SMILES strings for all components in the crystal structures, and the stoichiometry and nature of the components were established. Components with a positive charge were designated as cations, those with a negative charge as anions, and those with separation of charges within the same compound as zwitterions (which could also be anions or cations depending on the overall charge). Cations and zwitterions were further classified as quaternary (Q4) if the positive charge was not due to proton transfer (e.g. N+ bonded to four other C atoms). The SMILES of neutral components were checked and flagged as water, solvent (if within the 18 most common solvent types in the CSD) or main molecular component. Most of the total 276k retrieved crystal structures passed successfully through the pKa calculator, but some failed due to errors, disorder or uncommon SMILES strings. The final dataset-1 contained nearly 259k crystal structures with calculated pKa values.
Dataset-1 was then filtered for structures containing at least one acid–base pair, and thus one ΔpKa value, resulting in dataset-2, containing over 148k crystal structures. A Python script was written to analyse all data. The number of protons transferred in each crystal structure was recorded, as well as the location of the strongest acid and base. If the strongest acid and base were contained within the same molecule, ΔpKa was classified as ΔpKa,self and these data were used for the analysis of trends in zwitterions and neutral compounds. If the strongest acid and base were contained within different molecules in the crystal, this was classified as a standard ΔpKa. Second strongest acids and bases were also considered and ΔpKa,II was recorded for relevant structures.
Full interaction maps
Full interaction maps (FIMs)45 were calculated for pairs of acids and bases using a water oxygen as a probe and displaying only the third contour with the standard setting of 6.0 (higher localised special probability). This was done using Mercury version 2021.2.0.46Hydrogen bond analysis in salts and co-crystals with ΔpKa ≈ 0
In total, 818 structures of co-crystals and monovalent salts with ΔpKa ≈ 0 (within an absolute tolerance of 1 unit, ΔpKa values between −0.5 and 0.5) were identified in dataset-2. These crystal structures were loaded into Conquest and the hydrogen-bonding environments of the acid–base pairs were analysed. First, the set was filtered to structures containing an acid–base contact involving a carboxylic acid/carboxylate. This resulted in a subset of 531 structures. The ancillary hydrogen bonds (HBs) around the carboxylic acid/carboxylate were then analysed further and structures grouped into three subsets: structures with 0, 1 or 2 ancillary HBs. For this purpose, Conquest queries were built for the different HB environments, with HBs identified as follows:• The HB donor is either an N or an O atom (no C atoms).
• The HB acceptor is either O or the O− in the carboxylic acid or carboxylate, respectively.
• The distance between the non-H atoms involved in the HB is less than the sum of their van der Waals radii.
• The angle of the HB (N/O–H⋯O/O−) is between 120 and 180°.
• Both intramolecular and intermolecular HBs were recorded.
Theoretical background
Gibbs free energy and ΔpKa
For the dissociation of a monoprotic acid (HA) in water, the equilibrium is quantified by the acid dissociation constant, KHAa:For a monoprotic base (B) accepting a proton in water, it is convenient also to quantify the equilibrium using the acid dissociation constant of the protonated base, 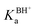 :
:
Since an equilibrium between HA and B in aqueous solution is a combination of the acid and base equilibria, the equilibrium constant can be expressed as a quotient of the individual acid dissociation constants:
| HA(aq) + B(aq) ⇌ A−(aq) + BH+(aq) |
Taking logarithms equates the log of the equilibrium constant for the proton transfer reaction in water to ΔpKa:
Using the thermodynamic relation between the standard Gibbs free energy of a reaction and its equilibrium constant, the standard free energy change for proton transfer between the acid and base in water is related to ΔpKa as follows:
At 298 K, 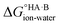 = −5.71 ΔpKa. Thus, positive values of ΔpKa correspond to negative
= −5.71 ΔpKa. Thus, positive values of ΔpKa correspond to negative 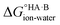 and therefore favour proton transfer from acid to base. Negative values of ΔpKa correspond to positive
and therefore favour proton transfer from acid to base. Negative values of ΔpKa correspond to positive 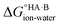 and favour non-ionised acid and base. Each additional unit of ΔpKa changes
and favour non-ionised acid and base. Each additional unit of ΔpKa changes 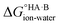 by ±5.71 kJ mol−1. For ΔpKa = 0,
by ±5.71 kJ mol−1. For ΔpKa = 0, 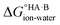 = 0, giving equal quantities of ionised and non-ionised species in water. Most pKa data refer to an aqueous solution at 298 K. However, the values may change drastically in other solvents and media.47
= 0, giving equal quantities of ionised and non-ionised species in water. Most pKa data refer to an aqueous solution at 298 K. However, the values may change drastically in other solvents and media.47
Extension to molecular crystals
The formation of a multi-component molecular crystal comprising an acid and a base may yield either a salt if proton transfer occurs or a co-crystal if there is no proton transfer. A thermochemical cycle summarising the associated free energy changes is shown in Fig. 2. For the co-crystal, the free energy of formation is simply the lattice free energy relative to the non-interacting molecules in the gas phase,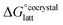 (assuming no significant conformational change for the molecules upon crystallisation). For the salt, the free energy of formation is the sum of the free energy for proton transfer in the gas phase,
(assuming no significant conformational change for the molecules upon crystallisation). For the salt, the free energy of formation is the sum of the free energy for proton transfer in the gas phase, 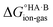 , plus the lattice free energy of the salt relative to the non-interacting ions in the gas phase,
, plus the lattice free energy of the salt relative to the non-interacting ions in the gas phase, 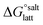 . Hence, the formation of a salt or co-crystal (under thermodynamic control) depends on the balance between the free energy for proton transfer in the gas phase and the difference between the lattice free energies of the salt and co-crystal:
. Hence, the formation of a salt or co-crystal (under thermodynamic control) depends on the balance between the free energy for proton transfer in the gas phase and the difference between the lattice free energies of the salt and co-crystal: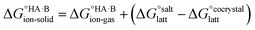 | (1) |
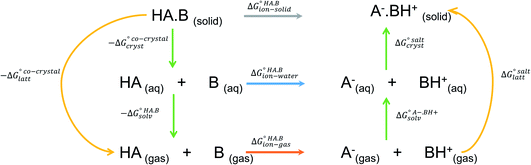 | ||
| Fig. 2 Thermochemical cycle summarising the free energy changes associated with the formation of a molecular salt or co-crystal. | ||
If 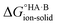 < 0, a salt will be favoured over a co-crystal. Conversely, if
< 0, a salt will be favoured over a co-crystal. Conversely, if 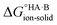 > 0, a co-crystal will be preferred.
> 0, a co-crystal will be preferred.
Evaluating 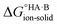 : the gas-phase route
: the gas-phase route
Since temperature and entropic effects remain challenging to compute and their relative changes are typically small,48 the standard free energy differences can be approximated to potential energy changes at 0 K, so: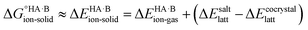 | (2) |
Although less commonly reported than pKa values, proton affinities (PA) in the gas phase can be measured or computed, which enables 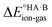 to be determined as follows:
to be determined as follows:
| PA(acid) = ΔE°{A−(g) + H+(g) → HA(g)} |
| PA(base) = ΔE°{B(g) + H+(g) → BH+(g)} |
The second term in eqn (2) is usually highly negative because lattice energies of salts are significantly more negative than those of co-crystals due to the coulombic contributions in the salt, and the first term in eqn (2) is usually highly positive (energy is required for proton transfer). It is the balance between 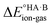 and (ΔEsaltlatt − ΔEco-crystallatt) that determines whether a co-crystal would form.
and (ΔEsaltlatt − ΔEco-crystallatt) that determines whether a co-crystal would form.
In this context, ΔpKa can be viewed as a proxy estimate for 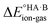 . In general, the strengths of acids and bases in aqueous solution do not necessarily correspond to the proton affinities in the gas phase, but a good linear dependence between the gas phase and aqueous acidity has been shown for organic acids of the type typically found in molecular crystals.49 If HA is a strong acid and B is a strong base (leading to a large positive ΔpKa),
. In general, the strengths of acids and bases in aqueous solution do not necessarily correspond to the proton affinities in the gas phase, but a good linear dependence between the gas phase and aqueous acidity has been shown for organic acids of the type typically found in molecular crystals.49 If HA is a strong acid and B is a strong base (leading to a large positive ΔpKa), 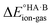 is likely to be less positive and amply compensated by the lattice energy gain of the salt. If HA and B are a weak acid/base (leading to a negative ΔpKa),
is likely to be less positive and amply compensated by the lattice energy gain of the salt. If HA and B are a weak acid/base (leading to a negative ΔpKa), 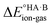 will have a larger positive value which could outweigh the energy gain of the salt lattice and therefore favour the co-crystal. For intermediate cases, the balance is delicate.
will have a larger positive value which could outweigh the energy gain of the salt lattice and therefore favour the co-crystal. For intermediate cases, the balance is delicate.
If a crystal structure (or structures) is known, the difference in lattice energy between the salt and co-crystal can be explicitly calculated for a given system.‡ For example, Mohamed et al. have shown the energetic balance between a salt and co-crystal for a series of pyridine/carboxylic acid crystals.50 In this series, the acid and base interact directly in the crystal structure so the salt/co-crystal balance can be explored by shifting the acid proton across an O–H⋯N hydrogen bond. In some cases, a single-well potential was found with a clearly favoured position (either co-crystal or salt), but other cases showed a very shallow potential with very little energetic difference between either situation.50 Similar studies on a series of hydrazone/dicarboxylic acid crystals produced comparable results.51 Further to this, commonly applied DFT-D methods have been shown to often result in incorrect proton transfer in acid–base cocrystals.53 Hence, the second term in eqn (2) may need careful consideration on a crystal-by-crystal basis. The biggest limitation here, of course, is the requirement to determine the crystal structure(s) in order to make the calculations. To predict salt/co-crystal formation from the molecular structure alone, the entire process would require crystal structure prediction (CSP) of both the co-crystal and salt systems followed by accurate computation of the lattice energies.52 Hence, the full evaluation of eqn (2) is generally impractical as a predictive tool.
Evaluating 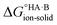 : the aqueous route
: the aqueous route
Following the thermochemical cycle in Fig. 2, 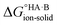 can be calculated from aqueous solution data as follows:
can be calculated from aqueous solution data as follows: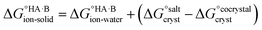 | (3) |
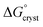 is the standard free energy change upon crystallisation of the salt or co-crystal from the constituent components in aqueous solution. This is the opposite process to that defining the solubility product, and hence
is the standard free energy change upon crystallisation of the salt or co-crystal from the constituent components in aqueous solution. This is the opposite process to that defining the solubility product, and hence 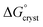 =
= 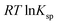 , where Ksp is the product of the molar concentrations of the molecular constituents in solution. The first term of eqn (3) has been shown earlier to be −2.3RTΔpKa, so eqn (3) can be re-written as:
, where Ksp is the product of the molar concentrations of the molecular constituents in solution. The first term of eqn (3) has been shown earlier to be −2.3RTΔpKa, so eqn (3) can be re-written as: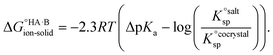 | (4) |
Using eqn (4), the sign of 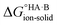 and, hence, the relative thermodynamic stability of the salt and co-crystal, can be visualised through a simple diagram (Fig. 3). For each ΔpKa value, the value of
and, hence, the relative thermodynamic stability of the salt and co-crystal, can be visualised through a simple diagram (Fig. 3). For each ΔpKa value, the value of 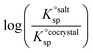 at which the free energy of proton transfer is 0 represents the boundary between the co-crystal and salt regions. This diagram illustrates neatly the ΔpKa rule. Co-crystals dominate when ΔpKa < 0. When ΔpKa > 4, salts dominate in most solubility ratio ranges. In the intermediate region of ΔpKa, the outcome is strongly sensitive to the relative solubility product of the salt versus the co-crystal.
at which the free energy of proton transfer is 0 represents the boundary between the co-crystal and salt regions. This diagram illustrates neatly the ΔpKa rule. Co-crystals dominate when ΔpKa < 0. When ΔpKa > 4, salts dominate in most solubility ratio ranges. In the intermediate region of ΔpKa, the outcome is strongly sensitive to the relative solubility product of the salt versus the co-crystal.
While ΔpKa can easily be measured or calculated, the second term in eqn (4) cannot be quantified unless both a co-crystal and a salt exist for the system, and the solubility products can be measured. This is almost never the case. Hence, eqn (4) is no more practical than eqn (2) as a general predictive tool.
Finally, it should be stressed that the balance between ΔpKa and the solubility ratio may be complex. For example, in the case where an acid becomes significantly weaker than the expectation in aqueous solution due to a change to a poorly solvating solvent, this may be compensated by a change in the relative solubilities of the co-crystal and the salt. For example, upon changing from water to an organic solvent, the effective ΔpKa may decrease, but this is likely to be compensated by a decrease in the solubility product of the salt relative to the co-crystal. An example of such behaviour is seen for cediranib maleate.54 Hence, the applicability of expectations based on an aqueous environment must be carefully considered when transferring to other solvents.
Practical application of the ΔpKa rule
Although the preceding sections add theoretical context to ΔpKa as a predictor for salt/co-crystal formation, the practical application of the ΔpKa rule is effectively based on empirical evidence. While it is unclear when the observation that salts would typically form for acid and bases with ΔpKa > 3 was made, this knowledge has been used for decades in the pharmaceutical industry. In 2012, Cruz-Cabeza probed the rule in the CSD and showed that ΔpKa > 4 almost always leads to salts and ΔpKa < −1 almost always leads to co-crystals. In the intermediate region, the probability of salt formation was found to follow the empirical trend:| Pobs(salt, %) = 17 ΔpKa + 28 |
In this context, with over 1 million crystal structures now available in the CSD, we set out in this work to probe further the experimental observations of salt and co-crystal formation, in order to shed light on the impact of crystal composition (particularly hydration), the location of the acid and base groups, the local hydrogen-bonding environment and the possibility of further proton transfers on the ΔpKa rule.
Results
Impact of solvation on the potential energy of acid–base proton transfer
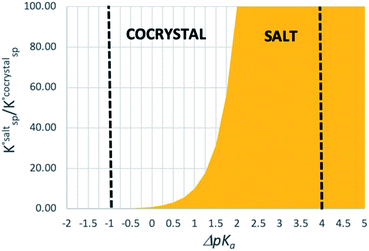
To demonstrate the effect of the acid–base relative strength, as well as solvation, on the ionisation of acid–base pairs, we selected acetic acid (AA) as a model acid together with three bases with increasing base strength: THF, pyridine (PYR) and trimethylamine (TMA). The computed ΔpKa and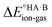 values in the gas phase are summarised in Fig. 4. As expected, as ΔpKa increases,
values in the gas phase are summarised in Fig. 4. As expected, as ΔpKa increases, 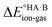 decreases, from 605 kJ mol−1 for AA:THF to 330 kJ mol−1 for AA:TMA.
decreases, from 605 kJ mol−1 for AA:THF to 330 kJ mol−1 for AA:TMA.
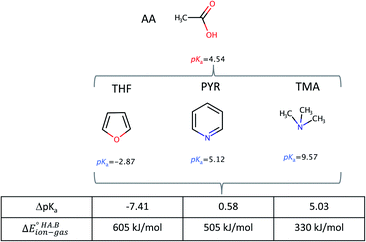 | ||
| Fig. 4 Calculated ΔpKa values and gas-phase proton transfer energies for acid–base pairs formed between AA with three bases (THF, PYR, TMA) of increasing strength. | ||
To expand on these values, and to illustrate the impact of solvation, the potential energy curve for proton transfer for each acid–base pair was calculated in different solvation environments: (a) gas-phase; (b) toluene; (c) 2-heptanone; (d) water. The solution environments were accounted for implicitly using SMD solvation models. Toluene and 2-heptanone were chosen because their dielectric constants (toluene = 2.3, 2-heptanone = 12) are similar to those anticipated for neutral molecular solids and molecular salts, respectively.55 Hence, they are intended to give a coarse approximation of the situation that may be found in the crystalline state. They are not necessarily implied to be common laboratory solvents (indeed, 2-heptanone is rare in practice). For the calculations, the AA molecule was located next to the base so that an A–H⋯B hydrogen bond was formed, and the geometry was optimised. The potential energy was then calculated as a function of the position of H+ within the A–H⋯B hydrogen bond, as outlined in the Methods section. The results are shown in Fig. 5.
For AA:THF (ΔpKa = −7.4), none of the environments favour proton transfer from acid to base because of the high 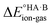 value for this pair. For AA:TMA (ΔpKa = 5.0), a similar situation is seen in the gas phase, but there is a progressive emergence of an energy minimum for proton transfer as the dielectric constant of the solvent increases. In aqueous solution, the minimum is pronounced and the ionised species are favoured over the neutral species by over 20 kJ mol−1. For AA:PYR (ΔpKa = 0.6), an intermediate situation is seen, whereby the curve for aqueous solution resembles that for AA:TMA in 2-heptanone. Hence, the balance between
value for this pair. For AA:TMA (ΔpKa = 5.0), a similar situation is seen in the gas phase, but there is a progressive emergence of an energy minimum for proton transfer as the dielectric constant of the solvent increases. In aqueous solution, the minimum is pronounced and the ionised species are favoured over the neutral species by over 20 kJ mol−1. For AA:PYR (ΔpKa = 0.6), an intermediate situation is seen, whereby the curve for aqueous solution resembles that for AA:TMA in 2-heptanone. Hence, the balance between 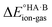 and the extent to which the ionised species are stabilised by solvation is clearly seen. To extend this picture to the solid state, the key question is how the crystal lattice impacts the outcome. The empirical evidence established for the ΔpKa rule suggests that the effect of the lattice is never sufficient to influence the outcome for acid–base pairs with ΔpKa < −1 or ΔpKa > 4, but that it can have a significant effect in the intermediate region. The remainder of this paper considers whether existing crystallographic information can be used to enhance the predictive power of the ΔpKa rule in the intermediate region.
and the extent to which the ionised species are stabilised by solvation is clearly seen. To extend this picture to the solid state, the key question is how the crystal lattice impacts the outcome. The empirical evidence established for the ΔpKa rule suggests that the effect of the lattice is never sufficient to influence the outcome for acid–base pairs with ΔpKa < −1 or ΔpKa > 4, but that it can have a significant effect in the intermediate region. The remainder of this paper considers whether existing crystallographic information can be used to enhance the predictive power of the ΔpKa rule in the intermediate region.
Ionisation and solvation statistics in the CSD (dataset-1)
Dataset-1 contains 258![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 719 crystal structures of organic compounds containing between one and four different molecular components. Dataset-1 was analysed by crystal type and composition, as described in the Methods section. Crystals with only one main component were classified either as neutral (no proton transfer) or zwitterionic, with the further distinction that some zwitterions are not the result of proton transfer (referred to as zwitterion-Q4). Multi-component systems were classified as co-crystals (neutral main components), co-crystals containing zwitterions, salts, salts-Q4 (quaternary salts) and ionic co-crystals. Some more complex systems were found, for example salts with multiple anion/cations, but these were not analysed further. A summary of the classification data is given in Table 1.
719 crystal structures of organic compounds containing between one and four different molecular components. Dataset-1 was analysed by crystal type and composition, as described in the Methods section. Crystals with only one main component were classified either as neutral (no proton transfer) or zwitterionic, with the further distinction that some zwitterions are not the result of proton transfer (referred to as zwitterion-Q4). Multi-component systems were classified as co-crystals (neutral main components), co-crystals containing zwitterions, salts, salts-Q4 (quaternary salts) and ionic co-crystals. Some more complex systems were found, for example salts with multiple anion/cations, but these were not analysed further. A summary of the classification data is given in Table 1.
| Crystal type | #MCa | Compositionb | N | Percentage of dataset (%) | ||
|---|---|---|---|---|---|---|
| Unsolvated | Hydrate | Solvate | ||||
| a #MC = number of main components. b N = neutral non solvent or zwitterion; Z = zwitterion; Z+ = cationic zwitterion; Z− = anionic zwitterion; C+ = cation; A− = anion; Q4 = quaternary. | ||||||
| Neutral | 1 | N | 215![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 491 491 |
92 | 4 | 5 |
| Zwitterion | 1 | Z | 2112 | 60 | 34 | 6 |
| Zwitterion-Q4 | 1 | Q4–Z | 3677 | 86 | 10 | 4 |
| Co-crystal | 2 | N N | 9464 | 89 | 6 | 5 |
| Co-crystal with Z | 2 | N Z | 349 | 73 | 21 | 6 |
| Co-crystal with ZQ4 | 2 | N Q4–Z | 197 | 85 | 7 | 8 |
| Salt | 2 | C+ A− | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 610 |
72 | 23 | 5 |
| Salt Q4 | 2 | Q4–C+ A− | 6479 | 65 | 27 | 8 |
| Salt with Z | 2 | Z+ A− | 181 | 66 | 33 | 1 |
| Salt with Z | 2 | C+ Z− | 138 | 69 | 28 | 3 |
| Salt with Z | 2 | Q4–Z+ A− | 123 | 64 | 33 | 3 |
| Co-crystal | 3 | N N N | 248 | 91 | 6 | 3 |
| Ionic co-crystal | 3 | C+ A− N | 1364 | 76 | 20 | 4 |
| Ionic co-crystal | 3 | C+ A− Z | 85 | 82 | 18 | 0 |
| Ionic co-crystal | 4 | C+ A− N N | 46 | 100 | 0 | 0 |
The most common types of crystals in the dataset are those containing only one neutral component, followed by salts, co-crystals and quaternary salts. Of these crystal structures, 10% contain ionised species (salts or (zwitter)ionic co-crystals), of which almost 73% involve proton transfer and 27% are quaternary salts. The transfer of a single proton is most common amongst all of the salts, being observed in 74% of the structures, followed by the transfer of two protons in 23% of the structures. Zwitterions are observed in only 3% of the dataset, so structures with zwitterions remain relatively rare in the CSD. Zwitterionic compounds that are not a result of proton transfer (zwitterion-Q4) are more common than zwitterionic forms that arise from self-proton transfer. This is likely to be a simple consequence of the chemical space represented in the CSD, which reflects to a large extent the common preferences of synthetic chemists. Whilst quaternary systems are analysed here for the purpose of general statistics, these are not relevant to the ΔpKa rule and thus are removed for the subsequent sections and analyses.
Most interesting in the current context is the relationship between salt/co-crystal formation and the hydration/solvation of the crystals. Whilst solvates make up only a small percentage of all crystal types, hydrates are much more common. In part, this is to be expected due the ubiquitous nature of water and its frequent use as a solvent, and several authors have discussed reasons why hydration is particularly common in molecular crystals.21,56–59 However, while hydrates constitute up to 6% of crystals containing only neutral (non-zwitterion) species, the percentage increases significantly to around 30% for crystals containing ions and/or zwitterions.
ΔpKa in multi-component crystals
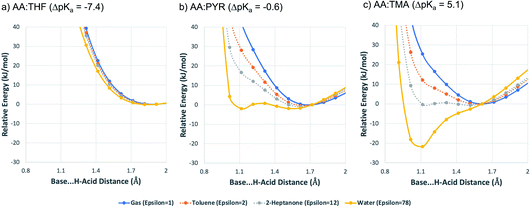
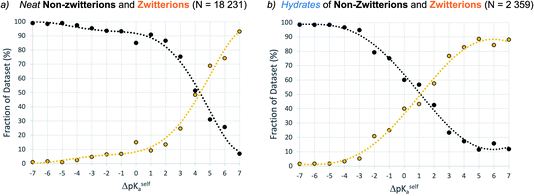
Dataset-2 is a subset of dataset-1 containing all structures with at least one acid–base pair, and thus one ΔpKa value. This set was used to determine the relative occurrence of co-crystals, mono-ionised salts and multi-ionised salts as a function of ΔpKa. The first comparison involves the relative distribution of co-crystals versus mono-ionised salts where ΔpKa is calculated as the difference between the strongest acid and the strongest base (which must be in different molecules). The results are shown in Fig. 6, where the data have been separated into unsolvated (neat) co-crystals and salts (Fig. 6a) and hydrates of co-crystals and salts (Fig. 6b).The result for neat co-crystals and salts is very similar to that presented by Cruz-Cabeza in 2012, with just a small shift to higher ΔpKa values at which the percentage of the dataset is 50%:50% for co-crystals and salts. The percentage value in the plot can be considered as the probability for an acid/base system of a given ΔpKa to be ionised when crystallised in an unsolvated form. In Fig. 6a, the co-crystal:salt equivalence point is observed at ΔpKa ≈ 1.4, compared to ΔpKa ≈ 1 in the 2012 study. Interestingly, the data for hydrates of co-crystals and salts is significantly shifted to the left, with the equivalence point in that distribution found at ΔpKa ≈ −0.5. The intermediate region of the plot (−3 < ΔpKa < 2) deviates noticeably from a sigmoidal shape. This may be influenced by the relatively smaller sample size, or it may indicate a greater degree of uncertainty in the apparent trend when applied to crystalline hydrates.
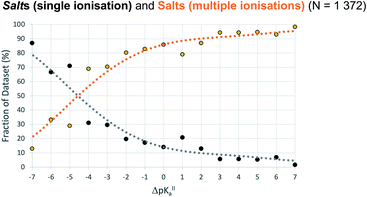
ΔpKa for second proton transfer (ΔpKa,II)
For crystals in dataset-2 with the possibility for two proton transfers (i.e. with calculated values for both ΔpKa and ΔpKa,II), Fig. 7 shows the relative occurrence of mono-ionised salts versus di-ionised salts as a function of ΔpKa,II. The intent here is to examine the effect of the crystal lattice of the mono-ionised salt on the second ionisation of an acid/base system. The number of observations in this case is reduced considerably compared to the co-crystal/salt dataset in Fig. 6, and thus more noise is seen on the apparent sigmoidal curves. Also, because of the smaller number of observations, the data are not separated into unsolvated versus hydrated forms. The data in Fig. 7 show a considerable shift to ΔpKa,II = −4.5 for the crossing point between the mono-ionised and di-ionised salts compared to that for the formation of any salt versus co-crystal as a function of ΔpKa. Fig. 8 shows the number of proton transfers (0, 1 or 2) plotted against ΔpKa and ΔpKa,II in this dataset. Considering only ΔpKa, the 50% probability of forming any salt (one or two proton transfers) falls between ΔpKa = 0 to 1, consistent with the expectations for co-crystals and salts seen in Fig. 6a. When looking at ΔpKa,II, however, the point of 50% probability for forming any salt (either one or two proton transfers) remains around ΔpKa,II ≈ 0, but the probability of forming a salt with two proton transfers is clearly much greater than that of forming a salt with one proton transfer. Hence, where there is the possibility for two proton transfers, the choice is more frequently between a co-crystal and a divalent salt, with monovalent salts being far less common. This is consistent with the indications in Fig. 7, and highlights that the ΔpKa rule does not apply within the same limits for ΔpKa and ΔpKa,II where there is a possibility for a second proton transfer. Here, of course, the stoichiometry of the acid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) base could play a key role when the acid and/or base itself does not have two acid/basic sites but rather two molecules of the acid/base are required per molecule of base/acid. Practically, this emphasises the importance of exploring a larger range of acid–base ratios and stoichiometries during salt screening, especially for potential divalent salts.
base could play a key role when the acid and/or base itself does not have two acid/basic sites but rather two molecules of the acid/base are required per molecule of base/acid. Practically, this emphasises the importance of exploring a larger range of acid–base ratios and stoichiometries during salt screening, especially for potential divalent salts.
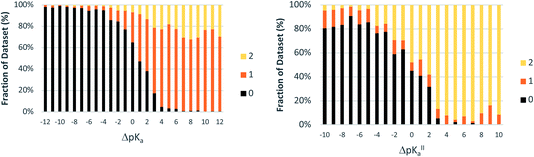 | ||
| Fig. 8 Relative occurrence (%) of salts with 0, 1 or 2 proton transfers as a function of ΔpKa and ΔpKa,II (bins of one ΔpKa value). The dataset is the same as that used to produce Fig. 7. | ||
ΔpKa in zwitterions
Data were retrieved for unsolvated forms (one main component only) and hydrates (one main component plus water) of molecules potentially able to exist as a zwitterion (i.e. with a calculated ΔpKa,self value). Fig. 9 shows that the equivalence point in the distribution of neutral and zwitterionic forms occurs at ΔpKa,self ≈ 4.1, which is significantly higher than that found for multi-component crystals. Again, hydration has the same effect as in multi-component systems, lowering the equivalence point in the zwitterion set to ΔpKa,self ≈ 1. It must be stressed that the data computed here are macro ionisation constants, which refer to the behaviour of the whole molecule to act as an acid or base, without any information on the microspecies that may be involved. Where the acid and base groups are sufficiently far apart within the molecule, it could be assumed that they would act independently, so ΔpKa,self is a meaningful measure. Where the acid and base groups are not independent (e.g. in close proximity in the molecule or linked through resonance effects), this could have a significant influence on ΔpKa,self. Hence, while Fig. 9 serves as a guideline for potential self-proton transfer, the application of ΔpKa,self to predict zwitterion formation should be viewed with a greater degree of caution since here the micro-ionisation constants play an important role.Discussion
When transferring ΔpKa values from the aqueous environment to make predictions about potential proton transfer in the solid state, the significant change in solvation environment can impact the overall expectations. Analysis of crystal structures in the CSD suggests in general that when ΔpKa is sufficiently negative (<−1) or sufficiently positive (>+4), the influence of this change in environment is unlikely to overturn the indication of salt/co-crystal formation provided by ΔpKa. When ΔpKa lies in the intermediate range, however, the thermodynamic preference for proton transfer is strongly dependent on the solvation environment. The important new result in this paper is the demonstration that crystal composition has an important influence on the ΔpKa rule. Most notably, the point of 50% probability for salt formation is shifted to lower ΔpKa for crystalline hydrates compared to unsolvated forms. Indeed, the data show that salt formation in crystalline hydrates mirrors almost perfectly aqueous solution data: thus, for crystalline hydrates of acid/bases, ΔpKa > 0 should result in a salt and ΔpKa < 0 should result in a co-crystal. This finding begs the question as to which is the consequence of which: does hydration occur because of proton transfer? Or does proton transfer occur because of hydration?In the regions where the non-ionised versus the ionised probabilities cross, a linear correlation can be found. The fitted equations in Table 2 may prove valuable for prediction of proton transfer in molecular crystals of various nature and compositions.
| System: neutral (a) vs. ionised (b) | Range | ΔpKa cross | P obs (ion, %) | R 2 |
|---|---|---|---|---|
| a Ionisation, second ionisation or self-ionisation as appropriate. | ||||
| Monovalent vs. multivalent salt | [−7, 0] | −4.2 | 11ΔpKIIa + 96 | 0.89 |
| Hydrated co-crystal vs. hydrated monovalent salt | [−5, 4] | −0.6 | 10ΔpKa + 56 | 0.94 |
| Hydrated neutral vs. hydrated zwitterion | [−3, 5] | 1.1 | 11ΔpKselfa + 38 | 0.98 |
| Cocrystal vs. monovalent salt | [−2, 4] | 1.3 | 14ΔpKa + 32 | 0.98 |
| Neutral vs. zwitterion | [1, 7] | 4.1 | 15ΔpKselfa − 12 | 0.97 |
Concerning unsolvated co-crystals versus salts, the data suggest that unsolvated forms of acid–base pairs are usually worse at solvating the ionic species than water. To compensate for this, ΔpKa must be positive for ionisation to occur. In order to illustrate this observation, we have selected two examples of benzoic acid forming a salt and a co-crystal with two different bases with ΔpKa values between 1 and 2. Using the Mercury full interaction maps (FIMs) tool with a water oxygen as probe, we can visualise the ancillary hydrogen bonds (aHBs) where water is involved with the acid–base pair in aqueous solution in its non-ionised form versus its ionised form (Fig. 10). In aqueous solution, water forms one aHB with the carbonyl of the carboxylic acid in its neutral form whilst forming two strong aHBs with the carboxylate. For the crystal outcome to be predicted solely by ΔpKa, the level of solvation of the acid–base pair in solution must be maintained in the solid state. In such a scenario, a positive ΔpKa will imply salt formation, whilst a negative ΔpKa will imply co-crystal formation. If solvation in the crystal is worse than in water (fewer aHBs), then the ΔpKa value for the switch between salt and co-crystal must be shifted to higher values. In PUTMAU (Fig. 10), for example, there are no other HB donors in the acid or base, so no aHBs are possible and, thus, the outcome is a co-crystal. In HOMWEN (Fig. 10), however, there is a hydroxyl group available on the base able to form an aHB with the carboxylate, and thus a salt is observed in the solid state. For an acid and base with a ΔpKa between 1 and 2, the experimentally derived probability for a salt to form would be between 50–60% (Table 2). In that scenario, a higher number of aHBs should result in a salt, whilst a lower number should result in a co-crystal.
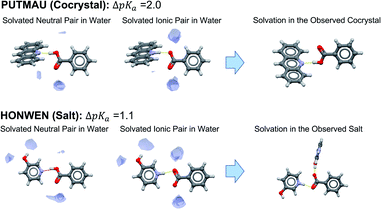 | ||
| Fig. 10 Visualisation of water solvation of non-ionised versus ionised acid–base pairs with full interaction maps versus the resulting ionisation and interactions observed in their crystals. | ||
To illustrate further the importance of crystalline aHBs to the ionisation outcome, we analyse the number of aHBs in acid–base co-crystals and salts with a ΔpKa ≈ 0 (Table 3). 147 crystal structures were found where the carboxylic acid/carboxylate was involved in two aHBs, 247 in one aHB and 137 in no aHBs (Table 3).
| N total | Salt% | Co-crystal% | |
|---|---|---|---|
| 2 aHBs A/A− | 147 | 54% | 46% |
| 1 aHBs A/A− | 247 | 12% | 88% |
| 0 aHBs A/A− | 137 | 3% | 96% |
Acid–base crystalline complexes able to afford two aHBs generate a solvation environment similar to water. Interestingly, nearly 50% of the 147 crystals with two aHBs are salts and the other 50% are co-crystals, mirroring the behaviour expected in aqueous solution where ΔpKa ≈ 0. When only one or no aHBs are possible, co-crystals clearly dominate over salts. Here, when a reduction of aHBs occurs, the nature and strength of those aHBs would matter, with stronger HBs better able than weaker aHBs to stabilise the ionic species. This effect is clearly seen in the case of double ionisation where the ΔpKa,II values for the switch between salt and co-crystal are shifted to negative values.
Conclusions
The ΔpKa rule is widely used in crystal engineering for the design of salts and co-crystals, particularly for pharmaceutical compounds. Its origin is experimental, but associated with the thermodynamics of acid–base aqueous equilibria. There is indeed a simple thermodynamic relationship between ΔpKa for an acid and a base and the corresponding free energy for proton transfer in aqueous solution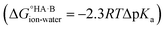 . Transferring this relationship to the solid state, although clearly convenient, comes with several challenges. Solvation plays a key role in the ionisation reaction and moving the acid–base species from aqueous solution (where the ΔpKa defines their relative acid strength) into the crystals shifts the ΔpKa expectations for ionisation to occur (as seen from experimentation). This experimental shift observation is what we refer to as the ΔpKa rule. The rule works well for more extreme cases of ΔpKa but loses its predictive power at ΔpKa values between −1 and 4, where proton transfer in the solid state becomes a fine balance between the “inherent” tendency for proton transfer and the influence of the crystalline environment.
. Transferring this relationship to the solid state, although clearly convenient, comes with several challenges. Solvation plays a key role in the ionisation reaction and moving the acid–base species from aqueous solution (where the ΔpKa defines their relative acid strength) into the crystals shifts the ΔpKa expectations for ionisation to occur (as seen from experimentation). This experimental shift observation is what we refer to as the ΔpKa rule. The rule works well for more extreme cases of ΔpKa but loses its predictive power at ΔpKa values between −1 and 4, where proton transfer in the solid state becomes a fine balance between the “inherent” tendency for proton transfer and the influence of the crystalline environment.
To illustrate the important role of the solvation environment on the ionisation outcome in the crystalline state, we have examined the applicability of the ΔpKa rule in crystalline systems with different compositions. This reveals that the point of equal probability of salt/co-crystal formation lies at ΔpKa ≈ 1.1 for neat (unsolvated) forms, but at around 0 for hydrates. In zwitterions, an even more positive ΔpKa value of 4.1 is seen, whilst in multi-protic salts the point is negative, around ΔpKa ≈ −4.2. New probability equations for ionisation (based on linear fittings to the CSD observations) are provided to enhance the predictive power of the ΔpKa rule in the intermediate region for systems of various compositions.
We have also highlighted the importance of solvation in this intermediate region of ΔpKa values for a few illustrative examples. Acid–base pairs that are stabilised by strong solvation in the crystalline state are more likely to be ionised than acid–base pairs that are not involved in any ancillary hydrogen bonds in the crystal. Finally stoichiometry and its impact to the hydrogen-bonding environment of the acid–base complex can also play a role.60 We anticipate that this contribution will be useful for future applications of the ΔpKa rule. The herein derived probability equations for crystals of various compositions, combined with an analysis of possible aHBs, can undoubtedly enhance the ΔpKa rule’s predictive power in the intermediate region.
Author contributions
AJCC initiated the project and performed the CSD searches and calculations. All authors contributed to the discussions, drafting of the paper and improvement of the data and made important contributions to the theoretical fundamentals. The authors thank Prof. Roger Davey for helpful discussions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AJCC thanks the Royal Society for an Industry Fellowship in AstraZeneca.Notes and references
- J. Manchester, G. Walkup, O. Rivin and Z. You, J. Chem. Inf. Model., 2010, 50, 565–571 CrossRef CAS PubMed.
- D. D. Perrin, B. Dempsey and E. P. Serjeant, pKa Prediction for Organic Acids and Bases, Springer, 1981, vol. 1 Search PubMed.
- C. Lim, D. Bashford and M. Karplus, J. Phys. Chem., 1991, 95, 5610–5620 CrossRef CAS.
- D. A. Haynes, W. Jones and W. D. S. Motherwell, J. Pharm. Sci., 2005, 94, 2111–2120 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- M. Sadakiyo, T. Yamada and H. Kitagawa, J. Am. Chem. Soc., 2009, 131, 9906–9907 CrossRef CAS PubMed.
- J. S. Stevens, S. Coultas, C. Jaye, D. A. Fischer and S. L. M. Schroeder, Phys. Chem. Chem. Phys., 2020, 22, 4916–4923 RSC.
- J. S. Stevens, M. Walczak, C. Jaye and D. A. Fischer, Chem.–Eur. J., 2016, 22, 15600–15604 CrossRef CAS PubMed.
- C. C. Wilson, N. Shankland and A. J. Florence, J. Chem. Soc., Faraday Trans., 1996, 92, 5051–5057 RSC.
- J. S. Stevens, S. J. Byard and S. L. M. Schroeder, J. Pharm. Sci., 2010, 99, 4453–4457 CrossRef CAS PubMed.
- S. Tothadi, T. R. Shaikh, S. Gupta, R. Dandela, C. P. Vinod and A. K. Nangia, Cryst. Growth Des., 2021, 21, 735–747 CrossRef CAS.
- P. T. Edwards, L. K. Saunders, A. R. Pallipurath, A. J. Britton, E. A. Willneff, E. J. Shotton and S. L. M. Schroeder, Cryst. Growth Des., 2021, 21(11), 6332–6340 CrossRef CAS.
- L. Rajput, M. Banik, J. R. Yarava, S. Joseph, M. K. Pandey, Y. Nishiyama and G. R. Desiraju, IUCrJ, 2017, 4, 466–475 CrossRef CAS PubMed.
- L. H. Thomas, A. J. Florence and C. C. Wilson, New J. Chem., 2009, 33, 2486–2490 RSC.
- M.-M. Blum, M. Mustyakimov, H. Rüterjans, K. Kehe, B. P. Schoenborn, P. Langan and J. C.-H. Chen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 713–718 CrossRef CAS PubMed.
- S. M. Reutzel-Edens, Pharmaceutical Salts and Co-crystals, Royal Society of Chemistry, 2011, pp. 212–246 Search PubMed.
- T. Wang, J. S. Stevens, T. Vetter, G. F. S. Whitehead, I. J. Vitorica-Yrezabal, H. Hao and A. J. Cruz-Cabeza, Cryst. Growth Des., 2018, 18, 6973–6983 CrossRef CAS.
- S. M. Berge, L. D. Bighley and D. C. Monkhouse, J. Pharm. Sci., 1977, 66, 1–19 CrossRef CAS PubMed.
- A. T. Serajuddin, Adv. Drug Delivery Rev., 2007, 59, 603–616 CrossRef CAS PubMed.
- D. P. Elder, R. Holm and H. L. De Diego, Int. J. Pharm., 2013, 453, 88–100 CrossRef CAS PubMed.
- C. B. Aakeröy, M. E. Fasulo and J. Desper, Mol. Pharmaceutics, 2007, 4, 317–322 CrossRef PubMed.
- G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 8342–8356 CrossRef CAS PubMed.
- G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967 CrossRef CAS PubMed.
- M. Karimi-Jafari, L. Padrela, G. M. Walker and D. M. Croker, Cryst. Growth Des., 2018, 18, 6370–6387 CrossRef CAS.
- M. K. Corpinot and D.-K. Bučar, Cryst. Growth Des., 2019, 19, 1426–1453 CrossRef CAS.
- A. Nangia and G. R. Desiraju, Supramolecular Synthons and Pattern Recognition, in Topics in Current Chemistry, E. Weber, Springer, Berlin, 1999, vol. 198 Search PubMed.
- G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311–2327 CrossRef CAS.
- J. A. Bis, P. Vishweshwar, D. Weyna and M. J. Zaworotko, Mol. Pharmaceutics, 2007, 4, 401–416 CrossRef CAS PubMed.
- P. Gilli, L. Pretto and G. Gilli, J. Mol. Struct., 2007, 844–845, 328–339 CrossRef CAS.
- P. Gilli, L. Pretto, V. Bertolasi and G. Gilli, Acc. Chem. Res., 2009, 42, 33–44 CrossRef CAS PubMed.
- B. R. Bhogala, S. Basavoju and A. Nangia, CrystEngComm, 2005, 7, 551–562 RSC.
- A. J. Cruz-Cabeza, CrystEngComm, 2012, 14, 6362–6365 RSC.
- S. L. Childs, G. P. Stahly and A. Park, Mol. Pharmaceutics, 2007, 4, 323–338 CrossRef CAS PubMed.
- G. Ramon, K. Davies and L. R. Nassimbeni, CrystEngComm, 2014, 16, 5802–5810 RSC.
- A. Lemmerer, S. Govindraju, M. Johnston, X. Motloung and K. L. Savig, CrystEngComm, 2015, 17, 3591–3595 RSC.
- A. Mukherjee and G. R. Desiraju, Cryst. Growth Des., 2014, 14, 1375–1385 CrossRef CAS.
- ChemAxon version 21.13, https://www.chemaxon.com Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- Avogadro version 1.1.1, https://avogadro.cc Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72(2), 171–179 CrossRef CAS PubMed.
- P. A. Wood, T. S. G. Olsson, J. C. Cole, S. J. Cottrell, N. Feeder, P. T. A. Galek, C. R. Groom and E. Pidcock, CrystEngComm, 2013, 15, 65–72 RSC.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- B. G. Cox, Acids and Bases: Solvent Effects on Acid-Base Strength, Oxford University Press, Oxford, New York, 2013 Search PubMed.
- Y. Abramov, G. Sun, Y. Zhou, M. Yang, Q. Zeng and Z. Shen, Cryst. Growth Des., 2019, 19, 7132–7137 CrossRef CAS.
- I. E. Charif, S. M. Mekelleche, D. Villemin and N. Mora-Diez, J. Mol. Struct.: THEOCHEM, 2007, 818, 1–6 CrossRef CAS.
- S. Mohamed, D. A. Tocher, M. Vickers, P. G. Karamertzanis and S. L. Price, Cryst. Growth Des., 2009, 9, 2881–2889 CrossRef CAS.
- L. Mazur, I. Materek, A. D. Bond and W. Jones, Cryst. Growth Des., 2019, 19, 2663–2678 CrossRef CAS.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C.-A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H.-Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459 CrossRef CAS PubMed.
- L. M. LeBlanc, S. G. Dale, C. R. Taylor, A. D. Becke, G. M. Day and E. R. Johnson, Angew. Chem., Int. Ed., 2018, 57, 14906–14910 CrossRef CAS PubMed.
- P. Praphanwittaya, P. Saokham, P. Jansook and T. Loftsson, J. Drug Delivery Sci. Technol., 2021, 62, 102359 CrossRef CAS.
- T. G. Cooper, K. E. Hejczyk, W. Jones and G. M. Day, J. Chem. Theory Comput., 2008, 4, 1795–1805 CrossRef CAS PubMed.
- G. R. Desiraju, J. Chem. Soc., Chem. Commun., 1991, 426–428 RSC.
- L. Infantes, L. Fábián and W. D. Sam Motherwell, CrystEngComm, 2007, 9, 65–71 RSC.
- A. Bajpai, H. S. Scott, T. Pham, K.-J. Chen, B. Space, M. Lusi, M. L. Perry and M. J. Zaworotko, IUCrJ, 2016, 3, 430–439 CrossRef CAS PubMed.
- H. D. Clarke, K. K. Arora, H. Bass, P. Kavuru, T. T. Ong, T. Pujari, L. Wojtas and M. J. Zaworotko, Cryst. Growth Des., 2010, 10, 2152–2167 CrossRef CAS.
- P. Stainton, E. Nauha, T. Grecu, J. F. McCabe, T. Munshi, I. Scowen, H. C. Stephen Chan, S. Nilsson and N. Blagden, Cryst. Growth Des., 2022, 22(3), 1665–1679 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1fd00081k |
| ‡ If a classical modelling approach is used, the ionisation term and the lattice energy terms will be computed separately. However, if a quantum modelling approach is used, the lattice energy will be optimised together with the ionisation state. A single optimisation of a crystal structure with DFT-d will result in either a salt or a co-crystal for a single well potential scenario since it will optimise the total energy of the lattice simultaneously. |
| This journal is © The Royal Society of Chemistry 2022 |