Open Access Article
Open Access ArticleCharacterisation of intergrowth in metal oxide materials using structure-mining: the case of γ-MnO2†
Nicolas P. L.
Magnard
,
Andy S.
Anker
 ,
Olivia
Aalling-Frederiksen
,
Andrea
Kirsch
,
Olivia
Aalling-Frederiksen
,
Andrea
Kirsch
 and
Kirsten M. Ø.
Jensen
and
Kirsten M. Ø.
Jensen
 *
*
Department of Chemistry and Nano-Science Center, University of Copenhagen, 2100 Copenhagen Ø, Denmark. E-mail: kirsten@chem.ku.dk
First published on 20th September 2022
Abstract
Manganese dioxide compounds are widely used in electrochemical applications e.g. as electrode materials or photocatalysts. One of the most used polymorphs is γ-MnO2 which is a disordered intergrowth of pyrolusite β-MnO2 and ramsdellite R-MnO2. The presence of intergrowth defects alters the material properties, however, they are difficult to characterise using standard X-ray diffraction due to anisotropic broadening of Bragg reflections. We here propose a characterisation method for intergrown structures by modelling of X-ray diffraction patterns and pair distribution functions (PDF) using γ-MnO2 as an example. Firstly, we present a fast peak-fitting analysis approach, where features in experimental diffraction patterns and PDFs are matched to simulated patterns from intergrowth structures, allowing quick characterisation of defect densities. Secondly, we present a structure-mining-based analysis using simulated γ-MnO2 superstructures which are compared to our experimental data to extract trends on defect densities with synthesis conditions. We applied the methodology to a series of γ-MnO2 samples synthesised by a hydrothermal route. Our results show that with synthesis time, the intergrowth structure reorders from a R-like to a β-like structure, with the β-MnO2 fraction ranging from ca. 27 to 82% in the samples investigated here. Further analysis of the structure-mining results using machine learning can enable extraction of more nanostructural information such as the distribution and size of intergrown domains in the structure. Using this analysis, we observe segregation of R- and β-MnO2 domains in the manganese oxide nanoparticles. While R-MnO2 domains keep a constant size of ca. 1–2 nm, the β-MnO2 domains grow with synthesis time.
Introduction
Due to the increasing need for sustainable technologies, a high interest has grown for functional materials based on earth abundant elements. Manganese dioxide MnO2 is an interesting compound in that perspective. Manganese oxide crystallises in several polymorphs including layered structures, tunnel structures, as well as spinel, rutile, and hollandite structures. These show a range of different electrochemical properties, allowing for targeted materials design for e.g., energy technologies.1–6 In this study, we focus on the γ-MnO2 polymorph in the MnO2 family. γ-MnO2 is of great interest as it is frequently used in commercial batteries as an electrode material and is investigated for secondary battery systems.7–10 However, the structural complexity of γ-MnO2 has made it difficult to fully map its relations between synthesis, structure and properties. The structure can be represented as an intergrowth of β-MnO2 (P42/mnm) and R-MnO2 (Pnam) slabs (Fig. 1). β-MnO2 crystallises in the rutile structure and is built from single-chains of edge-sharing [MnO6] octahedra, which are connected through corner-sharing octahedra along the a- and b-axis. R-MnO2 is closely related but contains double-chains of edge-sharing [MnO6] octahedra along the a-axis. The mixing, or intergrowth, of these two parent structures within the same O2− hcp sublattice results in the γ-MnO2 structure as illustrated in Fig. 1.11–14 The intergrowth structure can be considered a sub-ordered sequence of faults along a common crystallographic direction, here the a-axis, within the O2− hcp sublattice.12,14 The structure is also referred to as containing “De Wolff defects”, named after P. M. De Wolff who was one of the first to work on the characterisation of this phase.15 A consequence of intergrowth is a huge variability in the structure of different γ-MnO2 samples, which heavily influences the material properties.3,16–18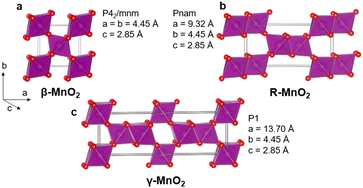 | ||
| Fig. 1 β-MnO2 (a) and R-MnO2 (b) can randomly be stacked along their common a-axis to form an intergrowth γ-MnO2 structure (c). | ||
However, the defects make the characterisation of γ-MnO2 challenging. The structural disorder gives rise to anisotropic broadening of Bragg reflections in powder diffraction patterns from γ-MnO2, and analysis beyond e.g., standard Rietveld refinement is required. In the past decades, several approaches using X-ray diffraction (XRD) have been developed to characterise the γ-MnO2 structure. A first approach was proposed by De Wolff,15 who related the broadening of specific Bragg peaks in R-MnO2-like γ-MnO2 to the amount of β-MnO2 domains. Later, Chabre and Pannetier12 interpreted De Wolff defects using a statistical model of the intergrowth structure. By defining a De Wolff defect distribution to describe the intergrowth rate, they modelled a library of γ-MnO2 XRD patterns. From this library, they were able to find patterns in the line position and broadening and determined empirical rules to estimate the intergrowth rate of γ-MnO2 for real samples from their diffraction patterns. Another approach has been used by Simon et al., who performed multi-phase Rietveld refinements on patterns from γ-MnO2 samples using the R-MnO2 and β-MnO2 structures, as well as a highly disordered ε-MnO2 model, where Mn4+ ions partially occupy all octahedral sites in the O2− hcp sublattice.19 This provided good agreement between the model and experimental data and allowed quantification of the different phases. The intergrowth in γ-MnO2 have also been characterised using Pair Distribution Function (PDF) analysis. The PDF is obtained by Fourier transforming the normalised and corrected total scattering data, and can provide information on the local and medium range structure in materials. Using PDF, Galliez et al.20 characterised γ-MnO2 samples by fitting their PDFs with the β-MnO2 and R-MnO2 parent structures. This approach gave information about the fractions of parent structures in γ-MnO2 samples, but was not able to account for the De Wolff defect distribution in the structure.
In a broader context, several tools have been developed for characterisation of planar faults in various crystal structures. In DIFFaX,21 faulted crystal structures are modelled by defining the unit layers that the system consists of along with a stacking fault probability for each layer, which allows calculation of scattering intensities. The scattered intensity of the faulted structure is calculated analytically using the structure factor of individual unit layers and an inter-layer interference term that account for the stacking probability of the different layers. This method was used by Chabre and Pannetier in their analysis of the effect of De Wolff defects in γ-MnO2 in XRD patterns.12 DIFFaX+, developed by Leoni et al.22 allows to directly refine stacking probabilities in order to quantitatively estimate defect densities. A similar methodology has been implemented in the FullProf suite software package through the FAULTS program, developed by Casas-Cabanas et al.23 A tool for simulating XRD patterns from structures with stacking faults has also been implemented in TOPAS by Coelho et al.24,25 This approach is based on the generation of supercells, from which individual scattering signals can be calculated. Simulated XRD patterns are then obtained by averaging over these signals. Other approaches in the literature are also based on modelling supercells for calculation of scattering patterns.26,27 Planar defects in nanocrystalline materials have furthermore been studied with PDF analysis, where the unit layers can be accurately described by the local range of the PDF and medium range by modelling faulted supercells.28–33
In this paper, we develop a new method for intergrowth characterization. We combine analysis of γ-MnO2 XRD patterns and PDFs, which allows to investigate which of the two methods is better suited for characterization of intergrown systems such as γ-MnO2. First, a large database of intergrowth superstructures with varying De Wolff defect distributions is constructed, using the statistical model developed by Chabre and Pannetier,12 and XRD patterns and PDFs from these structures are simulated. We then use the modelled patterns to establish trends in XRD/PDF peak intensity and shape with intergrowth parameters, which allows development of a peak-fitting method for estimation of defect densities. Secondly, we use the structures in the database for ‘structure-mining’ through Rietveld analysis against experimental data from hydrothermally synthesized manganese oxide nanoparticles. This analysis allows identification of the best fitting structure for a given dataset, so that trends on defect densities in a series of samples can be extracted. Thirdly, the structure-mining results are given to a machine learning algorithm which makes it possible to extract information on the size of domains in the intergrowth samples. This gives new insight into the formation and growth of γ-MnO2 intergrowths.
Methods
Sample synthesis
All γ-MnO2 samples have been synthesised using a soft chemistry route. The synthesis method is adapted from the protocol used by Wang et al.34 MnSO4 and (NH4)2S2O8 are dissolved in deionised (DI) water. The synthesis was conducted hydrothermally at 150 °C for 2 h, 3.5 h and 5 h with a starting concentration of Mn2+ ions of 0.7 M and a Mn2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S2O82− ratio of 5
S2O82− ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 using a Teflon-lined steel autoclave. The autoclaves were then left to cool down at room temperature after heating. The as-synthesised black solid was filtered and washed 3 times each with DI water and ethanol before being left to dry at room temperature. The samples were labelled sample 1, 2 and 3, corresponding to heating time of 2, 3.5 and 5 h, respectively.
3 using a Teflon-lined steel autoclave. The autoclaves were then left to cool down at room temperature after heating. The as-synthesised black solid was filtered and washed 3 times each with DI water and ethanol before being left to dry at room temperature. The samples were labelled sample 1, 2 and 3, corresponding to heating time of 2, 3.5 and 5 h, respectively.
XRD and X-ray total scattering measurements
The samples were put in Kapton tubes and XRD as well as X-ray total scattering patterns were measured at the I15-1 beamline at Diamond Light Source, United Kingdom. Scattering patterns from an empty Kapton tube and from a Si standard sample were measured as well. The Kapton tube data were used for background subtraction and the Si standard was used to account for instrumental broadening of the Q-space peaks. The total scattering data were acquired on a Perkin Elmer XRD 1611 CP3 2D detector with a pixel size of 100 × 100 μm2. The XRD data were collected on a Perkin Elmer XRD 4343 CT 2D detector with a pixel size of 150 × 150 μm2. The sample to detector distances were 283 mm (total scattering) and 670 mm (XRD) using a wavelength of 0.1618 Å.The 2D images were integrated using Dawn.35 PDF data were obtained by Fourier transformation of the normalised and corrected total scattering patterns using xPDFSuite36 with a Qmin value of 1.0 Å−1 and a Qmax value of 23 Å−1 after subtracting the scattering contribution of the Kapton tube.
Transmission electron microscopy (TEM)
Transmission electron microscopy images have been recorded with a Tecnai T20 G2 S-TEM with HT 200 keV and a LaB6 filament. The samples were prepared by dropcasting a suspension of MnO2 nanoparticles in ethanol on lacey carbon coated copper TEM grids. The ImageJ37 software was used for image processing and analysis.Results and discussion
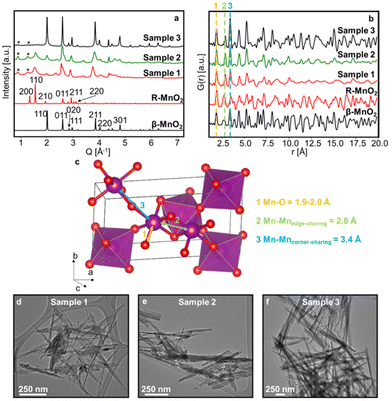
Three γ-MnO2 samples with different amounts of De Wolff defects were synthesised. To achieve different defect densities, the samples were hydrothermally treated for 2 h (sample 1), 3.5 h (sample 2) and 5 h at 150 °C (sample 3), respectively. Fig. 2a and b shows experimental XRD patterns and PDFs obtained for sample 1, 2 and 3 along with calculated patterns of β-MnO2 and R-MnO2. The preparation of the samples differs only by synthesis time, and we can observe that the longer the synthesis (sample 3), the structure of the samples becomes closer related to β-MnO2. The samples prepared with shorter syntheses times, sample 1 and 2, show reflections from both phases, indicating a structure containing features from both β-MnO2 and R-MnO2. For all three samples, some reflections in the XRD patterns are broader than others, such as the 110 peak of R- and β-MnO2 at 1.5 and 2.0 Å−1 in comparison to the 011 peak of β- and R-MnO2 around 2.5 and 2.6 Å−1, highlighted by the dotted line in Fig. 2a. This anisotropic broadening is coupled with a small shift of the peak position of the 110 peaks of the parent structures from one sample to the other. According to DIFFaX simulations from Chabre and Pannetier,12 this peak shift is related to changes in the De Wolff defect distribution, confirming the presence of intergrown structures in our γ-MnO2 samples. Micro-twinning along the 201 and 601 planes of the R-MnO2 parent structure can also happen in γ-MnO2 samples, but only affects the peak position of these particular reflections, according to DIFFaX calculations of Chabre and Pannetier.12 We do not observe any such significant effect here. In addition to γ-MnO2, we observe impurities of α-MnO2, indicated by stars in Fig. 2a. No evidence of a significant fraction of remaining Mn2+ ions from the precursors could be observed. Mn2+ containing compounds would likely give rise to a Mn–O peak around 2.2 Å in the PDF,38 which is not observed in our experimental data. Furthermore, synthesis of manganese oxides often leads to the formation of manganese dioxide hydrate MnO(OH)2 that give rise to a peak on the XRD data around 0.5 Å−1.39 Such a peak is not observed in our experimental data.The PDFs of the three samples (Fig. 2b) show similarities in peak positions, but differ in relative intensities. They also clearly reflect different sizes of the crystallites, or at least their coherent scattering domains, which increases from sample 1 to 3, as less damping of the PDF signal is seen at high r values. TEM images of the synthesised samples (Fig. 2d–f and Fig. S1†) do indeed show that samples 1, 2 and 3 show needle-shaped particles whose diameter increase with synthesis time, and we estimate them to be ca. 7 nm, 15 nm, and 54 nm, respectively. According to previous work, the long dimension of the needles can be assigned to the [001] direction of the β- and R-MnO2 structures,7,40–43 such that the intergrowth direction is along the diameter of the needles. This anisotropic shape can also explain partially the anisotropic broadening of the peaks on XRD data. However, the effect of De Wolff defects is prominent as it gives rise to even smaller intergrown domains within the sample.
Creation of γ-MnO2 supercells with various De Wolff defect distributions
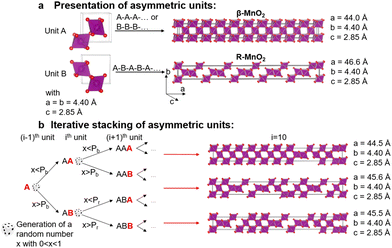
To characterise the defect chemistry of the three samples, we first investigate how different De Wolff defect distributions generally affect the XRD patterns and PDFs. The first step for the development of the methodology was therefore to generate a database of γ-MnO2 supercells containing various De Wolff defect distributions using the approach sketched in Fig. 3. To do so, rules based on the study from Chabre and Pannetier12 were applied. First, a pair of asymmetric units A and B (Fig. 3a) were identified and described in a primitive cell. Both consist of a pair of [MnO6] octahedra sharing one corner. However, for A, one of the Mn atoms is placed at the origin of the cell and the other one at (1/2, 1/2, 1/2), whereas for B the Mn atoms are placed at (0, 1/2, 1/2) and (1/2, 1/2, 0). Stacking of 2 similar units A–A or B–B with a stacking vector (aβ, 0, 0), (aβ being the a cell parameter in the structure) yields a regular β-MnO2 structure. In contrast, stacking of two different units A–B or B–A yields a regular R-MnO2 structure. Here, the stacking vector is (aR/2, ±0.026bR, 0), with aR and bR being the a and b cell parameters of R-MnO2. The slight shift (±0.026) along the b-axis needs to be added to adjust for corner-sharing [MnO6] octahedra in the R-MnO2 structure. To keep a straight structure, the shift along the b-axis alternates from one sequence to the other. As such, the unit B will be shifted by +0.026bR along the b-axis with respect to unit A in a stacking sequence A–B, whereas an opposite shift of −0.026bR along the b-axis is applied in a B–A sequence.The statistical approach of Chabre and Pannetier12 involves the definition of De Wolff defect distribution probabilities Pb and Pr. Pb corresponds to the probability of having a regular β-MnO2 stacking, i.e. an A–A or a B–B sequence and Pr corresponds to the probability of having a regular R-MnO2 stacking, i.e. an A–B or a B–A sequence. A combination of these two probabilities gives the respective phase fractions of β-MnO2 domains (%β-MnO2) and R-MnO2 domains (%R-MnO2) by eqn (1) and (2):
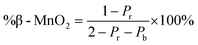 | (1) |
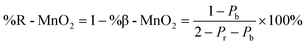 | (2) |
We generate the supercells with varying Pr and Pb using a simple method based on iterative stacking of asymmetrical units A and B. The process is based on setting the value of Pb, Pr and of a random number x (between 0 and 1), which is generated in each stacking step as shown in Fig. 2b. The following rules were used: if the ith and (i − 1)th units are the same, i.e. A and A or B and B, the type of the (i + 1)th unit to stack depends on Pb and x. If x < Pb, the stacking remains regular (A–A–A or B–B–B) representing β-MnO2. If x > Pb, the opposite unit is stacked (resulting in A–B–A or B–A–B), thus generating stacking faults in the β-MnO2 structure. Conversely, if the i-th and (i − 1)th units are different, i.e. A–B or B–A, the nature of the (i + 1)th unit depends on Pr. If x < Pr, the same unit present in the (i − 1)th step is added, resulting in A–B–A or B–A–B structures, corresponding to a regular R-MnO2 sequence. If x > Pr, the same unit is stacked (resulting in A–B–B or B–A–A) creating a stacking fault in the R-MnO2 structure.
We generated such superstructures in the whole (Pb, Pr) parameter space, varying both probabilities between 0.01 and 0.99 with an increment of 0.01, yielding 9801 different supercells. The starting point was sequence A–A. Each of them consists of 250 stacked sequences. The a cell parameter of the supercell is calculated by summing up all individual a-components of the stacking vectors for the whole supercell, ranging from 900 Å to 950 Å.
Pattern simulation and peak-fitting analysis
Using the database of 9801 supercells generated above, we first use a simple, peak-fitting analysis to estimate the defect distribution in our experimental samples from the appearance of the scattering patterns and PDFs. XRD and PDF patterns were calculated from each of the supercells using TOPAS Academic.44 In both cases, the isotropic atomic displacement parameters (ADP) of manganese and oxygen Biso were set to 0.2 Å2. A Gaussian profile with a peak width based on a Caglioti polynomial, U![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(θ)2 + V
tan(θ)2 + V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(θ) + W45 with U = 0.42, V = −0.36 and W = 0.70 was used.
tan(θ) + W45 with U = 0.42, V = −0.36 and W = 0.70 was used.
PDFs from the superstructures were calculated in an r-range up to 20 Å with a Qdamp of 0.04 Å−1 and a Qmax of 23 Å−1 to model instrumental parameters close to those of a real experiment.
Fig. 4a and d show contour plots of the simulated XRD patterns and PDFs for supercells for which eqn (1) satisfies the condition %β-MnO2 = Pb (and conversely eqn (2) satisfies the condition %R-MnO2 = Pr) in the range 0% ≤ %β-MnO2 ≤ 100%. The modelled XRD patterns show good agreement with those previously reported.12,46 When %β-MnO2 is close to 0%, the PDF and XRD pattern show features and Bragg peaks of pure R-MnO2 (Fig. 4b). Similarly, when %β-MnO2 tends towards 100%, XRD peaks sharpen, i.e. the structure orders back again. At %β-MnO2 = 100%, the XRD patterns and PDFs show similar features to the ones calculated from β-MnO2 as shown in Fig. 4c and f, respectively.
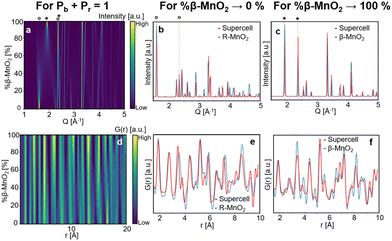 | ||
| Fig. 4 Modelled XRD patterns (a) and PDFs (d) from supercells for which eqn (1) satisfies the condition %β-MnO2 = Pb, 110 (1.5 Å−1 and 2.0 Å−1) and 011 (ca. 2.6 Å−1) reflections of R-MnO2 and β-MnO2 are shown by (°) and (*), respectively. Modelled XRD patterns (b) and PDFs (e) for %β-MnO2 → 0% (red curve) compared to parent R-MnO2 (blue curve). Modelled XRD patterns (c) and PDFs (f) for %β-MnO2 → 100% (red curve) compared to parent β-MnO2 (blue curve). | ||
When the β-MnO2 fraction deviates from the two end members (0% < %β-MnO2 < 100%), reflections from both parent structures can be observed. Some reflections strongly broadened, indicating a loss of long-range order in the γ-MnO2 structure. These are for instance the 110 reflections of both β- and R-MnO2 reflecting disorder along the a-axis. On the contrary, 011 reflections are not affected by the intergrowth.
The simulated data show that an estimate of the β-MnO2 fraction can be obtained from the intensity ratio between the 011 reflections of R- and β-MnO2. For the simulated XRD patterns we extract the intensities and FWHMs by fitting Pseudo-Voigt functions to these peaks. An example of such a fit is shown in Fig. S2a.† With increasing β-MnO2 fraction, a decrease of the intensity ratio (I011R/I011β) can be observed. By fitting an empirical quadratic function (eqn (3)) to the calculated data points, the intensities of the 011 reflection of the β- and R-phases can be linked to their structure factors F(hkl) and to %-β-MnO2viaeqn (3):
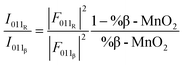 | (3) |
This procedure can be compared to a simple phase quantification in a binary mixture system, where the intensity ratio of two peaks is proportional to the ratio of the phase fractions, weighted by the ratio of their squared structure factors. The fitted (I011R/I011β) ratio is plotted as function of %β-MnO2 in Fig. 5a. We note that some data points (%β-MnO2 < 20%, Fig. 5a) do not follow the same trend. This can be attributed to the fact that the 011 reflections of β- and R-MnO2 have very similar d-spacings. In the case where the structure of a γ-MnO2 sample is closely related to those of one of the parents, its reflections will dominate the XRD pattern. In that situation it becomes difficult to fit two peaks as the XRD would show a strong reflection next to a weak one and some lack of convergence may thus occur.
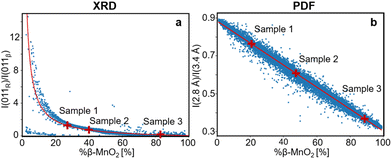 | ||
| Fig. 5 (a) Intensity ratio between 011R and 011β lines from the modelled XRD patterns plotted against the β-MnO2 fraction (%β-MnO2, blue dots) and fitted using eqn (3) (red solid line). (b) Intensity ratio between PDF peaks at 2.8 Å and 3.4 Å from the modelled PDFs plotted against %β-MnO2 (blue dots) and fitted using a linear function (red solid line). | ||
While this intensity ratio can inform on %β-MnO2 from XRD patterns, a second relation is needed to fully quantify the stacking disorder within γ-MnO2 intergrowth. Once %-β-MnO2 is determined, we still need to find Pb or Pr as they are all related to each other through eqn (1). Determining these three values would allow not only to get an estimate of the fraction of both parent structures, but also how their domains are distributed within the intergrowth. For this purpose, the ratio between the FWHM of 011R and 110R is calculated for all simulated XRD patterns of the γ-MnO2 superstructures. While the first reflection is not impacted by the intergrowth (its structure factor does not have any contribution from the position of atoms along the a-axis) the second one is. Therefore, a given fraction of R-MnO2 in the intergrowth will impact the relative broadening of these two reflections which will depend on the domain size of R-MnO2. The calculated ratio of XRD patterns of all supercells having the same β-MnO2 fraction are then plotted against Pr and are shown in Fig. S3.† When values for Pr and %β-MnO2 have been established, Pb can be calculated using eqn (1).
We can now calculate the β-MnO2 fraction, Pb and Pr for our three experimental XRD datasets of sample 1, 2 and 3. The Bragg peak intensity ratio was determined for each of the three samples by fitting Pseudo-Voigt functions to the 110R, 110β, 011β and 011R reflections of the experimental data as shown in Fig. S4a, d and g.† The corresponding β-MnO2 fraction can be estimated from the ratio of intensities as presented in eqn (3). Once this value is determined, Pr is estimated using the fitted FWHM of 011R and 110R and, Pb is calculated using eqn (1). The resulting %β-MnO2, Pb and Pr for the three samples are listed in Table 1. The β-MnO2 fraction gradually increases from sample 1 to 3. This can be related to the chemistry of the system. The chosen synthesis pathway leads initially to a metastable R-MnO2 phase that reorders into β-MnO2 as the synthesis progresses. Conversely, the structure becomes more and more ordered, as Pb and Pr both increase with synthesis time. Besides having more and more β-MnO2 blocks in the structure, the β- and R-MnO2 blocks tend to segregate with time.
| Sample | %β-MnO2 XRD | P b XRD | P r XRD | %β-MnO2 PDF | P b PDF | P r PDF |
|---|---|---|---|---|---|---|
| Sample 1 | 27 | 0.53 | 0.83 | 21 | 0.4 | 0.84 |
| Sample 2 | 40 | 0.72 | 0.81 | 48 | 0.69 | 0.72 |
| Sample 3 | 82 | 0.97 | 0.9 | 87 | 0.98 | 0.87 |
Having established a simple method for intergrowth characterisation from XRD data, we can use a similar approach for PDF analysis. We first identify peaks arising from specific motifs in the β-MnO2 and R-MnO2 structure. The PDF peak at 2.8 Å can be attributed to the Mn–Mn distance between two [MnO6] edge-sharing octahedra, while the peak at 3.4 Å arises from the Mn–Mn distance between two [MnO6] corner-sharing octahedra as shown in Fig. 2c. R-MnO2 contains more edge-sharing octahedra in its structure (4) than β-MnO2(2). Conversely, a manganese atom has less 2nd neighbours at 3.4 Å in R-MnO2 (where it has 4) than β-MnO2 (with 8 neighbours). The intensity ratio between the height of the two peaks can thus be used as a measure for %β-MnO2. We calculated the ratio for each of the simulated PDFs by fitting Gaussian functions to the two peaks, an example of the fitting procedure is shown in Fig. S2b.† The results are plotted as a function of %β-MnO2 in Fig. 5b. In contrast to the XRD analysis, a linear trend is observed for the PDF analysis. This can be explained by the fact that the amount of edge- and corner-sharing octahedra changes linearly when switching from blocks of β-MnO2 to blocks of R-MnO2. The obtained data can be fitted using a linear regression (red line, Fig. 5b). The %β-MnO2 fractions of sample 1, 2 and 3 were calculated by this approach and are reported in Table 1.
As in the XRD analysis, a second trend is used to quantify Pb and Pr once %β-MnO2 is determined. The intensity ratio between the peaks at 5.3 Å and 5.7 Å is calculated for γ-MnO2 superstructures and plotted as a function of Pb for superstructures with a given %β-MnO2 in Fig. S5.† Examples of fits are shown in Fig. S2c.† The two peaks used here correspond to second and third nearest neighbour in a (2 × 1) channel and while the former is present in both β- and R-MnO2 structures, the latter can only be found in R-MnO2. However, because in an intergrown structure a β-MnO2 block can be next to a R-MnO2 block, these two peaks may arise as well. Therefore, the ratio of these two peaks contain information about how many β-MnO2 blocks are connected to R-MnO2 blocks, i.e. the stacking probabilities Pr and Pb. The calculated ratio can be fitted using a linear function. Again, we can use these correlations to determine the defect density in our three samples. For each experimental PDF, the %β-MnO2 is first calculated and used to extract the corresponding Pb value shown in Table 1. Knowing both %β-MnO2 and Pb, Pr can be determined using eqn (1). Using the described procedure, we can now estimate %β-MnO2, Pb and Pr for the experimental samples 1, 2 and 3 and the fitting of the PDF peaks is shown in Fig. S4b, c, e, f, h, and i.† The results are summarised in Table 1. We are thus able to get a full picture of the intergrowth in γ-MnO2 using PDF analysis.
As seen in Table 1, the values extracted from the XRD and PDF analysis are of the same order of magnitude. However, some variations can be observed, especially regarding the estimation of Pb and Pr. In general, the peak analysis from PDF gives higher values than those obtained from XRD. This could imply that some other effects influence the intensity of PDF peaks in the local range. Indeed, other types of defects, such as micro-twinning and proton-induced defects may be seen in R-MnO2-like intergrowth samples (as in sample 1).12,13,47,48 Those may alter the short-range order in the crystal, and thus the intensity of the first peaks of the PDF. The proton-induced defects consist of substitution of Mn4+ by Mn3+ along with the formation of hydroxyl groups on the neighbouring O2− site, or by compensation of a manganese vacancy by four hydroxyl groups. Such defects may have a large impact on the properties of the material,49 however, characterization of these is outside the scope of this paper, and will be addressed in a future study. Finally, some stacking faults in the MnO2 O2− hcp sublattice has been predicted50 but no experimental evidence of such stacking events has been reported.
Structure refinement and structure-mining
The peak-fitting-approach presented above gives a good first estimate of the defect density in the materials. However, to further extend our analysis and to identify the best model to describe the data, we use ‘structure-mining’. Here, the structures generated above are fitted to the experimental data, and the trends in the goodness of fits of the different models are investigated. In order to optimise calculation time, Pb and Pr were limited to (0.0 < Pb < 1.0, 0.5 < Pr < 1.0) for sample 1, (0.5 < Pb < 1.0, 0.5 < Pr < 1.0) for sample 2 and (0.5 < Pb < 1.0, 0.0 < Pr < 1.0) for sample 3 according to the results of the peak-fitting analysis.All the structure refinements were performed using TOPAS.44 For the XRD analysis, the supercell cell parameters a, b and c and the isotropic atomic displacement parameters (ADP) for both manganese and oxygen were refined along with background and peak shape parameters, as described further in Table S1 in the ESI.† To minimise the number of refinement parameters, all atomic coordinates in the supercell are expressed as a function of the ones in the asymmetric unit. To achieve that, a translational operation in accordance with the stacking sequence in the supercell is applied to the atoms in each layer. In addition, the hollandite α-MnO2 structure was added as a secondary phase. A similar approach was used for the PDF analysis.
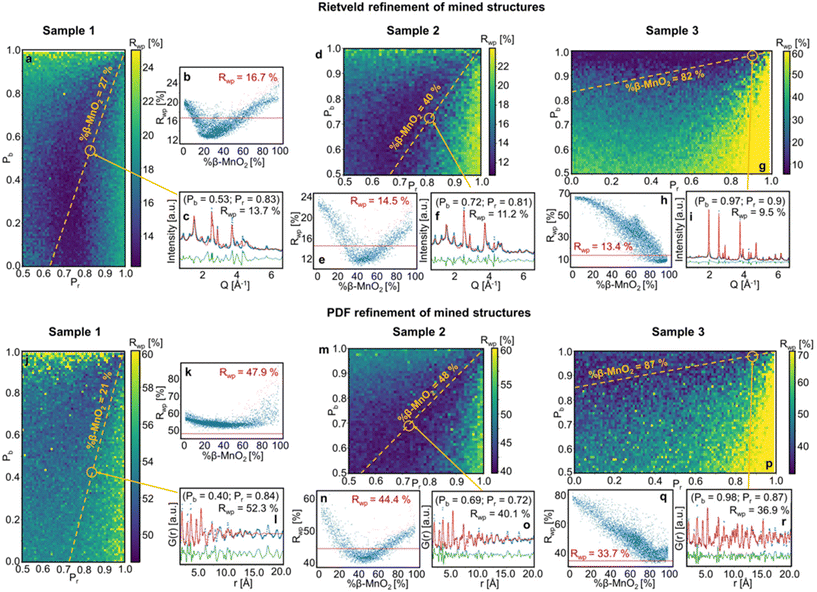
Fig. 6 shows the Rwp values obtained for the fitting of mined structures for samples 1, 2 and 3. The Rwp values are represented in a colour map, where the Pr and Pb values used for the superstructure generation are plotted on the x- and y-axes. The results are also represented in one dimension as a function of β-MnO2 fraction of the refined superstructures (Fig. 6b–q). The Rwp value corresponding to a simple two-phase refinement using the two parent structures (β-MnO2 and R-MnO2) on the same experimental dataset is shown as a red vertical line (Fig. 6b–q).
When performing refinements of the mined superstructures on the three samples, we see that the lowest Rwp values are systematically clustered in a region of the (Pb, Pr) space (dark blue regions). This is the case for both the XRD and PDF analysis, which means we can use this region as a β-MnO2 fraction estimate: for sample 1, we estimate the β-MnO2 fraction to be in the range 20–40%, sample 2 in the range 40–60% and for sample 3 in the range 80–100% (see Fig. 6b–q respectively). The fact that a whole range of supercells yielded similar fits, i.e. similar Rwp values, implies that in the case of such intergrown system, a single model is not sufficient to describe the material structure, as also seen from the poor fit quality for especially sample 1 which is further discussed below. This can be related to the random nature of the stacking of R- and β-MnO2 blocks in the supercell. Indeed, some key structural motifs in different quantities may be present in all the superstructures that yielded a good fit in the blue area on Fig. 6a–g and j–p. The idea of structural motifs will be further investigated in the next section.
When comparing the results of the fitting of mined structures on sample 1, 2 and 3 for XRD and PDF (Fig. 6b–q respectively) as a function of %β-MnO2, we observe that the dip in the Rwp around the best fits is deeper for the XRD superstructure refinements than for PDF. This indicates that XRD is more sensitive to disorder in the intergrowth sequence than PDF. XRD probes the average structure of a material while PDF probes the local structure. Defects such as intergrowth affect the long-range structure, which is better characterised in XRD.
The results of the peak-fitting analysis were also compared to the ones from the structure-mining approach. The fit of the superstructures corresponding to the (Pb, Pr) values obtained from the peak-fitting analysis of samples 1, 2 and 3 are shown in Fig. 6c–i (XRD) and l–r (PDF). The Pr and Pb values identified from the peak-fitting analysis fall into the region where superstructures fitted better to the experimental data than a two-phase mixture of the parent structures. However, some discrepancies are still observed, especially for sample 1 and 2. This is more clearly seen in Fig. S6,† showing a zoom of the low Q region of the Rietveld refinements along with the low r region or the PDF refinements presented in Fig. 6. For the Rietveld refinement of the XRD data, the intensity of some reflections is not fully described, including the 110R and 110β reflections. Furthermore, the 201R reflection at 2.4 Å−1 is not matched in position or in intensity. In r-space, the intensity of the first peaks, at 1.90 Å, 2.88 Å and 3.40 Å are not well described. The discrepancies in the fits can arise from different effects. Firstly, the limited size of the supercells (250 asymmetric units) may not provide a sufficient statistical average of the De Wolff defects distribution in the sample, which affects the description of the peak intensities in the XRD patterns. A second effect, as observed from TEM (Fig. 2 and Fig. S1†), is the particle shape, which affects the Bragg peak width and r-dependent PDF peak intensity. Finally, as discussed above, the γ-MnO2 structures can contain several types of defects, i.e. De Wollf or intergrowth defects, microtwinning and H-related defects. All of them impact the XRD patterns and PDFs. The aim of the present work is to develop a simple and fast method, building on structure mining, which can reveal trends in De Wolff defect densities. Therefore, our structure refinements may miss some of the information hidden in the scattering signal of the samples as we focus here on only one aspect of the problem.
The Rwp values for the corresponding superstructures and for the two-phase refinement of the parent structures are compared and summarised in Table 2. The superstructure refinements on experimental data generally yield a better fit than the refinement of the simple mix of the parent structures, with Rwp values being ca. 3% systematically lower. An exception arises for the PDF refinements of sample 1 and 3. For sample 1, the Rwp values obtained for analysis in both Q- and r-space are higher than those of the two other samples. Broader reflections in Q-space as well as a rapid damping of the PDF in direct space imply that sample 1 contains smaller crystallites, as also seen from our TEM analysis.
| Sample | Refinement | R wp, super-structures (%) | R wp, β-MnO2 + R-MnO2 (%) |
|---|---|---|---|
| Sample 1 | Rietveld | 13.7 | 16.7 |
| 52.3 | 47.9 | ||
| Sample 2 | Rietveld | 11.2 | 14.5 |
| 40.0 | 44.4 | ||
| Sample 3 | Rietveld | 9.5 | 13.4 |
| 36.9 | 33.6 |
Nanostructure analysis
In order to extract more information from the structure-mining process, we use our recently published approach for structure analysis, namely the Machine Learning-based Motif Extractor (ML-MotEx).51 The idea of ML-MotEx is to give the results from a large set of structure refinements to an explainable ML algorithm, which learns to predict the goodness-of-fit value for a structural refinement to the experimental data. Most importantly, the use of an explainable ML algorithm makes it possible to obtain information on the effect that each feature of the model has on the fit quality. ML-MotEx uses a Gradient Bosting Decision Tree (GBDT)52 to predict the Rwp value from structural information. SHAP (SHapley Additive exPlanation)53,54 values are used to explain each feature's effect on the Rwp value by taking into consideration the full dataset given as input. While the magnitude of the SHAP value quantifies the importance of a feature, its sign signifies whether the presence of the feature in the model affects the Rwp value positively or negatively, as described further below. The method is also described in detail in our recent publication.51We here want to use the ML-MotEx method to extract information on the nanostructure of the samples, i.e. determine the size of the R-MnO2 and β-MnO2 domains present in the intergrowth structures. Results from each of the 2500 superstructure refinements, performed on both XRD and PDF data, were used as input parameters for ML-MotEx. The structural features investigated using explainable ML were the β-MnO2 fraction, Pb and Pr, and the intergrowth sequence of each supercell. This input allows to investigate what structural features are important for the fit quality.42 The intergrowth sequence of a superstructure is generated from the asymmetric unit sequence used to build it (presented in Fig. 3). By taking the asymmetric unit at the ith and (i − 1)th position we determine whether a “block” constituting the intergrowth sequence corresponds to β- or R-MnO2.
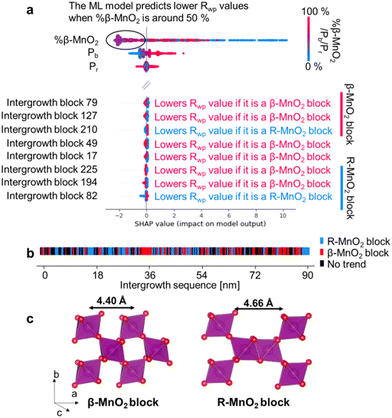
Fig. 7a shows the results of using ML-MotEx on the PDF measured on sample 2. ML-MotEx on the XRD and PDF obtained for samples 1 and 3 are shown in Fig. S7 in the ESI.† For each fit, a SHAP value is obtained for all of the features. We first consider the %β-MnO2 fraction, which we also investigated from the XRD and PDF analysis above. In the figure, the feature value (i.e. here %β-MnO2) is shown on the colour axis, where red represents a low %β-MnO2 fraction, while blue represents a high %β-MnO2 fraction. The SHAP values obtained for this feature show that when %β-MnO2 is either high (red/∼100%) or low (blue/∼0%), the SHAP values are positive. This means that the Rwp values are increased in these fits. Conversely, medium %β-MnO2 values (purple, ca. 50%) show negative SHAP values and thus lower the Rwp value. This agrees well with the results from the analysis in Fig. 6e, where we determined %β-MnO2 to be 48% for sample 2. The SHAP analysis also suggests that the Rwp value of the refinements can be pushed down by having a low Pb value. This is new information as refinements of the mined structures shown in Fig. 6m did not indicate a region of better fits for particularly low Pb values. Finally, the SHAP analysis shows that the Pr value does not seem to have a strong effect on the fit quality.
To get deeper understanding of the influence of De Wolff defect distribution on the fit, we next investigate the effect of the intergrowth sequence itself on the refinements through the SHAP analysis. We correlate here the nature of individual intergrowth block within the intergrowth sequence to the Rwp values using the SHAP analysis. As each block in the sequence is directly related to the structure refined to the experimental data, it is possible to establish a correlation between each intergrowth block and the Rwp value when investigating the whole range of supercells refined to one single experimental dataset. The influence of the intergrowth sequence on the fit quality is illustrated in Fig. 7b, where “intergrowth block X” parameters refer to a specific block in the 250-block long intergrowth sequence. Here, a positive feature value (red colour in Fig. 7a) refers to a β-MnO2 block. Conversely, a negative feature value (blue colour in Fig. 7a) refers to a block of R-MnO2. As an example, the SHAP value for intergrowth block 79 in Fig. 7a is red in the negative region which means that the Rwp value of the refinement is decreased if the unit is a β-MnO2 block. Conversely, the SHAP value is blue in the positive region so a R-MnO2 block will increase the Rwp of the refinement. The SHAP analysis performed on XRD results of sample 2, along with PDF and XRD results of samples 1 and 3 are shown in Fig. S7.†
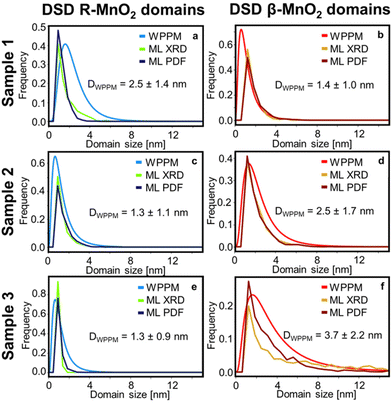
Based on the interpretation of SHAP values given above, we search for any continuous R- or β-MnO2 domains. First, we sort the intergrowth sequence blocks by whether it is more beneficial for the refinement to have them as a β- or a R-MnO2 block, i.e. when the SHAP value of a given block should rather be negative or positive to push down the Rwp value of the refinement. Then, we screen the complete intergrowth sequence to search for sequences of consecutive “preferentially β-MnO2 block” or “preferentially R-MnO2 block” and count the number of similar blocks in these sub-sequences. The result of this analysis is shown in Fig. 7b where blocks of R- and β-MnO2 are shown in blue and red, respectively. One can notice that these blocks are not randomly distributed in the intergrowth sequence but rather segregated into some small domains of a few consecutive R- or β-MnO2 blocks. We extract the size of these continuous domains of R-MnO2 and β-MnO2 by multiplying this number to the unit cell parameter a of R- and β-MnO2. The number of domains of a given size is counted and normalised by the total number of domains. The resulting domain size distributions are plotted as a function of size to build a Domain Size Distribution (DSD) function. This process is carried out for the results from structural refinements performed on both XRD and PDF data for sample 1, 2 and 3 and shown in Fig. 8. The results show small domain sizes of 1–2 nm depending on the sample and the parent structure (either R- or β-MnO2), as discussed below.
As a reference for the approach presented above, we also analysed the line profile of individual reflections for both R- and β-MnO2 in the experimental data using Whole Powder Pattern Modelling (WPPM). We carry out this analysis independently of the structure mining approach. This method, detailed in ESI Notes 1,† was used in order to determine the domain size distribution in the intergrowth direction, i.e. the [100] direction for both β-MnO2 and R-MnO2 domains. The software PM2K developed by Leoni et al.55 was used to estimate the DSD of β-MnO2 and R-MnO2 domains based on the 110R and 110β reflections of the XRD patterns of the three samples. The coefficients of the Caglioti-based instrumental profile were determined by analyzing the XRD pattern from the Si standard beforehand and a Chebyshev polynomial function was used to model the background. A lognormal function was used to model the DSD of β-MnO2 and R-MnO2 domains and the average domain size and standard deviation in the corresponding directions were determined. The fitting of the peaks is shown in Fig. S8.† From the lognormal distribution center μ and variance σ2, the average crystallite size (Daverage) and standard deviation of the crystallite size distribution (s.d.) can be derived as shown in eqn (4) and (5) below:
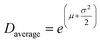 | (4) |
| s.d. = (e2μ+σ2(eσ2 − 1)) | (5) |
Finally, as we aim to determine the DSD of R- and β-MnO2 domains along the [100] direction, we need to make some assumptions since we use the 110 reflection which has a contribution in the [100] and [010] directions. We assume that the size of the domains is large along the [010] direction (no intergrowth in this direction) and we correct the size by using the relation (a2 + b2)1/2/a, i.e., 21/2/2 for β-MnO2 domains, and ca. 1.11 for R-MnO2 domains. By doing that, we can consider the same dimension for the results from DSD and ML-MotEx as the latter is already looking at number of intergrowth blocks along the [100] direction. The DSDs extracted from the WPPM analyses are plotted in Fig. 8 and compared to the ones obtained by ML-MotEx.
The DSD analysis show some differences between sample 1, 2 and 3. The R-MnO2 DSDs, which is centred around 1.0 nm, become narrower with increasing synthesis time. For instance, the average crystallite size estimated from WPPM is 2.5 ± 1.4 nm for sample 1 and 1.3 ± 0.9 nm for sample 3. This corresponds to only one to two unit cells of regular R-MnO2 domains within the intergrowth structure. Meanwhile, the β-MnO2 DSD shows a narrow distribution of small domains of 1.4 ± 1.0 nm in sample 1, which broadens and shifts towards larger domain size in sample 2 (2.5 ± 1.7 nm) and 3 (3.7 ± 2.2 nm). Similar trends in size are seen from the ML-Motex results. From this observation, it seems that in γ-MnO2, the intergrowth structure is stabilised by small R-MnO2 domains, around which β-MnO2 domains may grow. This is in line with theoretical studies from Sun et al. where they showed that the R-MnO2 structure is the most thermodynamically stable MnO2 polymorph at small crystallite sizes up to 5 nm.56 Beyond that size, β-MnO2 becomes the most thermodynamically stable MnO2 polymorph. The calculated DSD of the supercells determined by the peak-fitting method are shown in Fig. S9† and show similar trends as those that we observe using WPPM and ML. While the R-MnO2 DSD remains the same from sample 1 to 3, the β-MnO2 domains in the supercell become larger, although shifting towards larger values than expected for sample 3, with domain sizes ranging up to 12 nm. Because we investigate here only one single supercell, there can only exist a limited number of large domains, in opposition to the ML results where these large domains are mitigated by having some intergrowth blocks that are estimated are as neither “preferentially β-MnO2 block” or “preferentially R-MnO2 block”.
The similarity between the WPPM and our ML-MotEx-based method illustrates the crystal intergrowth observed can be compared to a stack of ultra-small nano-sized domains of each parent crystal structure, giving rise to the anisotropic line broadening in XRD patterns. Although the model did not account for all the effects impacting the XRD pattern of an intergrown crystal (peak asymmetry, microstrain), this approach gives a good description of the nanostructure.
For the 3 samples that we characterised, the size of the β- and R-MnO2 domains are ca. 1–2 nm, which corresponds also to the range in which the PDF data are refined. This observation can explain why only a few superstructures yielded a better refinement than that done with the two separate parent structures. Because PDF probes short-range order in a material, intergrowth systems can be treated as a binary mixture of the parent structures. While PDF analysis can thus be used to estimate the β-MnO2 and R-MnO2 fractions, XRD is more sensitive with respect to the way the two crystal structures are intergrown, i.e. the effect of Pb and Pr. However, in a case of an intergrowth structure that shows a high amount of disorder and where Bragg peaks can no longer be observed, PDF can still provide the missing information.
Conclusion
We have developed a method to characterise crystal intergrowth in γ-MnO2 using a combination of XRD and PDF analysis which is potentially applicable to many other systems. Our samples were hydrothermally synthesised γ-MnO2, where different synthesis times led to different defect densities. Our aim was to characterize the intergrowth density, and analyse the size of the domains present in the structure.We first simulated XRD and PDF patterns from a large database of γ-MnO2 structure models generated with different intergrowth densities. By considering trends in the simulated patterns, we developed a simple peak-fitting approach to estimate the defect density. This peak-fitting approach allowed us to obtain an estimate for the three parameters characterising the intergrowth, namely the β-MnO2 fraction, Pb and Pr.
To further characterise the materials, we used a structure-mining approach. Again using our database of γ-MnO2 structure models, we refined large subsets of these structures against our experimental data. Using the fit qualities obtained, we picked the best fitting structure for each sample and its corresponding intergrowth parameters. As the synthesis time of γ-MnO2 is increased from 2 to 5 hours, the intergrowth structure reorders from a R-like to a β-like structure, with segregation of R- and β-MnO2 domains. Our structure-mining approach also shows that structures with a fairly broad distribution of Pb and Pr lead to similar fit qualities. This suggests that it is in general difficult to assign one specific model to describe the structure of such disordered samples.
To address this issue, and to analyse the nanostructure in the samples, we characterised the size of the intergrowth domains in the three samples. Here, we applied an explainable machine learning algorithm, ML-MotEx, to extract information from the 2500 fits done for the structure-mining approach. ML-MotEx extracts the size of domains of both parent structures that help to yield a better fit of the structure, thus comparing crystal intergrowth structures to a mere stack of ultra-small nano-sized domains of two parent structures. The results showed that while R-MnO2 domains keep a constant size, β-MnO2 domains tend to grow as synthesis is carried out for longer time. The study furthermore showed that XRD is more suitable than PDF to characterise crystal intergrowths. The intergrowth affects especially the long-range order, which is better investigated with XRD.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is part of a project that has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme (grant agreement no. 804066). We are grateful to the Villum Foundation for financial support through a Villum Young Investigator grant (VKR00015416). Funding from the Danish Ministry of Higher Education and Science through the SMART Lighthouse is gratefully acknowledged. We acknowledge Diamond Light Source for time on Beamline I15-1 under Proposal CY21791-4. We thank Phillip Chapter for collecting data during remote beamtime. TEM images were collected at the DTU Nanolab, the National Centre for Nano Fabrication and Characterization at the Technical University of Denmark.References
- L. I. Hill, A. Verbaere and D. Guyomard, J. Power Sources, 2003, 119–121, 226–231 CrossRef CAS.
- S. Devaraj and N. Munichandraiah, J. Phys. Chem. C, 2008, 112, 4406–4417 CrossRef CAS.
- K. Galliez, P. Deniard, D. Lambertin, S. Jobic and F. Bart, J. Nucl. Mater., 2013, 438, 261–267 CrossRef CAS.
- D. M. Robinson, Y. B. Go, M. Mui, G. Gardner, Z. Zhang, D. Mastrogiovanni, E. Garfunkel, J. Li, M. Greenblatt and G. C. Dismukes, J. Am. Chem. Soc., 2013, 135, 3494–3501 CrossRef CAS PubMed.
- Y. Meng, W. Song, H. Huang, Z. Ren, S. Y. Chen and S. L. Suib, J. Am. Chem. Soc., 2014, 136, 11452–11464 CrossRef CAS PubMed.
- T. R. Juran, J. Young and M. Smeu, J. Phys. Chem. C, 2018, 122, 8788–8795 CrossRef CAS.
- F. Y. Cheng, J. Chen, X. L. Gou and P. W. Shen, Adv. Mater., 2005, 17, 2753–2756 CrossRef CAS.
- M. Chamoun, W. R. Brant, C.-W. Tai, G. Karlsson and D. Noréus, Energy Storage Mater., 2018, 15, 351–360 CrossRef.
- I. Vasiliev, B. A. Magar, J. Duay, T. N. Lambert and B. Chalamala, J. Electrochem. Soc., 2018, 165, A3517–A3524 CrossRef CAS.
- M. M. Thackeray, M. H. Rossouw, A. de Kock, A. P. de la Harpe, R. J. Gummow, K. Pearce and D. C. Liles, J. Power Sources, 1993, 43, 289–300 CrossRef CAS.
- C. Godart, M. Latroche, C. Freticny and C. Levy-Clement, Phys. Status Solidi A, 1992, 132, 253–268 CrossRef CAS.
- Y. Chabre and J. Pannetier, Prog. Solid State Chem., 1995, 23, 1–130 CrossRef CAS.
- A. Le Gal La Salle, S. Sarciaux, A. Verbaere, Y. Piffard and D. Guyomard, J. Electrochem. Soc., 2000, 147, 945 CrossRef CAS.
- L. I. Hill and A. Verbaere, J. Solid State Chem., 2004, 177, 4706–4723 CrossRef CAS.
- P. M. De Wolff, Acta Crystallogr., 1959, 12, 341–345 CrossRef CAS.
- C. Poinsignon, M. Amarilla and F. Tedjar, J. Mater. Chem., 1993, 3, 1227–1229 RSC.
- S. Jouanneau, S. Sarciaux, A. Le Gal La Salle and D. Guyomard, Solid State Ionics, 2001, 140, 223–232 CrossRef CAS.
- K. Galliez, P. Deniard, C. Payen, D. Lambertin, F. Bart, H.-J. Koo, M.-H. Whangbo and S. Jobic, Inorg. Chem., 2015, 54, 1194–1196 CrossRef CAS PubMed.
- D. Simon, R. Morton and J. Gislason, J. Adv. X-ray Anal., 2004, 47, 267–280 CAS.
- K. Galliez, P. Deniard, P.-E. Petit, D. Lambertin, F. Bart and S. Jobic, J. Appl. Crystallogr., 2014, 47, 552–560 CrossRef CAS.
- M. M. J. Treacy, J. M. Newsam and M. W. Deem, Proc. R. Soc. London, Ser. A, 1991, 433, 499–520 CrossRef.
- M. Leoni, A. F. Gualtieri and N. Roveri, J. Appl. Crystallogr., 2004, 37, 166–173 CrossRef CAS.
- M. Casas-Cabanas, M. Reynaud, J. Rikarte, P. Horbach and J. Rodríguez-Carvajal, J. Appl. Crystallogr., 2016, 49, 2259–2269 CrossRef CAS.
- A. A. Coelho, J. S. O. Evans and J. W. Lewis, J. Appl. Crystallogr., 2016, 49, 1740–1749 CrossRef CAS.
- C. M. Ainsworth, J. W. Lewis, C.-H. Wang, A. A. Coelho, H. E. Johnston, H. E. A. Brand and J. S. O. Evans, Chem. Mater., 2016, 28, 3184–3195 CrossRef CAS.
- W. A. Sławiński, D. S. Wragg, D. Akporiaye and H. Fjellvåg, Microporous Mesoporous Mater., 2014, 195, 311–318 CrossRef.
- S. Bette, T. Takayama, V. Duppel, A. Poulain, H. Takagi and R. E. Dinnebier, Dalton Trans., 2019, 48, 9250–9259 RSC.
- A. S. Masadeh, E. S. Bozin, C. L. Farrow, G. Paglia, P. Juhas, S. J. L. Billinge, A. Karkamkar and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115413 CrossRef.
- X. Yang, A. S. Masadeh, J. R. McBride, E. S. Božin, S. J. Rosenthal and S. J. L. Billinge, Phys. Chem. Chem. Phys., 2013, 15, 8480–8486 RSC.
- A. Kudielka, S. Bette, R. E. Dinnebier, M. Abeykoon, C. Pietzonka and B. Harbrecht, J. Mater. Chem. C, 2017, 5, 2899–2909 RSC.
- S. Bette, T. Takayama, K. Kitagawa, R. Takano, H. Takagi and R. E. Dinnebier, Dalton Trans., 2017, 46, 15216–15227 RSC.
- A. M. Pütz, M. W. Terban, S. Bette, F. Haase, R. E. Dinnebier and B. V. Lotsch, Chem. Sci., 2020, 11, 12647–12654 RSC.
- S. Mangelsen, B. R. Srinivasan, U. Schürmann, L. Kienle, C. Näther and W. Bensch, Dalton Trans., 2019, 48, 1184–1201 RSC.
- X. Wang and Y. Li, J. Am. Chem. Soc., 2002, 124, 2880–2881 CrossRef CAS PubMed.
- J. Filik, A. Ashton, P. Chang, P. Chater, S. Day, M. Drakopoulos, M. Gerring, M. Hart, O. Magdysyuk and S. Michalik, J. Appl. Crystallogr., 2017, 50, 959–966 CrossRef CAS PubMed.
- X. Yang, P. Juhas, C. L. Farrow and S. J. L. Billinge, 2014, eprint, DOI:10.48550/arXiv.1402.3163.
- M. D. Abràmoff, P. J. Magalhães and S. J. Ram, J. Biophotonics Int., 2004, 11, 36–42 Search PubMed.
- K. Pussi, J. Gallo, K. Ohara, E. Carbo-Argibay, Y. V. Kolen'ko, B. Barbiellini, A. Bansil and S. Kamali, Condens. Matter, 2020, 5, 19 CrossRef CAS.
- K. S. Abou-El-Sherbini, M. Askar and R. Schöllhorn, Solid State Ionics, 2002, 150, 407–415 CrossRef CAS.
- F. Cheng, J. Zhao, W. Song, C. Li, H. Ma, J. Chen and P. Shen, Inorg. Chem., 2006, 45, 2038–2044 CrossRef CAS PubMed.
- C. Wang, Y. Zeng, X. Xiao, S. Wu, G. Zhong, K. Xu, Z. Wei, W. Su and X. Lu, J. Energy Chem., 2020, 43, 182–187 CrossRef.
- X. Zhang, P. Yu, D. Zhang, H. Zhang, X. Sun and Y. Ma, Mater. Lett., 2013, 92, 401–404 CrossRef CAS.
- D. Su, H.-J. Ahn and G. Wang, J. Mater. Chem. A, 2013, 1, 4845–4850 RSC.
- A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218 CrossRef CAS.
- G. Caglioti, A. Paoletti and F. P. Ricci, Nucl. Instrum. Methods, 1958, 3, 223–228 CrossRef CAS.
- O. Schilling and J. Dahn, J. Appl. Crystallogr., 1998, 31, 396–406 CrossRef CAS.
- J.-R. Hill, C. M. Freeman and M. H. Rossouw, J. Solid State Chem., 2004, 177, 165–175 CrossRef CAS.
- D. Balachandran, D. Morgan, G. Ceder and A. van de Walle, J. Solid State Chem., 2003, 173, 462–475 CrossRef CAS.
- P. Ruetschi, J. Electrochem. Soc., 1984, 131, 2737 CrossRef CAS.
- T. X. Sayle, C. R. A. Catlow, R. R. Maphanga, P. E. Ngoepe and D. C. Sayle, J. Cryst. Growth, 2006, 294, 118–129 CrossRef CAS.
- A. S. Anker, M. Juelsholt, S. L. Skjærvø, I. Kantor, D. R. Sørensen, S. J. L. Billinge and R. Selvan, ChemRxiv, 2022 DOI:10.26434/chemrxiv-22022-v26431vfx.
- T. Chen and C. Guestrin, Presented in part at the Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, California, USA, 2016.
- S. M. Lundberg, G. Erion, H. Chen, A. DeGrave, J. M. Prutkin, B. Nair, R. Katz, J. Himmelfarb, N. Bansal and S.-I. Lee, Nat. Mach. Intell., 2020, 2, 56–67 CrossRef PubMed.
- S. M. Lundberg and S.-I. Lee, Proceedings of the 31st International Conference on Neural Information Processing Systems, 2017, pp. 4765–4774.
- M. Leoni, T. Confente and P. Scardi, Z. Kristallogr., 2006, 249–254 Search PubMed.
- W. Sun, D. A. Kitchaev, D. Kramer and G. Ceder, Nat. Commun., 2019, 10, 573 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dt02153f |
| This journal is © The Royal Society of Chemistry 2022 |