Elliptic dichroism in strong-field ionization of atoms subjected to tailored laser fields
Wilhelm
Becker
 *a and
Dejan B.
Milošević
*a and
Dejan B.
Milošević
 abc
abc
aMax-Born-Institut, Max-Born-Strasse 2a, 12489 Berlin, Germany. E-mail: wbecker@mbi-berlin.de
bUniversity of Sarajevo – Faculty of Science, Zmaja od Bosne 35, 71000 Sarajevo, Bosnia and Herzegovina. E-mail: milo@bih.net.ba
cAcademy of Sciences and Arts of Bosnia and Herzegovina, Bistrik 7, 71000 Sarajevo, Bosnia and Herzegovina
First published on 25th February 2022
Abstract
The differential ionization rate for strong-field ionization by tailored laser fields of atomic systems averaged over the magnetic quantum number satisfies particular inversion and reflection symmetries. The symmetries of the elliptic-dichroism parameter, which is related to the change of sign of the ellipticity of the laser field, are considered in detail, with particular emphasis on high-order above-threshold ionization. The general results are illustrated by the examples of an elliptically polarized laser field and a bi-elliptical orthogonally polarized two-color (BEOTC) field. For the BEOTC field the differential ionization rate and the elliptic-dichroism parameter are investigated for the ω–2ω and ω–3ω field combinations and for various relative phases between the laser-field components. The inversion and reflection symmetries of the photoelectron momentum distribution in the polarization plane of the field depend on the parities of r and s in the rω--sω BEOTC field combination and on the relative phase between the field components. We suggest that, by analyzing the symmetry properties of the measured momentum distribution of the elliptic-dichroism parameter, one can identify the mechanism of strong-field ionization. If the rescattering mechanism is dominant one can use these distributions to obtain information about the atomic and molecular structure and dynamics.
1 Introduction
Dichroic effects provide a versatile tool for modern physics and chemistry.1 For photoionization, two limiting cases can be identified: photoelectric circular dichroism (PECD) refers to a backward/forward asymmetry of the electron yield in the propagation direction of the incident circularly polarized laser beam, which is observed for a target of nonoriented chiral molecules. In contrast to earlier dichroic effects, this is due to the electric rather than the magnetic dipole. Hence the effect is substantial and has important applications especially for chiral recognition in the gas phase. Alternatively, circular (or elliptical) dichroism in the angular distribution (CDAD) refers to the effect of a change of the polarization state of the incident light on the momentum distribution within the polarization plane of photoelectrons released by a usually nonchiral target: “…, the CDAD effect disappears in directions parallel to the photon beam, whereas PECD asymmetry is maximized in these directions. Conversely, the PECD asymmetry disappears in directions perpendicular to the photon beam where the maximum CDAD asymmetry can be found”.1 CDAD can be used to analyze the interaction of light with a nonchiral target in order to assess the relative weight of nonadiabatic versus adiabatic ionization mechanisms. In other words, it allows one to attribute features of the momentum distribution to processes that require or do not require interaction of the freed electron with the parent ion.The first theoretical formulation of PECD was given in ref. 2 and the first observations were reported in ref. 3 and 4. Dichroic effects were observed in one-photon ionization and subsequently also in multiphoton ionization,5,6 above-threshold ionization (ATI)7 and, in general, in strong-field ionization.8–11 Currently, in addition to the photo-ion circular dichroism (PICD),12 PECD appears to open up the best avenue towards efficient chiral recognition.4,13 The term PECD has also been used for backward/forward asymmetries caused by orthogonally polarized two-color (OTC) fields.14
Left-right asymmetries in the photoelectron angular distributions of ATI by an elliptically polarized laser field were first reported in ref. 15, which has initiated many subsequent studies.16–20 In the present paper we consider CDAD, more precisely elliptic dichroism (EDAD) in strong-field ionization and, in particular, in above-threshold ionization (ATI) and high-order above-threshold ionization (HATI).
High-order strong-laser-field-driven processes are usually explained using the three-step model: the electron, temporarily liberated from an atom or molecule (this is the first or ionization step) may be driven back by the field (propagation step) to interact with the parent ion in the third step. If this interaction is elastic backscattering, then in the resulting process (called HATI) the electron can significantly increase its energy. Another possibility is recombination of this electron with the parent ion followed by emission of a high-energy photon (this is the so-called high-order harmonic generation). We also mention nonsequential multiple ionization, the process in which the recolliding electron kicks out one or more electrons of the parent ion. Such three-step processes have been usually examined using linearly polarized fields since the electron, driven by such a field, can readily revisit the parent ion. In the more general case of an elliptically polarized field, the liberated electron, if it starts with zero momentum, will “miss” its parent ion (i.e., in the language of quantum mechanics, the overlap of the corresponding wave packets will be small), so that the probability of the afore-mentioned high-order processes becomes lower and lower with increasing ellipticity.
For linear polarization and elastic rescattering by the angle 180° (backscattering) the final electron energy can be as high as 10Up (Up is the electron ponderomotive energy in the laser field), which is five times larger than the maximum energy of the directly ionized (ATI) electrons. The electron can rescatter in any direction, including forward scattering. In this case, the corresponding final electron energy is lower (<2Up). Usually, electrons that do not undergo rescattering (called direct electrons) make the main contribution in this energy region. However, Coulomb effects can enhance the contribution of the forward-scattered electrons since the Coulomb scattering cross section is very large for small angles.21 In fact, the low-energy structures (LES) in the energy region <0.1Up, discovered in 200922,23 (see Section 4 in ref. 24), were attributed to forward scattering.25 In addition to the LES, the forward-scattered electrons in the region (1–2)Up generate various interesting structures especially off the polarization axis,26 most of which have been observed. By interference with the direct electrons, they cause the spiderlike structures known as holograms.27,28 In our quantum-orbit nomenclature, these orbits are denoted as νμ = 10.29,30
More recently, it has been confirmed that there are more complex field configurations that also allow the electron to return to its parent ion so that high-order processes can occur more easily. Such, so-called tailored, fields consist of two or more field components having different frequencies and polarizations (see, for example, the special issue about dynamics in tailored ultrashort light fields31). For example, a bicircular field is a superposition of two coplanar counter-rotating circularly polarized fields having different frequencies. The HATI process in such a field was considered, for example, in ref. 32 where the improved strong-field approximation, which we will use in the present paper, was presented in detail. As another example, the helicity asymmetry of HATI by an intense bicircular field was analyzed in ref. 18. The helicity-asymmetry parameter defined in this reference is a special case of the elliptic-dichroism parameter to be introduced in the present paper. More recently, circular dichroism in biharmonic ionization of atoms was investigated in ref. 20. Another example of a tailored field is the OTC field, which consists of two linearly polarized components with orthogonal polarizations and commensurable frequencies. A detailed list of references devoted to strong-field processes in OTC fields can be found in ref. 33. Bicircular and OTC fields are special cases of a bi-elliptical OTC (BEOTC) field, which was introduced in ref. 34. As far as we know, the HATI process in a BEOTC field has not been investigated yet. This will make up a major part of this paper.
We will focus on the symmetries obeyed by the angle-resolved spectrum or the velocity map of the liberated electron. A parametric plot of the vector potential of the driving field may exhibit two kinds of symmetries, rotational symmetries and inversion symmetry (r → −r) on the one hand and reflection symmetry with respect to one or several planes (e.g. x → −x or y → −y) on the other.18 The first type preserves the direction of the time evolution of the vector potential while the second one reverses it. The overall shape of the velocity map of the released electron is closely related to the symmetries of the vector potential. ATI electrons, which are described by the lowest-order term of a Born expansion of the ionization amplitude in terms of the binding potential, observe both of the afore-mentioned symmetries. In contrast, HATI electrons undergo rescattering. Hence, they are only captured by the next-order term of the Born series, which allows for one additional interaction with the binding potential. This term depends on the time evolution of the field: ionization precedes rescattering. Therefore, the momentum distribution of the HATI electrons only reproduces the first type of symmetries, which does not depend on the direction of the time evolution. A reversal of the helicities of the driving field corresponds to time reversal. Hence, it leaves the first type intact but not the second. This is most clearly brought out by the dichroism parameter to be defined below. Nonzero values of this parameter immediately pinpoint regions where rescattering makes the dominant contributions. The other way around, given a momentum distribution obtained from an experiment or from numerical solution of the time-dependent Schrödinger equation, an analysis of the field symmetries preserved versus those violated allows one to conclude whether or not electrons with certain momenta have undergone rescattering.
We will analyze in detail the dependence of the differential ionization rate and the elliptic dichroism parameter on the parameters of the BEOTC field. We will start our scrutiny with the simpler case of just one elliptically polarized field and investigate the effect of the sign of the ellipticity especially on the various low-energy structures. In Subsection 2.1 we briefly sketch the formalism that we will utilize, viz. the strong-field approximation for both the direct and the rescattered electrons. In Subsection 2.2 we introduce the fields that we will investigate, discuss their symmetry properties and the ensuing symmetries of the angle-resolved spectrum of the liberated electrons. Section 3 exhibits the results for the two field configurations, Subsection 3.1 for the elliptically polarized field and Subsection 3.2 for the BEOTC field. We compare the results for two wavelengths, 1300 and 2000 nm. The final Section 4 presents conclusions. We use atomic units throughout the paper.
2 Theory
2.1 Differential ionization rate and the improved strong-field approximation
The differential ionization rate for detection of an electron with the momentum p and with absorption of n photons from the laser field is given by32,35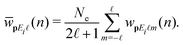 | (1) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (there are 2
(there are 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1 orbitals enumerated by m). Since each orbital can be occupied by two electrons with opposite values of the spin projections we have Ne = 2(2
+ 1 orbitals enumerated by m). Since each orbital can be occupied by two electrons with opposite values of the spin projections we have Ne = 2(2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1). For the He atom it is
+ 1). For the He atom it is ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = m = 0, while for the other inert gases (Ne, Ar, Kr, Xe) we have
= m = 0, while for the other inert gases (Ne, Ar, Kr, Xe) we have ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, m = 0, ±1. We will illustrate our theoretical results using the example of the Ar atom, which has the ionization potential Ip = 15.76 eV.
= 1, m = 0, ±1. We will illustrate our theoretical results using the example of the Ar atom, which has the ionization potential Ip = 15.76 eV.
Within the improved strong-field approximation we have32,35–37
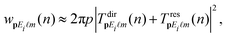 | (2) |
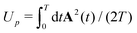 is the ponderomotive energy, T = 2π/ω the period, and ω the fundamental angular frequency of the laser field. We use the dipole approximation and the length gauge with the electric field vector E(t) = −dA(t)/dt. The so-called direct-ionization T-matrix element is
is the ponderomotive energy, T = 2π/ω the period, and ω the fundamental angular frequency of the laser field. We use the dipole approximation and the length gauge with the electric field vector E(t) = −dA(t)/dt. The so-called direct-ionization T-matrix element is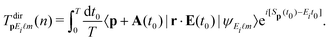 | (3) |
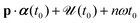 , where A(t) = dα(t)/dt and
, where A(t) = dα(t)/dt and 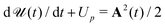 . In our approach, the ground-state wave functions ψEi
. In our approach, the ground-state wave functions ψEi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m are calculated using the Hartree–Fock–Roothan method and presented in the form of a linear combination of Slater-type orbitals.32,35
m are calculated using the Hartree–Fock–Roothan method and presented in the form of a linear combination of Slater-type orbitals.32,35
The rescattering T-matrix element 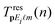 describes the so-called three-step process (see the review articles36,37 and references therein) in which the liberated electron returns to the parent ion and rescatters off it (i.e., off the corresponding potential V(r), which we model by a double Yukawa potential as described in ref. 35 and 38), reaching the detector with the final momentum p. It is given by
describes the so-called three-step process (see the review articles36,37 and references therein) in which the liberated electron returns to the parent ion and rescatters off it (i.e., off the corresponding potential V(r), which we model by a double Yukawa potential as described in ref. 35 and 38), reaching the detector with the final momentum p. It is given by
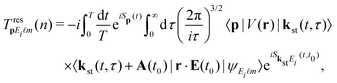 | (4) |
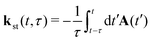 is the stationary electron momentum, SqE(t,t0) ≡ Sq(t0) − Et0 − Sq(t) and the term Sq(t) − Eit0 can be replaced by
is the stationary electron momentum, SqE(t,t0) ≡ Sq(t0) − Et0 − Sq(t) and the term Sq(t) − Eit0 can be replaced by 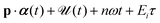 . As before, the double integral in eqn (4) can be calculated numerically or using the saddle-point method. The matrix elements in eqn (3) and (4) can be calculated analytically. For inert gases with
. As before, the double integral in eqn (4) can be calculated numerically or using the saddle-point method. The matrix elements in eqn (3) and (4) can be calculated analytically. For inert gases with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 the matrix element for m = 0 is equal to zero, so that only the contributions with m = ±1 have to be taken into account in (1).
= 1 the matrix element for m = 0 is equal to zero, so that only the contributions with m = ±1 have to be taken into account in (1).
2.2 Inversion and reflection symmetries
An elliptically polarized laser field with the frequency ω1 = rω (r integer), amplitude E1 and ellipticity ε1 has the form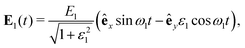 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ =
θ = ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) ·êx and tan
·êx and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = py/px. To cover the most general case where pz ≠ 0, the ionization potential Ip has to be replaced by Ip + pz2/2.
θ = py/px. To cover the most general case where pz ≠ 0, the ionization potential Ip has to be replaced by Ip + pz2/2.
The exact differential ionization rate w(p,ε) ≡ wpEi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(n) for the field (5) (with the notation ε = ε1) satisfies the inversion symmetry (twofold symmetry) w(−p,ε) = w(p,ε), i.e., w(θ) = w(θ + π). This can be shown by rewriting the transition amplitude in the interaction representation as39
m(n) for the field (5) (with the notation ε = ε1) satisfies the inversion symmetry (twofold symmetry) w(−p,ε) = w(p,ε), i.e., w(θ) = w(θ + π). This can be shown by rewriting the transition amplitude in the interaction representation as39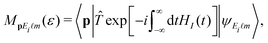 with
with ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) the time ordering operator, HI(t) = eiH0tr·E(t)e−iH0t and H0 = (−i∂/∂r)2/2 + V(r). Introducing the parity operator
the time ordering operator, HI(t) = eiH0tr·E(t)e−iH0t and H0 = (−i∂/∂r)2/2 + V(r). Introducing the parity operator ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) we have
we have ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |p〉 = |−p〉 and
|p〉 = |−p〉 and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ψEi
|ψEi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m〉 = (−1)
m〉 = (−1)![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) |ψEi
|ψEi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m〉, where we used the following relation for the spherical harmonics:
m〉, where we used the following relation for the spherical harmonics: ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) Y
Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(ϑ,φ) = Y
m(ϑ,φ) = Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(π − ϑ,φ + π) = (−1)
m(π − ϑ,φ + π) = (−1)![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) Y
Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(ϑ,φ). We get
m(ϑ,φ). We get 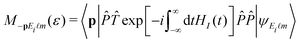 . The parity operator changes the sign of the exponent in the time-ordered exponential. Using the substitution t → t + T/2 and the relation E1(t + T/2) = −E1(t) we obtain that, up to a phase factor, M−pEi
. The parity operator changes the sign of the exponent in the time-ordered exponential. Using the substitution t → t + T/2 and the relation E1(t + T/2) = −E1(t) we obtain that, up to a phase factor, M−pEi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(ε) is equal to MpEi
m(ε) is equal to MpEi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(ε) so that the relation w(−p,ε) = w(p,ε) is proven for the exact ionization rate.
m(ε) so that the relation w(−p,ε) = w(p,ε) is proven for the exact ionization rate.
There are additional exact symmetries related to a change of the sign of the ellipticity, i.e., a change of the handedness.39 They are valid for the differential ionization rate (1), which is averaged over the magnetic quantum number m. In order to prove these symmetries we introduce the operators ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) x and
x and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) y of the reflections about the x and y axes in the polarization plane and use the relations
y of the reflections about the x and y axes in the polarization plane and use the relations ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) xY
xY![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(ϑ,φ) = Y
m(ϑ,φ) = Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(ϑ,π − φ) = Y
m(ϑ,π − φ) = Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) −m(ϑ,φ) and
−m(ϑ,φ) and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) yY
yY![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(ϑ,φ) = Y
m(ϑ,φ) = Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(ϑ,−φ) = Y
m(ϑ,−φ) = Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) −m(ϑ,φ). As in the above derivation of the inversion symmetry, it can be proven that, up to a phase factor, M−pxpyEi
−m(ϑ,φ). As in the above derivation of the inversion symmetry, it can be proven that, up to a phase factor, M−pxpyEi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) −m(−ε) is equal to MpxpyEi
−m(−ε) is equal to MpxpyEi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(ε). A similar derivation can be done for the y component. The only difference is that for py → −py it is not necessary to perform the time translation t → t + T/2 because a simultaneous application of
m(ε). A similar derivation can be done for the y component. The only difference is that for py → −py it is not necessary to perform the time translation t → t + T/2 because a simultaneous application of ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) y and the operation ε → −ε leaves the field E1(t) unchanged. Therefore, denoting
y and the operation ε → −ε leaves the field E1(t) unchanged. Therefore, denoting ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (p,ε) ≡
(p,ε) ≡ ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) pEi
pEi![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (n), we have
(n), we have ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (−px,py,−ε) =
(−px,py,−ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (px,−py,−ε) =
(px,−py,−ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (px,py,ε), i.e.,
(px,py,ε), i.e., ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (π − θ,−ε) =
(π − θ,−ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (−θ,−ε) =
(−θ,−ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ,ε) or
(θ,ε) or
![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ,−ε) = (θ,−ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (π − θ,ε). (π − θ,ε). | (6) |
![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (−θ) =
(−θ) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ).
(θ).
For the direct electrons, we have the fourfold symmetry:39![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(θ,ε) =
dir(θ,ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(π − θ,ε) =
dir(π − θ,ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(−θ,ε), and the symmetry
dir(−θ,ε), and the symmetry ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(p,ε) =
dir(p,ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(p,−ε) upon a change of helicity. This symmetry can be proven using time inversion, i.e., the substitution t → −t, which leads to
dir(p,−ε) upon a change of helicity. This symmetry can be proven using time inversion, i.e., the substitution t → −t, which leads to 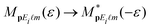 so that the rate (1) for the direct electrons is unchanged. This symmetry is not valid for the rescattering amplitude since in this case the time ordering is important (rescattering follows ionization and not vice versa). If we define the elliptic-dichroism parameter40
so that the rate (1) for the direct electrons is unchanged. This symmetry is not valid for the rescattering amplitude since in this case the time ordering is important (rescattering follows ionization and not vice versa). If we define the elliptic-dichroism parameter40
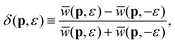 | (7) |
![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(p,ε) =
dir(p,ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(p,−ε) has the consequence that δdir(p,ε) = 0. The above-mentioned exact symmetries lead to the relations
dir(p,−ε) has the consequence that δdir(p,ε) = 0. The above-mentioned exact symmetries lead to the relations ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ,ε) =
(θ,ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ + π,ε) and
(θ + π,ε) and ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ,ε) −
(θ,ε) − ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ,−ε) =
(θ,−ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (π − θ,−ε) −
(π − θ,−ε) − ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (π − θ,ε), so that
(π − θ,ε), so that 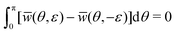 . That is, the exact ionization rate integrated over all angles is independent of the sign of the ellipticity. Therefore, to analyze dichroism, the restricted angle interval θ ∈ [0,π/2] should be used. In this case we define
. That is, the exact ionization rate integrated over all angles is independent of the sign of the ellipticity. Therefore, to analyze dichroism, the restricted angle interval θ ∈ [0,π/2] should be used. In this case we define 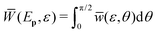 where the integration extends only over one hemisphere and introduce the angle-integrated elliptic-dichroism parameter40
where the integration extends only over one hemisphere and introduce the angle-integrated elliptic-dichroism parameter40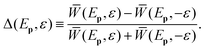 | (8) |
In ref. 34, we considered the so-called BEOTC (bi-elliptical orthogonal two-color) field. It consists of the elliptically polarized field E1(t), eqn (5), having the x axis as the major axis and a second coplanar elliptically polarized field E2(t) with the y axis as the major axis and with the frequency ω2 = sω (s integer), amplitude E2, and ellipticity ε2:
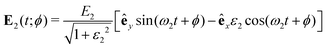 | (9) |
| E(t;ϕ) = E1(t) + E2(t;ϕ). | (10) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) x and
x and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) y and a change of sign of the ellipticities, the symmetry of the averaged rate depends on the parity of r and s and the shift of the relative phase. This is summarized in the following relations:
y and a change of sign of the ellipticities, the symmetry of the averaged rate depends on the parity of r and s and the shift of the relative phase. This is summarized in the following relations: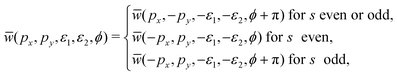 | (11) |
3 Numerical results
3.1 Elliptical field
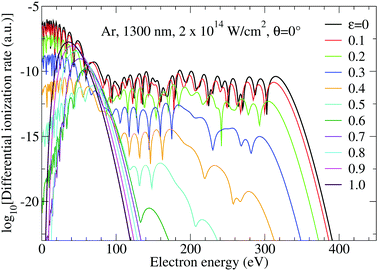
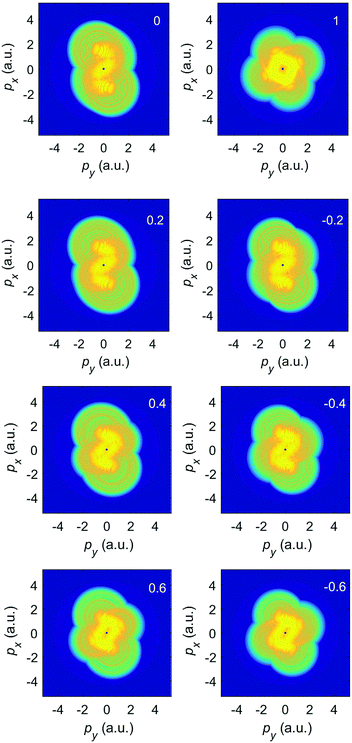
We first consider ionization of Ar atoms by a monochromatic elliptically polarized laser field with the intensity I = E12 = 2 × 1014 W cm−2 and the frequency ω1 = ω corresponding to the fundamental wavelength of 1300 nm. In Fig. 1 we present the differential ionization rate for emission in the direction of the semi-major axis of the polarization ellipse (θ = 0°) for various values of the ellipticity ε1 = ε, as indicated in the panel, calculated from eqn (2) incorporating both the direct and the rescattered electrons. The plateau of the rescattered electrons is longest for linear polarization (ε = 0; the plateau extends up to 10Up, i.e. up to 316 eV), while it is completely absent for circular polarization (ε = 1). With increasing ellipticity both the plateau height and its length quickly decrease and a multiplateau structure in the spectrum of the rescattered electrons appears. This is explained using quantum-orbit theory in ref. 41 and 42. The spectrum of the direct electrons extends up to about 2Up = 63 eV.
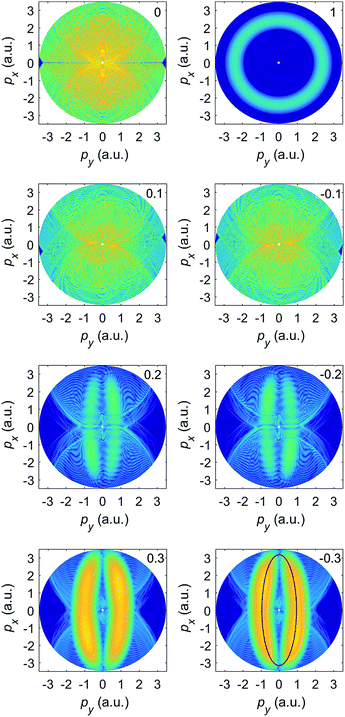
Fig. 2 exhibits the corresponding photoelectron momentum distributions for various ellipticities, evaluated again from eqn (2). For linear polarization (upper left panel) the spectrum has the characteristic form of a figure eight, elongated in the direction of the major axis of the polarization ellipse (x axis).37 For circular polarization (upper right panel) the spectrum has the form of a ring; see, e.g., ref. 36. In the remaining panels we compare the photoelectron momentum distributions for positive (left panels) and negative (right panels) ellipticities. We see that the spectrum of the direct electrons, which occupies the center of the panels and corresponds to comparatively low energies, exhibits the fourfold symmetry, while the spectrum of rescattered electrons, which is clearly visible for ε = ±0.2 and ±0.4, only exhibits the twofold symmetry ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ) =
(θ) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ + π). Opposite helicities are related by the symmetry (6), i.e.
(θ + π). Opposite helicities are related by the symmetry (6), i.e. ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ,−ε) =
(θ,−ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (π − θ,ε) =
(π − θ,ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (−θ,ε). For the larger values of ε, rescattering is too weak to make a difference, cf.Fig. 1. Hence, already for ε = 0.6 the fourfold symmetry of the direct electrons is essentially restored.
(−θ,ε). For the larger values of ε, rescattering is too weak to make a difference, cf.Fig. 1. Hence, already for ε = 0.6 the fourfold symmetry of the direct electrons is essentially restored.
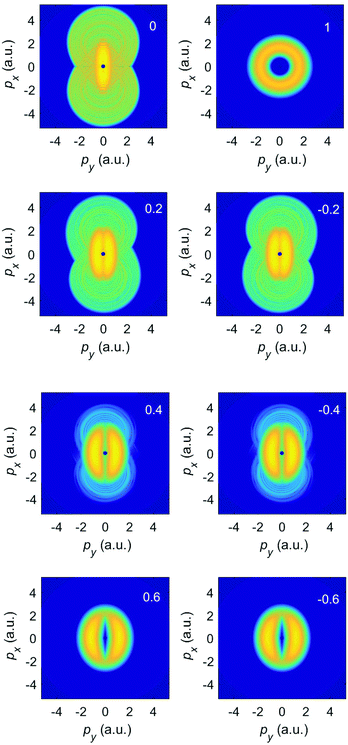 | ||
| Fig. 2 The logarithm of the differential ionization rate (in a.u.) of Ar atoms, presented in false colors in the photoelectron momentum plane, for ionization by an elliptically polarized field with the ellipticity indicated in the upper right corner of each panel. Both direct and rescattered electrons are included. The false-color scale covers 13 orders of magnitude (the logarithm of the rate is between −6 to −19). The other laser parameters are as in Fig. 1. | ||
In Fig. 3 we display the elliptic-dichroism parameter δ(p,ε), eqn (7), for two values of the ellipticity. We see that δ(p,ε) exhibits the twofold symmetry (θ ↔ θ + π) and it changes its sign for θ → −θ and θ → π − θ, which is in accordance with the relation δ(p,−ε) = −δ(p,ε). At the center of each panel we have δ(p,ε) ≈ 0, since in this region the contribution of the direct electrons is dominant. The central region expands with increasing ε due to the increasing dominance of the direct electrons. The fact that dichroic effects become less noticeable for larger ellipticities may seem counterintuitive, but a moment of thought shows that it is due to the reduced role of rescattering. In the limit of circular polarization, there is no dichroism at all, cf. the upper right panel of Fig. 2.
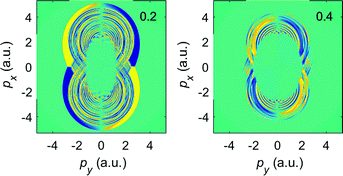 | ||
| Fig. 3 The elliptic-dichroism parameter presented in false colors in the photoelectron momentum plane for ionization of Ar atoms by an elliptically polarized field with ellipticity ε = 0.2 (left panel) and ε = 0.4 (right panel), corresponding to the spectra shown in Fig. 2. The false-color scale changes from −1 (blue) to +1 (yellow). The other laser parameters are as in Fig. 1. | ||
Fig. 4 shows the angle-integrated elliptic-dichroism parameter Δ(Ep,ε), eqn (8), for the fixed electron energies Ep = 2Up, 3Up,…,9Up. For energies lower than 2Up, for which the direct electrons are dominant, Δ(Ep,ε) is approximately zero (not shown). For energies from Ep = 2Up to 4Up it is close to zero for large ellipticities, while for smaller ellipticities, for which the contribution of the rescattered electrons is noticeable, it takes on some small values. For Ep = 4Up, Δ(Ep,ε) has a minimum of −0.19 for ε = 0.57, while for lower energies minima appear for smaller values of the ellipticity and the corresponding value of |Δ(Ep,ε)| is lower. For larger values of the energy and ellipticity the ionization rate is negligibly small and, due to loss of numerical precision owing to roundoff errors, the calculated parameter Δ(Ep,ε) is meaningless. For energies from Ep = 5Up to 9Up the parameter |Δ(Ep,ε)| increases with increasing ellipticities and exhibits oscillations.
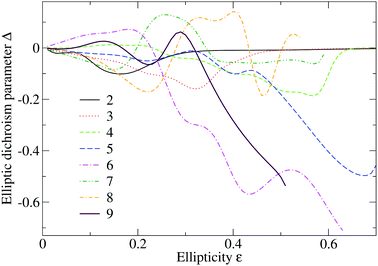 | ||
| Fig. 4 Angle-integrated elliptic-dichroism parameter as a function of the ellipticity for electron energies in units of Up as indicated. Both direct and rescattered electrons are included. The laser parameters are as in Fig. 1. | ||
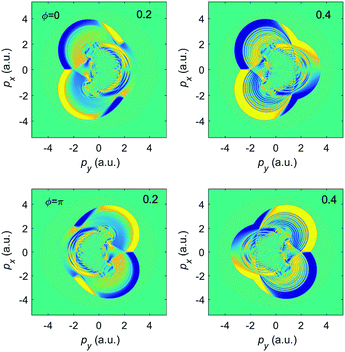
As we have mentioned in the introduction, for longer wavelengths the various low-energy structures become more pronounced. Therefore, we will now present results for a wavelength of 2000 nm, keeping the other parameters the same. Still, the direct electrons dominate the low-energy spectra except when the contribution of the forward-scattered electrons is enhanced by the Coulomb potential. In Fig. 5 we present the results for the differential ionization rate similarly as in Fig. 2, but now taking into account only the rescattering T-matrix element (4) and for the photoelectron energy lower than 2.2Up. For linear polarization, the spectrum in the top left panel has a characteristic rhombus- or diamond-like shape (compare Fig. 5 in ref. 43), while for circular polarization it has the form of a ring, similar to the upper right panel of Fig. 2. So, interestingly, for circular polarization the rescattering contribution (4) is largely proportional to the direct contribution (3). For the ellipticity ε = ±0.1 (second line) the diamond-like structure has become slightly tilted and deformed, in opposite directions for opposite helicity, and the rate satisfies the symmetries for the rescattered electrons explained above. However, for the central part of the spectrum, for py = 0 and |px| < 1 the rescattered-electron-induced difference between the spectra for ε = 0.1 and ε = −0.1 is hardly visible. This part contains the LES, which for linear polarization is located at |px| ≈ 0.75 a.u. For ε = ±0.1, a cross-like pattern in the middle of the plot appears to augment the LES; interestingly, the vertical arm does not tilt with the ellipticity while the horizontal does. For the ellipticity ε = ±0.2 a new structure has appeared: two elongated vertical kidney-shaped distributions parallel to the major polarization axis at about py = ±0.75 a.u., which together look like the two halves of a coffee bean. For larger ellipticities this structure persists and becomes even more pronounced. Its shape approaches the total distribution (direct plus rescattered), which for the shorter wavelenght of 1300 nm is shown in Fig. 2, in the same way as the rescattering contribution for circular polarization approaches the total contribution (upper right panels of Fig. 2 and 5).
Momentum distributions of the direct electrons only are analyzed in ref. 44 and 45. With increasing ellipticity the shapes of the rescattering momentum distributions appear to become closer to those of the direct electrons. However, the yields are not the same. This becomes evident by inspection of the elliptic-dichroism parameter, which we present in Fig. 6 for ellipticities from 0.1 to 0.4. For ε > 0.2, the kidney structures appear and immediately dominate the momentum distribution. However, the elliptic-dichroism parameter only observes the symmetries of the rescattered electrons and not the fourfold symmetry of the direct electrons. While this is so, the complicated rescattering structures, which characterize the plot for linear (ε = 0) and slightly elliptical (ε = 0.1) polarization, have completely disappeared for ε > 0.3. Recalling that δ(p,ε) = 0 for the direct electrons, we conclude that by measuring the elliptic-dichroism parameter it is possible to determine which electrons, direct or rescattered, dominate the strong-field ionization process. If the elliptic-dichroism parameter is different from zero and obeys the symmetries visible in Fig. 6, then we can say that the contribution of the shortest rescattering quantum orbit is dominant. This can be important for understanding the strong-field ionization process and explaining various experimentally observed structures.26–28,37 We have in mind the low-energy structures on and off the polarization axis, as well as the spiderlike structures known as holograms, laser-induced electron diffraction which can be used for imaging ultrafast molecular dynamics, etc. It would be interesting to see how these structures change with introducing laser ellipticity and how they will manifest themselves in the momentum distributions of elliptic dichroism.
 | ||
| Fig. 6 The elliptic-dichroism parameter presented in false colors in the photoelectron momentum plane for ionization of Ar atoms by an elliptically polarized field with the ellipticities denoted in the upper right corner of each panel. The false-color scale changes from −1 (blue) to +1 (yellow). The other laser parameters are as in Fig. 5, which is based on the rescattered electrons only. | ||
Comparing the spectra calculated above and the corresponding results for the elliptical dichroism on the one hand with experimental data on the other is difficult due to the effect of the Coulomb potential, which in our work is not fully incorporated beyond the wave functions of the initial bound state and the description of rescattering in the first-order Born approximation. It is well known since the early days of ATI that experimentally measured spectra for ionization of rare-gas atoms by elliptically polarized fields violate the fourfold symmetry predicted by the strong-field approximation for the direct electrons and only preserve the twofold inversion symmetry.15 This reduction from fourfold to twofold symmetry is reproduced by theory once the action of the Coulomb potential is taken into account.46–48 The coffee-bean like structures, which are so obvious in Fig. 2 and 6, are also well known except that both in experiments and in simulations that incorporate the Coulomb potential (such as CTMC (classical-trajectory Monte Carlo) simulations49–52) the two halves of the coffee bean are shifted versus one another along the major polarization axis, owing to the action of the Coulomb potential on the liberated electron. (We mention in passing that for the shorter wavelength of 400 nm the coffee-bean structure is not yet visible and the spectrum is completely dominated by the ATI rings52). The two halves of the coffee bean start shifting at or just below ε = 0.2 (see Fig. 2 and 6), in agreement with ref. 53, which presents both CTMC theory and experiments on rare gases.
At the same ellipticity of about ε = 0.2, the population along the major polarization axis starts thinning out (notice, especially, Fig. 2 for |ε| = 0.4). For |ε| ≥ 0.6, the spectrum begins to approach the characteristics of circular polarization with its rotational symmetry, and the population along the major axis rises again.44 We remark in passing that the staircase structure of the spectrum observed and discussed in ref. 41 and 42 (cf. also Fig. 1) only develops along the major axis. In general, the electron population is concentrated about the curve p = −A(t) as predicted by the simple-man model. The maxima of the momentum distribution correspond to those times t where the electric field |E(t)| is maximal, that is, where the modulus of the vector potential is minimal,44i.e., in the direction of the minor polarization axis. For ε = −0.3, the curve A(t) is displayed in the lower right panel of Fig. 5.
3.2 BEOTC field
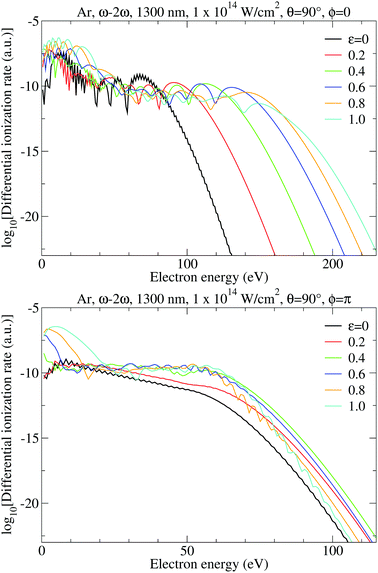
In this subsection we analyze the photoelectron spectra for ionization of Ar atoms by ω–2ω (r = 1 and s = 2) and ω–3ω (r = 1 and s = 3) BEOTC fields having the fundamental wavelength 1300 nm. For simplicity we suppose that the component ellipticities and intensities are equal, i.e., that ε1 = ε2 = ε and I1 = E12 = I2 = E22 = 1 × 1014 W cm−2. The relative phase is fixed to ϕ = 0 or to ϕ = π.In Fig. 7 we present the differential ionization rate for the ω–2ω BEOTC field for the ellipticities ε = 0, 0.2, 0.4, 0.6, 0.8, 1.0, for the electron emission angle θ = 90°, and for the relative phase ϕ = 0 (upper panel) and ϕ = π (lower panel), calculated from eqn (2) with both direct and rescattered electrons included. In all cases presented the rescattering plateau is clearly visible. For the OTC field (ε = 0) and for ϕ = 0 the plateau exhibits pronounced fast oscillations and the cutoff is at 80 eV, while for ϕ = π the plateau is more inclined and without fast oscillations, while the cutoff is at 60 eV. For larger ellipticities the plateau is almost two times longer for the relative phase ϕ = 0 than for ϕ = π. Clearly, the relative phase ϕ can serve as a powerful control parameter.
More information about the ionization process is contained in the photoelectron momentum distributions, presented in Fig. 8 for the relative phase ϕ = 0 and for various ellipticities, similarly to the case of the elliptically polarized monochromatic field in Fig. 2. The top left and right panels correspond, respectively, to the two limiting cases of the OTC field (ε = 0) and the bicircular field (ε = 1) and their momentum distributions agree with previous results.32,54 From the remaining panels we see that the rotational and reflection symmetries, which are characteristic for the OTC and bicircular fields, are violated for our more general BEOTC field. Comparing the left and right panels confirms that the simultaneous reversal of the sign of px and the sign of the ellipticity is a symmetry transformation. This is in accordance with the rule (11) (the s = 2 case in the second line).
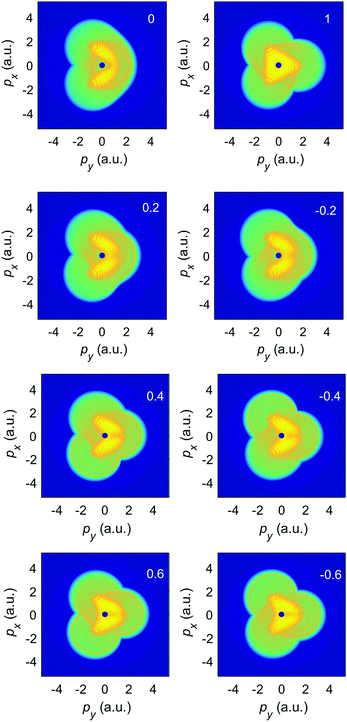 | ||
| Fig. 8 The logarithm of the differential ionization rate (in a.u.) of Ar atoms, presented in false colors in the photoelectron momentum plane, for ionization by an ω–2ω BEOTC field with the ellipticity ε = ε1 = ε2 denoted in the upper right corner of each panel, and with the relative phase ϕ = 0. Both the direct and the rescattered electrons are included. The false-color scale covers 13 orders of magnitude (the logarithm of the rate extends from −6 down to −19). The other laser parameters are as in Fig. 7. | ||
Numerical results for the same BEOTC field parameters as in Fig. 8, but with only the direct electrons included are shown in Fig. 9, for the ellipticities denoted in the upper right corner of each panel. We see that the momentum distributions are concentrated about the momenta on a parametric plot of p = −A(t0), which is depicted by a red curve in each panel. This is as predicted by the simple-man model. The curve is also an approximate solution of the saddle-point equation for the direct electrons (in the saddle-point approximation the integral over the ionization time in eqn (3) can be approximated by a sum over the saddle-point solutions t0s of the equation [p + A(t0s)]2 = −2Ip36,45). The momentum distributions in Fig. 9 satisfy the same reflection symmetries as the parametric plots, regardless of the time evolution of each curve (clockwise or counterclockwise). These symmetries are broken once rescattering is taken into account, as is clear by comparison with Fig. 8.
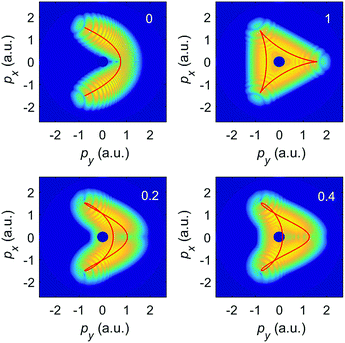 | ||
| Fig. 9 The logarithm of the differential ionization rate (in a.u.) of Ar atoms, presented in false colors in the photoelectron momentum plane, for ionization by the same BEOTC field as in Fig. 8, but with only the direct electrons included. The false-color scale covers 6 orders of magnitude (the logarithm of the rate extends from −6 down to −12). The red curves depict the negative vector potential −A(t0) for ellipticities as denoted in the upper right corner of each panel. | ||
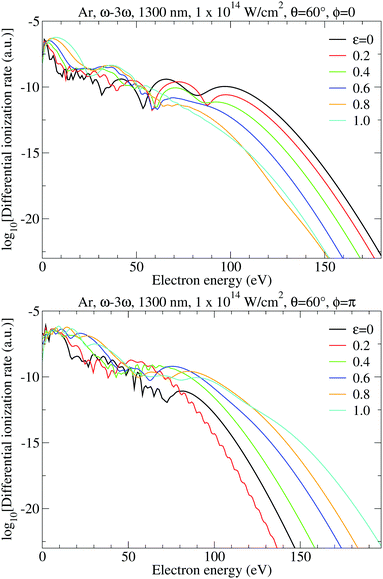
Fig. 10 displays the differential ionization rate similarly to Fig. 7 but for the ω–3ω BEOTC field and for the emission angle θ = 60°. For the relative phase ϕ = 0 the plateau length decreases with increasing ellipticities, while for ϕ = π the plateau is longer for higher ellipticities.
For an ω–3ω BEOTC field the spectra in Fig. 11 satisfy inversion symmetry, i.e., the photoelectron momentum distribution is invariant with respect to the transformation p → −p. However, they are not invariant with respect to the simultaneous change of the sign of the ellipticity and one of the momentum components, as was the case in Fig. 8. To obtain symmetry, it is also necessary to change the relative phase by π (see Fig. 13).
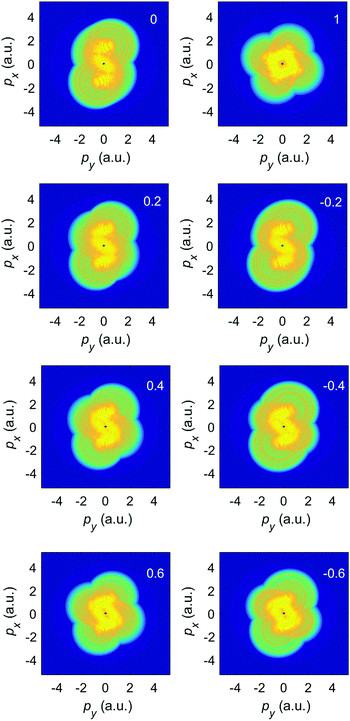 | ||
| Fig. 11 The logarithm of the differential ionization rate (in a.u.) of Ar atoms, presented in false colors in the photoelectron momentum plane, for ionization by an ω–3ω BEOTC field with the ellipticity ε = ε1 = ε2 denoted in the upper right corner of each panel, and with the relative phase ϕ = 0. Both the direct and the rescattered electrons are included. The false-color scale covers 13 orders of magnitude (the logarithm of the rate is between −6 and −19). The other laser parameters are as in Fig. 10. | ||
Comparing the left panels of Fig. 12 with the right panels of Fig. 8 shows that the momentum distributions for the ω–2ω BEOTC field are invariant with respect to the simultaneous transformations ε ↔ −ε, py ↔ −py, and ϕ ↔ ϕ + π, in agreement with the rule (11). On the other hand, comparing the left panels of Fig. 13 with the right panels of Fig. 11 we conclude that for the ω–3ω BEOTC field, in addition to the inversion symmetry, two symmetry transformations are valid: (i) ε ↔ −ε, ϕ ↔ ϕ + π, px ↔ −px and (ii) ε ↔ −ε, ϕ ↔ ϕ + π, py ↔ −py. This is again in accordance with the rule (11).
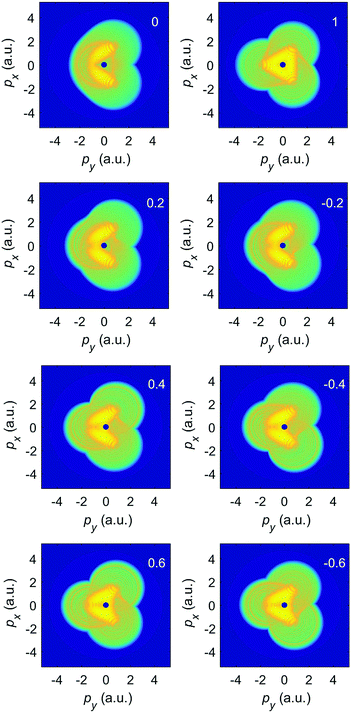 | ||
| Fig. 12 Same as Fig. 11, but for the ω–2ω BEOTC field with the relative phase ϕ = π. | ||
 | ||
| Fig. 13 The logarithm of the differential ionization rate (in a.u.) of Ar atoms, presented in false colors in the photoelectron momentum plane, for ionization by an ω–3ω BEOTC field with the ellipticity ε = ε1 = ε2 denoted in the upper right corner of each panel, and with the relative phase ϕ = π. The false-color scale covers 13 orders of magnitude (the logarithm of the rate is between −6 and −19). The other laser parameters are as in Fig. 10. | ||
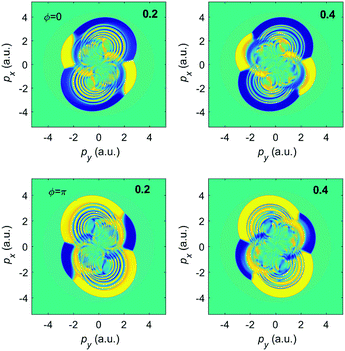
In Fig. 14 we show the elliptic-dichroism parameter δ(p,ε), eqn (7), for two values of the ellipticity. We see that δ(p,ε) changes its sign for px → −px, i.e., θ → π − θ, as required by eqn (11) and the relation δ(p,−ε) = −δ(p,ε). In addition, we see that the symmetry transformation ε ↔ −ε, ϕ ↔ ϕ + π, py ↔ −py, is also satisfied.
 | ||
| Fig. 14 The elliptic-dichroism parameter δ(p,ε) presented in false colors in the photoelectron momentum plane for ionization of Ar atoms by an ω–2ω BEOTC field with ellipticity ε = 0.2 (left panels) and ε = 0.4 (right panels) and relative phase ϕ = 0 (upper panels) and ϕ = π (lower panels) corresponding to the spectra of Fig. 8 (ϕ = 0) and Fig. 12 (ϕ = π). The false-color scale changes from −1 (blue) to +1 (yellow). The other laser parameters are as in Fig. 7. | ||
Fig. 15 displays the elliptic dichroism parameter for the ω–3ω BEOTC field. Now the inversion symmetry p → −p is satisfied for all phases and ellipticities. In addition, the above-mentioned symmetries (i) and (ii) are also satisfied. Especially for the higher ellipticity ε = 0.4, the plots identify regions of very high contrast wherein ionization into a final state with certain momenta (px.py) is much more likely by a field with one value of the helicity rather than its opposite. There are also extended regions, especially near the center of the plot, where the rate of ionization is practically independent of the helicity indicating that rescattering plays hardly any role for these final-state momenta.
 | ||
| Fig. 15 The elliptic-dichroism parameter presented in false colors in the photoelectron momentum plane for ionization of Ar atoms by an ω–3ω BEOTC field with ellipticity ε = 0.2 (left panels) and ε = 0.4 (right panels) and relative phase ϕ = 0 (upper panels) and ϕ = π (lower panels), corresponding to the spectra of Fig. 11 (ϕ = 0) and Fig. 13 (ϕ = π). The false-color scale changes from −1 (blue) to +1 (yellow). The other laser parameters are as in Fig. 10. | ||
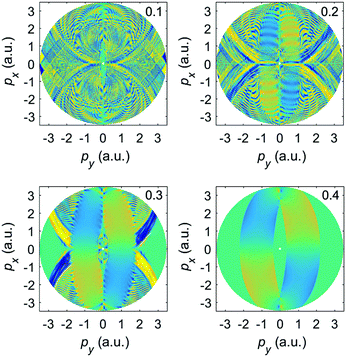
Finally, we will focus on comparatively low momenta and the transition from the pure OTC field (ε = 0) towards the bicircular field (ε = 1). Fig. 16 exhibits enlargements of the panels of Fig. 8 with positive ellipticity, with only rescattered electrons included, and with a color scale that is more adapted to the analysis of the central region. The ponderomotive potential of the ω field component is 0.58 a.u.; for linear polarization the first LES corresponds to the momentum 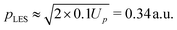 , which should set the stage also for the LESs due to the OTC or BEOTC fields. For ε = 0, this region is rather thinly populated. The structures that are visible observe the px → −px symmetry of the OTC field. With increasing ε various much more pronounced structures develop. They are all characterized by a strong violation of the afore-mentioned symmetry. For larger momenta, some spiral arms start to develop as they are characteristic of the bicircular field where their directionality is related to the relative helicity of the bicircular field.18,32 However, in the present case the arms protrude in either direction. For further increasing ellipticity, the spectra approach those of the bicircular field and the pertinent rotational symmetry. Interestingly, this happens more quickly in the outer momentum regions.
, which should set the stage also for the LESs due to the OTC or BEOTC fields. For ε = 0, this region is rather thinly populated. The structures that are visible observe the px → −px symmetry of the OTC field. With increasing ε various much more pronounced structures develop. They are all characterized by a strong violation of the afore-mentioned symmetry. For larger momenta, some spiral arms start to develop as they are characteristic of the bicircular field where their directionality is related to the relative helicity of the bicircular field.18,32 However, in the present case the arms protrude in either direction. For further increasing ellipticity, the spectra approach those of the bicircular field and the pertinent rotational symmetry. Interestingly, this happens more quickly in the outer momentum regions.
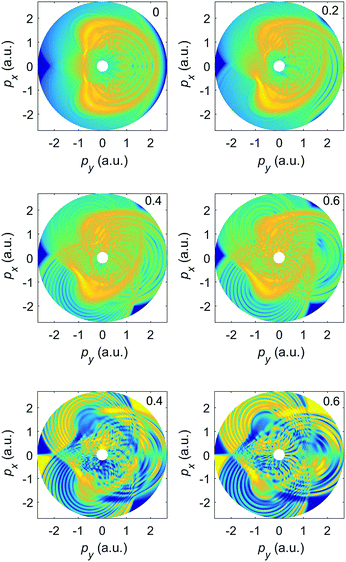 | ||
| Fig. 16 Enlargement of the central parts of Fig. 8 for the same parameters but positive ellipticities only and with only the rescattered electrons included. The color scale includes five orders of magnitude. The bottom panel shows the corresponding elliptic-dichroism parameter for the ellipticities ε = 0.4 and ε = 0.6. | ||
The bottom panel of Fig. 16 exhibits the elliptic-dichroism parameter for ε = 0.4 and ε = 0.6. We can see that δ(p,ε) is large in an extended region of the spectrum about (px,py) = (−1,−1) a.u. The upper right panel of Fig. 14 presents the spectrum due to both the direct and the rescattered electrons. This plot shows a large region with momenta |px| ≤ 1 and |py| ≤ 2 where δ(p,ε) ≈ 0. This reveals that overall rescattering contributes little to this region, even though taken by itself its helicity asymmetry is strong. We conclude that by measuring the momentum distribution of the elliptic-dichroism parameter one can obtain information about the significance of rescattering, i.e., information about the rescattering target.
4 Conclusions
Low-energy photoelectrons liberated in strong-field ionization of atoms are mostly generated as direct electrons, i.e. electrons that directly go to the detector after ionization. On the other hand, electrons reach high energies as a consequence of rescattering off their parent ion. Due to their different ionization mechanism the photoelectron momentum distributions display different characteristics for direct and rescattered electrons. For ionization by an elliptical field, in addition to the twofold inversion symmetry![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (−p) =
(−p) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (p), which is obeyed by all electrons, the direct-electron spectra satisfy the fourfold symmetry
(p), which is obeyed by all electrons, the direct-electron spectra satisfy the fourfold symmetry ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(θ) =
dir(θ) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(π − θ) =
dir(π − θ) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(−θ) and they do not depend on the sign of the ellipticity, i.e.
dir(−θ) and they do not depend on the sign of the ellipticity, i.e. ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(p,ε) =
dir(p,ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) dir(p,−ε). Therefore, the elliptic-dichroism parameter is equal to zero for the direct electrons. This symmetry is not valid for the rescattered electrons since for these electrons the time-inversion symmetry is violated: the time ordering—first ionization and then rescattering—is crucial. However, instead of this symmetry, the photoelectron spectra for elliptical polarization satisfy the symmetry
dir(p,−ε). Therefore, the elliptic-dichroism parameter is equal to zero for the direct electrons. This symmetry is not valid for the rescattered electrons since for these electrons the time-inversion symmetry is violated: the time ordering—first ionization and then rescattering—is crucial. However, instead of this symmetry, the photoelectron spectra for elliptical polarization satisfy the symmetry ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (π − θ,−ε) =
(π − θ,−ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (−θ,−ε) =
(−θ,−ε) = ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) (θ,ε). The resulting symmetries of the elliptic-dichroism parameter are analyzed in detail in the first part of the paper. An important discovery is that for ellipticities higher than |ε| = 0.2 the electron momentum distribution forms a structure parallel to the major polarization axis that is reminiscent of a coffee bean. For further increasing ellipticity, the momentum dependence of the elliptic-dichroism parameter simplifies more and more, indicating that fewer and fewer quantum orbits contribute. A quantum-orbit analysis of the low-energy structures for elliptical polarization has not been carried out yet. Analyzing the symmetry properties of the measured momentum distribution of the elliptic-dichroism parameter the mechanism of strong-field ionization can be identified. If rescattering is the dominant mechanism we can use the elliptic-dichroism distributions to obtain information about the atomic and molecular structure and dynamics. For example, one can explore the evolution of a molecular shape resonance along a chemical bond as it is stretching, as has been done for a linearly polarized field in ref. 55. Or one can trace the subfemtosecond molecular dynamics as was done in ref. 56 for an elliptically polarized laser field.
(θ,ε). The resulting symmetries of the elliptic-dichroism parameter are analyzed in detail in the first part of the paper. An important discovery is that for ellipticities higher than |ε| = 0.2 the electron momentum distribution forms a structure parallel to the major polarization axis that is reminiscent of a coffee bean. For further increasing ellipticity, the momentum dependence of the elliptic-dichroism parameter simplifies more and more, indicating that fewer and fewer quantum orbits contribute. A quantum-orbit analysis of the low-energy structures for elliptical polarization has not been carried out yet. Analyzing the symmetry properties of the measured momentum distribution of the elliptic-dichroism parameter the mechanism of strong-field ionization can be identified. If rescattering is the dominant mechanism we can use the elliptic-dichroism distributions to obtain information about the atomic and molecular structure and dynamics. For example, one can explore the evolution of a molecular shape resonance along a chemical bond as it is stretching, as has been done for a linearly polarized field in ref. 55. Or one can trace the subfemtosecond molecular dynamics as was done in ref. 56 for an elliptically polarized laser field.
We also considered the BEOTC field for which the above-mentioned symmetries are, in general, violated. Rather, we have identified particular symmetries that depend on the parity of r and s for the rω–sω BEOTC field that we used and on the relative phase between the field components. These symmetries are summarized in relation (11) and the preceding text. All the afore-mentioned symmetries of the photoelectron momentum distributions and the elliptic-dichroism parameter are illustrated by plots obtained using calculations based on the (improved) strong-field approximation.
We restricted ourselves to equal ellipticities and intensities for the two BEOTC components. In general, exploiting the possibilities of this parameter space, certainly the appearance of dichroic effects can be greatly expanded. An example is the investigation of the effect of the intensity ratio57 and the ellipticities58 of the bicircular field components on high-order harmonic generation. The analysis described above of the elliptic-dichroism parameter in atomic (H)ATI by the BEOTC field, and, in general, in tailored fields, can be generalized to molecular systems. For this we can use our molecular improved strong-field approximation (see ref. 59 and references therein). In the future we will investigate how elliptic dichroism depends on molecular parameters such as the internuclear distance and the molecular orientation. The molecular structure and its symmetry are imprinted in the interference minima that are observed in the photoelectron momentum distributions in HATI by a linearly polarized laser field. This was predicted in ref. 59 and observed in ref. 60 and 61. We expect that such interferences in tailored fields will be particularly noticeable in the momentum distribution of the elliptic-dichroism parameter, analogous to that presented in Fig. 14 and 15 for the argon atom. As another example, the position within a molecule where the electron is photo-emitted can be resolved, see the recent work62 in which an OTC field was applied. Extension to a BEOTC field and study of the elliptic dichroism will yield additional transverse information.
Author contributions
All authors contributed equally to the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support by the Ministry of Science, Higher Education and Youth, Canton Sarajevo, Bosnia and Herzegovina, and the Alexander von Humboldt Foundation.References
- I. Powis, Adv. Chem. Phys., 2008, 138, 267 CrossRef CAS.
- B. Ritchie, Phys. Rev. A, 1976, 13, 1411 CrossRef.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187 CrossRef PubMed.
- L. Nahon, G. A. Garcia, C. J. Harding, E. Mikajlo and I. Powis, J. Chem. Phys., 2006, 125, 114309 CrossRef PubMed.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Kohler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 51, 5001 CrossRef CAS PubMed.
- C. S. Lehmann, N. B. Ram, I. Powis and M. H. M. Janssen, J. Chem. Phys., 2013, 139, 234307 CrossRef PubMed.
- C. Lux, A. Senftleben, C. Sarpe, M. Wollenhaupt and T. Baumert, J. Phys. B, 2016, 49, 02LT01 CrossRef.
- S. Beaulieu, A. Ferré, R. Géneaux, R. Canonge, D. Descamps, B. Fabre, N. Fedorov, F. Légaré, S. Petit, T. Ruchon, V. Blanchet, Y. Mairesse and B. Pons, New J. Phys., 2016, 18, 102002 CrossRef.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, J. Rist, M. Weller, A. Hartung, M. Pitzer, L. P. H. Schmidt, T. Jahnke, R. Dörner and M. S. Schöffler, Phys. Rev. Res., 2019, 1, 033045 CrossRef CAS.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, M. Hofmann, J. Rist, M. Weller, A. Hartung, L. P. H. Schmidt, T. Jahnke, H. Braun, T. Baumert, J. Stohner, P. V. Demekhin, M. S. Schöffler and R. Dörner, Phys. Rev. Lett., 2021, 126, 083201 CrossRef CAS PubMed.
- K. Fehre, et al. , Phys. Rev. Lett., 2021, 127, 103201 CrossRef CAS PubMed.
- C. S. Lehmann and K. Weitzel, Phys. Chem. Chem. Phys., 2020, 22, 13707 RSC.
- A. Comby, E. Bloch, C. M. M. Bond, D. Descamps, J. Miles, S. Petit, S. Rozen, J. B. Greenwood, V. Blanchet and Y. Mairesse, Nat. Commun., 2018, 9, 5212 CrossRef CAS PubMed.
- P. V. Demekhin, A. N. Artemyev, A. Kastner and T. Baumert, Phys. Rev. Lett., 2018, 121, 253201 CrossRef CAS PubMed.
- M. Bashkansky, P. H. Bucksbaum and D. W. Schumacher, Phys. Rev. Lett., 1988, 60, 2458 CrossRef CAS PubMed.
- T. Jahnke, Th Weber, A. L. Landers, A. Knapp, S. Schössler, J. Nickles, S. Kammer, O. Jagutzki, L. Schmidt and A. Czasch, et al. , Phys. Rev. Lett., 2002, 88, 073002 CrossRef CAS PubMed.
- J. Hofbrucker, A. V. Volotka and S. Fritzsche, Phys. Rev. Lett., 2018, 121, 053401 CrossRef CAS PubMed.
- A. Gazibegović-Busuladžić, W. Becker and D. B. Milošević, Opt. Exp., 2018, 26, 12684 CrossRef PubMed.
- J. Hofbrucker, B. Böning, A. V. Volotka and S. Fritzsche, Phys. Rev. A, 2021, 104, 013102 CrossRef CAS.
- A. V. Volotka, J. Hofbrucker and S. Fritzsche, Phys. Rev. A, 2021, 104, L031103 CrossRef CAS.
- L. Guo, S. S. Han, X. Liu, Y. Cheng, Z. Z. Xu, J. Fan, J. Chen, S. G. Chen, W. Becker, C. I. Blaga, A. D. DiChiara, E. Sistrunk, P. Agostini and L. F. DiMauro, Phys. Rev. Lett., 2013, 110, 013001 CrossRef CAS PubMed.
- C. I. Blaga, F. Catoire, P. Colosimo, G. G. Paulus, H. G. Muller, P. Agostini and L. F. DiMauro, Nat. Phys., 2009, 5, 335 Search PubMed.
- W. Quan, Z. Lin, M. Wu, H. Kang, H. Liu, X. Liu, J. Chen, J. Liu, X. T. He, S. G. Chen, H. Xiong, L. Guo, H. Xu, Y. Fu, Y. Cheng and Z. Z. Xu, Phys. Rev. Lett., 2009, 103, 093001 CrossRef CAS PubMed.
- P. Agostini and L. F. DiMauro, Adv. At., Mol., Opt. Phys., 2012, 61, 117 CAS.
- F. H. M. Faisal, Nat. Phys., 2009, 5, 319 Search PubMed.
- M. Möller, F. Meyer, A. M. Sayler, G. G. Paulus, M. F. Kling, B. E. Schmidt, W. Becker and D. B. Milošević, Phys. Rev. A, 2014, 90, 023412 CrossRef.
- Y. Huismans, et al. , Science, 2011, 331, 61 CrossRef CAS PubMed.
- D. D. Hickstein, P. Ranitovic, S. Witte, X.-M. Tong, Y. Huismans, P. Arpin, X. Zhou, K. E. Keister, C. W. Hogle, B. Zhang, C. Ding, P. Johnsson, N. Toshima, M. J. J. Vrakking, M. M. Murnane and H. C. Kapteyn, Phys. Rev. Lett., 2012, 109, 073004 CrossRef PubMed.
- W. Becker, S. P. Goreslavski, D. B. Milošević and G. G. Paulus, J. Phys. B, 2014, 47, 204022 CrossRef.
- D. B. Milošević, Phys. Rev. A, 2014, 90, 063414 CrossRef.
- M. Lein and M. Wollenhaupt, J. Mod. Opt., 2018, 64, 949 CrossRef.
- D. B. Milošević and W. Becker, Phys. Rev. A, 2016, 93, 063418 CrossRef.
- D. Habibović, A. Gazibegović-Busuladžić, M. Busuladžić, A. Čerkić and D. B. Milošević, Phys. Rev. A, 2020, 102, 023111 CrossRef.
- D. B. Milošević and W. Becker, Phys. Rev. A, 2020, 102, 023107 CrossRef.
- D. B. Milošević, Strong-field approximation and quantum orbits, in Computational strong-field quantum dynamics: Intense Light-Matter Interactions, ed. D. Bauer, De Gruyter Textbook, Berlin, 2016, Chap. VII, pp. 199–221 Search PubMed.
- W. Becker, F. Grasbon, R. Kopold, D. B. Milošević, G. G. Paulus and H. Walther, Adv. At., Mol., Opt. Phys., 2002, 48, 35 CAS.
- W. Becker, S. P. Goreslavski, D. B. Milošević and G. G. Paulus, J. Phys. B, 2018, 51, 162002 CrossRef.
- E. Hasović, M. Busuladžić, A. Gazibegović-Busuladžić, D. B. Milošević and W. Becker, Laser Phys., 2007, 17, 376 CrossRef.
- W. Becker, M. Kleber, A. Lohr, G. G. Paulus, H. Walther and F. Zacher, Laser Phys., 1998, 8, 56 CAS.
- A. Gazibegović-Busuladžić, D. B. Milošević and W. Becker, Phys. Rev. A, 2004, 70, 053403 CrossRef.
- R. Kopold, D. B. Milošević and W. Becker, Phys. Rev. Lett., 2000, 84, 3831 CrossRef CAS PubMed.
- P. Salières, B. Carré, L. Le Déroff, F. Grasbon, G. G. Paulus, H. Walther, R. Kopold, W. Becker, D. B. Milošević, A. Sanpera and M. Lewenstein, Science, 2001, 292, 902 CrossRef PubMed.
- W. Becker and D. B. Milošević, Chin. Opt. Lett., 2015, 13, 070006 CrossRef.
- G. G. Paulus, F. Zacher, H. Walther, A. Lohr, W. Becker and M. Kleber, Phys. Rev. Lett., 1998, 80, 484 CrossRef CAS.
- A. Jašarević, E. Hasović, R. Kopold, W. Becker and D. B. Milošević, J. Phys. A: Math. Theor., 2020, 53, 125201 CrossRef.
- S. Basile, F. Trombetta and G. Ferrante, Phys. Rev. Lett., 1988, 61, 2435 CrossRef CAS PubMed.
- S. P. Goreslavski, G. G. Paulus, S. V. Popruzhenko and N. I. Shvetsov-Shilovski, Phys. Rev. Lett., 2004, 93, 233002 CrossRef CAS PubMed.
- S. V. Popruzhenko, G. G. Paulus and D. Bauer, Phys. Rev. A, 2008, 77, 053409 CrossRef.
- D. Shafir, H. Soifer, C. Vozzi, A. S. Johnson, A. Hartung, Z. Dube, D. M. Villeneuve, P. B. Corkum, N. Dudovich and A. Staudte, Phys. Rev. Lett., 2013, 111, 023005 CrossRef CAS PubMed.
- M. Li, Y. Liu, H. Liu, Q. Ning, L. Fu, J. Liu, Y. Deng, C. Wu, L.-Y. Peng and Q. Gong, Phys. Rev. Lett., 2013, 111, 023006 CrossRef PubMed.
- J. Yu, X. Sun, Y. Shao, M. Li, Q. Gong and Y. Liu, Phys. Rev. A, 2015, 92, 043411 CrossRef.
- H. Xie, M. Li, S. Luo, Y. Li, Y. Zhou, W. Cao and P. Lu, Phys. Rev. A, 2017, 96, 063421 CrossRef.
- M. Li, M.-M. Liu, J.-W. Geng, M. Han, X. Sun, Y. Shao, Y. Deng, C. Wu, L.-Y. Peng, Q. Gong and Y. Liu, Phys. Rev. A, 2017, 95, 053425 CrossRef.
- D. Habibović, W. Becker and D. B. Milošević, Symmetry, 2021, 13, 1566 CrossRef.
- F. Brausse, F. Bach, F. Krečinić, M. J. J. Vrakking and A. Rouzée, Phys. Rev. Lett., 2020, 125, 123001 CrossRef CAS PubMed.
- V. Hanus, S. Kangaparambil, S. Larimian, M. Dorner-Kirchner, X. Xie, M. S. Schöffler, G. G. Paulus, A. Baltuška, A. Staudte and M. Kitzler-Zeiler, Phys. Rev. Lett., 2019, 123, 263201 CrossRef CAS PubMed.
- D. B. Milošević, Phys. Rev. A, 2018, 98, 033405 CrossRef.
- D. B. Milošević, J. Phys. B, 2015, 48, 171001 CrossRef.
- M. Busuladžić, A. Gazibegović-Busuladžić, D. B. Milošević and W. Becker, Phys. Rev. Lett., 2008, 100, 203003 CrossRef PubMed.
- M. Okunishi, R. Itaya, K. Shimada, G. Prümper, K. Ueda, M. Busuladžić, A. Gazibegović-Busuladžić, D. B. Milošević and W. Becker, Phys. Rev. Lett., 2009, 103, 043001 CrossRef CAS PubMed.
- R. P. Sun, X. Y. Lai, S. G. Yu, Y. L. Wang, S. P. Xu, W. Quan and X. J. Liu, Phys. Rev. Lett., 2019, 122, 193202 CrossRef CAS PubMed.
- W. Xie, J. Yan, M. Li, C. Cao, K. Guo, Y. Zhou and P. Lu, Phys. Rev. Lett., 2021, 127, 263202 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |