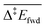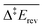Open Access Article
Open Access ArticleThe role of oxygenated species in the catalytic self-coupling of MeOH on O pre-covered Au(111)
R.
Réocreux
 a,
I.
Fampiou
a,
I.
Fampiou
 b and
M.
Stamatakis
b and
M.
Stamatakis
 *a
*a
aThomas Young Centre and Department of Chemical Engineering, University College London, Roberts Building, Torrington Place, London, WC1E 7JE, UK. E-mail: m.stamatakis@ucl.ac.uk
bDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, Massachusetts 02138, USA
First published on 20th January 2020
Abstract
The oxidation of alcohols plays a central role in the valorisation of biomass, in particular when performed with a non-toxic oxidant such as O2. Aerobic oxidation of methanol on gold has attracted attention lately and the main steps of its mechanism have been described experimentally. However, the exact role of O and OH on each elementary step and the effect of the interactions between adsorbates are still not completely understood. Here we investigate the mechanism of methanol oxidation to HCOOCH3 and CO2. We use Density Functional Theory (DFT) to assess the energetics of the underlying pathways, and subsequently build lattice kinetic Monte Carlo (kMC) models of increasing complexity, to elucidate the role of different oxygenates. Detailed comparisons of our simulation results with experimental temperature programmed desorption (TPD) spectra enable us to validate the mechanism and identify rate determining steps. Crucially, taking into account dispersion (van der Waals forces) and adsorbate–adsorbate lateral interactions are both important for reproducing the experimental data.
Introduction
The oxidation of alcohols is a well-established method to obtain a wide variety of organic compounds with oxidation states ranging from −II (methanol) to +IV (CO2). Albeit very versatile in that regard, the oxidation of alcohols nonetheless requires the development of complex oxidative agents1 or catalysts2,3 in order to avoid the combustion route and obtain compounds with the desired oxidation states (e.g. carbonyls, acids or esters).4 Heterogeneous catalysis can provide a means for selective alcohol oxidations, especially in the context of biomass valorisation, whereby atom economy and ease of product separation are key. Here, we shall only focus on the oxidation of alcohols to carboxylic acids and esters (oxidation state +II) of energetic and industrial relevance.Among the mildest heterogeneous catalysts, platinum group metals (Pt, Pd) exhibit appreciable conversions for aerobic oxidation in water to carboxylic acids.5 The ability of these metals to activate O2 is essential to their activity.6 However, the undesired consequence of such a property is self-oxidation, which leads to metal oxides, thereby impacting the activity of the catalyst.7 Selectivity issues exist as well, since platinum group metals can also yield decomposition products via C–C cleavages, as well as CO2 and water via over-oxidation.5,8 On the other hand, gold, as the noblest metal, remains metallic under oxidative conditions. Although the splitting of O2 on pure gold is highly activated in the gas phase or in neutral aqueous media, it becomes more facile under basic conditions,9 and as a matter of fact, gold is one of the most effective catalysts for the oxidation of alcohols to carboxylates when used under basic conditions.5
Selective alcohol oxidation in the gas phase over gold catalysts has also been achieved. Of particular interest for our work is the oxidation of methanol to methyl formate using O2 as an oxidant on a nanoporous silver-doped gold AgεAu1−ε catalyst (ε = 0.01–0.03).10 The silver sites activate O2 without the use of water or a base and initiate the oxidation cascade, the mechanism of which has been progressively elucidated over the last three decades. In the late 80s, the pioneering work by Madix and co-workers showed that surface oxygen adatoms on coinage metals (Cu, Ag, Au) have Brønsted and Lewis basic properties and can be used to perform X–H cleavages (X = C, N, O, S).11–13 Reacting methanol on O pre-covered gold surfaces yields different products, namely, formaldehyde (CH2O), hydrogen (H2), water (H2O), carbon dioxide (CO2), and methyl formate (HCOOCH3).13–15 Experimental mechanistic investigations have provided a description of the main features of the overall mechanism (see Fig. 1). For instance, vibrational spectroscopy has showed that adsorbed methanol (when dosed above 150 K) reacts quantitatively with the O adatoms to form CH3O (methoxy).15 After a first C–H activation (potentially assisted by O, OH or another CH3O),14,15 CH2O (formaldehyde) is formed and can readily associate with the remaining amount of either CH3O or O, yielding H2COOCH3 (hemiacetal alkoxide) and H2COO (methanediolate), respectively. Further C–H activations produce HCOOCH3 (methyl formate, the coupling product) and CO2 (over-oxidation product), which both desorb. Among the sequence of steps involved in the formation of the coupling product, H/D isotopic substitutions have showed that the desorption of HCOOCH3 is limited by the C–H activation step from CH3O.15 Moreover, 16O/18O substitution shows that the nucleophilic addition of O onto CH2O to H2COO is reversible.16 Other molecules desorb, such as H2O (essentially resulting from O deprotonation of CH3OH into CH3O by O), CH3OH (re-hydrogenation of CH3O from aliphatic hydrogen) and unreacted CH2O.
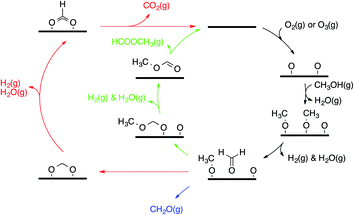 | ||
| Fig. 1 General mechanism for methanol oxidation over gold (represented as a thick horizontal line). The green arrows highlight the coupling while the red ones highlight the over-oxidation route. | ||
This understanding of the main features of the mechanism has paved the way for the successful extension of this chemistry to other alcohols (aliphatic alcohols,16–18 allylic alcohol19), aldehydes,20 and nucleophiles (amines).21 Remarkably, this mechanism translates to catalytic systems employing nanoporous gold as a catalyst (moderate temperatures and ambient pressures).10,22,23 Reece et al. have recently proved this transferability of the kinetic parameters of a set of elementary steps from surface science to catalysis, showing narrow pressure and material gaps.24,25 Even if the main features of the mechanism have been described, several aspects are still elusive to experiments, i.e. the precise role of O, OH and CH3O as bases and the details of the over-oxidation route (for instance how formate gets deprotonated).
Previous theoretical studies based on Density Functional Theory (DFT) have also shed light on the role of the different species on Au(111) under UHV conditions. The early work by Xu et al.16,26 substantiated the experimental mechanism by computing the reaction and activation energies of the main elementary steps. Comparing both the coupling and over-oxidation routes, Liu et al.27 provided qualitative insight into the influence of the coverage of oxygen adatoms on the selectivity of the catalyst. Yet, the role of OH was not investigated. Wang et al.28 studied the over-oxidation reactions extensively (neglecting the coupling route) and proposed different mechanisms under kinetic and thermodynamic controls. In spite of the significance of these early studies, van der Waals corrections were not common at the time and were therefore not included in their work. More recent work by Kabeer et al.29 has showed that vdW interactions are critical to describe the interaction of alkoxides on gold surfaces. Moreover, the complexity of the reaction network (wide and branched) requires a kinetic analysis to bridge the gap between molecular properties (such as activation/reaction energies) and macroscopic behaviours. Such an analysis can be achieved using the energetic span model introduced by Kozuch and Shaik,30–32 which can be generalised to the understanding of Temperature Programmed Desorption/Reaction (TPD/TPR) experiments.33
However, to understand in detail non-steady state behaviours, pressure/coverage effects, or the relative contribution of one mechanistic pathway versus another, kinetic simulations become necessary. Such simulations constitute a valuable tool for the analysis of complex reaction networks obtained from DFT calculations, especially when the energetic landscapes of different pathways are close, indicating a tendency for competition.34 Kinetic simulations can be performed within two different formalisms, either using mean-field deterministic equations or performing stochastic (Monte-Carlo) simulations. The former neglects spatial correlations and “averages out” the effect of lateral interactions, whereas the latter describes each adsorbate individually (as an entity occupying a specific site), and explicitly accounts for correlation. In spite of its computational cost (which is still negligible compared to the DFT mechanistic inspection), the stochastic approach allows for a detailed description of interactions between species, and provides insight into the influence of clustering/surface exclusion on the kinetics of a mechanism.35–37
Here we study the Temperature Programmed Oxidation (TPO) of methanol to methyl formate on the O pre-covered Au(111) surface. To understand the exact role of the different oxygenates under reacting conditions, we first re-examine the mechanism including weak van der Waals interactions. We carefully consider both the coupling route and one possible over-oxidation pathway previously described in the literature. Additionally, we have performed DFT-parameterised kinetic Monte-Carlo (kMC) simulations of the TPO spectra, which reproduce and rationalise the experimental observations. This multi-scale approach provides a dynamic description of the catalytic surface under reaction conditions and allows for the identification of the role of each species present on the surface during the course of the oxidation.
Computational details
Our approach relies on two theories. On the one hand, we determine the mechanism and its energetics at the atomistic level using ab initio calculations (DFT). On the other hand, this enables the calculation of rate constants from transition state theory (TST), and the subsequent parameterisation of a kMC model, which captures the chemistry at the catalyst level.Density function theory calculations
All the atomistic simulations were performed using periodic DFT as implemented in the Vienna Ab initio Simulation Package (version 5.4).38–40 The electronic exchange and correlation potential was modelled using the PBE-TS functional,41 which accounts for weak dispersion interactions between atomic structures. The core electrons were treated using the Projected Augmented Wave (PAW)42 method and the valence electronic density was expanded on a plane wave basis set with an energy cut-off of 400 eV. When solving the Kohn–Sham equations, the electronic density was optimised until the associated energy reaches the threshold of 10−6 eV.In all of our DFT calculations we focused on the Au(111) surface. We used a lattice constant of 4.162 Å, which was obtained by minimising the energy the FCC unit cell of Au. The system was described using a unit cell containing a 4 layer p(4 × 4) slab and 23 Å of vacuum, in order to avoid the interaction between two periodic images along the coordinate perpendicular to the slab. The atoms of the two lower layers were fixed at their bulk positions, relaxing the coordinates of all the other atoms of the periodic cell, until forces drop below 0.02 eV Å−1. The Brillouin zone was sampled using a 7 × 7 × 1 Monkhorst–Pack k-point mesh.43
Stable intermediates were located using the Conjugate Gradient algorithm. Transition states were first approached using the climbing image Nudge Elastic Band method,44,45 before switching to Dimer46,47 and/or Quasi-Newton algorithms. All structures were characterised by running vibrational analyses, checking in particular that transition states are indeed first-order saddles, containing exactly one imaginary frequency.
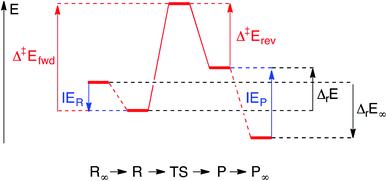
Each elementary step is energetically characterised by the reaction energies (ΔrE and ΔrE∞), the forward and reverse activation energies (Δ‡Efwd and Δ‡Erev) and the interaction energies of the reactants (IER) and the products (IEP), which are defined in Fig. 2. To take into account the thermodynamic barrier that needs to be overcome in order to bring the reactants together in the ready-to-react configuration, we further define the apparent forward and reverse activation energies as follows:
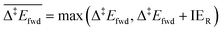 | (i) |
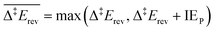 | (ii) |
Graph-theoretical kinetic Monte-Carlo simulations
The simulations were performed with the graph-theoretical kinetic Monte-Carlo framework as implemented in software Zacros (version 2.0) developed by Stamatakis and co-workers.48,49 Each event is described using a forward rate constant kfwd from state R to state P (representing the reactants and the products, respectively) and a reverse rate constant krev from state P to state R. They can be computed from DFT and TST as follows: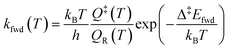 | (iii) |
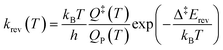 | (iv) |
| Δ‡Efwd − Δ‡Erev = ΔrE | (v) |
For our kMC simulations of methanol oxidative coupling on Au(111), different scenarios were considered. They consist of a different initial state (chemical composition) and a different sub-set of elementary steps as described in the results section. Simulations are performed with or without lateral interactions, that is taking into account or neglecting the IER or IEP for each elementary step. In the former case, appropriate energetic interactions terms are included in a cluster expansion Hamiltonian and the activation energies are computed via Brønsted–Evans–Polanyi relations, as per the previously published approach.49 For each scenario, 10 kMC simulations are performed and averaged to give the final TPO spectra. The simulations are run on a periodic lattice, which consists of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 sites: 5100 top sites and 10
300 sites: 5100 top sites and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 three-fold sites (fcc/hcp treated as one site type). The coverages are reported in units of a monolayer (ML), defined as the number of adsorbates on the surface normalised with respect to the number of top sites.
200 three-fold sites (fcc/hcp treated as one site type). The coverages are reported in units of a monolayer (ML), defined as the number of adsorbates on the surface normalised with respect to the number of top sites.
Results and discussion
DFT results
Since we aim at modelling TPD experiments where desorption plays a key role, it is very important to estimate the adsorption energies accurately. Previous studies investigating the oxidation of methanol on O-precovered Au(111) used Generalised Gradient Approximation (GGA) functionals with no corrections for dispersion interactions. As shown in Table 1, these functionals (PW91 and PBE) greatly underestimate the adsorption of closed-shell adsorbates on Au(111). When adding the Tkatchenko–Scheffler correction for vdW interactions, the adsorption energies become closer to the experimental values available in the literature.After thus validating the PBE-TS functional, we turned our attention to the reaction network of methanol oxidation on O-precovered Au(111), and performed DFT calculations to elucidate the underlying elementary steps (Table 2). For each step, we report all the energies appearing in Fig. 2 and eqn (i) and (ii). The elementary steps are grouped into different types. The first one corresponds to the desorption processes. Most of the species show low (CO2 and H2) to moderate (CH2O, CH3OH, H2O, HCOOCH3) affinities to Au(111). Only the associative adsorption of H2 has been considered as an activated process, as it involves bond cleavage. The activation energy thereof 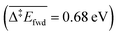 is comparable to other DFT studies,52 which surprisingly over-estimate the experimental barrier of 0.28 eV associated with a desorption peak at 110 K.53 At such a low temperature however, quantum tunnelling of the nuclei might dominate. This has for example been described for PdCu(111) single-atom alloys, on which a similar barrier of 0.65 eV for the associative desorption of H2 without tunnelling is decreased down to approximately 0.3 eV when treating nuclear quantum effects properly.54
is comparable to other DFT studies,52 which surprisingly over-estimate the experimental barrier of 0.28 eV associated with a desorption peak at 110 K.53 At such a low temperature however, quantum tunnelling of the nuclei might dominate. This has for example been described for PdCu(111) single-atom alloys, on which a similar barrier of 0.65 eV for the associative desorption of H2 without tunnelling is decreased down to approximately 0.3 eV when treating nuclear quantum effects properly.54
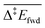 and
and 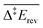 are the apparent activation energies as defined in Fig. 2. The energies are given in eV and do not include zero-point energy corrections
are the apparent activation energies as defined in Fig. 2. The energies are given in eV and do not include zero-point energy corrections
| Reaction number | Reaction | Δ‡Efwd | Δ‡Erev | ΔrE | IER | IEP | ΔrE∞ | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Desorption | R1 | CH3OH → CH3OH(g) | 0.44 | 0.00 | 0.44 | — | — | 0.44 | 0.00 | 0.44 |
| R2 | CH2O → CH2O(g) | 0.32 | 0.00 | 0.32 | — | — | 0.32 | 0.00 | 0.32 | |
| R3 | HCOOCH3 → HCOOCH3(g) | 0.42 | 0.00 | 0.42 | — | — | 0.42 | 0.00 | 0.42 | |
| R4 | CO2 → CO2(g) | 0.21 | 0.00 | 0.21 | — | — | 0.21 | 0.00 | 0.21 | |
| R5 | H + H → H2(g) | 0.66 | 0.64 | 0.02 | 0.02 | — | 0.68 | 0.64 | 0.04 | |
| R6 | H2O → H2O(g) | 0.30 | 0.00 | 0.30 | — | — | 0.30 | 0.00 | 0.30 | |
| CH3OH/CH3O | R7 | CH3OH → CH3O + H | 1.70 | 0.53 | 1.17 | — | 0.06 | 1.70 | 0.59 | 1.11 |
| R8 | CH3OH + O → CH3O + OH | 0.26 | 0.26 | 0.00 | −0.24 | −0.10 | 0.26 | 0.26 | −0.14 | |
| R9 | CH3OH + OH → CH3O + H2O | 0.03 | 0.00 | 0.03 | −0.26 | −0.15 | 0.03 | 0.00 | −0.08 | |
| CH3O/CH2O | R10 | CH3O → CH2O + H | 0.76 | 0.41 | 0.35 | — | 0.06 | 0.76 | 0.46 | 0.29 |
| R11 | CH3O + O → CH2O + OH | 0.43 | 1.55 | −1.12 | 0.13 | −0.03 | 0.56 | 1.55 | −0.96 | |
| R12 | CH3O + OH → CH2O + H2O | 0.70 | 1.91 | −1.21 | 0.09 | −0.25 | 0.79 | 1.91 | −0.88 | |
| R13 | CH3O + CH3O → CH3OH + CH2O | 0.66 | 1.79 | −1.14 | 0.15 | −0.17 | 0.81 | 1.79 | −0.82 | |
| AN2 | R14 | CH2O + CH3O → H2COOCH3 | 0.24 | 0.83 | −0.59 | 0.01 | — | 0.25 | 0.83 | −0.58 |
| R15 | CH2O + O → H2COO | 0.10 | 0.54 | −0.43 | −0.14 | — | 0.10 | 0.54 | −0.57 | |
| R16 | CH2O + OH → H2COOH | 0.06 | 0.61 | −0.56 | −0.03 | — | 0.06 | 0.61 | −0.58 | |
| H2COOCH3/HCOOCH3 | R17 | H2COOCH3 → HCOOCH3 + H | 0.53 | 1.19 | −0.66 | — | 0.00 | 0.53 | 1.19 | −0.65 |
| R18 | H2COOCH3 + O → HCOOCH3 + OH | 0.23 | 2.36 | −2.13 | 0.15 | −0.07 | 0.38 | 2.36 | −1.91 | |
| R19 | H2COOCH3 + OH → HCOOCH3 + H2O | 0.71 | 2.63 | −1.92 | −0.08 | −0.18 | 0.71 | 2.63 | −1.82 | |
| H2COO/HCOO | R20 | H2COO → HCOO + H | 0.28 | 1.34 | −1.06 | — | 0.31 | 0.28 | 1.65 | −1.37 |
| R21 | H2COO + O → HCOO + OH | 0.12 | 3.00 | −2.87 | 0.22 | −0.03 | 0.34 | 3.00 | −2.62 | |
| R22 | H2COO + OH → HCOO + H2O | 0.20 | 3.16 | −2.96 | 0.14 | −0.28 | 0.34 | 3.16 | −2.54 | |
| HCOO/CO2 | R23 | ϰ2-HCOO → ϰ1-HCOO | 0.78 | 0.13 | 0.65 | — | — | 0.78 | 0.13 | 0.65 |
| R24 | ϰ1-HCOO → H + CO2(g) | 0.05 | 0.99 | −0.94 | — | — | 0.05 | 0.99 | −0.94 | |
| R25 | ϰ2-HCOO + O → OH + CO2(g) | 0.94 | 2.49 | −1.55 | 0.01 | — | 0.94 | 2.49 | −1.54 | |
| R26 | ϰ2-HCOO + OH → H2O + CO2(g) | 1.18 | 2.60 | −1.43 | −0.03 | — | 1.18 | 2.60 | −1.46 | |
| Water chemistry | R27 | H2O → H + OH | 1.80 | 0.56 | 1.24 | — | 0.07 | 1.80 | 0.63 | 1.17 |
| R28 | OH → O + H | 1.96 | 0.60 | 1.36 | — | 0.11 | 1.96 | 0.71 | 1.26 | |
| R29 | OH + OH → H2O + O | 0.05 | 0.29 | −0.24 | 0.11 | −0.21 | 0.17 | 0.29 | 0.09 |
Upon adsorption of CH3OH, the first key step is the formation of the methoxy CH3O intermediate. Without the help of a base, the O–H cleavage is extremely endothermic (ΔrE > 1 eV) and more difficult than the desorption of CH3OH (ΔrE = 0.44 eV). This is consistent with the experimental observation that, when adsorbed on Au(111), methanol desorbs at a low temperature without reacting.14 The addition of surface O or OH dramatically lowers the kinetic barrier of this O–H cleavage and makes the production of the co-adsorbed configuration (CH3O + OH or CH3O + H2O) athermic. When considering the diffusion of the species, the overall acid/base reaction becomes slightly exothermic (ΔrE∞ ∼ −0.1 eV). Because of the significance of the role of O/OH to opening new routes, we have investigated their influence on the various subsequent C–H cleavages.
The C–H cleavage of CH3O to CH2O is moderately activated and can happen on its own (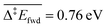 , without zero-point energy corrections). O lowers the apparent activation energy to 0.56 eV whereas OH increases it to 0.79 eV. The same trend is seen for the C–H cleavage from the coupling product H2COOCH3 to methyl formate HCOOCH3. On the CO2 route however, O and OH do not offer preferred alternative pathways for the C–H cleavage of H2COO to HCOO and HCOO to CO2. Concerning the latter step, it is worth noting that formate HCOO needs to go through a configurational change from bidentate ϰ2-HCOO to monodentate ϰ1-HCOO to be able to dehydrogenate. The actual rate-limiting step is this configurational change
, without zero-point energy corrections). O lowers the apparent activation energy to 0.56 eV whereas OH increases it to 0.79 eV. The same trend is seen for the C–H cleavage from the coupling product H2COOCH3 to methyl formate HCOOCH3. On the CO2 route however, O and OH do not offer preferred alternative pathways for the C–H cleavage of H2COO to HCOO and HCOO to CO2. Concerning the latter step, it is worth noting that formate HCOO needs to go through a configurational change from bidentate ϰ2-HCOO to monodentate ϰ1-HCOO to be able to dehydrogenate. The actual rate-limiting step is this configurational change 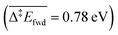 while the C–H cleavage from the monodentate configuration happens with almost no barrier
while the C–H cleavage from the monodentate configuration happens with almost no barrier 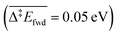 . Similar ϰ1/ϰ2 configurational equilibrium has been reported on different metals,55,56e.g. on Pt(111) monodentate ϰ1-HCOO is also less stable and also more reactive towards C–H activation.56
. Similar ϰ1/ϰ2 configurational equilibrium has been reported on different metals,55,56e.g. on Pt(111) monodentate ϰ1-HCOO is also less stable and also more reactive towards C–H activation.56
The compounds with higher oxidation states (HCOOCH3 and HCOO) are obtained from the coupling of formaldehyde (an electrophile) with O, OH or CH3O, which are nucleophiles on top of their aforementioned reactivity as Brønsted bases. For each nucleophile, the coupling reaction is exothermic (ΔrE∞ ∼ −0.6 eV). The structures of the three transition states are given in Fig. 3. The highest barrier is found for the coupling of CH2O with methoxy CH3O and is associated with an earlier transition state, as evidenced by the C⋯O distance in the transition state (see Fig. 3). O and OH, as less bulky nucleophiles, exhibit lower activation energies. Even if OH seems to be the most reactive species, experimental studies suggest that OH is either only transient (with an undetectable surface concentration) or more strongly solvated with water molecules.57 It is therefore likely that the coupling with OH is more complicated than described here and could involve more steps (de-coordinating water from OH to make it reactive), or it could be that it just never happens.
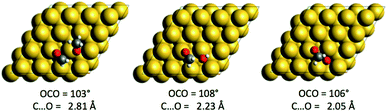 | ||
| Fig. 3 Structures of the three transition states associated with the AN2 of O, OH and CH3O onto CH2O. | ||
Because of the extensive branched reaction network underpinning this system, we need kinetic analysis to be able to assess how the proposed mechanism performs, and to explain macroscopic behaviours. Intuitively, we would not expect any methyl formate to be formed on the surface since the coupling of formaldehyde with O (and OH) is less activated 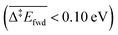 than with methoxy CH3O
than with methoxy CH3O 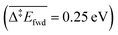 . However, this is without considering the entropic contribution of the transition state, which is very loose for the coupling with CH3O and tighter for the coupling with O (see the variation of the C–O distances, from 2.03 Å to 2.81 Å, in the transition states in Fig. 3). Moreover the usual approximation of considering the diffusion of surface species as faster than all other steps is not valid for O
. However, this is without considering the entropic contribution of the transition state, which is very loose for the coupling with CH3O and tighter for the coupling with O (see the variation of the C–O distances, from 2.03 Å to 2.81 Å, in the transition states in Fig. 3). Moreover the usual approximation of considering the diffusion of surface species as faster than all other steps is not valid for O 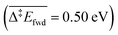 . kMC simulations are thus needed for capturing such complexities and describing these effects properly. For the purpose of analysis, we have considered three scenarios in our kMC simulations, focusing on different sets of elementary steps, and starting the system from different initial states. For each scenario, the kMC simulations have been performed twice: with and without the lateral interactions involved in the reactant and product states.
. kMC simulations are thus needed for capturing such complexities and describing these effects properly. For the purpose of analysis, we have considered three scenarios in our kMC simulations, focusing on different sets of elementary steps, and starting the system from different initial states. For each scenario, the kMC simulations have been performed twice: with and without the lateral interactions involved in the reactant and product states.
First scenario: the chemistry of methoxy only
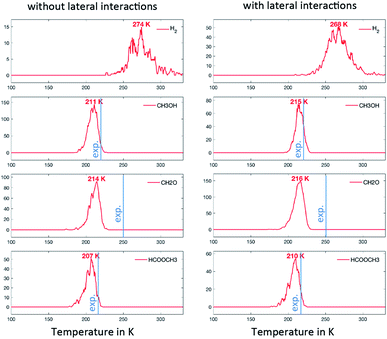
In the first scenario, the initial state considers only CH3O on the surface. This corresponds to the assumption that the deposited CH3OH molecules have quantitatively reacted with surface O to produce H2O (assumed to desorb as soon as it is formed) and CH3O. The simulations are therefore initiated with 0.01 ML or CH3O on the surface and only take into account the steps that do not involve O or OH (i.e. R1, R2, R3, R5, R7, R10, R13, R14 and R17). The associated TPDs are given in Fig. 4. Hydrogen desorbs at 274 K, while HCOOCH3, CH3OH and CH2O desorb almost simultaneously at around 210 K. The analysis of the surface species shows that, from this temperature, significant amounts of CH3O are converted to CH2O. The reaction is therefore limited by the C–H activation step from CH3O to CH2O, in accordance with experimental evidence based on the kinetic isotope effect.15 In spite of the simplifications, this scenario already reproduces the desorption peaks of these molecules well, with a deviation compared to the experiments of about 30 K. Since OHx (x = 0, 1, 2) are not explicitly taken into account (only implicitly via the presence of CH3O that can only be produced with OHx), we do not see water and CO2 coming off the surface. It is worth noting here that the lateral interactions do not exert a strong influence on position of the peak in this scenario (as shown in Fig. 4).Second and third scenarios: the chemistry of methoxy in presence of oxygen adatoms
In the second scenario, we have added 0.02 ML of O. This should in principle open various reactive routes. To progressively build on the complexity of the reaction network, we have first considered only the elementary steps associated with the successive recombination of H with O and OH to form water (R27, R28 and R29) and the reactions of the over-oxidation route (R15, R20, R23 and R24), in addition to the steps of the first scenario. This set of elementary steps is closely related to that chosen by Reece et al. in their kinetic model based on experimental kinetic parameters.25 The two-step C–H cleavage of formate (HCOO) into CO2 (configurational change and C–H scission) is modelled as a single elementary step, using the kinetic parameters of the configurational change (which is rate determining). The corresponding TPDs are given in Fig. 5. When lateral interactions are neglected, we see, in addition to the peaks discussed above, a peak for CO2 at ∼260 K and a peak for H2O at ∼280 K. These two peaks are seen experimentally, although, in the case of water, the major peak is still not reproduced with our simulations. When adding the lateral interactions, most surface oxygen reacts with formaldehyde to ultimately produce CO2, yielding a noisier spectrum for water (as less water desorbs) and a more defined spectrum for CO2. This results from the strong attractive interaction between CH2O with O (−0.14 eV) that dramatically increases the probability that they meet (especially at low temperature). Although there is experimental evidence of water desorbing concomitantly with CO2 around 275 K, the main desorption peak is seen around 220 K. O must therefore be involved in protonation/deprotonation steps at an early stage of the simulation.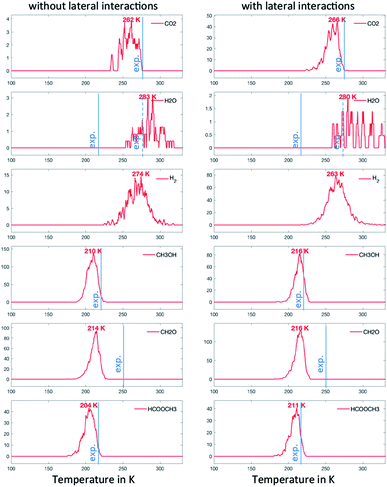 | ||
| Fig. 5 TPO spectra of methanol on Au(111) for scenario #2. Temperature ramp is 10 K s−1. The initial coverages are: 0.1 ML of CH3O and 0.02 ML in O. | ||
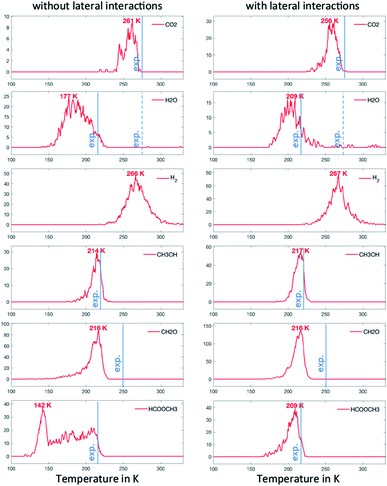
To address this problem, in our last scenario (Fig. 6), we have considered the same set of elementary steps and have added the C–H activation steps that become easier in the presence of O (i.e. CH3O + O = CH2O + OH and H2COOCH3 + O = HCOOCH3 + OH, referred to as R11 and R18 in Table 2). The production of CH2O, CH3OH and H2 remains essentially comparable with the previous simulations and agrees well with experimental observations. Interestingly, the desorption of HCOOCH3 now appears as bimodal (Fig. 6, left panel). The first peak at 142 K corresponds to the C–H activation of CH3O enabled by the presence of O, while the second one corresponds to the unassisted C–H activation of CH3O (catalysed by the surface in the absence of a base). If the first peak were observed experimentally, it would probably appear around 185 K,15 which is the normal desorption temperature of HCOOCH3 (PBE-TS underestimates its adsorption energy, see Table 1). However, there is no such evidence. Moreover, water is also produced 50 K too early, as a direct consequence of the high reactivity of O with CH3O, producing first OH and then H2O. It is therefore likely that our initial configuration (CH3O only with extra O) is too reactive when neglecting lateral interactions. When lateral interactions are included (Fig. 6, right panel), the low temperature water peak is shifted to higher temperatures and now matches the experimental data. More importantly, HCOOCH3 now desorbs in one peak, correcting the main deviation to experiments seen in the 3rd scenario without lateral interactions (Fig. 6, compare left and right panels). These two observations can be attributed to the increase of the overall activation energy of O + CH3O → OH + CH2O from Δ‡Efwd = 0.43 eV to 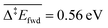 when including the repulsive interaction IER = 0.13 eV.
when including the repulsive interaction IER = 0.13 eV.
 | ||
| Fig. 6 TPO spectra of methanol on Au(111) for scenario #3. Temperature ramp is 10 K s−1. The initial coverages are: 0.1 ML of CH3O and 0.02 ML in O. | ||
The last major deviation compared to the experimental TPO spectra is in the desorption of CH2O. Experimentally the peak is very broad, starting at about 180 K and expanding to 400 K.15 This very likely results from a strong attractive interaction with water (−0.25 eV, see R12 in Table 2), which has not been included in our models. Other interactions might play a key role at low temperatures. As shown in Table 2, the lateral interactions of CH3OH with O and OH (−0.24 and −0.26 eV respectively) and H2O with O (−0.21 eV) are also strong and dominate over the reaction energies. It would therefore be no surprise that the oxygen atoms surrounded by water molecules would be less reactive than the bare oxygen atoms considered in our simulations. A better description of the initial complex equilibrium is therefore required to fully address the chemistry of the surface at very low temperatures, which is part of future work. Nevertheless, it is already remarkable that a DFT-parametrised model (involving no fitting to experimental data) gives us this amount of insight on such a complex system.
Conclusions
The present work adopts a multi-scale approach in the modelling of the TPO of methanol on O-precovered Au(111). Using DFT we have investigated the different elementary steps possible for the formation/cleavage of O–H and C–H bonds as well as different coupling reactions between electrophiles and nucleophiles. We have shown that the presence of O lowers the activation energies of the C–H cleavages involved in the coupling pathway, but does not affect those of the over-oxidation route. We then built three different kinetic models, progressively incorporating complexity by adding relevant elementary steps (intrinsic reactivity of CH3O, role of O to form CO2 and role of O in C–H activations) and lateral interactions. These models reproduce the salient features of the TPO spectra, in particular, the desorption temperatures of CO2 and the coupling product (methyl formate), as well as the water desorption when excess O is included in the initial state. Still though, deviations from the experimental observations (for example the width of the peaks) suggest that the initial state of the systems should be studied more thoroughly to explain the chemical equilibrium between the different species, as well as how they interact with each other in a tightly connected network of adsorbates. This understanding is of great importance considering that gold is also a prominent catalyst for alcohol oxidation in condensed phases, such as basic liquid water.9 This however remains challenging58 as it requires a high number of DFT calculations in order to get enough data to describe the interactions between the different adsorbates (O, OH, H2O, CH3O and CH3OH) properly.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported as part of Integrated Mesoscale Architectures for Sustainable Catalysis, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award DE-SC0012573. The authors acknowledge Prof. C. Friend, Prof. R. Madix and Dr C. Reece for fruitful discussions.References
- H. Tohma and Y. Kita, Adv. Synth. Catal., 2004, 346(23), 111–124 CrossRef CAS.
- D. Morton and D. J. Cole-Hamilton, J. Chem. Soc., Chem. Commun., 1988, 17, 1154–1156 RSC.
- N. Sieffert, R. Réocreux, P. Lorusso, D. J. Cole-Hamilton and M. Bühl, Chem.–Eur. J., 2014, 20, 4141–4155 CrossRef CAS.
- J. Clayden, N. Greeves and P. D. Wothers, Organic Chemistry, Oxford Uni., 2012, DOI:10.1007/s00897010513a.
- S. E. Davis, M. S. Ide and R. J. Davis, Green Chem., 2013, 15(1), 17–45 RSC.
- M. M. Montemore, M. A. Van Spronsen, R. J. Madix and C. M. Friend, Chem. Rev., 2018, 118(5), 2816–2862 CrossRef CAS.
- A. P. Markusse, B. F. M. Kuster, D. C. Koningsberger and G. B. Marin, Catal. Lett., 1998, 55(3–4), 141–145 CrossRef CAS.
- M. S. Ide, D. D. Falcone and R. J. Davis, J. Catal., 2014, 311, 295–305 CrossRef CAS.
- Q. Gu, P. Sautet and C. Michel, ACS Catal., 2018, 8(12), 11716–11721 CrossRef CAS.
- A. Wittstock, V. Zielasek, J. Biener, C. M. Friend and M. Bäumer, Science, 2010, 327, 319–322 CrossRef CAS.
- R. J. Madix, Science, 1986, 233(4769), 1159–1166 CrossRef CAS.
- D. A. Outka and R. J. Madix, Surf. Sci., 1987, 179, 361–376 CrossRef CAS.
- D. A. Outka and R. J. Madix, J. Am. Chem. Soc., 1987, 109(6), 1708–1714 CrossRef CAS.
- J. Gong, D. W. Flaherty, R. A. Ojifinni, J. M. White and C. B. Mullins, J. Phys. Chem. C, 2008, 112(14), 5501–5509 CrossRef CAS.
- B. Xu, X. Liu, J. Haubrich, R. J. Madix and C. M. Friend, Angew. Chem., Int. Ed., 2009, 48(23), 4206–4209 CrossRef CAS.
- B. Xu and C. M. Friend, Faraday Discuss., 2011, 152, 307–320 RSC.
- B. Xu, R. J. Madix and C. M. Friend, J. Am. Chem. Soc., 2010, 132(46), 16571–16580 CrossRef CAS.
- J. Gong and C. B. Mullins, J. Am. Chem. Soc., 2008, 130(49), 16458–16459 CrossRef CAS.
- G. M. Mullen, L. Zhang, E. J. Evans, T. Yan, G. Henkelman and C. B. Mullins, Phys. Chem. Chem. Phys., 2015, 17(6), 4730–4738 RSC.
- B. Xu, R. J. Madix and C. M. Friend, Acc. Chem. Res., 2014, 47(3), 761–772 CrossRef CAS.
- B. Xu, C. M. Friend and R. J. Madix, Faraday Discuss., 2011, 152, 241–252 RSC.
- K. M. Kosuda, A. Wittstock, C. M. Friend and M. Bäumer, Angew. Chem., Int. Ed., 2012, 51(7), 1698–1701 CrossRef CAS.
- M. L. Personick, B. Zugic, M. M. Biener, J. Biener, R. J. Madix and C. M. Friend, ACS Catal., 2015, 5(7), 4237–4241 CrossRef CAS.
- C. Reece, M. Luneau and R. J. Madix, ACS Catal., 2019, 9(5), 4477–4487 CrossRef CAS.
- C. Reece, E. A. Redekop, S. Karakalos, C. M. Friend and R. J. Madix, Nat. Catal., 2018, 1(11), 852–859 CrossRef CAS.
- B. Xu, J. Haubrich, T. A. Baker, E. Kaxiras and C. M. Friend, J. Phys. Chem. C, 2011, 115(9), 3703–3708 CrossRef CAS.
- S. Liu, P. Jin, D. Zhang, C. Hao and X. Yang, Appl. Surf. Sci., 2013, 265, 443–451 CrossRef CAS.
- L. Wang, C. He, W. Zhang, Z. Li and J. Yang, J. Phys. Chem. C, 2014, 118(31), 17511–17520 CrossRef CAS.
- F. Cheenicode Kabeer, W. Chen, R. J. Madix, C. M. Friend and A. Tkatchenko, J. Phys. Chem. C, 2017, 121(50), 27905–27914 CrossRef CAS.
- S. Kozuch and J. M. L. Martin, ChemPhysChem, 2011, 12(8), 1413–1418 CrossRef CAS.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44(2), 101–110 CrossRef CAS.
- A. M. Ruppert, M. Jȩdrzejczyk, N. Potrzebowska, K. Kaźmierczak, M. Brzezińska, O. Sneka-Płatek, P. Sautet, N. Keller, C. Michel and J. Grams, Catal. Sci. Technol., 2018, 8(17), 4318–4331 RSC.
- R. Réocreux, C. A. Ould Hamou, C. Michel, J. B. Giorgi and P. Sautet, ACS Catal., 2016, 6, 8166–8178 CrossRef.
- M. Salciccioli, M. Stamatakis, S. Caratzoulas and D. G. Vlachos, Chem. Eng. Sci., 2011, 66, 4319–4355 CrossRef CAS.
- M. Stamatakis and D. G. Vlachos, ACS Catal., 2012, 2(12), 2648–2663 CrossRef CAS.
- M. K. Sabbe, M. F. Reyniers and K. Reuter, Catal. Sci. Technol., 2012, 2(10), 2010–2024 RSC.
- M. Andersen, C. Panosetti and K. Reuter, Front. Chem., 2019, 7, 1–24 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- V. G. Ruiz, W. Liu, E. Zojer, M. Scheffler and A. Tkatchenko, Phys. Rev. Lett., 2012, 146103 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 134106 CrossRef.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010 CrossRef CAS.
- A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123, 224101 CrossRef.
- M. Stamatakis and D. G. Vlachos, J. Chem. Phys., 2011, 134(21), 214115 CrossRef.
- J. Nielsen, M. D’Avezac, J. Hetherington and M. Stamatakis, J. Chem. Phys., 2013, 139(22), 224706 CrossRef.
- R. Réocreux, C. Michel, P. Fleurat-Lessard, P. Sautet and S. N. Steinmann, J. Phys. Chem. C, 2019, 123(47), 28828–28835 CrossRef.
- B. C. Krüger, G. B. Park, S. Meyer, R. J. V. Wagner, A. M. Wodtke and T. Schäfer, Phys. Chem. Chem. Phys., 2017, 19, 19896–19903 RSC.
- M. T. Darby, R. Réocreux, E. C. H. Sykes, A. Michaelides and M. Stamatakis, ACS Catal., 2018, 8(6), 5038–5050 CrossRef CAS.
- M. Pan, D. W. Flaherty and C. B. Mullins, J. Phys. Chem. Lett., 2011, 2(12), 1363–1367 CrossRef CAS.
- G. Kyriakou, E. R. M. Davidson, G. Peng, L. T. Roling, S. Singh, M. B. Boucher, M. D. Marcinkowski, M. Mavrikakis, A. Michaelides and E. C. H. Sykes, ACS Nano, 2014, 8(5), 4827–4835 CrossRef CAS.
- J. J. Sims, C. A. Ould Hamou, R. Réocreux, C. Michel and J. B. Giorgi, J. Phys. Chem. C, 2018, 122(35), 20279–20288 CrossRef CAS.
- S. N. Steinmann, C. Michel, R. Schwiedernoch, J.-S. Filhol and P. Sautet, ChemPhysChem, 2015, 16, 2307–2311 CrossRef CAS.
- R. G. Quiller, T. A. Baker, X. Deng, M. E. Colling, B. K. Min and C. M. Friend, J. Chem. Phys., 2008, 129(6), 064702 CrossRef CAS.
- R. Réocreux and C. Michel, Current Opinion in Green and Sustainable Chemistry, 2018, 10, 51–59 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |