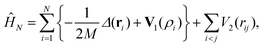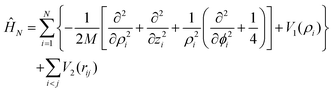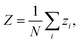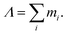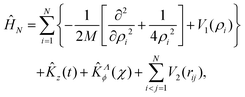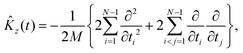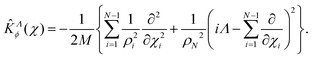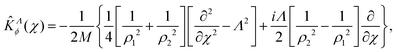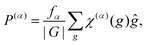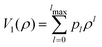Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A nuclear spin and spatial symmetry-adapted full quantum method for light particles inside carbon nanotubes: clusters of 3He, 4He, and para-H2†
María Pilar
de Lara-Castells
 *a and
Alexander O.
Mitrushchenkov
*a and
Alexander O.
Mitrushchenkov
 *b
*b
aInstituto de Física Fundamental, IFF-CSIC, Serrano 123, E-28006 Madrid, Spain. E-mail: Pilar.deLara.Castells@csic.es
bMSME, Univ. Gustave Eiffel, CNRS UMR 8208, Univ. Paris Est Creteil, F-77454 Marne-la-Vallée, France. E-mail: Alexander.Mitrushchenkov@univ-eiffel.fr
First published on 14th December 2020
Abstract
We present a new nuclear spin and spatial symmetry-adapted full quantum method for light fermionic and bosonic particles under cylindrical carbon nanotube confinement. The goal is to address Fermi–Dirac and Bose–Einstein nuclear spin statistics on an equal footing and to deliver excited states with a similar accuracy to that of the ground state, implementing ab initio-derived potential models as well. The method is applied to clusters of up to four (three) 4He atoms and para-H2 molecules (3He atoms) inside a single-walled (1 nm diameter) carbon nanotube. Due to spin symmetry effects, the bound states energy landscape as a function of the angular momentum around the tube axis becomes much more complex and rich as the number of 3He atoms increase compared to the spinless 4He and para-H2 counterparts. Four bosonic 4He and para-H2 particles form pyramidal-like structures which are more compact as the particle mass and the strength of the inter-particle interaction increases. They feature stabilization of the collective rotational motion as bosonic quantum rings bearing persistent rotational motion and superfluid flow. Our results are brought together with two key experimental findings from the group of Jan-Peter Toennies: (1) the congestion of spectral profiles in doped 3He droplets as opposed to the case of 4He droplets (S. Gebenev, J. P. Toennies and A. F. Vilesov, Science, 1998, 279, 2083); (2) the onset of microscopic superfluidity in small doped clusters of para-H2 molecules (S. Grebenev, B. G. Sartakov, J. P. Toennies and A. F. Vilesov, Science, 2000, 289, 1532), but at the reduced dimensionality offered by the confinement inside carbon nanotubes.
1 Introduction
Being composed by the lightest atoms and molecules in nature, aggregates of helium and molecular hydrogen are the most paradigmatic cases of finite quantum systems, with the atoms and molecules being held together by weak dispersion forces. The solvation of molecular dopant with helium atoms and hydrogen molecules has allowed to find evidences for the onset of superfluid behaviour at microscopic level and to show the role of the Fermi–Dirac or Bose–Einstein nuclear spin statistics. The molecular spectroscopic measurements in helium droplets by the group of Professor Jan-Peter Toennies demonstrated the existence of very different spectral profiles depending on the considered isotope, 3He or 4He:1,2 As first observed for sulfur hexafluoride, SF63,4 and carbonyl sulfide, OCS,1 the spectra of molecular impurities inside 4He droplets attain a very well resolved profile with sharp rotational lines. In contrast, the spectra of OCS inside 3He droplets exhibited broad (about 1 cm−1) spectral profiles, with the temperature of the drop (about 0.1 K) being below the superfluid transition temperature in bulk 3He (Tλ = 3 × 10−3 K). Moreover, a well-resolved spectral profile was recovered after adding 4He atoms to 3He droplets.1 Since 4He atoms can be considered as composite spin-less bosonic particles while 3He atoms are fermionic with a nuclear spin equal to 1/2, the essential role of nuclear spin statistics on microscopic superfluidity was demonstrated. Further experimental observations by the same group5,6 indicated the onset of molecular superfluidity even in small doped clusters of spin-less bosonic para-H2 (or ortho-D2) molecules. Further theoretical7,8 and combined experimental-theoretical evidences9 on the superfluidity of small para-H2 clusters have been found.The cylindrical confinement provided by carbon nanotubes has offered the possibility of studying the pronounced quantum behaviour of 4He atoms and H2 molecules at reduced dimensionality. This way, very recent measurements have demonstrated the formation of two-dimensional (2D) 4He layers on the outer surface of a single-walled carbon nanotubes (SWCNTs).10 Also, an experimental study11 of gas adsorption at low (2–5 K) temperature revealed a quenched propagation of 4He atoms through carbon nanopores with diameters below 7 Å despite of their small kinetic diameter. The application of orbital-free helium density functional theory to carbon nanotubes immersed in a helium nanodroplet provided theoretical explication that the experimental observations stem from the exceptionally high zero-point energy of 4He as well as its tendency to form 2D layers upon adsorption at low temperatures. These conclusions were further confirmed by applying more accurate ab initio potential modelling along with a wave-function (WF)-based approach.12 Moreover, the quest for the occurrence or either quasi-superfluid or quasi-crystalline behavior of para-H2 molecules when confined in SWCNTs has recently motivated an intense theoretical research.13–15 For the case of molecular deuterium, our recent theoretical work has provided conclusive evidence for the transition from molecular aggregation to quantum solid-like packing in a SWCNT of 1 nm diameter,16 confirming a previous study using an embedding approach in a broader (ca. 1.4 nm) SWCNT.17 Altogether, these studies12–18 have highlighted the key role played by the quantum nature of the nuclear degrees of freedom in the confined helium, hydrogen, or deuterium motion.
The present work is aimed to provide a new symmetry- and spin-adapted full quantum approach capable to describe fermionic particles of spin 1/2 (3He atoms) as well spin-less bosonic particles (4He atoms and para-H2 molecules) inside SWCNTs. A similar case of 3He, 4He and para-H2 particles around a molecular dopant was successfully treated by the Full-Configuration-Interaction-type Nuclear Orbital (FCI-NO) approach (see, e.g., ref. 8). This FCI-NO treatment was able to accurately deal with the hard-core interaction problem,19 and to automatically include all the nuclear-statistic-induced (bosonic or fermionic) effects. It handled the many-body problem by expanding the Hamiltonian operator with quantum single-particle basis functions followed by an efficient diagonalization technique.20 The method was rooted on a previous Hartree–Fock-type implementation21 which was applied to explain the role of Boson–Fermion statistics on the differences in the spectra obtained by Toennies and collaborators1 depending on the considered isotope (3He or 4He).22 The FCI-NO method resembles the traditional CI method of quantum electronic structure theory and was originally developed for doped fermionic 3He clusters19,23,24 and further extended for bosonic systems (for a mini-review see ref. 25) composed by 4He atoms26 or para-H2 molecules.8 As the method presented in this work, one key advantage of the FCI-NO technique was its capability of providing solvent states with accuracy similar to that for the ground state. This capability was used to characterize collective rotational motion,8 and to provide insights into the experimental measurements indicating the onset of microscopic superfluid behaviour on doped para-H2 clusters by Toennies and collaborators.5,6
The FCI-NO method can not be directly applied to the case of SWCNT as the ‘dopant’ species. In fact, a heavy dopant in helium (or molecular hydrogen) clusters can be considered as providing a reference coordinate system fixed in space, for the helium (or molecular hydrogen) motion.8,19,23–25 This ansatz is similar to the adiabatic approach in electronic structure calculations, where the nuclear framework is considered fixed and provides a coordinate system for electrons. Therefore, the electronic WF can be expanded as a sum of products of ‘molecular orbitals’, with each of them being well localized in space. Similarly, the FCI-NO technique uses an expansion of products of ‘nuclear orbitals’, being centered at the molecular dopant and fixed in space. In the present case, the SWCNT ‘dopant’ is also fixed in space but is infinitely long and uniform in one direction. By assuming the coordinate axis Z along the tube axis, the overall motion of the cluster along Z is thus free. Consequently, the spectrum is continuous, with the total WF being delocalized along Z. In order to obtain the bound states, the motion of the cluster center-of-mass (COM) along the coordinate Z needs to be explicitly separated. We know that the total WF, corresponding to a zero momentum along Z and the target bound state, must be independent on Z. Unfortunately, this condition is impossible to satisfy when the WF is taken as a product of one particle ‘orbitals’. Thus, unless all orbitals do not depend on Z, the artificial COM kinetic energy will contaminate the total energy. This difficulty is reminiscent to the problem of separating the overall COM in theories where the quantum motion of electrons and nuclei is tentatively described on an equal footing using orbital-like approaches (see, e.g., ref. 27 and references therein). In the present work, this issue is solved by recasting the Hamiltonian in internal coordinates and incorporating an adaptation to the spin- and spatial-symmetry of the confined fermionic and bosonic particles.
A consistently accurate description of the interaction between the confined species and the SWCNT is achieved through the application of ab initio-derived pairwise additive potential models for both helium12 and hydrogen.17 For the specific case of van-der-Waals-dominated adsorbate/(carbon-based) surface interactions,12,17,28–30 its adequacy relies on the excellent transferability properties found for the parameters accounting for the dispersion contribution upon increasing the size of clusters modelling the extended systems.28 More difficult, dispersionless contributions are mostly of short-range nature and the usage of small cluster models can be also justified. Therefore, different analytical forms are employed to model the dispersionless and dispersion contributions, with the model parameters being computed at ab initio level on short and narrow carbon nanotubes and then scaled to the actual systems. The detailed energy decomposition offered by the ab initio method applied – density functional theory (DFT)-based symmetry-adapted perturbation theory (SAPT(DFT))31,32 – has rendered such strategy successful and efficient when describing the adsorption of molecular and atomic species to inner and outer surfaces of carbon nanotubes.12,17,33
The article is structured as follows. Section 2 presents the method developed in this work. Section 3 illustrates its application to the cluster of quantum particles (3,4He atoms and para-H2 molecules) inside a SWCNT of 1 nm diameter. We emphasize on the interplay between the mass of the given particles, the strength of the corresponding pair interactions, and their nuclear (fermionic or bosonic) spin statistics, as well as on the onset for the stabilization of collective rotational motion. Finally, Section 4 summarizes our main findings and presents an outline of future perspectives.
2 Method
2.1 Setting up the problem
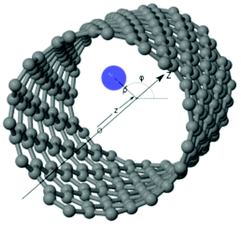
The method presented in this work has been developed to allow the calculation of the bound states of N identical atoms or molecules trapped inside a SWCNT. These atoms or molecules will be referred with the term ‘pseudo-nuclei’ (PNs), having been described as point-like particles of mass M. The total interaction of the PN cluster with the SWCNT is represented as a sum of one-particle terms, describing the interaction of the SWCNT with a single PN, and the interaction between the PNs. The latter is written as a sum of pairwise terms. We assume that the corrugation is negligible so that the interaction of each PN with the SWCNT (which is assumed to be infinitely long) depends only on the distance of the PN from the nanotube axis, V1 = V1(ρ). The interaction between each pair of (identical) PNs is assumed to be a function of just the PN–PN distance, V2 = V2(rij). Then, the total Hamiltonian operator can be written as a function of the 3 N Cartesian coordinates of the PNs asUsing cylindrical coordinates (xi,yi,zi → ρi,ϕi,zi) for each PN (see Fig. 1), together with a Jacobian transformation of the volume to keep the Hamiltonian ‘explicitly Hermitian’, 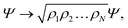 it takes the form
it takes the form
| rij2 = ρi2 + ρi2+ (zi − zj)2 − 2ρiρjcos(ϕi − ϕj). |
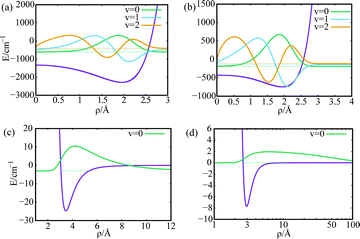
Considering a SWCNT of 1 nm diameter and helicity index (11,4), the He–CNT and H2–CNT one-particle potentials V1(ρ) are presented in the upper panels of Fig. 2 [panels (a) and (b)] along with a few supported bound states. It can be seen that the carbon wall is impenetrable, with the PN–SWCNT being dispersion-dominated. As can be observed in the lower panels of Fig. 2 [panels (c) and (d)], the two-particle interaction V2(rij) between the PNs is much weaker than the PN–SWCNT interaction, specially in the case of helium. Notice the huge zero-point energies for the 4He–SWCNT (ca. 500 cm−1) and 4He–4He vibrational motions.
Since the center-of-mass coordinate leads to a continuum spectrum, the Hamiltonian has to be recast in internal coordinates which do not contain the overall Z-translation
We introduce the following internal coordinates for the z degrees of freedom
z1…zN → t1…tN−1,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z, Z, |
| ti = zi − zN. |
The angular relative coordinates are defined instead as
| ϕ1…ϕN → χ1…χN−1,Φ = ϕN, |
| χi = ϕi − ϕN. |
It should be mentioned that the definition of the overall rotation coordinate is not unique. We use Φ = ϕN instead of 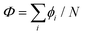 as this definition allows to keep integer factors (and thus a periodic behavior) for the coordinates χi. As the WF in coordinates ϕi must be a single-valued function, it can be represented as a sum of products of factors exp
as this definition allows to keep integer factors (and thus a periodic behavior) for the coordinates χi. As the WF in coordinates ϕi must be a single-valued function, it can be represented as a sum of products of factors exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) imiϕi, with all mi values being integers. Moving to internal coordinates, the corresponding overall rotational motion can be separately collected into the factor
imiϕi, with all mi values being integers. Moving to internal coordinates, the corresponding overall rotational motion can be separately collected into the factor 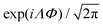 with the overall rotation quantum number Λ given by
with the overall rotation quantum number Λ given by
After separating the coordinates Z and Φ, a Λ-dependent Hamiltonian of 3N − 2 internal coordinates is obtained as
riN2 = ρi2 + ρN2 + ti2 − 2ρiρNcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χi. χi. |
The kinetic energy operator along the Z axis can be expressed as
For Λ > 0, the angular kinetic energy contribution contains complex terms. Yet, the whole Hamiltonian matrix can be kept real if the total WF is separated into two terms, symmetric and anti-symmetric with respect to a simultaneous change of sign of all χi coordinates, correspondingly, and the anti-symmetric term is taken with the imaginary factor ‘i’.
2.2 Adaptation to the symmetry of the problem
The total WF of a system composed by N identical particles must be symmetric (for bosonic particles, e.g., 4He atoms) or anti-symmetric (e.g., 3He atoms) with respect to the exchange of any two particles. Moreover, the Hamiltonian expressed in both Cartesian and internal coordinates must be invariant under zi → −zi and, for Λ = 0, ϕi → −ϕi transformations.While z and ϕ symmetries are equally present in the internal Hamiltonian, and thus can be easily accounted for, the incorporation of the full permutation symmetry of all N particles (i.e., the SN group) is more complicated. The irreducible representations of this group are described by Young diagrams. The fully symmetric (anti-symmetric) solution for bosons (fermions) correspond to the {N} ({1,1,…,1}) Young diagrams. The case of fermions is even more complex as the spin symmetry has to be incorporated as well. Using the FCI-NO approach,8 all these symmetry properties can be easily implemented via the second quantization technique. The employment of internal coordinates makes the symmetry adaptation far more complex. The internal Hamiltonian is explicitly invariant under any exchange between the first N − 1 particles, and not invariant when the particle labelled as N is involved. It means that we can use only the SN−1 symmetry group representations explicitly and it is necessary to further perform a SN → SN−1 reduction. This aspect is discussed in detail below.
The case of N = 2 is special and the full permutation symmetry can be explicitly taken into account. Thus, if the angular coordinates are settled as 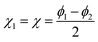 and
and 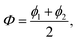 the exchange of the two particles 1 ↔ 2 simply corresponds to
the exchange of the two particles 1 ↔ 2 simply corresponds to
| ρ1 ↔ ρ2; t → −t; χ → −χ. |
Notice that the factor 1/2 in the definition of χ makes the WF periodic in χ, with the associated quantum number being m = m1 − m2. The overall rotational quantum number Λ = m1 + m2 is always integer. Yet, an additional constraint must be imposed on the χ dependence as both m1 and m2 are integers and thus the parity of m should be the same as the parity of Λ. In other words, the wave-function must be ±invariant under the χ → χ + π transformation with a phase +1 for even Λ and −1 for odd Λ. This condition is satisfied when using properly adapted basis functions, as explained in Section 2.4. The angular kinetic energy in these coordinates is expressed as
To conclude this subsection, let us describe how a given explicit symmetry is imposed into the Hamiltonian. As iterative Davidson-type techniques are used for the Hamiltonian diagonalization (see Section 2.4), the employment of symmetry-adapted basis functions is not efficient. Instead, we use a projection technique and, specifically, character-based projectors. The projector to a given irreducible representation α of the symmetry group is expressed as,34
2.3 Reduction SN → SN−1 and incorporation of the spin symmetry
As mentioned above, the Hamiltonian expressed in internal coordinates does not explicitly include the symmetry group SN. Yet, the solution must belong to the SN representation as the original Hamiltonian features this symmetry. In order to identify the specific SN representation, the symmetries of the solutions are tested a posteriori.An acceptable solution for the case of spinless bosons must belong to the {N} Young diagram. By removing the coordinate of the particle labelled as N, this solution might only correspond to the {N − 1} diagram of the SN−1 group as it must obviously be symmetric with respect to any permutation of first N − 1 PNs. However, the solution that transforms as the {N − 1} representation of the SN−1 symmetry group may correspond not only to the {N} but also to the {N − 1,1} diagram of SN. To verify that the good {N} solution has been obtained, we calculate a ‘symmetry factor Q’ as:
| Q ≡ 〈Ψ(1 ↔ N)|Ψ〉. |
Then, from general theory of the SN group representations,35 it can be shown that the factor Q for the solution corresponding to {N} ({N − 1,1}) is equal to 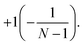 Therefore, the factor Q can be used to select the correct solutions. The details of its calculation when applying the DVR technique are given in Section 2.4. It involves a modification in the grid, and thus this factor may also serve as an indicator of the accuracy of the numerical treatment (grid quality) itself.
Therefore, the factor Q can be used to select the correct solutions. The details of its calculation when applying the DVR technique are given in Section 2.4. It involves a modification in the grid, and thus this factor may also serve as an indicator of the accuracy of the numerical treatment (grid quality) itself.
A similar approach can be used for the fermionic case. Here we may have degenerate solutions belonging to different representations of the SN−1 subgroup so that several Q factors need to be calculated. We provide full details for bosonic and fermionic cases with explicit expressions for N = 2, 3, and 4 in Section S1 of the ESI.† It is also stressed that the differences between the energies of correct (pure fermionic or bosonic) solutions and those corresponding to solutions which do not satisfy the associated full SN symmetry serve as an estimate of the magnitude of exchange effects. In the calculations presented in this work, these energy differences have been of the order of a few wave-numbers.
2.4 Implementation: discrete variable representation (DVR) approach
To evaluate the matrix elements of the internal Hamiltonian, we use the Discrete Variable Representation (DVR) approach36 as in our previous works,16,17,33,37 with the basis set obtained as a direct product of functions for the different coordinates. The main advantage is that the potential term V2 is diagonal in the DVR basis so that it needs to be evaluated just on the set of DVR grid points.To fully account for the stronger V1 interaction, we use the potential-optimized (using V1) PO-DVR method38 (see also ref. 16). The underlying DVR functions are 2D harmonic oscillator functions as they ‘absorb’ the 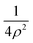 singular term at ρ = 0 into the kinetic energy contribution. As the N = 1 excitation energies are much larger than the clusters formation energies (because of the V2 contributions are much smaller than the V1 contributions), a few PO-DVR functions are sufficient. The good performance of such a basis has been assessed by the fast convergence of the total energies with the number of PO-DVR grid points along the ρ coordinates, nρ.
singular term at ρ = 0 into the kinetic energy contribution. As the N = 1 excitation energies are much larger than the clusters formation energies (because of the V2 contributions are much smaller than the V1 contributions), a few PO-DVR functions are sufficient. The good performance of such a basis has been assessed by the fast convergence of the total energies with the number of PO-DVR grid points along the ρ coordinates, nρ.
Sinc-DVR functions are employed for both t- and χ-coordinates. The number of functions on the t-coordinate and the grid interval is chosen to ensure the convergence of the bound-state WFs and energies. Sinc-DVR functions are defined for the angular coordinates χ on the interval [0…2π], with the kinetic energy adjusted to the periodicity of the WFs. These functions are symmetrized with respect to the χ → 2π − χ transformation and the anti-symmetric functions are taken with phase factor i so that the Hamiltonian matrix is kept as real. For the particular N = 2 case, the Sinc-DVR functions are also symmetrized with respect to the χ → χ + π transformation so that even-m and odd-m functions can be distinguished.
The diagonalization of the resulting Hamiltonian matrix is performed using the Jacobi–Davidson (JD) algorithm.39 In contrast with standard Davidson algorithms, the JD technique has been found to be very robust and capable of providing converged energies even for ill-behaved ‘hard-core’ interactions such as the short-range He–He interaction in doped helium clusters.19,20,24
As explained above, the factors Q are evaluated to assign correctly the permutation symmetry. Their explicit expression is:
| Qij = 〈Ψi(1 ↔ N)|Ψj〉 = 〈Ψi(ρi′,ti′,χi′)|exp(−iΛχ1)|Ψj〉. |
3 Results
3.1 Interaction potentials
As mentioned in the introduction, we have used previously developed ab initio-derived potential models for the PN–SWCNT interaction (PN = He, H2), using different analytical forms for the dispersionless and dispersion energy contributions. To preserve the cylindrical symmetry of the system, the very small corrugation appearing along the azimuthal degree of freedom ϕ is ignored. Moreover (see e.g., ref. 12), the adsorbate-SWCNT interaction is almost constant along the Z axis, decaying slowly at the borders. Then, considering long nanotubes, we can assume that the interaction potential depends only on ρ. The atomic structure of the SWCNT is implicitly considered through the SAPT(DFT) calculations used to fit the parameters of the employed pairwise potential model.12,17 For convenience, the details are given in Section S2 of the ESI.† The adequacy of the potential model has been attested in previous works on both the He–SWCNT (see Fig. 2 of ref. 12) and the H2–SWCNT (see Fig. 3 of ref. 17) interactions. In order to employ these potentials within the DVR approach, they were fit to the polynomials of ρ:The parameters of these polynomial fits are provided in Section S2 of the ESI.†
To model the He–He interaction, we have employed the very accurate potential of Cencek et al.,40 which includes nonadiabatic and relativistic corrections. For the H2–H2 interaction, the rotationally-averaged potential energy surface reported by Hinde41 has been employed instead, as in our previous works.16,17
3.2 Bound states of (3,4He)N and (para-H2)N clusters (N < 4)
Table 1 summarizes the results for the bound states of (3,4He)N and (para-H2)N clusters inside the SWCNT(11,4) tube for N ≤ 3. To better understand the spatial structure of the WFs, Fig. 3, 4 and 6 provide plots of 2D densities for N = 2, N = 3 and N = 4 correspondingly. The 2D density is the square of the WF integrated over all but two coordinates. For completeness, Section S3 of the ESI,† provides also 1D densities. The densities corresponding to ortho-D2 molecules are also included for comparison purposes. For illustrative purposes, Fig. 5 presents the classical structures that can be extracted from the maximum values of the 2D densities corresponding to (4He)N clusters.| N | S | Λ | z-Symm | E, cm−1 | E bind, cm−1 | Dissociation channel | Q |
|---|---|---|---|---|---|---|---|
| 4He | |||||||
| 1 | 0 | −192.734 | |||||
| 1 | 1.430 | ||||||
| 2 | 5.620 | ||||||
| 2 | 0 | + | −386.381 | 0.912 | 4He(m = 0) + 4He(m = 0) | ||
| 1 | + | 2.291 | 0.050 | 4He(m = 1) + 4He(m = 0) | |||
| − | 2.229 | 0.113 | id. | ||||
| 2 | + | 2.822 | 0.950 | 4He(m = 1) + 4He(m = 1) | |||
| 3 | + | 7.906 | 0.055 | 4He(m = 2) + 4He(m = 1) | |||
| − | 7.855 | 0.107 | id. | ||||
| 3 | 0 | + | −580.174 | 1.059 | 4He2(Λ = 0) + 4He(m = 0) | 0.998 | |
| 1 | + | 1.836 | 0.652 | 4He2(Λ = 0) + 4He(m = 1) | 1.005 | ||
| 2 | + | 3.221 | 0.659 | 4He2(Λ = 2) + 4He(m = 0) | 0.993 | ||
| 3 | + | 4.233 | 1.077 | 4He2(Λ = 2) + 4He(m = 1) | 0.992 | ||
| 3He | |||||||
| 1 | 0 | −188.739 | |||||
| 1 | 2.011 | ||||||
| 2 | 7.791 | ||||||
| 2 | 0 | 0 | + | −377.795 | 0.317 | 3He(m = 0) + 3He(m = 0) | |
| 1 | 1 | + | 1.307 | 1.021 | 3He(m = 1) + 3He(m = 0) | ||
| 0 | 2 | + | 3.956 | 0.383 | 3He(m = 1) + 3He(m = 1) | ||
| 1 | 3 | + | 9.010 | 1.110 | 3He(m = 2) + 3He(m = 1) | ||
| 3 | 1/2 | 0 | − | −566.735 | 0.519 | 3He2(Λ = 0, S = 0) + 3He(m = 0) | 0.497 |
| 1/2 | 1 | − | 1.459 | 0.051 | 3He2(Λ = 1, S = 1) + 3He(m = 0) | −0.497 | |
| 1/2 | 1 | + | 1.119 | 0.390 | id. | 0.498 | |
| 3/2 | 1 | − | 1.052 | 0.457 | id. | −0.993 | |
| 1/2 | 2 | − | 3.441 | 0.080 | 3He2(Λ = 1, S = 1) + 3He(m = 1) | −0.498 | |
| 1/2 | 2 | + | 3.112 | 0.408 | id. | 0.496 | |
| 3/2 | 2 | − | 3.061 | 0.460 | id. | −0.995 | |
| 1/2 | 3 | − | 5.933 | 0.236 | 3He2(Λ = 2, S = 0) + 3He(m = 1) | 0.495 | |
| H2 | |||||||
| 1 | 0 | −607.393 | |||||
| 1 | 2.651 | ||||||
| 2 | 0 | + | −1223.909 | 9.123 | H2(m = 0) + H2(m = 0) | ||
| 1 | + | 7.962 | 3.812 | H2(m = 1) + H2(m = 0) | |||
| − | 6.100 | 5.674 | id. | ||||
| 2 | + | 5.191 | 9.234 | H2(m = 1) + H2(m = 1) | |||
| 3 | 0 | + | −1843.514 | 12.212 | (H2)2(Λ = 0) + H2(m = 0) | 0.996 | |
| 1 | + | 2.989 | 11.874 | (H2)2(Λ = 0) + H2(m = 1) | 1.005 | ||
| 2 | + | 5.555 | 11.848 | (H2)2(Λ = 2) + H2(m = 0) | 0.988 | ||
| 3 | + | 7.830 | 12.224 | (H2)2(Λ = 2) + H2(m = 1) | 0.990 | ||
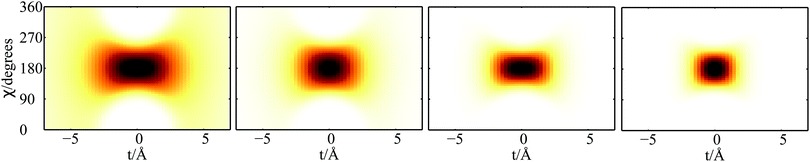 | ||
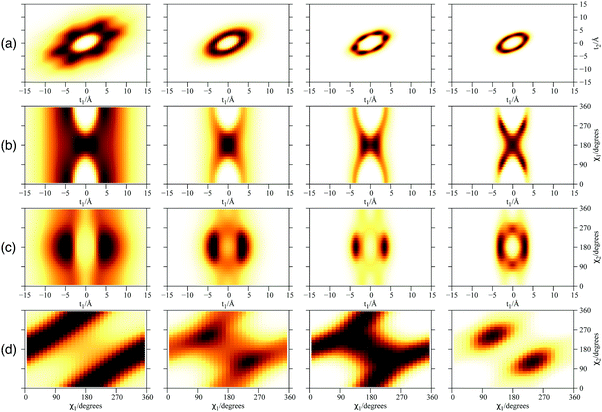
| Fig. 3 Plot of 2D densities in t and χ coordinates for PN2⊂SWCNT(11,4) complexes. Left to right: PN = 3He, 4He, para-H2, ortho-D2. | ||
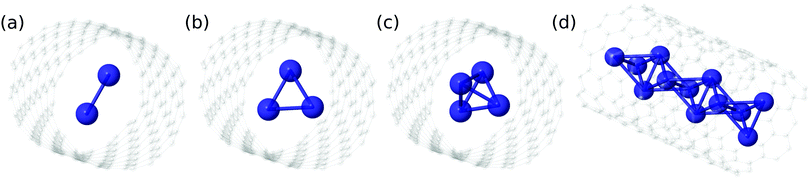 | ||
| Fig. 5 Classical structures that can be associated with the maximum values of the 2D densities corresponding to (4He)N clusters (see also Fig. 4 and 6). | ||
Considering the lowest-energy bound states, we can observe that the values of the binding energies of (ortho-H2)N complexes are at least 10 times larger than those associated to (4He)N clusters. Comparing the two helium isotopes, we notice that the binding energy of (4He)N complexes is twice as large as for (3He)N clusters. It is remarkable that, in contrast with the free dimer, the confined (3He)2 system is bound (although by just −0.3 cm−1), despite of the free Z motion. In fact, according to a previously developed one-dimensional model (see Section S3 of the ESI of ref. 12), the effective 3He–3He interaction along the tube axis would be very similar to that of the free dimer in such a narrow nanotube of 1 nm. This finding can be explained as follows: the confinement causes the single 3He distribution to be much more localized along the ρ direction. By accounting for the z symmetry and according to the obtained density distributions, the two 3He atoms can place themselves at opposite sides of the nanotube diameter and not along the tube axis. Then, the attractive V2 interaction makes possible that such configuration is bound, even at the price of a slightly increased kinetic energy (ϕ localization).
The differences between the bound states of confined 3He and 4He atoms for N = 1 originates from the higher zero-point energy (the mass) of the former. Due to the spin symmetry, however, the levels structure for N > 1 and the 3He isotope (as well as the dissociation channels for N = 3) differs much from the 4He counterpart. While there is only one bound state for Λ = 0, the number of states of opposite t-symmetry for Λ > 0 increases sharply as the number of 3He atoms grow. In particular, notice that a significant number of bound states have very close energies already for the (3He)3 cluster. Of course, this trend is expected to be even more pronounced for larger N values. This outcome is reminiscent to that reported for doped 3He clusters at both Hartree–Fock22 and FCI-NO levels.25 In both studies,22,25 the congested profile of the experimental spectra in doped 3He droplet1 was attributed to the high energy degeneracy exhibited by fermionic clusters.
We can also observe from Table 1 that collective rotational states for (4He)N clusters with Λ = N are associated to larger binding energies, as opposed to those of (3He)N clusters. However, no energy minima are obtained at Λ = N for either 4He or para-H2 bosonic particles. This feature would signal the stabilization of collective rotational motion which, importantly, is found upon the aggregation of four bosonic particles (see Section 3.3).
It worth stressing that the clusters dissociation often breaks the symmetry in t, which is present in all bound states (see Table 1). For example, the (4He)2 cluster with Λ = 1 dissociate to two 4He atoms with different overall rotation quantum numbers (m = 0 and m = 1). It indicates the onset of t-symmetry breaking at infinite distance, which would have to be accounted for in dynamical studies of the helium motion in SWCNTs. This feature also correlates (at least for the 4He isotope) with the fact of having (nearly degenerate) states that are anti-symmetric in t for N = 2 and odd Λ values. Indeed, for even Λ values, the dissociation channel is symmetric and the anti-symmetry in t is not present. States with odd Λ values are not symmetric in t and the dissociative WF is in fact a combination of ± states. For N = 3, all the dissociation channels are obviously non symmetric as combinations of the channels of the helium dimer and a single helium atom. However, anti-symmetric in t states are not bound in this case.
As mentioned above, WFs bearing the same Λ value can be either symmetric or anti-symmetric with respect to the z → −z exchange. The relatively large values for the splittings between ± states (see Table 1) come from the fact that the fragments wave functions (WFs) are very diffused. As a result, their overlaps are significant and contribute to the splittings. For instance, anti-symmetric WFs should be zero at z = 0 in contrast with symmetric WFs. This additional restriction results in noticeable energy differences. The reason why the values of the splittings are large can be also understood as follows: the nanotube is large enough to hold two PNs with the same z value (i.e., t = 0). As the repulsive interaction is due to V2, which has the minimum (of just a few cm−1) at about 3 Å, such a configuration is just slightly penalized (if ever). It is additionally slightly penalized by the rotational kinetic energy term, due to an increased localization along the ϕ coordinates. Thus, the barrier corresponding to the PN's exchange (or the end-over-end rotation) is found to be quite low. Actually, for N = 2, such t = 0 configuration corresponds to the ground state. This feature can be viewed making an analogy to a 1D model potential with two symmetric wells and a barrier. When the barrier is low enough, the splittings between symmetric and anti-symmetric solutions become large. In our case, it is difficult to plot an effective 1D V2 potential along the z coordinate as all internal coordinates (t, χ and, to a lesser extent, ρ) are strongly coupled.
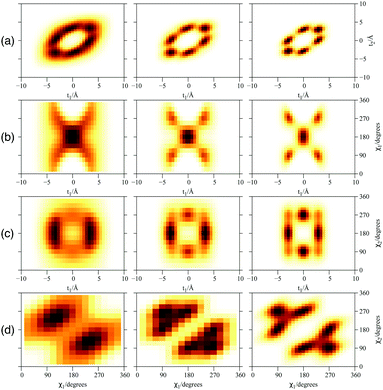
Focusing now on the 2D densities (Fig. 3–6), we observe that all systems present long tails in the t coordinates, though more compact than those of the free 4He2 dimer. All the 2D densities for the (PN)2⊂SWCNT(11,4) systems (see Fig. 3) indicate that the most probable structure is a dimer with the inter-nuclear axis perpendicular to the tube axis. The delocalization trend as the particle mass decreases and the strength of the inter-particle interaction decreases is very pronounced. The analysis of the 2D densities of the (PN)3⊂SWCNT(11,4) systems is even more appealing (see Fig. 4).43 For instance, it can be seen that, for PN = 4He and ortho-D2, the WF bears a maximum at t1,2 = 0, which can be attributed to a triangular structure. In stark contrast, for PN = 3He and para-H2, the density along the t coordinate has an hexagonal-like shape which would correspond to an structure lying aligned along the tube axis. Actually, 4He atoms also execute wide amplitude motion between triangular and aligned-type structures so that the corresponding 2D density in the χ coordinates deviates noticeably from that of D2 molecules. Hence, three D2 molecules and 4He atoms form a very flexible triangular structure (see also Fig. 5) while H2 and 3He atoms are delocalized along the tube axis. It is clear that the mass of the quantum particle is the dominant factor followed by the strength of the inter-particle interaction.
3.3 The special case of (4He)4 and (para-H2)4 clusters
Fig. 6 presents the plots of the ground-state 2D densities of PN4 clusters (PN = 4He, para-H2, and ortho-D2), comparing them with the case of ortho-D2 molecules reported in ref. 16. It can be observed that, whatever the bosonic particle be, the most probable structure is pyramidal-like. However, it features an increasing spatial delocalization when going from ortho-D2 through para-H2 to 4He particles. On the one hand, although para-H2 molecules are twice as light as 4He atoms, the three times deeper attractive well of the pair potential (see Fig. 1) causes the structure of the (para-H2)4 cluster being more compact that the 4He counterpart. In fact, the extended profile of the 2D densities in the χ coordinates reflects a quasi-independent relative rotational motion of two (4He)2 dimers lying orthogonal to the tube axis. On the other hand, since ortho-D2 molecules are twice as heavy as para-H2 molecules, the solid-like nature of the (ortho-D2)4 structure (a regular tetrahedron) becomes even more apparent than the (para-H2)4 counterpart. Interestingly, (para-H2)4 clusters also adopt a (vibrationally averaged) tetrahedral geometry under spherical nanoconfinement in clathrate hydrate cages.44,45 These similarities indicate that the aggregation of multiple H2 molecules is driven by quantum nuclear effects and very weak dispersive H2–H2 interactions rather than the much more stronger H2–SWCNT (or H2-cage) energy contribution.We have also investigated the stabilization of collective rotational motion. To this end, the lowest-state energies of the PN4⊂SWCNT(11,4) systems are represented at each Λ value (the so-called yrast states) in Fig. 6 (see also Table 2). As found for doped para-H28 and confined ortho-D216 clusters, four 4He atoms or para-H2 molecules are necessary for the appearance of the collective rotational states as energy minima such as that presented at Λ = N (see Fig. 7). The occurrence of energy minima in yrast lines at Λ = νN (ν being an integer) has been connected with the onset of a superfluid behaviour and persistent flow in quantum rings made of 4He atoms by Bloch.46 Actually, bosonic symmetry is a necessary but not a sufficient condition. For instance, the stabilization of collective rotational motion is not featured by (PN)N clusters with N < 4 (PN = 4He, para-H2, see Table 1). As previously discussed,8 such singularities appear when the hard-core H2–H2 (or 4He–4He) repulsive interaction is intensified. This situation occurs, e.g., when a belt around a dopant molecule is close to completion with 4He atoms or H2 molecules. Such behaviour has been derived for bosonic particles featuring an infinity repulsive interaction when confined in a 1D ring.47 However, we remark that our outcome is issued from highly accurate full quantum calculations and not a theoretical model.
| S | Λ | z-Symm | E, cm−1 | ΔE, cm−1 | Q | n ρ /nt/nχ |
|---|---|---|---|---|---|---|
| (4He)4 | ||||||
| 0 | 0 | + | −776.022 | 0 | 0.963 | 1/30/8 |
| 1 | + | 2.661 | 0.925 | |||
| 2 | + | 3.758 | 0.979 | |||
| 3 | + | 5.252 | 0.930 | |||
| 4 | + | 5.230 | 0.978 | |||
| (para-H2)4 | ||||||
| 0 | 0 | + | −2481.168 | 0 | 0.979 | 1/25/8 |
| 1 | + | 10.299 | 0.963 | |||
| 2 | + | 12.291 | 0.984 | |||
| 3 | + | 15.336 | 0.976 | |||
| 4 | + | 9.936 | 0.991 | |||
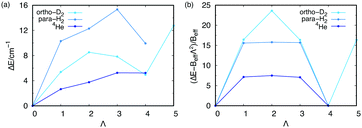 | ||
| Fig. 7 (a) ΔE values (energy differences with the ground state) for the lowest-energy states of the PN4⊂SWCNT(11,4) (PN = 4He, para-H2, ortho-D2) systems as a function of Λ. See also Table 2. (b) The same but after subtracting the overall rotational term BeffΛ2 (in units of Beff). The Beff term is evaluated from the ΔE value for Λ = N. Notice the periodicity of the resulting function in panel (b) (see ref. 16 for the details). | ||
As for the case of ortho-D2 molecules,16 a classical analysis of the potential minima landscape leads to the prediction of a quasi-1D chain of pyramidal-like structures as the number of 4He atoms and para-H2 molecules increase (see Fig. 5). Because the well-depth of the V1 potential is much larger than the V2 counterpart, the 4He atoms and the H2 molecules can be considered as fixed at a distance ρmin from the nanotube axis, where ρmin is the position of the V1 potential minimum. Then, the rest of the geometry is defined by V2. By requiring that all rij distances have the values at which the V2 potential minimum is located, the numbers of variables and conditions are the same for N = 4 so that the potential minimum is just a single point in the parameter space. Considering the z-extension of the pyramidal structure for N = 4, we can conclude that the structure for N ≫ 4 is a 1D chain of pyramidal-shaped structures (see Fig. 5), exhibiting a high delocalization when being formed by 4He atoms.
4 Conclusions
This work addresses the characterization of multiple quantum particles inside carbon nanotubes and, in particular, in identifying the role of the nuclear spin statistics of the considered particles. It has been motivated by the experimental evidence of microscopic superfluidity (and its lack) in doped 4He (3He) droplets and para-H2 clusters by the group of Professor Jan-Peter Toennies (see, e.g., ref. 1, 2, 5 and 6), but at the reduced dimensionality offered by confinement inside carbon nanotubes. For this purpose, we have developed a highly accurate full quantum method which is capable of dealing with Fermi–Dirac and Bose–Einstein nuclear spin statistics of the confined quantum particles on an equal footing, delivering excited and disentangled states with similar accuracy to the ground state, and using ab initio-derived potential models. In contrast with orbital-based techniques, we numerically solve the Schrödinger differential equation for the wave function with the full set of independent variables represented via a DVR grid so that the energy convergence has just to be ensure vs. the grid parameters and the grid size. In order to illustrate its performance, we have applied our new method to clusters of up to four (three) 4He atoms and para-H2 molecules (3He atoms) inside a single-walled carbon nanotube of 1 nm diameter.The energy landscape of the bound states as a function of the angular momentum around the tube axis reveals very different profiles for clusters of 3He and 4He atoms. Due to the spin of the fermionic 3He atom, the increasingly congested structure of the energy spectrum is evident as the number of 3He atoms increases, in contrast with the spin-less (bosonic) 4He counterpart. This finding is in line to that reported for doped 3He clusters:22,25 the calculated spectral profile of the dopant molecule becomes increasingly more congested upon augmentation of the number of 3He atoms, explaining the experimental observations in doped 3He droplets.1 The wave-function and density analysis of (PN)3 clusters (PN = 3He, 4He, and para-H2) indicates the occurrence of wide amplitude motions, specially for the 3He isotope due its lighter mass and weakness of the He–He interaction. As for ortho-D2,16 evidence of stabilization of collective rotational motion and persistent flow,46 is found in clusters of four bosonic para-H2 molecules and 4He atoms, forming tetrahedral pyramidal-like structures. Remarkably, the main findings (arrangement in an unique (vibrationally averaged) tetrahedral geometry and exhibition of collective rotational motion) are shared with those uncovered for the case of spherical confinement in clathrate hydrate by Bačić and collaborators.44,45 In our case of cylindrical confinement, the analysis of the potential minima landscape serves to predict a 1D chain of pyramidal-like structures along the tube axis as the resulting condensed matter system as the number of bosonic particles increases.
Pushing our understanding beyond common intuition, the present study along with previous works16,17 point out that the transition from van der Waals-type molecular aggregation to quasi-1D condensed matter systems under cylindrical carbon nanotube confinement is driven by purely dispersive inter-adsorbate interactions together with quantum nuclear effects and not the much more stronger adsorbate-tube interaction forces. As a future perspective, we are aimed to adapt our Full Configuration Interaction Nuclear Orbital (FCI-NO) approach, originally developed for doped helium clusters, to the present case in which the carbon nanotube acts as the ‘dopant’ species. The essential advantage of this ansatz is that the WF is expanded using products of nuclear orbitals, allowing the employment of second quantization techniques and an automatic inclusion of Fermi–Dirac and Bose–Einstein nuclear spin statistical effects. This would imply the choice of an orbital representation such that the equality 〈Z〉 = 0 is satisfied. For this purpose, one path is the imposition of the symmetry on the z coordinate for each orbital, and the follow-up subtraction of the center-of-mass kinetic energy. Whatever the specific strategy for further developments be, we hope that the highly accurate method presented in this work will serve to produce the necessary benchmark results.
Conflicts of interest
There are no conflicts to declare.Appendix
The basis sets used for helium clusters are as follows: 400 radial (2D oscillator) basis functions for N = 1; 5 PO-DVR (as obtained from 400 functions for N = 1) radial functions, 641 sinc-DVR functions on the interval [−160:160]a0 for t, and 120 sinc-DVR functions for χ, for N = 2; and 5 PO-DVR radial functions, 81 sinc-DVR functions on the interval [−40:40]a0 for ti, 30 sinc-DVR functions for χi, for N = 3. These basis sets ensure that the energy values are converged to better than 0.01 cm.−1 Although the same number of t,χ basis functions for N = 2 as for N = 3 would be sufficient, the larger basis set was used just to obtain finer plots of the densities and wave functions. The size of Hamiltonian matrix for Λ = 0 with these basis sets was 480.750 for N = 2 and 369.056.250 for N = 3. For Λ > 0, the size was twice as large (the symmetry for χ is broken due to the Λ-dependent term in the Hamiltonian).Acknowledgements
We thank Zlatko Bačić for attracting our attention to the similarities between confinement of multiple H2 molecules under carbon nanotubes and clathrate hydrate cages. This work has been partly supported by the Spanish Agencia Estatal de Investigación (AEI) and the Fondo Europeo de Desarrollo Regional (FEDER, UE) under Grant No. MAT2016-75354-P. We are thankful to CESGA super-computer facilities (Spain) for providing computational resources. MPdLC thanks Patricia López-Caballero for her help in the edition of this manuscript, as well as Andreas W. Hauser for his collaboration on previous works addressing confinement in carbon nanotubes.References
- S. Gebenev, J. P. Toennies and A. F. Vilesov, Science, 1998, 279, 2083–2086 CrossRef PubMed.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622 CrossRef CAS PubMed.
- S. Goyal, D. L. Schutt and G. Scoles, Phys. Rev. Lett., 1992, 69, 933–936 CrossRef CAS PubMed.
- M. Hartmann, R. E. Miller, J. P. Toennies and A. Vilesov, Phys. Rev. Lett., 1995, 75, 1566–1569 CrossRef CAS PubMed.
- S. Grebenev, B. G. Sartakov, J. P. Toennies and A. F. Vilesov, J. Chem. Phys., 2010, 132, 064501 CrossRef PubMed.
- S. Grebenev, B. G. Sartakov, J. P. Toennies and A. F. Vilesov, Science, 2000, 289, 1532–1535 CrossRef CAS PubMed.
- Y. Kwon and K. B. Whaley, Phys. Rev. Lett., 2002, 89, 273401 CrossRef PubMed.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, J. Phys. Chem. Lett., 2011, 2, 2145–2151 CrossRef CAS.
- H. Li, R. J. Le Roy, P.-N. Roy and A. R. W. McKellar, Phys. Rev. Lett., 2010, 105, 133401 CrossRef PubMed.
- A. Noury, J. Vergara-Cruz, P. Morfin, B. Plaçais, M. C. Gordillo, J. Boronat, S. Balibar and A. Bachtold, Phys. Rev. Lett., 2019, 122, 165301 CrossRef CAS PubMed.
- T. Ohba, Sci. Rep., 2016, 6, 28992 CrossRef CAS PubMed.
- A. W. Hauser, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Phys. Chem. C, 2017, 121, 3807–3821 CrossRef CAS.
- M. Rossi and F. Ancilotto, Phys. Rev. B, 2016, 94, 100502 CrossRef.
- G. Ferré, M. C. Gordillo and J. Boronat, Phys. Rev. B, 2017, 95, 064502 CrossRef.
- A. Del Maestro and M. Boninsegni, Phys. Rev. B, 2017, 95, 054517 CrossRef.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, J. Phys. Chem. Lett., 2020, 11, 5081–5086 CrossRef CAS PubMed.
- M. P. de Lara-Castells, A. W. Hauser, A. O. Mitrushchenkov and R. Fernández-Perea, Phys. Chem. Chem. Phys., 2017, 19, 28621–28629 RSC.
- A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. Lett., 2016, 7, 4929–4935 CrossRef CAS PubMed.
- M. P. de Lara-Castells, G. Delgado-Barrio, P. Villarreal and A. O. Mitrushchenkov, J. Chem. Phys., 2006, 125, 221101 CrossRef CAS PubMed.
- M. P. de Lara-Castells, A. Mitrushchenkov, G. Delgado-Barrio and P. Villarreal, Few-Body Systems, 2009, 45, 233–236 CrossRef CAS.
- M. P. de Lara-Castells, D. López-Durán, G. Delgado-Barrio, P. Villarreal, C. Di Paola, F. A. Gianturco and J. Jellinek, Phys. Rev. A, 2005, 71, 033203 CrossRef.
- D. López-Durán, M. P. de Lara-Castells, G. Delgado-Barrio, P. Villarreal, C. Di Paola, F. A. Gianturco and J. Jellinek, Phys. Rev. Lett., 2004, 93, 053401 CrossRef PubMed.
- M. P. de Lara-Castells, G. Delgado-Barrio, P. Villarreal and A. O. Mitrushchenkov, J. Chem. Phys., 2009, 131, 194101 CrossRef CAS PubMed.
- M. P. de Lara-Castells, N. F. Aguirre, P. Villarreal, G. Delgado-Barrio and A. O. Mitrushchenkov, J. Chem. Phys., 2010, 132, 194313 CrossRef PubMed.
- N. F. Aguirre, P. Villarreal, G. Delgado-Barrio, A. O. Mitrushchenkov and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2013, 15, 10126–10140 RSC.
- N. F. Aguirre, P. Villarreal, G. Delgado-Barrio, A. O. Mitrushchenkov and M. P. de Lara-Castells, Chem. Phys. Lett., 2013, 555, 12–18 CrossRef CAS.
- N. F. Aguirre, P. Villarreal, G. Delgado-Barrio, E. Posada, A. Reyes, M. Biczysko, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Chem. Phys., 2013, 138, 184113 CrossRef PubMed.
- M. P. de Lara-Castells, M. Bartolomei, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 194701 CrossRef PubMed.
- M. P. de Lara-Castells, A. W. Hauser and A. O. Mitrushchenkov, J. Phys. Chem. Lett., 2017, 8, 4284–4288 CrossRef CAS PubMed.
- M. P. de Lara-Castells and A. W. Hauser, Phys. Life Rev., 2020, 32, 95–98 CrossRef PubMed.
- A. J. Misquitta, R. Podeszwa, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 2005, 123, 214103 CrossRef PubMed.
- A. Heßelmann, G. Jansen and M. Schütz, J. Chem. Phys., 2005, 122, 014103 CrossRef PubMed.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, Phys. Chem. Chem. Phys., 2019, 21, 3423–3430 RSC.
- E. Wigner and J. Griffin, Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra, Academic Press, 1959 Search PubMed.
- R. Pauncz, The Symmetric Group in Quantum Chemistry, Taylor & Francis, 1995 Search PubMed.
- Z. Bačic and J. C. Light, Annu. Rev. Phys. Chem., 1989, 40, 469–498 CrossRef.
- A. W. Hauser, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Phys. Chem. C, 2017, 121, 3807–3821 CrossRef CAS.
- J. Echave and D. C. Clary, Chem. Phys. Lett., 1992, 190, 225–230 CrossRef CAS.
- G. L. G. Sleijpen and H. A. V. der, SIAM J. Matrix Anal. A., 1996, 17, 401–425 CrossRef.
- W. Cencek, M. Przybytek, J. Komasa, J. B. Mehl, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 2012, 136, 224303 CrossRef.
- R. J. Hinde, J. Chem. Phys., 2008, 128, 154308 CrossRef PubMed.
- Under the considered cylindrical environment, the overall Λ value remains a good quantum number throughout the dissociation, and thus it must match the sum of the λ values of the two fragments.
- We note that due to the explicit symmetry of the first N − 1 particles taken into account, it is sufficient to consider just the (four) provided 2D densities for N > 2. The other densities, related by (N − 1) transpositions, are identical. For instance, the 2D density in t2, χ2 coordinates is the same as in t1, χ1 coordinates.
- F. Sebastianelli, M. Xu and Z. Bačić, J. Chem. Phys., 2008, 129, 244706 CrossRef PubMed.
- A. Witt, F. Sebastianelli, M. E. Tuckerman and Z. Bačić, J. Phys. Chem. C, 2010, 114, 20775–20782 CrossRef CAS.
- F. Bloch, Phys. Rev. A, 1973, 7, 2187–2191 CrossRef.
- M. Manninen, S. Viefers and S. Reimann, Physica E Low Dimens. Syst. Nanostruct., 2012, 46, 119–132 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the method, the ab initio-derived potential model, and additional figures presenting 1D densities. See DOI: 10.1039/d0cp05332e |
| This journal is © the Owner Societies 2021 |