Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Designing new SRP density functionals including non-local vdW-DF2 correlation for H2 + Cu(111) and their transferability to H2 + Ag(111), Au(111) and Pt(111)†
Egidius W. F.
Smeets
 and
Geert-Jan
Kroes
and
Geert-Jan
Kroes
 *
*
Univeristeit Leiden, Leiden Institute of Chemistry, Einsteinweg 55, 2333 CC, Leiden, The Netherlands. E-mail: g.j.kroes@chem.leidenuniv.nl; Tel: +31 71 527 4396
First published on 19th November 2020
Abstract
Specific reaction parameter density functionals (SRP-DFs) that can describe dissociative chemisorption molecular beam experiments of hydrogen (H2) on cold transition metal surfaces with chemical accuracy have so far been shown to be only transferable among different facets of the same metal, but not among different metals. We design new SRP-DFs that include non-local vdW-DF2 correlation for the H2 + Cu(111) system, and evaluate their transferability to the highly activated H2 + Ag(111) and H2 + Au(111) systems and the non-activated H2 + Pt(111) system. We design our functionals for the H2 + Cu(111) system since it is the best studied system both theoretically and experimentally. Here we demonstrate that a SRP-DF fitted to reproduce molecular beam sticking experiments for H2 + Cu(111) with chemical accuracy can also describe such experiments for H2 + Pt(111) with chemical accuracy, and vice versa. Chemically accurate functionals have been obtained that perform very well with respect to reported van der Waals well geometries, and which improve the description of the metal over current generalized gradient approximation (GGA) based SRP-DFs. From a systematic comparison of our new SRP-DFs that include non-local correlation to previously developed SRP-DFs, for both activated and non-activated systems, we identify non-local correlation as a key ingredient in the construction of transferable SRP-DFs for H2 interacting with transition metals. Our results are in excellent agreement with experiment when accurately measured observables are available. It is however clear from our analysis that, except for the H2 + Cu(111) system, there is a need for more, more varied, and more accurately described experiments in order to further improve the design of SRP-DFs. Additionally, we confirm that, when including non-local correlation, the sticking of H2 on Cu(111) is still well described quasi-classically.
1 Introduction
Hydrogen (H2) dissociation on various transition metal surfaces is an example of an intensely studied activated elementary surface reaction within surface science. Chemically accurate computation of rate-controlling states is essential in order to accurately describe the complex overall processes that take place during heterogeneous catalysis under real world conditions.1–5 Industrially H2 dissociation is an important step in the production of methanol from CO2 over a Cu/ZnO/Al2O3 catalyst.6–8 Additionally H2 dissociation is an important process in the production of syngas and ammonia.4 Increasing the predictive power of theoretical models of heterogeneous catalysis potentially has an important financial impact on the chemical industry.9An important step to increasing the predictive power of theoretical models is to create density functionals (DFs) that are chemically accurate for specific systems,1,10–13i.e. DFs that can describe reaction barrier heights to within 1 kcal mol−1.5 A next step is to investigate what ingredients of a DF that is chemically accurate for one system might make it transferable to another system without loss of accuracy. Presently, specific reaction parameter (SRP) density functional theory (DFT) is the only method that can describe the interaction of H2 with metal surfaces with demonstrated chemical accuracy, while simultaneously being computationally cheap enough to make large comparative studies feasible. Therefore the design of accurate DFs is highly important to the field. The availability of transferable specific reaction parameter density functionals (SRP-DFs) has the potential to greatly speed up theoretical heterogeneous catalysis research. It does so by avoiding the need to design a new DF for each system of interest. The availability of transferable SRP-DFs would greatly improve the predictive power of theory for systems for which only sparse experimental results have been published.
The fitting of SRP-DFs is meticulous work and presently14 requires experimental data as reference data.1,10–13,15 Transferability of a DF among systems in which one specific molecule interacts with surfaces of different metals has so far only been reported for the DF designed for CH4 dissociation on Ni(111),13 which could also describe the dissociation of CH4 on Pt(111) with chemical accuracy,16 where Ni and Pt belong to the same group. So far, for SRP-DFs fitted to reproduce molecular beam adsorption experiments for H2 interacting with transition metals transferability was shown among systems in which H2 interacts with different faces of the same metal,17,18 but not among systems where the interaction is with surfaces of different metals.12,15,19,20
The transferability of a SRP-DF that was fitted for the CH4 + Ni(111) system to the CH4 + Pt(111) system suggests that non-local correlation may be an important ingredient for a transferable DF, as this SRP-DF contains non-local correlation. For this reason here we investigate the design of new SRP-DFs that include non-local correlation for H2 + transition metal systems. In this work we present two new SRP-DFs featuring GGA exchange but using non-local correlation. These DFs were fitted to experiments on the H2 + Cu(111) system, since theoretically10,12,21–44 and experimentally45–61 this is the best studied system. For this system we can have the most confidence that discrepancies between theory and experiment can be attributed to either shortcomings in DF design or the limitations of using the Born–Oppenheimer static surface (BOSS) model. It is well known that the BOSS model works well for activated H2 dissociation on cold metals.23,27–29,62 Additionally we evaluate the performance of a SRP-DF that was fitted to the H2 + Pt(111) system11 for the H2 + Cu(111) system.
In undertaking this study we have two aims. The first is to identify features of the newly constructed SRP-DFs that increase their transferability to other systems. Since we use the BOSS model, a direct assessment of the quality of a given DF is really only possible for molecular beam dissociative chemisorption experiments on reasonably cold metal surfaces. Apart from the H2 + Cu(111) system we will consider such experiments for the H2 + Pt(111) system63,64 and the H2 + Ag(111) system.54 For the latter two systems there exists some uncertainty about the validity of the molecular beam parameters describing the experiments.19,65 We however feel that, although there are some uncertainties in the parameters describing the experiments, nevertheless valuable insights on transferability can be derived by analysing the predicted reactivity of the SRP-DFs considered here.
Our second aim is to analyse the limits of our dynamical model to the extent that this is possible. We hope that a detailed analysis of the H2 + Cu(111) system's large body of experimental work45–61 will indicate how to proceed with improving the theoretical description of this system. To this end we will analyse both associative desorption experiments47,51 and dissociative chemisorption experiments.45,46 Naturally, our primary motive is to achieve chemical accuracy. We have also carried out a full quantum mechanical molecular beam simulation by carrying out a large number of fully initial-state resolved quantum dynamical (QD)66,67 calculations for the H2 + Cu(111) system. This is important because the inclusion of a van der Waals well in the PES might lead to discrepancies between quasi-classical trajectory (QCT)68 and QD results compared to the good agreement that was obtained for these two methods for the H2 + Cu(211) system36 using the SRP48 DF,10,62 which does not employ non-local correlation.
For the H2 + Cu(111) system it is known that the effect of surface motion cannot readily be ignored for specific observables at high surface temperature62 (Ts). Analysing associative desorption and dissociative chemisorption experiments as linked through detailed balance,69 might allow us to disentangle the effects of surface motion and the non-adiabatic contributions of electron–hole pair (ehp) excitations, a methodology that was suggested by Shuai et al.70 for the H2 + Au(111) system. If detailed balance is applicable then an analysis of both associative desorption and dissociative chemisorption experiments should yield the same result. A detailed analysis might therefore allow us to identify which dynamical effects not included in the BOSS model may have to be included in future work. Here we will make a direct comparison to experimental effective barrier (E0(ν, J)) parameters.47 Even though a complementary molecular beam dissociative chemisorption experiment is not available for the associative desorption experiment of Shuai et al.70 on H2 + Au(111), we extend our analysis also to this system. We note that it is also possible to simulate associative desorption directly by running trajectories starting around the transition state using Metropolis sampling of the initial conditions,71–75 and that this has also been done for H2 and D2 desorbing from Cu(111). However, the calculations published so far do have limitations. The early work72,73 used a PES that is an approximate fit39 to unconverged DFT calculations40 using the PW91 DF,76 and the statistical accuracy of the results of the later work75 was limited by the number of ab initio molecular dynamics (AIMD) trajectories that could be run. However, an interesting aspect of the later work75 is that the effects of surface atom motion and electron–hole pair excitation could also be investigated.
Furthermore we will treat vibrationally and rotationally inelastic scattering for the H2 + Cu(111) system, since the opinion has been voiced that these properties might be extra sensitive to the van der Waals well, which is present in potential energy surfaces (PESs) computed here with the use of non-local correlation.24
For the H2 + Ag(111) system the only molecular beam dissociative chemisorption experiments we are aware of are those of Hodgson and coworkers.54 We will also make a comparison to initial-state resolved associative desorption experiments for this system,77,78 as was recently done by Jiang and Guo79 using quantum dynamics calculations on a permutation invariant polynomial (PIP) neural network potential80 and in work done in our group.12,19 Earlier experimental work on the H2 + Ag(111) system suggested that H2 prefers to physisorb on silver surfaces,81–83 and that the dissociation of H2 on silver is endothermic,84 exhibiting a relatively low barrier for associative desorption of H2.84–86 For this reason some earlier experimental studies have focused on scattering at low translational energies of H2 from Ag(111)87–90 and Ag(110).91 Recent theoretical studies that addressed the effects of electron–hole pair excitation have shown very interesting effects at low translational energies with respect to inelastic scattering and dynamical steering.92–94 The non-adiabatic energy loss during the dynamics was however shown to be small.94 This is in agreement with work on H2 + Cu(111), which also showed little effect of electron–hole pair excitation on sticking.22,95 Therefore we presume the BOSS model to be accurate enough for our first aim, which is to identify the features of SRP-DFs that contribute to their transferability.
Our DFT calculations using van der Waals correlation functionals96,97 also yield results regarding the geometry and the depth of the van der Waals wells for the systems investigated, and we will compare these results to the experimental results for the systems investigated here. In many cases the experimental results come from an analysis of experiments on selective adsorption.59,61,89,90,98–104 In these experiments, an increase or a dip is observed in a peak for a diffractive (corrugation mediated selective adsorption, CMSA105,106) or a rotational (rotationally mediated selective adsorption, RMSA98) transition if the translational energy goes through a value that coincides with the energy between two parallel translational or hindered rotational metastable states, respectively. In the final state, the H2 molecule is trapped in the van der Waals well close to the surface.100,103 Information about the resonance energies that are present can be used to reconstruct the shape of the potential, and thus the van der Waals well geometries and well depths. The H2-(111) metal–surface systems investigated here exhibit little corrugation. For this reason experiments using RMSA of HD, in which rotational excitation is used to probe the bound levels of the gas-surface potential, have been particularly important for gathering information concerning van der Waals interactions in these systems. The off-center position of the center of mass of HD results in very pronounced resonances when using the RMSA technique.61,98–101 Experimentalists have also been able to carry out RMSA measurements using H2 or D2 instead of HD.89,90,102 van der Waals well depths can also be obtained from the temperature dependence of the Debye–Waller attenuation of peaks for (rotationally) inelastic diffraction,107,108 from potential inversion using calculations on (rotationally inelastic) diffractive scattering using the eikonal approximation,107 and from potential inversion using measurements on phonon-assisted RMSA (also called rotationally mediated focused inelastic resonances, RMFIR109). Concerning the systems investigated here, studies using experiments to analyze the van der Waals interaction have been performed for H2 + Cu(111),59,61 H2 + Ag(111),89,90,101 H2 + Au(111),61 and H2 + Pt(111).98–100,110
This paper is organized as follows. Section 2 covers the computational methods used, with Section 2.1 discussing the coordinate system we use. Section 2.2 details the construction of SRP-DFs, and Section 2.3 the interpolation of the PESs based on SRP DFT data. The QCT and QD methods are described in Sections 2.4 and 2.5, respectively. The way in which we calculate observables is discussed in Section 2.6, and the computational details are summarized in Section 2.7.
Section 3 is the results section. Section 3.1 concerns the electronic structure of the investigated systems and the fitted PESs for these systems. Section 3.2 concerns simulations of molecular beam sticking experiments for three H2 (D2) + metal systems. Initial-state resolved reaction probabilities are presented in Section 3.3, and Section 3.4 presents parameters, E1/2(ν, J), that can be used to compare with associative desorption experiments. Rotational quadrupole alignment parameters, which characterize the dependence of reaction on the alignment of H2 relative to the surface (parallel or end-on) are presented in Section 3.5 for the D2 + Cu(111) system. Rotationally and vibrationally inelastic scattering of H2 from Cu(111) is considered in Section 3.6. State distributions of molecules desorbing from Au(111) are presented in Section 3.7.
The discussion is presented in Section 4. Calculated metal properties are discussed in Section 4.1, and static properties of the calculated PESs in Section 4.2. Molecular beam sticking results are discussed in Section 4.3. In Section 4.4 we analyze initial-state resolved reaction probabilities, and compare extracted E1/2(ν, J) parameters with values extracted from associative desorption experiments on H2 + Cu(111) and Au(111). We also compare initial-state resolved reaction probabilities computed with theory with experimental data for H2 + Ag(111), and the state distributions of molecules desorbing from Au(111). In Section 4.4 we also discuss theoretical and experimental values of rotational quadrupole alignment parameters for D2 + Cu(111). The inelastic scattering of H2 from Cu(111) is discussed in Section 4.5 The quality of the QCT results is evaluated by comparison with QD results for H2 + Cu(111) in Section 4.6. Section 4.7 contains an overview of the comparison theory-experiment for all the H2–metal surface systems we treat in this work. The transferability of the created SRP-DFs is discussed in Section 4.8. In Section 4.9 we discuss how and when qualitative differences in the adiabatic descriptions of molecular beam sticking and associative desorption can be interpreted as a possible signature of the role of ehp excitation. Conclusions are presented in Section 5.
2 Methodology
2.1 Coordinate system
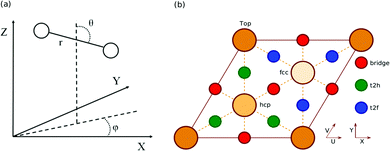
All calculations in this work are carried out using the BOSS model.10 This means that the atoms of the metal slab are fixed to their ideal lateral positions, and that we only take into account the six molecular degrees of freedom (DOF) of the impinging H2 (D2) molecule (see Fig. 1a). Three of the DOFs taken into account are the centre of mass (COM) coordinates X, Y and Z, where (X,Y) describes the lateral position of the molecule and Z describes the molecule–surface distance. The other DOFs are the H2 bond length r, the polar orientation angle with respect to the surface normal θ and the azimuthal angle ϕ. The geometry of the (111) face of an fcc metal together with its high symmetry sites is shown in relation to the coordinate system used in Fig. 1b.2.2 SRP DFT
We use periodic DFT calculations to construct PESs, testing DFs at the GGA, the meta-GGA (mGGA), and GGA + non-local correlation level, where non-local correlation refers to either vdW-DF1 non-local correlation96 or vdW-DF2 non-local correlation97 (see the types of DF defined in Table 1). In many cases we test a DF that is a SRP-DF for at least one of the four systems considered. In the present context a SRP-DF is constructed by taking a weighted average of a DF that overestimates the sticking probability, and one DF that underestimates the sticking probability for the system of interest.10 More specifically, the mixing often occurs for the exchange part of the DF, as was done for many of the previously developed SRP-DFs.11,13,16,26| Name | Type | Exchange | Correlation |
|---|---|---|---|
| B86SRP68-DF2 | vdW-DF | 0.68 B86r111 + 0.32 RPBE112 | vdW-DF297 |
| MS-B86bl12 | mGGA | MS-B86bl12 | revTPSS113 |
| MS-PBEl12 | mGGA | MS-PBEl12 | revTPSS113 |
| optPBE-DF1114 | vdW-DF | optPBE114 | vdW-DF196 |
| PBE115 | GGA | PBE115 | PBE115 |
| PBEα57-DF211 | vdW-DF | PBEα = 0.57116 | vdW-DF297 |
| PBEsol117 | GGA | PBEsol117 | PBE115 |
| RPBE112 | GGA | RPBE112 | PBE115 |
| SRP4862 | GGA | 0.52 PBE115 + 0.48 RPBE112 | PBE117 |
| SRPsol63-DF2 | vdW-DF | 0.63 PBEsol117 + 0.37 RPBE112 | vdW-DF297 |
| vdW-DF196 | vdW-DF | revPBE118 | vdW-DF196 |
| vdW-DF297 | vdW-DF | rPW86119 | vdW-DF297 |
The SRP-DFs developed in this work are all DFs in which the exchange part is taken at the GGA level, and the exchange correlation functional takes the following form:
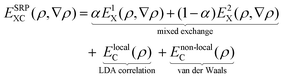 | (1) |
2.3 Construction of the PESs
A continuous representation of the PESs is obtained by the interpolation of DFT results calculated on a grid using the corrugation reducing procedure (CRP).120 The method we use is analogous to that used by Wijzenbroek et al.,41 but we used denser grids to represent the full six dimensional molecule–surface interaction potential and the three dimensional atom–surface interaction potential to further increase the accuracy of the resulting CRP120 PESs with respect to the underlying DFT calculations. Details are presented in the ESI.†2.4 Quasi-classical dynamics
The QCT calculations presented in this work are carried out on six dimensional PESs and assume quasi-classical initial conditions.68 This means that we take into account the quantum mechanical energies of the impinging H2 and D2 molecules in their initial rovibrational states. The method used is described more fully in ref. 121. The equations of motion are integrated using the method of Stoer and Bulirsch.122When simulating a molecular beam experiment 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories are propagated per energy point, and when calculating initial-state resolved reaction probabilities 50
000 trajectories are propagated per energy point, and when calculating initial-state resolved reaction probabilities 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories are propagated per energy point. All trajectories start in the gas phase, at Zgas = 8 Å. For all QCT calculations we use a time step of dt = 0.001 fs. Trajectories are assumed to result in reaction if r becomes bigger then some critical value rc (2.2 Å) and in scattering if Z becomes bigger then Zgas which is also the starting point of all trajectories.
000 trajectories are propagated per energy point. All trajectories start in the gas phase, at Zgas = 8 Å. For all QCT calculations we use a time step of dt = 0.001 fs. Trajectories are assumed to result in reaction if r becomes bigger then some critical value rc (2.2 Å) and in scattering if Z becomes bigger then Zgas which is also the starting point of all trajectories.
2.5 Quantum dynamics
Six dimensional quantum dynamics (QD) calculations are performed by solving the time-dependent Schrödinger equation,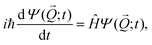 | (2) |
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ,t) denotes the nuclear wave function of H2 at time t with
,t) denotes the nuclear wave function of H2 at time t with ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) being the position vector. Furthermore we employ the following Hamiltonian in order to take into account the six degrees of freedom of H2:
being the position vector. Furthermore we employ the following Hamiltonian in order to take into account the six degrees of freedom of H2: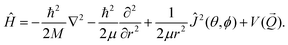 | (3) |
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ) is the six dimensional PES. The scattered wave packet is analysed using the scattering matrix formalism,125 yielding fully initial-state resolved S-matrix elements for vibrationally, rotationally, and diffractionally inelastic scattering. From the S-matrix elements the corresponding state-to-state probabilities
) is the six dimensional PES. The scattered wave packet is analysed using the scattering matrix formalism,125 yielding fully initial-state resolved S-matrix elements for vibrationally, rotationally, and diffractionally inelastic scattering. From the S-matrix elements the corresponding state-to-state probabilities 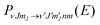 for scattering at the incident energy E can be obtained.66,67 Subsequently the sticking probability can be computed66,67 by subtracting the sum of the scattering probabilities from one.
for scattering at the incident energy E can be obtained.66,67 Subsequently the sticking probability can be computed66,67 by subtracting the sum of the scattering probabilities from one.
Further information on how we construct the initial wave packet can be found in Section S2 of the ESI.† Table S1 (ESI†) presents parameters describing all the initial wave packets used, and Table S2 (ESI†) shows the rovibrational states taken into account in the molecular beam simulations of sticking with the QCT and QD methods.
2.6 Computation of observables
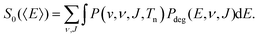 | (4) |
| P(v,ν, J,Tn)dv = Pflux(v;Tn)dv × Pint(ν, J,Tn). | (5) |
| Pflux(v;Tn)dv = Cv3e−(v−v0)2/α2dv | (6) |
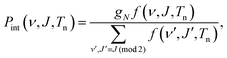 | (7) |
| f(ν, J,Tn) = (2J + 1) × e(−(Eν,0−E0,0)/kBTvib) × e(−(Eν,J−Eν,0)/kBTrot). | (8) |
In the QCT calculations presented in this work the probability distribution P(v, ν, J, Tn) is randomly sampled as described in ref. 121. All parameters describing molecular beam experiments used for the calculations presented here can be found in Table S3 (ESI†). The reaction probability is then computed by dividing the number of adsorbed trajectories, Nads, by the total number of calculated trajectories, N, i.e. Pr = Nads/N.
We compute initial-state selected but degeneracy averaged reaction probabilities, Pdeg(E, ν, J), as:
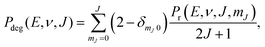 | (9) |
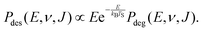 | (10) |
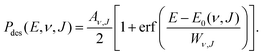 | (11) |
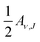 . Using eqn (11), E0(ν, J) also is the inflexion point of the reaction probability curve if the saturation value Aν,J corresponds to the absolute saturation value. Wν,J represents the width of the reaction probability curve.
. Using eqn (11), E0(ν, J) also is the inflexion point of the reaction probability curve if the saturation value Aν,J corresponds to the absolute saturation value. Wν,J represents the width of the reaction probability curve.
If the proportionality factor implicit in eqn (10) would also be measured in the experiment (for instance, because the exact state-selective flux would have been measured), it should be possible to directly extract absolute values of the initial-state selected reaction probabilities from the experiment by assuming detailed balance. In this case, the directly extracted Aν,J value would be the true saturation value of the reaction probability. These values could then be directly compared to computed degeneracy averaged initial-state resolved reaction probabilities (eqn (9)).
In practice, even if the prefactor in eqn (10) is not measured in associative desorption, it is still possible to extract normalized values from a wholly experimental procedure, if measured sticking probabilities are also available. This has been done for H2 + Cu(111)47,51 and D2 + Cu(111).45,47,62 In this method, which we call Method A1, essentially the sticking probability is described in terms of the initial-state selected probabilities extracted from the associative desorption experiments, thereby obtaining the saturation values describing the latter. Method A1 is described more fully in the ESI.†
If no sticking experiments are available, as for the H2 + Au(111) system also studied here, the experimentalists may chose not to normalize the extracted reaction probabilities in an absolute sense. However, the extracted reaction probabilities may still be normalized relative to one another. This was done in recent experiments on H2 and D2 + Au(111), in which Aν,J was set to one for (ν = 0,J = 6) H2 and for (ν = 0,J = 0) D2, and the Aν,J values for different (ν, J) states of H2 and D2, respectively, reflected the values of the reaction probabilities relative to these reference states.70 We will call this Method A2, where the A in A2 emphasizes that this method is also wholly experimental.
If no measured sticking probabilities are available for the system of interest, one may still choose to normalize reaction probabilities extracted from associative desorption experiments, but now with reference to theory.47,70 We label such methods with “B” to emphasize that the normalization is done with reference to theory. In the methods we are aware of, the experimentalists define a translational energy Emax(ν, J), which is the maximum translational energy for which the not yet normalized value can still be accurately extracted using eqn (10).47,70 At higher E this becomes difficult because the desorption flux becomes small due to the exponential factor in eqn (10), leading to too much noise in the determined Pdeg(E,ν, J). Parameters can then be described in two ways (Methods B1 and B2). Briefly, in Method B1 the saturation parameters are determined by setting them equal to the theoretical reaction probability computed for E = Emax(ν, J). The E1/2(ν, J) parameters is then determined as the energy at which the computed reaction probability equals half the saturation value. Method B2 aims to improve upon this. Method B1 was previously followed in experimental papers to enable comparison with theory for H2, D2 and HD desorbing from Cu surfaces,47 and for H2 and D2 desorbing from Au(111).70 Further details of Methods B1 and B2 are presented in the ESI.†
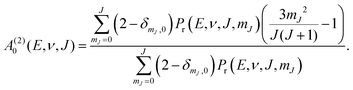 | (12) |
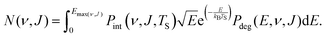 | (13) |
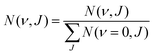 | (14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν = 0 can then calculated as:
ν = 0 can then calculated as: | (15) |
2.7 Computational details
All the electronic structure calculations were carried out by performing plane wave periodic DFT calculations using a user modified version of the Vienna Ab Initio Simulation Package127–130 (VASP). The modification of the computer package concerns an interface to VASP with the LibXC density functional library.131 The standard VASP projector augmented wave (PAW) potentials132 and vdW-DF correlation96,97 as implemented in VASP133,134 were used for all calculations at the GGA level except for the SRP48 calculations on Pt(111), for which the standard VASP ultrasoft pseudopotentials135 and PBE correlation115 were used. Calculations done using a mGGA use mGGA correlation (see Table 1).All calculations at the GGA level presented in this work have been carried out using a plane wave cutoff energy of 450 eV together with smearing of 0.2 eV using the Methfessel–Paxton method of order 1. The input parameters for calculations with a mGGA DF can be found in ref. 12. Lattice constants have been calculated using a four atom bulk unit cell and a 28 × 28 × 28 Monckhorst–Pack k-point grid. All metal slabs consist of six layers of which the bottom two layers were fixed at the ideal bulk interlayer distance. Slab relaxation has been carried out using a 1 × 1 supercell, a 32 × 32 × 1 Γ-centered k-point grid and a vacuum distance of 16 Å. PES calculations have been carried out using a 3 × 3 supercell, a 11 × 11 × 1 Γ-centered k-point grid and a vacuum distance of 16 Å.
3 Results
3.1 Electronic structure
| Cu | Ag | Au | Ni | Pd | Pt | |
|---|---|---|---|---|---|---|
| Exp. | −1.0%,56,58 −0.7%57 | −2.5%,137 −0.5%138 | 1.5%139 | −0.07%56 | 1.3%140 | 1.1%141 |
| SRP4810 | −1.3%10 | −0.6%19 | 0.6%142 | −1.0%20 | 0.0% | 1.0% |
| VdW-DF196 | −0.2% | 0.1% | 1.6% | −1.1% | 0.7% | 1.3% |
| vdW-DF297 | 0.0% | 0.5% | 2.1% | −1.1% | 0.8% | 1.5% |
| B86SRP68-DF2 | −0.4% | −0.1% | 1.3% | −1.1%20 | 0.7% | 1.2% |
| SRPsol63-DF2 | −0.4% | −0.2% | 1.4% | −1.1% | 0.6% | 1.0% |
| PBEα57-DF211 | −0.4% | 0.0% | 1.5% | −0.8%20 | 0.6% | 0.8% |
| optPBE-DF1114 | −0.8%41 | −0.2% | 1.0% | 0.2% | 0.8% | |
| MS-B86bl12 | −1.0% | −0.5% | 1.0% | 0.3% | 1.0% | |
| PBE115 | −0.3%143 | −0.2%143 | 1.0%143 | −0.5%143 | 0.9%143 | |
| PBEsol117 | −0.4%143 | −0.1%143 | 0.8%143 | 0.6%143 | 0.8%143 |
| Bridge | t2b | hcp | ξ | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| E b | r b | Z b | E b | r b | Z b | E b | r b | Z b | ||
| SRP4810,41 | 0.636 | 1.030 | 1.172 | 0.887 | 1.396 | 1.394 | 1.047 | 1.539 | 1.269 | 0.411 |
| B86SRP68-DF2 | 0.725 | 1.045 | 1.169 | 0.936 | 1.380 | 1.392 | 1.056 | 1.379 | 1.273 | 0.331 |
| SRPsol63-DF2 | 0.712 | 1.045 | 1.167 | 0.925 | 1.379 | 1.392 | 1.038 | 1.373 | 1.270 | 0.326 |
| PBEα57-DF2 | 0.720 | 1.063 | 1.142 | 0.934 | 1.385 | 1.390 | 1.035 | 1.373 | 1.268 | 0.315 |
| optPBE-DF141 | 0.712 | 1.053 | 1.165 | 0.915 | 1.382 | 1.396 | 1.070 | 1.427 | 1.271 | 0.358 |
| MS-B86bl12 | 0.683 | 0.997 | 1.205 | 0.895 | 1.351 | 1.391 | 1.079 | 1.369 | 1.266 | 0.396 |
Barrier heights and positions for H2 + Ag(111), Au(111) and Pt(111) are shown in Tables S5, S6 and S7 (ESI†) respectively. With respect to the H2 + Pt(111) system the most striking result is that only the PBEα57-DF211 and MS-PBEl12 DFs exhibit a double barrier structure for the top-to-bridge (t2b) geometrie whereas the other DFs tested do not. The PBEα57-DF211 SRP-DF is the only DF that predicts a negative early barrier to reaction for this reaction.
We have checked the fit accuracy of our CRP120 PES for the B86SRP68-DF2 DF for H2 + Cu(111) using ∼4900 randomly sampled geometries. Based on all the randomly sampled points taken together our CRP120 fit has a root mean square (rms) error of 31 meV. When only looking at the 3538 geometries that have an interaction energy of H2 with the surface lower then 4 eV the rms error reduces to 8 meV (∼0.2 kcal mol−1). Our CRP120 PES is thus highly accurate with respect to the underlying electronic structure calculations. Since the other PESs calculated for this paper have been constructed in the same manner, we presume their accuracy with respect to the electronic structure calculations to be similar, and high enough for our purposes.
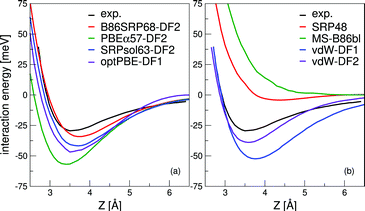 | ||
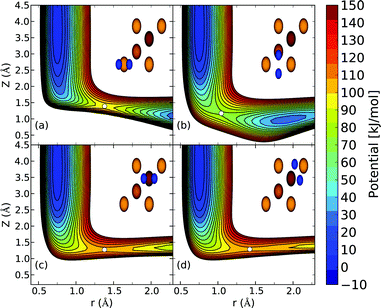
| Fig. 3 The computed interaction energy of H2 parallel to the Cu(111) surface above a top site (ϕ = 0°,θ = 90°) is compared with experimental results59 (black). Panel (a) shows the calculated van der Waals well for the B86SRP68-DF2 (red), PBEα57-DF2, SRPsol63-DF2 and optPBE-DF141 DFs, and panel (b) for the SRP48,10 MS-B86bl,12 vdW-DF196 and vdW-DF297 DFs. | ||
All van der Waals well depths and geometries for the systems and DFs investigated in this work are tabulated in Table S8 (ESI†). With respect to the van der Waals well depths for H2 + Ag(111), H2 + Au(111), and H2 + Pt(111) we find depths that are in good agreement with experimental work61,90,99,110 for the B86SRP68-DF2 DF.
3.2 Molecular beam sticking probabilities
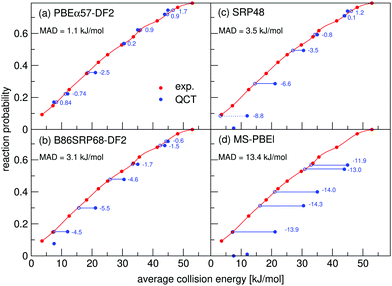
Molecular beam sticking probabilities computed with five DFs for H2 and D2 reacting on Cu(111) are shown in Fig. 4, comparing to experimental results of Auerbach and coworkers45,51 and Rendulic and coworkers.46 Fig. S5 (ESI†) shows the comparison with an additional experiment for the five DFs discussed here, namely for the pure D2 molecular beams of Auerbach and coworkers.45 The difference between theory and experiment is assessed by determining how far the theoretical result needs to be shifted along the incidence energy axis to be superimposed on a spline interpolated curve going through the experimental results. Values of the mean absolute deviation (MAD) are calculated as the mean of the absolute number of these shifts for a particular set of molecular beam experiments. From the MAD values it can be seen that all five DFs considered describe the experiments on H2 + Cu(111) shown in Fig. 4 with chemical accuracy. Fig. 5 shows comparisons to two additional sets of molecular beam experiments of Auerbach and coworkers45,51 for H2 reacting on Cu(111) for a more limited set of DFs.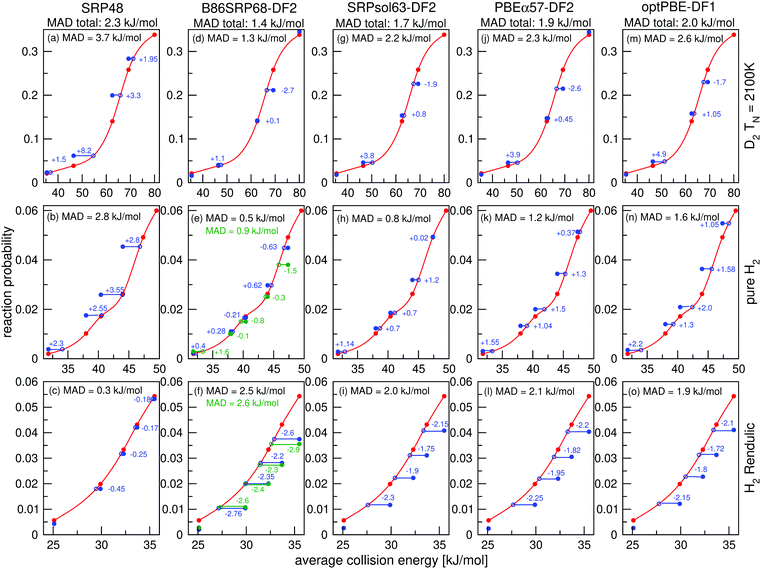 | ||
| Fig. 4 Molecular beam sticking probabilities for H2 and D2 reacting on Cu(111) for three sets of molecular beam experiments, as computed with five SRP-DFs. Experimental results are shown in red,45,46,51 QCT results are shown in blue, and QD results are shown in green in two panels (panels e and f). The values next to each data point denote the shift along the translational energy axis from the computed reaction probability to the interpolated experimental reaction probability in kJ mol−1. The MAD values are the mean value of the energy differences for each experiment. | ||
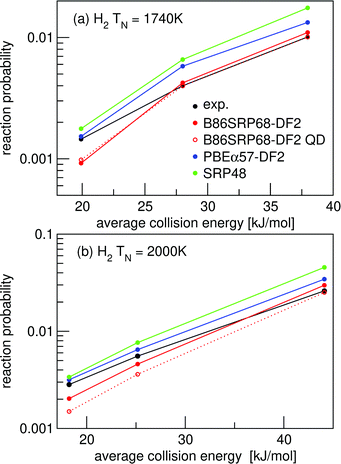 | ||
| Fig. 5 Molecular beam sticking probabilities for H2 reacting on Cu(111). Experimental values are shown in black,51 computed reaction probabilities are shown for the B86SRP68-DF2 (red), PBEα57-DF2 (blue), and the SRP48 (green) DFs. The solid lines correspond to QCT calculations, the dashed lines to QD calculations. | ||
For the B86SRP68-DF2 DF QD results are also shown for the experiments concerning H2 in Fig. 4e, f and in Fig. 5. Note that in these figures the QCT results are based on more rovibrational states than those included in the QD calculations (see Table S2, ESI†). In Fig. 6 we also explicitly compare QCT and QD results obtained while averaging over the same rovibrational states, and compare those to the QCT results shown in Fig. 4e, f and in Fig. 5. Fig. S6 (ESI†) shows the same data as shown in Fig. 6, but with the reaction probability on a log-scale. Table S9 (ESI†) displays the computed MADs for all experiments considered.
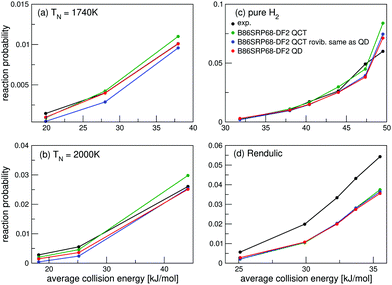 | ||
| Fig. 6 Molecular beam sticking probabilities for H2 reacting on Cu(111). Experimental values are shown in black,51 B86SRP68-DF2 QCT results are shown in green, B86SRP68-DF2 QCT results based on the same rovibrational states as taken into account in the QD calculations in blue, and B86SRP68-DF2 QD results in red. | ||
Fig. 7 shows molecular beam sticking experiments for D2 reacting on Ag(111). Experimental results of Hodgson and coworkers144 are also shown. The calculated results are obtained using the pure D2 molecular beam parameters of Auerbach and coworkers45 obtained from experiments on Cu(111). The DFs treated in this work, as well as the MS-PBEl mGGA,12 reproduce the experiment to almost within chemical accuracy. The SRP48 DF19,62 yields the worst and the MS-PBEl12 the best performance.
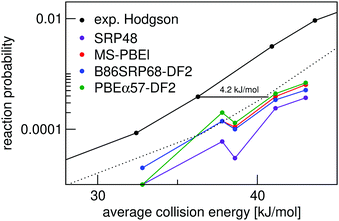 | ||
| Fig. 7 Molecular beam sticking probability as a function of the average incidence energy for D2 reacting on Ag(111). Experiment is shown in black.144 QCT results are shown for the following DFs: SRP48 (purple),19 MS-PBEl (red),12 B86SRP68-DF2 (blue), and PBEα57-DF2 (green). The dotted line represents the experimental curve shifted by 4.2 kJ mol−1, denoting the limit to chemical accuracy. | ||
In Fig. 8 molecular beam sticking probabilities for D2 reacting on Pt(111) for three DFs are shown, comparing to the molecular beam experiments of Luntz et al.64 A comparison to the experimental results of Cao et al.60 is shown in Fig. S7 (ESI†). For the comparison to the experiment of Luntz et al.64 the molecular beam parameters of Groot et al.145 are used, while Cao et al.60 have actually reported their molecular beam parameters. Fig. 8a shows that the B86SRP68-DF2 DF describes the experiment64 with overall chemical accuracy, albeit that the energy shifts are larger than 4.2 kJ mol−1 at the lowest energies. However, Fig. S7a (ESI†) shows that the experiments of Cao et al.60 are not described to within chemical accuracy using the B86SRP68-DF2 DF. The SRP48 and MS-PBEl DFss are not able to describe either experiment to within chemical accuracy.
 | ||
| Fig. 8 Molecular beam sticking probabilities for D2 reacting on Pt(111) for (a) the PBEα57-DF2, (b) B86SRP68-DF2, (c) SRP48 and (d) MS-PBEl DFs. Experimental results are shown in red,64 QCT results in blue. The values next to each data point denote the shift along the translational energy axis from the computed reaction probability to the interpolated experimental reaction probability. | ||
The parameters describing the beams used in the experiment can be found in Table S3 (ESI†). MADs and mean signed deviations (MSDs) for all simulated molecular beam experiments considered here can be found in Table S9 (ESI†).
3.3 Initial-state resolved reaction probabilities
Initial-state resolved reaction probabilities will be presented for H2 reacting on both Cu(111) and Ag(111). Fig. 9 shows fully initial-state resolved reaction probabilities for H2 reacting on Cu(111), as obtained with the QD and QCT methods. At the level of degeneracy averaged reaction probabilities the agreement is very good (Fig. 9a and c), but the QD method predicts a slightly larger orientational dependence of the reaction probability (Fig. 9b). Fig. S8 (ESI†) shows a comparison of degeneracy averaged reaction probabilities obtained using the QD and QCT method for the 20 rovibrational states included in the QD calculations. The agreement between the QD and QCT method is very good for all states, though there are some differences for the J < 3 rovibrational states.Fig. 10 shows degeneracy averaged initial-state resolved reaction probabilities for H2 and D2 reacting on Ag(111). A comparison is made to reaction probabilities extracted from associative desorption experiments assuming detailed balance.77,78 The agreement with experiment seems best for D2 and when using the MS-PBEl mGGA.12 Note, however, that the Pdeg(E, ν, J) extracted from experiments were not normalized, but simply assumed to saturate at unity, making it hard to perform an accurate comparison with experiment.
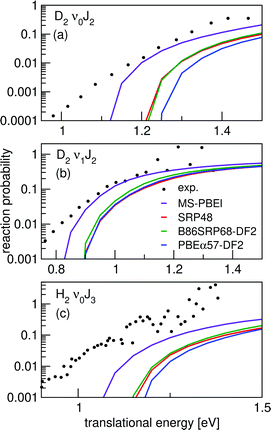 | ||
| Fig. 10 Initial-state selected reaction probabilities Pdeg(E, ν, J) computed for H2 (D2) + Ag(111) using the MS-PBEl (purple), SRP4819 (red), B86SRP68-DF2 (green) and the PBEα57-DF2 (blue) DFs are shown as a function of translational energy, comparing with values with values extracted from associative desorption experiments.77,78 Results are shown for D2 (ν = 0,J = 2) (a), D2 (ν = 1,J = 2) (b), and H2 (ν = 0,J = 3) (c). | ||
3.4 E 1/2(ν, J) parameters
E 1/2(ν, J) parameters calculated for H2 (D2) + Cu(111) using Methods A1 and B1 are shown in Fig. 11 and 12, respectively, also comparing with experiment.47 Using Method B1, the DFs that include non-local correlation qualitatively reproduce the rotational hindering observed experimentally for (ν = 0), i.e. the increase of E1/2(ν, J) parameters with increasing J for low J before decreasing with increasing J. A third degree polynomial has been fitted to the calculated E1/2(ν, J) parameters, which describes the dependence of the E1/2(ν, J) parameters on J. The polynomials are shown, without the energy axis offset resulting from the fit to a third degree polynomial, in Fig. S9 (ESI†).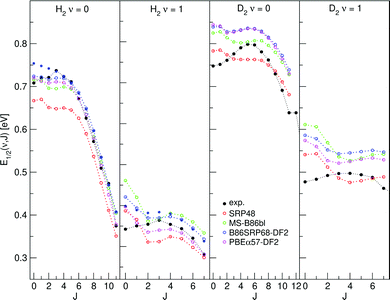 | ||
| Fig. 11 E 1/2(ν, J) parameters as a function of J obtained using Method A1 for H2 and D2 reacting on Cu(111). Red circles represent the SRP48 values,62 green circles the MS-B86bl values,12 blue circles represent the B86SRP68-DF2 values with the solid blue circles corresponding to QD calculations, magenta circles represent the PBEα57-DF2 values, and solid black circles represent experimental results.47 | ||
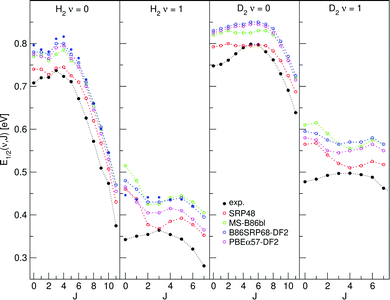 | ||
| Fig. 12 E 1/2(ν, J) parameters as a function of J obtained using Method B1 for H2 and D2 reacting on Cu(111). Red circles represent the SRP48 values,62 green circles the MS-B86bl values,12 blue circles the B86SRP68-DF2 values with the solid blue circles corresponding to QD calculations, magenta circles represent the PBEα57-DF2 values, and solid black circles represent experimental results.47 | ||
E 1/2(ν, J) parameters calculated for H2 (D2) + Au(111) using Method B2 are shown in Fig. 13, also comparing to experiment.70
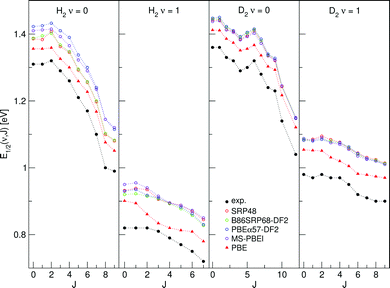 | ||
| Fig. 13 E 1/2(ν, J) parameters as a function of J obtained using Method B2 for H2 and D2 reacting on Au(111), experimental values are shown in black.70 Red circles represent the SRP48 values,142 green circles the B86SRP68-DF2 values, blue circles the PBEα57-DF211 values, purple circles the MS-PBEl12 values and red triangles the PBE values.142 | ||
Accompanying MAD and mean signed deviations (MSD) values of the computed E1/2(ν, J) parameters from the experimental values are presented in Table S10 (ESI†) for both H2 (D2) + Cu(111) and H2 (D2) + Au(111).
3.5 Rotational quadrupole alignment parameters Cu(111)
In Fig. 14 we compare calculated rotational quadrupole alignment parameters using the QCT method to experimental ones for D2 desorbing from Cu(111).49 Note that a positive A(2)0(ν, J) indicates a preference for parallel reaction, a negative value a preference for perpendicular reaction, and zero means the reaction proceeds independent of D2 orientation. We observe only a monotonous increase of the rotational quadrupole alignment parameters with decreasing translational energy, indicating that at translational energies close to the reaction threshold molecules prefer to react in a parallel orientation.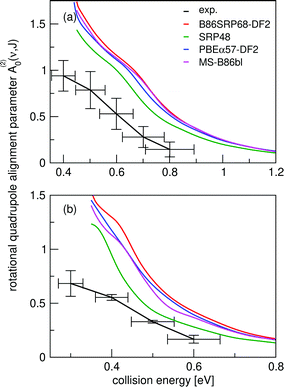 | ||
| Fig. 14 Panel (a) shows rotational quadrupole alignment parameter, A(2)0(ν = 0,J = 11), and panel (b) shows the rotational quadrupole alignment parameter A(2)0(ν = 1,J = 6) for D2 reacting with Cu(111). Experimental results are shown in black.49 Theoretical results using the QCT method are shown for the B86SRP68-DF2 (red), SRP4810 (green), PBEα57-DF211 (blue), and the MS-B86bl12 (magenta) DFs. | ||
3.6 Inelastic scattering of H2 from Cu(111)
Vibrationally inelastic scattering probabilities, P(ν = 0,J→ν = 1,J = 3) for H2 scattering from Cu(111) are shown in Fig. 15 for scattering from the initial J = 1, 3 and 5 states. Results were obtained using the QD method. The onset of the vibrational inelastic scattering probabilities is correlated with the onset of reactivity for each particular state. The DFs yield similar results for the initial (ν = 0,J = 5) rovibrational state, except that the SRP48 DF yields smaller vibrational excitation probabilities for E > 0.8 eV (panel c). For the (ν = 0,J = 1) and (ν = 0,J = 3) initial rovibrational states the differences are larger (panels a and b).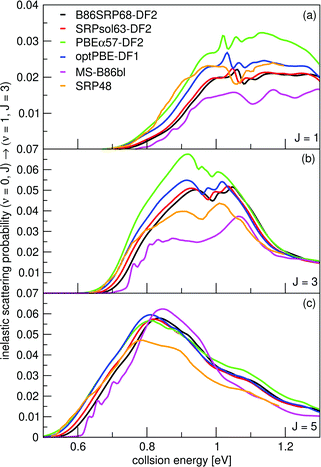 | ||
| Fig. 15 Vibrationally inelastic scattering probabilities for P(ν = 0,J → ν = 1,J = 3). Shown are results for J = 1 (a), J = 3 (b), and J = 5 (c). QD results for the following DFs are shown: B86SRP68-DF2 (black), SRPsol63-DF2 (red), PBEα57-DF2 (green), optPBE-DF1 (blue), MS-B86bl (magenta), and SRP4824 (orange). | ||
Fig. 16 shows the ratio of rotationally elastic and inelastic scattering probabilities P(ν = 1,J = 0 → ν = 1,J = 2)/P(ν = 1,J = 0 → ν = 1,J = 0) computed with two DFs and comparing with experiment.54 Note that both curves need to be shifted by 40 meV in order to overlap with the onset of the experimental curves measured for a surface temperature of 300 K.54
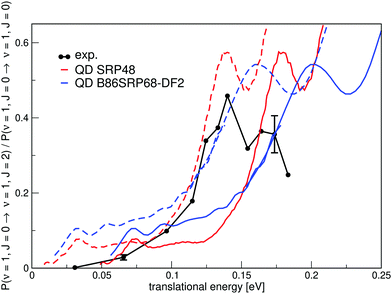 | ||
| Fig. 16 A comparison of the ratios of theoretical and experimental rotationally inelastic scattering probabilities P(ν = 1,J = 0 → ν = 1,J = 2)/P(ν = 1,J = 0 → ν = 1,J = 0) for H2 impinging on Cu(111). Experimental results are shown in black54 with the error bars representing maximum deviations in repeated measurements constituting estimated standard deviations. QD results for the SRP48 DF are shown in red10 and QD results for the B86SRP68-DF2 DF are shown in blue. Dashed lines constitute the calculated ratio's of rotationally inelastic scattering shifted by 40 meV. | ||
3.7 Rovibrational state populations of H2 and D2 desorbing from Au(111)
Fig. 17 shows rovibrational state populations of H2 and D2 desorbing from Au(111). Here we plot ln[N/gN(2J + 1)] versus the rotational energy, with N being the total population for each (ν, J) state (see eqn (13)) and gN(2J + 1) being the statistical weight for rotational level J.70 For D2, gN = 2 for even J and 1 for odd J; for H2, gN = 1 for even J and 3 for odd J. In such a plot a Boltzmann distribution will appear as a straight line.70 Here we integrate eqn (13) up to Emax(ν, J).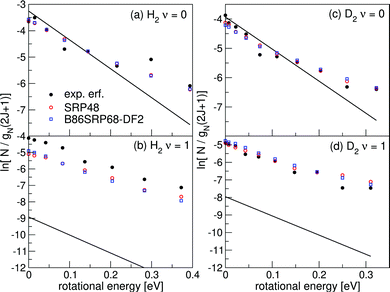 | ||
| Fig. 17 Rovibrational state populations of H2 and D2 desorbing from Au(111) are shown versus the rotational energy. Experimental results are shown in black,70 theoretical results are shown in red for the SRP48 DF142 and in blue for the B86SRP68-DF2 DF. The straight lines represent Boltzmann distributions for the surface temperature of the experiment. | ||
Fig. S10 (ESI†) shows the rovibrational state populations of H2 desorbing from Au(111) as reported in by Shuai et al.70 together with the values we calculate using eqn (13) with an upper integration limit of 5 eV to be in line with the procedure used by Shuai et al.70 as outlined in a private communication.146
Table 4 shows the ratio of the fluxes of molecules desorbing in the first excited and in the vibrational ground state for both H2 and D2 desorbing from Au(111). The ratios are calculated using eqn (15) and are solely based on the rovibrational states for which results are shown in Fig. 17. Again, here we integrate eqn (13) up to Emax(ν, J).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν = 0 molecules desorbing from Au(111) as measured in experiments70 and computed with the SRP48 and B86SRP68-DF2 DFs
ν = 0 molecules desorbing from Au(111) as measured in experiments70 and computed with the SRP48 and B86SRP68-DF2 DFs
| H2 | D2 | |
|---|---|---|
| Exp.70 | 0.552 | 0.424 |
| SRP48 | 0.250 | 0.473 |
| B86SRP68-DF2 | 0.249 | 0.522 |
4 Discussion
Our aim has been to develop new SRP-DFs that include non-local correlation for the H2 + Cu(111) system, and afterwards assess the transferability of these DFs to other systems. The reason for taking this approach, instead of fitting the DF to best reproduce experiments on all systems shown in the Results section, is that numerous experimental results are available for the reaction of H2 and D2 on Cu(111).45–55 For the non-copper systems discussed in this work experimental results are sparse,17,70 and there is discussion about the validity of the available parameters describing the molecular beams used in the experiments on H2 (D2) + Ag(111) and Pt(111).19,60,64,65The good agreement between different dissociative chemisorption experiments45,46,51 on the reaction of H2 (D2) + Cu(111), and their resultant constraints for a to be developed SRP-DF, provides an opportunity to design the best performing SRP-DF for this system yet reported. The DF that best describes sticking probabilities obtained from dissociative chemisorption molecular beam experiments for H2 (D2) + Cu(111), will be considered the best performing DF. We choose this definition since our calculations are carried out using the BOSS model. From the literature it is known that the BOSS model works rather well for activated H2 dissociation on cold metals.23,27–29,62,147
Comparisons to experimental results obtained from associative desorption experiments will not be included in the assessment of the quality of the newly constructed SRP-DFs for two reasons. The first reason is that associative desorption experiments are carried out at high surface temperatures. Since we have carried out calculations using the BOSS model we neglect surface temperature effects. The second reason is that in obtaining state-specific information from associative desorption experiments requires the assumption of detailed balance, which is strictly speaking not applicable if an electronically non-adiabatic process is involved and energy exchange with the surface is allowed. Since neither process can be ruled out we feel it safer to base our judgement on the sticking experiments. We still discuss the valuable experimental results on associative desorption since they do provide insight into the reaction dynamics. However, as we will discuss, it is fraught with difficulty to make a direct quantitative comparison between calculations on dissociative chemisorption and associative desorption experiments without improving our dynamical model by incorporating phonons and ehp excitations, which is challenging to do.148–150 Recently, this has been done for H2 + Cu(111)75 using ab initio molecular dynamics with electronic friction (AIMDEF) calculations employing the PBE115 DF. It is hard to draw firm conclusions from this work on the effect of electron–hole pair excitation as the statistical accuracy of the AIMDEF calculations is limited through the small number of AIMDEF trajectories.
4.1 Metal properties
Using a GGA DF for a theoretical description of gas surface dynamics is in most cases a compromise between a good description of the metal slab and a good description of the interaction of a molecule with the metal slab.151 Table S4 (ESI†) shows the calculated lattice constants for all DFs investigated in this work. Highly accurate results are only achieved using PBEsol117 and our previously developed mGGA MS-B86bl.12 All our candidate SRP-DFs yield improved results over the vdW-DF1,96 vdW-DF2,97 and SRP4810 DFs. We generally see a large improvement in the calculated lattice constant if a DF has at least one component with a μ value closer to the second gradient expansion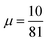 , as used in the PBEsol,117 MS-B86bl,12 SRPsol63-DF2 and the B86SRP68-DF2 DFs.
, as used in the PBEsol,117 MS-B86bl,12 SRPsol63-DF2 and the B86SRP68-DF2 DFs.
When looking at the relaxations of the interlayer distance of the two top most layers relative to the bulk interlayer distance (Table 2) no clear trend can be discerned. The best performing DF is again MS-B86bl.12 We do note that the SRP48 DF appears to produce top interlayer distances that on the whole are closer to the experimental values than DFs obtained combining GGA exchange DFs with vdW-DF2 non-local correlation. The reason for this is unclear.
4.2 Static PES properties
The experimental van der Waals well depth that has been measured for H2 + Cu(111)59 can provide us with a constraint when fitting a new SRP-DF for this system. The new SRP-DFs we present here are B86SRP68-DF2 and SRPsol63-DF2 (Table 1). The two original van der Waals DFs, namely vdW-DF196 and vdW-DF2,97 yield wells that are too deep, especially for vdW-DF1,96 as also found in earlier work152 (Fig. 3b, see also Table S8, ESI†). The two previous SRP-DFs for this system produce a very tiny (SRP4810) or no (MS-B86bl12) van der Waals well at all (Fig. 3b). Of the four DFs considered in Fig. 3b, the vdW-DF297 DF produces the best results. Other exploratory calculations carried out by us showed that using vdW-DF196 correlation yields van der Waals wells that are much to deep and too close to the surface, although they are not shown here. The better performance of vdW-DF2 correlation is most likely due to the large-N asymptote correction used in this DF.97Fig. 3a shows the same van der Waals well depth for the SRP-DFs that include vdW-DF2 correlation, and one SRP-DF that includes vdW-DF1 correlation. These four DFs are all chemically accurate with respect to the reactivity of H2 on Cu(111), as can be seen from the MAD values in Fig. 4. The PBEα57-DF2 DF has originally been fitted to reproduce experiments for H2 (D2) + Pt(111),11 and the optPBE-DF1114 DF has previously been shown to be chemically accurate H2 (D2) + Cu(111).41 The exchange part of the optPBE-DF1 DF was optimized to reduce intermediate range effects to avoid double counting when combining it with non-local vdW-DF1 correlation.114 It is clear that the choice of exchange functional greatly impacts the depth and position of the van der Waals well. The difference between the depths of the deepest and the shallowest van der Waals well obtained with the non-standard DFs using vdW-DF2 non-local correlation97 (Fig. 3a, 23.4 meV) is greater than the difference between the depths of the vdW-DF1 and vdW-DF2 wells (Fig. 3b, 13.4 meV, see also Table S8, ESI†). It can also been seen that going from PBEα57-DF2 to SRPsol63-DF2 the calculated van der Waals well more closely resembles experiment.59 The closest agreement with experiment is achieved using the B86SRP68-DF2 DF.
All van der Waals wells computed by us are tabulated in Table S8 (ESI†), also comparing with experimental van der Waals wells that have been reported for H2 + Cu(111),59,61 H2 + Ag(111),90 H2 + Au(111)61 and H2 + Pt(111).99,110 With respect to the Cu(111) well depth the experimental results are in reasonable agreement with each other. However, the position reported by Harten et al.61 is somewhat closer to the surface. This difference in the Z dependence of the van der Waals well can be attributed to ambiguities in the bound state level assignments from the Feshbach resonances in the earlier experiment,104 and it has been remarked that the results obtained later59 are in fact also consistent with the earlier measurements.104 Additionally we suspect that the reported van der Waals wells for H2 + Ag(111)90 and H2 + Au(111)61 might possibly be too close to the surface104 for the same reason. This drawback of using the RMSA technique98 might be alleviated by redoing the potential inversion on the basis of the original data on Feshbach resonances with more advanced theoretical models,153e.g., using an analysis in which the molecule–surface potential is not laterally averaged. In yet a different approach, instead of using the RMSA approach98 Poelsema et al.110 presented a combined thermal energy atom scattering/thermal desorption spectroscopy (TEAS/TDS) study of the H2 + Pt(111) system, obtaining van der Waals well geometries that were subsequently accurately reproduced by theory.11 For the H2 + metal(111) systems studied here it would certainly be advantageous if additional experimental data were to become available addressing the van der Waals interaction, using either a sophisticated analysis of results for RMSA studies or through combined TEAS/TDS studies. New experiments would allow for a better comparison between theory and experiment with respect to the predictions obtained by the inclusion of non-local correlation in DFT calculations on the systems addressed here.
We can however say that the B86SRP68-DF2 DF yields van der Waals well depths that agree well with experiments for the highly activated systems H2+ Cu(111), H2 + Ag(111) and H2 + Au(111). For the weakly activated H2 + Pt(111) system the B86SRP68-DF2 appears to somewhat underestimate the depth of the van der Waals well, while the SRP DF for this system (PBEα57-DF2) yields a value in the range of the experimental values.
4.3 Molecular beam sticking
It is clear from the total MAD values that all DFs evaluated in Fig. 4 are chemically accurate with respect to the three sets of molecular beam experiments for H2 (D2) + Cu(111) shown in Fig. 4, and that the agreement between theory and experiment is good for all molecular beam conditions. The theoretical results shown here were obtained using the BOSS model. The experiments of Michelsen et al.45 and Rettner et al.53 considered here employed a low surface temperature of 120 K, the experiment of Berger et al.46 was reportedly done on a ‘cold’ surface, and from the literature it is known that the BOSS model works well for activated H2 dissociation on cold metals.23,26–29 Another advantage of fitting a SRP-DF to these sets of molecular beam experiments is that they cover both H2 and D2 for very different experimental conditions with respect to the nozzle temperature, the average collision energy, and the width of the velocity distributions.10
The B86SRP68-DF2 DF exhibits a MAD of 1.4 kJ mol−1 for the experiments shown in Fig. 4, which is the lowest value obtained with the five DFs discussed. Of the DFs that include non-local correlation the B86SRP68-DF2 DF also performs best with respect to the calculated lattice constants, as can be seen in Table S4 (ESI†). In addition it performs best with respect to the shape and depth of the van der Waals well. We therefore select the B86SRP68-DF2 DF as the new, and most accurate, SRP-DF for the H2 + Cu(111) system. From this point onward we will mainly focus on the results obtained with the newly selected B86SRP68-DF2 DF and the PBEα57-DF211 DF, and on how the performance of these two DFs compares to that of the original SRP4810 DF and of our previously developed mGGA DFs.12
In the ESI† one additional comparison to experiment is made in Fig. S5, concerning pure D2 molecular beams.45 This comparison highlights a limitation of assessing the quality of a candidate SRP-DF by computing the mean distance along the incidence energy axis from the computed S0 value to interpolated experimental values. In this experiment the average translational energy does not monotonically increase with increasing nozzle temperature. Due to the high sensitivity of the sticking probability to the width of the velocity distribution of the molecular beam, the sticking probability also does not monotonically increase with the average translational energy. In Fig. S5 (ESI†) the application of our quality assessment strategy leads, in some cases, to large deviations with respect to the interpolated experimental results (note, however, that only for one data point and for one DF chemical accuracy was not achieved, see Fig. S5c, ESI†). Our quality assessment strategy works best if the reactivity increases monotonically with increasing average translational energy.
Fig. 6a and b show that for narrow low average translational energy molecular beams51 the QD method predicts slightly larger sticking probabilities compared to QCT sticking probabilities calculated from the same set of rovibrational states. This small gap between QD and QCT sticking probabilities based on the same set of rovibrational states is slightly bigger then what was obtained for H2 + Cu(211) when using the SRP48 DF.36 Though this suggests that quantum effects might play a small role in the dynamics, it is also possible that the slightly higher sticking probability predicted by QD is due to the underlying reaction probability curves for specific included rovibrational states showing more structure than for H2 + Cu(211).36 Since the molecular beam sticking probabilities are very small in Fig. 6a and b, they could be very sensitive to increased structure (and noise) in the underlying reaction probability curves. We shall further discuss the differences between fully initial-state resolved QD and QCT reaction probabilities in Section 4.6.
Fig. 6c and d show very good agreement between QD and QCT results, also for the QCT results that were based on more initial rovibrational states. Only for the highest nozzle temperature points in Fig. 6c (see Table S3, ESI†) taking into account more initial rovibrational states in the QD than those listed in Table S2 (ESI†) might be advisable. This is also the reason that QD now predicts a somewhat lower sticking probability than QCT in Fig. 4e. The QD and QCT results based on the same set of initial rovibrational states in Fig. 6c and d are however in good agreement at these high nozzle temperature points, indicating that for all but the lowest average translational energies H2 + Cu(111) is well described quasi-classically.
Note that for a nozzle temperature of 2000 K we take into account all rovibrational states that have a Boltzmann weight >0.001. Highly excited rovibrational states, either with high ν, high J, or both, yield high reaction probabilities at low translational energies, therefor the effect of not taking into account these rovibrational states might be larger than expected from their Boltzmann weight. It is however computationally very expensive to take into account all initial rovibrational states that have a Boltzmann weight >0.001 at a nozzle temperature of 2300 K in the QD calculations, i.e. the nozzle temperature for the point in Fig. 6c where the QCT results and the QCT results based on the same, smaller, set of initial rovibrational states as the QD calculations diverge most. Doing this would nearly double the amount of wave packet calculations, and these additional calculations would also require larger basis sets.
The discrepancy between theory and experiment at low incidence energies for the SRP48 and B86SRP68-DF2 DFs most likely arises because these DFs exhibit a too high early barrier to reaction at the top site minimum barrier geometry (see Table S7, ESI†). These two DFs also do not posses the double barrier structure for the t2b site that the PBEα57-DF2 DF predicts. The MS-PBEl functions does predict a double barrier structure for the t2b site. The early t2b barrier predicted by the MS-PBEl DF is however very high when compared to results obtained with the other DFs, which is most likely the root cause of its poor performance for this system.
The molecular beam experiments of Cao et al.60 are not as well described by the B86SRP68-DF2 DF, as can be seen in Fig. S7 (ESI†). However we note that the increase of the MAD value in going from Fig. 8a to Fig. S7a (ESI†) is similar in size to what was reported for the PBEα57-DF2 DF65 (see Table S9, ESI†). Earlier work from our group has shown that the experimental results of Luntz et al.64 and Cao et al.60 are in good agreement with each other for the lower incidence energies but somewhat diverge for the higher incidence energies.65 The possible origins of the discrepancy between these two sets of experimental data are discussed in ref. 65. Here it was surmised that at high average incidence energies the reaction probabilities of Cao et al.60 are most likely somewhat underestimated compared to the results of Luntz et al.64 because the average incidence energies are somewhat underestimated in the experiment of Cao et al.60
Although we are not yet able to describe the molecular beam experiment with chemical accuracy, the improvement of the DFs that include non-local correlation over the SRP48 DF again suggests that non-local correlation is an important ingredient for constructing SRP-DFs describing H2 + metal systems that incorporate GGA exchange. The MS-PBEl mGGA12 does not include non-local correlation but performs similarly well as the GGA based SRP-DFs that do include non-local correlation. Perhaps further improvement is possible by adding non-local correlation to the MS-PBEl DF.
4.4 Associative desorption
In this work we have not included MDEF calculations in which the effect of ehp excitations is modeled as a classical friction force. In our previous work36 the MDEF method shifted the E1/2(ν, J) parameters to slightly higher values since, again, we model an associative desorption experiment using a dissociative chemisorption calculations. Including the effect of ehp excitations in the dynamics here then has a similar effect in both cases, and shifts the E1/2(ν, J) parameters to slightly higher energies. However, as mentioned in our previous work,36 if ehp excitations are important then assuming detailed balance to extract degeneracy averaged reaction probability curves is, strictly speaking, not correct. More specifically, we would expect that if we applied electronic friction to the simulation of an associative desorption experiment in the manner discussed here, the predicted translational energy distributions would shift to higher energies as opposed to lower energies as expected in a direct simulation of associative desorption. In other words: extracting E1/2(ν, J) parameters from dissociative chemisorption calculations applying electronic friction would shift our E1/2(ν, J) parameters to higher energies instead of the expected lower energies, because the effective barrier would go up. However, we note that the MDEF calculations in our previous work36 only shifted the trend in E1/2(ν, J) parameters to slightly higher values on the energy axis and did not influence the observed trend in their J-dependence. This is in accordance with very recent direct simulations of associative desorption of H2 from Cu(111)75 using AIMD and AIMDEF calculations and the PBE DF, which find little effect of ehp excitations modeled at the local density friction approximation (LDFA)154 level.
In Section 4.10 we will further discuss how a combined analysis of dissociative chemisorption and associative desorption experiments might be used in the future to determine a possible fingerprint of non-adiabatic effects.
4.4.1.1 E 1/2(ν, J) parameters Cu(111). The comparison of the measured E0(ν, J) parameters values with the E1/2(ν, J) parameters computed using Method B1 is shown in Fig. 12. The Emax(ν, J) parameters needed in this method (see eqn (S4), ESI†) were taken from Tables S4 and S6 of ref. 47. The comparison of the experimental E0(ν, J) parameters with theoretical E1/2(ν, J) parameters extracted using Method A1 is presented in Fig. 11. In this method we used A = 0.325 for H2 and A = 0.513 for D2, as obtained in ref. 47.
Table S10 (ESI†) presents MAD and MSD values obtained with both methods. The following conclusions can be drawn: for almost all DFs Method A1 (based fully on experiments) yields the lowest MAD and MSD values. The only exception occurs for H2 + Cu(111) when using the SRP48 DF, for which Method B1 gives a lower MAD value (41 meV), although the difference with Method A1 (43 meV) is quite small. From this point of view, Method A1 works better.
The use of Method A1 for H2 would seem to yield conclusions that are more consistent with the conclusions from the comparisons of the sticking probabilities. Specifically, the mGGA DF and the DFs containing non-local van der Waals correlation all perform better than SRP48 DF for H2. Nonetheless, SRP48 performs best for D2, regardless of whether Method A1 or B1 is used. We also note that the better behavior of the other DFs in procedure A1 is to some extent suspect due to the rather low A value employed for H2 (0.325). This A value is much lower than the A value extracted for D2 in Method A1 (0.513). This may well be a simple artifact resulting from the method followed: the A value determined for D2 is likely to be more accurate because the sticking experiments were done for a kinetic energy up to 0.83 eV,45 whereas the sticking experiments for H2 only went up to about 0.5 eV.51 This suggest that the A-value for D2 (Fig. S1c, ESI†) is much more accurate than for H2 (Fig. S1a, ESI†), and it is not clear why the A value for H2 should differ much from it. Furthermore, the A value established for H2 in Method A1 is much lower than the A-values established for H2 in Method B1 (see also Fig. S1a and c, ESI†), while for D2 the A values extracted with the two methods resemble each other, and the A values extracted with Method B1 for H2, much more (see Fig. S1b–d, ESI†).
Finally, we note at this stage the E1/2(ν, J) parameters computed using Method A1 do, in general, not reproduce the subtle trend found experimentally that the E0(ν, J) parameters first increase somewhat with J (see Fig. 11) (attributed to rotational hindering45,47,51).
The E1/2(ν, J) parameters calculated using Method B1 (especially the ones calculated with DFs incorporating non-local van der Waals correlation) better reproduce this subtle rotational hindering effect (Fig. 12). The reasonable performance of Method B1 is also clear from Fig. S9 (ESI†), which presents a third degree polynomial fit to the E1/2(ν, J) parameters as a function of J obtained using the B1 method. The polynomial fits are shown without the energy axis offset. DFs that include non-local correlation reproduce the subtle rotational hindering effect, DFs that do not include non-local correlation do not or hardly show rotational hindering. Additionally, for H2, the agreement with the experimental dependence of the E0(ν, J) parameters on J improves when using the QD method for vibrationally exited molecules.
That DFs including non-local correlation better reproduce the subtle rotational hindering effect with the use of Method B1 is wholly due to the rovibrational state dependence of the Emax(ν, J) parameters. The extracted degeneracy averaged reaction probabilities in fact monotonically increase with increasing J (Fig. S8, ESI†), and this is true for all DFs used in this work. Reproducing rotational hindering based on these degeneracy averaged reaction probability curves is therefore not possible when selecting the same A value for all rovibrational states, as done with Method A1.
The E1/2(ν, J) parameters calculated using both Methods A1 and B1 do reproduce the clear trend (Fig. 11 and 12) that at high J the E0(ν, J) parameters decrease with J (attributed to energy transfer from rotation to the reaction coordinate as the rotational constant decreases when the molecule stretches to reach the dissociation barrier25,36,126).
We are aware of one single PES that does reproduce the rotational hindering effect as observed in the experiment, namely the LEPS PES39 used by Dai and Light37 for six-dimensional QD calculations. As discussed in the ESI,† we have investigated whether the rotational hindering observed by Dai and Light37 could be due to their QD calculations being unconverged. We find that this is not the case, but that the observed difference with our calculations using the best SRP-DF (B86SRP68-DF2) only arises for J < 3, suggesting that the rotational hindering effect is very subtle (see Fig. S4, ESI†). Further research is needed to check whether the difference between the calculations could be due to the LEPS fit39 being inaccurate, the underlying electronic structure calculations being unconverged,39,40 or both. See the ESI† for further details.
Reported density functional molecular dynamics (DFMD) calculations that include surface motion have shown that at low translational energies surface temperature effects somewhat increase the reactivity of D2 reacting on Cu(111).23,62 Increased reactivity at low translational energies might lower calculated E1/2(ν, J) parameters for both Methods A1 and B1. We have extracted E1/2(ν, J) parameters using both Methods A1 and B1 from Nattino et al.62 The results are shown in Fig. 18. The reported data was obtained using the SRP48 DF.62 There were only three rovibrational states for which a data point was available at a translational energy higher than the maximum kinetic energy sensitivity of the experiment.47 To validate the obtained E1/2(ν, J) parameters we have also extracted E1/2(ν, J) parameters using the same methodology for the reported logistics function fits to BOSS direct dynamics data.62 The good agreement for both Methods A1 and B1 between our SRP48 E1/2(ν, J) parameters and those obtained from logistics function fits to BOSS direct dynamics data validates this comparison. For both the A1 and B1 method the single point for (ν = 0,J = 11) suggests that a small decrease can be expected from allowing the surface to move, for the (ν = 1,J = 6) point this is not so clear. There is however a dramatic decrease of the E1/2(ν, J) parameter for (ν = 1,J = 4). This is a clear indication that, at least for low J, taking into account surface motion leads to lower E1/2(ν, J) parameters, and this might thus be partly responsible for the observed rotational hindering. The decrease of the E1/2(ν = 1,J = 4) value with the introduction of surface motion is less pronounced when using the A1 method.
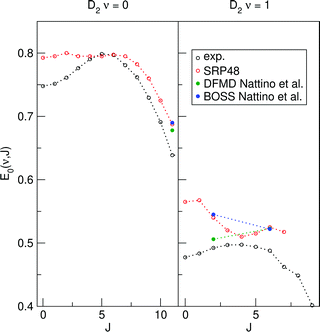 | ||
| Fig. 18 E 1/2(ν, J) parameters as a function of J for D2 reacting on Cu(111). Closed symbols pertain to E1/2(ν, J) parameters calculated using the A1 method, open symbols refer to the B1 method. Experimental results are shown in black,47 SRP48 results calculated in this work are shown in red. DFMD (green) and BOSS (blue) results obtained using the SRP48 DF have been extracted from ref. 62. | ||
Note however that the E0(ν, J) parameters are extremely sensitive to the quality of the logistics function fits. The agreement between our SRP48 E1/2(ν, J) parameters and those obtained from logistics function fits to BOSS direct dynamics for which no data point existed at a translational energy higher then the maximum kinetic energy sensitivity to which the experiment was sensitive was not so good.
The above observations warrant the following tentative conclusions: within the BOSS approximation, the mGGA DF and the DFs containing non-local correlation perform best for sticking. However, assuming Method B1 to be best, the SRP48 performs best for associative desorption. For associative desorption and again within the BOSS approximation, the two different methods (A1 and B1) for extracting the E1/2(ν, J) parameters describing the reaction probabilities extracted from associative desorption experiments yield rather different results. It follows that, at this stage, the associative desorption experiments are not as useful as the sticking experiments for assessing the accuracy of theory. Hopefully this can be changed in future by taking into account surface atom motion and ehp excitation in the theory, and by computing associative desorption fluxes directly from theory, as was recently done using the PBE DF by Galparsoro et al.75
4.4.1.2 E 1/2(ν, J) parameters Au(111). The comparison of the measured E0(ν, J) values with the E1/2(ν, J) parameters computed using Method B2 is shown in Fig. 13. The Emax(ν, J) parameters needed in this method (see eqn (S4), ESI†) have been obtained from a private communication,146 and have been plotted in Fig. S2 (ESI†) against the E0(ν, J) parameters extracted from the measurements.70 We note that the Emax(ν, J) parameters typically equal
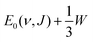 for the ν = 0 states and
for the ν = 0 states and 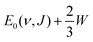 for the ν = 1 states, where W = 0.31 eV for ν = 0 and 0.29 eV for ν = 170 (see Fig. S2, ESI†). This means that Method B1 will yield unreliable values for the E1/2(ν, J) parameters. It also means that Method B2 relies heavily on extrapolation in the method to determine the A values by anchoring the measured reaction probabilities to the reaction probabilities computed at Emax(ν, J). One should therefore exercise extreme caution when comparing the theory to experiment.
for the ν = 1 states, where W = 0.31 eV for ν = 0 and 0.29 eV for ν = 170 (see Fig. S2, ESI†). This means that Method B1 will yield unreliable values for the E1/2(ν, J) parameters. It also means that Method B2 relies heavily on extrapolation in the method to determine the A values by anchoring the measured reaction probabilities to the reaction probabilities computed at Emax(ν, J). One should therefore exercise extreme caution when comparing the theory to experiment.
Table S10 (ESI†) shows the MAD end MSD values obtained with Method B2 for H2 + Au(111). The following tentative conclusions can be drawn: the E1/2(ν, J) parameters computed with the mGGA DF tested here and with all DFs employing van der Waals correlation substantially overestimate the measured E0(ν, J) parameters, with MAD values of approximately 0.1 eV for H2. The PBE DF would appear to perform best, with a MAD value of 46 meV for H2. This conclusions agrees with the observation that PBE reaction probabilities142 allowed better fits of the measured time-of-flight spectra of H2 and D2 desorbing from Au(111)70 than the SRP48 reaction probabilities.
A caveat here is that the experiment was performed with a surface temperature of 1063 K, while all calculations were performed using the BOSS model. Allowing surface motion during the dynamics would lead to broadening of the sticking probability curves.23,29,155,156 A higher sticking probability at lower translational energies could potentially lower the theoretical E1/2(ν, J) parameters. Additionally, we have performed our calculations on an unreconstructed Au(111) surface because the surface unit cell of reconstructed Au(111) is at present too big to map out a full PES using DFT calculations. Earlier work in our group indicated that the barriers to H2 dissociation are somewhat higher on the reconstructed Au(111) surface and that using an unreconstructed surface might lead to the underestimation of dynamical barrier heights by about 50 meV (∼1 kcal mol−1),142 which would lead to slightly higher E1/2(ν, J) parameters and therefore to increased disagreement with the measured values.
We are not able to resolve the contradiction posed by Shuai et al.70 that the vibrational efficacies computed with the SRP48 DF are in good agreement with experiment (as may be derived from Fig. 13) but that the ratio of desorbed molecules in the vibrational ground state versus the vibrationally excited state is not (see Table 4). The good reproduction of the J dependence of the E0(ν, J) parameters by theory (Fig. 13) suggests that the reactivity of the individual rovibrational states relative to each other is accurately described by theory as long as states are considered with the same vibrational level. Previously reported experiments implied that the recombination of H2 on Au(111) is coupled to the electronic degrees of freedom of the metal.157–160 In line with Shuai et al.70 we think that non-adiabatic effects together with surface motion effects and surface reconstruction represent the most likely causes for the lower translational energy distributions of the desorbing H2 (ν = 0) molecules compared to theory. If molecular beam dissociative chemisorption experiments on a reasonably cold surface would become available for this system (like for H2 + Ag(111)) this would allow for a more direct comparison to experiment of QCT and MDEF calculations. Molecular beam adsorption experiments would also allow us to check if the absolute reactivity predicted by the DFs shown here is in agreement with experiment. Therefore, at present, we cannot corroborate or refute the conclusion reached by Shuai et al.,70 namely that the experimentally observed lower translational energy distributions compared to theoretical predictions (see Fig. 1 of Shuai et al.70) is most likely due to ehp excitations in the desorption dynamics.
Fig. S10 (ESI†) shows the state distributions of molecules desorbing from Au(111) as reported by Shuai et al.70 in their Fig. 2 together with experimental results calculated by us using eqn (13), an upper integration limit of 5 eV, and our normalization procedure, which were the boundary conditions and integration parameters suggested to us by Shuai et al.70,146 As can be seen from Fig. S10 (ESI†) our “experimental results” calculated using eqn (13) and the error function fits reported in ref. 70 are in good agreement with the experimental results reported by Shuai et al.,70i.e. the calculated curves have the correct shape and can, to a good approximation, be superimposed on one another, provided that they are shifted by a constant value as explained in the caption of Fig. S10 (ESI†). However, we are not able to reproduce the normalization strategy employed by Shuai et al.70 Also when we shift the SRP48 (ν = 0) and (ν = 1) curves by the same value we cannot exactly superimpose our computed SRP48 results with their computed SRP48 results for both vibrational states simultaneously. It is not clear to us how this discrepancy arises.
The relative populations for the (ν = 0) and (ν = 1) rovibrational states is not affected by this discrepancy. The difference between our work and Shuai et al.70 with respect to the ν = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν = 0 ratios arises because we use Emax(ν, J) as the upper integration limit in eqn (13). Shuai et al.70 have used 5 eV as the upper integration limit.146 The only reason we choose Emax(ν, J) as the upper integration boundary is because the reported error function fits are only reliable below Emax(ν, J), for some rovibrational states the error function fits can yield sticking probabilities much larger than unity for high kinetic energies. The ratios we calculate are shown in Table 4. We note that when we use the upper integration limit of 5 eV, we reproduce the ν = 1
ν = 0 ratios arises because we use Emax(ν, J) as the upper integration limit in eqn (13). Shuai et al.70 have used 5 eV as the upper integration limit.146 The only reason we choose Emax(ν, J) as the upper integration boundary is because the reported error function fits are only reliable below Emax(ν, J), for some rovibrational states the error function fits can yield sticking probabilities much larger than unity for high kinetic energies. The ratios we calculate are shown in Table 4. We note that when we use the upper integration limit of 5 eV, we reproduce the ν = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν = 0 ratios reported by Shuai et al.70 In our view only integrating up to Emax(ν, J) is a more fair way of calculating the N(ν, J) populations, though on the scale of Fig. 17 the difference between integrating to Emax(ν, J) or 5 eV would not be visible. Note that the overwhelming majority of the area under the Gaussian fits to the time-of-flight curves, as reported in Tables S1–S4 of ref. 70, lies well below Emax(ν, J). Note also that we calculate the ν = 1
ν = 0 ratios reported by Shuai et al.70 In our view only integrating up to Emax(ν, J) is a more fair way of calculating the N(ν, J) populations, though on the scale of Fig. 17 the difference between integrating to Emax(ν, J) or 5 eV would not be visible. Note that the overwhelming majority of the area under the Gaussian fits to the time-of-flight curves, as reported in Tables S1–S4 of ref. 70, lies well below Emax(ν, J). Note also that we calculate the ν = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν = 0 ratios only using the rovibrational states shown in Fig. 17, which is the same set of rovibrational states used by Shuai et al.70
ν = 0 ratios only using the rovibrational states shown in Fig. 17, which is the same set of rovibrational states used by Shuai et al.70
In Fig. 17 the difference between the desorbing populations computed with the SRP48 and B86SRP68-DF2 SRP-DFs is minimal. The agreement between theory and experiment is best for D2, although the qualitative agreement between theory and experiment is reasonable for both H2 and D2. It can be seen in Table 4 that there is only a reasonable agreement for D2 with respect to the ν = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν = 0 population ratios. The theoretical ν = 1
ν = 0 population ratios. The theoretical ν = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν = 0 population ratio for H2 is however too low, a result similar to what was reported by Shuai et al.70 The difference between theory experiment can perhaps be explained by the experimental time-of-flight distributions being much broader than the theoretical ones, see Fig. 1 of ref. 70. Taking into account surface motion in the theoretical calculations might well improve the agreement with experiment with respect to both the rovibrational state distributions of desorbing molecules as well as the ν = 1
ν = 0 population ratio for H2 is however too low, a result similar to what was reported by Shuai et al.70 The difference between theory experiment can perhaps be explained by the experimental time-of-flight distributions being much broader than the theoretical ones, see Fig. 1 of ref. 70. Taking into account surface motion in the theoretical calculations might well improve the agreement with experiment with respect to both the rovibrational state distributions of desorbing molecules as well as the ν = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν = 0 population ratio.
ν = 0 population ratio.
In Fig. 10 we see that, especially for D2, the MS-PBEl mGGA DF has the best agreement with the initial-state selected reaction probabilities extracted from the associative desorption experiments. The good performance of the MS-PBEl DF can be explained by the slightly earlier barriers, as discussed in our previous work.12 The DFs that include non-local correlation do not show such a large improvement over the SRP48 DF, while they do for sticking.
Without new experimental work for this system, especially molecular beam experiments covering a wide range of translational energies and nozzle temperatures, it will be difficult to further improve the theoretical description of this system. Additional experiments (e.g. a molecular beam sticking experiment on D2 seeded in H2 and going op to a translational energy of 0.8 eV as done for H2 + Cu(111)45) would also allow us to assess more accurately if the dynamics predicted by the MS-PBEl mGGA or the dynamics predicted by the GGA based SRP-DFs that do and do not include non-local correlation are more in line with experimental observations.
Note that the B86SRP68-DF2, PBEα57-DF211 and MS-B86bl12 DFs are in good agreement with each other for both the (ν = 0,J = 11) state (Fig. 14a) and the (ν = 1,J = 6) state (Fig. 14b), but that these three DFs predict slightly higher rotational quadrupole alignment parameters than the SRP48 DF.26 Given that the SRP48 rotational quadrupole alignment parameters were decreased, but still somewhat too large when surface atom motion was introduced,26 the present results suggest that the SRP48 DF yields the best description of this observable.
4.5 Inelastic scattering of H2 from Cu(111)
In this section we will discuss inelastic scattering results for H2, obtained with QD. We start with the vibrationally inelastic scattering results for H2 shown in Fig. 15. We specifically show QD results since the previously voiced expectation that vibrationally inelastic scattering should be well described using the QCT method for translational energies above the lowest barrier to reaction163 has been shown not to hold.24 Here we discuss the inelastic scattering probability P(ν = 0, J → ν = 1, J = 3) for three different initial J states. Panels a and b suggest that for (J = 1) and (J = 3) and for the DFs that use non-local correlation the vibrationally inelastic scattering probability is correlated with the depth of the van der Waals well (see Table S5, ESI†). A deeper van der Waals well is correlated with higher vibrationally inelastic scattering probabilities. Fig. 15c shows that for (J = 5) all DFs yield vibrational excitation probabilities in reasonable agreement with each other. Bringing TOF spectra for vibrational excitation from (ν = 0,J) to (ν = 1,J = 3) in better agreement with experimental results would require a substantial increase of the vibrational excitation probabilities computed with the SRP48 DF (by a factor of 2–3),24,163 which is obtained with none of the DFs tested. We conclude that better agreement with experiment probably requires a different dynamical model, as suggested also by earlier work.24,163From the computed ratio of rotationally inelastic scattering probabilities P(ν = 1, J = 0 → ν = 1, J = 2)/P(ν = 1, J = 0 → ν = 1, J = 0) shown in Fig. 16 it is clear that the B86SRP68-DF2 DF performs not as good as the SRP48 DF.10 The shifted SRP48 curve follows the experiment more closely. Both curves need to be shifted by 40 meV in order to better overlap with the experiment performed using a surface temperature of 300 K.54 The overlap with experiment of the shifted curves only holds until 0.14 eV, but the experimentalists noted that at higher energies the measurements became more difficult.54 It is rather surprising that both computed ratios need to be shifted by roughly the same amount in order to overlap with experiment, since the SRP48 DF overestimates the initial sticking probability in molecular beam experiment while the B86SRP68-DF2 DF does not. From the literature it is also known that including surface motion during the dynamics might lead to broadening, and an earlier onset, of inelastic scattering probabilities.23,29 We speculate that allowing surface motion and ehp excitation during the dynamics might obviate the need for the shift in order to superimpose the calculated curves with experiment.
4.6 QD vs. QCT for H2 + Cu(111)
In Fig. 9 initial state-resolved reaction probabilities are shown calculated using the B86SRP68-DF2 DF. Here the (J = 0) and (J = 1) state for both the vibrational ground state and the first vibrationally excited state are shown because the differences between the QD and QCT method are most prevalent for the low lying rotational states. The QD reaction probability curves show more structure than was shown for H2 + Cu(211),36 but the agreement between the QD and QCT method for degeneracy averaged reaction probabilities (Fig. 9a and c) is still very good. From the comparison between QD and QCT degeneracy averaged reaction probabilities shown in Fig. S8 (ESI†) it can be seen that the differences between the QD and QCT method get smaller with increasing J for J > 3, though small differences remain even for high J states.The biggest difference between the QD and QCT method are observed in Fig. 9b. Here we show fully initial-state resolved reaction probabilities, thereby distinguishing between a 'cartwheeling' molecules rotating in a plane parallel to the surface normal (mJ = 0) and a 'helicoptering' molecules rotating in a plane perpendicular to the surface normal. In line with our previous work, we observe that QD predicts a slightly larger preference for molecules reacting parallel to the surface. The rovibrational states shown in Fig. 9 are the same rovibrational states shown in Fig. 2 of our previous work for H2 reacting on Cu(211),36 in which the agreement for degeneracy averaged reaction probabilities was nearly perfect.
In recent experimental work kaufmannCu211 have reported a previously unobserved “slow reaction channel” for H2 associatively desorbing from Cu(111) and Cu(211). In this channel, the reaction could be facilitated by trapping on the surface and distortion of the surface due to thermal motion forming a reactive site.47 Even though our PES now contains a van der Waals well that might facilitate trapping during the reaction dynamics, we do not yet see evidence of the recently reported slow reaction channel for H2 + Cu(111).47 The translational energy range used in our calculations overlaps with the translational energies at which the slow channel reactivity was observed.47 We can therefore rule out quantum effects (like tunneling, see ref. 36) during the dynamics as the origin of this slow reaction channel for H2 + Cu(111), as we did before for H2 + Cu(211).36 We therefore propose, as done earlier for H2 + Cu(211),36 that the slow reaction channel reported by Kaufmann et al.47 originates from the very high surface temperature of 923 K used in the associative desorption experiments. Presently it is not possible to take surface motion explicitly into account in QD calculations, and it is challenging to do so in QCT calculations.148–150 Galparsoro et al.75 likewise did not yet find evidence for the slow reaction channel in their AIMD calculations.
4.7 Overall description of systems
When looking at the H2 + Ag(111) and H2 + Au(111) systems considered in this work together, one stark realization is that further development of chemically accurate DFs for H2 reacting on transition metal surfaces is still heavily stymied by a lack of experimental data. This is bad news as presently semi-empirical DFT seems to be the only path to extracting chemically accurate information on barriers to reaction. Relying on non-empirical constraints on DF design is not yet feasible, as illustrated by the poor performance of the SCAN164 DF for H2 + Cu(111).12 Additionally, taking another step upwards on Jacob's ladder from a GGA or mGGA towards hybrid DFs is computationally very expensive, if not prohibitively so.For both the activated and non-activated reactions of H2 on transitions metals there is now only a single well studied system, namely H2 + Cu(111) (and maybe H2 + Pt(111)65). What we mean by well studied is that there should be different kinds of well described experiments. For example, a combination of an associative desorption experiment and a dissociative chemisorption experiment should be available, or sticking probabilities for normal and off-normal incidence. It is also critical that the experimental conditions are described accurately.15,19,20,65,142
Without new and detailed experiments on, at least, the related H2 + Pd(111) and H2 + Ag(111) or H2 + Au(111) systems it is not possible to grasp the overarching trends in reactivity imposed by the position of these metals in the periodic table. In many aspects we are dancing in the dark with respect to DF design. The consequence of this is that, presently, theory can only provide models with limited predictive power.
The large amount of experimental45–61,165,166 and theoretical work10,12,18,21–44,155,167,168 available have allowed us to get the best description of this system so far. We can however not yet point to one DF that is clearly the best DF for this system. Currently two DFs compete for being the best DF for this system, namely B86SRP68-DF2 and MS-B86bl.12 The latter has a better description of the metal and might therefor be better when looking at diffraction probabilities. The MS-B86bl DF however misses any description of van der Waals forces. In all our simulations for the H2 + Cu(111) system the B86SRP68-DF2 and MS-B86bl DFs perform similarly well. With the information available now one might argue that the MS-B86bl DF is the best DF for this system since its description of the metal is much better than provided by the B86SRP68-DF2 DF, and because the effect of including non-local correlation is only apparent when calculating E1/2(ν, J) parameters for this system. The MS-B86bl DF is however not transferable to weakly activated systems. In our view, the DFs that are more generally applicable, i.e. the B86SRP68-DF2 and PBEα57-DF2 DFs, are currently the best DFs. A good next step could be to use non-local correlation together with the MS-B86bl DF.
Shuai et al.70 suggested that the PBE DF is better then the SRP48 DF because calculated time-of-flight distributions correlated slightly less worse with experimental observations for the PBE DF. This assertion implicitly assumes the validity of detailed balance for this system. The main conclusion of the experimentalists was however that the bad agreement between theory and experiment points toward strong non-adiabatic effects, which, if true, would invalidate the assumption of detailed balance.70
4.8 Transferability
So far SRP-DFs fitted to reproduce molecular beam adsorption experiments for H2 and D2 where shown to be transferable among crystal faces of the same metal,17,18 but not among different metals.19,20 Here we show examples in which a SRP-DF that was fitted to reproduce molecular beam experiments of the activated late barrier system of H2 reacting on Cu(111) can also describe the non-activated early barrier system of D2 reacting on Pt(111) with chemical accuracy, and vice versa. Transferability to a different substrate of a SRP-DF fitted to reproduce gas-surface experiments has only been reported for CH4 dissociation on Ni(111)13 to CH4 dissociation on Pt(111).16The SRP48 DF for H2 + Cu(111) is not transferable to the H2 + Ag(111) system19 or to the H2 + Pt(111) system. We have previously shown that a SRP-DF based on the mGGA that does not include non-local correlation (MS-PBEl12) greatly improves the transferability from H2 + Cu(111) to H2 + Ag(111),12 but Fig. 8 shows that this DF is not transferable to the weakly activated H2 + Pt(111) system.
The only group of DFs that might be considered transferable between both highly activated and weakly activated systems are DFs that include non-local correlation. We demonstrated that a SRP-DF fitted to H2 + Pt(111), PBEα57-DF2,11 can describe H2 + Cu(111) with overall chemical accuracy and that a new SRP-DF fitted to H2 + Cu(111), B86SRP68-DF2, can describe the D2 + Pt(111) experiments of Luntz et al.64 with chemical accuracy. We speculate that the transferability between the Cu(111) and Pt(111) systems might be improved by taking into account relativistic corrections in our DFT calculations beyond those already included in the PAW potentials,132 which at this accuracy level might be important.169,170
Both the B86SRP68-DF2 and PBEα57-DF2 DFs more or less predict the same reactivity for the H2 + Ag(111) system. It is not possible however to call the DFs transferable to this system, yet. The lack of well described dissociative chemisorption experiments for this system does not yet allow us to make a broad statement about the accuracy of the theoretical description of this system. At present our description appears to be just shy of chemical accuracy.
4.9 Adiabatic description of S0 and E1/2(ν, J), a possible fingerprint for ehp excitations
The assumption of detailed balance entails that associative desorption is the inverse of dissociative chemisorption. In an adiabatic picture there is just one reason for a possible divergence of the obtained reaction probabilities. This is based on surface temperature, which is usually much higher in the associative desorption experiments than in the sticking experiments. This might lead to a breakdown of the detailed balance assumption that is usually involved when modeling associative desorption experiments with calculations on dissociative chemisorption. We note that it might be possible to model the associative desorption experiment directly,75,171–173 thereby negating the need to invoke the principle of detailed balance and investigate if associative desorption is indeed the inverse of dissociative chemisorption.Including ehp excitations in dissociative chemisorption calculations would lower the reactivity thereby increasing the effective barrier.22 Including ehp excitations in hypothetical associative desorption calculations, where molecules would start at the transition state and then desorb, would probably shift the translational energy distributions of desorbing molecules to lower energies and lead to lower effective barriers. When accounting for the effect of surface temperature, the difference in predicted reactivity as embodied by the E1/2(ν, J) parameters obtained by including ehp excitations in associative desorption and dissociative chemisorption calculations, and their differences with results from adiabatic calculations, might then be taken to be a fingerprints for the effect of ehp excitation.
For H2 + Cu(111) we know from DFMD calculations62 and other approaches23,29,155,156 that the effect of surface motion on the reactivity in dissociative chemisorption is small, even for high surface temperatures. Fig. 18 shows some evidence that the broadening of reaction probability curves might affect the calculated E1/2(ν, J) parameters for low J. However, in an adiabatic picture, assuming detailed balance there should be no difference between calculations on dissociative adsorption and associative desorption.
We believe that this suggests a reason for only the SRP48 DF being chemically accurate for H2 + Cu(111) for both dissociative chemisorption and associative desorption, since it overestimates the former and underestimates the latter predicted reactivity. The new SRP-DFs that are very accurate for dissociative chemisorption on cold surfaces, for which the BOSS model is valid,23,27–29,62,147 must underestimate the reactivity obtained from associative desorption by at least the extent to which surface temperature would increase the reactivity in dissociative chemisorption. Any remaining discrepancy can be safely attributed to the effect of ehp excitations.
The analysis of the H2 + Au(111) system is more complicated due to the lack of dissociative chemisorption experiments and the current inability to take into account surface reconstruction (and thereby surface motion). Without at least either a dissociative chemisorption experiment or calculations using a reconstructed surface using the BOSS model, it is not yet possible to disentangle the contributions of the surface temperature, surface reconstruction and ehp excitations to the reactivity. Additionally, more detailed associative desorption and dissociative chemisorption experiments for the H2 + Ag(111) system would allow for a systematic investigation into the effect of ehp excitations on reactivity for highly activated late barrier reactions.
5 Conclusions
We have constructed new SRP-DFs that include non-local correlation for the H2 (D2) + Cu(111) system and assessed the transferability of these DFs to the H2 (D2) + Ag(111), H2 (D2) + Au(111) and H2 (D2) + Pt(111) systems. All newly tested and developed DFs are based on GGA-exchange and use non-local correlation to describe dissociative chemisorption of H2 (D2) on Cu(111) within chemical accuracy, and, to the extent that it can be assessed, improve the transferability to the other systems discussed in this work over the previously reported SRP48 and MS-B86bl SRP-DFs.The new SRP-DFs improve the description of the metal over the previously available SRP-DFs based on mixing GGA exchange, especially concerning calculated lattice constants. In general, the new SRP-DFs with non-local correlation exhibit higher and later barriers to reaction in combination with a slightly lower energetic corrugation. We also find that vdW-DF2 non-local correlation performs better than vdW-DF1 correlation for all tried combinations with different exchange functionals, except when the exchange part of a functional was specifically optimized for use with vdW-DF1 correlation. The B86SRP68-DF2 functional best reproduces the measured van der Waals well depths for H2 + Cu(111), H2 + Ag(111) and H2 + Au(111).
SRP-DFs that include non-local correlation, namely B86SRP68-DF2 and PBEα57-DF2, are transferable from the highly activated late barrier H2 + Cu(111) system to the weakly activated earlier barrier H2 + Pt(111) system and vice versa. This feat could not be demonstrated with GGA and mGGA SRP-DFs that do not include non-local correlation. Assessing the transferability of the tested and developed SRP-DFs to H2 + Ag(111) and H2 + Au(111) is difficult due to the lack of well characterized molecular beam experiments. The SRP-DFs that include non-local correlation predict similar results for molecular beam sticking of D2 + Ag(111), which are just shy of chemical accuracy. However it should be noted that there is some discussion about the validity of the beam parameters describing this particular molecular beam experiment.
A detailed analysis of associative desorption experiments on Cu(111) suggest that accurate calculation of E1/2(ν, J) parameters requires an improvement of our dynamical model. Describing the surface degrees of freedom might close the gap between the excellent description of dissociative chemisorption and the good description of associative desorption, for molecules in the vibrational ground state. Any discrepancy in predicted reactivity between simulated associative desorption and dissociative chemisorption remaining after taking into account the effect of surface atom motion can then most likely be attributed to ehp excitation. Lack of additional experiments for the H2 + Au(111) system, specifically a well described dissociative chemisorption experiment, presently keeps us from disentangling the effects of surface reconstruction, surface temperature and ehp excitation for this system.
We have carried out a full molecular beam simulation for the H2 + Cu(111) system using the QD method and the B86SRP68-DF2 DF for sticking in this system, which is the best performing DF for this system, and which includes non-local correlation. Overall H2 + Cu(111) is very well described quasi-classically when looking at molecular beam reaction probabilities or degeneracy averaged reaction probabilities. At the level of molecular beam sticking, and degeneracy averaged reaction probabilities, the differences between the QD and QCT method are very small. The QD method predicts slightly higher reaction probabilities for molecular beam sticking for very narrow low average translational energy molecular beams when comparing to QCT results based on the same set of initial rovibrational states. When looking at initial-state resolved reaction probabilities the QD method predicts a somewhat larger orientational dependence of the reaction, in favor of molecules reacting in a parallel orientation. With respect to vibrationally and rotationally inelastic scattering of H2 from Cu(111) the B86SRP68-DF2 DF performs almost as well as the previous best SRP-DF for this system, namely the SRP48 DF.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Dr M. F. Somers for the fruitful discussions about the different dynamical models employed in this work, as well as Dr E. N. Ghassemi. Without her previous work on most of the systems treated here this paper would not have been possible. Lastly we would like to thank our student B. Hagedoorn BSc, whose bachelor thesis constituted the start of the H2 + Au(111) project. We would also like to thank Dr S. Kaufmann for useful discussions and for providing us with the Emax(ν, J) parameters from the experiments of H2 (D2) + Au(111). This work was supported financially through a NWO/CW TOP grant (No. 715.017.001), and by a grant of supercomputer time from NWO Exacte en Natuurwetenschappen (NWO-ENW, grant number 2019.015).References
- G.-J. Kroes, J. Phys. Chem. Lett., 2015, 6, 4106–4114 CrossRef CAS.
- C. A. Wolcott, A. J. Medford, F. Studt and C. T. Campbell, J. Catal., 2015, 330, 197–207 CrossRef CAS.
- M. K. Sabbe, M.-F. Reyniers and K. Reuter, Catal. Sci. Technol., 2012, 2, 2010–2024 RSC.
- G. Ertl, Angew. Chem., Int. Ed., 2008, 47, 3524–3535 CrossRef CAS.
- G.-J. Kroes, Science, 2008, 321, 794–797 CrossRef CAS.
- K. Waugh, Catal. Today, 1992, 15, 51–75 CrossRef CAS.
- L. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384 CrossRef CAS.
- M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr and B.-L. Kniep, et al. , Science, 2012, 336, 893–897 CrossRef CAS.
- G. B. Park, T. N. Kitsopoulos, D. Borodin, K. Golibrzuch, J. Neugebohren, D. J. Auerbach, C. T. Campbell and A. M. Wodtke, Nat. Rev. Chem., 2019, 1–10 Search PubMed.
- C. Daz, E. Pijper, R. Olsen, H. Busnengo, D. Auerbach and G. Kroes, Science, 2009, 326, 832–834 CrossRef.
- E. N. Ghassemi, M. Wijzenbroek, M. F. Somers and G.-J. Kroes, Chem. Phys. Lett., 2017, 683, 329–335 CrossRef.
- E. W. F. Smeets, J. Voss and G.-J. Kroes, J. Phys. Chem. A, 2019, 123, 5395–5406 CrossRef CAS.
- F. Nattino, D. Migliorini, G.-J. Kroes, E. Dombrowski, E. A. High, D. R. Killelea and A. L. Utz, J. Phys. Chem. Lett., 2016, 7, 2402–2406 CrossRef CAS.
- K. Doblhoff-Dier, J. Meyer, P. E. Hoggan and G.-J. Kroes, J. Chem. Theory Comput., 2017, 13, 3208–3219 CrossRef CAS.
- J. Boereboom, M. Wijzenbroek, M. Somers and G. Kroes, J. Chem. Phys., 2013, 139, 244707 CrossRef CAS.
- D. Migliorini, H. Chadwick, F. Nattino, A. Gutiérrez-González, E. Dombrowski, E. A. High, H. Guo, A. L. Utz, B. Jackson and R. D. Beck, et al. , J. Phys. Chem. Lett., 2017, 8, 4177–4182 CrossRef CAS.
- E. N. Ghassemi, E. W. F. Smeets, M. F. Somers, G.-J. Kroes, I. M. Groot, L. B. Juurlink and G. Füchsel, J. Phys. Chem. C, 2019, 123, 2973–2986 CrossRef CAS.
- L. Sementa, M. Wijzenbroek, B. Van Kolck, M. Somers, A. Al-Halabi, H. F. Busnengo, R. Olsen, G.-J. Kroes, M. Rutkowski and C. Thewes, et al. , J. Chem. Phys., 2013, 138, 044708 CrossRef CAS.
- E. Nour Ghassemi, M. Somers and G.-J. Kroes, J. Phys. Chem. C, 2018, 122, 22939–22952 CrossRef CAS.
- T. Tchakoua, E. W. F. Smeets, M. Somers and G.-J. Kroes, J. Phys. Chem. C, 2019, 123, 20420–20433 CrossRef CAS.
- Ž. Šljivančanin and B. Hammer, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 085414 CrossRef.
- P. Spiering and J. Meyer, J. Phys. Chem. Lett., 2018, 9, 1803–1808 CrossRef CAS.
- P. Spiering, M. Wijzenbroek and M. Somers, J. Chem. Phys., 2018, 149, 234702 CrossRef CAS.
- G.-J. Kroes, J. Juaristi and M. Alducin, J. Phys. Chem. C, 2017, 121, 13617–13633 CrossRef CAS.
- M. Somers, D. McCormack, G.-J. Kroes, R. Olsen, E. Baerends and R. Mowrey, J. Chem. Phys., 2002, 117, 6673–6687 CrossRef CAS.
- F. Nattino, C. Díaz, B. Jackson and G.-J. Kroes, Phys. Rev. Lett., 2012, 108, 236104 CrossRef.
- G.-J. Kroes and C. Daz, Chem. Soc. Rev., 2016, 45, 3658–3700 RSC.
- C. Díaz, R. A. Olsen, D. J. Auerbach and G.-J. Kroes, Phys. Chem. Chem. Phys., 2010, 12, 6499–6519 RSC.
- M. Wijzenbroek and M. F. Somers, J. Chem. Phys., 2012, 137, 054703 CrossRef CAS.
- D. A. McCormack, G.-J. Kroes, R. A. Olsen, J. A. Groeneveld, J. N. van Stralen, E. J. Baerends and R. C. Mowrey, Faraday Discuss., 2000, 117, 109–132 RSC.
- D. A. McCormack, G.-J. Kroes, R. A. Olsen, J. A. Groeneveld, J. N. van Stralen, E. J. Baerends and R. C. Mowrey, Chem. Phys. Lett., 2000, 328, 317–324 CrossRef CAS.
- J. Chen, X. Zhou and B. Jiang, J. Chem. Phys., 2019, 150, 061101 CrossRef.
- G. Darling and S. Holloway, J. Chem. Phys., 1994, 101, 3268–3281 CrossRef CAS.
- S. Sakong and A. Groß, Surf. Sci., 2003, 525, 107–118 CrossRef CAS.
- G.-J. Kroes, E. Pijper and A. Salin, J. Chem. Phys., 2007, 127, 164722 CrossRef CAS.
- E. W. F. Smeets, G. Füchsel and G.-J. Kroes, J. Phys. Chem. C, 2019, 123, 23049–23063 CrossRef CAS.
- J. Dai and J. C. Light, J. Chem. Phys., 1998, 108, 7816–7820 CrossRef CAS.
- J. Dai and J. C. Light, J. Chem. Phys., 1997, 107, 1676–1679 CrossRef CAS.
- J. Dai and J. Z. Zhang, J. Chem. Phys., 1995, 102, 6280–6289 CrossRef CAS.
- B. Hammer, M. Scheffler, K. W. Jacobsen and J. K. Nørskov, Phys. Rev. Lett., 1994, 73, 1400 CrossRef CAS.
- M. Wijzenbroek, D. M. Klein, B. Smits, M. F. Somers and G.-J. Kroes, J. Phys. Chem. A, 2015, 119, 12146–12158 CrossRef CAS.
- G. Füchsel, K. Cao, S. Er, E. W. F. Smeets, A. W. Kleyn, L. B. F. Juurlink and G.-J. Kroes, J. Phys. Chem. Lett., 2018, 9, 170–175 CrossRef.
- G.-J. Kroes, M. Pavanello, M. Blanco-Rey, M. Alducin and D. J. Auerbach, J. Chem. Phys., 2014, 141, 054705 CrossRef.
- H. A. Michelsen and D. J. Auerbach, J. Chem. Phys., 1991, 94, 7502–7520 CrossRef CAS.
- H. Michelsen, C. Rettner, D. Auerbach and R. Zare, J. Chem. Phys., 1993, 98, 8294–8307 CrossRef CAS.
- H. Berger, M. Leisch, A. Winkler and K. Rendulic, Chem. Phys. Lett., 1990, 175, 425–428 CrossRef CAS.
- S. Kaufmann, Q. Shuai, D. J. Auerbach, D. Schwarzer and A. M. Wodtke, J. Chem. Phys., 2018, 148, 194703 CrossRef.
- G. Anger, A. Winkler and K. Rendulic, Surf. Sci., 1989, 220, 1–17 CrossRef CAS.
- H. Hou, S. Gulding, C. Rettner, A. Wodtke and D. Auerbach, Science, 1997, 277, 80–82 CrossRef CAS.
- G. Comsa and R. David, Surf. Sci., 1982, 117, 77–84 CrossRef CAS.
- C. Rettner, H. Michelsen and D. Auerbach, J. Chem. Phys., 1995, 102, 4625–4641 CrossRef CAS.
- C. Rettner, D. Auerbach and H. Michelsen, J. Vac. Sci. Technol., A, 1992, 10, 2282–2286 CrossRef CAS.
- C. Rettner, H. Michelsen and D. Auerbach, Chem. Phys., 1993, 175, 157–169 CrossRef CAS.
- A. Hodgson, P. Samson, A. Wight and C. Cottrell, Phys. Rev. Lett., 1997, 78, 963 CrossRef CAS.
- H. Michelsen, C. Rettner and D. Auerbach, Surf. Sci., 1992, 272, 65–72 CrossRef CAS.
- T. Okazawa, F. Takeuchi and Y. Kido, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075408 CrossRef.
- S. Lindgren, L. Walldén, J. Rundgren and P. Westrin, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 576 CrossRef CAS.
- K. Chae, H. Lu and T. Gustafsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 14082 CrossRef CAS.
- S. Andersson and M. Persson, Phys. Rev. Lett., 1993, 70, 202 CrossRef CAS.
- K. Cao, G. Füchsel, A. W. Kleyn and L. B. Juurlink, Phys. Chem. Chem. Phys., 2018, 20, 22477–22488 RSC.
- U. Harten, J. P. Toennies and C. Wöll, J. Chem. Phys., 1986, 85, 2249–2258 CrossRef CAS.
- F. Nattino, A. Genova, M. Guijt, A. S. Muzas, C. Daz, D. J. Auerbach and G.-J. Kroes, J. Chem. Phys., 2014, 141, 124705 CrossRef.
- K. Cao, R. van Lent, A. Kleyn and L. Juurlink, Chem. Phys. Lett., 2018, 706, 680–683 CrossRef CAS.
- A. Luntz, J. Brown and M. Williams, J. Chem. Phys., 1990, 93, 5240–5246 CrossRef CAS.
- E. N. Ghassemi, M. F. Somers and G.-J. Kroes, J. Phys. Chem. C, 2019, 123, 10406–10418 CrossRef CAS.
- E. Pijper, G.-J. Kroes, R. A. Olsen and E. J. Baerends, J. Chem. Phys., 2002, 117, 5885–5898 CrossRef CAS.
- G.-J. Kroes and M. F. Somers, J. Theor. Comput. Chem., 2005, 04, 493–581 CrossRef CAS.
- L. M. Raff and M. Karplus, J. Chem. Phys., 1966, 44, 1212–1229 CrossRef CAS.
- M. Cardillo, M. Balooch and R. Stickney, Surf. Sci., 1975, 50, 263–278 CrossRef CAS.
- Q. Shuai, S. Kaufmann, D. J. Auerbach, D. Schwarzer and A. M. Wodtke, J. Phys. Chem. Lett., 2017, 8, 1657–1663 CrossRef CAS.
- A. Perrier, L. Bonnet, D. Liotard and J.-C. Rayez, Surf. Sci., 2005, 581, 189–198 CrossRef CAS.
- A. Perrier, L. Bonnet and J.-C. Rayez, J. Phys. Chem. A, 2006, 110, 1608–1617 CrossRef CAS.
- A. Perrier, L. Bonnet and J.-C. Rayez, J. Chem. Phys., 2006, 124, 194701 CrossRef CAS.
- C. Daz, A. Perrier and G. Kroes, Chem. Phys. Lett., 2007, 434, 231–236 CrossRef.
- O. Galparsoro, S. Kaufmann, D. J. Auerbach, A. Kandratsenka and A. M. Wodtke, Phys. Chem. Chem. Phys., 2020, 22, 17532–17539 RSC.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
- M. Murphy and A. Hodgson, Surf. Sci., 1997, 390, 29–34 CrossRef CAS.
- M. Murphy and A. Hodgson, Phys. Rev. Lett., 1997, 78, 4458 CrossRef CAS.
- B. Jiang and H. Guo, Phys. Chem. Chem. Phys., 2014, 16, 24704–24715 RSC.
- B. Jiang and H. Guo, J. Chem. Phys., 2014, 141, 034109 CrossRef.
- G. Lee and E. Plummer, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 7250 CrossRef CAS.
- P. Sprunger and E. Plummer, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 14436 CrossRef CAS.
- P. Avouris, D. Schmeisser and J. Demuth, Phys. Rev. Lett., 1982, 48, 199 CrossRef CAS.
- F. Healey, R. Carter, G. Worthy and A. Hodgson, Chem. Phys. Lett., 1995, 243, 133–139 CrossRef CAS.
- D. H. Parker, M. E. Jones and B. E. Koel, Surf. Sci., 1990, 233, 65–73 CrossRef CAS.
- G. Lee, P. Sprunger, M. Okada, D. Poker, D. Zehner and E. Plummer, J. Vac. Sci. Technol., A, 1994, 12, 2119–2123 CrossRef CAS.
- H. Asada, Surf. Sci., 1979, 81, 386–408 CrossRef.
- J. M. Horne, S. C. Yerkes and D. R. Miller, Surf. Sci., 1980, 93, 47–63 CrossRef CAS.
- C.-f. Yu, K. B. Whaley, C. S. Hogg and S. J. Sibener, Phys. Rev. Lett., 1983, 51, 2210 CrossRef CAS.
- C. Yu, K. B. Whaley, C. S. Hogg and S. J. Sibener, J. Chem. Phys., 1985, 83, 4217–4234 CrossRef CAS.
- L. Mattera, R. Musenich, C. Salvo and S. Terreni, Faraday Discuss., 1985, 80, 115–126 RSC.
- R. J. Maurer, Y. Zhang, H. Guo and B. Jiang, Faraday Discuss., 2019, 214, 105–121 RSC.
- Y. Zhang, R. J. Maurer, H. Guo and B. Jiang, Chem. Sci., 2019, 10, 1089–1097 RSC.
- R. J. Maurer, B. Jiang, H. Guo and J. C. Tully, Phys. Rev. Lett., 2017, 118, 256001 CrossRef.
- A. S. Muzas, J. I. Juaristi, M. Alducin, R. D. Muiño, G.-J. Kroes and C. Daz, J. Chem. Phys., 2012, 137, 064707 CrossRef CAS.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS.
- K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- J. P. Cowin, C.-F. Yu, S. J. Sibener and J. E. Hurst, J. Chem. Phys., 1981, 75, 1033–1034 CrossRef CAS.
- J. P. Cowin, C.-F. Yu, S. J. Sibener and L. Wharton, J. Chem. Phys., 1983, 79, 3537–3549 CrossRef CAS.
- J. P. Cowin, C.-F. Yu and L. Wharton, Surf. Sci., 1985, 161, 221–233 CrossRef CAS.
- C.-F. Yu, C. S. Hogg, J. P. Cowin, K. B. Whaley, J. C. Light and S. J. Sibener, Isr. J. Chem., 1982, 22, 305–314 CrossRef CAS.
- J. Perreau and J. Lapujoulade, Surf. Sci., 1982, 122, 341–354 CrossRef CAS.
- A. Kaufhold and J. P. Toennies, Surf. Sci., 1986, 173, 320–336 CrossRef CAS.
- S. Andersson, L. Wilzén and M. Persson, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 2967 CrossRef CAS.
- J. Lennard-Jones and A. Devonshire, Nature, 1936, 137, 1069–1070 CrossRef CAS.
- H. Hoinkes and H. Wilsch, Helium Atom Scattering from Surfaces, Springer, 1992, pp. 113–172 Search PubMed.
- M. F. Bertino, F. Hofmann and J. P. Toennies, J. Chem. Phys., 1997, 106, 4327–4338 CrossRef CAS.
- P. Nieto, E. Pijper, D. Barredo, G. Laurent, R. A. Olsen, E.-J. Baerends, G.-J. Kroes and D. Faras, Science, 2006, 312, 86–89 CrossRef CAS.
- M. Bertino, S. Miret-Artés, J. Toennies and G. Benedek, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 9964 CrossRef CAS.
- B. Poelsema, K. Lenz and G. Comsa, J. Phys.: Condens. Matter, 2010, 22, 304006 CrossRef.
- I. Hamada, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121103 CrossRef.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Phys. Rev. Lett., 2009, 103, 026403 CrossRef.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2009, 22, 022201 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- G. K. Madsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195108 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800 CrossRef.
- H. Busnengo, A. Salin and W. Dong, J. Chem. Phys., 2000, 112, 7641–7651 CrossRef CAS.
- G. Füchsel, M. del Cueto, C. Díaz and G.-J. Kroes, J. Phys. Chem. C, 2016, 120, 25760–25779 CrossRef.
- J. Stoer and R. Bulirsch, Introduction to numerical analysis, Springer Science & Business Media, 2013, vol. 12 Search PubMed.
- R. Kosloff, Time-Dependent Quantum Molecular Dynamics, Springer, 1992, pp. 97–116 Search PubMed.
- D. Kosloff and R. Kosloff, J. Comput. Phys., 1983, 52, 35–53 CrossRef CAS.
- G. G. Balint-Kurti, R. N. Dixon and C. C. Marston, Int. Rev. Phys. Chem., 1992, 11, 317–344 Search PubMed.
- R. N. Zare and W. G. Harter, Phys. Today, 1989, 42, 68 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, SoftwareX, 2018, 7, 1–5 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. c. v. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102 CrossRef.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef.
- P. Haas, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085104 CrossRef.
- P. Statiris, H. Lu and T. Gustafsson, Phys. Rev. Lett., 1994, 72, 3574 CrossRef CAS.
- E. Soares, G. Leatherman, R. Diehl and M. Van Hove, Surf. Sci., 2000, 468, 129–136 CrossRef CAS.
- R. Nichols, T. Nouar, C. Lucas, W. Haiss and W. Hofer, Surf. Sci., 2002, 513, 263–271 CrossRef CAS.
- H. Ohtani, M. Van Hove and G. Somorjai, Surf. Sci., 1987, 187, 372–386 CrossRef CAS.
- D. L. Adams, H. Nielsen and M. A. Van Hove, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 4789 CrossRef CAS.
- M. Wijzenbroek, D. Helstone, J. Meyer and G.-J. Kroes, J. Chem. Phys., 2016, 145, 144701 CrossRef.
- A. Patra, J. E. Bates, J. Sun and J. P. Perdew, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E9188–E9196 CrossRef CAS.
- C. Cottrell, R. Carter, A. Nesbitt, P. Samson and A. Hodgson, J. Chem. Phys., 1997, 106, 4714–4722 CrossRef CAS.
- I. Groot, H. Ueta, M. Van der Niet, A. Kleyn and L. Juurlink, J. Chem. Phys., 2007, 127, 244701 CrossRef CAS.
- S. Kaufmann, personal communication.
- C. Y. Wei, S. P. Lewis, E. J. Mele and A. M. Rappe, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 10062–10068 CrossRef CAS.
- K. Shakouri, J. Behler, J. Meyer and G.-J. Kroes, J. Phys. Chem. Lett., 2017, 8, 2131–2136 CrossRef CAS.
- N. Gerrits, H. Chadwick and G.-J. Kroes, J. Phys. Chem. C, 2019, 123, 24013–24023 CrossRef CAS.
- N. Gerrits, K. Shakouri, J. Behler and G.-J. Kroes, J. Phys. Chem. Lett., 2019, 10, 1763–1768 CrossRef CAS.
- L. Schimka, J. Harl, A. Stroppa, A. Grüneis, M. Marsman, F. Mittendorfer and G. Kresse, Nat. Mater., 2010, 9, 741–744 CrossRef CAS.
- K. Lee, K. Berland, M. Yoon, S. Andersson, E. Schröder, P. Hyldgaard and B. I. Lundqvist, J. Phys.: Condens. Matter, 2012, 24, 424213 CrossRef.
- G. Darling and S. Holloway, J. Chem. Phys., 1990, 93, 9145–9156 CrossRef CAS.
- J. Juaristi, M. Alducin, R. D. Muiño, H. F. Busnengo and A. Salin, Phys. Rev. Lett., 2008, 100, 116102 CrossRef CAS.
- A. Mondal, M. Wijzenbroek, M. Bonfanti, C. Daz and G.-J. Kroes, J. Phys. Chem. A, 2013, 117, 8770–8781 CrossRef CAS.
- M. Bonfanti, M. F. Somers, C. Daz, H. F. Busnengo and G.-J. Kroes, Z. Phys. Chem., 2013, 227, 1397–1420 CAS.
- S. Mukherjee, F. Libisch, N. Large, O. Neumann, L. V. Brown, J. Cheng, J. B. Lassiter, E. A. Carter, P. Nordlander and N. J. Halas, Nano Lett., 2012, 13, 240–247 CrossRef.
- E. Hasselbrink, Surf. Sci., 2009, 603, 1564–1570 CrossRef CAS.
- B. Schindler, D. Diesing and E. Hasselbrink, J. Chem. Phys., 2011, 134, 034705 CrossRef.
- B. Schindler, D. Diesing and E. Hasselbrink, J. Phys. Chem. C, 2013, 117, 6337–6345 CrossRef CAS.
- J. C. Polanyi, Science, 1987, 236, 680–690 CrossRef CAS.
- J. C. Polanyi, Angew. Chem., Int. Ed. Engl., 1987, 26, 952–971 CrossRef.
- G.-J. Kroes, C. Daz, E. Pijper, R. A. Olsen and D. J. Auerbach, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20881–20886 CrossRef CAS.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef.
- M. Gostein, H. Parhikhteh and G. Sitz, Phys. Rev. Lett., 1995, 75, 342 CrossRef CAS.
- E. Watts and G. O. Sitz, J. Chem. Phys., 2001, 114, 4171–4179 CrossRef CAS.
- G.-J. Kroes, G. Wiesenekker, E. Baerends and R. Mowrey, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 10397 CrossRef CAS.
- A. Salin, J. Chem. Phys., 2006, 124, 104704 CrossRef CAS.
- R. Olsen, G. Kroes and E. Baerends, J. Chem. Phys., 1999, 111, 11155–11163 CrossRef CAS.
- R. Olsen, P. Philipsen and E. Baerends, J. Chem. Phys., 2003, 119, 4522–4528 CrossRef CAS.
- G. Mills, G. Schenter, D. E. Makarov and H. Jónsson, Chem. Phys. Lett., 1997, 278, 91–96 CrossRef CAS.
- G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- G. Mills and H. Jónsson, Phys. Rev. Lett., 1994, 72, 1124 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05173j |
| This journal is © the Owner Societies 2021 |