Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Inter-adsorbate forces and coherent scattering in helium spin-echo experiments
David J.
Ward
 *a,
Arjun
Raghavan†
*a,
Arjun
Raghavan†
 a,
Anton
Tamtögl
a,
Anton
Tamtögl
 b,
Andrew P.
Jardine
a,
Emanuel
Bahn
b,
Andrew P.
Jardine
a,
Emanuel
Bahn
 a,
John
Ellis
a,
Salvador
Miret-Artès
a,
John
Ellis
a,
Salvador
Miret-Artès
 c and
William
Allison
a
c and
William
Allison
a
aCavendish Laboratory, J.J. Thomson Ave., Cambridge, CB3 0HE, UK. E-mail: djw77@cam.ac.uk
bInstitute of Expermental Physics, Graz University of Technology, Petersgasse 16, 8010, Graz, Austria
cCSIC Institute of Fundamental Physics, Serrano 123, Madrid, 28006, Spain
First published on 7th October 2020
Abstract
In studies of dynamical systems, helium atoms scatter coherently from an ensemble of adsorbates as they diffuse on the surface. The results give information on the co-operative behaviour of interacting adsorbates and thus include the effects of both adsorbate–substrate and adsorbate–adsorbate interactions. Here, we discuss a method to disentangle the effects of interactions between adsorbates from those with the substrate. The result gives an approximation to observations that would be obtained if the scattering was incoherent. Information from the experiment can therefore be used to distinguish more clearly between long-range inter-adsorbate forces and the short range effects arising from the local lattice potential and associated thermal excitations. The method is discussed in the context of a system with strong inter-adsorbate interactions, sodium atoms diffusing on a copper (111) surface.
1 Introduction
Helium atom scattering is well established as a sensitive probe of surface processes and particularly for studies of the dynamics of pristine and adsorbate covered surfaces.1 Atoms are known to scatter strongly and coherently from the electron density at a surface. Thus, the technique is particularly powerful in analysing vibrations that have weight at, or near, the surface.2–4 The resulting inelastic scattering gives both the energy and wavelength dependence of the excitations. Helium atoms are also sensitive to changes in the electron density as adsorbed atoms and molecules move on an otherwise flat surface.5–7 Scattering under these circumstances generates quasi-elastic intensity, where time correlations in the intensity reflect the time-dependence of motion in the target. The present work is concerned with the diffusion of adsorbates and, in particular, the analysis of quasi-elastic scattering in helium spin-echo measurements when strong inter-adsorbate forces are present.The scattering of any wave from a dynamical assembly of particles encodes information on the factors that underlie motion within the assembly. The difficulties of extracting that information from fluctuations in the scattered intensity have been recognised since the earliest experiments of dynamical light-scattering.8 In the case of a system in equilibrium, it was argued that the time-scales of thermal excitation, inter-particle forces and the time-resolution in the experiment all have an effect on the observations.9 The degree of coherence in the scattering process also has an important contribution to the outcome of an experiment.10
In a classical, kinematic approximation, the amplitude scattered from a moving particle, j, with position, rj(t), will depend on the momentum transfer, ΔK, and time, t, as follows
| Aj(ΔK,t) = f(ΔK)exp[−iΔK·rj(t)], | (1) |
When the scattering is coherent then the amplitudes from the individual adsorbates sum to give a total amplitude
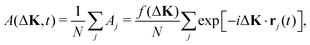 | (2) |
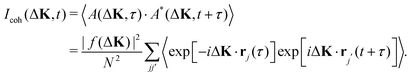 | (3) |
The angle brackets indicate an ensemble average, which is equivalent to an average over the time variable, τ, when the dynamics are ergodic.
When the scattering is incoherent the intensity from each adsorbate,
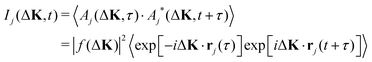 | (4) |
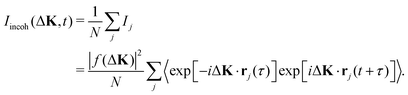 | (5) |
Here the normalisation ensures that, when all adsorbates scatter in phase, the coherent and incoherent intensities are equal.
The incoherent intensity (eqn (5)) is determined entirely by the self-correlation of individual scattering centres, j, whereas the coherent intensity (eqn (3)) includes correlations between all pairs of particles, j and j′. Cases where the motion is co-operative and where correlations between particles are important would clearly generate differences in the two measures of intensity fluctuation. Since co-operative motion requires some degree of interaction between the adsorbates, differences between the coherent and incoherent intensities reflect the nature of inter-particle forces. Incoherent scattering is regarded as having a more intuitive interpretation since it is indicative of the local adsorbate–substrate potential and the thermal excitations that control the dynamics.10 In contrast, coherent scattering will show, in addition, the effects of interactions.
Helium scattering is inherently a coherent scattering technique. However, there is a direct advantage in having access to both coherent and incoherent scattering intensities when analysing data from surface systems. In a typical diffusion study the aim is first to establish the energy landscape on which the particles move. The landscape is defined by the principal adsorption sites and the transition states for diffusion. Incoherent scattering provides a simple method that helps to distinguish the effects of the local energy landscape from long-range interactions that are generated by forces acting between the adsorbates. In that way, simple dynamical models, such as idealised hopping14,15 can be used to generate a first-cut model of the landscape before inter-adsorbate forces are considered. A more complete analysis can then proceed by analysing the strength and range of the forces that contribute to the coherent scattering. In this way a better, self-consistent description of the experimental data can be obtained.
The relationship between coherent and incoherent lineshapes is known qualitatively as de Gennes narrowing,16 though the interpretation in terms of cooperative behaviour remains a topic for debate.17 A quantitative relationship between the incoherent and coherent correlation functions has only been established for approximate systems such as site-to-site hopping motion of weakly interacting particles in three-dimensional space (3-D).10,18,19 Here, we explore the validity of the quantitative approach for the study of strongly interacting adsorbates, in a 2-D system, where the effects of correlated motion dominate the scattering.
The approach we take in the present work is first to establish a ‘typical’ system of strongly-correlated adsorbates. Here we consider sodium atoms moving on a copper (111) surface, for which both a model landscape and an interaction model are available.20 We use simulations based on the Langevin molecular-dynamics framework to deduce the coherent and incoherent scattering intensities, upon the assumption of point scatterers. The analysis indicates that 3-D models10,18 have validity when applied to strongly correlated motion in this 2-D system. Experimental results from the Na/Cu(111) system are then analysed and we demonstrate that a suitable form-factor for scattering can be constructed. The form-factor then allows us to obtain an incoherent scattering intensity from the measurements of coherent scattering.
2 Analysis of coherent and incoherent scattering
Intensity correlation functions, as given in eqn (3) and (5), are known as Intermediate Scattering Functions (ISF) in the neutron scattering literature. The interpretation of these correlation functions forms the basis of the quasi-elastic scattering technique. For unconfined lateral diffusion of the adsorbates, the long-time limit of the correlation function is assumed to decay exponentially, I(ΔK,t) ∼ exp[−α(ΔK,t)].21 In general, therefore, the intensity correlation function has a characteristic ‘lineshape’ that may be written as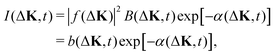 | (6) |
The quantitative relationship between coherent and incoherent lineshapes has been studied theoretically, in the context of neutron scattering10,18 and dynamical light scattering.9 These studies use approximations to make the algebra tractable. Typically they involve the interpretation of weakly interacting systems in 3-D. Examples include the diffusion of dilute interstitial particles, or diffusion in alloys. Usually, the motion is assumed to occur in the absence of an external potential,9 or on a well-defined lattice in the regime where hops are the dominant dynamical process, giving a quasi-elastic scattering lineshape that is a simple exponential.10,18,19,24 In the case of hopping, the incoherent dephasing rate, αincoh, is then assumed to have the form derived by Chudley and Elliott14
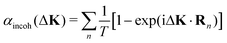 | (7) |
The dephasing rates for coherent and incoherent scattering encode the time dependence of the motion and, when interactions are present, they will have a different dependence on ΔK. In the limit of weak interactions between scattering centres, the relationship between the two dephasing rates is known.10,18 Derivations use a self-consistent field calculation within linear-response theory,18 or obtain a similar result using transition-state theory.10 In both derivations, the dephasing rates for coherent and incoherent scattering are related by the prefactor for coherent scattering, Bcoh(ΔK,t = 0), so that
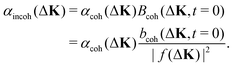 | (8) |
Sinha and Ross18 were the first to include the motion of spatially extended objects having a defined form-factor, |f(ΔK)|2, and hence derive eqn (8) in the form given. In their case the extended object was a lattice distortion surrounding a moving interstitial atom; however, their argument is equally applicable to scattering from the distribution of electronic charge surrounding a moving adsorbate, as in the present work. The prefactor for coherent scattering, bcoh(ΔK,t = 0), is known as either the quasi-elastic contribution to the structure factor18 or the intensity due to short range order.10
Eqn (8) is significant as it shows that measurements of coherent scattering can be used, in principle, to deduce the dephasing rates for incoherent scattering. The method outlined above is widely used in weakly-interacting 3-D systems but the approximations are untested in the context systems with strong spatial correlation, such as diffusion in 2-D, and for a strongly scattering probe such as helium atoms. In the present paper we explore the value of eqn (8) in the context of surface systems with strong correlations in the motion. We show that incoherently scattered intensity can be deduced from measurements of coherent helium scattering, at a good level of approximation.
3 Numerical simulations of coherent and incoherent scattering
The motion of adsorbates on a periodic surface may be reproduced with various forms of molecular dynamics simulations. In the present work we are concerned with the calculation of scattering from the adsorbates and, for that purpose, the Langevin, or Generalised-Langevin framework provides a convenient and well established method to understand the motion.25–29 Here, the dynamical coordinates of the adsorbates are treated explicitly while the substrate interactions are represented by an adiabatic potential-energy surface. Thermal excitation is represented by a combination of random forces and an appropriate frictional force and it is possible to include an explicit description of inter-adsorbate interactions.Differences in the calculated intensity correlations using the Langevin or Generalised-Langevin equations depend on the frequency spectrum of the thermal noise; however, those differences disappear as the correlation-time extends beyond any correlations in the noise spectrum.28 For these reasons we adopt the computationally more efficient Langevin approach. The equation of motion for the dynamical coordinates, rj, is
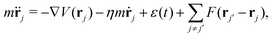 | (9) |
The equations of motion may be integrated for discrete time steps, δt, building up a ‘trajectory’, ri(t), for each adsorbate. Sample trajectories for two atoms taken from a simulation are shown in Fig. 1. The simulation includes 500 interacting sodium atoms on a copper[111] surface at a temperature of 155 K. The adiabatic potential, coverage of Θ = 0.025 monolayer defined with respect to the saturation coverage and friction η = 0.43 ps−1 are taken from ref. 20 and correspond to values that describe the experimental data discussed below. Kohn–Lau32 dipole–dipole inter-adsorbate forces are included, parameterised according to ref. 20. The trajectories in Fig. 1 map out a honeycomb structure on which hopping between sites takes place. A honeycomb trajectory arises when both hcp and fcc sites of the (111) surface act as adsorption sites.33 Adsorbates spend a significant time at one adsorption site until gaining sufficient energy to overcome the energy barrier between sites. Occasional long hops are evident in the trajectories. In these instances the adsorbate traverses two or more barriers, before becoming trapped again at a particular adsorption site. The fraction of the long hops, relative to single jumps, depends on the friction25 and those that are evident in Fig. 1 are consistent with the low friction used in the simulation. Co-operative motion due to the effects of interactions between adsorbates cannot easily be seen from a superficial inspection of trajectories such as in Fig. 1, but the effects are clearly apparent in the correlation functions we discuss below.
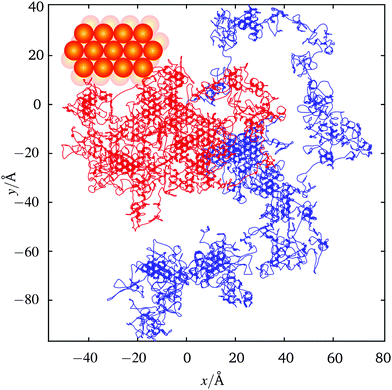 | ||
Fig. 1 Sample trajectories for two representative adsorbates (red and blue) out of a simulation of 500 interacting species. The simulation data was collected during a total run time of 6500 ps. Parameters, such as the adiabatic potential, coverage (Θ = 0.025 monolayer) and friction (η = 0.43 ps−1) are the same as those reported in ref. 20 and correspond to values that describe the experimental data discussed below. Both fcc and hcp sites have a local minimum in the potential and the system temperature is such that single hops between adjacent sites dominate the motion. Occasionally, the trajectories exhibit long hops due to the low value of the friction η. Inset shows the real space atomic structure of the substrate, measurements and simulations reported are performed on the [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ] direction which is aligned with the y axis. ] direction which is aligned with the y axis. | ||
We calculate the coherent and the incoherent scattering intensities defined in eqn (3) and (5) using the relevant amplitudes, A(ΔK,t) according to (2) and Aj(ΔK,t) according to (1) respectively, where the phase factor, aj(ΔK,t) = exp[−iΔK·rj(t)], is constructed from the trajectory, r(t). Its temporal Fourier transform
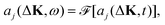 | (10) |
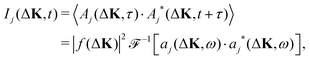 | (11) |
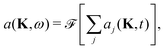 | (12) |
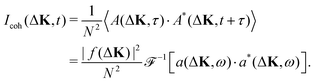 | (13) |
In general the intensity correlation functions are more complex than the single exponential decay assumed in the derivation of eqn (8) and complete analytic forms are only known for a limited number of simple systems.22,23,28 Fortunately, it is not necessary to know the analytic form of the amplitude in order to explore the validity of eqn (8). We do, however, need to determine the two key quantities, αcoh(ΔK), and, bcoh(ΔK,t = 0).
In the work below we use a similar procedure to analyse the intensity correlation functions from the numerical simulations and the experimental data, taking the form-factor, |f(ΔK)|2 = 1, in the simulations. First, the dephasing rates, α(ΔK), for coherent and incoherent scattering are extracted by fitting the simulated intensities, Iincoh and Icoh, at long times to a decaying exponential boexp[−α(ΔK,t)]35 (see also Supplementary Information of Rittmeyer et al.20). Second, we extract the ‘short time scale’ contribution to the structure factor using a Gaussian, b1exp[−(t/σ)2], where the width parameter, σ, approximates the ballistic motion and any remaining terms, at short times. The quasi-elastic contribution to the structure factor from eqn (6) is then given by,
| bcoh(ΔK,t = 0) = bo + b1. | (14) |
Fig. 2 shows results from simulations of Na/Cu(111) using trajectories such as those in Fig. 1. Blue data points (Fig. 2(a)) give the dephasing rate for coherent scattering as a function of momentum transfer in the [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ] direction. The results are characteristic of strong repulsive forces between the adsorbates36 that are evident in the pronounced maximum and subsequent dip observed for ΔK < 0.5 Å−1. Scatter in the data points arises from the statistical uncertainty of the simulations.
] direction. The results are characteristic of strong repulsive forces between the adsorbates36 that are evident in the pronounced maximum and subsequent dip observed for ΔK < 0.5 Å−1. Scatter in the data points arises from the statistical uncertainty of the simulations.
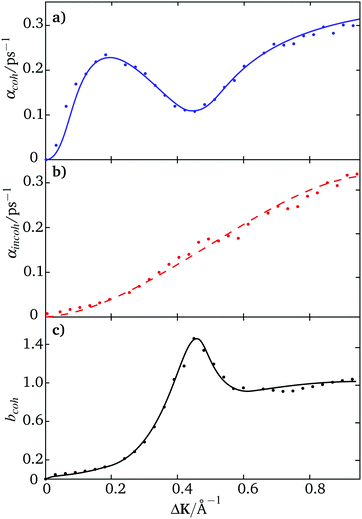 | ||
Fig. 2 Analysis of trajectory data for scattering along the [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ] direction (y-axis in inset to Fig. 1). Panel (a) shows the coherent dephasing rates, αcoh(ΔK) calculated using parameters according to ref. 20. The dephasing rates for coherent scattering, shown as blue data points with a line to guide the eye, are extracted from the long-time limit of the intensity correlation function (see text). Panel (b) shows incoherent dephasing rates, αincoh(ΔK), as a dashed red line. The rates are calculated in the same way as in (a) but using eqn (5). The red data points are deduced from results in panels (a) and (c), with f(ΔK) = 1. The black points in panel (c) show the quasi-elastic contribution to the structure factor, bcoh(ΔK,t = 0) (see text) with the solid line to guide the eye. Values that deviate from unity indicate the effects of inter-adsorbate interactions on the resulting dephasing rates. ] direction (y-axis in inset to Fig. 1). Panel (a) shows the coherent dephasing rates, αcoh(ΔK) calculated using parameters according to ref. 20. The dephasing rates for coherent scattering, shown as blue data points with a line to guide the eye, are extracted from the long-time limit of the intensity correlation function (see text). Panel (b) shows incoherent dephasing rates, αincoh(ΔK), as a dashed red line. The rates are calculated in the same way as in (a) but using eqn (5). The red data points are deduced from results in panels (a) and (c), with f(ΔK) = 1. The black points in panel (c) show the quasi-elastic contribution to the structure factor, bcoh(ΔK,t = 0) (see text) with the solid line to guide the eye. Values that deviate from unity indicate the effects of inter-adsorbate interactions on the resulting dephasing rates. | ||
Fig. 2(b) shows the corresponding dephasing rates for incoherent scattering. In this case the results, deduced from eq:incohintensity, are shown by the red line. Note that the statistical variation is much less than in panel (a) as the incoherent intensities are averaged over all trajectories in addition to the averaging over repeated simulation runs which also takes place in the calculation of the coherent intensities. The data points in the middle panel are calculated from eqn (8) using values of αcoh in panel (a) and values of the quasi-elastic contribution to the structure factor, bcoh(ΔK,t = 0) shown in Fig. 2(c). The main feature in panel (c) is the dramatic decrease in bcoh(ΔK,t = 0) as ΔK approaches zero and a similar effect is evident in the experiment (see later). The strong inter-adsorbate interactions maintain the separation of the adsorbates and stabilise structures where interference in the scattered amplitudes from neighbouring adsorbates interfere destructively, giving rise to the low scattered intensity at small ΔK. The converse is evident in the peak between 0.4–0.5 Å−1, where the same structures tend to scatter constructively and the corresponding scattered intensity is higher.
The excellent agreement between the two estimates of the incoherent dephasing rates (red points and solid line in In Fig. 2(b)) supports both the analytic model,18eqn (8) and our method of analysis.
For the analysis leading to Fig. 2 we have taken the adsorbates to be point scatterers and the corresponding form-factor for scattering f(ΔK) = 1 in eqn (8). We now turn to the analysis of experiment and, in particular, the determination of the experimental form-factor.
4 Experimental measurements and the form-factor
There are significant differences between intensity correlation functions from experimental and from numerical simulation. In the experiment there are contributions from inelastic scattering, due to substrate phonons,1 and purely elastic scattering from static features on the surface contributes to the total intensity. In addition, the form-factor for scattering from the mobile species, |f(ΔK)|2, must be extracted from the ΔK dependence of the scattered intensity.Contributions from inelastic scattering are removed by a Fourier filter, applied in the frequency domain,20,35 while scattering from static structures is accounted for by subtracting a constant term so that the intensity has the same form as eqn (6) and I(ΔK,t) → 0 as t → ∞.
The coherent intensity can then be analysed in the same way as the simulations (see above). In order to extract an approximate dephasing rate for incoherent scattering according to eqn (8), we need a corresponding approximation to the ΔK dependence of the form-factor. Earlier works, such as measurements using time-of-flight methods,37 have been analysed on the basis of a power law to approximate the form-factor
| |f(ΔK)|2 = CΔK−n. | (15) |
Ellis et al.37 found the exponent to be, n = 3 in the case of Xe atoms on a Pt(111) surface. However, the value of n will depend on the nature of the scattering object. For example, a value n = 2 at small values of ΔK, is predicted for scattering from a 1-D object such as a step.38
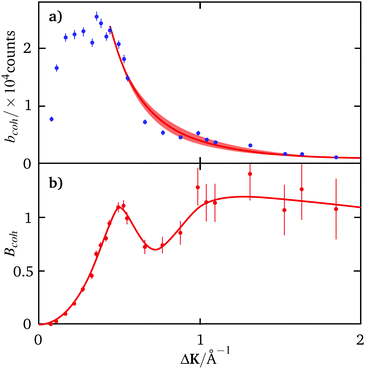
In the present analysis, we treat n as a free parameter and determine the value that best describes the ΔK dependence of the measured intensity at large momentum transfers, where Bcoh(ΔK,t = 0) is approximately constant. Fig. 3(a) shows the measured quasi-elastic intensity, bcoh(ΔK,t = 0), as blue data points together with the best-fit to the form-factor, |f(ΔK)|2 according to (15) (red curve). A value of n = 2.2 ± 0.2 describes the trend in the data for 0.44 < ΔK< 2 Å−1. At smaller values of ΔK the intensity deviates markedly from ΔK−n and we attribute the effect to the expected decrease in quasi-elastic intensity noted in Fig. 2(c), above.
Fig. 3(b) shows the amplitude of the quasi-elastic lineshape, Bcoh(ΔK,t = 0) = bcoh(ΔK,t = 0)/|f(ΔK)|2, derived from the data in panel (a). The result shows the same features as observed in the trajectory simulations (Fig. 2(c), above) namely, a reduction in quasi-elastic intensity as ΔK → 0, followed by a maximum corresponding to diffraction from quasi-static structures. The fact that these features emerge strongly from such a simple model for the form-factor (eqn (15)) suggests that the procedure is robust.
Fig. 4 shows the coherent and incoherent dephasing rates obtained from coherent scattering data. Blue points in panel (a) are coherent dephasing rates derived from the time-dependence of the experimental data while the red points in lower panel (b) show incoherent rates deduced using eqn (8) and the amplitude of the quasi-elastic lineshape, Bcoh(ΔK,t = 0), shown in Fig. 3(b). The differences between the red and blue data are as expected. In particular, the shape of the incoherent data (red points) is clearly quadratic at small values of ΔK indicating diffusive behaviour in the absence of correlated motion, as would be expected for hopping according to eqn (7).
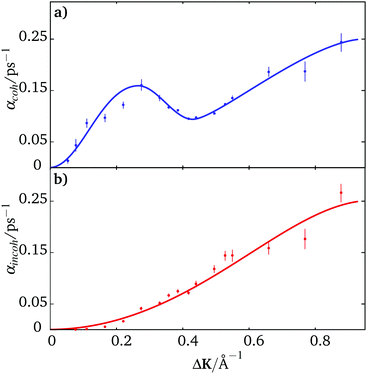 | ||
| Fig. 4 Top panel (a) shows the dephasing rate α(ΔK) for coherent scattering in blue. In the lower panel (b) red points show the dephasing rate for incoherent scattering obtained by scaling the blue data points by Bcoh(ΔK,t = 0) = bcoh(ΔK,t = 0)/|f(ΔK)|2 according to eqn (8). The lines are drawn as a guide to the eye. | ||
5 Conclusions
The results presented above show that it is possible to remove the influence of inter-adsorbate correlations leading to data equivalent to an incoherent scattering experiment. The data can then be analysed using simple models to give an approximation to the energy landscape before including inter-adsorbate interactions in a more complete analysis.Our simulations use a molecular-dynamics approach, which includes both inter-cell and intra-cell motion. However, the analysis would be identical for a simulation using Monte-Carlo methods where the trajectories for each adsorbate are generated by random hops on a specified lattice.39 The resulting lineshape (eqn (6)) is simpler to analyse, since intra-cell motion is absent, but the results should be the same, as long as the Monte-Carlo algorithm generates the correct statistical occupancy of sites.10
The form-factor in helium scattering is relatively little studied and it is a significant challenge, if eqn (8) is to be applied more widely in quasi-elastic scattering experiments with helium atoms. In the present case, variations in the scattered intensity can be attributed to the form-factor at large ΔK and to a variation in the quasi-elastic contribution to the structure factor at low ΔK. Furthermore the form-factor is well described by a simple power law in dependence of ΔK. For systems having greater complexity in the dynamics, such as the motion of molecules, the analysis may be more difficult. Hence wider experimental studies of the scattering form-factor would provide a significant benefit to the analysis method that has been outlined here.
A further factor in the success of the present work may be a fortuitous choice of the adsorbate coverage in relation to the strength of the interactions and the surface temperature. The low coverage and the strong pairwise forces together ensure that the quasi-elastic contribution to the structure factor deviates from unity only at small values of ΔK ≤ 0.6 Å−1 as in Fig. 2(c). Thus the effect of adsorbate interactions are evident in a region of ΔK-space that is clearly different from the effects of the shorter range of forces from the substrate potential. The latter will be most evident at larger ΔK. Similarly, the temperature in the present work is low enough to allow strong correlations to emerge in the adsorbate dynamics, which in turn suggests large differences between coherent and incoherent scattering. At higher temperatures the differences between coherent and incoherent will be reduced as the thermal forces dominate the dynamics. It follows that, in the high-temperature limit, it would be difficult to distinguish between thermal forces and pairwise forces from the ΔK dependence of the dephasing rates. In that regime a two-bath model for interactions would then be appropriate.30,31
Although the derivation of eqn (8) assumed weak forces, which suggests the results should be approximate for the strongly correlated dynamics of sodium diffusing on copper, it is nevertheless remarkably successful. Our results use stronger interactions, applied in a dynamical range with more highly correlated motion than earlier work10 and they support the suggestion that the method (eqn (8)) has a wider application than is implied by the approximation used in its derivation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge use of and support by the Cambridge Atom Scattering Facility (https://atomscattering.phy.cam.ac.uk) and EPSRC award EP/T00634X/1. One of us (AT) acknowledges financial support provided by the FWF (Austrian Science Fund) within the project J3479-N20. One of us (SMA) would like to acknowledge the Ministerio de Ciencia, Universidades e Innovacion (Spain) for the grant with Ref. FIS2017-83473-C2-1-P. We thank the Cavendish Workshop, particularly Rik Balsod, for making the titanium dispenser that was critical for taking the experimental data.References
- G. Benedek and J. P. Toennies, Atomic Scale Dynamics at Surfaces, Springer Berlin Heidelberg, Berlin, Heidelberg, 2018, vol. 63, pp. 1–562 Search PubMed.
- G. Benedek, S. Miret-Artés, J. R. Manson, A. Ruckhofer, W. E. Ernst and A. Tamtögl, J. Phys. Chem. Lett., 2020, 11, 1927–1933 CrossRef CAS.
- G. Benedek, J. R. Manson and S. Miret-Artés, Adv. Mater., 2020, 32, 2002072 CrossRef CAS.
- A. Tamtögl, D. Campi, M. Bremholm, E. M. J. Hedegaard, B. B. Iversen, M. Bianchi, P. Hofmann, N. Marzari, G. Benedek, J. Ellis and W. Allison, Nanoscale, 2018, 10, 14627–14636 RSC.
- G. Alexandrowicz and A. P. Jardine, J. Phys.: Condens. Matter, 2007, 19, 305001 CrossRef.
- A. P. Jardine, G. Alexandrowicz, H. Hedgeland, W. Allison and J. Ellis, Phys. Chem. Chem. Phys., 2009, 11, 3355–3574 RSC.
- G. Fratesi, G. Alexandrowicz, M. I. Trioni, G. P. Brivio and W. Allison, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235444 CrossRef.
- Y. Yan and J. Clarke, Adv. Colloid Interface Sci., 1989, 29, 277–318 CrossRef CAS.
- P. N. Pusey, J. Phys. A: Math. Gen., 1975, 8, 1433–1440 CrossRef.
- M. Leitner and G. Vogl, J. Phys.: Condens. Matter, 2011, 23, 254206 CrossRef.
- P. Fouquet, H. Hedgeland and A. P. Jardine, Zeitschrift für Physikalische Chemie, 2010, 224, 61–81 CrossRef CAS.
- I. Calvo-Almazán, M. Sacchi, A. Tamtögl, E. Bahn, M. M. Koza, S. Miret-Artés and P. Fouquet, J. Phys. Chem. Lett., 2016, 7, 5285–5290 CrossRef.
- A. Jones, A. Tamtögl, I. Calvo-Almazán and A. Hansen, Sci. Rep., 2016, 6, 27776 CrossRef.
- C. T. Chudley and R. J. Elliott, Proc. Phys. Soc., 1961, 77, 353–361 CrossRef.
- F. E. Tuddenham, H. Hedgeland, A. P. Jardine, B. A. J. Lechner, B. J. Hinch and W. Allison, Surf. Sci., 2010, 604, 1459–1475 CrossRef CAS.
- P. de Gennes, Physica, 1959, 25, 825–839 CrossRef CAS.
- B. Wu, T. Iwashita and T. Egami, Phys. Rev. Lett., 2018, 120, 135502 CrossRef.
- S. Sinha and D. Ross, Phys. B + C, 1988, 149, 51–56 CrossRef CAS.
- M. Leitner, B. Sepiol, L. Stadler, B. Pfau and G. Vogl, Nat. Mater., 2009, 8, 717–720 CrossRef CAS.
- S. P. Rittmeyer, D. J. Ward, P. Gütlein, J. Ellis, W. Allison and K. Reuter, Phys. Rev. Lett., 2016, 117, 1–5 CrossRef.
- P. S. M. Townsend and J. Ellis, J. Chem. Phys., 2018, 149, 194705 CrossRef.
- J. L. Vega, R. Guantes and S. Miret-Artés, J. Phys.: Condens. Matter, 2004, 16, S2879–S2894 CrossRef CAS.
- R. Guantes, J. L. Vega, S. Miret-Artés and E. Pollak, J. Chem. Phys., 2004, 120, 10768–10779 CrossRef CAS.
- P. C. Clapp and S. C. Moss, Phys. Rev., 1966, 142, 418–427 CrossRef CAS.
- T. Ala-Nissila, R. Ferrando and S. C. Ying, Adv. Phys., 2002, 51, 949–1078 CrossRef CAS.
- S. Miret-Artés and E. Pollak, J. Phys.: Condens. Matter, 2005, 17, S4133–S4150 CrossRef.
- A. P. Jardine, H. Hedgeland, G. Alexandrowicz, W. Allison and J. Ellis, Prog. Surf. Sci., 2009, 84, 323–379 CrossRef CAS.
- P. S. M. Townsend and D. J. Ward, J. Phys. Commun., 2018, 2, 075011 CrossRef.
- N. Avidor, P. S. Townsend, D. J. Ward, A. P. Jardine, J. Ellis and W. Allison, Comput. Phys. Commun., 2019, 242, 145–152 CrossRef CAS.
- R. Martínez-Casado, J. L. Vega, A. S. Sanz and S. Miret-Artés, J. Phys.: Condens. Matter, 2007, 19, 305002 CrossRef.
- R. Martínez-Casado, J. L. Vega, A. S. Sanz and S. Miret-Artés, Phys. Rev. Lett., 2007, 98, 1–4 CrossRef.
- W. Kohn and K. Lau, Solid State Commun., 1976, 18, 553–555 CrossRef CAS.
- B. A. J. Lechner, H. Hedgeland, J. Ellis, W. Allison, M. Sacchi, S. J. Jenkins and B. J. Hinch, Angew. Chem., Int. Ed., 2013, 52, 5085–5088 CrossRef CAS.
- J. Ellis and A. P. Graham, Surf. Sci., 1997, 377-379, 833–842 CrossRef CAS.
- D. J. Ward, Doctoral thesis, University of Cambridge, 2013 Search PubMed.
- G. Alexandrowicz, A. P. Jardine, H. Hedgeland, W. Allison and J. Ellis, Phys. Rev. Lett., 2006, 97, 156103 CrossRef CAS.
- J. Ellis, A. P. Graham and J. P. Toennies, Phys. Rev. Lett., 1999, 82, 5072–5075 CrossRef CAS.
- A. M. Lahee, J. R. Manson, J. P. Toennies and C. Wöll, J. Chem. Phys., 1987, 86, 7194 CrossRef CAS.
- A. Tamtögl, M. Sacchi, N. Avidor, I. Calvo-Almazán, P. S. M. Townsend, M. Bremholm, P. Hofmann, J. Ellis and W. Allison, Nat. Commun., 2020, 11, 278 CrossRef.
Footnote |
| † Current address: Department of Physics, University of Illinois at Urbana-Champaign – 1110 W. Green St., Urbana, IL 61801. |
| This journal is © the Owner Societies 2021 |