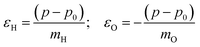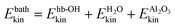Vibrational energy relaxation of interfacial OH on a water-covered α-Al2O3(0001) surface: a non-equilibrium ab initio molecular dynamics study
Giacomo
Melani
 *ac,
Yuki
Nagata
*ac,
Yuki
Nagata
 b and
Peter
Saalfrank
b and
Peter
Saalfrank
 *c
*c
aInstitut für Chemie, Universität Zürich, Winterthurerstrasse 190, CH-8057 Zürich, Switzerland. E-mail: giacomo.melani@chem.uzh.ch
bMax-Planck Institute für Polymerforschung, Ackermannweg 10, 55128 Mainz, Germany
cInstitut für Chemie, Universität Potsdam, Karl-Liebknecht-Straße 24-25, D-14476 Potsdam-Golm, Germany. E-mail: peter.saalfrank@uni-potsdam.de
First published on 28th August 2020
Abstract
Vibrational relaxation of adsorbates is a sensitive tool to probe energy transfer at gas/solid and liquid/solid interfaces. The most direct way to study relaxation dynamics uses time-resolved spectroscopy. Here we report on a non-equilibrium ab initio molecular dynamics (NE-AIMD) methodology to model vibrational relaxation of OH vibrations on a hydroxylated, water-covered α-Al2O3(0001) surface. In our NE-AIMD approach, after exciting selected O–H bonds their coupling to surface phonons and to the water adlayer is analyzed in detail, by following both the energy flow in time, as well as the time-evolution of Vibrational Density of States (VDOS) curves. The latter are obtained from Time-dependent Correlation Functions (TCFs) and serve as prototypical, generic representatives of time-resolved vibrational spectra. As most important results, (i) we find a few-picosecond lifetime of the excited modes and (ii) identify both hydrogen-bonded aluminols and water molecules in the adsorbed water layer as main dissipative channels, while the direct coupling to Al2O3 surface phonons is of minor importance on the timescales of interest. Our NE-AIMD/TCF methodology is powerful for complex adsorbate systems, in principle even reacting ones, and opens a way towards time-resolved vibrational spectroscopy.
I. Introduction
Water-covered metal oxides play an important role in many areas of surface science, with applications ranging from heterogeneous catalysis over electrochemistry to geochemistry.1 Tremendous effort has been investigated in recent years to characterize various water/metal oxide interfaces,2–9 which improved our molecular-level understanding of their surface physical chemistry. Vibrational spectroscopy is a powerful tool to do so. Notably, surface-sensitive Vibrational Sum Frequency (VSF) spectroscopy has been employed for silica/water,10 quartz/water,11 or alumina (Al2O3)/water12 interfaces. Here we concentrate on the latter, as a particularly well studied model system for insulating metal oxides.While most of the vibrational studies above are of the steady-state type, a more direct account of dynamics is provided by time-resolved spectroscopy, e.g., VSF in a pump–probe mode.13 Time-resolved spectroscopy can give direct information on energy transfer between an adsorbate and the surface, which is central for the understanding of adsorbate bonding but also for more applied issues, such as energy storage or bond-selective chemistry. In the pump–probe variant of VSF spectroscopy,14 a spectrally narrow IR (infrared) pulse is used to excite/pump an adsorbate vibration, which is then probed by two spatially and temporarily overlapping IR and visible pulses which generate a VSF signal that is recorded as a function of frequency and the delay time Δt, between pump and probe pulses. Both steady-state and time-resolved VSF spectra have recently been recorded for water-covered α-Al2O3(0001) surfaces by Borguet et al.,15–17 for example, focusing primarily on the hydrogen-bonded spectral region and on the effects of interfacial electrolytes on O–H stretching vibrations.
In own recent work, in a combined experimental/theoretical effort, the so-called Al–I terminated α-Al2O3(0001) surface18–22 as the most stable alumina surface in vacuum,19–22 further a hydroxylated α-Al2O3(0001),21,23 as well as O-terminated α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02)24 and O-terminated α-Al2O3(11
02)24 and O-terminated α-Al2O3(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0)25 surfaces, all in contact with small amounts of water were studied with steady-state VSF spectroscopy, mostly to characterize the vibrations of interfacial O–H (or O–D) bonds. From the theory side, periodic Density Functional Theory (DFT) was used, either stationary and together with Normal Mode Analysis (NMA),20,21,24,25 or in the form of ab initio molecular dynamics (AIMD) in combination with Time-dependent Correlation Function (TCF) methods,22,23 to characterize adsorbate vibrations. The AIMD/TCF approach is computationally costly but also very powerful, as it accounts for Vibrational Density Of States (VDOS) curves and even for spectra, IR and VSF,22,23 beyond the harmonic approximation and it explicitly includes the effects of temperature, which allows for direct comparison between simulations and experiments.
0)25 surfaces, all in contact with small amounts of water were studied with steady-state VSF spectroscopy, mostly to characterize the vibrations of interfacial O–H (or O–D) bonds. From the theory side, periodic Density Functional Theory (DFT) was used, either stationary and together with Normal Mode Analysis (NMA),20,21,24,25 or in the form of ab initio molecular dynamics (AIMD) in combination with Time-dependent Correlation Function (TCF) methods,22,23 to characterize adsorbate vibrations. The AIMD/TCF approach is computationally costly but also very powerful, as it accounts for Vibrational Density Of States (VDOS) curves and even for spectra, IR and VSF,22,23 beyond the harmonic approximation and it explicitly includes the effects of temperature, which allows for direct comparison between simulations and experiments.
The motivation for our present, theoretical work is to extend the previous AIMD/TCF simulations explicitly to the time-dependent domain, by initially vibrationally exciting specific O–H chromophores of a water-covered alumina surface, and follow their dynamics after increasing time delays, in the spirit of a pump–probe vibrational analysis. Specifically, we shall consider a water-covered, hydroxylated α-alumina interface (see below), and excite high-frequency O–H vibrations associated with non-hydrogen bonded aluminol groups, i.e., quasi-free O–H units attached to surface Al ions. In fact, this surface was extensively studied by us before,21,23 and currently corresponding pump–probe VSF experiments are underway to study vibrational relaxation.26 We shall try, on the basis of non-equilibrium ab initio molecular dynamics (NE-AIMD) simulations, to (i) model the vibrational energy relaxation times of excited surface aluminols in H2O/α-Al2O3(0001) and (ii) understand the vibrational relaxation mechanism and energy flow in this system. (iii) A third goal for this work is to extend the known NE-AIMD methodology,27 to calculate time-resolved vibrational spectra for complex interfaces. For that, NE-AIMD will be combined with time-windowed TCF methods, with time-dependent correlation functions serving to compute spectra I(ω,Δt) as needed for interpreting pump–probe IR/VSF signals, for example. Here, we shall not make the full step to pump–probe IR/VSF spectra, though, and compute time-resolved VDOS curves instead, i.e., time-resolved power spectra that can be seen as a generic precursors to real spectra. On top, the VDOS curves help to analyze the relaxation process, complementary to other tools, such as kinetic energy analysis.
Concerning the vibrational energy redistribution it is common practice to define a “vibrational lifetime”, as the population decay time of the excited chromophore's v = 1 state to the ground state, v = 0, i.e., Pv=1(t) ∝ exp(−t/τ). Note that this definition holds strictly for quantum mechanics and for T = 0 only and in fact, neither in experiment nor in our classical theory as here one necessarily operates with Pv=1(t) curves but uses related measures instead. For excited O–H stretching vibrations at non-metallic interfaces, a wide range of lifetimes can be expected. In case when the OH bond was part of a hydrogen-bonded network, e.g., a water layer, time-resolved VSF experiments for the air/water interface gave lifetimes ≤1 ps.14,28 Here the excited interfacial OH relaxes efficiently thanks to its direct coupling with H2O bending overtones, which then allows further relaxation into the hydrogen bonding modes. If, on the other hand, an isolated O–H stretch mode, say, was directly coupled to surface phonons only, one could expect much longer lifetimes. In this case the high-frequency O–H mode can only relax via slow multi-phonon processes, because the Debye frequency of the surface is much lower. For α-alumina, the Debye frequency is in the order of 1000 cm−1, so three to four phonons would be required for relaxation at least. Multi-phonon relaxation is indeed a slow process: an extreme example is the C–O stretch mode of carbon monoxide on NaCl(100), with τ ∼ 4 ms.29 Another example, chemically closer to α-alumina is represented by the O–H stretching relaxation of interfacial silanols in silica. For this system, early time-resolved vibrational spectroscopy measurements30,31 indicated a lifetime in the order of 100 ps. In the present study, the excited O–H chromophores are neither strongly H-bonded nor in contact with surface phonons only (there are water molecules around, see below), so an intermediate situation may be expected. In fact, we shall find lifetimes in the order of several picoseconds below.
Our paper is organized as follows. In the next Section II, the model of the interface studied here, hydroxylated α-Al2O3(0001) with additional water will be introduced and static DFT and canonical AIMD calculations on this system done in ref. 23 will be reviewed that are of relevance also for the present study. In Section III, the NE-AIMD methodology used here will be introduced, analysis methods will be described together with the NE-AIMD/TCF approach to time- and frequency resolved VDOS spectra. In Section IV we present results, i.e., (i) lifetime calculations based on kinetic-energy analysis, (ii) subsystem-resolved energy flows to unravel the relaxation mechanism, (iii) time- and frequency resolved VDOS spectra for lifetime estimates, and as the precursors for time-resolved vibrational spectra just mentioned. A final Section V summarizes and concludes this work.
II. The surface model, static DFT and canonical AIMD calculations
A. The water/aluminol interface model
As the pump–probe VSF experiments26 were done on a α-Al2O3(0001) surface sample exposed to air or to liquid water at room temperature, we employed a surface model that roughly represents α-alumina at low/medium water coverage. The model is the same as used in ref. 23 for the interpretation of vibrational spectra of water-covered α-alumina(0001). It consists of a hydroxylated alumina surface which forms from the so-called Al-terminated, UHV-stable (0001) surface.18,32–34 The latter has an atomic-layer sequence Al–O3–Al–Al–O3–Al–R, where “R” stands for a repetition of the Al–O3–Al sequence into the bulk (when referring to a 1 × 1 cell). When exposed to water, the top layer Al-atoms are removed and the topmost O layer is saturated with hydrogen – the hydroxylated surface (HS) has formed. The atomic-layer sequence of the HS is (HO)3–Al–(Al–O3–Al)–R. Within a 2 × 2 cell, which we use here, we have twelve terminating OH bonds, or aluminols. We consider in addition, five Al layers and two oxygen layers, giving a simulation cell of composition Al20O36H12. In our model, on top of the upper surface layer we adsorb eight intact water molecules. We refer to this system as the “Hydroxylated Surface +2 MonoLayers” (2ML) model, or HS + 2ML as in ref. 23. The HS + 2ML structure was found particularly stable by Density Functional Theory (DFT) calculations, due to the formation of a honeycomb-like layer network consisting of water hexagons.23The high stability is due to the formation of hydrogen bonds between some of the aluminol OH groups and molecular H2O. In the model of Fig. 1, four of the twelve aluminol OH groups are non-hydrogen bonded (“quasi-free”), while eight are involved in H-bonds. The water layer appears to be also very rigid during AIMD trajectories, which makes this distinction between hb- (hydrogen-bonded) and nhb-aluminols (non-hydrogen bonded) valid on all timescales considered here and in ref. 23. As seen in Fig. 1, the quasi-free aluminols can come in “upright” and more “parallel” orientations relative to the surface. We note that in geometry optimization, NMA and AIMD only the uppermost three atomic layers plus the hydrogens of our HS + 2ML were allowed to move, while the lower layers were kept frozen at bulk geometries.21,23 The same protocol was followed in the AIMD simulations for the present work.
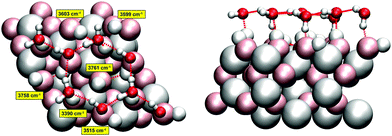 | ||
| Fig. 1 Top (left) and side views (right) of the hydroxylated α-Al2O3(0001) surface (2 × 2), with additional eight water molecules (HS + 2ML). Our model has a stoichiometric composition of 92 atoms (Al20O36H12·(H2O)8). Surface atoms are shown as “van der Waals spheres” in pale colors, water thin films in a “ball-and-stick” representation (H in white, Al in grey and O in red, surface atoms large, water atoms small). Hydrogen bonds are indicated by dashed red lines. In the left panel, for some of the O–H groups harmonic frequencies, calculated at the PBE + D2 level of theory, are indicated in wavenumbers. In particular, there are four non-hydrogen-bonded aluminol OH groups, two of them “upright” and with very high frequencies (3758 cm−1 and 3761 cm−1), and two of them in “parallel” orientation with lower frequencies (3603 cm−1 and 3599 cm−1). Even lower frequencies are found for hydrogen-bonded aluminols – two examples are shown. In AIMD, only the uppermost three atomic layers (an O layer and a double-layer of Al) plus the adsorbate atoms were allowed to move, while the lower layers were kept frozen at PBE + D2 bulk geometries.21 | ||
B. Stationary DFT and canonical AIMD calculations
For the HS + 2ML model shown in Fig. 1, we performed geometry optimization, NMA, and AIMD simulations,23 all at the Kohn–Sham35 DFT (KS-DFT) level of theory, employing the Perdew–Burke–Ernzerhof (PBE)36 exchange–correlation functional and a projector-augmented plane-wave basis (PAW)37 as implemented in the Vienna Ab initio Simulation Package (VASP).38–40 Dispersive van der Waals interactions were included by Grimme's empirical D2 method.41 For all calculations a 3 × 3 × 1 k-point mesh and a kinetic energy cutoff of 400 eV were used. The 2 × 2 cell slab models used have an extension of 9.66 Å × 9.66 Å × 31.41 Å (20 Å of vacuum in the z-direction) and employ 3D periodic boundary conditions.In ref. 23, besides NMA for harmonic frequency analysis, we also modelled vibrational spectra (Vibrational Densities of States, VDOS, IR and VSF) of the hydroxylated α-alumina(0001) surface without (HS) and with (HS + 2ML) additional water, using AIMD at 300 K with the Nosé–Hoover thermostat.42–44 Specifically, we fully employed surface-specific Velocity–Velocity Autocorrelation Functions (VVAFs) to calculate ssp-polarized VSF spectra.45 AIMD showed that the aluminol OH bonds on the hydroxylated (0001) surface, are orientationally flexible at room temperature: within a ps-timescale, they can switch from the “upright” position (polar angle (θOH) less than 45°) to a “parallel” one, where the bonds are almost flat with respect to the (0001) surface plane. With an additional water layer, this flexibility is somewhat hindered. Further details about the orientational behaviour of aluminols OH can be found in ref. 23. In all AIMD calculations a timestep of 0.2 fs was adopted.
In ref. 23, the following characteristic frequencies/frequency ranges for HS + 2ML were found by NMA:
• parallel aluminols show vibrational frequencies around 3600 cm−1 if not involved in accepting hydrogen bonds from nearby water molecules;
• non-hydrogen bonded upright aluminols have higher vibrational frequencies, in the range of 3750–3760 cm−1;
• hydrogen-bonded aluminol OH and water–OH groups are both red-shifted with respect to the quasi-free OH groups, to a range between 3000–3500 cm−1;
• water bending modes are found around 1600–1660 cm−1;
• below ∼1100 cm−1, one finds H2O librational modes, aluminol OH bending, substrate phonons and water layer vibrations, respectively.
For illustration, we show in Fig. 1, left, some selected aluminol vibrational frequencies. Special attention will be given to non-hydrogen bonded aluminol OH groups, two of them “upright” and with very high frequencies (3758 cm−1 and 3761 cm−1) in the static model, and two of them in “parallel” orientation with lower frequencies (3603 cm−1 and 3599 cm−1). From the AIMD vibrational spectra at room temperature, which contain anharmonicity and temperature effects, rather similar values are obtained – mainly broadened w.r.t. to NMA stick spectra.23 In particular the high-frequency modes are only slightly red-shifted relative to the NMA frequencies, by a few wavenumbers: the non-hydrogen bonded aluminol OH vibrations give rise to a VDOS peak centered at slightly under 3750 cm−1, with a Full Width at Half Maximum (FWHM) of around 35 cm−1 (see ref. 23 and below). Our theoretical observations are in agreement with published experimental VSF spectra.12,21 (It should also be noted, however, that other works see only weak or no signals in this high-frequency range for water-covered α-alumina(0001) surfaces and α-alumina particles.46) Within our model, at an IR excitation frequency of around 3700 cm−1, we can reasonably expect that mainly the quasi-free aluminol OH groups are excited. Further, due to selection rules for IR light polarized perpendicular to the surface, notably the “upright” non-hydrogen bonded OH bonds should be excitable.
III. Non-equilibrium NE-AIMD and NE-AIMD/TCF approaches
A. AIMD calculations after vibrational excitation by “velocity swapping”
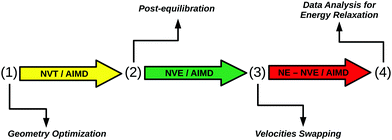
In order to model the IR preexcitation and subsequent relaxation, measured by time-resolved VSF, we employ a combination of equilibrium and non-equilibrium AIMD methods. Specifically, a protocol illustrated in Fig. 2 is followed, consisting of the following steps:(1) Starting geometry and equilibration phase: a geometry optimization at the PBE + D2 level of theory is done for the initial HS + 2ML structure. From there, five canonical NVT/AIMD trajectories at 300 K are run, each 24 ps long.
(2) Post-equilibration phase: starting from the end points of phase (1), five microcanonical NVE/AIMD trajectories are run, first for 10 ps, then for another 10 ps. The post-equilibration phase is introduced to remove spurious effects caused by coupling with the thermostat. The two different end times of phase (2) are used to test the influence of the length of the post-equilibration phase. We will loosely refer to phase (2) also as the “equilibrium NVE” phase.
(3) IR excitation by “velocity swapping”, subsequent non-equilibrium dynamics: the two end times of phase (2) (10 ps and 20 ps after equilibration phase (1)), are used as starting times for two sets of non-equilibrium AIMD simulations after “IR excitation” (NEQ1, NEQ2), called also “non-equilibrium NVE” in what follows. Both for NEQ1 and NEQ2, five NVE/AIMD trajectories are run after “swapping” of nuclear velocities of specific O–H bonds, all 10 ps long.
(4) Analysis: data are analyzed for energy relaxation.
Let us specify stage (3) of the scheme in Fig. 2, where atom velocities of selected O–H bonds associated with interfacial aluminols are “swapped”.47 This step is used to mimic an experimental IR excitation in the pump–probe scheme. The interaction of a single vibrational chromophore with IR light involves the absorption of a vibrational quantum of energy, ħω0. In our AIMD scheme, this excess energy is assumed to be fully converted into kinetic energy of atoms involved in excited aluminols. In this way, swapping of atom velocities enables us to perform non-equilibrium simulations, without the need of more complex techniques (e.g., explicit coupling to an IR pulse). The “kinetic energy-only model” used here does not include any atom displacements initially, along (unknown) vibrational coordinates. Of course, the excess energy stored in the O–H bonds at the beginning of phase (3), will rapidly and periodically be transferred into potential energy, and then be redistributed into other modes. For further features of the original equilibrium/non-equilibrium AIMD model, see ref. 27, 47 and 48.
The velocity swapping itself proceeds as follows. First, as an idealization we only swap velocities of H- and O-atoms associated with an excited aluminol. This is achieved by choosing, as swapped velocities 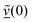 at time t = 0 (the time at the end of phase (2)):47
at time t = 0 (the time at the end of phase (2)):47
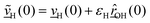 | (1) |
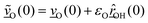 | (2) |
In the equations above,
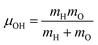 is the O–H bond reduced mass and
is the O–H bond reduced mass and 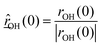 the unit vector along the OH bond. The excess energy is represented by ΔE and in our simulations this value is taken as ħω0 = 3750 cm−1 per excited bond, in order to account for our computed frequencies (see above). Velocities
the unit vector along the OH bond. The excess energy is represented by ΔE and in our simulations this value is taken as ħω0 = 3750 cm−1 per excited bond, in order to account for our computed frequencies (see above). Velocities 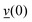 are those prior to swapping.
are those prior to swapping.
Only selected aluminol OH bonds are pre-excited in our AIMD simulations. Specifically, due to IR frequency and dipole orientation issues as described above, we excite only non-hydrogen bonded, “upright” aluminols. This is achieved in practice by analyzing at the end of phase (2), polar angles θOH of all non-hydrogen-bonded aluminols. Then, if θOH < 45° (the angle roughly separating “upright” from “parallel”), the O and H atom velocities of the considered aluminol are velocity swapped, otherwise not. According to this method, not all (four, see Fig. 1) non-hydrogen bonded aluminols are usually excited at the beginning of phase (3).
B. Analysis of NE-AIMD results
In order to analyze the dynamics, two sets of calculations were carried out. In a first set, we analyzed the time-dependent, ensemble-average kinetic energies of atoms or atom groups after excitation. Analyzing the kinetic energy of the excited aluminol OH groups and fitting them to analytic functions, defines a vibrational relaxation time. Analyzing the kinetic energy content in other subsystems, such as hydrogen-bonded aluminols, the water layer, or the alumina surface, gives insight into the pathways of energy flow, i.e., into the relaxation mechanism.An alternative analysis method, is to employ “instantaneous kinetic energy spectral densities” for non-equilibrium MD, as proposed in ref. 27 and 48–50. These are obtained via Fourier transforming mass-weighted velocity–velocity autocorrelation functions in individual time windows along the AIMD trajectories. Here we use a variant of this approach by considering the Fourier transforms of non-mass weighted VVAFs, by which we obtain Vibrational Density Of States (VDOS) curves as a function of both frequency ω and delay time Δt. The latter is an approximation to a time-dependent vibrational spectrum. We should point out that a similar procedure has been proposed by Lesnicki et al. to study vibrational relaxation of water, with special application for the liquid and the CaF2/H2O interface,51,52 but here the computed spectral densities are directly obtained by VVAFs. The analysis based on VDOS(ω,Δt) can also be done atomwise or for various subsystems of HS + 2ML. Specifically, the total VDOS(ω,Δt) is calculated from real parts of the Fourier transforms as
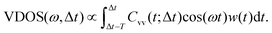 | (3) |
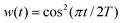 . Further, the VVAFs Cvv(t;Δt), which indirectly depend on time Δt, are computed as
. Further, the VVAFs Cvv(t;Δt), which indirectly depend on time Δt, are computed as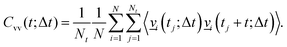 | (4) |
IV. Results and discussion
A. Time-dependent average kinetic energies and relaxation
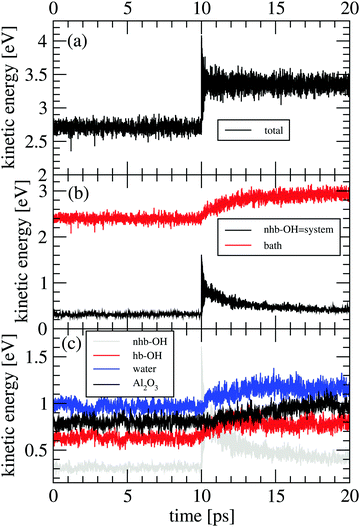
In the following section results from the non-equilibrium AIMD trajectories are reported, for the HS + 2ML system shown in Fig. 1 with excited non-hydrogen bonded aluminols. We will only refer to trajectory-averaged properties in time intervals 10 ps before and 10 ps after “IR excitation” and quantities derived thereof. For this purpose, we average all ten trajectories sampled during this time and do not distinguish between NEQ1 and NEQ2 groups anymore. In fact, averaging separately over the two groups gives very similar results.We first show in Fig. 3(a), the total kinetic energy 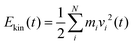 for phases (2) and (3). In this figure, t = 10 ps refers to the instant of “IR excitation”. We note that the velocity swapping at t = 10 ps, leads to a total kinetic energy gain by around 1.4 eV (from ∼2.7 to ∼4.1 eV), right after the excitation. Given ħω0 = 3750 cm−1 (0.46 eV), this corresponds to the excitation of around three aluminols on average, with one quantum each. Since only sufficiently upright non-hydrogen bonded aluminols are excited, this reflects the fact that not all four nhb-upright aluminols found in the static structure of Fig. 1 are excited in average, due to their dynamical fluctuations.23
for phases (2) and (3). In this figure, t = 10 ps refers to the instant of “IR excitation”. We note that the velocity swapping at t = 10 ps, leads to a total kinetic energy gain by around 1.4 eV (from ∼2.7 to ∼4.1 eV), right after the excitation. Given ħω0 = 3750 cm−1 (0.46 eV), this corresponds to the excitation of around three aluminols on average, with one quantum each. Since only sufficiently upright non-hydrogen bonded aluminols are excited, this reflects the fact that not all four nhb-upright aluminols found in the static structure of Fig. 1 are excited in average, due to their dynamical fluctuations.23
A more detailed analysis of the time evolution of the kinetic energy before and after velocity swapping is provided in panels Fig. 3(b) and (c), for different subsystems of the HS + 2ML model. In particular, we report averaged Ekin values for four different subsystems:
• the four non-hydrogen bonded aluminols, among them the excited, “upright” OH bonds (“nhb-OH”);
• the hydrogen-bonded aluminols (“hb-OH”);
• the water molecules forming the adsorbed layer (“H2O”);
• and the remaining surface atoms (“Al2O3”).
A still quite coarse-grained picture of the relaxation dynamics is provided in Fig. 3(b), showing the kinetic energy of a “system” containing the non-hydrogen bonded aluminols only, Esyskin = Enhb-OHkin, and a “bath”, 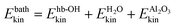 comprising all the movable rest. The black curve in panel (b) clearly reflects a quasi-exponential decay for excited aluminols (the “system”), while the average “bath” kinetic energy (red) follows an incremental trend which reaches a new steady-state like condition within the last picoseconds of the non-equilibrium AIMD. From the “system” curve, we may extract a vibrational relaxation time, τ, for the non-hydrogen bonded aluminols, by fitting their average kinetic energy, Enhb-OHkin, for t > t0, with an exponential curve:
comprising all the movable rest. The black curve in panel (b) clearly reflects a quasi-exponential decay for excited aluminols (the “system”), while the average “bath” kinetic energy (red) follows an incremental trend which reaches a new steady-state like condition within the last picoseconds of the non-equilibrium AIMD. From the “system” curve, we may extract a vibrational relaxation time, τ, for the non-hydrogen bonded aluminols, by fitting their average kinetic energy, Enhb-OHkin, for t > t0, with an exponential curve:
| Enhb-OHkin(t − t0) = Enhb-OHkin(t0)e−(t−t0)/τ + ΔEnhb-OHkin. | (5) |
In Fig. 3(c), we further disentangle the kinetic energy flow from the “system” into various “bath” subsystems. From the three subsystem curves shown there, we note that both neighbouring water molecules 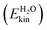 and hydrogen-bonded aluminols (Ehb-OHkin) are quite effective channels for accepting vibrational energy from the non-hydrogen bonded aluminols: the average kinetic energies of the water layer and the hb-OH bonds increase rapidly within the first 2–3 ps after vibrational excitation of the chromophores, reaching a new plateau corresponding to a “hot ground state” after 5 ps. In contrast, surface atoms
and hydrogen-bonded aluminols (Ehb-OHkin) are quite effective channels for accepting vibrational energy from the non-hydrogen bonded aluminols: the average kinetic energies of the water layer and the hb-OH bonds increase rapidly within the first 2–3 ps after vibrational excitation of the chromophores, reaching a new plateau corresponding to a “hot ground state” after 5 ps. In contrast, surface atoms 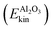 seem to increase their kinetic energy more slowly, time-delayed (after 5–6 ps), and to a lesser extent. Within the present model at least, a direct energy transfer from the excited aluminols to the alumina surface phonons is of minor importance for the relaxation process, in contrast to more “lateral” transfer to neighbouring water molecules or aluminol groups. This is consistent with the mismatch of frequencies, with O–H vibrations being much more energetic than surface phonons. It is also in line with test AIMD calculations according to which excited aluminol O–H vibrations, within the present model at least, on a hydroxylated but otherwise water-free alumina surface, showed no signs of vibrational relaxation up to timescales of ten picoseconds whatsoever (not shown here).
seem to increase their kinetic energy more slowly, time-delayed (after 5–6 ps), and to a lesser extent. Within the present model at least, a direct energy transfer from the excited aluminols to the alumina surface phonons is of minor importance for the relaxation process, in contrast to more “lateral” transfer to neighbouring water molecules or aluminol groups. This is consistent with the mismatch of frequencies, with O–H vibrations being much more energetic than surface phonons. It is also in line with test AIMD calculations according to which excited aluminol O–H vibrations, within the present model at least, on a hydroxylated but otherwise water-free alumina surface, showed no signs of vibrational relaxation up to timescales of ten picoseconds whatsoever (not shown here).
B. Time-dependent vibrational densities of states (VDOS)
The second analysis tool mentioned earlier is the time-windowed VDOS according to eqn (3). In what follows, we evaluate VDOS(ω,Δt) during phase (3) of our AIMD trajectories, at ten snapshot times Δt = 1, 2,…, 10 ps after “IR excitation”. The VDOS curves are shown in Fig. 4. For comparison, we will also refer to VDOS curve obtained from equilibrium NVT/AIMD calculations (300 K) done in ref. 23, and a NVE/AIMD spectrum for Δt = 0, i.e., from prior to the excitation step.Looking first at the equilibrium situation, which is shown in Fig. 4(a), black curve, we find the narrow, “upright” nhb-aluminol peak at 3750 cm−1 mentioned earlier, while hydrogen-bonded aluminol and water–OH groups form a broad band from about 3000 to 3600 cm−1. At around 1600 cm−1 we see the water bending modes and below ∼1200 cm−1 water librational, OH bending, substrate phonons and water layer vibrations, all similar to those found from NMA. The assignment comes from NMA and also from atomic or subsystem analysis of the VDOS, as outlined in ref. 23. Note that the low-frequency band has the highest VDOS, followed by the higher-frequency regions.
Let us look now at the time evolution of VDOS(ω,Δt) in the non-equilibrium situation, shortly after “IR excitation” of selected nhb-aluminol chromophores, at Δt = 1 ps. The corresponding VDOS is also shown in Fig. 4(a), blue curve, and also in Fig. 4(b) when zoomed into the O–H stretching range [3000, 4000] cm−1. In this case, we note the very intense peak around 3600 cm−1. This peak in the VDOS at Δt = 1 ps arises from the vibrationally excited non-hydrogen bonded aluminols and is now most intense. Its position at a lower frequency compared to the room temperature equilibrium situation, not centered around 3750 cm−1, can be explained by taking into account both the anharmonicity of the pre-excited O–H bond and the classical motion of nuclei.27,48 In contrast, at room temperature without O–H pre-excitation, the trajectories explore predominantly the harmonic, low-energy portion of the O–H potential curve.
With increasing delay time Δt after pre-excitation, we see from Fig. 4 that the 3600 cm−1 peak looses intensity, and is being blue-shifted towards a vibrational frequency of ∼3740 cm−1. In the classical dynamics picture, the blue-shift arises from the fact that O–H vibrations loose energy and amplitude, and the corresponding trajectories then also start to probe the harmonic low-energy regions of the O–H potential curves. The ∼3740 cm−1 signal is rather stable in position and intensity, after a few ps. Some, smaller modifications of VDOS curves can be also noticed for the hydrogen-bonded modes, located between 3000 and 3500 cm−1, as seen in Fig. 4. Further, the distinct H2O bending-mode peak around 1600 cm−1 and the low-frequency modes below 1100 cm−1 change in intensity while their position remains largely unaffected.
The VDOS spectrum at Δt = 10 ps closely reflects all the features of the equilibrium 300 K spectrum, as can be most clearly seen from Fig. 4(a). This spectrum is also similar to the non-equilibrium, pre-excitation spectrum at Δt = 0, which has been added in Fig. 4(b) (in red). Remaining differences between VDOS(ω,Δt = 10 ps) and the equilibrium 300 K spectrum can be due to the fact that shorter time-intervals have been used for Fourier transformation in the Δt-resolved case, and also since the system contains more energy and thus has a higher effective temperature after excitation. Altogether, the time-resolved spectrum reflects the approach to thermal equilibrium, following the excitation.
All of these findings are also qualitatively consistent with what has been found above for the relaxation process, from kinetic energy distributions. In order to directly address the spectral changes due to vibrational energy redistribution in time, we define the following function, ΔVDOS(Δt), by integrating for a given Δt over frequency, and referring to VDOS(0), which is the VDOS sampled within the last 1 ps of the equilibrium-NVE phase (2), i.e., right before velocity swapping:
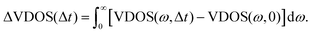 | (6) |
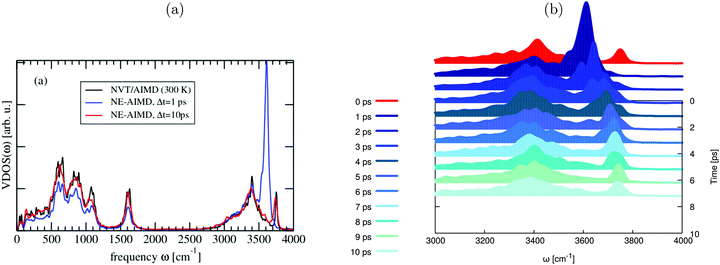
In Fig. 5, we report the integrated VDOS curves for different delay times, i.e., ΔVDOS(Δt) in eqn (6). We employ again a constant time interval of 1 ps. The analysis is done for the total HS + 2ML system, but also for subsystems. In particular, we consider hydrogen- and non-hydrogen bonded aluminols (“hb-OH” and “nhb-OH”), their sum (“aluminols, (nhb + hb)-OH”), the water layer (“H2O”), and the surface (“Al2O3”).
Since each total VVAF is normalized, the integrated total spectral density doesn’t change as a function of time, so that the total ΔVDOS(t) remains constant at 0 (dashed black curve). On the other hand, spectral densities of individual subsystems manifest significant changes during the 10 ps of propagation. The ΔVDOS(Δt) of non-hydrogen bonded aluminols (red), suddenly increase between 0 (end of phase (2)) and 1 ps, then progressively decay by at least 85% within the 10 ps propagation time. As we would expect, the integrated spectral densities of hydrogen-bonded aluminols (blue), water layer (magenta) and surface atoms (in green) have an increasing behaviour within at least the very first 2 or 3 ps after 1 ps. This can be interpreted as a vibrational energy flow into these subsystems, which are all part of the “bath”. We also see that the water layer seems most affected, followed by the hydrogen-bonded aluminols and the surface, which shows only very small changes in ΔVDOS(Δt). While the inactivity of the surface atoms in relaxation is obvious, the relative importance of individual water molecules vs. hydrogen-bonded aluminols is debatable, because there are more water atoms than hydrogen-bonded aluminols. At longer times, for the various bath subsystems, we see oscillatory behaviours. These are probably due to energy exchange within different dissipating channels, but also finite size effects cannot be excluded.
Due to the relative inactivity of the surface atoms, the blue ΔVDOS curve, which is associated with both non-hydrogen bonded and hydrogen-bonded aluminols, is close to a mirror image of the integrated spectral density of all water molecules (magenta). This reinforces the hypothesis that vibrational energy relaxation happens by coupling to modes of energy between 3000 and 3500 cm−1, which are located in the hydrogen-bonded VDOS band. Further, when looking at the black solid and the magenta ΔVDOS curves, we also notice that spectral densities of hydrogen-bonded aluminols and water molecules evolve almost symmetrically, which may indicate an efficient energy exchange between these two, strongly hydrogen-bonded subsystems.
Finally, by inspection of Fig. 5, we could also deduce that the main relaxation happens within the first 4 ps or so, and shows signatures of non-exponential behaviour. This timescale is somewhat slower than the one derived from kinetic energy analysis (∼2 ps). In passing, we note that preliminary experimental results for this system suggest indeed O–H relaxation times in the order of a few picoseconds.26 All of this indicates that the present situation with an O–H chromophore which is relatively weakly coupled to a surface and water environment, will lead to lifetimes between “short” (sub-ps) and “long” (many ps or even longer), the latter two for strongly and very weakly coupled systems, respectively.
V. Summary and conclusions
To summarize, the analysis of both kinetic energy and vibrational state densities provides qualitative and partially quantitative tools to unravel the energy redistribution of excited upright non-hydrogen bonded aluminols, which were the focus of this work. Our calculations suggest that the latter subsystem of the HS + 2ML surface is characterized by a vibrational band located between 3700 and 3800 cm−1, outside the other high-frequency bands which are associated with hydrogen-bonded modes. The analysis of non-equilibrium AIMD trajectories shows that, once the non-hydrogen bonded, upright aluminols are excited, they relax rapidly within the first picoseconds of propagation. Relaxation times obtained either via an exponential fit of their average kinetic energy, or by looking at the time-evolution of the frequency-integrated spectral densities, both suggest a “lifetime” between 2 and 4 ps. Compared to other studies reporting on O–H vibrational dynamics, especially the analysis of Borguet et al.,15–17 our findings indicate an intermediate relaxation timescale for an O–H chromophore with weak coupling to its aqueous environment. Our tools also allow us to disentangle the role of various other subsystems of the HS + 2ML model for the relaxation process. Indeed, we can identify as main dissipative channels both hydrogen-bonded aluminols and, in their sum even more important, water molecules in the adsorbed water layer. In general, hydrogen-bonded modes with frequencies between 3000 and 3500 cm−1 act as efficient pathways for the redistribution of the initial excess of kinetic energy in quasi-free, high-frequency O–H aluminols.Methodologically, here we combined non-equilibrium AIMD methods with time-dependent correlation function techniques. The vibrational excitation is simulated by employing a “velocities swapping” method, which allows for a mode-selective perturbation by adding a given excess of kinetic energy, i.e. a vibrational quantum in our approach, all within the framework of classical dynamics. The relatively high increase of kinetic/thermal energy, accompanied with the inherent structural fluctuations of AIMD trajectories, while causing on one hand an overall heating of the system, higher than in the actual experiments, can also account for multi-photonic excitations as the ones due to spectrally-broad exciting IR pulses.
On a more general level, it shall be underlined that while the AIMD approach is “costly”, it has the advantage of also allowing to treat reactive processes, and it is completely general, i.e., not restricted to a system class for which a force field, say, has been parametrized. Further, the NE-AIMD/TCF methodology opens the way to real, time-resolved vibrational spectra, e.g., time-resolved IR or VSF spectra. In this case, dipole–dipole auto- or dipole-polarizability cross-correlation functions need to be determined, which can also be done with the help of velocity–velocity autocorrelation functions.22,23,45 Work along these lines is in progress in our laboratory.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank R. Kramer Campen (Duisburg-Essen) and his group for sharing some experimental results prior to publication, and for most useful discussions. We also acknowledge fruitful discussions with Tillmann Klamroth (Potsdam), Marcella Iannuzzi (Zurich) and Peter Hamm (Zurich). The authors thank the Deutsche Forschungsgemeinschaft (DFG) for financial support through project Sa 547/9 and the North-German Supercomputing Alliance (HLRN) for providing HPC resources that have contributed to the research results reported in this work. One of us (P. S.) takes the opportunity to thank Jan Peter Toennies for his continuous support, interest in our work, and the many fruitful discussions over meanwhile about 30 years – when he first approached P. S. regarding a paper on quantum size effects in lead films resulting from his thesis.References
- O. Bjørneholm, M. H. Hansen, A. Hodgson, L.-M. Liu, D. T. Limmer, A. Michaelides, P. Pedevilla, J. Rossmeisl, H. Shen, G. Tocci, E. Tyrode, M.-M. Walz, J. Werner and H. Bluhm, Water at interfaces, Chem. Rev., 2016, 116, 7698–7726 CrossRef PubMed.
- G. E. Brown, V. E. Henrich, W. H. Casey, D. L. Clark, C. Eggleston, A. Felmy, D. W. Goodman, M. Grätzel, G. Maciel, M. I. McCarthy, K. H. Nealson, D. A. Sverjensky, M. F. Toney and J. M. Zachara, Metal oxide surfaces and their interactions with aqueous solutions and microbial organisms, Chem. Rev., 1999, 99, 77–174 CrossRef CAS PubMed.
- H.-J. Freund, H. Kuhlenbeck and V. Staemmler, Oxide surfaces, Rep. Prog. Phys., 1996, 59, 283 CrossRef CAS.
- M. A. Henderson, The interaction of water with solid surfaces: Fundamental aspects revisited, Surf. Sci. Rep., 2002, 46, 1–308 CrossRef CAS.
- M.-P. Gaigeot, M. Sprik and M. Sulpizi, Oxide/water interfaces: How the surface chemistry modifies interfacial water properties, J. Phys.: Condens. Matter, 2012, 24, 124106 CrossRef PubMed.
- Y. Wang and C. Wöll, IR spectroscopic investigations of chemical and photochemical reactions on metal oxides: Bridging the materials gap, Chem. Soc. Rev., 2017, 46, 1875–1932 RSC.
- R. Mu, Z. Zhao, Z. Dohnalek and J. Gong, Structural motifs of water on metal oxide surfaces, Chem. Soc. Rev., 2017, 46, 1785–1806 RSC.
- M. E. McBriarty, G. F. von Rudorff, J. E. Stubbs, P. J. Eng, J. Blumberger and K. M. Rosso, Dynamic stabilization of metal oxide/water interfaces, J. Am. Chem. Soc., 2017, 139, 2581–2584 CrossRef CAS PubMed.
- Z.-J. Zhao, Z. Li, Y. Cui, H. Zhu, W. F. Schneider, W. N. Delgass, F. Ribeiro and J. Greeley, Importance of metal-oxide interfaces in heterogeneous catalysis: a combined DFT, microkinetic, and experimental study of water-gas shift on Au/MgO, J. Catal., 2017, 345, 157–169 CrossRef CAS.
- Q. Du, E. Freysz and Y. R. Shen, Vibrational spectra of water molecules at quartz/water interfaces, Phys. Rev. Lett., 1994, 72, 238 CrossRef CAS PubMed.
- S. Ong, X. Zhao and K. B. Eisenthal, Polarization of water molecules at a charged interface: Second harmonic studies of the silica/water interface, Chem. Phys. Lett., 1992, 191, 327–335 CrossRef CAS.
- L. Zhang, C. Tian, G. A. Waychunas and Y. R. Shen, Structures and charging of α-alumina (0001)/water interfaces studied by sum-frequency vibrational spectroscopy, J. Am. Chem. Soc., 2008, 130(24), 7686–7694 CrossRef CAS PubMed.
- J. A. McGuire and Y. R. Shen, Ultrafast vibrational dynamics at water interfaces, Science, 2006, 313(5795), 1945–1948 CrossRef CAS PubMed.
- S. Nihonyanagi, S. Yamaguchi and T. Tahara, Ultrafast dynamics at water interfaces studied by vibrational sum frequency generation spectroscopy, Chem. Rev., 2017, 117, 10665–10693 CrossRef CAS PubMed.
- A. Tuladhar, S. M. Piontek and E. Borguet, Insights on interfacial structure, dynamics, and proton transfer from ultrafast vibrational sum frequency generation spectroscopy of the alumina(0001)/water interface, J. Phys. Chem. C, 2017, 121, 5168–5177 CrossRef CAS.
- M. DelloStritto, S. M. Piontek, M. L. Klein and E. Borguet, Relating interfacial order to sum frequency generation with ab initio simulations of the aqueous Al2O3(0001) and (11
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) interfaces, J. Phys. Chem. C, 2018, 122, 21284–21294 CrossRef CAS.
0) interfaces, J. Phys. Chem. C, 2018, 122, 21284–21294 CrossRef CAS. - S. M. Piontek, A. Tuladhar, T. Marshall and E. Borguet, Monovalent and divalent cations at the α-Al2O3(0001)/water interface: How cation identity affects interfacial ordering and vibrational dynamics, J. Phys. Chem. C, 2019, 123(30), 18315–18324 CrossRef CAS.
- T. Kurita, K. Uchida and A. Oshiyama, Atomic and electronic structures of α-Al2O3 surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155319 CrossRef.
- J. Wirth and P. Saalfrank, The chemistry of water on α-alumina: Kinetics and nuclear quantum effects from first principles, J. Phys. Chem. C, 2012, 116, 26829–26840 CrossRef CAS.
- H. Kirsch, J. Wirth, Y. Tong, M. Wolf, P. Saalfrank and R. K. Campen, Experimental characterization of unimolecular water dissociative adsorption on α-alumina, J. Phys. Chem. C, 2014, 118, 13623–13630 CrossRef CAS.
- Y. Tong, J. Wirth, H. Kirsch, M. Wolf, P. Saalfrank and R. K. Campen, Optically probing Al–O and O–H vibrations to characterize water adsorption and surface reconstruction on α-alumina: an experimental and theoretical study, J. Chem. Phys., 2015, 114, 054704 CrossRef PubMed.
- G. Melani, Y. Nagata, R. Kramer Campen and P. Saalfrank, Vibrational spectra of dissociatively adsorbed D2O on Al-terminated α-Al2O3(0001) surfaces from ab initio molecular dynamics, J. Chem. Phys., 2019, 150, 244701 CrossRef PubMed.
- G. Melani, Y. Nagata, J. Wirth and P. Saalfrank, Vibrational spectroscopy of hydroxylated α-Al2O3(0001) surfaces with and without water: An ab initio molecular dynamics study, J. Chem. Phys., 2018, 149, 014707 CrossRef PubMed.
- J. Wirth, H. Kirsch, S. Wlosczyk, Y. Tong, P. Saalfrank and R. K. Campen, Characterization of water dissociation on α-Al2O3(1
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02): theory and experiment, Phys. Chem. Chem. Phys., 2016, 18, 14822 RSC.
02): theory and experiment, Phys. Chem. Chem. Phys., 2016, 18, 14822 RSC. - S. Heiden, Y. Yue, H. Kirsch, J. Wirth, P. Saalfrank and R. K. Campen, Water dissociative adsorption on α-Al2O3(1
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 20) is controlled by surface site undercoordination, density, and topology, J. Phys. Chem. C, 2018, 122, 6573–6584 CrossRef CAS.
20) is controlled by surface site undercoordination, density, and topology, J. Phys. Chem. C, 2018, 122, 6573–6584 CrossRef CAS. - R. K. Campen, et al., to be published.
- J. Jeon, J. H. Lim, S. Kim, H. Kim and M. Cho, Simultaneous spectral and temporal analyses of kinetic energies in nonequilibrium systems: Theory and application to vibrational relaxation of OD stretch mode of HOD in water, J. Phys. Chem. A, 2015, 119, 5356–5367 CrossRef CAS PubMed.
- C.-S. Hsieh, R. K. Campen, M. Okuno, E. H. G. Backus, Y. Nagata and M. Bonn, Mechanism of vibrational energy dissipation of free OH groups at the air-water interface, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18780–18785 CrossRef CAS PubMed.
- H.-C. Chang and G. E. Ewing, Infrared fluorescence from a monolayer of CO on NaCl(100), Phys. Rev. Lett., 1990, 65, 2125–2128 CrossRef CAS PubMed.
- E. J. Heilweil, M. P. Casassa, R. R. Cavanagh and J. C. Stephenson, Temperature dependence of the vibrational population lifetime of OH(v = 1) in fused silica, Chem. Phys. Lett., 1985, 117, 185–190 CrossRef CAS.
- M. P. Casassa, E. J. Heilweil, J. C. Stephenson and R. R. Cavanagh, Time-resolved measurements of OH(v = 1) vibrational relaxation on SiO2 surfaces: Isotope and temperature dependence, J. Chem. Phys., 1986, 84, 2361–2364 CrossRef CAS.
- V. A. Ranea, W. F. Schneider and I. Carmichael, DFT characterization of coverage dependent molecular water adsorption modes on α-Al2O3(0001), Surf. Sci., 2008, 602, 268–275 CrossRef CAS.
- V. A. Ranea, I. Carmichael and W. F. Schneider, DFT investigation of intermediate steps in the hydrolysis of α-Al2O3(0001), J. Phys. Chem. C, 2009, 113, 2149–2158 CrossRef CAS.
- S. Wippermann, W. G. Schmidt, P. Thissen and G. Grundmeier, Dissociative and molecular adsorption of water on α-Al2O3(0001), Phys. Status Solidi C, 2010, 7(2), 137–140 CrossRef CAS.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, 1133–1138 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Hafner, Ab initio, molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio, molecular dynamics for open-shell transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(17), 13115–13118 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Nosé, A molecular dynamics method for simulations in the canonical ensemble, Mol. Phys., 1984, 52, 255–268 CrossRef.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- T. Ohto, K. Usui, T. Hasegawa, M. Bonn and Y. Nagata, Toward ab initio molecular dynamics modeling for sum-frequency generation spectra; an efficient algorithm based on surface-specific velocity-velocity correlation function, J. Chem. Phys., 2015, 143, 124702 CrossRef PubMed.
- N. G. Petrik, P. L. Huestis, J. A. LaVerne, A. B. Aleksandrov, T. M. Orlando and G. A. Kimmel, Molecular water adsorption and reactions on α-Al2O3(0001) and α-Alumina particles, J. Phys. Chem. C, 2018, 122(17), 9540–9551 CrossRef CAS.
- Y. Nagata, S. Yoshimune, C.-S. Hsieh, J. Hunger and M. Bonn, Ultrafast vibrational dynamics of water disentangled by reverse nonequilibrium ab initio molecular dynamics simulations, Phys. Rev. X, 2015, 5, 021002 Search PubMed.
- J. Jeon, C.-S. Hsieh, Y. Nagata, M. Bonn and M. Cho, Hydrogen bonding and vibrational energy relaxation of interfacial water: A full DFT molecular dynamics simulation, J. Chem. Phys., 2017, 147, 044707 CrossRef PubMed.
- T. Yagasaki, J. Ono and S. Saito, Ultrafast energy relaxation and anisotropy decay of the librational motion in liquid water: A molecular dynamics study, J. Chem. Phys., 2009, 131, 164511 CrossRef PubMed.
- J. Jeon and M. Cho, Redistribution of carbonyl stretch mode energy in isolated and solvated N-methylacetamide: Kinetic energy spectral density analyses, J. Chem. Phys., 2011, 135, 214504 CrossRef PubMed.
- D. Lesnicki and M. Sulpizi, A microscopic interpretation of pump-probe vibrational spectroscopy using ab initio molecular dynamics, J. Phys. Chem. B, 2018, 122, 6604–6609 CrossRef CAS PubMed.
- D. Lesnicki, Z. Zhang, M. Bonn, M. Sulpizi and E. H. G. Backus, Surface charges at the CaF2/water interface allow very fast intermolecular vibrational-energy transfer, Angew. Chem., Int. Ed., 2020, 59, 13116–13121 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2021 |