Open Access Article
Open Access ArticleCollision-driven state-changing efficiency of different buffer gases in cold traps: He(1S), Ar(1S) and p-H2(1Σ) on trapped CN−(1Σ)†
Lola
González-Sánchez
 a,
Ersin
Yurtsever
a,
Ersin
Yurtsever
 b,
Barry P.
Mant
b,
Barry P.
Mant
 c,
Roland
Wester
c,
Roland
Wester
 c and
Franco A.
Gianturco
c and
Franco A.
Gianturco
 *c
*c
aDepartamento de Química Física, University of Salamanca, Plaza de los Caídos sn, 37008 Salamanca, Spain
bDepartment of Chemistry, Koç University, Rumelifeneri yolu, Sariyer, TR-34450, Istanbul, Turkey
cInstitut für Ionenphysik und Angewandte Physik, Universität Innsbruck, Technikerstr. 25, 6020, Innsbruck, Austria. E-mail: francesco.gianturco@uibk.ac.at
First published on 17th August 2020
Abstract
We employ potential energy surfaces (PES) from ab initio quantum chemistry methods to describe the interaction of the CN−(1Σ) molecule, one of the small anions often studied at low temperatures, with other possible gases which can be employed as buffer in cold ion traps: the He and Ar atoms and the p-H2 molecule. These PESs are used to calculate from quantum multichannel dynamics the corresponding state-changing rate constants between the populated rotational states of the anion, the latter being in its electronic and vibrational ground states. The different cross sections for the collision-driven quenching and excitation processes at low temperatures are compared and further used to model CN− cooling (de-excitation) efficiency under different trap conditions. The interplay of potential coupling strength and mass-scaling effects is discussed to explain the differences of behaviour among the buffer gases. The advantages of being able to perform collisional cooling at higher trap temperatures when using Ar and p-H2 as buffer gases are also discussed.
1 Introduction
Cold and ultracold controllable atomic and molecular systems attract great interest because the quantum nature of the world is visibly manifested at low and ultralow temperatures, and research on such systems can provide new insight into the quantum theory of matter and of matter–light interactions. Such an understanding is crucial for the progress of many areas of physics as well as the development of future quantum technologies.Ion trapping techniques were developed in the 1950s by Hans Dehmelt and Wolfgang Paul, who shared the 1989 Nobel Prize in physics for their work.1 The two most commonly employed types of ion traps are radio-frequency quadrupole traps, or Paul traps and Penning traps2,3 (invented by Dehmelt, but named after Frans Penning), which rely on static electric and magnetic fields. Penning traps are generally not used in combination with cold buffer-gas cooling,4 since the orbital motion of the trapped ions would not be stable under collisions. Instead, buffer-gas cooling has been used extensively in Paul traps.4 In recent years, the development of more sophisticated methods involving octupole ion traps, which strongly suppress disturbances of ion-atom collisions due to micromotion throughout the extended volume of the atom trap,5,6 has allowed the study of a variety of molecular anions trapped and stabilized via collisional cooling induced by the chosen buffer gas, often helium.7 Hence, molecular ions can be cooled in collisions with cold neutral atoms, thereby generating the efficient cooling of rotational and vibrational degrees of freedom during collisions with the trapped anions. This general cooling can be applied to molecular ions and ionic clusters of almost arbitrary size and complexity, albeit limiting the experiments to temperatures above about 4 K due to the limitations from standard cryostats based on the He buffer gas.
We also know however that, in principle at least, simple molecular anions could be cooled efficiently to millikelvin temperatures using Doppler or Sisyphus cooling in Paul or in Penning traps.8 Additionally, photodetachment cooling has been tried and shown that even lower temperatures could be accessed during the process.9
For the preparation of the trapped anions into their lowest internal states by collisions with neutrals to be efficient, the system has to exhibit a large ratio of elastic or rotationally inelastic collisions to reactive collisions, since the latter could lead to a loss of the original ions by the opening of possible charge-exchange channels.10 This last requirement therefore explains the preference for using one of the noble gases as the buffer gas in the cold ion traps. It is therefore of direct interest when modelling possible operating conditions in the traps to know the size and temperature dependence of the collision-induced state-changing processes for the molecular anion under study as the buffer gas selected is replaced by another, to test a broader range of operating conditions. In our previous work11–14 we have examined a variety of small molecular anions and discussed the relative importance of their inelastic collision rate constants involving rotational states at different trap temperatures. Recent experimental work in our group has also been directed to photo-detachment studies of the CN− anion with He as the buffer gas of choice.15,16
In the present study, we shall therefore revisit the behaviour of the CN− anion collisional inelastic rate constants involving rotational states active at the temperatures we shall consider for the cold traps. In particular, we shall obtain from first principle quantum calculations the relative sizes of its state-changing rotationally inelastic rate coefficients when using He, Ar or p-H2 as buffer gases in the traps. We will then compare the cooling kinetics of these different systems as possible buffer gases and show that the heavier gases can more rapidly cool the trapped anion even at higher temperatures than using He.
In the recent literature, there have been several papers which have dealt with rotational excitations of molecular anions of astrophysical interest with other partners such as He and H2. For example, in the work of Walker et al.17 the rotationally inelastic rate coefficients were calculated for the C6H− anion interacting with He and H2. It was found that the rate coefficients for H2 collisions for Δj = −1 transitions are of the order of 10−10 cm3 s−1, a factor of 2 to 4 greater than those for He. Additionally, Lara-Moreno et al.18 have recently presented calculations for the rotational state-changing collisions involving the C3N− anion with He as a partner where the rate coefficients for the rotational transitions between 1 and 300 K were reported. The same authors19 have also extended their calculations for C3N− to collisions with H2 as a partner and found unexpected similarities between the rate coefficients of the rotational de-excitations of CN−, C3N−, and C6H−. It therefore becomes interesting to further extend the comparison for the CN− anion by including a heavier noble gas like Ar, one which is also employed as a buffer gas for experiments in cold traps.
2 Interaction potentials and ab initio calculations
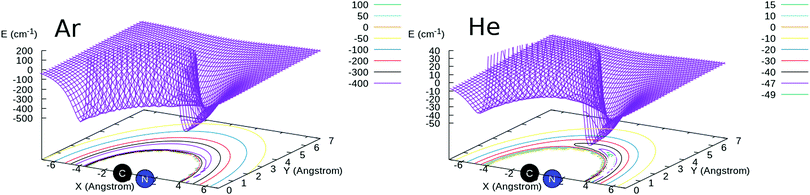
For the CN−/Ar system, ab initio calculations were carried out in the present work using the MOLPRO suite of quantum chemistry codes.20,21 The CN− bond distance was kept fixed at 1.181431 Å throughout the calculation of the potential energy points. The post-Hartree–Fock treatment was carried out using the CCSD(T) method as implemented in MOLPRO22,23 and complete basis set (CBS) extrapolation using the aug-cc-pVTZ, aug-cc-pVQZ and aug-cc-pV5Z basis sets24,25 was carried out. The basis-set-superposition-error (BSSE)26 was also included for all the calculated points so that the full interaction was obtained with and without the inclusion of the BSSE correction and the two sets of results were compared as discussed below.The 2D RR-PES (R,θ) was calculated using 56 points in R from 2.5 to 25.0 Å and 19 angular values from 0 to 180°, for a total of 1064 grid points. We report in Fig. 1 a pictorial representation of the new RR-PES compared with one describing the interaction with He atoms, already described in detail in our earlier work.16 We will therefore not report again all aspects of those calculations but only show the results in comparison with the new PES for CN−/Ar. In both systems, we see that the largest attractive wells are located along the linear structures, with the deeper one on the side of the N-atom of the anion. However, we also see that the strengths of the attractive wells are very different, with the one for the Ar partner being nearly one order of magnitude larger on both sides of the target molecule. This is obviously due to the larger number of electrons in the Ar atom and on its much larger dipole polarizability that dominates the long-range attractive terms. Its value is 1.383 a03 for He,27 to be compared with 11.070 a03 for Ar.28 We also see that, in the case of Ar, the interaction well depths at the two linear ends of the molecule are much more similar to each other than in the case of He, a feature that we shall further discuss below in terms of spatial anisotropy differences between the two systems.
Another pictorial presentation of the RR-PESs for both systems, a form which will be used in the scattering calculations discussed below, is obtained by numerically generating the radial coefficients of the multipolar expansion of the RR-2D potential energy surfaces:
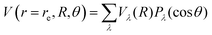 | (1) |
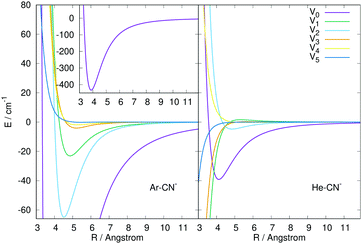 | ||
| Fig. 2 Comparison of the numerically computed multipolar coefficients of the two expansions using eqn (1), of the RR-PES describing the interaction of He and Ar with the CN− anion. See main text for further details. | ||
The panel in the left of the Fig. 2 reports the lower six terms of expansion of eqn (1) for the newly computed interaction of Ar with CN−, while the panel on the right shows for comparison the same terms but for the CN−/He interaction computed previously.16 The following comments can be made: (i) the relative depths of the two spherical terms of the multipoles is clearly visible in the inset on the left panel for Ar and in the right panel for the He partner. The one for the Ar atom is about one order of magnitude larger than that in the case of He; (ii) the next two anisotropic terms with λ = 1 and 2 also show for the Ar case the presence of strongly attractive wells and steeply repulsive walls at short range, while the data for He in the right panel show instead that only the λ = 2 term has a shallow well before the repulsive region; (iii) the next three anisotropic coefficients for the Ar PES remain uniformly repulsive at short range with increasingly shallower wells slightly further out. On the other hand, for the case of the He partner only the λ = 4 term remains repulsive with essentially no well, while all the other are strongly attractive at short range.
In conclusion, the comparison of the interaction potentials for the two atoms indicates, as expected, a much larger strength and greater spatial extension of the CN−/Ar RR-PES compared with that of CN−/He, a difference which will be evident when we shall discuss below the differences in the computed state-changing cross sections and rate coefficients.
In order to further check the importance that the inclusion of the BSSE correction could have on the new calculations for the Ar interaction with CN−, we have carried out the same set of calculations of this new PES with and without the inclusion of the BSSE correction. We know, in fact, that such corrections for weakly interacting systems like those including an anionic molecule with a closed-shell neutral gas, as is the case here, are usually slightly affecting the overall depth of the attractive wells while leaving the overall angular anisotropy unaffected: such minor changes usually result only in a correspondingly small effect on the spherical component of the multipolar expansion of the 2D PES. The actual comparison of the results is shown in the curves of Fig. 3. The solid lines report the calculations obtained when the BSSE correction was included, while the dashed lines indicate the calculated PES points without the inclusion of the BSSE correction. As expected, we see that the anisotropic coefficients, those which will drive the relative flux distribution into the final inelastic channels during collisions, are essentially unchanged in the two cases, with only a minor modification of the well depth of the spherical component. We therefore expect that the use of either PES will not make much of a difference when carrying out the inelastic dynamics, a point that we shall further discuss below when calculating inelastic cross sections and rate coefficients.
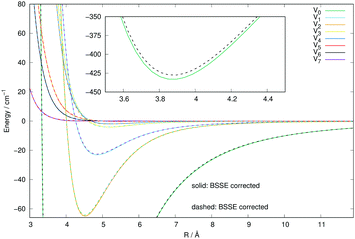 | ||
| Fig. 3 Comparison of the numerically computed multipolar coefficients of the two expansions using eqn (1), of the RR-PES describing the interaction of Ar with the CN− anion when either including the BSSE correction (solid lines) or omitting it (dashed lines). See main text for further details. | ||
The CN−/H2 PES has already been obtained from ab initio calculations and employed to obtain rotationally inelastic collisions using the full dimensionality of the problem.29 In fact, the CN−/H2 system, with both molecules treated as rigid rotors, is characterized by three angles θ, θ′ and ϕ and the distance R between the centres of masses. The final V(R,θ,θ′,ϕ) potential is therefore a 4D potential energy surface between the two partners. In the calculations reported by Kłos and Lique, they found that there were not significant differences between the inelastic cross sections for the two species (para and ortho) of H2 and therefore that the collisional rates for the p-H2 (j = 0) and for the o-H2 (j = 1) were found to be very similar.29 For collisions at low temperatures (T ≤ 100 K), the rotational excitation probability of H2 itself is fairly low since the energy spacing between the j = 0 and j = 2 levels in p-H2 is much larger than in the case of CN−.16,29 We shall therefore only consider as a partner of the anion the p-H2 (j = 0) system. In this case, only the leading terms of the 4D multipolar expansion needs to be kept, thereby allowing the resulting RR-PES to be simplified to the lower 2D dimensionality as indicated by eqn (1).16,29 We will not report this 2D PES again here, but note that its general features are stronger than in the case of He and more similar to those shown above for the Ar partner. Such differences will be further analysed in the following sections.
3 Quantum dynamics: cross sections and rate coefficients
Below we briefly outline the computational method to obtain rotationally inelastic cross sections and rate coefficients for the scattering of CN− with He, Ar and p-H2 (j = 0). The standard time-independent formulation of the Coupled-Channel (CC) approach to quantum scattering will not be repeated in detail (see for example Taylor30 for a general formulation) since we have already discussed it in many of our earlier works.31–33 Hence, only a short outline will be given.For the case where no chemical modifications occur in the molecule by the impinging projectile, the total scattering wave function can be expanded in terms of asymptotic target rotational eigenfunctions (within the rigid rotor approximation) which are taken to be spherical harmonics and whose eigenvalues are given by Bj(j + 1), where B is the rotational constant for the closed-shell CN− anion: 1.87239 cm−1.16 The channel components for the CC equations are therefore expanded into products of total angular momentum J eigenfunctions and of radial functions to be determined via the solutions of the CC equations,31,32i.e. the familiar set of coupled, second order homogeneous differential equations:
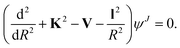 | (2) |
| (N′ − YN) = J′ − YJ | (3) |
In the present calculations we have generated a broad range of state-to-state rotationally inelastic cross sections from the collisional interaction of CN− with Ar and compared them with our earlier results of the collisions of the same anion with He atoms.16 Once the state-to-state inelastic integral cross sections are known, the rotationally inelastic rate constants kj→j′(T) can be evaluated as the convolution of the cross sections over a Boltzmann distribution of the relative collision energies:
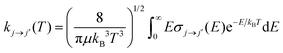 | (4) |
4 Results and discussion
Following the quantum method outlined earlier, we have carried out new calculations for CN−/Ar rotationally inelastic collisions over largely the same range of energies already studied for collisions of the same anion with He and p-H2 (j = 0), both data already discussed in our earlier work.16 We shall therefore employ those earlier cross sections and rate coefficients for the comparisons we shall present in the current work. For the CN−/Ar calculations, we have extended the radial range on integration out to Rmax = 90 Å for the higher energies and further out to Rout = 750 Å at the lowest energies considered. The extension is done, within our own scattering code, by using the long-range exponents of the dominant terms which progress as R−4 and as R−5 with coefficients obtained by numerical interpolation from the outermost computed radial values of the ab initio potential.We have employed a set of coupled rotational levels up to jmax = 21 for the lower energies and extended that range up to jmax = 30 for the higher collision energies. Such index values correspond to the number of rotational states included in the full Coupled-Channel treatment of the quantum dynamics.
The range of total angular momentum values was taken up to Jtot = 200. The energy range was varied with different energy intervals in the following way: 0.01–0.1 cm−1, ΔE = 0.001 cm−1, 0.1–1 cm−1, ΔE = 0.01 cm−1, 1–100 cm−1, ΔE = 0.1 cm−1. 100–200 cm−1, ΔE = 0.2 cm−1, 200–500 cm−1, ΔE = 1 cm−1.
We have included the calculation of all physical transitions that involved rotational levels up to j = 10 for the molecular anion and some of the resulting observables will be presented below.
We carried out the multichannel quantum dynamics calculations using both the RR-PES which included the BSSE correction, and the RR-PES without the inclusion of the BSSE correction. As expected, both sets of inelastic rate coefficients turned out to be nearly identical at all energies considered, thus confirming the lack of any effect from such modification of the RR-PES on the quantum inelastic dynamics. Therefore, all the results presented below were obtained via the RR-PES which did not include the BSSE modification. A direct comparison of some of the final rates will be shown below to confirm the present comment.
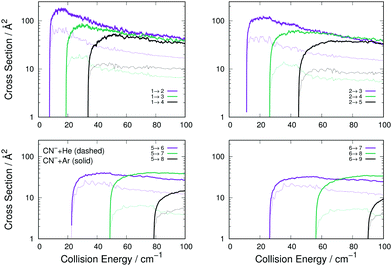
The data reported by Fig. 4 present a range of transitions from various initial rotational states of the CN− molecule in collision with either Ar (thick solid lines) or He (thin dashed lines). The following comments can be made:
(i) The transitions with Δj = 1 are the largest in size and behaviour for both systems, a result which is independent of the initial level since all such transitions in all panels follow this trend. This feature indicates the dominance of the λ = 1 multipolar coefficient of Fig. 2 for the dynamical coupling of both He and Ar with the anion's rotational states. (ii) All excitation cross sections decrease in size, for both systems, as Δj increases, indicating again the importance of the direct coupling from λ = 1 multipolar coefficient of Fig. 2 for He and Ar with the anion in relation to the other dynamical coupling coefficients. (iii) Furthermore, the inelastic transitions, with all values of Δj, remain for the He partner always smaller than those obtained for Ar. This indicates that the two sets of potential coupling coefficients (Fig. 2) for the CN−–He RR-PES are uniformly smaller than those pertaining to the CN−/Ar system.
Rotationally inelastic collision processes involving CN− with He atoms and p-H2 (j = 0) molecules have been already discussed in our earlier work,16 where we highlighted that the interaction between H2 and CN− also leads to Associative Detachment (AD) processes with the destruction of the anionic molecule.34 This process, however, turns out to be rather slow under cold trap conditions. It thus follows that the use of p-H2 as a partner in cold traps could also still be an interesting alternative for which one can assess through calculations how feasible would be to use it as a buffer gas at higher temperatures than the more usual He noble gas.
It is therefore useful to compare the relative collision-driven cooling efficiency of that molecular partner with the one of Ar, since the interaction of H2 with CN− is already known to be stronger than that with He.16 We have employed the reduced 2D form of the relevant PES for the case of the p-H2 partner already presented in earlier work.29
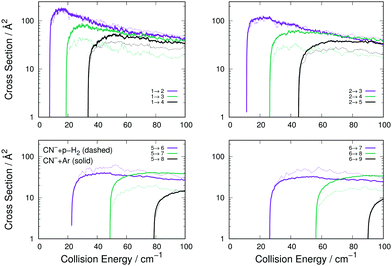
The following considerations can be made from the comparison between the two sets of cross sections in Fig. 5: (i) the transitions with Δj = 1 are of very similar size and behaviour for both systems, a result which turns out to be independent of the initial level since all such transitions are similar in size and energy behaviour; (ii) all excitation cross sections decrease in relative size, for both systems, as Δj increases, indicating the dominance of the λ = 1 multipolar coefficients for the dynamical coupling for both Ar and p-H2 colliding CN−; (iii) additionally, as Δj increases, the inelastic cross sections for p-H2 become smaller than those obtained for Ar. This is an indication that the potential coupling coefficients with λ > 1 remain relatively stronger for the CN−/Ar case than they are for the CN−/p-H2 case, as we have already discussed in our earlier work,16 showing that the λ = 2 and 3 multipolar coefficients for the p-H2 case are similar in the dynamical coupling strength of their repulsive regions.
On the whole, the comparison with a molecular system like p-H2 indicates that the Ar atom has a comparable-to-higher collisional excitation/de-excitation efficiency involving rotational states of CN−. This aspects will be further discussed below when comparing the state-changing rotational rate coefficients at different trap temperatures.
We now turn to the de-excitation (rotational cooling) processes, reporting in Fig. 6 for CN−/Ar, compared with the same processes for CN−/He.
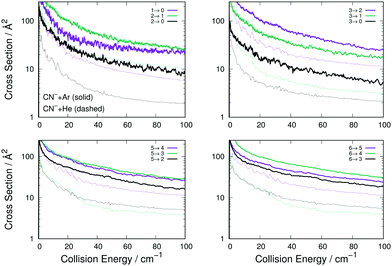 | ||
| Fig. 6 Computed de-excitation cross sections for rotational states of CN− interacting with Ar (thick lines) and with He (thin dashes) atoms. The notation is the same already used in Fig. 4 and 5. See main text for further details. | ||
The comparison of the four panels of Fig. 6 follows the general behaviour already discussed for the rotational excitation collisions reported by Fig. 4. All the Ar-driven state-changing processes are always larger in size than those involving He atoms, this being true across the energy range examined and for all types of Δj changing transitions we have considered. The comparison of the similar types of transitions between Ar and p-H2 partners follow closely the same relative size behaviour already shown by the excitation processes of Fig. 6: transitions with Δj = 1 are similar in size and energy dependence, while those with Δj > 1 are larger for the Ar projectile than for p-H2 and therefore are not shown in an additional figure.
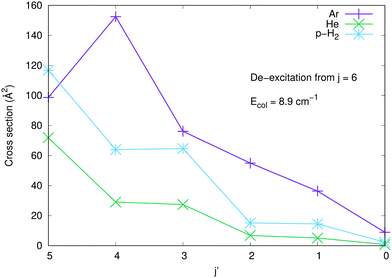
To further underline the relative behaviour of the inelastic cross sections, we report in the panels of Fig. 7 the computed relative efficiency (state-to-state cross sections) for the collisional cooling of CN− rotational levels interacting with Ar (crosses), He (× marks) and p-H2 (star marks). The greatest cooling efficiency is clearly displayed by the Ar-driven collisions, while both p-H2 and He turn out to be less efficient partners, with the p-H2 partner showing intermediate size for its cooling cross sections. All these comparative features will be more directly analysed when looking at the computed inelastic rate coefficients over the range of temperatures of interest in an ion trap.
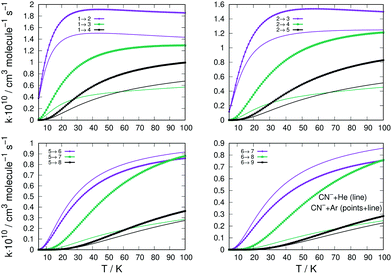
The state-changing excitation rate coefficients were computed by numerical quadrature of the corresponding cross sections as indicated by eqn (4). The ones involving the lower rotational levels for the CN−/Ar and CN−/He are given in the four panels of Fig. 8. They report excitation processes from up to j = 6 levels and are given by thick lines for the former system and by plain thin lines for the latter. The excitation processes are from different initial levels and in each panel the transitions with the Δj = 1, 2 and 3 excitations are shown as colour-coded in each panel.
The following considerations can be made by perusing the panels of Fig. 8: (i) all excitation rates involving Ar as a partner are consistently larger, for nearly all the considered transitions, than those obtained with He as a buffer gas; (ii) the marked difference is provided by the Δj = 1 excitations, where we see that for excitations from j = 1 and j = 2 the rate coefficients with He are close to those for Ar and remain so up to higher T values; (iii) the same transitions with Δj = 1, but starting from more excited levels like j = 5 and j = 6 (lower two panels in the figure), are now larger for the He atom as a partner than they are for the Ar atom. A possible explanation for this difference of behaviour between the two systems could be suggested by the specific shape of the radial multipolar coefficients of the two PESs compared in the panels of Fig. 2. We know that the direct potential coupling during the multichannel dynamics comes from the torque applied during the collision by the anisotropic potential with λ = 1 terms. This means that the differences in the shapes of the radial coefficients can tell us about the relative efficiency of such coupling during the collisions. For the case of the interaction CN− with Ar, reported in the left panel of Fig. 2, we see that the term in question has an attractive well before its repulsive wall at shorter distances. On the other hand, the same term for the interaction with He, right-panel of the same figure, has a very deep attractive well in the short range of radial distances. Such difference suggests that the He projectile can penetrate more closely to the target than the Ar atom and therefore apply for a longer range of action the transition-driving torque generated as a direct coupling by this multipolar term. The difference becomes less marked for the λ > 1 terms, which are now between the two systems in a relative order of size as that already seen for the excitations from j = 1 and j = 2. It means that now the reduced-mass difference in the kinematics takes over and the Ar projectile becomes only slightly more efficient in inducing rotational transitions.
To verify with a specific numerical example that to use the RR-PES with and without including the BSSE correction does not change the size and relative behaviour of the collision rate coefficients, we report in the figure below Fig. 9 a comparison for a set of excitation rate constants involving the initial rotational level of CN− colliding with the Ar atom.
One can clearly see from all the different collision rate constants reported in that figure that to employ a BSSE-corrected PES, at least for the case of anionic partner interacting with a noble gas, leaves the final rate constants essentially unchanged.
The data reported by the four panels of Fig. 10 describe now the state-changing inelastic rate coefficients for the transitions involving de-excitation (rotational cooling) processes, comparing the relative behavior of Ar and He as possible buffer gases. The organization of the data presented in the four panels of this figure is the same as that given into the similar panels of Fig. 8.
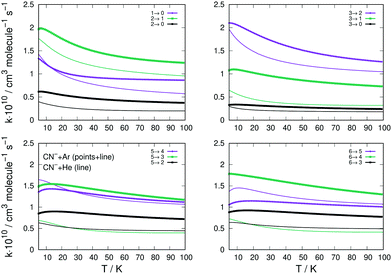 | ||
| Fig. 10 Same sets of state-changing rates as in Fig. 8, but here for the behaviour of de-excitation (cooling) processes for Ar (thick lines) and He (plain thin lines) in collision with CN−. The reported rate coefficients have been multiplied by 1010 cm3 s−1. See main text for further comments. | ||
We clearly see that the majority of the rotational cooling rates for Ar as an atomic partner are larger than those we have obtained for the He as a buffer gas. This happens for all transitions, from all initial rotational states chosen and for all the Δj values selected. The only difference in behaviour is that shown by the Δj = −1 de-excitation from the j = 5 level, where we see that the He partner is very close in magnitude to that from CN−/Ar process (lower left panel Fig. 10). This behaviour of the rotational cooling processes is in accord with what we had already discussed before for the rotation excitation inelastic rates of Fig. 8.
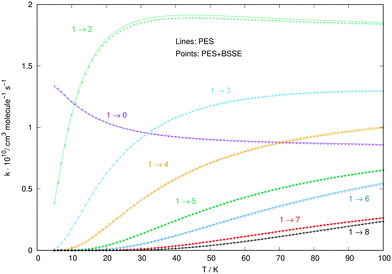
A similar comparison of collision-driven rotational excitation rate coefficients is reported in the four panels of Fig. 11, where Ar and p-H2 are now the two different partners of the molecular anion. For the latter, the rates were calculated by Kłos and Lique and obtained from the Basecol database.35 The following comments can be made: (i) all the excitation rate coefficients involving transitions with Δj = 1 changes are much larger for the p-H2 partner than those for the Ar atom. This indicates again that the strength of the coupling potentials is stronger for the former system than it is for the latter; (ii) as one considers excitations with Δj > 1, we see that the p-H2 partner still generates larger rate coefficients, although without them being very much larger than in the case of Ar. It is therefore the different strengths of the multipolar potential coefficients with λ > 1 in the two different partners which controls the efficiency of the direct coupling dynamics. One should also note that the reduced mass for the CN−/p-H2 is the smallest one for the three systems we are considering here.
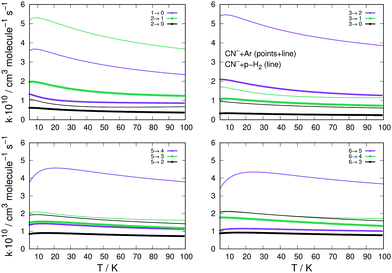 | ||
| Fig. 11 Computed excitation rates comparing the results for the Ar partner (thick lines) with the p-H2 case (thin plain lines). The reported rate coefficients have been multiplied by 1010 cm3 s−1. The transitions are the same as those in Fig. 10. See main text for further discussion. | ||
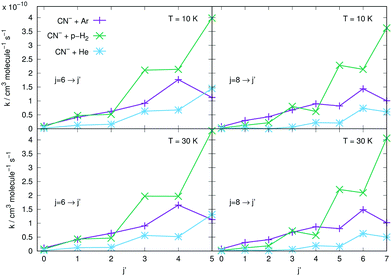
The results reported in the four panels of Fig. 12 present a comparison between different rotation cooling transitions, showing the behaviour of three different collision partners with CN−: He, Ar and p-H2. The two left-side panels in the figure report de-excitation rates from the initial j = 6 level of the anion into all its lower levels, while the right-side panels report the same type of processes but starting from the j = 8 initial rotational state. The temperatures of the rates considered also change from T = 10 K (upper panels) to T = 30 K in the lower two panels of the same figure. The following comments can be made: (i) all transitions involving state changes with Δj ≤ −3 for all three collision partners indicate the cooling rates for collisions with p-H2 to be the largest of the series, with that with Δj = −1 being the largest for both initial states and at both temperatures; (ii) all cooling transitions involving the Ar partner show that those with Δj = −1 are smaller than those with Δj = −2, as to be expected from the behaviour of the coupling potential terms already discussed earlier. The size of the inelastic rates with Δj ≥ −3 are now uniformly smaller, due to the increase of the involved energy gaps and the decrease of the coupling strength of the anisotropic potential, as discussed before in this section; (iii) the cooling rate coefficients pertaining to the He atom as a collision partner are smaller than those for Ar and for p-H2 at all temperatures and for both initial states examined, with the exclusion of the Δj = −1 transitions from the j = 6 state, which are larger than those for Ar. It is once more the relative interplay of the λ = 1 radial coefficient of the multipolar potential expansion in Fig. 2, the larger energy gap for that transition compared with that from j = 8, and the changes in the reduced mass for the case of the Ar projectile (the largest of the three systems) which provide the structural explanation of such differences in the dynamics.
5 Comparison of cooling kinetics in an ion trap
Given the information obtained from the calculations of the previous section, we are now in a position to follow the microscopic evolutions of the anion's rotational state populations by setting up the corresponding rate equations describing such evolution as induced by collisional energy transfer with the buffer gas in the trap as36,37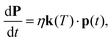 | (5) |
Both the vector p(t) values at t = tinitial and the collisional temperature T of the trap corresponding to the mean collisional energy between the partners are quantities to be specifically selected in each computational run and will be discussed in detail in the examples presented below. We shall disregard for the moment the inclusion of the state-changing rates due to spontaneous radiative processes in the trap. These quantities are already known to be smaller than the collision-controlled rates between the lower rotational levels of such systems, as already shown by us in earlier studies,16 and are therefore not expected to have any significant effect under the present trap conditions.
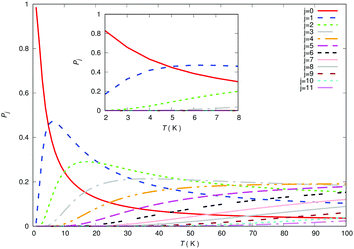
It may be useful at this point to be reminded of the relative populations of the rotational states of the trapped anion over a range of temperatures achievable in the traps. The corresponding steady-state populations are reported by the panels of Fig. 13. The importance of such populations for the present evolution kinetics will be further discussed below.
It is important to note at this point that, if the rate coefficients of the k(T) matrix in eqn (5) satisfy the detailed balance between state-changing transitions, then as t → ∞, the initial distribution will approach that of the effective equilibrium temperature of the buffer gas as felt by the ions in the trap, at least from a theoretical standpoint. These asymptotic solutions correspond to the steady-state conditions in the trap and can be obtained by solving the corresponding homogeneous form of equations given as dp(t)/dt = 0.
We solved the homogeneous equations by using the singular-value decomposition technique (SVD),36 already employed by us in previous studies. The non-homogeneous eqn (5), starting from our tinitial of 100 K to analyse the evolution kinetics at the various lower T values considered, as shown below. They were solved using the Runge–Kutta method for different translational temperatures of the trap. Since the role of the gas density is simply that of a scaling factor in the kinetics equations, we present in the figures values which are among those likely to be employed in trap experiments.5
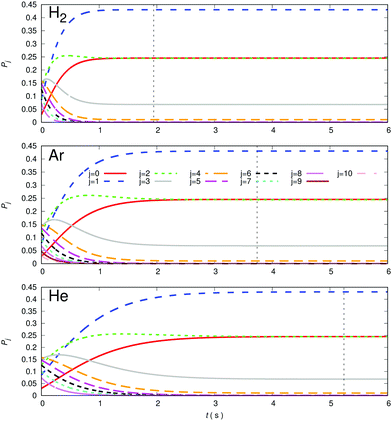
A comparison of the kinetic evolutions of the different populations of the rotational states of the trapped anion, at the lowest trap temperature of 10 K and choosing the same density of 1010 cm−3 for p-H2 (top panel), Ar (central panel) and He (bottom panel) is presented in the different panels of Fig. 14 below. The lighter He atom generates less efficient rotational state-changing collision dynamics than is the case for Ar and the p-H2 partner appear as the most efficient at these low temperatures.
The vertical lines shown in each of the panels of Fig. 14 indicate the time value for which thermal equilibrium of the state populations at the chosen 10 K temperature is achieved. We see how markedly different are these values for the three gases, suggesting again the most efficient to be molecular hydrogen in comparison with the other two atoms. This differences in collisional de-excitation efficiency will be further examined in the other figures of this section. It is important to note at this point that our computational definition of reaching the steady-state population at the chosen trap temperature is that of following the j = 0 population until it remains unchanged to its 4th decimal place. This definition has been followed throughout our present calculations.
It is important to note now that Fig. 14 is simply presenting a numerical experiment to indicate the differences in cooling dynamics exhibited by the three different gases at an arbitrary low T (in this case 10 K) below that selected to compute the evolution of the cooling dynamics in the trap after loading the molecular anion (T = 100 K). We should be reminded, in fact, that the physical boiling points of these buffer gases are really very different at ambient pressures, a feature that will play an important role in the present discussion of the comparative results. For p-H2 that value is 20.28 K, while for Ar is 83.8 K and for He is 4.22 K. The temperature value chosen above for our numerical experiment would therefore be only physically viable for He but not for the other two. However, to compare their behaviour at the same T value helps us to better visualize their different collisional efficiently in cooling the trapped anion of this study.
It is also of note to mention here that, under the low-pressure trap conditions the buffer gasses can be employed below their boiling points without substantial losses via condensation in the trap, as shown in earlier work by members of our group,37 where the use of Ar as a buffer gas was carried out down to about 55 K with marginal losses due to condensation effects. More physically realistic, and significant, operating conditions will be further discussed via the simulations presented below, the aim being to suggest easier (higher T) operating conditions, but still without efficiency losses, which can be attained by changing the buffer gas from He.
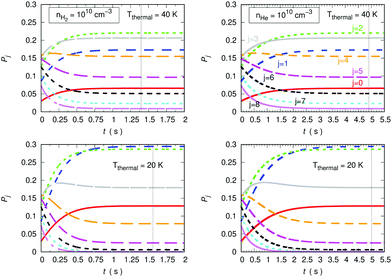
The data reported by the two columns shown in Fig. 15 clearly show the marked differences of behaviour of the population evolution of the rotational states of the trapped anion when the buffer gas is changed from He to p-H2. The vertical lines indicated in all panels report the time values for which the steady-state population is reached in the trap, where the collisional evolution has been started with T = 100 K. At both the considered temperatures the hydrogen buffer is clearly more efficient in driving rotational de-excitation processes in the trapped molecular anion. In fact, our calculations indicate a factor of more than three faster cooling (de-excitation) in the case of p-H2 in comparison with the He gas. Furthermore, the higher T values show the expected, slightly shorter time delay value in relation to that exhibited by the lower temperature in the lower panels of the same figure.
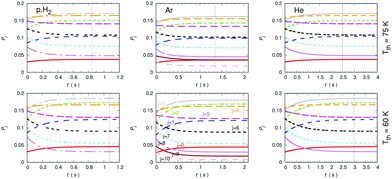
A further comparison of the de-excitation efficiency exhibited by all three possible buffer gases is reported in the three sets of panels of Fig. 16. The temperatures of choice correspond now to higher values, chosen so that the Ar buffer gas in the trap is expected to remain in the gas phase or with only marginal losses by condensation, as discussed in earlier work from members of our group.37 The higher T values are shown by the three upper panels while the lower temperatures taken as an example are reported in the three lower panels. The trap density of both buffer gases has been kept the same, as indicated in the figure, and the initial uploading temperature of the molecular gas has been selected to be 100 K for starting the collisional de-excitation process. The steady-state condition has been defined before in relation to the previous figures.
The data in the panels of that figure indicate once more the marked changes in de-excitation efficiency displayed by the different choices of buffer gases. The panels associated with the lower temperature of our example indicate that rotational levels up to j = 10 are being populated in the anion although only the j = 9 level is being significantly populated. The exclusion, for the calculations involving the He buffer, of the j = 9 and 10 in the network of coupled evolutionary equations does not change significantly the present results. The vertical lines report, as before, the time value at which the steady-state population of the anion rotational levels reaches the stated trap temperature. The panels for the Ar gas indicate a time interval, at both temperatures, which shows to be intermediate between the longest time delays reported for the He gas and the shortest ones indicated for the p-H2 example. The change of that time interval with changing T to higher values does not alter this ratio nor shortens the actual time delay values by much.
The Ar buffer gas, as discussed earlier when the collisional rate constants were compared in the previous section, is clearly seen to be less efficient than p-H2 in terms of collisional de-excitation capability (cooling): the vertical lines for the atomic gas, in relation of those shown by the latter molecular buffer gas, are around 40% slower on the present timescale than those associated with the latter. On the other hand, the He gas provides, as already discussed in our analysis of its dynamics in the previous Section, the lest efficient buffer gas for the present molecular anion. We can therefore say that either Ar or p-H2 would be buffer gases which can be used at higher trap temperatures and exhibit a markedly higher cooling efficiency than that of the He buffer gas. Such differences are obviously a consequence of the detailed quantum dynamics of the state-changing collisional rate constants which we have examined in the previous section.
6 Conclusions
In the present study we have analysed in detail the quantum collisions which can take place in a cold trap, over a range of trap temperatures chosen as examples, when the initial molecular anion which is trapped there (in our case the CN− anion) is made to interact with different choices for the buffer gas employed to drive the collisional de-excitations of the molecular rotational levels present at an initial temperature of 100 K, i.e. markedly larger than that expected to be reached in the trap after collisional thermalisation with the buffer gas of choice.The quantum calculations were carried out using accurate ab initio potential energy surfaces describing the interaction with the title molecular anion and three different buffer gases: He, Ar and p-H2. The relevant inelastic cross sections which we have computed via the quantum Coupled-Channel (CC) method have involved all the lower-lying rotational states of CN− up to j = 10, with the latter state found to be only marginally populated at the highest temperatures considered in this study.
The corresponding state-changing, rotationally inelastic rate coefficients were obtained for all three gases considered and found to be different in size within the series of gases, with those induced by Ar and p-H2 being fairly close to each other and those associated with the He gas being markedly smaller. As a consequence of the quantitative differences between collisional rate constants found by our calculations, we have further found that the evolutionary kinetics of the rotational state populations for the trapped anion changes depending on the actual buffer gas being considered. Hence, our analysis of the time delays obtained from the calculations clearly shows that the p-H2 is the most efficient gas in driving collisional de-populations of the higher rotational levels of the trapped anion, with Ar being just after it and behaving very similarly. On the other hand, the He gas is invariably found to be the slowest in driving collisional de-excitation processes, albeit being able to go down to lower temperatures as those achieved by the other two gases. In conclusion, our present calculations indicate that different choices for the buffer gas can provide a more rapid thermalization kinetics in the trapped anions and can achieve this improvement at higher temperatures than those indicated by He as a buffer of choice.
It follows from the present findings that whenever the trap conditions are not going to be operating below 60 K or so, it may be possible to employ a different buffer gas from He, thereby reducing the time delays needed to bring the trapped molecular anion's rotational populations down to the selected trap temperature.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to professor F. Lique for kindly providing us with the original routine to generate the CN−/p-H2 potential energy surface. FAG and RW acknowledge the financial support of the Austrian FWF agency through the research grant no. P29558-N36. One of us (L. G.-S.) further thanks the MINECO (Spain) for the awarding of grant PGC2018-09644-B-I00.Notes and references
- W. Paul, Rev. Mod. Phys., 1990, 62, 531–540 CrossRef CAS.
- F. M. Penning, Physica, 1936, 3, 873 CrossRef.
- H. G. Dehmelt, Adv. At. Mol. Phys., 1968, 3, 52–72 Search PubMed.
- W. M. Itano, J. C. Bergquist, J. J. Bollinger and D. J. Wineland, Phys. Scr., 1995, T59, 106–120 CrossRef CAS.
- R. Wester, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154001 CrossRef.
- O. Asvany and S. Schlemmer, Int. J. Mass Spectrom., 2009, 279, 147–155 CrossRef CAS.
- J. Deiglmayr, A. Göritz, T. Best, M. Weidemüller and R. Wester, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 043438 CrossRef.
- J. Fesel, S. Gerber, M. Doser and D. Comparat, Phys. Rev. A, 2017, 96, 031401(R) CrossRef.
- S. Gerber, J. Fesel, M. Doser and D. Comparat, New J. Phys., 2018, 20, 023024 CrossRef.
- F. H. J. Hall, M. Aymar, N. Bouloufa-Maafa, O. Dulieu and S. Willitsch, Phys. Rev. Lett., 2011, 107, 243202 CrossRef PubMed.
- L. González-Sánchez, E. Bodo and F. A. Gianturco, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 022703 CrossRef.
- M. Hernández Vera, F. A. Gianturco, R. Wester, H. da Silva Jr., O. Dulieu and S. Schiller, J. Chem. Phys., 2017, 146, 124310 CrossRef PubMed.
- L. González-Sánchez, R. Wester and F. A. Gianturco, ChemPhysChem, 2018, 19, 1866 CrossRef PubMed.
- F. A. Gianturco, O. Y. Lakhmanskaya, M. Hernández Vera, E. Yurtsever and R. Wester, Faraday Discuss., 2018, 212, 117–135 RSC.
- M. Simpson, M. Nötzold, T. Michaelsen, B. Bastian, J. Meyer, R. Wild, F. A. Gianturco, M. Milovanovic, V. Kokoouline and R. Wester, 2020, in preparation.
- L. González-Sánchez, B. P. Mant, R. Wester and F. A. Gianturco, Astrophys. J., 2020, 897, 75 CrossRef.
- K. M. Walker, F. Lique, F. Dumouchel and R. Dawes, Mon. Not. R. Astron. Soc., 2016, 466, 831–837 CrossRef.
- M. Lara-Moreno, T. Stoecklin and P. Halvick, Mon. Not. R. Astron. Soc., 2017, 467, 4174–4179 CrossRef CAS.
- M. Lara-Moreno, T. Stoecklin and P. Halvick, Mon. Not. R. Astron. Soc., 2019, 486, 414–421 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, et al., MOLPRO, version 2019.2, a package of ab initio programs, 2019, see https://www.molpro.net Search PubMed.
- C. Hampel, K. A. Peterson and H.-J. Werner, Chem. Phys. Lett., 1992, 190, 1–12 CrossRef CAS.
- M. J. O. Deega and P. J. Knowles, Chem. Phys. Lett., 1994, 227, 321–326 CrossRef.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1993, 98, 1358 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1994, 100, 2975 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- A. C. Newell and R. C. Baird, J. Appl. Phys., 1965, 36, 3751–3759 CrossRef CAS.
- D. R. Johnston, G. J. Oudemans and R. H. Cole, J. Chem. Phys., 1960, 33, 1310 CrossRef CAS.
- J. Kłos and F. Lique, Mon. Not. R. Astron. Soc., 2011, 418, 271–275 CrossRef.
- J. R. Taylor, Scattering Theory The Quantum Theory of Nonrelativistic Collisions, Dover, 2006 Search PubMed.
- R. Martinazzo, E. Bodo and F. A. Gianturco, Comput. Phys. Commun., 2003, 151, 187 CrossRef CAS.
- D. López-Durán, E. Bodo and F. A. Gianturco, Comput. Phys. Commun., 2008, 179, 821 CrossRef.
- L. González-Sánchez, F. A. Gianturco, F. Carelli and R. Wester, New J. Phys., 2015, 17, 123003 CrossRef.
- S. V. Jerosimić, F. A. Gianturco and R. Wester, Phys. Chem. Chem. Phys., 2018, 20, 5490 RSC.
- M.-L. Dubernet, M. H. Alexander, Y. A. Ba, N. Balakrishnan, C. Balanca, C. Ceccarelli, J. Cernicharo, F. Daniel, F. Dayou, M. Doronin, F. Dumouchel, A. Faure, N. Feautrier, D. R. Flower, A. Grosjean, P. Halvick, J. Klos, F. Lique, G. C. McBane, S. Marinakis, N. Moreau, R. Moszynski, D. A. Neufeld, E. Roueff, P. Schilke, A. Spielfiedel, P. C. Stancil, T. Stoecklin, J. Tennyson, B. Yang, A. M. Vasserot and L. Wiesenfeld, Astron. Astrophys., 2013, 553, A50 CrossRef.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in FORTRAN, Cambridge University Press, New York, 1993 Search PubMed.
- J. Mikosch, H. Kreckel, R. Wester, R. Plašil, J. Glosik, D. Gerlich, D. Schwalm and A. Wolf, J. Chem. Phys., 2004, 121, 11030 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: An additional folder containing the multipolar coefficients for the new CN−/Ar RR-PES, a Fortran routine for generating the actual PES values and all the computed state-to-state inelastic rate coefficients as been made available by the authors. See DOI: 10.1039/d0cp03440a |
| This journal is © the Owner Societies 2021 |