Open Access Article
Open Access ArticleMechanical properties of cell- and microgel bead-laden oxidized alginate-gelatin hydrogels†
T.
Distler‡
 *a,
L.
Kretzschmar‡
b,
D.
Schneidereit
c,
S.
Girardo
*a,
L.
Kretzschmar‡
b,
D.
Schneidereit
c,
S.
Girardo
 d,
R.
Goswami
d,
R.
Goswami
 d,
O.
Friedrich
d,
O.
Friedrich
 c,
R.
Detsch
a,
J.
Guck
de,
A. R.
Boccaccini
c,
R.
Detsch
a,
J.
Guck
de,
A. R.
Boccaccini
 *a and
S.
Budday
*a and
S.
Budday
 *b
*b
aInstitute of Biomaterials, Department of Materials Science and Engineering, Friedrich-Alexander-University Erlangen-Nürnberg, 91058 Erlangen, Germany. E-mail: thomas.distler@fau.de; aldo.boccaccini@fau.de
bInstitute of Applied Mechanics, Department of Mechanical Engineering, Friedrich-Alexander-University Erlangen-Nürnberg, 91058 Erlangen, Germany. E-mail: silvia.budday@fau.de
cInstitute of Medical Biotechnology, Department of Chemical and Biological Engineering, Friedrich-Alexander-University Erlangen-Nürnberg, 91056 Erlangen, Germany
dMax Planck Institute for the Science of Light and Max-Planck-Zentrum für Physik und Medizin, Erlangen-Nürnberg, 91058 Erlangen, Germany
eChair of Biological Optomechanics, Department of Physics, Friedrich-Alexander-University Erlangen-Nürnberg, 91058 Erlangen, Germany
First published on 5th March 2021
Abstract
3D-printing technologies, such as biofabrication, capitalize on the homogeneous distribution and growth of cells inside biomaterial hydrogels, ultimately aiming to allow for cell differentiation, matrix remodeling, and functional tissue analogues. However, commonly, only the mechanical properties of the bioinks or matrix materials are assessed, while the detailed influence of cells on the resulting mechanical properties of hydrogels remains insufficiently understood. Here, we investigate the properties of hydrogels containing cells and spherical PAAm microgel beads through multi-modal complex mechanical analyses in the small- and large-strain regimes. We evaluate the individual contributions of different filler concentrations and a non-fibrous oxidized alginate-gelatin hydrogel matrix on the overall mechanical behavior in compression, tension, and shear. Through material modeling, we quantify parameters that describe the highly nonlinear mechanical response of soft composite materials. Our results show that the stiffness significantly drops for cell- and bead concentrations exceeding four million per milliliter hydrogel. In addition, hydrogels with high cell concentrations (≥6 mio ml−1) show more pronounced material nonlinearity for larger strains and faster stress relaxation. Our findings highlight cell concentration as a crucial parameter influencing the final hydrogel mechanics, with implications for microgel bead drug carrier-laden hydrogels, biofabrication, and tissue engineering.
1. Introduction
Hydrogels are three-dimensional polymer networks of high water content,1,2 which have found a wide range of applications in the context of tissue engineering (TE). Synthetic hydrogels such as polyethylene glycol (PEG),3 2-hydroxyethyl methacrylate (HEMA)-based hydrogels,4 poly(oxazoline)s (POx),5 or polyacrylamide (PAAm), as well as naturally derived hydrogels such as alginate, gelatin, collagen, or fibrin matrices,6–9 have been used in various biomedical applications.1 Frequently, these include the delivery of cells,10–14 growth factors,15–17 or drugs,18–22in vitro tissue and tumor models,23–25 and tissue engineering (TE) matrices.2,26–30The role of biopolymer hydrogels in TE is to chemically and physically mimic the extracellular matrix (ECM) environment to facilitate controlled cell adhesion, proliferation, differentiation, and matrix remodeling.7,26 Therefore, not only chemical properties of hydrogels such as surface functionality or water absorption capacity play an important role,1 but also the mechanical characteristics of artificial ECM materials need to be known and tuned according to their intended application.31–35 Previous studies have shown that neural progenitor or pre-osteoblast cells are more likely to adhere, differentiate, and proliferate when the artificial ECM has similar properties to the native ECM.36,37
Importantly, the mechanical characteristics of biomaterial hydrogels can be tuned by various means, such as composition,32,35,38–42 chemical functionalities,43 microstructure,44 and cross-linking mechanisms.45–47 Research on the mechanical properties of materials for TE, therefore, has been frequently focused on a single stiffness value and how it affects cell adhesion, proliferation, and differentiation.48,49 However, the nonlinear behavior of the native tissue ECM and of many artificial ECM materials requires a more complex mechanical assessment to fully reconstitute nonlinearity and time-dependent mechanical characteristics.35,50,51
Despite the fact that advanced scaffold fabrication techniques, such as biofabrication approaches embedding cells inside a 3D-printed hydrogel matrix,52–62 are a major research focus in TE lately, little is known on how cells incorporated into a material influence the final mechanical properties of the cell–matrix composite.50,63,64 Consequently, there is a pressing need to understand how cell concentration might affect the mechanical properties of specific hydrogel systems. Interestingly, van Oosten et al.50 showed that the response of fibrin-based hydrogels to tension is stiffer than that to compression (different from native brain tissue51), which was inverted when cells were embedded inside the gels.50 Hence, cells inside hydrogels can significantly alter the qualitative compression–tension asymmetry behavior, likely to be dependent on the hydrogel system investigated. In addition, cell density and growth combined with ECM production have been shown to alter the mechanical properties of hydrogels during TE construct maturation and represent crucial parameters for successful TE. For instance, human cancer-associated fibroblasts embedded in collagenI/Matrigel™ hydrogels were found to stiffen the material with increasing cell number,63 which was associated with matrix remodeling caused by the cells inside the matrix during incubation and was overcome by the inhibition of ROCK 1/2 kinases.63 Significant increases of aggregate and Young's modulus were also found in agarose hydrogels incubated with different cell densities over time.64 The effect was linked to the increasing glycosaminoglycan (GAG) and collagen content in the ECM, synthesized by the embedded cells.64
Mechanical tissue- and organ-substitutes, to be used as, e.g., soft tissue phantoms or surgical models, have been engineered using various hydrogels.38,50,65–67 We previously found that alginate-based gels without embedded cells can imitate mechanical characteristics of brain tissue.38 In contrast to fibrin-based hydrogels,50 the matrix material showed a stiffer behavior for compression than for tension, mimicking the asymmetry found in native brain tissue.38,51 Yet, matrices different from pristine alginate are required to allow for matrix remodeling, cell proliferation, and hydrogel degradation, to ensure successful TE approaches.43
To overcome the limited cell–material interaction and degradation behavior of pristine alginate, advanced alginate-based hydrogels have been introduced,19,61,68 which include derivatives with increased cell–material interaction through specific integrin binding motifs28,69–72 and proteins,31,73,74 combined with a tailored degradation behavior through oxidation of the alginate.75–78 Aldehyde groups resulting from the oxidation process allow for reversible covalent bonds between the oxidized alginate and amine groups of proteins such as gelatin,68,79–82 increasing their protein binding capacity and cell adhesion properties.28 The applicability of oxidized alginate-gelatin (ADA-GEL) hydrogels has been demonstrated in several TE applications,75 including bioprinting approaches embedding cells.60,82–87 However, the influence of cells embedded in ADA-GEL hydrogels on the detailed resulting complex mechanical characteristics still remains unknown. ADA-GEL hydrogels consist of ionically crosslinked oxidized alginate polysaccharide combined with reversibly, covalently bound gelatin, which contrasts with fibrous, network-building collagen or fibrin-based hydrogels, on which the impact of cell-fillers has been investigated before.50 We have shown in previous studies by second harmonic generation (SHG) imaging that ADA-GEL does not possess highly ordered fibrillar structures,84,88 hence can be assumed as a non-fibrillar hydrogel. Its non-fibrous crosslinking structure renders ADA-GEL as an excellent candidate to study the effect of cellular fillers on the mechanical properties of non-fibrous hydrogel matrices, especially as this hydrogel proved its potential for TE75,76 and biofabrication82,84,85,89,90 applications.
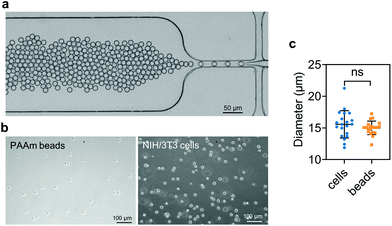
The goal of this work is to investigate the influence of increasing cell density on the mechanical properties of ionically cross-linked ADA-GEL hydrogels. In addition, we aim to evaluate whether PAAm microgel beads can mimic the effect of embedded cells as a filler model system. PAAm microgel beads have shown the potential to mimic cells with respect to their diameter and elasticity, and to allow for a comparison between different mechanical assessment techniques, such as atomic force microscopy (AFM) and real-time deformability cytometry (RT-DC).91 Due to their mechanical similarities to cells, PAAm beads have been used as stress sensors,91–93 for the calibration of RT-DC measurements,94 and to build 3D colloidal scaffolds with spatially differing mechanical layers for cell growth, migration and mechanosensitivity studies.95 Here, we investigate the mechanical properties of hydrogels containing PAAm microgel beads and embryo mouse fibroblast (NIH/3T3) cells for small and large deformations under compression, tension, and torsional shear loadings. We specifically investigate time-dependent and nonlinear effects to systematically study the influence of different filler concentrations and potential differences between PAAm microgel beads and cells inside the hydrogel matrix. To underpin the mechanical characterization, we assess bead and cell distributions inside the gels using multiphoton microscopy techniques.
2. Materials and methods
2.1. Oxidized alginate synthesis
Sodium alginate (PH 176, VIVAPHARM alginate, JRS PHARMA GmbH & Co. KG, Rosenberg, Germany) was oxidized following an adapted protocol of controlled oxidization as described previously.78 In brief, sodium alginate (10 g) was oxidized using 9.375 mmol sodium metaperiodate (Sigma Aldrich, Germany) in 100 ml of a water–ethanol (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 v/v) for 6 hours in the absence of light. The oxidation reaction was quenched using 10 ml of ethylene-glycol (Sigma Aldrich, Germany) and the solution was dialyzed against ultrapure water (UPW, Type II, MilliQ) using dialysis tubes (Molecular Weight Cut-off (MWCO): 6–8 kDa, Spectra/Por, Spectrum Laboratories, US) for three days. The water was changed daily to ensure the complete extraction of the oxidant, ethanol, and reaction byproducts. The oxidized alginate (alginate dialdehyde, ADA) was frozen overnight and lyophilized for 72 h to yield a dry product.
50 v/v) for 6 hours in the absence of light. The oxidation reaction was quenched using 10 ml of ethylene-glycol (Sigma Aldrich, Germany) and the solution was dialyzed against ultrapure water (UPW, Type II, MilliQ) using dialysis tubes (Molecular Weight Cut-off (MWCO): 6–8 kDa, Spectra/Por, Spectrum Laboratories, US) for three days. The water was changed daily to ensure the complete extraction of the oxidant, ethanol, and reaction byproducts. The oxidized alginate (alginate dialdehyde, ADA) was frozen overnight and lyophilized for 72 h to yield a dry product.
2.2. Hydrogel formulation
Hydrogel precursor solution was obtained by dissolving 7.5% (w/v) ADA in Dulbecco's phosphate-buffered saline (DPBS, Gibco, Germany) and 7.5% (w/v) gelatin (GEL) (Typ A, from porcine skin, Bloom 300, Sigma Aldrich, USA) in UPW under continuous stirring at 37 °C. Both solutions were passed through 0.45 m (ADA) and 0.22 m (GEL) syringe filters (Rotilabo®, Carl Roth GmbH & Co. KG, Germany), respectively. ADA and GEL were mixed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio and stirred until a homogeneous solution with a final concentration of 3.75%/3.75% (w/v) ADA-GEL was obtained.
1 ratio and stirred until a homogeneous solution with a final concentration of 3.75%/3.75% (w/v) ADA-GEL was obtained.
2.3. Cell culture and maintenance
To assess the influence of cells on the mechanical properties of hydrogel samples, NIH/3T3 cells (passage P7-P28) (murine embryo fibroblasts 3T3, ATCC® CRL-1658™, ATCC, USA) were used. The cells were cultured using a high glucose Dulbecco's Modified Eagle's Medium (DMEM, Gibco, Germany), supplemented with bovine calf serum, L-glutamine, sodium pyruvate and penicillin–streptomycin (Gibco, Germany), at 37 °C under a controlled humidified atmosphere (98% air, 5% CO2) in an incubator. Cells were passaged by washing with DPBS and detaching using 0.25% Trypsin/EDTA (Gibco, Germany).2.4. Preparation of polyacrylamide microgel beads
PAAm beads were produced as described previously.91 Briefly, a polydimethylsiloxane (PDMS)-based flow-focusing microfluidics device interfaced with a pressure-based microfluidics controller (Fluigent MFCS-EX) was used to produce pre-gel monodisperse droplets in oil (Fig. 1a). The pre-gel mixture was obtained by dissolving acrylamide (7.6% w/v), bis-acrylamide (0.2% w/v) and ammonium persulphate (0.8% w/v) in 10 mM TRIS buffer (all Sigma Aldrich, Germany). The oil (HFE-7500, 3M™, USA) solution was prepared by dissolving ammonium Krytox surfactant (1.5% w/w), TEMED (0.4% v/v) and N-hydroxysuccinimide ester (NHS, 0.1% w/v), (Sigma Aldrich, Germany). After production, the droplets dispersed in the oil solution were incubated overnight at 65 °C to complete the polymerization. Finally, the beads were washed three times by centrifugation and resuspended in 1× PBS. To functionalize the beads with Alexa Fluor™ 488 Hydrazide (Thermo Fisher Scientific, USA), the beads were re-suspended in 50 mM HEPES (Carl Roth, Germany) dissolved in UPW. After incubation overnight, the functionalized PAAm microgel beads were washed three times with 1× PBS and stored at 4 °C until further use.2.5. Sample preparation
To study the influence of embedded cells and PAAm microgel beads on the mechanical behavior of ADA-GEL hydrogels, we chose different filler densities between 1 million fillers per ml and 8 million fillers per ml, as summarized in Table 1. Table 1 additionally reports the number of specimens and the corresponding passages of NIH/3T3 cells for the different test series. Cells were counted using the Trypan blue (Gibco, Germany) exclusion method with a Neubauer counting chamber (Paul Marienfeld GmbH & Co. KG, Germany). The cells were centrifuged and then dispersed in the hydrogel precursor solution after carefully removing the cell medium. PAAm microgel beads were treated analogously, except for the use of Trypan blue.| Study | Pure ADA-GEL | 1 million per ml | 2 million per ml | 4 million per ml | 6 million per ml | 8 million per ml | |
|---|---|---|---|---|---|---|---|
| Beads | No. of samples | n = 5 | n = 5 | n = 5 | n = 5 | — | n = 6 |
| Cells | No. of samples | n = 5 | n = 5 | n = 5 | n = 5 | n = 5 | n = 5 |
| Cell passage | — | P7 | P12 | P15 | P28 | P24 | |
We fabricated ADA-GEL cylinders using a custom-designed platinum-catalyzed silicone model (Ecoflex™ 00-50, Smooth-On Inc., USA). The mold negative for the casting of ten cylinders (d = 8 mm, h = 4 mm) was first fabricated from polylactic acid (PLA) using a polymer 3D-printer (Ultimaker 2+, Ultimaker, Netherlands). Next, the silicone mold was placed in Petri dishes (d = 92 mm, Sarstedt, Germany) and 200 l of hydrogel precursor solution were pipetted into each mold. The solution was carefully spread to the edges of the mold to allow for a flat specimen surface and to avoid bubbles. The hydrogels were left to set for 20 min to allow partial gelatin solidification, followed by crosslinking using 0.1 M CaCl2. After five minutes, the mold was removed after detaching the specimens by using a spatula. The samples were allowed to additionally crosslink for five minutes before detaching them with the spatula from the Petri dish. Afterwards, the samples were cross-linked for another 35 minutes, so that a total crosslinking time of 45 minutes was reached. An exemplary crosslinked ADA-GEL sample is illustrated in Fig. 2a. We finally transferred the samples into DMEM, which was chosen as the storing and testing medium for the mechanical analyses.
2.6. Experimental setup
For the mechanical measurements, a Discovery HR-3 rheometer (TA Instruments, New Castle, USA) was used. To maximize adhesion between the specimens and the geometry of the rheometer, sandpaper was attached to the upper and lower specimen holder before mounting the samples by using instant glue (Cyanacrylat, Henkel AG & Co. KGaA, Germany), as described in ref. 38. Before starting the testing protocol, an axial force of 0.03 N was applied to ensure contact between the geometry and the specimen. As the samples were fixed for microstructural analyses after mechanical testing, we refrained from testing the samples immersed in fluid. Instead, we carefully hydrated the specimens with DMEM, as illustrated in Fig. 2b. All mechanical measurements were performed at room temperature (22 °C, RT), as hydrogel degradation may have affected the results at elevated temperatures.78 When testing fluorescent PAAm microgel bead-laden ADA-GEL samples, the setup was covered using a black cardboard to avoid photobleaching.The testing protocol combined different loading conditions, loading modes (compression, tension, torsional shear), strains, and strain rates to appropriately characterize both the small- and large-strain response of these nonlinear and viscoelastic materials, as summarized in Table 2. Each sample was measured for ∼25 minutes, keeping the hydrogel surrounded by DMEM at all times. The protocol started with a frequency sweep from 0.1 to 10 Hz at a maximum shear strain of 1% to quantify the small-strain behavior of the hydrogels. Subsequently, cyclic compression–tension experiments with a maximum strain of 15% and a loading velocity of 40 m s−1 were performed, followed by stress relaxation experiments at a maximum strain of 15% and a holding time of 300 s each. Finally, two sets of cyclic shear experiments were performed with maximum strains of 15% and 30%, and an angular frequency of 0.3333 rad s−1 and 0.1667 rad s−1, respectively, followed by a shear stress relaxation test at 30% maximum shear strain (reached within 1 s) with a holding time of 300 s. After mechanical testing, the ADA-GEL samples were carefully removed from the geometries by using a scalpel and stored in DMEM for subsequent microstructural investigations.
| Loading condition | Max. strain | Loading rate |
|---|---|---|
| Frequency sweep | 1% | 0.1–10 Hz |
| Cyclic compression and tension | 15% | 40 m s−1 |
| Compression stress relaxation | 15% | Undefined |
| Tension stress relaxation | 15% | Undefined |
| Cyclic shear | 15% | 0.3333 rad s−1 |
| Cyclic shear | 30% | 0.1667 rad s−1 |
| Shear stress relaxation | 30% | 0.1 s (rise time) |
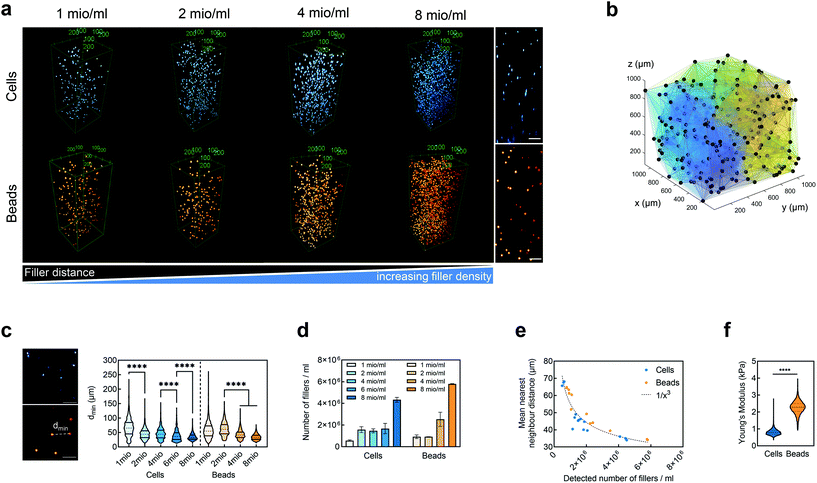
2.7. Analysis of filler distribution
To analyze the distribution of cells inside the ADA-GEL hydrogels, cell-laden samples were stained for cell nuclei using 1 l ml−1 Hoechst 33342 (Hoechst 33342, H3570, Invitrogen™, Germany) solution (in HBSS) for 40 minutes in the absence of light. The specimens were washed with Hank's Balanced Salt Solution (HBSS, Sigma Aldrich, Germany) and fixed using 4% formaldehyde (Sigma Aldrich, Germany) for 20 minutes. All samples were stored in HBSS at 4 °C before imaging.2.8. Multiphoton microscopy
The distribution of cells and beads inside ADA-GEL hydrogels was analyzed using a multiphoton microscope (TriMScope II, LaVision BioTec, Bielefeld, Germany). Hoechst stained cells were excited using a modelocked ps-pulsed Ti:Sa laser (Chameleon Vision II, Coherent, Santa Clara, USA) at 810 nm wavelength. The cell-sample's fluorescence was recorded using a 450/30 nm single bandpass filter (Chroma Technology group, Acal BFi Germany GmbH, Germany) and a non-descanned transmission photomultiplier tube (PMT). The Alexa488-conjugated bead fluorescence was recorded using a 525/50 nm (Chroma Technology group, Acal BFi Germany GmbH, Germany) single bandpass filter and the same PMT. A 25× HC FLUOTAR L objective (Leica Microsystems GmbH, Germany) was used throughout the imaging. Voxel sizes of 0.4 × 0.4 × 1 m3 in images with a field of view of 400 m2 were recorded, maintaining pixel counts of 512 × 512 pixels (X–Y) and 1292 pixels (Z).2.9. Image analysis
All images were processed using Fiji (NIH).96 For image quantification, image volumes of 0.4 × 0.4 × 1 mm3 were recorded. The nearest neighbour distance dmin among cells and beads was calculated from 3D reconstructions of the imaged volumes using Matlab (MathWorks Inc, US), and was defined as the smallest distance among all proximate neighbours (N > 294) of each individual filler inside the hydrogel volume. The number of fillers was quantified from three individual volumes per concentration. The mean nearest neighbour distance was calculated for each individual volume (n = 3) per concentration.2.10. Real-time deformability cytometry (RT-DC)
Cell and bead elasticity were assessed using RT-DC, as described previously.91,97 Briefly, NIH/3T3 cells and PAAm beads were suspended in MC 0.5% (w/v) in 1× PBS (3 × 106 ml−1) and flow-focused in a 30 m narrow square channel, applying a total flow rate of 0.12 and 0.24 l s−1, respectively. The flow rate was adapted to account for sufficient deformation inside the narrow channel, in the range of 0.005–0.05 for further calculation of the Young's modulus. The cell and bead deformation vs. size was analyzed in real-time and a method based on numerical simulations was used to calculate their Young's modulus.98 The deformation d is defined by the following equation97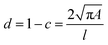 | (1) |
2.11. Data analysis and material modeling
To describe the macroscopic deformation of each tested specimen, we used the nonlinear equations of continuum mechanics and introduced the deformation map φ(X,t), which maps tissue from the undeformed, unloaded configuration to the deformed, loaded configuration.99 The deformation gradient F(X,t) = ∇Xφ(X,t) maps line elements in the undeformed sample to the corresponding line elements in the deformed sample, where X and x denote the position vectors in the unloaded and loaded configurations, respectively. The principal stretches λi, i = 1, 2, 3, are the square roots of the eigenvalues of the left and right Cauchy Green tensors defined by b = FFT and C = FTF, where [F] = diag{λ1,λ2,λ3}. We assumed that the samples deformed homogeneously in compression and that the filled ADA-GEL hydrogels are incompressible due to their high water content, characterized by det F = 1.In uniaxial compression and tension, we computed the stretch as λ = 1 + Δz/H, with specimen height H and z-displacement Δz. The corresponding Piola stress Pzz was calculated as the measured force fz divided by the cross-sectional area A of the specimen in the unloaded reference configuration, i.e. Pzz = fz/A. Under the assumption of uniform deformation and for unconfined lateral surfaces, the deformation gradient F yields
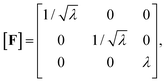 | (2) |
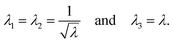 | (3) |
We model the compression–tension response of the samples by considering the modified one-term Ogden model strain-energy function for a hyperelastic, incompressible material 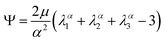 , where α denotes the nonlinearity parameter and μ the classical shear modulus.51,100 We can then express the Piola stress tensor PΨ as the derivative of the strain-energy function Ψ with respect to the deformation gradient F.99 For an incompressible hyperelastic material with det F = 1, we obtain
, where α denotes the nonlinearity parameter and μ the classical shear modulus.51,100 We can then express the Piola stress tensor PΨ as the derivative of the strain-energy function Ψ with respect to the deformation gradient F.99 For an incompressible hyperelastic material with det F = 1, we obtain
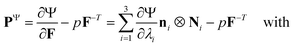 | (4) |
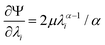 | (5) |
To calibrate the shear modulus μ and nonlinearity parameter α, we used the nonlinear least-squares algorithm lsqnonlin in MATLAB and minimized the objective function
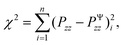 | (6) |
To evaluate the ‘goodness of fit’, we determined the coefficient of determination R2 = 1 − Sres/Stot, where 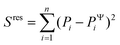 is the sum of squares of residuals with the experimental data values Pi, the corresponding model data values PΨi, and the number of data points n, and
is the sum of squares of residuals with the experimental data values Pi, the corresponding model data values PΨi, and the number of data points n, and 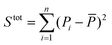 is the total sum of squares with the mean of the experimental data
is the total sum of squares with the mean of the experimental data 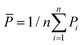 .
.
2.12. Statistical analysis
All statistical analyses were performed using either the Statistics Toolbox in MATLAB® (MathWorks, US) or GraphPad Prism software (GraphPad Software, US). A p-value lower than 0.05 was considered to be significant. Multi-comparison tests with separate Tukey-Kramer tests were performed between the different bead and cell concentrations. We evaluated maximum stresses in compression, tension, and torsional shear, as well as the compression–tension asymmetry, Young's modulus, and the nonlinearity parameter α. Comparisons between two groups were performed using Student's or Welch's t-tests (normally distributed) or Mann-Whitney U tests (non-parametric). Statistically significant differences among mean ranks (nearest neighbour distance analysis) were tested for non-parametric Kruskal-Wallis test with Dunn's multiple comparisons post-hoc test.3. Results
3.1. Imaging
We embedded cells and beads at different filler concentrations inside ADA-GEL hydrogels and assessed the distribution of the fillers using multiphoton microscopy (Fig. 3a). An intact, spherical cell-shape was confirmed without indication of fragmented or spread cells in the autofluorescence channel. Increasing the filler density of cells (blue, Hoechst) and beads (orange colored, AF488) led to a decrease in the distance between neighbouring fillers (Fig. 3a–c). From the multiphoton microscopy data, we reconstructed the 3D filler distribution inside the hydrogels (Fig. 3b) and calculated the nearest distance between two individual neighbouring cells and beads in 3D from the reconstructions (Fig. 3c). The mean distance between cells in 1 mio ml−1 cell-containing ADA-GEL hydrogels was approx. 67 ± 4 μm. Increasing the cell density from 4 million per ml to 6 and 8 million per ml led to a significantly (****p < 0.0001) decreased nearest neighbour distance (Fig. 3c, Videos S1 and S2, ESI†). Increasing the content of beads from 2 million per ml to 4 and 8 million per ml significantly decreased the median nearest neighbour distance from >50 μm to approx. 33 μm (Fig. 3c). The number of fillers detected in the hydrogel showed a noticeable increase from 2, 4, and 6 million cells per ml to 8 million cells per ml (Video S1, ESI†), with similar amounts of cells detected in the 2, 4, and 6 mio ml−1 hydrogels (Fig. 3d). For bead-laden hydrogels, an increase in detected bead density was monitored from 2 to 4 million per ml, and 4 to 8 million per ml (Fig. 3c). Plotting the mean nearest neighbour distance as a function of the detected amount of fillers, we observed that the mean neighbour distance decreases at approx. 1/x3 with detected number of fillers inside the hydrogels (Fig. 3e). The Young's modulus of the cells was significantly (****p < 0.0001) lower in comparison to the polyacrylamide beads (Fig. 3f), as cell stiffness was in the range of 0.6 ± 0.1 kPa and bead stiffness was at 2.2 ± 0.1 kPa, assessed via real-time deformability cytometry (Fig. 3f).3.2. Small-strain behavior of cell- and bead-laden hydrogels
Fig. 4a and b show the storage (G′) and loss (G′′) moduli for cell- and bead-laden ADA-GEL samples over a frequency range of 0.01 to 10 Hz. In general, G′ and G′′ are in the same range for both bead- and cell-laden ADA-GEL specimens. Independent of the filler and its concentration, the storage moduli slightly increase with increasing frequency. While bead densities between 2 and 8 million beads per ml in Fig. 4a, left, show similar results to pure ADA-GEL with only a slight decrease in the storage modulus with increasing bead density, the gel with the lowest bead concentration of one million beads per ml exhibits a significantly higher value of G′. However, the theoretical volume fraction of one million beads per ml was approximately 0.2% of the bulk hydrogel (Table 3). Considering the variance of the assessment (Fig. S1, ESI†) and the fact that an increase in G′ was solely observed for one million beads per ml but not for further increasing bead concentrations, the data do not allow for a strong conclusion on the observed effect. Concerning cell-laden ADA-GEL hydrogels in Fig. 4a, right, the storage moduli for densities of up to 4 million cells per ml alternate around the results of pure ADA-GEL samples. However, we observe a significant decrease in G′ when the cell density is increased to 6 or 8 million cells per ml. This may be attributed to the increasing amount (Fig. 3a and d) of softer (Fig. 3f) cells inside the hydrogels, with significantly reduced distance between individual cells (p < 0.0001, Fig. 3c). In general, the effect of cell inclusions on G′ is more pronounced than for the inclusions of PAAm microgel beads, especially for high cell concentrations >4 million per ml.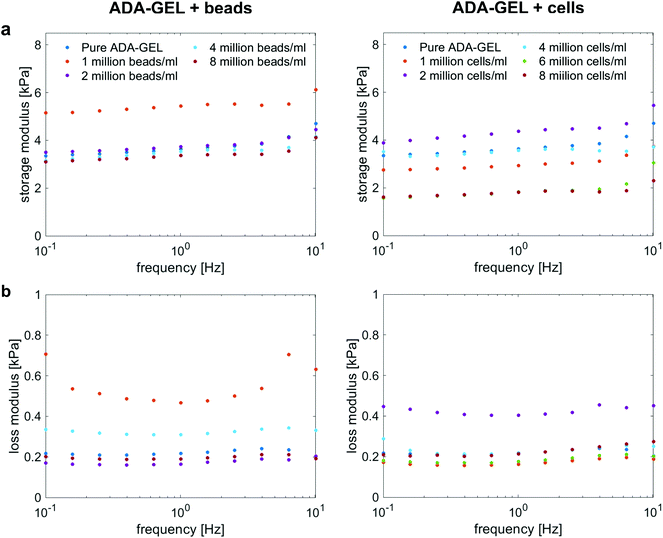 | ||
| Fig. 4 Storage (a) and loss (b) moduli for ADA-GEL samples with different cell and PAAm microgel bead densities, respectively, at 1% strain over a frequency range from 0.1 Hz to 10 Hz. | ||
| Beads | Cells | |||||
|---|---|---|---|---|---|---|
| Density (ml−1) | Volume (%) | Analytical E (kPa) | Experimental E (kPa) | Volume (%) | Analytical E (kPa) | Experimental E (kPa) |
| Pure ADA-GEL | — | — | 11.3 ± 0.9 | — | — | 11.3 ± 0.9 |
| 1 million | 0.2 | 11.3 | 10.8 ± 1.4 | 0.3 | 11.3 | 9.6 ± 1.4 |
| 2 million | 0.5 | 11.3 | 10.8 ± 2.2 | 0.5 | 11.3 | 10.1 ± 1.0 |
| 4 million | 1.0 | 11.2 | 8.6 ± 1.2 | 1.0 | 11.2 | 10.1 ± 1.0 |
| 6 million | — | — | — | 1.6 | 11.1 | 4.0 ± 0.8 |
| 8 million | 1.9 | 11.2 | 9.8 ± 1.0 | 2.1 | 11.2 | 3.5 ± 0.9 |
The loss moduli for both bead- and cell-laden hydrogels slightly decrease up to a frequency of approximately 1 Hz, and then slightly increase again for higher frequencies. Similar to the storage moduli of ADA-GEL samples filled with beads, we observe the highest values for samples with a bead density of 1 million per ml, while all other concentrations show similar results to pure ADA-GEL. For cell-laden hydrogel samples, only the samples with 2 million cells per ml show significantly higher values than the pure ADA-GEL samples, while the data do not indicate a clear correlation between the cell- or bead-filler concentration and the viscoelastic properties of the hydrogels in the small strain (1%) regime (Fig. 4).
3.3. Large-strain behavior of cell- and bead-laden hydrogels
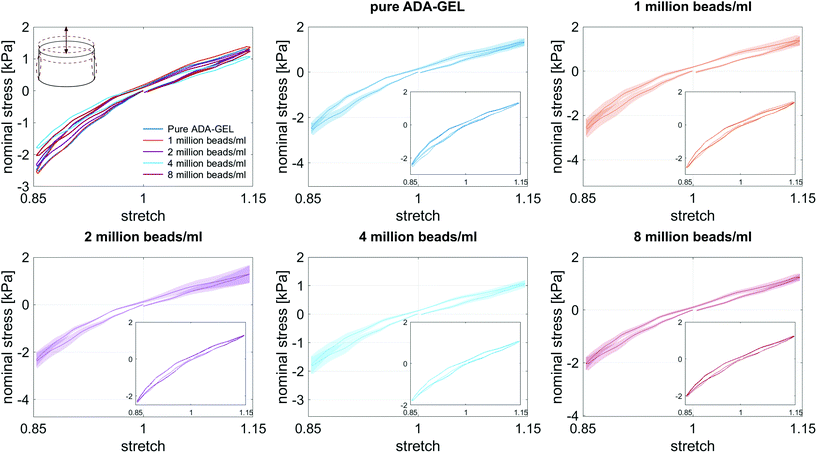
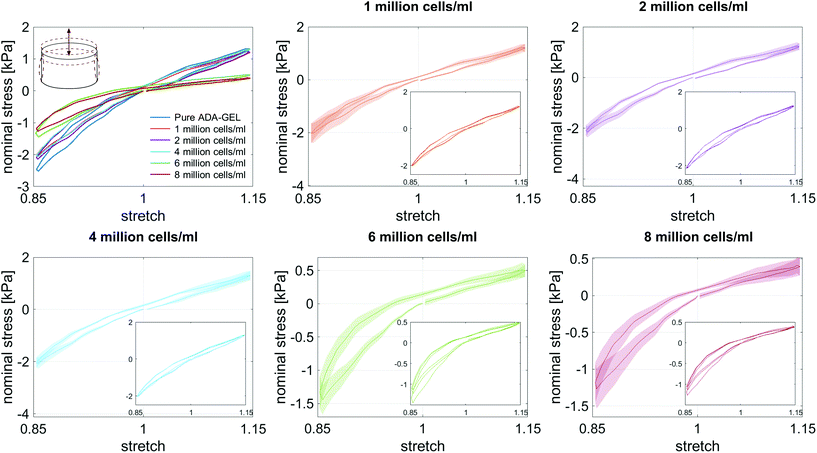
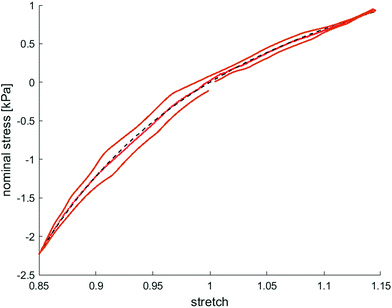
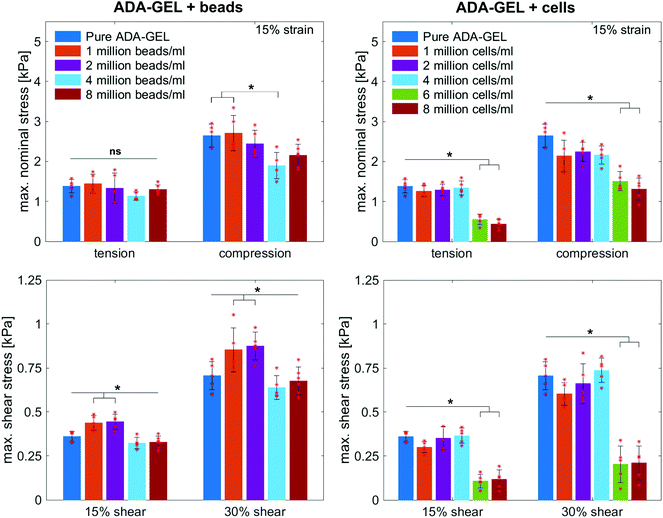
Fig. 8 illustrates the average maximum stresses with standard deviations during compressive loading up to 15% strain, tensile loading up to 15% strain, as well as torsional shear loadings up to 15% and 30%, respectively, for bead- and cell-laden hydrogels of different filler densities. In accordance with the observations in Fig. 5 and 6, the maximum nominal stresses are higher for compression than for tension for all hydrogels tested in this work. Regarding hydrogel samples filled with beads, we observe a slight decrease in the maximum stresses for bead densities of 4 and 8 million beads per ml, independent of the loading mode. Furthermore, in shear only, specimens with 1 and 2 million beads per ml show significantly higher stresses compared to all other concentrations and pure ADA-GEL. Regarding cell-laden hydrogels, the inclusion of lower concentrations (<6 mio ml−1) shows no significant effect on the maximum stresses compared to pure ADA-GEL. However, we observe significantly decreased stresses for all loading modes for higher cell densities of 6 and 8 million cells per ml. The drop in stresses for higher filler densities is much more pronounced for cell- than for bead-laden hydrogels. In both cases, the effect is more apparent in shear than in compression and tension.
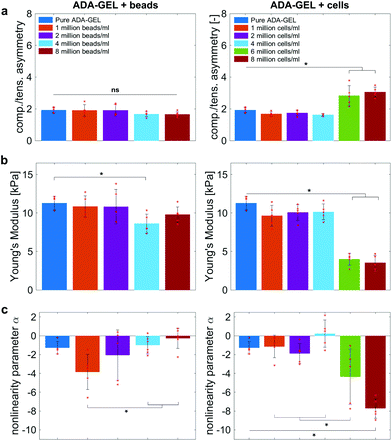
Fig. 9 compares the compression–tension asymmetry (a), the Young's modulus (b) and the nonlinearity parameter α (c) for bead- and cell-laden hydrogels of different filler densities. For most of the hydrogels investigated in this work, the compression–tension asymmetry takes on a value of approximately two, which yields that the compression response is twice as stiff as the response in tension. Only the high-cell-concentration hydrogels with 6 and 8 million cells per ml show a more pronounced asymmetry, where compression is more than three times stiffer than tension.
The Young's modulus significantly decreases for both high-bead- and high-cell-concentrations. Interestingly, the Young's modulus decreases for densities higher than 2 million per ml in bead-laden hydrogels, but only for densities higher than 4 million fillers per ml in cell-laden hydrogels. In accordance with the results from small-strain experiments, the drop in the Young's modulus is much more pronounced for the cell-laden hydrogels than for the bead-laden gels.
The drop in stiffness for higher filler concentrations is significantly higher than one would expect considering the low volume fractions of fillers, which hardly exceed 2% (Table 3), even for the highest concentrations of 8 million fillers per ml. A first analytical approximation for the effective stiffness of a matrix filled with a low volume fraction of linear elastic, spherical particles may be obtained using the following model for interaction-free defects,
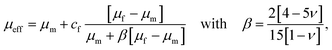 | (7) |
The nonlinearity parameter α mostly takes on negative values, which represents the stiffer response in compression than in tension. Values of α > 2 would yield the opposite trend. Samples with 1 million beads per ml have a significantly smaller α than samples with 4 and 8 million beads per ml. Again, the cell-laden samples show more significant trends than the bead-laden hydrogels. The samples with 6 and 8 million cells per ml show a significantly higher nonlinearity than other cell densities and pure ADA-GEL.
3.4. Time-dependent behavior
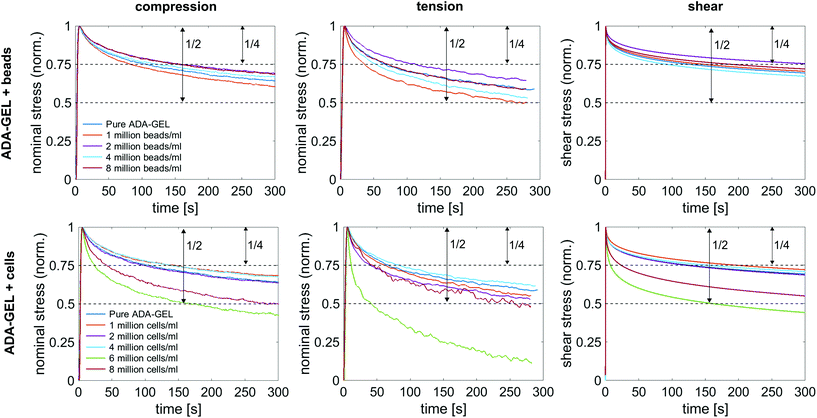
Fig. 10a shows the average normalized stress relaxation behavior in compression, tension, and torsional shear for bead- and cell-laden ADA-GEL samples of different concentrations. All tested samples did not reach equilibrium within 300 s. In general, the hydrogels relax fastest in tension and reach 3/4 of the initial stress earliest, which is reached latest in shear. Overall, a trend of faster relaxation can be observed with higher filler concentrations. Similar to the results in the previous sections, the hydrogels with high cell concentrations of 6 and 8 million cells per ml show a different behavior in comparison to lower cell concentrations, and relax significantly earlier to 3/4 of the initial stress. The only samples relaxing to a stress value below 50% of the initial stress were cell-laden hydrogels with 6 million cells per ml. Interestingly, those samples (n = 6) show a faster relaxation behavior than samples with 8 million cells per ml.4. Discussion
In this work, we have assessed the complex mechanical response of cell- and PAAm microgel bead-laden hydrogels with different filler concentrations. The mechanical properties of biomaterials play an important role for tissue engineering applications.8,32 Besides hydrogel degradation,101 stress relaxation102,103 especially has proven to be a crucial mechanical parameter that influences cell response. However, often only the mechanical properties of the matrix material are quantified by means of stiffness (Young's modulus) or unimodal viscoelastic (shear) rheological analyses. Only recently, a study on fibrous hydrogel materials has shown that the mechanical properties change through the inclusion of cells, not only quantitatively but also qualitatively.50Here, we have investigated the influence of cell- and PAAm microgel bead fillers on the mechanics of non-fibrous, alginate-gelatin-based hydrogels under compression, tension, and shear.38 We have combined small-strain and large-strain experiments to assess the distinct nonlinearity, compression–tension asymmetry, and viscoelasticity of this class of materials. This multi-modal mechanical assessment of oxidized alginate-gelatin hydrogels incorporating cells and PAAm microgel bead fillers has important applications for various tissue engineering applications.10,75,84,85,104
4.1. High filler concentrations over-proportionally soften the overall material response
The filler stiffness of PAAm microgel beads with an average Young's modulus of 2.2 kPa was significantly higher than the Young's modulus of the NIH/3T3 cells with approx. 0.6 kPa, as found here using RT-DC analysis (Fig. 3f). However, both fillers were significantly softer than the ADA-GEL matrix with a Young's modulus of approximately 11.3 kPa. For low concentrations, the fillers did not significantly affect the mechanical response neither in the small-strain (Fig. 4) nor in the large-strain regime (Fig. 5–8). This observation was expected as the theoretical volume fraction of the fillers in the hydrogel (ratio of the number of fillers times their volume divided by the total hydrogel volume) was generally very small and never exceeded 2.5%.However, inclusions of more than 2 million beads per ml or 4 million cells per ml led to a significant drop of stresses for the large-strain loading regime. Comparing the results for maximum shear strains of 15% and 30%, respectively, the drop is more pronounced for higher strains. For cell-containing gels even the small-strain stiffness quantified by the storage modulus during frequency sweeps drops significantly. In general, the stiffness drop is more pronounced for the cell-laden than for bead-laden hydrogels. This effect can be partially attributed to the stiffer response of the beads in comparison to the cells. Still, the inclusion of approximately 1% volume fraction of beads and 1.6% volume fraction of cells leads to a drop in the Young's modulus of 24% and 65%, respectively, which is disproportionally high in comparison to model suggestions of the impact of those filler contents. Therefore, we may conclude that other effects, such as a change of hydrogel cohesion or interference by the fillers in the ionic crosslinking and subsequent hydrogel network formation, affect final hydrogel stiffness. The guluronic acid chain assembly mediated by calcium ions results in the crosslinking of ADA.78,105 Hence, increasing the amount of fillers may alter the formation of a bulk, homogeneously crosslinked alginate network. The presence of beads and cells may differently decrease the effective crosslinking density in the final hydrogel. The fillers could act as macrostructural heterogeneities affecting the final number of elastic chains in the gel.106
The difference in Young's modulus drop could be a result from different interactions of the cells and the beads with the gel network and not only result from the difference of the intrinsic Young's modulus of the cells and beads. Despite the intrinsically higher stiffness of PAAm microgel beads, the approx. 2.5 times smaller stiffness drop of PAAm microgel containing hydrogels may be explained by potential crosslinking reactions between unreacted NHS groups on the PAAm microgel bead surface with ε-amino groups of lysine of gelatin. Together, those effects may counteract the stiffness drop in comparison to the cell-laden gels.
We have demonstrated through multiphoton microscopy techniques that the nearest neighbour distance of fillers inside the hydrogels scaled nonlinearly with increasing filler number (Video S1, ESI†). The mean distance dropped by almost 30% comparing 4 million and 6 million cells per ml. This might explain the sudden drop of stiffness when reaching 6 million cells per ml. The decreased mean filler distance may lead to a disruption in the homogeneous alginate-hydrogel formation in comparison with hydrogels without any spherical fillers. This effect was higher for the cells than for PAAm microgel beads, which can to some extent be attributed to their lower stiffness in comparison to the PAAm microgel beads as well as to the potential crosslinking of the gelatin with the PAAm microgel bead surface.
The PAAm microgel beads have to be assumed as microporous gel fillers. The pores could be filled by the hydrogel solution and a gelation inside the beads might occur, which cannot happen inside the cells. This may lead to differently hindered crosslinking of the bulk hydrogel due to the different interactions of beads and cells with the gel.
Additionally, cells exhibit a nonlinear elastic behavior and more pronounced viscous effects,18,107–109 while PAAm beads show an almost elastic response.91 We expect stress peaks in the matrix in the immediate vicinity of the fillers in the deformed state, preferably in the case of cell-laden hydrogels. The cells in the hydrogels were still in round shape without signs of cell spreading (Fig. 3a), indicating no strongly pronounced cell–material interaction directly after embedding the cells in the hydrogels and crosslinking. As a result, we assume less cell–material interaction with the bulk hydrogel in comparison to the potentially unreacted NHS groups on the functionalized PAAm-bead surface with the hydrogel. This difference to the PAAm beads may ultimately cause the loss of bulk hydrogel stiffness and explain the significant drop in the stiffness observed for cell-laden hydrogels at higher filler concentrations (≥6 mio ml−1). As the mechanical properties were assessed directly after embedding the cells in the hydrogels and crosslinking (∼45 min), we assume no release of matrix metalloproteinases (MMP) in that time frame, which could cause hydrogel degradation during prolonged in vitro cell culture.80,110–112
4.2. Hydrogels with high cell concentrations show more pronounced nonlinearity and viscous effects
Along with lower stiffness, the high-cell-concentration hydrogels show more pronounced conditioning during cyclic loading (Fig. 6) in comparison to bead-laden hydrogels (Fig. 5), larger hysteresis, and faster stress relaxation (Fig. 10). We attribute this observation to the nonlinear mechanical properties of the cells18,107–109 compared to the rather elastic PAAm microgel beads.91 While we did not observe a clear correlation between filler concentrations and viscous properties for the small strain (1%) regime (Fig. 4), large deformation loadings (15% strain) under multiple loading modes (compression, tension, shear, Fig. 5, 6, Fig. S9–S14, ESI†) revealed that high cell numbers >4 million per ml impact the nonlinearity, compression–tension asymmetry, conditioning behavior, and viscosity of the overall hydrogels, which is in contrast to the behavior observed for bead-laden hydrogels.Furthermore, we assume that a partial crosslinking of the beads with the hydrogel may explain the higher elastic than viscous response of PAAm bead-laden hydrogels (Fig. 5), and therefore, the less pronounced conditioning behavior and hysteresis. The PAAm beads might be fixed in the matrix due to potential bead–matrix interaction and move together with the matrix during deformation, while the cell movement may be not as synchronized with the matrix deformation due to a lack of interaction. Together with the intrinsic elastic properties of the PAAm microgel beads and the assumed lower interface interaction of cells with the hydrogel, this may explain the faster relaxation and higher viscous effects observed for the cell-laden hydrogels in compression–tension testing (Fig. 6), especially due to the inherent viscoelastic properties of cells and their cytoskeletal components.109,113
The absolute value of the nonlinearity parameter α increases significantly for high cell concentrations. In contrast, it decreases for high bead concentrations. This is in agreement with a recent study showing that cell embedding in fibrous hydrogel networks changed the behavior of the material from compression softening into compression stiffening.50 In the context of fibrous matrices, this effect was attributed to the alignment of collagenous fibers alongside the volume-conserving cell inclusions, orienting upon compression, and ultimately leading to the stiffening upon compression.50 The ADA-GEL hydrogels used in this study, in contrast, do not include collagenous fibrous structures, as shown by the absence of second harmonics in comparison to fibrillar collagen type I-based hydrogels.84,88 Therefore, the effect of hydrogel fiber alignment can be excluded and the main stress-bearing components are the ionic alginate network and the softer cellular inclusions, which leads to a different mechanical response and impact on hydrogel nonlinearity in comparison to fibrous cell-hydrogel systems.50
4.3. Cell embedding in biofabrication can alter the final hydrogel mechanics after crosslinking
Biofabrication, which comprises the simultaneous processing of cells and biomaterials to cell-laden constructs, has gained momentum in the past decade.52,53,58,114 Cell-laden hydrogels, or bioinks, are most commonly used in biofabrication processes.115 If one considers the relevance of the results obtained in relation to the printing techniques available in biofabrication, extrusion and inkjet printing are particularly relevant. While our results can be transferred primarily to hydrogels produced via extrusion printing due to the high viscosity of ADA-GEL (∼102–103 Pa s for low shear-rate regimes <1 s−1 (ref. 84)), low-viscosity bioinks are used in ink-jetting (approx. <10−2 Pa s,55 0.09–0.16 Pa s for ADA-GEL (unpublished data)). Additionally, depending on the geometry of the inkjet needle, very high shear forces can be generated here, which might influence the final cell response in 3D.116As cells are fillers with highly nonlinear mechanical properties,18,107–109 we found that they can significantly affect the final mechanical properties of the biofabricated construct. This has already been shown in a previous study on fibrous collagen-based hydrogels, which shifted their mechanical properties from compression softening to compression stiffening and thereby, reversed their compression–tension asymmetry by the addition of cells.50 We show in this study that incorporating cells in non-fibrous oxidized alginate-gelatin-based hydrogels84 can lead to decreased stiffness, as well as increased compression–tension asymmetry and nonlinearity at cell densities >6 million cells per ml. Cell concentrations of 100 million cells per ml have been utilized for cartilage tissue engineering applications.102 However, commonly, hydrogel materials are characterized prior to the incorporation of cells. As a result, the final mechanical properties of the cell-laden construct are hardly recapitulated by assessing the hydrogels without cellular filler, especially for high cell numbers. In this study, we have assessed the mechanical properties of cell-laden hydrogels directly after embedding cells inside the gels. The aim was to investigate the influence of cell density on the mechanical properties directly after fabrication, similar to biofabricates. We did not expect cell spreading or morphology changes as fibroblast cells have been shown to proliferate and spread in ADA-GEL only after approximately seven days.60 This was also confirmed by the spherical cell shape inside the hydrogels observed via multiphoton-microscopy analysis, since spread cells would have been visible via autofluorescence.84 Hence, our study provides insights into the influence of spherical cell fillers on the mechanical properties of hydrogels directly after fabrication and cross-linking, and prior to in vitro cell culture.
When facing limited resources in terms of limited capabilities to achieve high cell numbers due to, e.g., limited growth capabilities or high costs involved for cell culture, the assessment of the hydrogel mechanics prior to cell addition remains a valid approach. On the other hand, our results indicate that a true understanding of the final hydrogel mechanics with incorporated cells is important and may allow to better recapitulate cell growth, cell proliferation, and maturation in light of the real titab initio biofabricate mechanics (cell-containing-hydrogels), with important implications for future tissue engineering studies and material designs.
4.4. Implications for spherical filler based drug delivery applications and “gel-in-gel” hydrogels
Efforts have been made to engineer polymer microspheres for controlled drug release,117–120 as well as to incorporate polymer microspheres as drug delivery vesicles into hydrogels.121–123 Multi-phasic “gel-in-gel” materials have been recently discussed and are currently explored for tissue engineering applications.124 We used PAAm hydrogel microgel beads with a diameter of approx. 15 μm and stiffness of approx. 2 kPa in this study and show that such fillers can impact the overall mechanical properties of the resulting hydrogel after reaching a threshold concentration. This effect was primarily observed for cells, which have nonlinear mechanical properties. As a result, depending on the hydrogel or polymer material and its intrinsic mechanical nonlinearity, such fillers may influence the complex and time-dependent mechanical properties of the overall hydrogel. In addition, at high concentrations, the mean neighbour distance may influence drug diffusion from the fillers to the hydrogel bulk by changed drug concentration gradients. Regarding tissue engineering, the question arises as to which extent cytokines in the gel can cover a diffusion distance of approx. 30–70 m from cell-to-cell through a defined network density and polymer surface charge provided by the hydrogel.125–128Consideration should also be given to how the degradation rates of the matrix can be adjusted so that the network degrades within a defined time. Ultimately, this can influence controlled tissue development and diffusion.
The altered mechanics of the hydrogel and interaction of hydrogel bulk with the fillers may affect filler degradation and the release of embedded drugs upon deformation. Hence, we suggest to consider the impact of filler concentration and its intrinsic mechanical properties on the final hydrogel mechanics as well as the potential impact of filler-filler distance on drug-release kinetics. Our study further contributed to a better understanding of the potential impact of filler densities on the final hydrogel mechanics of non-fibrous, alginate-based hydrogels.
4.5. Limitations
This study focused on the influence of spherical PAAm microgel beads and cells as fillers on the resulting mechanical properties of oxidized alginate-gelatin hydrogels. The potential interaction of PAAm microgel beads with the hydrogel, specifically with the gelatin component due to the potential presence of unreacted NHS on the bead surface after Alexa Fluor 488™ bead modification, and its potential difference to the cell–material interface, was not comprehensively covered in this study, which we will investigate in future work. We did also not assess bead–material and cell–material interactions in detail. In addition, the deformation of cells and beads inside the hydrogels was not specifically monitored during mechanical deformation. We will assess the in situ deformation of cell- and microgel bead fillers during mechanical hydrogel deformation in future work.During image analysis, we observed that despite the adjustment of the cell concentration between 2, 4, and 6 million cells per ml, similar amounts of cells were detected inside the hydrogel volumes (n = 3). The results indicate ambiguity between theoretically counted cell density and the actual amount of cells detected in the hydrogels. However, despite the high penetration depth (1 mm) achieved by the multiphoton microscopy technique, the imaged hydrogel volumes (0.4 × 0.4 × 1 mm3, 0.16 mm3, 0.16 μl) only represent a small fraction of the bulk hydrogel sample (approx. 200 mm3) which was used for mechanical testing. Due to limited resources and imaging time, it was not possible to image volumes in the range of the complete bulk cylinder. This might have caused the difference between imaging and theoretical counting. In addition, counting cells and beads using Neubauer cell counting chambers might have introduced errors leading to discrepancies between the theoretical cell number and measured cell numbers from the imaging volumes. By utilizing automatic cell counters, we will address those potential error sources in the future. Secondly, the amount of imaged hydrogel volume would need to be increased to achieve a total imaged hydrogel volume, which better represents the entire sample.
Despite those challenges, the multiphoton imaging used here allowed us to confirm homogeneous cell and bead distribution inside the imaged volumes, suggesting homogeneous distribution in the bulk samples and an isotropic mechanical response (Fig. 3 and Fig. S10†). Besides the limitation of imaged volume, the technique was confirmed to be highly suitable for the assessment of cell- and PAAm microgel bead distribution inside hydrogel specimens beyond penetration depths achieved when using traditional fluorescence imaging techniques.129
5. Conclusions
We have demonstrated that low concentrations of NIH/3T3 fibroblast cells and PAAm microgel beads (1–4 mio ml−1) embedded in oxidized alginate-gelatin hydrogels only have a marginal impact on the overall complex mechanical material behavior. However, high cell concentrations (≥6 mio ml−1) inside the hydrogels led to a significant stiffness drop and increased material nonlinearity. This effect was more pronounced for cell than for PAAm microgel bead-laden hydrogels. We show that the inclusion of mechanically nonlinear cells can increase the compression–tension asymmetry of non-fibrous alginate-based hydrogels. Ultimately, the nonlinearity and viscous nature of the cell-containing hydrogels increase in comparison to cell-free hydrogels. The viscous contribution and nonlinearity of cells can, therefore, be a determinant for the final hydrogel bulk mechanics, with important implications towards biofabrication approaches and cell-containing hydrogel designs in tissue engineering.Author contributions
TD and SB conceptualized the study. TD, RD, and SB developed the methodology. LK performed the main mechanical experiments and data analysis. TD, LK, and SB wrote the first draft. LK, SG, RD, TD, and SB contributed to manuscript writing. TD, DS, and OF conceptualized and performed multiphoton microscopy imaging. DS conducted image data analysis and provided the MATLAB® image analysis code. TD and DS performed imaging data visualization. RG, SG, and JG conceptualized and performed microgel bead fabrication and RT-DC measurements. TD, LK, DS, SG, RG, OF, RD, JG, ARB, and SB contributed to data interpretation and commented on the manuscript. SB and ARB acquired funding and provided resources. SB supervised the overall project. All authors have reviewed and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge Lena Fischer (Institute of Biophysics, Prof. Ben Fabry, Dr Ingo Thievessen, FAU Erlangen-Nuremberg) for providing NIH/3T3 cells. In addition, financial support by the German Research Foundation (DFG) through the grants BU 3728/1-1 to SB and SFB 1270/1 - 299150580 to ARB, SFB-TRR225 project B06 to RD, B08 to OF, as well as the Emerging Talents Initiative to SB and the Emerging Fields Initiative by the FAU to SB and ARB is gratefully acknowledged.References
- E. Caló and V. V. Khutoryanskiy, Eur. Polym. J., 2015, 65, 252–267 CrossRef.
- J. L. Drury and D. J. Mooney, Biomaterials, 2003, 24, 4337–4351 CrossRef CAS.
- O. Chaudhuri, L. Gu, D. Klumpers, M. Darnell, S. A. Bencherif, J. C. Weaver, N. Huebsch, H. pyo Lee, E. Lippens, G. N. Duda and D. J. Mooney, Nat. Mater., 2015, 15, 326–334 CrossRef PubMed.
- O. Wichterle and D. Lim, Nature, 1960, 185, 117–118 CrossRef.
- J. Blöhbaum, I. Paulus, A.-C. Pöppler, J. Tessmar and J. Groll, J. Mater. Chem. B, 2019, 7, 1782–1794 RSC.
- Y. Li, J. Rodrigues and H. Tomas, Chem. Soc. Rev., 2012, 41, 2193–2221 RSC.
- N. A. Peppas, J. Z. Hilt, A. Khademhosseini and R. Langer, Adv. Mater., 2006, 18, 1345–1360 CrossRef CAS.
- K. Y. Lee and D. J. Mooney, Chem. Rev., 2001, 101, 1869–1880 CrossRef CAS PubMed.
- A. D. Augst, H. J. Kong and D. J. Mooney, Macromol. Biosci., 2006, 6, 623–633 CrossRef CAS PubMed.
- B. Balakrishnan and A. Jayakrishnan, Biomaterials, 2005, 26, 3941–3951 CrossRef CAS PubMed.
- Z. Wei, J. Zhao, Y. M. Chen, P. Zhang and Q. Zhang, Sci. Rep., 2016, 6, 1–12 CrossRef PubMed.
- G. Yang, Z. Xiao, X. Ren, H. Long, H. Qian, K. Ma and Y. Guo, PeerJ, 2016, 4, e2497 CrossRef PubMed.
- S. Duin, K. Schütz, T. Ahlfeld, S. Lehmann, A. Lode, B. Ludwig and M. Gelinsky, Adv. Healthcare Mater., 2019, 8, 1–14 Search PubMed.
- R. Costa-Almeida, I. Calejo, R. Altieri, R. M. A. Domingues, E. Giordano, R. L. Reis and M. E. Gomes, Biomed. Mater., 2019, 14, 034104 CrossRef CAS PubMed.
- V. E. Santo, A. M. Frias, M. Carida, R. Cancedda, M. E. Gomes, J. F. Mano and R. L. Reis, Biomacromolecules, 2009, 10, 1392–1401 CrossRef PubMed.
- C. Fu, X. Yang, S. Tan and L. Song, Sci. Rep., 2017, 7, 1–13 CrossRef CAS PubMed.
- C. R. Silva, P. S. Babo, M. Gulino, L. Costa, J. M. Oliveira, J. Silva-Correia, R. M. Domingues, R. L. Reis and M. E. Gomes, Acta Biomater., 2018, 77, 155–171 CrossRef CAS PubMed.
- C. W. Yung, W. E. Bentley and T. A. Barbari, J. Biomed. Mater. Res., Part A, 2010, 95, 25–32 CrossRef PubMed.
- K. Y. Lee and D. J. Mooney, Prog. Polym. Sci., 2012, 37, 106–126 CrossRef CAS PubMed.
- T. Garg, O. Singh, S. Arora and R. S. R. Murthy, Crit. Rev. Ther. Drug Carrier Syst., 2012, 29, 1–63 CrossRef CAS PubMed.
- M. K. Schesny, M. Monaghan, A. H. Bindermann, D. Freund, M. Seifert, J. A. Eble, S. Vogel, M. P. Gawaz, S. Hinderer and K. Schenke-Layland, Biomaterials, 2014, 35, 7180–7187 CrossRef CAS PubMed.
- C. Elvira, J. F. Mano, J. San Román and R. L. Reis, Biomaterials, 2002, 23, 1955–1966 CrossRef CAS PubMed.
- M. V. Monteiro, V. M. Gaspar, L. P. Ferreira and J. F. Mano, Biomater. Sci., 2020, 8, 1855–1864 RSC.
- B. Kundu, A. R. Bastos, V. Brancato, M. T. Cerqueira, J. M. Oliveira, V. M. Correlo, R. L. Reis and S. C. Kundu, ACS Appl. Mater. Interfaces, 2019, 11, 14548–14559 CrossRef CAS PubMed.
- R. A. Francescone III, M. Faibish and R. Shao, J. Visualized Exp., 2011, 55, 2–5 Search PubMed.
- R. Langer and J. P. Vacanti, Science, 1993, 260, 920–926 CrossRef CAS PubMed.
- J. Silva-Correia, J. M. Oliveira, J. S. G. Caridade, R. A. Sousa, J. F. Mano and R. L. Reis, J. Tissue Eng. Regener. Med., 2011, 5, e97–e107 CrossRef CAS PubMed.
- A. Grigore, B. Sarker, B. Fabry, A. R. Boccaccini and R. Detsch, Tissue Eng., Part A, 2014, 20, 2140–2150 CrossRef CAS PubMed.
- J. Li, C. Wu, P. K. Chu and M. Gelinsky, Mater. Sci. Eng., R, 2020, 140, 100543 CrossRef.
- B. B. Mendes, M. Gómez-Florit, R. A. Pires, R. M. Domingues, R. L. Reis and M. E. Gomes, Nanoscale, 2018, 10, 17388–17401 RSC.
- G. D. Nicodemus and S. J. Bryant, Tissue Eng., Part B, 2008, 14, 149–165 CrossRef CAS PubMed.
- F. Brandl, F. Sommer and A. Goepferich, Biomaterials, 2007, 28, 134–146 CrossRef CAS PubMed.
- W. F. Liu and C. S. Chen, Mater. Today, 2005, 8, 28–35 CrossRef.
- K. Franze, P. A. Janmey and J. Guck, Annu. Rev. Biomed. Eng., 2013, 15, 227–251 CrossRef CAS PubMed.
- M. Jaspers, S. L. Vaessen, P. V. Schayik, D. Voerman, A. E. Rowan and P. H. J. Kouwer, Nat. Commun., 2017, 8, 1–10 CrossRef PubMed.
- S. K. Seidlits, Z. Z. Khaing, R. R. Petersen, J. D. Nickels, J. E. Vanscoy, J. B. Shear and C. E. Schmidt, Biomaterials, 2010, 31, 3930–3940 CrossRef CAS PubMed.
- C. B. Khatiwala, S. R. Peyton and A. J. Putnam, Am. J. Physiol.: Cell Physiol., 2006, 290, C1640–C1650 CrossRef CAS PubMed.
- T. Distler, E. Schaller, P. Steinmann, A. R. Boccaccini and S. Budday, J. Mech. Behav. Biomed. Mater., 2020, 111, 103979 CrossRef CAS PubMed.
- L.-S. Wang, J. E. Chung, P. P.-Y. Chan and M. Kurisawa, Biomaterials, 2010, 31, 1148–1157 CrossRef CAS PubMed.
- J. W. Nichol, S. T. Koshy, H. Bae, C. M. Hwang, S. Yamanlar and A. Khademhosseini, Biomaterials, 2010, 31, 5536–5544 CrossRef CAS PubMed.
- C. Cha, S. R. Shin, X. Gao, N. Annabi, M. R. Dokmeci and X. Tang, Small, 2014, 10, 514–523 CrossRef CAS PubMed.
- L. A. Sawicki and A. M. Kloxin, Biomater. Sci., 2014, 2, 1612–1626 RSC.
- X. Li, Q. Sun, Q. Li, N. Kawazoe and G. Chen, Front. Chem., 2018, 6, 1–20 Search PubMed.
- N. Annabi, J. W. Nichol, X. Zhong, C. Ji, S. Koshy, A. Khademhosseini and F. Dehghani, Tissue Eng., Part B, 2010, 16, 371–383 CrossRef CAS PubMed.
- X. Zhao, N. Huebsch, D. J. Mooney and Z. Suo, J. Appl. Phys., 2010, 107, 1–5 Search PubMed.
- P. M. Kharkar, K. L. Kiick and A. M. Kloxin, Chem. Soc. Rev., 2013, 42, 7335–7372 RSC.
- S. A. Bencherif, A. Srinivasan, F. Horkay, J. O. Hollinger, K. Matyjaszewski and N. R. Washburn, Biomaterials, 2008, 29, 1739–1749 CrossRef CAS PubMed.
- J. W. Gunn, S. D. Turner and B. K. Mann, J. Biomed. Mater. Res., Part A, 2005, 72, 91–97 CrossRef PubMed.
- A. Banerjee, M. Arha, S. Choudhary, R. S. Ashton, S. R. Bhatia, D. V. Schaffer and R. S. Kane, Biomaterials, 2009, 30, 4695–4699 CrossRef CAS PubMed.
- A. S. van Oosten, X. Chen, L. Chin, K. Cruz, A. E. Patteson, K. Pogoda, V. B. Shenoy and P. A. Janmey, Nature, 2019, 573, 96–101 CrossRef CAS PubMed.
- S. Budday, G. Sommer, C. Birkl, C. Langkammer, J. Haybaeck, J. Kohnert, M. Bauer, F. Paulsen, P. Steinmann, E. Kuhl and G. A. Holzapfel, Acta Biomater., 2017, 48, 319–340 CrossRef CAS PubMed.
- J. Groll, T. Boland, T. Blunk, J. A. Burdick, D.-W. Cho, P. D. Dalton, B. Derby, G. Forgacs, Q. Li, V. A. Mironov, L. Moroni, M. Nakamura, W. Shu, S. Takeuchi, G. Vozzi, T. B. Woodfield, T. Xu, J. J. Yoo and J. Malda, Biofabrication, 2016, 8, 013001 CrossRef PubMed.
- L. Moroni, T. Boland, J. A. Burdick, C. De Maria, B. Derby, G. Forgacs, J. Groll, Q. Li, J. Malda, V. A. Mironov, C. Mota, M. Nakamura, W. Shu, S. Takeuchi, T. B. Woodfield, T. Xu, J. J. Yoo and G. Vozzi, Trends Biotechnol., 2018, 36, 384–402 CrossRef CAS PubMed.
- L. Ouyang, R. Yao, Y. Zhao and W. Sun, Biofabrication, 2016, 8, 035020 CrossRef PubMed.
- K. Hölzl, S. Lin, L. Tytgat, S. Van Vlierberghe, L. Gu and A. Ovsianikov, Biofabrication, 2016, 8, 032002 CrossRef PubMed.
- Y. Zhao, Y. Li, S. Mao, W. Sun and R. Yao, Biofabrication, 2015, 7, 1–11 CrossRef PubMed.
- N. Paxton, W. Smolan, T. Böck, F. Melchels, J. Groll and T. Jungst, Biofabrication, 2017, 9, 044107 CrossRef PubMed.
- V. Mironov, T. Boland, T. Trusk, G. Forgacs and R. R. Markwald, Trends Biotechnol., 2003, 21, 157–161 CrossRef CAS.
- D. B. Kolesky, R. L. Truby, A. S. Gladman, T. A. Busbee, K. A. Homan and J. A. Lewis, Adv. Mater., 2014, 26, 3124–3130 CrossRef CAS PubMed.
- T. Distler, F. Ruther, A. R. Boccaccini and R. Detsch, Macromol. Biosci., 2019, 19, 1–13 CrossRef PubMed.
- Y. S. Zhang and A. Khademhosseini, Science, 2017, 356, 1–10 Search PubMed.
- I. Apsite, J. M. Uribe, A. F. Posada, S. Rosenfeldt, S. Salehi and L. Ionov, Biofabrication, 2020, 12, 015016 CrossRef CAS PubMed.
- T. R. Cox and C. Madsen, Bio-Protoc., 2017, 7(1), e2101 Search PubMed.
- R. L. Mauck, S. L. Seyhan, G. A. Ateshian and C. T. Hung, Ann. Biomed. Eng., 2002, 30, 1046–1056 CrossRef PubMed.
- Z. Tan, D. Dini, F. R. y. Baena and A. E. Forte, Mater. Des., 2018, 160, 886–894 CrossRef CAS.
- A. E. Forte, S. Galvan, F. Manieri, F. R. y. Baena and D. Dini, Mater. Des., 2016, 112, 227–238 CrossRef CAS.
- A. Leibinger, A. E. Forte, Z. Tan, M. J. Oldfield, F. Beyrau, D. Dini and F. R. y. Baena, Ann. Biomed. Eng., 2015, 44, 2442–2452 CrossRef PubMed.
- R. Detsch, B. Sarker, T. Zehnder, G. Frank and A. R. Boccaccini, Mater. Today, 2015, 18, 590–591 CrossRef.
- S. N. Pawar and K. J. Edgar, Biomaterials, 2012, 33, 3279–3305 CrossRef CAS PubMed.
- Ø. Arlov, E. Öztürk, M. Steinwachs, G. Skjåk-Bræk and M. Zenobi-Wong, Eur. Cells Mater., 2017, 33, 76–89 CrossRef PubMed.
- M. Ø. Dalheim, J. Vanacker, M. A. Najmi, F. L. Aachmann, B. L. Strand and B. E. Christensen, Biomaterials, 2016, 80, 146–156 CrossRef CAS PubMed.
- K. Hozumi and M. Nomizu, Curr. Protoc. Cell Biol., 2018, 80, 1–15 Search PubMed.
- Y. S. Hsueh, Y. S. Chen, H. C. Tai, O. Mestak, S. C. Chao, Y. Y. Chen, Y. Shih, J. F. Lin, M. J. Shieh and F. H. Lin, Tissue Eng., Part A, 2017, 23, 185–194 CrossRef CAS PubMed.
- R. Silva, R. Singh, B. Sarker, D. G. Papageorgiou, J. A. Juhasz-Bortuzzo, J. A. Roether, I. Cicha, J. Kaschta, D. W. Schubert, K. Chrissafis, R. Detsch and A. R. Boccaccini, Int. J. Biol. Macromol., 2018, 114, 614–625 CrossRef CAS PubMed.
- S. Reakasame and A. R. Boccaccini, Biomacromolecules, 2018, 19, 3–21 CrossRef CAS PubMed.
- K. H. Bouhadir, K. Y. Lee, E. Alsberg, K. L. Damm, K. W. Anderson and D. J. Mooney, Biotechnol. Prog., 2001, 17, 945–950 CrossRef CAS PubMed.
- C. G. Gomez, M. Rinaudo and M. A. Villar, Carbohydr. Polym., 2007, 67, 296–304 CrossRef CAS.
- B. Sarker, D. G. Papageorgiou, R. Silva, T. Zehnder, F. Gul-E-Noor, M. Bertmer, J. Kaschta, K. Chrissafis, R. Detsch and A. R. Boccaccini, J. Mater. Chem. B, 2014, 2, 1470–1482 RSC.
- B. Balakrishnan, M. Mohanty, A. C. Fernandez, P. V. Mohanan and A. Jayakrishnan, Biomaterials, 2006, 27, 1355–1361 CrossRef CAS PubMed.
- B. Sarker, R. Singh, R. Silva, J. A. Roether, J. Kaschta, R. Detsch, D. W. Schubert, I. Cicha and A. R. Boccaccini, PLoS One, 2014, 9 DOI:10.1371/journal.pone.0107952.
- B. Sarker, T. Zehnder, S. N. Rath, R. E. Horch, U. Kneser, R. Detsch and A. R. Boccaccini, ACS Biomater. Sci. Eng., 2017, 3, 1730–1737 CrossRef CAS PubMed.
- T. Zehnder, B. Sarker, A. R. Boccaccini and R. Detsch, Biofabrication, 2015, 7, 025001 CrossRef PubMed.
- T. Zehnder, A. Boccaccini and R. Detsch, Biofabrication, 2017, 9, 25016 CrossRef PubMed.
- T. Distler, A. A. Solistio, D. Schneidereit, O. Friedrich, R. Detsch and A. R. Boccaccini, Biofabrication, 2020, 12, 045005 CrossRef CAS PubMed.
- N. Soltan, L. Ning, F. Mohabatpour, P. Papagerakis and X. Chen, ACS Biomater. Sci. Eng., 2019, 5, 2976–2987 CrossRef CAS PubMed.
- F. Ruther, T. Distler, A. R. Boccaccini and R. Detsch, J. Mater. Sci.: Mater. Med., 2019, 30, 1–14 CrossRef CAS PubMed.
- F. You, X. Wu, M. Kelly and X. Chen, Bio-Des. Manuf., 2020, 3, 48–59 CrossRef CAS.
- A. Weizel, T. Distler, D. Schneidereit, O. Friedrich, L. Bräuer, F. Paulsen, R. Detsch, A. R. Boccaccini, S. Budday and H. Seitz, Acta Biomater., 2020, 118, 113–128 CrossRef CAS PubMed.
- S. Hafeez, H. Ooi, F. Morgan, C. Mota, M. Dettin, C. van Blitterswijk, L. Moroni and M. Baker, Gels, 2018, 4, 85 CrossRef CAS PubMed.
- S. Schwarz, S. Kuth, T. Distler, C. Gögele, K. Stölzel, R. Detsch, A. Bocaccini and G. Schulze-Tanzil, Mater. Sci. Eng., C, 2020, 116, 111189 CrossRef CAS PubMed.
- S. Girardo, N. Traeber, K. Wagner, G. Cojoc, C. Herold, R. Goswami, R. Schluessler, S. Abuhattum, A. Taubenberger and F. Reichel, et al. , J. Mater. Chem. B, 2018, 6, 6245–6261 RSC.
- N. Traeber, K. Uhlmann, S. Girardo, G. Kesavan, K. Wagner, J. Friedrichs, R. Goswami, K. Bai, M. Brand and C. Werner, et al. , Sci. Rep., 2019, 9, 1–14 CAS.
- A. V. Taubenberger, S. Girardo, N. Träber, E. Fischer-Friedrich, M. Kräter, K. Wagner, T. Kurth, I. Richter, B. Haller, M. Binner, D. Hahn, U. Freudenberg, C. Werner and J. Guck, Adv. Biosyst., 2019, 3, 1–16 Search PubMed.
- B. Fregin, F. Czerwinski, D. Biedenweg, S. Girardo, S. Gross, K. Aurich and O. Otto, Nat. Commun., 2019, 10, 1–11 CrossRef PubMed.
- K. Wagner, S. Girardo, R. Goswami, G. Rosso, E. Ulbricht, P. Müller, D. Soteriou, N. Träber and J. Guck, Soft Matter, 2019, 15, 9776–9787 RSC.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J. Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- O. Otto, P. Rosendahl, A. Mietke, S. Golfier, C. Herold, D. Klaue, S. Girardo, S. Pagliara, A. Ekpenyong, A. Jacobi, M. Wobus, N. Töpfner, U. F. Keyser, J. Mansfeld, E. Fischer-friedrich and J. Guck, Nat. Methods, 2015, 12, 199–202 CrossRef CAS PubMed.
- M. Mokbel, D. Mokbel, A. Mietke, N. Träber, S. Girardo, O. Otto, J. Guck and S. Aland, ACS Biomater. Sci. Eng., 2017, 3, 2962–2973 CrossRef CAS PubMed.
- G. A. Holzapfel, Nonlinear Solid Mechanics: A Continuum Approach for Engineering Science, John Wiley & Sons, Chichester, 2000, vol. 24 Search PubMed.
- R. W. Ogden, Proc. R. Soc. London, Ser. A, 1972, 326, 565–584 CAS.
- C. M. Madl, B. L. Lesavage, R. E. Dewi, C. B. Dinh, R. S. Stowers, M. Khariton, K. J. Lampe, D. Nguyen, O. Chaudhuri, A. Enejder and S. C. Heilshorn, Nat. Mater., 2017, 16, 1233–1242 CrossRef CAS PubMed.
- H. P. Lee, L. Gu, D. J. Mooney, M. E. Levenston and O. Chaudhuri, Nat. Mater., 2017, 16, 1243–1251 CrossRef CAS PubMed.
- O. Chaudhuri, L. Gu, M. Darnell, D. Klumpers, S. A. Bencherif, J. C. Weaver, N. Huebsch and D. J. Mooney, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- H. Park and K. Y. Lee, J. Biomed. Mater. Res., Part A, 2014, 102, 4519–4525 CrossRef PubMed.
- P. S. Braccini I, Biomacromolecules, 2001, 2, 1089–1096 CrossRef PubMed.
- F. Di Lorenzo and S. Seiffert, Polym. Chem., 2015, 6, 5515–5528 RSC.
- A. Mietke, O. Otto, S. Girardo, P. Rosendahl, A. Taubenberger, S. Golfier, E. Ulbricht, S. Aland, J. Guck and E. Fischer-Friedrich, Biophys. J., 2015, 109, 2023–2036 CrossRef CAS PubMed.
- P. H. Wu, D. R. B. Aroush, A. Asnacios, W. C. Chen, M. E. Dokukin, B. L. Doss, P. Durand-Smet, A. Ekpenyong, J. Guck, N. V. Guz, P. A. Janmey, J. S. Lee, N. M. Moore, A. Ott, Y. C. Poh, R. Ros, M. Sander, I. Sokolov, J. R. Staunton, N. Wang, G. Whyte and D. Wirtz, Nat. Methods, 2018, 15, 491–498 CrossRef CAS PubMed.
- P. Kollmannsberger and B. Fabry, Annu. Rev. Mater. Res., 2011, 41, 75–97 CrossRef CAS.
- I. E. Collier, S. M. Wilhelm, A. Z. Eisen, B. L. Marmer, G. A. Grant, J. L. Seltzer, A. Kronberger, C. He, E. A. Bauer and G. I. Goldberg, J. Biol. Chem., 1988, 263, 6579–6587 CrossRef CAS.
- T. Xia, K. Akers, A. Z. Eisen and J. L. Seltzer, Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol., 1996, 1293, 259–266 CrossRef.
- B. Lelongt, G. Trugnan, G. Murphy and P. M. Ronco, J. Cell Biol., 1997, 136, 1363–1373 CrossRef CAS PubMed.
- O. Lieleg, K. M. Schmoller, M. M. A. E. Claessens and A. R. Bausch, Biophys. J., 2009, 96, 4725–4732 CrossRef CAS PubMed.
- A. Atala and J. Yoo, Essentials of 3D Biofabrication and Translation, Elsevier, 1st edn, 2015, pp. 440 Search PubMed.
- J. Malda, J. Visser, F. P. Melchels, T. Jüngst, W. E. Hennink, W. J. A. Dhert, J. Groll and D. W. Hutmacher, Adv. Mater., 2013, 25, 5011–5028 CrossRef CAS PubMed.
- S. J. Müller, E. Mirzahossein, E. N. Iftekhar, C. Bächer, S. Schrüfer, D. W. Schubert, B. Fabry and S. Gekle, PLoS One, 2020, 15, 1–15 Search PubMed.
- B. Xue, V. Kozlovskaya, F. Liu, J. Chen, J. F. Williams, J. Campos-Gomez, M. Saeed and E. Kharlampieva, ACS Appl. Mater. Interfaces, 2015, 7, 13633–13644 CrossRef CAS.
- S. Freiberg and X. X. Zhu, Int. J. Pharm., 2004, 282, 1–18 CrossRef CAS PubMed.
- N. K. Varde and D. W. Pack, Expert Opin. Biol. Ther., 2004, 4, 35–51 CrossRef CAS PubMed.
- K. K. Kim and D. W. Pack, Microspheres for Drug Delivery in BioMEMS and Biomedical Nanotechnology, ed. M. Ferrari, A. P. Lee and L. J. Lee, Springer, Boston, MA. DOI:10.1007/978-0-387-25842-3_2.
- R. Sharma, I. P. Smits, L. De La Vega, C. Lee and S. M. Willerth, Front. Bioeng. Biotechnol., 2020, 8, 1–12 CrossRef PubMed.
- M. Bahadoran, A. Shamloo and Y. D. Nokoorani, Sci. Rep., 2020, 10, 7–9 CrossRef PubMed.
- Y. Karamzadeh, A. Ansari Asl and S. Rahmani, J. Appl. Polym. Sci., 2020, 137, 1–11 CrossRef.
- S. Kühn, J. Sievers, A. Stoppa, N. Träber, R. Zimmermann, P. B. Welzel and C. Werner, Adv. Funct. Mater., 2020, 30 DOI:10.1002/adfm.201908857.
- T. Lühmann and H. Hall, Materials, 2009, 2, 1058–1083 CrossRef.
- C.-C. Lin, P. D. Boyer, A. A. Aimetti and K. S. Anseth, J. Controlled Release, 2010, 142, 384–391 CrossRef CAS PubMed.
- L. M. Weber, C. G. Lopez and K. S. Anseth, J. Biomed. Mater. Res., Part A, 2009, 90, 720–729 CrossRef PubMed.
- E. Axpe, D. Chan, G. S. Offeddu, Y. Chang, D. Merida, H. L. Hernandez and E. A. Appel, Macromolecules, 2019, 52, 6889–6897 CrossRef CAS PubMed.
- V. Crosignani, A. Dvornikov, J. S. Aguilar, C. Stringari, R. Edwards, W. W. Mantulin and E. Gratton, J. Biomed. Opt., 2012, 17, 116023 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/D0BM02117B |
| ‡ Equal contributions. |
| This journal is © The Royal Society of Chemistry 2021 |