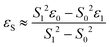Coupling of terminal iridium nitrido complexes

Abstract

The oxidative coupling of nitride ligands (N³⁻) to dinitrogen and its microscopic reverse, N₂-splitting to nitrides, are important elementary steps in chemical transformations, such as selective ammonia oxidation or nitrogen fixation. Here an experimental and computational evaluation is provided for the homo- and heterocoupling of our previously reported iridium(IV) and iridium(V) nitrides [IrN(PNP)]ⁿ (n = 0, +1; PNP = N(CHCHPtBu₂)₂). All three formal coupling products [(PNP)IrN₂Ir(PNP)]ⁿ (n = 0–+2) were structurally characterized. While the three coupling reactions are all thermodynamically feasible, homocoupling of [IrN(PNP)]⁺ is kinetically hindered. The contributing parameters to relative coupling rates are discussed providing qualitative guidelines for the stability of electron rich transition metal nitrides.

---

Sven Schneider

---

Introduction

The splitting of dinitrogen at ambient temperatures is a highly attractive reaction in the context of nitrogen fixation, yet still represents a challenging goal.¹ Ever since the seminal work of Cummins and co-workers about 20 years ago,² several other systems were reported to undergo the splitting of dinitrogen into well-defined nitrido complexes.³ The first reported and intensively examined example proceeds through diazenido dimer [(ArtBuN)₃Mo(NN)Mo(NtBuAr)₃]. Importantly, this linear μ-N₂ complex holds 10 π-electrons in the {MNNM}-core (Fig. 1a), finally resulting in the closed-shell nitride [NMo(NtBuAr)₃].^4,5 In comparison, the dimers [(ArtBuN)₃Mo (NN)Mo(NtBuAr)₃]ⁿ⁺ (n = 1–2) exhibit stronger degrees of N₂ activation due to depletion of a molecular orbital that is N–N antibonding in character. However, N₂-splitting is not observed due to destabilization of the nitrides upon oxidation. Similarly, Nishibayashi and co-workers examined the redox series [(depf)₂Cp*Mo(NN)MoCp*(depf)₂]ⁿ⁺ (n = 0–2; depf = 1,1′-bis(diethylphosphino)ferrocene), observing N₂ splitting for the 10 π-electron system (n = 0) and the reverse, nitride coupling, after oxidation of the resulting nitride.^3d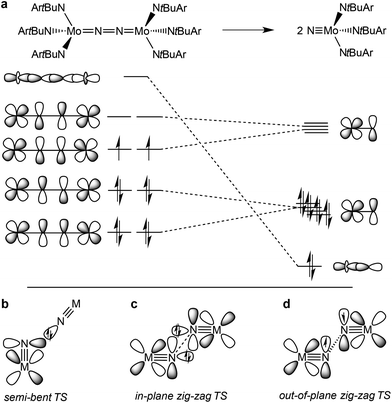

Fig. 1 Qualitative molecular orbitals relevant for N₂ splitting with Cummins’ complex (a) and schematic transition states that were proposed for N₂-splitting/coupling (b–d).

A similar picture arises for the reverse reaction, i.e. the coupling of terminal nitrides. Several authors reported the formation of dinitrogen bridged complexes upon reductive coupling of octahedral M^V nitrides (M = Fe, Ru, Os).⁶ These transient nitrides are typically formed in situ, e.g. by photolysis of M^III-azides, reduction of stable M^VI nitrides or oxidation of low-valent ammine complexes to give divalent ({M^IIN₂} or {M^IIN₂M^II}) or mixed valent {M^IIN₂M^III} dinitrogen complexes. Except for a few cases, it is not fully clear whether the reaction proceeds via M^V≡N homocoupling or coupling of M^V≡N with parent M^VI≡N. Importantly, within the simplified MO-picture (Fig. 1a) the M^II/II and M^II/III dinitrogen bridged complexes represent 12 and 11 π-electron {MNNM}-cores, respectively. However, some closed-shell nitrides also decay by nitride coupling underlining that the electronic configuration is not the only predictor for the thermochemistry of N₂-splitting/coupling.^7–9

In comparison, the relationship of electronic structure and kinetics received less attention. Ware and Taube examined the thermal decomposition of [Os^VINCl₃(py)₂] by nitride coupling to [Os^IIICl₃(py)₃].⁷ They pointed out that donation from a nitride lone-pair into an empty M≡N π*-orbital should be favored over a collinear approach of the two monomers and therefore proposed a semi-bent transition state (Fig. 1b). In line with such a polar transition state (TS), Seymore and Brown showed that heterocoupling of electrophilic Os^VI- and nucleophilic Mo^VI-nitrides is considerably faster than the respective homocoupling reactions.¹⁰ However, Burger and coworkers emphasized that nitride homocoupling should favor a symmetrical “non least-motion pathway” or in-plane zig-zag TS, which features mutual σ/π donor–acceptor interactions of the two monomer fragments (Fig. 1c).¹¹

Recently, we reported that photolysis of the iridium(II) azide [Ir(N₃)(PNP)] (1, PNP = N(CHCHPtBu₂)₂) results in the formation of iridium(IV) nitride [IrN(PNP)] (2, Scheme 1).¹² Spectroscopic and computational analysis suggested that 2 and the analogous rhodium compound are π-radicals with strong delocalization of the unpaired electron over the M≡N core, i.e. considerable “nitridyl” character.^12,13 In solution, these transient nitrides undergo clean coupling, e.g. to 12-π-electron N₂-complex [N₂{Ir(PNP)}₂] (3) in case of 2 (Scheme 1). The computed TS for a PMe₂-truncated model featured a mutual π/π MO-interaction as the most favorable pathway with an out of plane zig-zag arrangement of the two monomer radicals (Fig. 1d).¹² Alternatively, oxidation of 1 results in formation of isolable iridium(V) nitride [IrN(PNP)]⁺ (4), which in turn also gives 2 upon reduction (Scheme 1). In this context, we were interested whether the enhanced thermal stability of 4 can be attributed to thermodynamic or kinetic arguments. Here, we present a systematic experimental and computational study that addresses the stability of the iridium nitrides with respect to oxidative coupling.

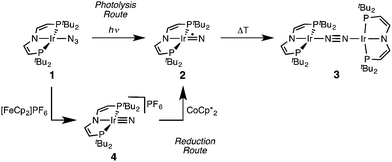Scheme 1 Syntheses of iridium(IV) and iridium(V) PNP nitrides 2 and 4 and coupling to iridium(I)/iridium(I) N₂-complex 4.¹²

Results and discussion

Synthesis of the [N₂{Ir(PNP)}₂]ⁿ⁺ (n = 0–2) redox series

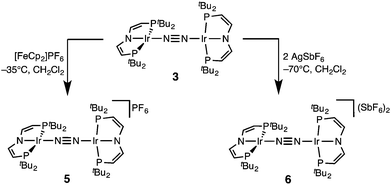
In a slightly improved synthetic protocol, the neutral dimer 3 can be obtained analytically pure in 66% yield on the iridium(V) nitride reduction route using Na/Hg with strict exclusion of light. Complex 3 was characterized by cyclic voltammetry (CV, see ESI†). The CV reveals three oxidative redox processes at E_1/2 = −0.27, 0.18, 0.35 V (vs. FeCp₂/FeCp₂⁺), respectively. While the Ir^I/I/Ir^I/II couple is fully reversible at r.t., the higher oxidations seem pseudo-reversible, as evidenced by the observation of small additional peaks upon cyclic back to low potentials. Hence, the electrochemical results suggest, that one- and two-electron oxidation of 3 could give isolable products.

Chemical oxidation of 3 with one equivalent of [FeCp₂]PF₆ in dichloromethane at −35 °C affords the isolation of Ir^I/II N₂-complex [N₂{Ir(PNP)}₂]PF₆ (5) as a temperature, light, and air sensitive dark green solid (Scheme 2). The X-band EPR spectrum of 5 in frozen solution (4 K) reveals a rhombic signal corresponding to an S = 1/2 system (ESI†). The large anisotropy of the g-tensor (g_x = 2.66, g_y = 2.12, g_z = 1.62) without resolved hyperfine coupling was similarly observed for several Ir^II(PNP) complexes with square-planar geometry.^5,14 From the CV data a comproportionation constant K_C is estimated to be around 10⁷. A large K_C like this is frequently stressed as a simple predictor for electronic delocalization in the mixed valent complex indicating stabilization due to resonance exchange.¹⁵ Note that K_C data should be treated with caution and is easily over-interpreted due to the many other parameters possibly contributing to electrochemical potentials.¹⁶ In fact, the bond parameters in the solid state indicate valence localization in the crystal (see below) and the DFT model of 5 also exhibits localization of the spin density on one of the two Ir(PNP) moieties (ESI†). In contrast, the ¹H NMR spectrum of 5 exclusively shows one set of paramagnetically shifted and broadened pincer ligand peaks (ESI†), suggesting rapid electron transfer between the N₂-bridged moieties on the NMR timescale (1–10⁻⁴ s). Unfortunately, detailed analysis of the NIR spectrum was hampered by the thermal instability of 5 and dication 6 (see below) and did not allow for a reliable assignment of intervalence charge transfer vs. interconfigurational electronic transitions. However, IR spectroscopy reveals the presence of a relatively intense band assignable to the N₂ stretching vibration both in solution (CH₂Cl₂: 1959 cm⁻¹) and in the solid state (nujol: 1960 cm⁻¹). The assignment was confirmed by DFT computations (ESI†) scaled to monomeric complex [Ir(N₂)(PNP)] (2077 cm⁻¹):¹² The experimental shift Δν_N2 = 117 cm⁻¹ is well reproduced by DFT (Δν_N2 = 115 cm⁻¹). This comparison also excludes the formation of monomeric [Ir(N₂)(PNP)]⁺, which should be blue shifted with respect to [Ir(N₂)(PNP)]. Importantly, the observation of an N₂-stretch confirms the presence of a permanent dipole, hence valence localization on the IR-timescale (∼10⁻¹⁴ s) also in solution providing an upper limit for the charge transfer rate. Similar properties between localized and delocalized mixed-valence (Class II–III) were found for N₂-bridged Os^II/III complexes.¹⁷ Unequivocal assignment of complex 5 requires further investigations.

Scheme 2 Chemical oxidation of iridium(I)/iridium(I) N₂-complex 3.

Confirmation of the molecular structure of 5 is provided by single-crystal X-ray diffraction (Fig. 2 and Table 1). Both Ir ions are in distorted square-planar coordination geometries and bridged by a linear, end-on bound N₂, as in parent 3. The structure features two crystallographically distinctly different Ir(PNP) fragments. For example, the Ir–N_PNP and Ir–N_N2 distances differ by 0.06 Å and 0.11 Å, respectively. Ir2 exhibits a longer bond to the PNP π-donor ligand and a shorter bond to the π-acceptor N₂ than Ir1. In that respect, Ir2 behaves similar to Ir in 3. Hence, the structural parameters suggest trapped oxidation states in the solid state with Ir1 and Ir2 being associated with the +2 and +1 valence states, respectively. Importantly, the N–N distance (1.136(6) Å) is identical with that in 3 (1.135(4) Å) and in [N₂{Ir(PCP)}₂] (1.134(2) Å; PCP = C₆H₃-2,6-(CH₂PtBu₂)₂)¹⁸ and close to free N₂ (1.097 Å) revealing a weak degree of N₂-activation upon oxidation.

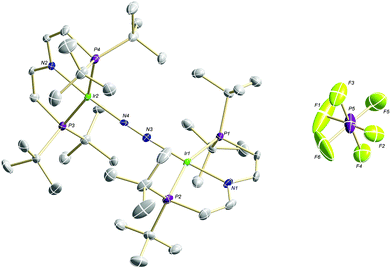Fig. 2 Molecular structure of 5 in the solid state (ellipsoids at 50% probability level, hydrogen atoms and solvent molecules omitted for clarity).

Table 1 Comparison of selected experimental and computed bond lengths and angles of 3, 5, and 6

	3		5		6
	Exp	DFT	Exp	DFT	Exp	DFT
a Computed spin ground–states: ^13, ^25, ^36.
Bond lengths (Å)
Ir–N2	1.937(3)/1.933(3)	1.922	1.984(5)/1.878(5)	1.988/1.855	1.954(3)	1.928
Ir–NPNP	2.041(3)/2.035(3)	2.055	1.973(4)/2.031(4)	1.969/2.059	1.983(3)	1.995
N–N	1.135(4)	1.136	1.136(6)	1.141	1.138(6)	1.140
Bond angles (°)
Ir–N–N	174.6(2)/172.3(3)	172.8	175.3(4)/174.6(4)	172.0/173.2	172.2(3)	173.2
N–Ir–N	173.6(2)/171.0(1)	172.0	172.8(2)/173.3(2)	169.9/171.6	168.0(1)	169.0

---

The reaction of 3 with two equivalents of AgSbF₆ at −70 °C in dichloromethane under the exclusion of light results in the immediate precipitation of metallic silver and formation of a deep red solution (Scheme 2). Monitoring by ¹H NMR spectroscopy reveals the formation of a new paramagnetic compound with one set of signals assignable to a PNP pincer ligand, yet not as clean as in case of 5 (ESI†). No signals were found by X-band EPR spectroscopy as expected for a non-Kramers system. Decomposition in solution above −50 °C into several unidentified paramagnetic compounds is indicated by new ¹H NMR signals upon warming. Importantly, the nitride 4 was not found as decomposition product.

The high lability of the product from double oxidation with respect to ambient temperatures and light hampered a more detailed spectroscopic characterization, so far. However, crystallization at low temperatures afforded red crystals of the dinitrogen bridged Ir^II/II complex [(N₂){Ir(PNP)}₂](SbF₆)₂ (6) that were suitable for X-ray diffraction. In contrast to mixed-valent complex 5, the molecular structure of 6 (Fig. 3 and Table 1) features two crystallographically equivalent Ir(PNP) fragments. The Ir–N_PNP (1.983(3) Å) and Ir–N_N2 (1.954(3) Å) bond lengths are very close to those of Ir1 in 5, supporting the valence state assignments for the structure of 5 and full oxidation of 6 to Ir^II/II. The N₂ bond length (1.138(6) Å) is identical within error compared to the parent Ir^I/I (1.135(4) Å) and Ir^I/II (1.136(6) Å) complexes, indicating that N₂ activation is negligible within the [N₂{Ir(PNP)}₂]ⁿ⁺ (n = 0–2) redox series.

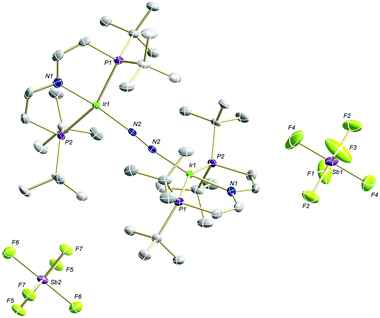Fig. 3 Molecular structure of 6 in the solid state (ellipsoids at 50% probability level, hydrogen atoms and solvent molecules omitted for clarity).

Nitride coupling to [N₂{Ir(PNP)}₂]ⁿ⁺ (n = 0–2)

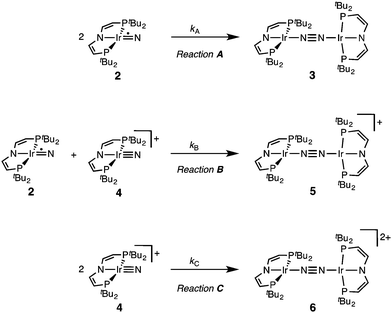
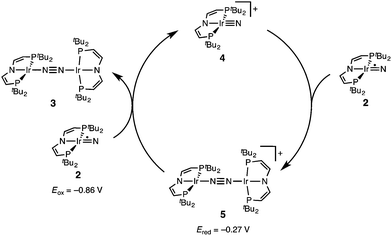
The successful preparation of 5 and 6 and the absence of N₂ activation upon oxidation of 3 suggest that the iridium(V) nitride 4 is only kinetically stabilized with respect to coupling. We previously reported the kinetics of iridium(IV) nitride coupling (Scheme 3, A): A second order rate-law in 2 was found with a rate constant at room temperature k = 1.1(2) M⁻¹ min⁻¹. Hence, this reaction is accompanied with a moderate kinetic barrier around ΔG^‡_{298 K} = 22 kcal mol⁻¹. In contrast, very slow decay is observed for iridium(V) nitride 4 over several days at elevated temperatures in dichloromethane, into several unidentified products. Furthermore, in contrast to 2, decomposition of 4 follows a rate law that is first-order in 4 (k = 0.474(9) d⁻¹; ESI†). Hence, the nitride coupling rate (Scheme 3, C) could not be directly derived, but the decomposition rate allows for an estimate of a lower limit for the kinetic barrier of nitride coupling (ΔG^‡_{313 K} > 25 kcal mol⁻¹).

Scheme 3 Nitride coupling reactions examined.

Coupling of the iridium(V) and iridium(IV) nitrides to mixed-valent 5 was also examined (Scheme 3, B). Spectro-electrochemical reduction of 4 (E_red = −0.86 V) at room temperature results in clean conversion to Ir^I/I complex 3 (E_ox = −0.27 V). The observation of an isosbestic point at 560 nm indicates the absence of long-lived intermediates on the experimental time-scale (ESI†). Moreover, the equimolar addition of 2 to 4 at −70 °C, where both pure nitrides are kinetically stable, results in immediate coupling to 5 (ESI†) confirming much more rapid coupling to 5 than to 3 or 6. Even the addition of a substoichiometric amount of 4 (10 mol%) to 2 at −70 °C results in the immediate formation with dimer 3 as the main product (ESI†). This observation can be rationalized with a redox-catalytic cycle (Scheme 4): Nitrides 2 and 4 undergo rapid coupling. The resulting dimer 5 is then reduced by starting material 2 to restore catalyst 4, which is in line with the potentials of redox couples 2/4 and 3/5, respectively. This mechanism also explains a previously reported observation for the two routes to iridium(IV) nitride 2 (Scheme 1): Unlike the photolysis route, the reduction route also yields considerable amounts of coupling product 3, even at low temperatures where coupling of pure 2 is not observed.

Scheme 4 Proposed mechanism of redox catalysis for the coupling of nitride 2.

Computational results

Our experimental results demonstrate a clear succession in nitride coupling rates (k_B > k_A > k_C). This result was rationalized by means of density functional theory (DFT). The energetics of the three coupling reactions (Scheme 3, A–C) were examined by DFT computations on the D3BJ-PBE0(Cosmo(THF))/def2-TZVP//D3BJ-PBE0/def2-SVP level of theory. The molecular structures of dimers 3, 5 and 6 are well reproduced with singlet (3), doublet (5) and triplet (6) ground states, respectively (Tables 1 and 2 and ESI†). Ferromagnetic coupling (J = 39 cm⁻¹) of the iridium(II) ions in 6 results in the triplet state being slightly more stable than the open shell singlet state by 0.4 kcal mol⁻¹. The computed electronic ground states resemble the simplified picture that arises from symmetry considerations (Fig. 1) for 12 (3), 11 (5) and 10 (6) π-electron configurations, respectively. Accordingly, the geometry of 5 is distorted along the Ir–N–N–Ir axis avoiding uneven occupation of degenerate π-MOs. Similarly, coplanar arrangement of the two Ir(PNP) fragments would also lift π-MO degeneracy due to mixing of the Ir–N–N–Ir π-manifold with PNP nitrogen lone-pairs. While such a coplanar conformation is not accessible with bulky PtBu₂ groups (see below), the PMe₂-truncated model of 5 favors such a conformation, emphasizing the importance of considering the full model.

Table 2 Calculated reaction electronic energies (ΔE including zero point energy) and free energies (ΔG) for the coupling reactions A–C in kcal mol⁻¹ and N–N distances in the transition states (D_N–N) in Å

Reaction	A		B		C
	^2 2 + ^22 → ^13		^2 2 + ^14 → ^25		^1 4 + ^14 → ^36
	ΔE	ΔG298 ^b	ΔE	ΔG298 ^b	ΔE	ΔG298 ^b
a With respect to encounter complexes (ESI). b With respect to starting complexes.
TS	6.9^a	21.0	1.2^a	10.1	13.8^a	29.3
Product	−121.8^b	−101.5	−115.6^b	−97.1	−91.3^b	−73.9
D N–N	2.057		2.003		1.841

---

Computational evaluation of reactions A–C (Scheme 3) fully reproduces our experimental results (Table 2 and ESI†). Nitride coupling is thermodynamically strongly favored for all three reactions. However, the driving force within the redox series 3 (ΔG₂₉₈ = −101.5 kcal mol⁻¹), 5 (ΔG₂₉₈ = −97.1 kcal mol⁻¹), and 6 (ΔG₂₉₈ = −73.9 kcal mol⁻¹) decreases, as expected from the destabilizing population of an Ir–N π*-antibonding orbital in 2. For reaction A, a kinetic barrier was computed (ΔG^‡₂₉₈ = 21.0 kcal mol⁻¹) that is in excellent agreement with experiment (≈ 22 kcal mol⁻¹).¹² It mainly arises from the entropic contribution with only a small electronic fraction. The transition state, ^BS(1,1)TS_A (Fig. 4A), was located on the open shell singlet surface at a rather long N–N distance (2.06 Å). The spin is eventually quenched at significantly smaller N–N distances, leading to the closed shell ground state of dimer 3. The TS structure features the two Ir(PNP) monomer fragments being essentially perpendicular to each other. The two Ir–N groups are offset from collinearity along both relative orientations of the Ir(PNP) planes resulting in an out-of-plane zig-zag transition state. The orthogonalized sets of natural frontier orbitals represent hybrid orbitals from SOMO/LUMO mixing of the nitride monomers. π/π-Orbital overlap between the two monomers is further increased by slightly tilting the two monomer fragments towards each other (Ir–N–N–Ir dihedral angle: 152°). The previously computed PMe₂-truncated model of reaction A also gave a good agreement for the driving force (ΔG₂₉₈ = −108.2 kcal mol⁻¹) but underestimation of the reaction barrier (ΔG^‡₂₉₈ = 13.7 kcal mol⁻¹).¹² In fact, the smaller model featured a distinctly different conformation for the TS with almost coplanar relative orientation of the two monomers. However, the minute electronic contributions to biradical coupling is almost identical for both models, while the entropic contribution seems underestimated in case of the small model presumably due to steric constraints for vibrational and rotational degrees of freedom of the tBu groups in the TS.

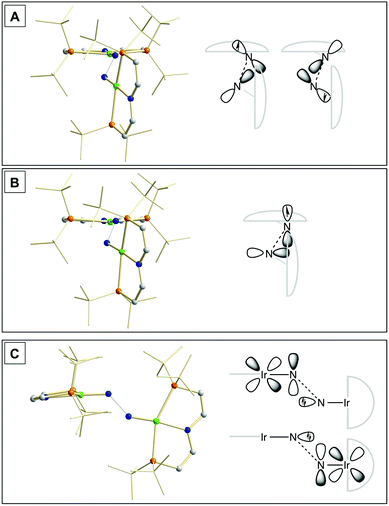Fig. 4 Transition state structures of ^BS(1,1)TS_A (A), ²TS_B (B) and ¹TS_C (C) and schematic representations of the NBO interactions.

Coupling of ²2 and ¹4 to ²5, was computed to be essentially electronically barrierless with a free energy of activation ΔG^‡₂₉₈ = 10.1 kcal mol⁻¹, confirming the experimentally observed rapid coupling reaction B. The transition state ²TS_B (Fig. 4B) exhibits strong structural similarities with ^BS(1,1)TS_A concerning the N–N distance (D_N–N = 2.00 Å) and the out-of-plane zig-zag relative orientation of the two nitride fragments (Ir–N–N–Ir dihedral angle: 142°). Accordingly, ²TS_B also features a π/π-interaction between the two monomers, here arising from orbital overlap of the SOMO (2) and LUMO (4) monomer orbitals, respectively. The spin density is equally distributed over the mixed-valent dimer indicating strong electronic coupling and charge delocalization in the TS.

In contrast, reaction C is associated with a considerably higher computed kinetic barrier (ΔG^‡₂₉₈ = 29 kcal mol⁻¹), which is in agreement with the enhanced thermal stability of 4. The transition state ¹TS_C (Fig. 4C) is located on the singlet surface. At a later stage there is a change to an open shell singlet and eventually the triplet ground state of ³6 (ESI†). ¹TS_C exhibits significant differences compared with ^BS(1,1)TS_A and ²TS_B: The two Ir–N bond vectors are almost parallel (Ir–N–N–Ir dihedral angle: 178°) and the offset from collinearity only along one of the Ir(PNP) planes results in an in-plane zig-zag transition state. The closed-shell σ/π-orbital interaction between the two monomers resembles the TS previously considered by Burger.¹¹ In the present case though different Ir–N π*-orbitals are involved on the two monomers, respectively, due to the perpendicular orientation of the two monomer fragments. Importantly, the N–N distance in ¹TS_C (1.84 Å) is considerably shorter compared with those in ^BS(1,1)TS_A and ²TS_B (both >2.00 Å) indicating that a stronger orbital interaction is necessary to overcome the kinetic barrier.

Hence, the computational evaluation confirms the order of relative coupling rates that was found experimentally (k_B > k_A > k_C). Albeit partitioning of TS energies into the contributing terms was not done within this study, the TS structures allow for a qualitative rationalization that is in line with the observed order: Coulombic repulsion of the two positively charged nitrides is expected to contribute to the higher barrier of reaction Cvs.A. In turn, the TS of reaction B exhibits strong charge delocalization over both monomer moieties, tantamount a stabilizing Coulombic effect. Besides these charge considerations, barrierless coupling of 2 and 4 involves direct overlap of the respective SOMO and LUMO orbitals while diradical coupling reaction A necessitates some electronic rearrangement within ^BS(1,1)TS_A with respect to ²2. However, in all three TSs relatively large N–N distances were found and NBO analysis of ¹TS_C reflects only a donor–acceptor interaction between electronically weakly perturbed monomers. Hence, these results suggest for the Coulombic interaction to be the main contributor to the computed order of reaction barriers.

Conclusions

We previously reported the coupling of iridium(IV) nitride 2 to the Ir^I/I N₂-bridged dimer 3.¹² In contrast, iridium(V) nitride 4 does not undergo coupling at room temperature. In the present paper, the other products of formal nitride coupling besides 3, i.e. the N₂-bridged Ir^I/II and Ir^II/II complexes 5 and 6, were synthesized and structurally characterized. None of the dimers reveal structural or spectroscopic features indicative of an appreciable degree of N₂-activation. These results suggest that nitride 4 is also inherently thermodynamically unstable with respect to N₂-coupling. This notion is supported by DFT computations, though indicating a considerably smaller driving force for homocoupling of 4vs.2. Examination of the kinetics of homo- and heterocoupling reactions A–C revealed the order k_B > k_A > k_C, also supported by DFT. Analysis of the TS structures indicate that the Coulombic interactions between the nitrides favor this order, leading to stabilization of ²TS_B by charge delocalization and repulsion within ¹TS_C. Hence, this work indicates some guidelines for thermodynamic and kinetic stabilization of electron rich transition metal nitrides.

Experimental section

Materials and methods

All experiments were carried out using Schlenk (argon atmosphere) and glove-box (argon atmosphere) techniques. All solvents were dried by passing through columns packed with activated alumina. Deuterated solvents were obtained from Euriso-Top GmbH, dried over Na/K (Toluene-d₈) or CaH₂ (CD₂Cl₂), distilled by trap-to-trap transfer in vacuo, and degassed by three freeze–pump–thaw cycles, respectively. [FeCp₂]PF₆ (SigmaAldrich) and AgSbF₆ (SigmaAldrich) were used as purchased. Silica gel 60 silanized was purchased from Merck KGaA and heated in vacuo for 5 days prior to use. 1, 4, and Na/Hg were prepared according to published procedures.^12,19

Irradiation was carried out with a Lot Oriel Xe-Short arc lamp. Cyclic voltammograms were recorded with a Metrohm Autolab PGSTAT101 using Ag/Ag⁺ reference-, glassy-carbon working- and Pt-wire counter-electrodes. Pt-net working-electrodes and a spectro-electrochemistry cuvette (0.1 cm optical pathway) were used for UV/VIS-spectroelectrochemical measurements in combination with an Avantes AvaSpec-2048×14 UV/VIS-spectrometer. Otherwise UV/VIS-spectra were recorded with an Agilent Cary 300 UV/VIS-spectrometer at room temperature with a 0.1 mM concentration in quartz cuvettes (1 cm optical pathway). NMR-spectra were recorded on a Bruker Avance 300/400 spectrometer and calibrated to the residual proton resonance of the solvent (CD₂Cl₂: δ_H = 5.32 ppm; δ_C = 54.00 ppm; Toluene-d₈: δ_H = 7.09, δ_C = 137.86). ³¹P-NMR chemical shifts are reported relative to external phosphoric acid (δ = 0.0 ppm). Signal multiplicities are abbreviated as: s (singlet), h (heptet), br (broad). Experimental X-band EPR spectra were recorded on a Bruker ELEXSYS-II E500 CW-EPR. The spectra were simulated by iteration of the anisotropic g-values, (super)hyperfine coupling constants, and line widths using the EPR-simulation program W95EPR developed by Prof. Dr Frank Neese. ESI-MS-experiments employed a micrOTOF-Q II instrument (Bruker Daltonik). IR spectra were recorded with a Thermo Scientific Nicolet iZ10 FT/IR spectrometer at r.t. IR spectra in solution were recorded with a thin layer IR cell.

Improved synthesis of [IrCl(PNP)]. To a suspension of [Ir(COE)₂Cl]₂ (53.8 mg, 60.0 μmol, 1.00 eq.) in THF (50 mL) (^tBu₂PCH₂CH₂)₂NH (43.4 mg, 120 μmol, 2.00 eq.) in THF (5 mL) is added. The reaction is stirred for 15 min at room temperature and benzoquinone (32.4 mg, 300 μmol, 5.00 eq.) is added. After stirring for 16 h at room temperature the suspension is extracted with THF (3 × 5 mL), silanized silica is added and the solvent is removed in vacuo under intense stirring. The solid is extracted with pentanes (5 × 5 mL), the solvent removed in vacuo and the remaining residue dissolved in benzene and lyophilized. (Yield: 56 mg, 95.9 μmol, 80%). NMR data were identical with the previously reported synthesis. Anal. Calc. for C₂₀H₄₀IrNP₂ (584.16): C, 41.12; H, 6.90; N, 2.40. Found: C, 41.41; H, 7.05; N, 2.15.

Improved synthesis of [(N₂){Ir(PNP)}₂] (3). Under the exclusion of light, [IrN(PNP)][PF₆] (50.0 mg, 70.7 μmol, 1.00 eq.) is dissolved in THF (3 mL) and NaHg (1 M, 1.24 g, 91.9 μmol, 1.30 eq.) is added and the solution is stirred for 1 min at room temperature. The solvent is removed in vacuo and the residue is extracted with benzene (6 × 0.8 mL). The product is isolated by column chromatography (2 cm silanized silica gel, 1.5 cm diameter; benzene). (Yield: 27.0 mg, 23.4 μmol, 66%). NMR data were identical with the previously reported synthesis. Anal. Calc. for C₄₀H₈₀Ir₂N₄P₂ (1125,44): C, 42.69; H, 7.17; N, 4.98. Found: C, 43.44; H, 7.32; N, 4.30.

Synthesis of [(N₂){Ir(PNP)}₂]PF₆ (5). Under the exclusion of light, 3 (5.0 mg, 4.4 μmol, 1.0 eq.) and [Fe(C₅H₅)₂]PF₆ (1.5 mg, 4.4 μmol, 1.0 eq.) are dissolved in DCM (2 mL) at −35 °C and stirred for 5 min. The solvent is removed in vacuo. The residue is exhaustively washed with toluene (–35 °C, 8 × 2 mL) to remove ferrocene, extracted with THF (−35 °C, 4 × 2 mL) and the solvent is removed in in vacuo. ¹H-NMR: (300 MHz, CD₂Cl₂, RT): δ = 39.1 (s br, 4H, CH), 5.21 (s br, 72H, PCCH₃) −129.0 (s br, 4H, CH). ¹H-NMR: (300 MHz, THF-d₈, RT): δ = 42.7 (s br, 4H, CH), 5.45 (s br, 72H, PCCH₃) −140.1 (s br, 4H, CH). ³¹P{¹H}-NMR: (121.49 MHz, CD₂Cl₂, RT): δ = −145.0 (h, ²J_PF = 711 Hz, PF₆). ESI-MS (m/z): [M]⁺ calcd for C₄₀H₈₀N₄P₄Ir₂ 1124.457; found: 1124.406.

Synthesis of [(N₂){Ir(PNP)}₂](SbF₆)₂ (6). Under the exclusion of light, 3 (4.0 mg, 3.6 μmol, 1.0 eq.) and AgSbF₆ (2.4 mg, 7.1 μmol, 2.0 eq.) are dissolved in DCM (−70 °C, 0.5 mL) and the solution is shaken for 1 min. ¹H-NMR: (400 MHz, CD₂Cl₂, −70 °C): δ = 29.09 (s br, 4H, CH), 21.78 (s br, 72H, PCCH₃) −11.25 (s br, 4H, CH).

Coupling of 2 in the presence of catalytic amounts of 4. [Ir(N₃)(PNP)] (5.0 mg, 8.5 mmol, 1.0 eq.) is dissolved in THF-d₈ (0.4 mL) and irradiated at −80 °C for 20 minutes. The solution is frozen with liq. N₂ and 4 (0.6 mg, 0.85 mmol 0.1 eq.) in DCM-d₂ (0.1 mL) is added to the frozen solid. The solution is thawed and NMR spectra were recorded at −70 °C (For an amount of 1 mol% of 3 only 0.01 mL of the DCM-d₂ solution is added).

Thermal stability of 4. 4 (5.3 mg, 7.5 mmol, 1.0 eq.) is dissolved in DCM-d₂ (0.54 mL) and naphthalene (1.9 mg, 15 mmol, 2.0 eq.) is added. The solution is heated to 40 °C for 5 days.

Crystallographic details

Suitable single crystals for X-ray structure determination were selected from the mother liquor under an inert gas atmosphere and transferred in protective perfluoro polyether oil on a microscope slide. The selected and mounted crystals were transferred to the cold gas stream on the diffractometer. Intensity data for 5 and 6 were obtained at 100 K on a Bruker D8 three-circle diffractometer, equipped with a PHOTON 100 CMOS detector and an INCOATEC microfocus source with Quazar mirror optics (λ = 0.71073 Å). The data obtained were integrated with SAINT and a multi-scan absorption correction with SADABS was applied. Both structures were solved and refined using the Bruker SHELX 2014 software package.²⁰ All non-hydrogen atoms were refined with anisotropic displacement parameters. All C–H hydrogen atoms were refined isotropically on calculated positions by using a riding model with their U_iso values constrained to 1.5 U_eq of their pivot atoms for terminal sp³ carbon atoms and 1.2 times for all other carbon atoms. Crystal structure determination of C₄₀H₈₀F₆Ir₂N₄P₅ (5): CCDC 1437698, M = 1270.33, orthorhombic, a = 13.1762(5), b = 13.3606(5), c = 28.3330(11) Å, U = 4987.8(3) ų, T = 100 K, space group P2₁2₁2₁ (no. 19), Z = 4, 78 343 reflections measured, 12 410 unique (R^int = 0.0589), which were used in all calculations. The final wR(F²) was 0.0454 (all data). Crystal structure determination of C₅₂H₁₀₄F₁₂Ir₂N₄O₃P₄Sb₂ (6): CCDC 1437699, M = 1813.17, monoclinic, a = 15.7367(8), b = 15.1562(7), c = 15.2970(8) Å, b = 113.649(2)°, U = 3342.1(3) ų, T = 100 K, space group P2/c (no. 13), Z = 2, 55 887 reflections measured, 8353 unique (R^int = 0.0446), which were used in all calculations. The final wR(F²) was 0.0600 (all data).

Computational details

DFT calculations were performed with the Turbomole 7.0 package²¹ applying the PBE0 ²² functional and Grimme's dispersion correction with Becke–Johnson damping (D3BJ).²³ Ahlrich's revised basis sets were used (def2-SVP for structure optimization and def2-TZVP for single point energies) with a full basis for all elements but Ir for which a Stuttgart–Dresden 60 electron core potential has been used, replacing the inner shell 1s–4f orbitals.²⁴ No symmetry restrains were imposed and the optimized structures were defined as minima (no negative eigenvalue) or transition states (one negative eigenvalue) by vibrational analyses at the same level of theory. In case of ¹TS_C a small second imaginary mode at −13 cm⁻¹ was observed. Solvent effects were accounted for by applying the COSMO model (ε = 7.6 for THF) in the single point calculations.²⁵ Final energies were obtained by adding zero point vibrational energies or enthalpies from the optimizations to the SCF energies, in short notified as D3BJ-PBE0(COSMO(THF))/def2-TZVP//D3BJ-PBE0/def2-SVP. The electronic structures of ^BS(1,1)TS_A and 6 were evaluated by the broken symmetry protocol and the open shell singlet (OSS) structures (BS1,1) were located. The energies of the (multi-determinant) OSS were estimated from the energy ε₀ of the optimized single-determinant broken symmetry solution and the energy ε₁ from a separate unrestricted triplet (m_s = 1) calculation at the same geometry with the same functional and basis set, using the approximate spin correction formula proposed by Yamagushi:²⁶

NBO analyses at the D3BJ-PBE0/def2-SV(P) level were performed with Gaussian 09 RevD.01 ²⁷ coupled to NBO6.0 ²⁸ using the structures optimized as described above.

Acknowledgements

The authors thank the European Research Council (Grant Agreement 646747) for generous support, Prof. K. Koszinowski for recording the ESI-MS data, and Prof. M. Bennati for access to EPR facilities and discussion.

References

1. H.-P. Jia and E. A. Quadrelli, Chem. Soc. Rev., 2014, 43, 547.
2. C. E. Laplaza and C. C. Cummins, Science, 1995, 268, 861.
3. Recent examples: (a) M. M. Rodriguez, E. Bill, W. W. Brennessel and P. L. Holland, Science, 2011, 334, 780; (b) T. J. Hebden, R. R. Schrock, M. K. Takase and P. Müller, Chem. Commun., 2012, 48, 1851; (c) I. Klopsch, M. Finger, C. Würtele, B. Milde, D. B. Werz and S. Schneider, J. Am. Chem. Soc., 2014, 136, 6881; (d) T. Miyazaki, H. Tanaka, Y. Tanabe, M. Yuki, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Angew. Chem., Int. Ed., 2014, 53, 11488.
4. (a) C. E. Laplaza, M. J. A. Johnson, J. C. Peters, A. L. Odom, E. Kim, C. C. Cummins, G. N. George and L. J. Pickering, J. Am. Chem. Soc., 1996, 118, 8623; (b) J. J. Curley, T. R. Cook, S. Y. Reece, P. Müller and C. C. Cummins, J. Am. Chem. Soc., 2008, 130, 9394; (c) A. S. Huss, J. J. Curley, C. C. Cummins and D. A. Blank, J. Phys. Chem. B, 2013, 117, 1429.
5. M. G. Scheibel, J. Abbenseth, M. Kinauer, F. W. Heinemann, C. Würtele, B. de Bruin and S. Schneider, Inorg. Chem., 2015, 54, 9290.
6. (a) L. A. P. Kane-Maguire, P. S. Sheridan, F. Basolo and R. G. Pearson, J. Am. Chem. Soc., 1970, 92, 5865; (b) J. D. Buhr and H. Taube, Inorg. Chem., 1979, 18, 2208; (c) C.-M. Che, H.-W. Lam, W.-F. Tong, T.-F. Lai and T.-C. Lau, J. Chem. Soc., Chem. Commun., 1989, 1883; (d) K. D. Demandis, T. J. Meyer and P. S. White, Inorg. Chem., 1997, 36, 5678; (e) O. Krahe, E. Bill and F. Neese, Angew. Chem., Int. Ed., 2014, 53, 8727.
7. D. C. Ware and H. Taube, Inorg. Chem., 1991, 30, 4605.
8. T. A. Betley and J. C. Peters, J. Am. Chem. Soc., 2004, 126, 6252.
9. Homocoupling of closed-shell iron(IV) nitride [FeN{PhB(CH₂PiPr₂)₃}] results in an N₂ Fe^I/I dimer with high-spin configuration, which therefore represents an 8 π-electron configuration within the {FeNNFe} core.⁸.
10. (a) S. B. Seymore and S. N. Brown, Inorg. Chem., 2002, 41, 462; (b) S. B. Seymore and S. N. Brown, Inorg. Chem., 2006, 45, 9540.
11. J. Schöffel, N. Susnjar, S. Nückel, D. Sieh and P. Burger, Eur. J. Inorg. Chem., 2010, 4911.
12. M. G. Scheibel, B. Askevold, F. W. Heinemann, E. J. Reijerse, B. de Bruin and S. Schneider, Nat. Chem., 2012, 4, 552.
13. M. G. Scheibel, Y. Wu, A. C. Stückl, L. Krause, E. Carl, D. Stalke, B. de Bruin and S. Schneider, J. Am. Chem. Soc., 2013, 135, 17719.
14. J. Meiners, M. G. Scheibel, M.-H. Lemée-Cailleau, S. A. Mason, M. B. Boeddinghaus, T. F. Fässler, E. Herdtweck, M. M. Khusniyarov and S. Schneider, Angew. Chem., Int. Ed., 2011, 50, 8184.
15. (a) M. D. Ward, Chem. Soc. Rev., 1995, 24, 121; (b) W. Kaim and B. Sarkar, Coord. Chem. Rev., 2007, 251, 584.
16. D. M. D'Alessandro and F. R. Keene, Dalton Trans., 2004, 3950.
17. K. D. Demadis, C. M. Hartshorn and T. J. Meyer, Chem. Rev., 2001, 101, 2655.
18. R. Ghosh, M. Kanzelberger, T. J. Emge, G. S. Hall and A. S. Goldman, Organometallics, 2006, 25, 5668.
19. S. H. Babcock, Inorg. Synth., 1939, 1, 10.
20. APEX2 v2014.9-0 (SAINT/SADABS/SHELXT/SHELXL), Bruker AXS Inc., Madison, WI, USA, 2014.
21. TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
22. J. P. Perdew, K. Burke and M. Ernzerhof, J. Chem. Phys., 1996, 105, 9982.
23. (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
24. (a) K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119; (b) D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123; (c) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297; (d) F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143.
25. A. Klamt and G. Schürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799.
26. (a) T. Onishi, Y. Takano, Y. Kitagawa, T. Kawakami, Y. Yoshioka and K. Yamaguchi, Polyhedron, 2001, 20, 1177; (b) S. Yamanaka, T. Kawakami, H. Nagao and K. Yamaguchi, Chem. Phys. Lett., 1994, 231, 25; (c) Q. Knijnenburg, D. Hetterscheid, T. M. Kooistra and P. H. M. Budzelaar, Eur. J. Inorg. Chem., 2004, 1204.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
28. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013.

---

Footnote

† Electronic supplementary information (ESI) available: Spectroscopic, electrochemical, kinetic, and mass spectrometric data and crystallographic and computational details. CCDC 1437698 and 1437699. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qi00267b

---