N-Heterocyclic carbene adducts to [Cp′FeI]₂: synthesis and molecular and electronic structure

Abstract

Addition of N-heterocyclic carbenes (L = 1,3-di-tert-butylimidazol-2-ylidene (ItBu), 1,3-di-iso-propyl-4,5-dimethylimidazol-2-yildene (IiPr₂Me₂), 1,3-mesitylimidazol-2-yildene (IMes) and 1,3-di-(2,6-di-isopropylphenyl)imidazol-2-yildene (IPr)) to the iron half-sandwich complex [Cp′FeI]₂ (Cp′ = η⁵-1,2,4-(Me₃C)₃C₅H₂, 1) forms the neutral, 16VE adducts [Cp′FeI(L)] (2–5) in moderate to excellent yields. These complexes were structurally characterised. The NHC ligand binds strongly to the Fe(II) atom, so that no exchange is observed on the NMR and chemical time scale. Fe(II) atoms in the starting material 1 adopt a high-spin configuration (S = 2) and are weakly antiferromagnetically coupled at low temperatures. Furthermore, in contrast to previous reports on related [(η⁵-C₅Me₅)FeCl(NHC)] systems, in which the Fe(II) atoms assume an intermediate spin (S = 1), no spin state change occurs upon coordination of the NHC ligand; the Fe(II) atoms in complexes 2–5 retain their high-spin state (S = 2) as shown by solid state magnetic susceptibility and zero-field ⁵⁷Fe Mössbauer spectroscopy investigations. Density functional theory (DFT) studies at the B3LYP level of theory also agree with a well separated S = 2 ground state for compounds 2–5. Surprisingly for Fe(II) high-spin systems, compounds 1–5 exhibit slow paramagnetic relaxation in their Mössbauer spectra; this can be traced to spin–spin and spin–lattice relaxation processes with unusually large spin–lattice relaxation barriers. A structural model is proposed that associates these processes with crystal packing effects.

---

Marc D. Walter

Marc D. Walter studied at the Technische Universität (TU) Kaiserslautern in Germany. He carried out his PhD (awarded in 2005) jointly with Helmut Sitzmann in Kaiserslautern and with Richard A. Andersen at the University of California, Berkeley. From 2006–2010, he was a postdoctoral research fellow with Maurice S. Brookhart at the University of North Carolina at Chapel Hill. In 2010, he has started his independent career at the TU Braunschweig (supported by the Emmy Noether Program of the Deutsche Forschungsgemeinschaft (DFG; German Research Foundation)). His research focuses on the activation and functionalization of small molecules using highly reactive organometallic complexes. In 2014 he received the DFG Heinz Maier-Leibnitz Prize and the Wöhler-BASF Young Investigator Award of the Wöhler-Vereinigung (the inorganic subdivision of the Gesellschaft Deutscher Chemiker (GDCh; German Chemical Society)). Since 2015 he is also supported by a DFG Heisenberg fellowship.

---

Introduction

The importance of 16VE piano stool complexes in catalysis has long been recognized and their electronic structure has been extensively investigated by computational methods. Extended-Hückel theory (EHT) calculations on the electronic structure and structural dynamics in [CpMn(CO)₂] were reported as early as 1977.¹ The first examples of Group 8 systems were synthesized in the late 1980s. Tilley and co-workers prepared diamagnetic [Cp*Ru(L)Cl] (Cp* = η⁵-C₅Me₅, L = P(iPr)₃, PCy₃) complexes that bind C₂H₄ and undergo oxidative addition with PhSiH₃ to yield [Cp*Ru(L)(H)(SiH₂Ph)].² A few years later Caulton and co-workers showed that the related systems [Cp*Ru(L)(OMe)] (L = PCy₃, P(iPr)₂Ph) react with H₂ to give [Cp*Ru(P(iPr)₂Ph)(H)₃] and MeOH.² Consequently the electronic structure of neutral ruthenium 16VE two-legged piano stools was analyzed by various computational methods.³ In the late 1990s, cationic 16VE iron complexes such as [Cp*Fe(dppe)]⁺ were introduced that exhibited an intermediate spin (S = 1) configuration;⁴ computational studies at the DFT and MP2 level of theory predicted either low (S = 0) or intermediate spin (S = 1) states for these systems depending on their molecular structure (C_s or C_2v symmetry).⁵ However, in contrast to the cationic derivatives, the isolation of neutral 16VE iron two-legged piano stools has been more challenging. For this purpose O-donor⁶ or N-donor⁷ functionalized cyclopentadienyl ligands were prepared. However, only the N-pyrrolidine derivative [{(C₄H₈N)(CH₂)₂C₅Me₄}FeCl] was obtained as a thermally stable, crystalline compound, and not many details were provided with respect to its physical properties.⁷ Similarly, attempts to isolate [Cp*Fe(acac)]) were unsuccessful.⁸ More recently several neutral 16VE two-legged iron piano stools [Cp*FeX(NHC)] (NHC = N-heterocyclic carbene, X = Cl, Ph) with intermediate spin configuration (S = 1) were reported and used for small molecule activation.⁹ In the course of our investigations we have shown that the iron half-sandwich [Cp′FeI]₂ (1, Cp′ = η⁵-1,2,4-(Me₃C)₃C₅H₂) represents a valuable starting material for further functionalization and small molecule activation.¹⁰ In this contribution we report on the synthesis and molecular and electronic structure of several N-heterocyclic carbene adducts to complex 1.

Results and discussion

Synthesis

The iron half-sandwich complex [Cp′FeI]₂ (Cp′ = η⁵-1,2,4-(Me₃C)₃C₅H₂, 1) dissociates in coordinating solvents such as diethyl ether, tetrahydrofuran or acetone into neutral 16VE fragments of the type [Cp′FeI(L)], but when the solvent is removed the dimeric structure is reestablished.^10b No spin state change is induced on coordination of these solvents; but because of the lability of these mono-solvent adducts, a stronger ligand is required for further characterization of such adducts. Recently, we have shown that, on addition of N,N′-dimethylaminopyridine (DMAP) to [Cp′FeN(SiMe₃)₂], the 16VE adduct [Cp′FeN(SiMe₃)₂(dmap)] is formed; it can be isolated in crystalline form and also exhibits a high-spin (S = 2) configuration in the solid state.^10d However, in solution a rapid equilibrium between [Cp′FeN(SiMe₃)₂(dmap)], [Cp′FeN(SiMe₃)₂] and free DMAP is observed. In contrast addition of DMAP to 1 induces ligand redistribution to [Cp′₂Fe] and insoluble [FeI₂(dmap)₂]. We reasoned that N-heterocyclic carbenes might represent good alternative ligands, since they are excellent σ-donors and are readily tunable in their electronic and steric properties.¹¹ Furthermore, several iron complexes bearing NHCs or NHC-derived ligand systems have been prepared and successfully employed in catalysis.¹² The addition of N-heterocyclic carbenes to dimer 1 does indeed form corresponding 16VE adducts 2–5 as crystalline products, isolable directly from the reaction mixture in moderate to excellent yields (Scheme 1).

Scheme 1 Preparation of NHC-adducts to [Cp′FeI]₂.

The paramagnetic adducts 2–5 were characterized by various spectroscopic techniques and elemental analyses. We were also keen to explore the stability of the NHC-adducts with respect to ligand exchange on the NMR and chemical time scales. To this end, free ItBu was added to C₆D₆ solutions of 2 and 5 and the ¹H NMR spectra were recorded. However, the NMR resonances of 2 and 5 remained unperturbed and sharp resonances attributed to free ItBu were detected in the diamagnetic region. These solutions were then allowed to stand at ambient temperatures for 8 days and the ¹H NMR spectra were recorded again, but unchanged spectra indicated that there is also no exchange on the chemical time scale. These observations imply that the NHC ligands bind strongly to the Fe(II) atom, which also raises questions regarding the spin state in these complexes. To address this aspect, the solid state molecular structures might provide some initial insights.

Molecular structure

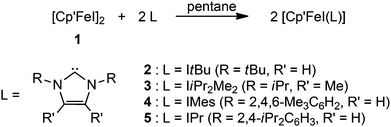
Crystals suitable for crystal X-ray diffraction were grown at ambient temperature (Table 1). The molecular structures of complexes 2–5 are shown in Fig. 1 and important bond distances are listed in Table 2.

Fig. 1 ORTEP diagrams of adducts 2–5 (thermal ellipsoids drawn at the 30% probability level).

Table 1 Crystallographic data

Compound reference	2	3	4	5
Chemical formula	C28H49FeIN2	C28H49FeIN2	C38H53FeIN2	C44H65FeIN2
Formula mass	596.44	596.44	720.57	804.73
Crystal system	Monoclinic	Monoclinic	Monoclinic	Orthorhombic
a/Å	26.809(5)	9.35317(12)	9.7691(4)	18.4790(4)
b/Å	15.1557(16)	18.27596(18)	38.5982(14)	16.7584(2)
c/Å	16.959(3)	17.01417(16)	9.6194(4)	26.7961(4)
α/°	90.00	90.00	90.00	90.00
β/°	120.93(2)	95.7372(8)	99.676(4)	90.00
γ/°	90.00	90.00	90.00	90.00
Unit cell volume/Å^3	5910.8(15)	2893.80(5)	3575.6(2)	8298.2(2)
Temperature/K	100(2)	100(2)	100(2)	100(2)
Space group	C2/c	P21/n	P21/c	Pbca
No. of formula units per unit cell, Z	8	4	4	8
Radiation type	Cu Kα	Mo Kα	Mo Kα	Cu Kα
Absorption coefficient, μ/mm^−1	12.397	1.605	1.312	8.970
No. of reflections measured	39 142	149 287	139 395	101 789
No. of independent reflections	5623	8415	8201	8484
R int	0.1274	0.0370	0.0748	0.0607
Final R1 values (I > 2σ(I))	0.0544	0.0199	0.0582	0.0267
Final wR(F^2) values (I > 2σ(I))	0.1212	0.0414	0.0957	0.0622
Final R1 values (all data)	0.0736	0.0251	0.0684	0.0327
Final wR(F^2) values (all data)	0.1304	0.0431	0.0982	0.0650
Goodness of fit on F^2	1.033	1.055	1.328	1.032
Δρ/e Å^−3	2.986/−1.643	0.444/−0.328	1.299/−1.358	0.436/−0.440

---

Table 2 Selected bond distances (Å) and angles (°)

	2	3	4	5
Fe–C1	2.307(5)	2.4095(11)	2.334(4)	2.3422(18)
Fe–C2	2.327(5)	2.3424(12)	2.368(4)	2.3769(19)
Fe–C3	2.374(5)	2.2792(12)	2.357(4)	2.3710(18)
Fe–C4	2.436(5)	2.3114(12)	2.379(4)	2.3410(18)
Fe–C5	2.345(5)	2.3660(12)	2.329(4)	2.2828(18)
Fe–C(Cp′) (ave)	2.3578 ± 0.0501	2.3417 ± 0.0500	2.3534 ± 0.0215	2.343 ± 0.0372
Fe–Cp′cent	2.02	2.00	2.02	2.00
Fe–Cp′plane	2.02	2.00	2.02	2.00
Fe–I	2.7658(9)	2.71039(19)	2.7128(6)	2.6883(3)
Fe–C18	2.151(5)	2.1244(12)	2.162(4)	2.1718(19)
Cp′cent–Fe–I	137.76	124.26	119.59	118.81
Cp′cent–Fe–C18	132.95	132.48	141.13	149.48
C18–Fe–I	91.26(14)	103.23(3)	99.07(9)	91.62(5)

---

The molecular structures of several Fe half-sandwich complexes have been reported,^10,13 and one important feature of these investigations is the correlation between the Cp_cent–Fe distance and the spin state of these molecules. This distance is ca. 1.7 Å in low-spin Fe(II) complexes, such as Cp′₂Fe (1.71 Å),^10b and increases to ca. 1.9–2.1 Å for Fe(II) compounds with a high-spin configuration, e.g. [Cp′FeI]₂ (1.93 Å).^10b With increasing spin state, metal–ligand antibonding orbitals are occupied, thus weakening the Fe–C bonds and therefore also increasing the variations in the Cp_cent–Fe distances. The coordination spheres around the Fe atom in the NHC-adducts 2–5 may be described as distorted trigonal planar, and the Cp_cent–Fe distances range between 2.00–2.02 Å, consistent with a d⁶ high-spin configuration of the Fe(II) atom. It is noteworthy that for the related Cp* complexes such as [Cp*FeCl(IiPr₂Me₂)] and [Cp*FeCl(IMes)], the Cp_cent–Fe distances are 1.78 and 1.93 Å, respectively.^9a Despite this large spread of values, the authors assumed that the Fe(II) atoms in both systems adopt an intermediate spin configuration.^9a Considering our observations on adducts 2–5 and assuming that the intermediate spin assignment is indeed correct, the Cp* ligand induces a stronger ligand field than the Cp′ ligand and therefore stabilizes the S = 1 spin configuration, which is not accessible for the Cp′-derived complexes 2–5. The increased electron-donating ability of Cp* compared to Cp′ was also indicated by electrochemical studies on various iron complexes with Cp* and Cp′ ligand systems.¹⁴ Another factor contributing to this apparent spin state change may be the significantly increased steric demand of the Cp′ relative to the Cp* ligand,¹⁵ which also destabilizes the intermediate spin state. The steric influence of alkyl substitution is also nicely demonstrated in the electronic properties of the corresponding manganocene systems; [Cp*₂Mn] (S = 1/2) is a low-spin molecule,¹⁶ while [Cp′₂Mn] (S = 5/2) adopts the high-spin state.¹⁷ The Fe–C(NHC) bond distances in complexes 2–5 are significantly longer than those found in the related [Cp*FeX(NHC)] (X = monoanionic ligand) derivatives,^9a but are in the range of those observed for three-coordinate, high-spin Fe–NHC complexes (2.096(2) to 2.184(2) Å), that are not Cp-stabilized such as [(NHC)Fe{N(SiMe₃)₂}₂] (NHC = IMes, IPr),¹⁸ [(IPr)Fe{N(SiMe₃)₂}{SePh}],¹⁹ [(IiPr₂Me₂)FeMes₂],²⁰ [(IPr)Fe{NHAr}₂] (Ar = C₆H₃-2,6-Cl₂, C₆H₃-2,6-iPr₂),²¹ [(NHC)Fe(CH₂SiMe₃)₂] and [(NHC)Fe(CH₂SiMe₃)(Cl)] (NHC = IPr and SIPr),²² [(NHC)Fe(CH₂SiMe₃)(Cl)] (NHC = IPr, IMes, SIPr, SiMes)²³ and [(IiPr₂Me₂)Fe(σ-CPh=CPh₂)₂].²⁴

Solid state magnetic susceptibility studies

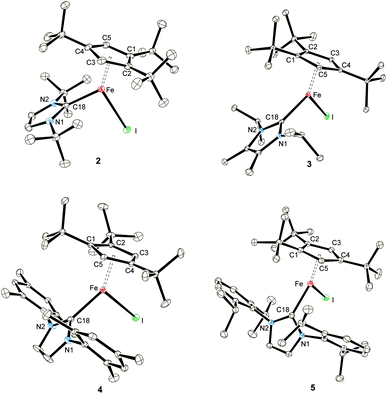
To provide further support for our assumption of d⁶ high-spin systems, solid state magnetic susceptibility data were recorded between 2 and 300 K (Fig. 2). Adducts 2–5 exhibit a magnetic moment of 5.2–5.4μ_B at 300 K, which is indeed consistent with our initial spin state assignment. The inverse molar magnetic susceptibilities (1/χ) for compounds 2–5 obey the Curie–Weiss law with Curie constants of 3.46(1), 3.67(2), 3.51(1) and 3.78(2) emu K mol⁻¹, respectively and very small Weiss temperatures of ca. +1 to −3 K indicating the absence of long-range magnetic ordering (see ESI‡ for details). Fig. 2 also shows the solid state magnetism of 1, whose magnetic moment 1 varies between μ_eff = 2.18μ_B (2 K) and 7.95μ_B (300 K). The value of 7.95μ_B corresponds to 5.62μ_B per Fe(II) centre, which is close to that of 5.3(2)μ_B (per Fe at 295 K) previously reported for the solution moment of 1 (recorded in C₆D₆).^10b Furthermore, the temperature dependence of μ_eff for complex 1 is indicative of antiferromagnetic coupling between two high-spin Fe(II) S = 2 centers at low temperature. Unfortunately, any attempt to fit the magnetic trace to a simple spin Hamiltonian has failed so far. Possible explanations may include potential impurities or a spin state change in the sample. To evaluate these possibilities we also recorded solid state Mössbauer spectra on 1 and the NHC-adducts 2–4 at variable temperatures. These results are described in detail in the next section and confirm the purity of the compounds.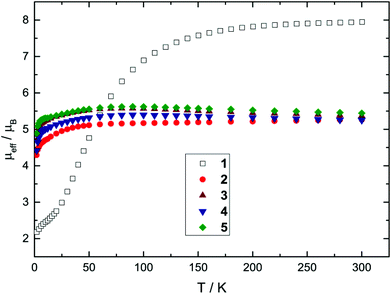

Fig. 2 Effective magnetic moment μ_effvs. T plots for 1 and NHC-adducts 2–5 (recorded in an applied magnetic field of 0.1 T).

⁵⁷Fe-Mössbauer spectroscopy studies

For iron complexes, Mössbauer spectroscopy provides an alternative physical method to probe the local electronic environment at the ⁵⁷Fe nucleus.^27,31 Extensive systematic studies on a series of iron compounds have resulted in approximate ranges of iron isomer shifts and quadrupole splittings depending on the formal Fe oxidation and spin state.²⁷ Despite the fact that ferrocene [(η⁵-C₅H₅)₂Fe] belonged to the first organometallic complexes to be investigated,³² the available database on other Cp-containing iron compounds other than ferrocene and ferrocenium derivatives is still underdeveloped. Furthermore, because of strong covalence in the metal–organic bonds and strong metal–ligand mixing in the molecular orbitals, an unambiguous assignment of the oxidation and spin state solely based on Mössbauer spectroscopy data is a difficult task; however, for complexes with the same spin state a reasonable correlation between the isomer shift and the formal iron oxidation state may be established.³¹ In the context of our current investigation we sought to expand the database of Cp-containing Fe-complexes with different formal oxidation states and spin configurations. Table 3 lists a few representative examples of Cp-derived organo-iron compounds. Zero-field Mössbauer spectroscopy measurements were carried out on polycrystalline samples of complexes 1–5 at temperatures between ca. 20 to 250 K. The isomer shift (δ) and quadrupole splitting (ΔE_Q) values found for the materials 1–5 lie in the typical range, that is generally observed for Fe(II) high-spin complexes,^27,31 which also corroborates the magnetic susceptibility studies (vide supra). Nevertheless, the isomer shifts of compounds 1–5 show only small changes depending on the different coordination sphere (Tables 3 and 4), whereby the marginal increase of δ with decreasing temperature can be predominantly attributed to the second order Doppler shift.^27,31 Furthermore, the quadrupole splitting also exhibits a marginal temperature dependence, and the ΔE_Q values for compounds 1, 3, 4 and 5 are in the range of 1.4–2.0 mm s⁻¹, while the ΔE_Q values of complex 2 are significantly larger at 3.0–3.1 mm s⁻¹ (Tables 3 and 4). The quadrupole splitting in general is influenced by the distribution of the valence electrons about the nucleus and the number, symmetry and type of the ligands surrounding the iron atom.^27,31,33 Thus, the difference in the ΔE_Q values within the series of NHC-adducts 2–5 may be correlated to their molecular structures. While the Fe–Cp′_cent distances within this series remain relatively invariant (2.00–2.02 Å), the Fe–I (2.6883(3) to 2.7658(9) Å) and the Fe–C18 (2.1244(12) to 2.1718(19) Å) distances vary appreciably as a function of the steric demand of the NHC ligand (Table 2). An associated effect is that the steric bulk of the NHC ligand also influences the Cp′_cent–Fe–I, Cp′_cent–Fe–C18 and C18–Fe–I bond angles. While it is difficult to obtain an unambiguous correlation between the structural data and ΔE_Q values, the quadrupole splitting appears to be sensitive to the Fe–I bond distance; the longer this distance, the larger the ΔE_Q values (see ESI‡ for details). Therefore complex 2 with the longest Fe–I bond distance (2.7658(9) Å) exhibits the largest ΔE_Q value (3.11 mm s⁻¹). Alternatively, recent studies have also established that secondary metal–ligand interactions may also influence the quadrupole splitting in low-coordinate iron complexes.³⁴ A closer examination of the coordination environment of the Fe atom in 2 reveals Fe⋯C distances of ca. 3.04 Å between the Fe atom and one methyl group of NHC-tBu substituents, which is certainly shorter than any other Fe⋯C contacts in compounds 3–5. Although these Fe⋯C distances in 2 are still significantly longer than Fe⋯C interactions of ca. 2.5 Å previously considered to be relevant,^34b we cannot exclude that secondary interactions may also contribute to the unusual ΔE_Q value in 2.

Table 3 Selected Mössbauer data for cyclopentadienyl-derived iron complexes^a

Oxidation state	Compound	Spin state	δ (mm s^−1)	ΔEQ (mm s^−1)
a Recorded in solid state on powdered samples at T = 100 K unless otherwise stated. Isomer shifts are specified relative to metallic iron at room temperature. b See ref. 14b (recorded at 77 K). c See ref. 25 (recorded at 4.2 K). d See ref. 25 (recorded at 77 K). e See ref. 26. f See ref. 27. g See ref. 28 (recorded at 80 K). h This work. i See ref. 29 (recorded at 4.2 K). j See ref. 30.
+I	[Cp′Fe(μ-C10H8)FeCp*]^b	S = 0	0.63	1.74
	[(η^5-C5H5)Fe][(η^6-C6Me6)]^c	S = 1/2	0.90	1.54
+II	[(η^5-C5H5)Fe][(η^6-C6Me6)]^+^d	S = 0	0.45	2.00
	[(η^5-C5H5)2Fe]^e	S = 0	0.53	2.45
	[(η^5-C5H5)Fe(CO)2I]^f	S = 0	0.23	1.83
	[Cp*Fe(dppp)][OTf]^g	S = 1	0.55	1.75
	[Cp′FeI]2 (1)^h	S = 2	1.03	1.91
	[Cp′FeI(ItBu)] (2)^h	S = 2	0.95	3.11
	[Cp′FeI(IiPr2Me2)] (3)^h	S = 2	0.86	1.53
	[Cp′FeI(IMes)] (4)^h	S = 2	0.98	1.75
	[Cp′FeI(IPr)] (5)^h	S = 2	0.99	1.59
+III	[(η^5-C5Me5)Fe(dppe)H][PF6]^i	S = 1/2	0.26	0.84
	[(η^5-C5H5)2Fe][BF4]^j	S = 1/2	0.61	—
	[Cp*Fe(dppe)(CO)H][PF6]^i	S = 1/2	0.30	0.72

---

Table 4 Temperature-dependent Mössbauer data for compounds 1–5^a

T (K)	δ (mm s^−1)	ΔEQ (mm s^−1)	H hf (T)	Γ HWHM (mm s^−1)	τ c ^−1 (10^9 s^−1)
a Recorded in solid state on powdered samples at various temperatures. Isomer shifts are specified relative to metallic iron at room temperature and were not corrected in terms of the second order Doppler shift. All spectra were analysed by a least-squares fitting routine based on the longitudinal relaxation model developed by Blume and Tjon.^35 b The parameter was held constant for the fit at the value given. c Measured on an independently prepared sample. d The T = 300 K spectrum of complex 1 was analysed with a least-squares fit to a Lorentzian doublet, since the fit with the Blume–Tjon relaxation model was only possible with a constant numerical value for the relaxation rate of τc^−1 > 50 × 10^9 s^−1 (i.e., the relaxation rate approaches the fast relaxation limit). e The two sub-spectra consist of volume fractions of 35 : 65 and 63 : 37 at T = 20 and 30 K, respectively.
Complex 1
4	1.116(22)	2.034(44)	53^b	0.190(7)	0.32(13)
10^c	1.087(22)	1.962(44)	53^b	0.195(8)	0.37(19)
30	1.116(18)	2.036(34)	53^b	0.190(6)	0.35(13)
40	1.097(13)	2.006(26)	53^b	0.191(6)	0.44(15)
50^c	1.062(10)	1.933(20)	53^b	0.175(5)	0.60(21)
75	1.066(4)	1.973(7)	53^b	0.158(3)	1.38(41)
100^c	1.027(4)	1.907(8)	53^b	0.148(6)	3.44(30)
125	1.042(2)	1.970(3)	53^b	0.151(3)	7.49(50)
150^c	1.006(3)	1.906(6)	53^b	0.137(5)	14(3)
175	1.011(2)	1.954(3)	53^b	0.139(3)	24(6)
200	0.994(2)	1.945(4)	53^b	0.141(4)	47(29)
300^d	0.923(3)	1.904(6)	(53^b)	0.131(6)	(>50)
Complex 2
20	0.966(4)	3.114(7)	53^b	0.189(6)	5.36(62)
100	0.946(4)	3.108(7)	53^b	0.176(7)	16(6)
200	0.896(3)	3.041(7)	53^b	0.145(7)	16(6)
Complex 3
20	0.878(4)	1.332(7)	50.2(1)	0.097(26)	0.0023(3)
30	0.813(45)	1.436(88)	50.2^b	0.185(23)	0.028(1)
40	0.921(11)	1.640(22)	50.2^b	0.150(14)	0.14(1)
40^c	0.916(65)	1.610(130)	50.2^b	0.156(10)	0.17(1)
60^c	0.916(7)	1.615(12)	50.2^b	0.159(6)	1.13(6)
80	0.886(3)	1.559(5)	50.2^b	0.142(4)	3.16(18)
100	0.856(3)	1.532(6)	50.2^b	0.154(5)	5.20(51)
120	0.867(2)	1.528(4)	50.2^b	0.141(3)	5.96(46)
150	0.865(2)	1.557(4)	50.2^b	0.141(3)	6.78(59)
200	0.830(4)	1.543(7)	50.2^b	0.132(7)	10(3)
250	0.806(3)	1.554(5)	50.2^b	0.140(6)	18(6)
Complex 4
20^e	0.960(48)	1.692(88)	56.1(4)	0.250(22)	0.006(3)
	0.861(20)	1.540(40)	56.1^b	0.328(50)	0.051(7)
30^e	0.982(94)	1.634(174)	56.1^b	0.280(13)	0.020(4)
	1.031(44)	1.900(44)	56.1^b	0.159(49)	0.080(3)
40	1.341(200)	2.480(410)	56.1^b	0.197(22)	0.085(6)
60	1.016(50)	1.890(98)	56.1^b	0.212(17)	0.35(3)
100	0.970(8)	1.790(15)	56.1^b	0.195(8)	1.68(11)
100^c	0.977(1)	1.705(12)	56.1^b	0.170(6)	1.57(8)
200	0.919(7)	1.673(14)	56.1^b	0.159(12)	10(3)
200^c	0.912(4)	1.660(8)	56.1^b	0.149(7)	7(1)
300^c	0.856(8)	1.616(15)	56.1^b	0.192(15)	14(8)
Complex 5
15^c	1.001(120)	1.600(240)	53^b	0.178(19)	0.17(2)
20^c	1.021(88)	1.628(176)	53^b	0.183(16)	0.18(2)
40	1.024(71)	1.648(144)	53^b	0.138(9)	0.16(1)
60^c	0.984(77)	1.568(152)	53^b	0.194(19)	0.25(3)
80	0.971(17)	1.582(34)	53^b	0.146(7)	0.53(3)
100	0.962(26)	1.568(50)	53^b	0.138(17)	0.97(14)
100^c	1.008(17)	1.604(32)	53^b	0.186(14)	1.03(10)
150	0.911(5)	1.484(9)	53^b	0.138(6)	3.29(30)
200^c	0.916(7)	1.498(14)	53^b	0.155(12)	6(2)
250	0.900(3)	1.471(6)	53^b	0.139(7)	13(4)

---

Nevertheless, all Mössbauer spectra obtained for compounds 1–5 clearly exhibit the characteristic line shape and temperature-dependent asymmetric line broadening (Fig. 3), indicating the presence of paramagnetic relaxation, which is slow or of the same order of magnitude as the ⁵⁷Fe nuclear Larmor precession time in the magnetic hyperfine field. For example for complexes 3 and 4 the relaxation time (τ_c) approaches the experimental time scale τ_M of the Mössbauer spectroscopy (τ_M approx. 10⁻⁷ to 10⁻⁹ s) at a temperature above T = 200 K and reaches the slow relaxation limit at ca. T = 20 K, resulting in a single, magnetically split hyperfine pattern (Fig. 3 and 5). It should be noted that these fully developed six-line Mössbauer spectra are not attributed to a long-range magnetic ordering, which is further substantiated by the observation of Curie–Weiss behaviour for all NHC-adducts 2–5 with small Weiss temperatures in the magnetic susceptibility measurements between T = 2 and 300 K (vide supra).

Fig. 3 Zero-field Mössbauer spectra of compound 3 recorded at T between 40 and 250 K (a) and T between 20 and 40 K (b).

This allows us to evaluate directly the magnitude of the magnetic hyperfine field at the ⁵⁷Fe nucleus site (H_hf), which is of the order of H_hf = 50.2(1) and 56.1(4) T at T = 20 K for complex 3 and 4, respectively. The main contributions to the internal magnetic field in zero-field Mössbauer spectroscopy experiments are the Fermi contact (H_F), the orbital (H_L) and dipolar (H_D) term.^33,36 In highly ionic compounds, the Fermi contact term is predominantly determined by the spin state S, and H_F can be estimated to be ca. 51 T,³⁷ which is in good agreement with the experimentally determined magnetic hyperfine field for compounds 3 and 4. However, since covalence plays a significant role in complexes 1–5, tending to (significantly) reduce the H_F value,^37a,38 the measured hyperfine field is likely not determined solely by the Fermi contact term; orbital and dipolar terms may also contribute, and applied-field Mössbauer spectroscopy would be useful to quantify these contributions.

The presence of slow paramagnetic relaxation is unusual for Fe(II) high-spin complexes such as the series of compounds presented in this study. For symmetric Fe(II) high-spin complexes, a non-zero orbital momentum combined with spin–orbit coupling (SOC) commonly results in strong orbital-phonon coupling and, therefore, in short correlation times τ_c relative to the ⁵⁷Fe nuclear Larmor precession time. Hence, we attribute the observation of slow paramagnetic relaxation for the complexes 1–5 to a more complete quenching of the orbital momentum and the presence of SOC in combination with a (large) negative axial zero-field splitting parameter D. This can be rationalized with a simple crystal field model. Because of the low molecular symmetry (C₁) the five-fold degeneracy of the Fe d-orbitals (3d⁶, ⁵D) is completely removed and the orbital momentum is thoroughly quenched (Fig. 4).

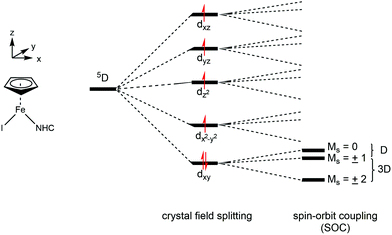Fig. 4 Schematic illustration of the crystal field splitting and spin–orbit coupling for the ⁵D (3d⁶) term.

Nevertheless, spin–orbit coupling mixes the wave functions of the orbital ground state and of close-lying excited orbital states and therefore partially restores the orbital momentum and splits the ground state d-orbital singlet into M_s = 0, ±1 and ±2 sublevels, separated by D and 3D, respectively. Large negative D values (combined with a small or vanishing rhombic zero-field splitting parameter E/D) then result in a virtually isolated M_s = ±2 ground state, which is well separated from the M_s = ±1 and 0 state by 3D and 4D, respectively, and gives rise to a highly anisotropic magnetic ground state. This supposition is the starting point for the discussion of the Mössbauer results presented below; and it is worth mentioning that – in general – every M_s sublevel, when thermally populated, will contribute to the experimentally observed Mössbauer spectrum with a different magnetic hyperfine field and quadrupole splitting. The observation of a fully developed magnetically split hyperfine pattern at low temperatures for compounds 3 and 4 (vide supra) is consistent with a large negative D and a virtually isolated M_s = ±2 ground state as proposed above.

Paramagnetic relaxation processes observed in zero-field Mössbauer spectroscopy can be analysed by the stochastic longitudinal relaxation model developed by Blume and Tjon, which assumes a constant orientation of the electric field gradient relative to the direction of the magnetic hyperfine field.³⁵ The magnetic hyperfine field then adopts two values, +H_hf and −H_hf, which corresponds to the virtually isolated M_s = ±2 ground state doublet derived by the proposed simple crystal field approach (vide supra). Although the Blume–Tjon model³⁵ does not consider isotropic paramagnetic relaxation, we found a perfect agreement between theory and experimental data. As an example, we show the spectra of complex 3 for selected temperatures in Fig. 3, and for further comparison, we also plot the low-temperature spectra of complexes 1–5 in Fig. 5.

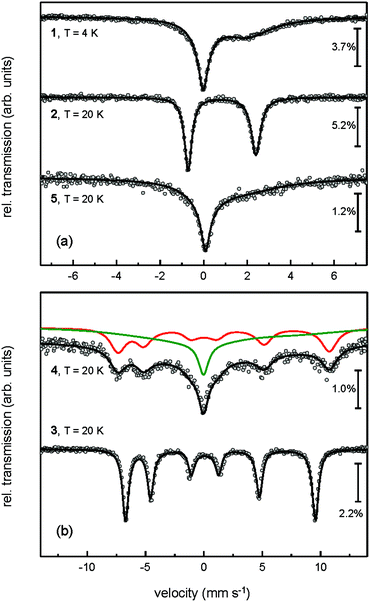Fig. 5 Zero-field Mössbauer spectra of complex 1 measured at T = 4 K and NHC-adducts 2–5 recorded at T = 20 K.

The numerical results of this analysis are summarised in Table 4. The strong correlation of the relaxation rate (τ_c⁻¹) and the magnitude of the local magnetic hyperfine field also prevents both parameters from being simultaneously fitted when the relaxation rate is too fast. For complexes 3 and 4 the magnetic hyperfine field determined by the measurement at T = 20 K was held constant for the fit at elevated temperatures. Furthermore for complexes 1, 2 and 5 we applied, as an approximation, the mean hyperfine field derived from compounds 3 and 4 of approx. 53 T; this was also fixed for the fit. With the exception of complex 4 at T = 20 and 30 K (vide infra), all measured spectra of compounds 1–5 could consistently be fitted with a single ⁵⁷Fe site (regardless of the temperature). Furthermore we found no indications of any iron-containing impurity phase. The line widths (Γ_HWHM; half-width at half-maximum) at temperatures above the slow relaxation limit (T > 50 K) range between approx. 0.14 and 0.19 mm s⁻¹ and are fairly close to the experimental line width of our spectrometer (ca. 0.13 mm s⁻¹), which further substantiates the overall good sample homogeneity. Nevertheless, for the 20 and 30 K spectra of compound 4 we have to consider an additional sub-spectrum to account for the experimental data, whereas above 30 K the spectra of 4 can be analysed well by a model assuming a single ⁵⁷Fe site. In the framework of the simple crystal field approach and the energy levels derived in combination with SOC (vide supra), the presence of a second sub-spectrum in the slow relaxation limit may be attributed to thermal occupation of the M_s = ±1 sublevel. Alternatively, we may associate the two sub-spectra with different volume fractions or two inequivalent ⁵⁷Fe sites that are characterised by crystal packing. When both fractions exhibit different degrees of spin–lattice coupling within the solid state solution, different relaxation barriers and relaxation rates are expected. Unfortunately we are unable to distinguish between these alternative explanations at the current stage. However, we can exclude the possibility that the second sub-spectrum observed at low temperatures results from sample decomposition, since deliberate exposure of 4 to air for ca. five minutes reveals a prominent Fe(III) high-spin Mössbauer doublet at T = 20 K (see ESI‡ for details).

To further quantify the temperature-dependent behaviour of the relaxation rate for compounds 1–5, we considered different relaxation processes, i.e. temperature-independent spin–spin (or quantum tunnelling) processes and temperature-dependent direct one-phonon Orbach and indirect two-phonon Raman type spin–lattice relaxation mechanisms using eqn (1)³⁹

1/τ_c = 1/τ₀ + ATⁿ + B/(exp(Δ/T) − 1) (1)

The 1/τ₀ term denotes the spin–spin relaxation, while the ATⁿ and B/(exp(Δ/T) − 1) terms describe the Raman and Orbach relaxation processes, respectively. The exponent of the Raman contribution was fixed to n = 7, which is appropriate for a non-Kramers doublet.³⁹ The Orbach relaxation barriers Δ obtained from these analyses are summarised in Table 5, along with the parameters A and B of the simulation of eqn (1); Fig. 6 shows the simulation of the experimental data to the eqn (1).

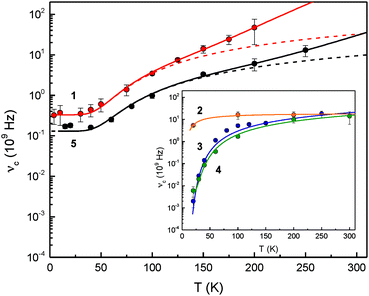Fig. 6 Temperature-dependent relaxation rates ν_c = τ_c⁻¹ for complexes 1–5. The broken lines consider only the spin–spin and Orbach relaxation term of eqn (1) to illustrate the different contributions from Orbach and Raman type spin–lattice relaxation mechanisms. The full line represents the result of a least-squares fitting routine based on eqn (1).

Table 5 Quantitative analysis of the temperature-dependent relaxation rates τ_c⁻¹ determined by zero-field Mössbauer spectroscopy^a

Complex	τ 0 ^−1 (10^9 s^−1)	Δ (K)	A (10^9 s^−1)	B (10^9 s^−1)
a The values were obtained by a least-squares fitting routine based on eqn (1). For compounds 1 and 5, a significant contribution of the Raman relaxation term was found, while for the other adducts this contribution can be neglected. b Since the relaxation rate of adduct 2 is in the vicinity of the fast relaxation limit above T = 20 K, we used an Arrhenius ansatz, i.e. τc^−1 = B exp(−Δ/T), to find a rough estimate for the relaxation barrier Δ based on the data points available. c The parameter was held constant for the fit at the numerical value.
1	0.33(18)	280(40)	2.4(1) × 10^−15	49(16)
2	—	<25^b^,^c	—	19^b^,^c
3	<2 × 10^−3^c	187(6)	—	19^c
4	<4 × 10^−3^c	217(7)	—	16^c
5	0.13(9)	275(44)	9.4(9) × 10^−17	14(5)

---

The Raman type relaxation is clearly relevant for compounds 1 and 5, whereas the temperature-dependent relaxation of compounds 2, 3 and 4 is sufficiently described solely by an Orbach type relaxation mechanism. Moreover, compound 2 shows relatively fast relaxation in the temperature range investigated. Therefore, the spin–spin and spin–lattice relaxation for this compound cannot be reliably quantified. In contrast, for 1 and 5 the relaxation processes associated with spin–spin interactions occur with relaxation rates in the range between approx. 0.13 × 10⁹ and 0.33 × 10⁹ s⁻¹, while for 3 and 4 the spin–spin contribution with an upper limit of 1/τ₀ < 0.002 × 10⁹ and 0.004 × 10⁹ s⁻¹, respectively, is significantly smaller than for the other complexes. The Orbach relaxation barriers for 3 and 4 are of the order of Δ = 200 K (139 cm⁻¹); in contrast adduct 2 shows a significantly smaller relaxation barrier with an upper limit of Δ < 25 K (17 cm⁻¹) and complexes 1 and 5 feature a larger Δ of ca. 280 K (194 cm⁻¹). To the best of our knowledge, the relaxation barriers evaluated in these systems are the largest spin–lattice relaxation barriers so far observed for any Fe(II) high-spin complexes.

Nevertheless, the differences in the relaxation processes observed for compounds 1–5 pose the questions whether these phenomena can be attributed to a structural property of these materials. In all cases the Fe(II) atoms are placed in a low-symmetry environment giving rise to a highly anisotropic magnetic M_s = ±2 ground state (vide supra). With the exception of the some variations for complexes 2–5 in the Fe–C18 and Fe–I bond distances and the Cp′–Fe–I, Cp′–Fe–C18 and I–Fe–C18 angles these molecules are structurally similar, so that the differences in the relaxation behaviour are presumably not only of molecular origin, but may also be associated with a different packing arrangement of these compounds. Within the series 1–5 two classes can clearly be distinguished, that is, those crystallising with four (compounds 3 and 4) or eight Fe(II) atoms (complexes 1,^10b2 and 5) in the unit cell (Table 1). More importantly, complexes with four Fe(II) atoms per unit cell reach (or at least approach) the slow relaxation limit below T = 40 K, whereas those with eight Fe(II) atoms/unit cell do not. The packing diagrams of complexes 1–5 are shown in the ESI‡ along with the arrangement and intermolecular Fe⋯Fe distances in the respective complexes. Qualitatively the following trends emerge: (1) the Fe atoms of complexes 3 and 4 are arranged in planes to form rhombuses or zig-zag chains, respectively. Furthermore the intermolecular Fe⋯Fe distances are similar, lying in the range 10.1 to 11.4 Å. This corresponds to the observation of low spin–spin relaxation rates of 1/τ₀ < 0.002 × 10⁹ and 0.004 × 10⁹ s⁻¹ for these compounds. In contrast, for complexes with significant higher spin–lattice (compounds 1, 2 and 5) and spin–spin (compounds 1 and 5) relaxation rates, the intermolecular Fe⋯Fe distances vary significantly ranging from 7.7 to 13.4 Å, and for dimer 1 the intramolecular Fe⋯Fe distance is even shorter at 3.53 Å. (2) Remarkably, the more symmetric the arrangement of the Fe atoms within the unit cell of the NHC-adducts 2–5, the higher the Orbach relaxation barrier, reaching ca. 280 K (194 cm⁻¹) for complex 5 in which the Fe atoms form a square prism. Although this is currently a rather crude phenomenological description, further work is in progress to unravel the correlation between slow paramagnetic relaxation and molecular structure and lattice contributions. This may also include applied-field Mössbauer spectroscopy, high-field EPR spectroscopy and AC magnetic susceptibility experiments.

Computational studies

Density functional theory (DFT) studies can be useful to understand the electronic structure in organometallic compounds. Given the discrepancy between the electronic structure of the [Cp*FeCl(NHC)] adducts^9a and our [Cp′FeI(NHC)] adducts 3 and 4 it was of interest to compare the relative stability of these complexes in different spin configurations (S = 0, 1 and 2) and also to evaluate their influence on the molecular structures of these molecules. For this purpose, we computed the adducts [Cp*FeCl(IiPr₂Me₂)], [Cp*FeCl(IMes)], 3 and 4 using two different DFT functionals, B3LYP and the dispersion-corrected B97D. We have previously used both functionals in our investigations of iron^10a,c,e and manganese⁴⁰ half-sandwich complexes. The relative free energies (ΔG⁰) of these compounds as a function of spin states are shown in Table 6.

Table 6 Relative free energies (ΔG⁰ in kcal mol⁻¹) computed for NHC-adducts in different spin configurations^a

	[Cp*FeCl (IiPr2Me2)]	[Cp*FeCl(IMes)]	3	4
a Computed at the B3LYP level of theory with the basis sets 6-311G(d,p) for Fe, C, H, N, Cl and SDD for I. Values given in parenthesis refer to the values obtained for B97D using the same basis sets.
S = 0	18.1 [4.3]	20.3 [4.8]	21.1 [5.9]	25.5 [9.9]
S = 1	2.5 [0.0]	3.6 [0.0]	3.0 [0.0]	6.0 [0.0]
S = 2	0.0 [5.2]	0.0 [3.6]	0.0 [3.1]	0.0 [2.5]

---

Computational methods in general are associated with uncertainties regarding the absolute values of the relative stabilities of the respective spin states; these are of the order of a few kcal mol⁻¹.⁴¹ This aspect becomes especially significant when the energy difference between spin states is small, as in this case between S = 2 and S = 1 (Table 6). Table 6 also shows that B97D overestimates dispersion and non-covalent interactions and therefore it predicts an intermediate spin configuration for [Cp*FeCl(IiPr₂Me₂)], [Cp*FeCl(IMes)], 3 and 4, which is clearly inconsistent with the experimental data provided above. In contrast, B3LYP, which neglects dispersion effects, is known to (artificially) overstabilize the high-spin state.^41,42

So while the electronic ground state might not be accurately determined computationally, DFT methods are known to predict reliably molecular structures of different spin states.⁴³ Therefore a comparison of the computed and experimental structures might be more conclusive (Table 7). A closer inspection reveals that only for [Cp*FeCl(IiPr₂Me₂)] does the computed Fe–Cp_cent distance agree with the experimental data in the intermediate spin configuration (S = 1), whereas for all other compounds this experimental Fe–Cp_cent distance is much closer to those computed for the high-spin state.

Table 7 Comparison between computed and experimental bond distances (Å)^a

	S = 0	S = 1	S = 2	X-ray data
a Computed at the B3LYP level of theory with a 6-311G(d,p) basis set for Fe, C, H, N, Cl and a SDD basis set for I. Values given in parenthesis refer to the values obtained for B97D using the same basis sets. b Crystal structure data taken from ref. 9a.
[Cp*FeCl (IiPr2Me2)]^b
Fe–Cpcent	1.66 [1.60]	1.81 [1.75]	2.00 [1.98]	1.78
Fe–Cl	2.260 [2.256]	2.283 [2.275]	2.300 [2.277]	2.2434(8)
Fe–C18	1.978 [1.917]	1.966 [1.890]	2.140 [2.065]	1.950(2)
[Cp*FeCl(IMes)]^b
Fe–Cpcent	1.67 [1.62]	1.82 [1.78]	1.99 [2.00]	1.93
Fe–Cl	2.262 [2.258]	2.285 [2.276]	2.324 [2.310]	2.2715(7)
Fe–C18	2.006 [1.925]	1.988 [1.911]	2.187 [2.045]	2.085(3)
Complex 3
Fe–Cpcent	1.70 [1.63]	1.85 [1.78]	2.01 [1.96]	2.00
Fe–I	2.662 [2.628]	2.693 [2.665]	2.765 [2.729]	2.71039(19)
Fe–C18	2.025 [1.954]	2.000 [1.927]	2.158 [2.074]	2.1244(12)
Complex 4
Fe–Cpcent	1.71 [1.64]	1.87 [1.80]	2.02 [1.99]	2.00
Fe–I	2.693 [2.680]	2.723 [2.712]	2.837 [2.822]	2.6883(3)
Fe–C18	2.060 [1.968]	2.027 [1.951]	2.187 [2.086]	2.1718(19)

---

Overall, our DFT computations suggest that the energy difference between the intermediate (S = 1) and high-spin (S = 2) state is small and varies between 2.5–6.0 kcal mol⁻¹ (with B3LYP), so that these 16VE adducts are also likely to adopt the maximum spin state. In addition, the qualitative crystal field splitting scheme of the d-orbitals (Fig. 4) is also found in our DFT analysis (see ESI‡ for details). While there is no ambiguity about the spin states of NHC-adducts 3 and 5 based on our experimental data, the situation differs for [Cp*FeCl(IiPr₂Me₂)] and [Cp*FeCl(IMes)].^9a For the least sterically encumbered derivative [Cp*FeCl(IiPr₂Me₂)] the computed energy difference between intermediate (S = 1) and high-spin (S = 2) state is the smallest within the series and the computed molecular structure for S = 1 is also very close to the experimental one. All these observations lend some support to the original spin state assignment for [Cp*FeCl(IiPr₂Me₂)],^9a but for [Cp*FeCl(IMes)] the computed high-spin geometry is closer to that of the experimental solid state structure. It appears probable that both spin states need to be considered for these adducts [Cp*FeX(NHC)] (X = monoanionic ligands), which might translate into substantial reactivity differences within this class of molecules.

Conclusion

In this manuscript we describe the synthesis of several NHC-adducts to [Cp′FeI]₂ (1). This leads to the homolytic cleavage of 1, but in contrast to literature reports on the related [Cp*FeCl(NHC)] adducts, the Fe(II) atoms in adducts 2–5 adopt a high-spin configuration, which is rare for 16VE iron half-sandwich complexes. The maximum spin state for these adducts was verified by solid state X-ray diffraction, magnetic susceptibility and zero-field ⁵⁷Fe-Mössbauer spectroscopy studies. Considering the discrepancy between the literature reports on [Cp*FeCl(NHC)]^9a and adducts 2–5 we also compared these systems by DFT computations, which indicated that only for the least sterically demanding complex [Cp*FeCl(IiPr₂Me₂)]^9a is the experimentally determined molecular structure consistent with an Fe(II) intermediate spin configuration, whereas in the other cases the computed high-spin structure is in better agreement with the experimental X-ray diffraction data. Nevertheless, the currently available data suggest that Cp* induces a stronger ligand field than Cp′. Therefore the intermediate spin state should be more readily accessible for the Cp* systems than for their Cp′ analogues. Considering the importance of spin states for the reactivity, this difference in ligand field strength might have important implications for spin-induced reaction barriers associated with these systems. Further investigations to address these questions are currently in progress and will be reported. In the course of our zero-field Mössbauer spectroscopy investigations we also observed intriguing paramagnetic relaxation behaviour for compounds 1–5. The analysis of the temperature-dependent relaxation rate reveals unusual large spin–lattice (Orbach) relaxation barriers for complexes 1 and 5 and indications for significant contributions of indirect two-phonon Raman relaxation processes. In all cases the low molecular symmetry of these complexes combined with spin–orbit coupling give rise to a highly anisotropic magnetic M_s = ±2 ground state, which may be noted as the physical origin of the magnetic dynamics observed. Further studies on these phenomena are currently in progress and will be reported in due course.

Experimental section

General procedures

All operations were performed in a glove box (Mbraun UNIlab, nitrogen atmosphere) or in an atmosphere of dry nitrogen using Schlenk techniques. ¹H NMR measurements were performed on Bruker AV300 and Bruker DRX 400 spectrometer. Elemental analyses (C, H) by combustion and gas chromatography were carried out using an Elementar varioMICRO. EI-MS spectra were recorded on a Thermofinnigan MAT 95 XL. A Bruker Vertex 70 spectrometer and a by Varian Cary 50 Scan were used for the collection of IR and UV/vis spectra, respectively. Solid state magnetic susceptibility studies were performed in quartz tubes as previously described⁴⁴ and the data were collected at a 7 T Quantum Design MPMS magnetometer utilizing a superconducting interference device (SQUID) and corrected for Pascal constants.⁴⁵

Materials

Pentane was dried by a solvent purification system from MBraun and stored over 4A molecular sieves under nitrogen. [Cp′FeI]₂ (1)^10b and the NHC ligands ItBu,⁴⁶ IiPr₂Me₂,⁴⁷ IMes⁴⁸ and IPr⁴⁸ were prepared according to literature procedures.

Synthesic procedures

[Cp′FeI(ItBu)] (2). Slow addition of a pentane (10 mL) solution of ItBu (90 mg, 0.5 mmol) to a pentane (10 mL) solution of 1 (208 mg, 0.25 mmol) resulted immediately in a precipitation of 2 as yellow crystalline material. Yield: 259 mg (0.43 mmol, 86%). ¹H NMR (300 MHz, C₆D₆, 300 K): δ = 34.9 (ν_1/2 = 300 Hz), 6.00 (vbr., ν_1/2 = 2140 Hz), −8.8 (ν_1/2 = 540 Hz), −15.0 (ν_1/2 = 756 Hz). Elemental analysis calcd (%) for C₂₈H₄₉FeIN₂: C 56.38, H 8.28, N 4.70; found: C 56.02, H 8.24, N 4.72. IR (ATR; cm⁻¹): 3110(w), 2954(m), 2903(m), 2863(m), 1479(m), 1460(m), 1398(m), 1367(s), 1354(m), 1230(s), 1200(s), 1146(m), 837(m), 740(s), 680(m), 626(m). UV/vis (THF, 22 °C, nm): 299 (sh, ε = 3330 L mol⁻¹ cm⁻¹), 371 (sh, ε = 830 L mol⁻¹ cm⁻¹). Mp: 197–202 °C (dec.).

[Cp′FeI(IiPr₂Me₂)] (3). Slow addition of a pentane (10 mL) solution of IiPr₂Me₂ (77 mg, 0.43 mmol) to a pentane (10 mL) solution of 1 (150 mg, 0.18 mmol) resulted in a color change from red to yellow-green. The solution was concentrated and the product was obtained as yellow-green crystals. Yield: 100 mg (0.17 mmol, 47%). ¹H NMR (300 MHz, C₆D₆, 300 K): δ = 33.0 (ν_1/2 = 360 Hz), 31.0 (ν_1/2 = 67 Hz), −15.2 (ν_1/2 = 240 Hz), −16.4 (ν_1/2 = 75 Hz), −18.2 (ν_1/2 = 120 Hz). Elemental analysis calcd (%) for C₂₈H₄₉FeIN₂: C 56.38, H 8.28, N 4.70; found: C 56.75, H 8.18, N 4.86. The EI mass spectrum showed a molecular ion at m/z = 596 amu. The parent isotope cluster was simulated: (calcd %, observd %): 594 (6, 7), 592 (2, 2), 596 (100, 100), 597 (35, 34), 598 (6, 5), 599 (1, 1). IR (ATR; cm⁻¹): 2958(m), 2902(m), 2868(m), 1460(m), 1383(m), 1356(s), 1236(m), 1219(m), 1134(m), 1110(m), 830(s), 752(m), 673(m). UV/vis (THF, 22 °C, nm): 325 (sh, ε = 3590 L mol⁻¹ cm⁻¹), 439 (sh, ε = 580 L mol⁻¹ cm⁻¹), 791 (ε = 75 L mol⁻¹ cm⁻¹). Mp: 184–218 °C (dec.).

[Cp′FeI(IMes)] (4). Slow addition of a pentane (7.5 mL) solution of IMes (100 mg, 0.36 mmol) to a pentane (10 mL) solution of 1 (150 mg, 0.18 mmol) resulted in the precipitation of red crystals. Yield: 150 mg (0.21 mmol, 58%). ¹H NMR (300 MHz, C₆D₆, 300 K): δ = 101.2 (ν_1/2 = 1110 Hz), 62.4 (ν_1/2 = 254 Hz), 16.9 (ν_1/2 = 220 Hz), −5.7 (ν_1/2 = 520 Hz), −20.4 (ν_1/2 = 660 Hz), −27.1 (ν_1/2 = 353 Hz), −67.7 (ν_1/2 = 780 Hz). Elemental analysis calcd (%) for C₃₈H₅₃FeIN₂: C 63.34, H 7.41, N 3.89; found: C 63.59, H 7.42, N 4.09. IR (ATR; cm⁻¹): 3167(w), 3134(w), 3101(w), 2949 (s), 2919(m), 2895(m), 2862(m), 1482(s), 1457(m), 1395(m), 1378(m), 1356(s), 1266(s), 1239(s), 926(m), 856(s), 823(s), 724(s), 671(s). UV/vis (THF, 22 °C, nm): 304 (ε = 3730 L mol⁻¹ cm⁻¹), 373 (sh, ε = 880 L mol⁻¹ cm⁻¹), 470 (sh, ε = 270 L mol⁻¹ cm⁻¹), 811 (ε = 30 L mol⁻¹ cm⁻¹). Mp: 168–184 °C (dec.).

[Cp′FeI(IDipp)] (5). A pentane (10 mL) solution of IDipp (117 mg, 0.3 mmol) was slowly added to a pentane (10 mL) solution of 1 (125 mg, 0.15 mmol). The reaction mixture changed color from red to orange-red and after one hour at ambient temperature the product was obtained as red crystals. Yield: 233 mg (0.29 mmol, 97%). Elemental analysis calcd (%) for C₄₄H₆₅FeIN₂: C 65.67, H 8.14, N 3.48; found: C 65.89, H 8.26, N 3.41. ¹H NMR (300 MHz, C₆D₆, 300 K): δ = 84.2 (ν_1/2 = 320 Hz), 42.8 (ν_1/2 = 760 Hz), very broad and strongly overlapping resonances at −4.5, −7.1, −8.1, −11.6, −15.1 (ν_1/2 ∼ 32 Hz), −17.8 (ν_1/2 ∼ 75 Hz), −21.6 (ν_1/2 ∼ 800 Hz), −23.1 (ν_1/2 ∼ 50 Hz), −26.5 (ν_1/2 ∼ 540 Hz), −39.5 (ν_1/2 ∼ 570 Hz). IR (ATR; cm⁻¹): 2961(s), 2925(m), 2865(m), 1538(s), 1457(s), 1383(s), 1356(s), 1240(m), 1201(m), 821(s), 799(s), 742(s), 671(m). UV/vis (n-hexane, 22 °C, nm): 306 (sh, ε = 2290 L mol⁻¹ cm⁻¹), 375 (sh, ε = 650 L mol⁻¹ cm⁻¹), 405 (sh, ε = 480 L mol⁻¹ cm⁻¹), 444 (sh, ε = 270 L mol⁻¹ cm⁻¹). Mp: 140–180 °C (dec.).

⁵⁷Fe-Mössbauer spectroscopy studies

Zero-field Mössbauer spectroscopy measurements were performed on a conventional transmission spectrometer with sinusoidal velocity sweep. Polycrystalline powders of complexes 1–5 were prepared with an area density corresponding to ca. 0.05–0.18 mg ⁵⁷Fe cm⁻² and were filled in sample containers made of Teflon or PEEK. The measurements on compounds 1, 3 and 5 were done with a CryoVac continuous flow cryostat with N₂ or Helium exchange gas. After positioning the sample containers, the sample chamber was evacuated and flushed five times with N₂ or Helium gas, respectively. The N₂ or Helium atmosphere was kept at ca. 10 mbar during the measurement. The temperature was measured with a calibrated Si diode located close to the sample container providing a temperature stability of better than 0.1 K. Furthermore, measurements on compounds 2 and 4 and on independently prepared samples of 3 and 5 were carried out with a Janis closed-cycle cryostat with comparable specifications, geometry and sample environments as described above. The activities of the Mössbauer sources used were about 25 mCi (CryoVac CFC) and 8 mCi (Janis CCR) of ⁵⁷Co in a rhodium matrix, which were stored at ambient temperatures during the measurement; the isomer shifts (δ) were specified relative to metallic iron at room temperature, but were not corrected in terms of second order Doppler shift.

Crystallographic details

Single crystals of each compound were examined in inert oil. Data collection was performed on various Oxford Diffraction diffractometers using monochromated Mo Kα or mirror-focused Cu Kα radiation (Table 1). Absorption corrections were performed on the basis of multiscans. The data were analysed using the SHELXL97 program.⁴⁹ CCDC 1432917–1432920.

Computational details

All calculations employed the B3LYP⁵⁰ and long-range dispersion-corrected Grimme's functional (B97D)⁵¹ and were carried out with Gaussian 09.⁵² No symmetry restrictions were imposed (C1). C, H, N, and Fe were represented by an all-electron 6-311G(d,p) basis set, whereas a SDD basis-set was used for I. The nature of the extrema (minima) was established with analytical frequencies calculations. The zero point vibration energy (ZPE) and entropic contributions were estimated within the harmonic potential approximation. Geometrical parameters were reported within an accuracy of 10⁻³ Å and 10⁻¹ degrees.

Acknowledgements

MDW gratefully acknowledges the financial support by the Deutsche Forschungsgemeinschaft (DFG) through the Emmy-Noether and the Heisenberg program (WA 2513/2 and WA 2513/6, respectively). We thank Prof. Dr Richard A. Andersen (UC Berkeley) for SQUID access, and Prof. Dr M. Bröring (Institut für Anorganische und Analytische Chemie) and Prof. Dr F. J. Litterst (Institut für Physik der Kondensierten Materie) at the TU Braunschweig for access to the ⁵⁷Fe-Mössbauer equipment. Prof. F. J. Litterst is also acknowledged for helpful and insightful discussions.

Notes and references

1. P. Hofmann, Angew. Chem., Int. Ed. Engl., 1977, 16, 536–537.
2. B. K. Campion, R. H. Heyn and T. D. Tilley, J. Chem. Soc., Chem. Commun., 1988, 278–280.
3. (a) T. J. Johnson, K. Folting, W. E. Streib, J. D. Martin, J. C. Huffman, S. A. Jackson, O. Eisenstein and K. G. Caulton, Inorg. Chem., 1995, 34, 488–499; (b) T. R. Ward, O. Schafer, C. Daul and P. Hofmann, Organometallics, 1997, 16, 3207–3215.
4. (a) P. Hamon, L. Toupet, J.-R. Hamon and C. Lapinte, Organometallics, 1996, 15, 10–12; (b) G. Argouarch, P. Hamon, L. Toupet, J.-R. Hamon and C. Lapinte, Organometallics, 2002, 21, 1341–1348.
5. K. Costuas and J.-Y. Saillard, Organometallics, 1999, 18, 2505–2512.
6. U. Siemeling, Chem. Ber., 1995, 128, 1135–1136.
7. K. Jonas, P. Klusmann and R. Goddard, Z. Naturforsch., B: J. Chem. Sci., 1995, 50, 394.
8. (a) E. E. Bunel, L. Valle and J. M. Manriquez, Organometallics, 1985, 4, 1680–1682; (b) R. A. Paciello, J. M. Manriquez and J. E. Bercaw, Organometallics, 1990, 9, 260–265.
9. (a) Y. Ohki, T. Hatanaka and K. Tatsumi, J. Am. Chem. Soc., 2008, 130, 17174–17186; (b) T. Hatanaka, Y. Ohki and K. Tatsumi, Chem. – Asian J., 2010, 5, 1657–1666; (c) T. Hatanaka, Y. Ohki, T. Kamachi, T. Nakayama, K. Yoshizawa, M. Katada and K. Tatsumi, Chem. – Asian J., 2012, 7, 1231–1242.
10. (a) M. D. Walter, J. Grunenberg and P. S. White, Chem. Sci., 2011, 2, 2120–2130; (b) M. D. Walter and P. S. White, New J. Chem., 2011, 35, 1842–1854; (c) M. D. Walter and P. S. White, Inorg. Chem., 2012, 51, 11860–11872; (d) M. D. Walter and P. S. White, Dalton Trans., 2012, 41, 8506–8508; (e) M. Maekawa, C. G. Daniliuc, P. G. Jones, J. Hohenberger, J. Sutter, K. Meyer and M. D. Walter, Eur. J. Inorg. Chem., 2013, 4097–4104.
11. (a) W. A. Herrmann and C. Köcher, Angew. Chem., Int. Ed. Engl., 1997, 36, 2162–2187; (b) F. E. Hahn and M. C. Jahnke, Angew. Chem., Int. Ed., 2008, 47, 3122–3172; (c) N-Heterocyclic Carbenes, ed. S. Díez-González, From Laboratory Curiosities to Efficient Synthetic Tools RSC, Cambridge, 2011; (d) M. N. Hopkinson, C. Richter, M. Schedler and F. Glorius, Nature, 2014, 510, 485–496.
12. K. Riener, S. Haslinger, A. Raba, M. P. Högerl, M. Cokoja, W. A. Herrmann and F. E. Kühn, Chem. Rev., 2014, 114, 5215–5272.
13. (a) G. Y. Vollmer, M. W. Wallasch, D. Saurenz, T. R. Eger, H. Bauer, G. Wolmershäuser, M. H. Prosenc and H. Sitzmann, Organometallics, 2015, 34, 644–652; (b) H. Bauer, D. Weismann, G. Wolmershäuser, Y. Sun and H. Sitzmann, Eur. J. Inorg. Chem., 2014, 2014, 3072–3084; (c) D. Weismann, Y. Sun, Y. Lan, G. Wolmershäuser, A. K. Powell and H. Sitzmann, Chem. – Eur. J., 2011, 17, 4700–4704; (d) M. W. Wallasch, D. Weismann, C. Riehn, S. Ambrus, G. Wolmershäuser, A. Lagutschenkov, G. Niedner-Schatteburg and H. Sitzmann, Organometallics, 2010, 29, 806–813; (e) M. Wallasch, G. Wolmershäuser and H. Sitzmann, Angew. Chem., Int. Ed., 2005, 44, 2597–2599; (f) H. Sitzmann, T. Dezember, W. Kaim, F. Baumann, D. Stalke, J. Kärcher, E. Dormann, H. Winter, C. Wachter and M. Kelemen, Angew. Chem., Int. Ed. Engl., 1997, 35, 2872–2875.
14. (a) M. Maekawa, C. G. Daniliuc, M. Freytag, P. G. Jones and M. D. Walter, Dalton Trans., 2012, 41, 10317–10327; (b) J. Malberg, E. Lupton, E.-M. Schnöckelborg, B. de Bruin, J. Sutter, K. Meyer, F. Hartl and R. Wolf, Organometallics, 2013, 32, 6040–6052.
15. A. Glöckner, H. Bauer, M. Maekawa, T. Bannenberg, C. G. Daniliuc, P. G. Jones, Y. Sun, H. Sitzmann, M. Tamm and M. D. Walter, Dalton Trans., 2012, 41, 6614–6624.
16. J. C. Smart and J. L. Robbins, J. Am. Chem. Soc., 1978, 100, 3936–3937.
17. M. D. Walter, C. D. Sofield, C. H. Booth and R. A. Andersen, Organometallics, 2009, 28, 2005–2019.
18. R. A. Layfield, J. J. W. McDouall, M. Scheer, C. Schwarzmaier and F. Tuna, Chem. Commun., 2011, 47, 10623–10625.
19. T. Pugh and R. A. Layfield, Dalton Trans., 2014, 43, 4251–4254.
20. L. Xiang, J. Xiao and L. Deng, Organometallics, 2011, 30, 2018–2025.
21. X. Wang, Z. Mo, J. Xiao and L. Deng, Inorg. Chem., 2013, 52, 59–65.
22. A. A. Danopoulos, P. Braunstein, M. Wesolek, K. Y. Monakhov, P. Rabu and V. Robert, Organometallics, 2012, 31, 4102–4105.
23. A. A. Danopoulos, P. Braunstein, N. Stylianides and M. Wesolek, Organometallics, 2011, 30, 6514–6517.
24. Y. Liu, L. Wang and L. Deng, Organometallics, 2015, 34, 4401–4407.
25. J. R. Hamon, D. Astruc and P. Michaud, J. Am. Chem. Soc., 1981, 103, 758–766.
26. R. D. Ernst, D. R. Wilson and R. H. Herber, J. Am. Chem. Soc., 1984, 106, 1646–1650.
27. P. Gütlich and J. Ensling, in Inorganic Electronic Structure and Spectroscopy, ed. E. I. Solomon and A. B. P. Lever, Methodology, J. Wiley & Sons, New York, 1999, vol. 1, pp. 161–213.
28. G. Argouarch, P. Hamon, L. Toupet, J.-R. Hamon and C. Lapinte, Organometallics, 2002, 21, 1341–1348.
29. P. Hamon, J.-R. Hamon and C. Lapinte, J. Chem. Soc., Chem. Commun., 1992, 1602–1603.
30. R. H. Herber and T. P. Hanusa, Hyperfine Interact., 1997, 108, 563–575.
31. P. Gütlich, E. Bill and A. X. Trautwein, Mössbauer Spectroscopy and Transition Metal Chemistry, Springer, Heidelberg, 2011.
32. (a) U. Zahn, P. Kienle and H. Eicher, Z. Phys. Chem., 1962, 166, 220–226; (b) G. K. Wertheim and R. H. Herber, J. Chem. Phys., 1963, 38, 2106–2111.
33. Mössbauer spectroscopy, ed. D. P. E. Dickson and F. J. Berry, Cambridge University Press, Cambridge, 1986.
34. (a) P. P. Power, Chem. Rev., 2012, 112, 3482–3507; (b) D. J. Evans, D. L. Hughes and J. Silver, Inorg. Chem., 1997, 36, 747–748.
35. M. Blume and J. A. Tjon, Phys. Rev., 1968, 165, 446–456.
36. (a) W. Marshall and C. E. Johnson, J. Phys. Radium, 1962, 23, 733; (b) C. E. Johnson, in I Hyperfine Interactions in Excited Nuclei, ed. G. Goldring and B. Kalis, Gordon & Breach, London, 1971, p. 803.
37. (a) W. M. Reiff, C. M. Frommen, G. T. Yee and S. P. Sellers, Inorg. Chem., 2000, 39, 2076–2079; (b) N. N. Greenwood and T. C. Gibb, Mössbauer Spectroscopy, Springer, New York, 1971.
38. C. E. Johnson, in Hyperfine Interaction in Excited Nuclei, ed. G. Goldring and R. Kalish, North-Holland, Amsterdam, 1978, vol. 3, p. 803.
39. A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, Oxford, 2012.
40. M. Maekawa, M. Römelt, C. G. Daniliuc, P. G. Jones, P. S. White, F. Neese and M. D. Walter, Chem. Sci., 2012, 3, 2972–2979.
41. (a) J. N. Harvey, Struct. Bonding, 2004, 112, 151–183; (b) M. Swart, J. Chem. Theory Comput., 2008, 4, 2057–2066.
42. I. Cacelli, D. W. Keogh, R. Poli and A. Rizzo, J. Phys. Chem. A, 1997, 101, 9801–9812.
43. S. Ye and F. Neese, Inorg. Chem., 2010, 49, 772–774.
44. M. D. Walter, M. Schultz and R. A. Andersen, New J. Chem., 2006, 30, 238–246.
45. C. J. O'Connor, Prog. Inorg. Chem., 1982, 29, 203–285.
46. A. J. Arduengo, H. Bock, H. Chen, M. Denk, D. A. Dixon, J. C. Green, W. A. Herrmann, N. L. Jones, M. Wagner and R. West, J. Am. Chem. Soc., 1994, 116, 6641–6649.
47. N. Kuhn and T. Kratz, Synthesis, 1993, 561–562.
48. L. Hintermann, Beilstein J. Org. Chem., 2007, 3, 22.
49. (a) G. M. Sheldrick, SHELXL-97, Program for the Refinement of Crystal Structure from Diffraction Data, University of Göttingen, Göttingen, Germany, 1997; (b) G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122.
50. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (b) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
51. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
52. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, E. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallington CT, 2009.

---

Footnotes

† Dedicated to Prof. Manfred Scheer on the occasion of his 60^th birthday.

‡ Electronic supplementary information (ESI) available: Crystallographic data as CIF, crystal packing diagrams, Curie–Weiss plots, UV/Vis and Mössbauer spectra and computational details. CCDC 1432917–1432920. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qi00235d

---