Azacyclo-auxiliary ligand-tuned SMMs of dibenzoylmethane Dy(III) complexes

Abstract

A series of four β-diketone mononuclear dysprosium complexes, namely, Dy(DBM)₃(bpy) (1), Dy(DBM)₃(phen)·Tol (2), Dy(DBM)₃(dpq)·Tol (3), and Dy(DBM)₃(dppz) (4) (bpy = 2,2′-bipyridine, phen = 1,10-phenanthroline, dpq = dipyrazine[2,3-f:2′,3′-h]quinoxaline, dppz = dipyrido[3,2-a:2′,3′-c]phenazine, Tol = toluene) have been isolated by the reactions of dibenzoylmethane (DBM), azacyclo-auxiliary ligands and DyCl₃·6H₂O. X-ray crystallographic analysis reveals that complexes 1–4 are all eight-coordinate mononuclear structures. The azacyclo-auxiliary ligands have a dramatic effect on the structure and magnetic characteristics of complexes 1–4, originating from the different degrees of deviation from the ideal coordination symmetries. Complexes 1 and 2 display a single relaxation mode under 0 Oe and complexes 3 and 4 display two single relaxation modes under 2000 Oe.

---

Introduction

Single-molecule magnets (SMMs) are paramagnetic molecular species exhibiting slow dynamics in their magnetization.¹ They have received considerable attention in the past two decades owing to their quantum tunneling of the magnetization,² which offers the opportunity of potential applications in high-density information memory storage, molecular spintronics and other devices.³ Thus far, a multitude of SMMs with various structures have been reported.⁴ Since the first lanthanide SMM was discovered,⁵ lanthanide ions have become highly promising candidates for the development of SMMs because of their large orbital angular momentum and high spin. Notably, the Dy(III) ion has a large magnetic moment with a Kramers ground state of ⁶H_15/2 and a large Ising-type magnetic anisotropy. It was thus employed to design a number of Dy-based SMMs with mononuclear, multinuclear and chain structures.⁶ It is known that the ligand field (LF) (not including the Dy(III) ion) plays a crucial role in the magnetic anisotropy of the Dy(III) ion by producing an easy axis magnetization to yield higher effective energy barriers for spin reversal and higher blocking temperatures of SMMs.⁷ In addition, the magnetism of Dy-based SMMs is also sensitive to tiny distortions in the coordination geometry resulting from the auxiliary ligands.⁸ Thus the auxiliary ligands play an essential role in designing Dy-based SMMs. It is well-known that β-diketones, good bidentate chelating ligands, are not only able to sensitize the luminescence of lanthanide complexes,⁹ but can also afford SMMs.^7b,10 Previously, the groups of Gao and Tang have reported simple acetylacetonate (acac) dysprosium complexes with capping nitrogen auxiliary ligands, affording the highest effective energy barriers of 187 K for [Dy(acac)₃(dppz)]·CH₃OH.¹¹ Subsequently, some fluorine-containing β-diketone dysprosium SMMs were developed,^8b,10b,12 by way of adjusting the coordination geometry around the Dy(III) ions through the replacement of the auxiliary ligands. Recently, our group designed and synthesized a series of new β-diketone dysprosium SMMs with oxygen-containing auxiliary ligands.^8a It provided an effective path to suppress the quantum tunneling of magnetization (QTM) which universally exists in lanthanide complexes. Although a host of β-diketone dysprosium SMMs have been studied, there is still no complete theory on the understanding of the dynamics of the magnetization in Dy(III) ion-based SMMs. To further study the effect of β-diketones and auxiliary ligands on Dy(III) ion-based SMMs, a series of azacyclo-auxiliary ligands were employed in reactions of dibenzoylmethane (DBM) with DyCl₃·6H₂O. As a result, a series of four β-diketone mononuclear dysprosium complexes 1–4 containing the azacyclo-auxiliary ligands have been isolated. Their crystal structures have been determined and their magnetism has been investigated. The correlation between the magnetism and structure has been studied.

Experimental section

Materials and instruments

Dysprosium oxide (Dy₂O₃, 99.99%) was purchased from Gan Zhou rare earth Chemical Plant (Jiang Xi, China). Other chemicals (98%, A. R.) were purchased from Shanghai D&R Finechem Co. (Shanghai, China). All chemicals except DyCl₃·6H₂O were obtained from commercial sources and used without further purification. DyCl₃·6H₂O was prepared by reaction of Dy₂O₃ and HCl in aqueous solution. Elemental (C, H and N) analyses were performed on a Perkin-Elmer 2400 analyzer. FT-IR spectra were collected on a Perkin-Elmer 100 spectrophotometer by using KBr pellets in the range of 4000–450 cm⁻¹. UV spectra were recorded on a Perkin-Elmer Lambda 35 spectrometer. Powder X-ray diffraction (PXRD) data were recorded on a Rigaku D/Max-3B X-ray diffractometer with CuKα as the radiation source (λ = 0.15406 nm) in the angular range θ = 5–50° at room temperature. The magnetic susceptibilities of complexes 1–4 were measured with a Quantum Design VSM superconducting quantum interference device (SQUID) magnetometer. Magnetic corrections were made by using Pascal's constants.

Synthesis of Dy(DBM)₃(bpy) (1)

A solution of DBM (0.3364 g, 1.5 mmol) and NaOH (0.0600 g, 1.5 mmol) in 10 ml CH₃OH was stirred for half an hour, then DyCl₃·6H₂O (0.1885 g, 0.5 mmol) and 2,2′-bipyridine (0.0781 g, 0.5 mmol) were added to the solution. The mixture was stirred for 24 h at room temperature. Single crystals suitable for X-ray analysis were obtained from toluene/petroleum ether within 5 to 7 days. Yield based on the reactant DBM: 0.4201 g (85.0%). Anal. Calcd for C₅₅H₄₁DyN₂O₆ (988.4): C, 66.83; H, 4.15; N, 2.83. Found: C, 66.80; H, 4.18; N, 2.85. IR (KBr, ν/cm⁻¹): 3433 (m), 1601 (s), 1553 (s), 1514 (s), 1413 (s), 1313 (s), 1218 (s), 1071 (s), 721 (s), 604 (m). UV-Vis (CH₃OH, λ_max/nm): 253, 350.

Synthesis of Dy(DBM)₃(phen)·Tol (2)

A solution of DBM (0.3364 g, 1.5 mmol) and NaOH (0.0600 g, 1.5 mmol) in 10 ml CH₃OH was stirred for half an hour, then DyCl₃·6H₂O (0.1885 g, 0.5 mmol) and 1,10-phenanthroline (0.0991 g, 0.5 mmol) were added to the solution. The mixture was stirred for 24 h at room temperature. Single crystals suitable for X-ray analysis were obtained from toluene/petroleum ether within 5 to 7 days. Yield based on the reactant DBM: 0.4805 g (87.0%). Anal. Calcd for C₆₄H₄₉DyN₂O₆ (1104.56): C, 69.59; H, 4.44; N, 2.54. Found: C, 66.60; H, 4.40; N, 2.58. IR (KBr, ν/cm⁻¹): 3440 (m), 1601 (s), 1553 (s), 1514 (s), 1413 (s), 1314 (s), 1218 (s), 1072 (s), 729 (s), 611 (m). UV-Vis (CH₃OH, λ_max/nm): 260, 350.

Synthesis of Dy(DBM)₃(dpq)·Tol (3)

A solution of DBM (0.3364 g, 1.5 mmol) and NaOH (0.0600 g, 1.5 mmol) in 10 ml CH₃OH was stirred for half an hour, then DyCl₃·6H₂O (0.1885 g, 0.5 mmol) and dipyrazine[2,3-f:2′,3′-h]quinoxaline (0.1160 g, 0.5 mmol) were added to the solution. The mixture was stirred for 24 h at room temperature. Single crystals suitable for X-ray analysis were obtained from toluene/petroleum ether within 5 to 7 days. Yield based on the reactant DBM: 0.9884 g (89.0%). Anal. Calcd for C₁₂₅H₉₀Dy₂N₈O₁₂ (2221.06): C, 67.59; H, 4.05; N, 5.05. Found: C, 67.60; H, 4.08; N, 5.08. IR (KBr, ν/cm⁻¹): 3435 (m), 1602 (s), 1554 (s), 1511 (s), 1415 (s), 1314 (s), 1219 (s), 1071 (s), 728 (s), 609 (m). UV-Vis (CH₃OH, λ_max/nm): 252, 350.

Synthesis of Dy(DBM)₃(dppz) (4)

A solution of DBM (0.3364 g, 1.5 mmol) and NaOH (0.0600 g, 1.5 mmol) in 10 ml CH₃OH was stirred for half an hour, then DyCl₃·6H₂O (0.1885 g, 0.5 mmol) and dipyrido[3,2-a:2′,3′-c]phenazine (0.1412 g, 0.5 mmol) were added to the solution. The mixture was stirred for 24 h at room temperature. Single crystals suitable for X-ray analysis were obtained from toluene/petroleum ether within 5 to 7 days. Yield based on the reactant DBM: 0.4792 g (86.0%). Anal. Calcd for C₆₃H₄₃DyN₄O₆ (1114.52): C, 67.89; H, 3.86; N, 5.03. Found: C, 67.91; H, 3.88; N, 5.05. IR (KBr, ν/cm⁻¹): 3435 (m), 1601 (s), 1553 (s), 1512 (s), 1413 (s), 1314 (s), 1218 (s), 1078 (s), 728 (s), 611 (m). UV-Vis (CH₃OH, λ_max/nm): 264, 350.

X-ray crystallography

Single-crystal X-ray data of complexes 1–4 were collected on an Oxford Xcalibur Gemini Ultra diffractometer with graphite-monochromated Mo Kα (λ = 0.71073 Å) at room temperature. Empirical absorption corrections based on equivalent reflections were applied. The structures of complexes 1–4 were solved by direct methods and refined by full-matrix least-squares methods on F² using the SHELXS-97 crystallographic software package.¹³ All non-hydrogen atoms are anisotropically refined. All crystal data and structure refinement details for complexes 1–4 are summarized in Table 1. Selected bond lengths and angles for complexes 1–4 are given in Tables S1 and S2 in the ESI.† CCDC no. 1062450–1062453 contain the supplementary crystallographic data for complexes 1–4, respectively.

Table 1 Crystal data and structure refinement for complexes 1–4

Complexes	1	2	3	4
a R 1 = ∑||Fo| − |Fc||/|Fo|. b wR2 = [∑w(Fo^2 − Fc^2)^2/∑w(Fo^2)^2]^1/2.
Empirical formula	C55H41DyN2O6	C64H49DyN2O6	C125H90Dy2N8O12	C63H43DyN4O6
Formula weight (g mol^−1)	988.4	1104.56	2221.06	1114.52
Color	Buff	Buff	Buff	Buff
Cryst syst.	Monoclinic	Monoclinic	Monoclinic	Monoclinic
Space group	P21/c	P21/c	P21/c	P21/c
a (Å)	13.3650(5)	30.1199(9)	25.036(5)	12.188(5)
b (Å)	22.5332(7)	19.6717(7)	19.728(5)	22.423(5)
c (Å)	16.1797(6)	19.7248(5)	25.887(4)	41.216(5)
α (°)	90	90	90	90
β (°)	109.799(5)	97.169(3)	120.839(14)	100.394(9)
γ (°)	90	90	90	90
V (Å^3)	4584.6(3)	11 595.8(6)	10 978(4)	11 079(5)
Z	4	8	4	8
ρ (g cm^−3)	1.432	1.160	1.344	1.336
μ (mm^−1)	1.683	1.333	1.415	1.403
F (000)	1996	4088	4496	4504
R 1 , [I > 2σ (I)]	0.0268	0.0574	0.0420	0.0779
wR1^b, [I > 2σ (I)]	0.0575	0.1425	0.1219	0.2090
R 1 , (all data)	0.0377	0.0986	0.0651	0.1121
wR2^b, (all data)	0.0622	0.1607	0.1438	0.2520
GOF on F^2	1.024	1.008	1.113	1.076

---

Results and discussion

Spectral analysis of complexes 1–4

Complexes 1–4 were synthesized as shown in the ESI, Scheme S1.† The IR spectra of complexes 1–4 exhibit typical broad absorptions in the region 3430–3440 cm⁻¹ which implies the presence of bidentate nitrogen donors. In addition, the C=N stretching frequencies of the donors (1615 cm⁻¹) are shifted to lower wavenumbers in complexes 1–4 (1601 cm⁻¹ in 1; 1601 cm⁻¹ in 2; 1602 cm⁻¹ in 3; 1601 cm⁻¹ in 4), which shows the involvement of the auxiliary nitrogen ligands to form complexes with the Dy(III) ions (Fig. S1 in the ESI†). The UV-vis spectra show that there are obviously absorption bands around 341 nm for DBM and 350 nm for complexes 1–4 (Fig. S2 in the ESI†); the absorption maxima are red-shifted 9 nm, which result from the singlet–singlet n-π* enol absorption of the β-diketonate.

PXRD analysis of complexes 1–4

Powder X-ray diffraction (PXRD) patterns of complexes 1–4 are in agreement with the simulated patterns (Fig. S3–S6 in the ESI†). PXRD analysis further demonstrates that the crystal structures of complexes 1–4 are truly representative of the bulk materials. The differences in intensity are due to the preferred orientation of the powder samples.

TG-DSC analysis of complexes 1–4

TG-DSC analyses (Fig. S7–S10 in the ESI†) of complexes 2 and 3 exhibit a gradual weight loss of 8.26% and 8.15%, respectively, in the first step, 28–110 °C, which corresponds to the loss of one toluene (calcd 8.34% and 8.30%), and then they undergo a single-step decomposition. In contrast, complexes 1 and 4 are more stable than complexes 2 and 3, meaning that there is no solvent in complexes 1 and 4.

Structural descriptions of complexes 1–4

X-ray crystallographic analysis reveals that complexes 1–4 are all mononuclear structures crystallizing in the monoclinic space group P2₁/c. In complexes 1–4, all three DBM and one auxiliary ligand are coordinated to the Dy(III) ion. The central Dy(III) ions are all eight-coordinated by six oxygen atoms from three DBM ligands and two nitrogen atoms from auxiliary ligands. For complex 1, the coordination geometry around the Dy(III) ion can be defined as distorted square antiprismatic (SAP) (Fig. 1a) in which δ₁–δ₄ and φ₁–φ₂ values are close to the angles of an ideal square antiprismatic geometry. The average bond lengths of Dy–O and Dy–N are 2.325 and 2.570 Å, respectively. The relevant dihedral angles are summarized in Table 2. In contrast, for complexes 2–4, there are two unique molecules existing in one unit that form [Dy(DBM)₃-auxiliary ligand]₂ pairs. For complex 2, both of the two crystallographically equivalent Dy(III) ions adopt a distorted square antiprismatic coordination geometry. Although the δ₁–δ₄ and φ₁–φ₂ values are slightly different, the values are close to the angles of an ideal square antiprismatic geometry (Fig. 1b and Table 2). For complex 3, the two crystallographically inequivalent Dy(III) ions adopt coordination geometries of square antiprismatic for the Dy1(III) ion and dodecahedral (DD) for the Dy2(III) ion. The δ₁–δ₄ and φ₁–φ₂ values for the Dy1(III) ion are 12.1, 19.5, 54.6, 49.8° and 24.1, 21.0°, respectively, which are close to the angles (0.0, 0.0, 52.4, 52.4° and 24.5, 24.5°) of an ideal square antiprismatic geometry. However, the δ₁–δ₄ and φ₁–φ₂ values for the Dy2(III) ion are 17.5, 33.1, 30.0, 35.7° and 0.6, 5.9°, respectively, which are close to the angles (29.5, 29.5, 29.5, 29.5° and 0.0, 0.0°) of an ideal dodecahedron (Fig. 1c and Table 3). Since complex 4 is comparable with complex 3, a detailed analysis of its coordination geometry is summarized in Table 4. However, for complex 4, the Dy1(III) ion has a distorted square antiprismatic geometry, whereas the Dy2(III) ion has a distorted bicapped trigonal prismatic (TP) geometry (Fig. 1d and Table 4). The average bond lengths of Dy–O and Dy–N are 2.314, 2.593 Å for Dy1 and 2.320, 2.588 Å for Dy2 in complex 2, 2.320, 2.574 Å for Dy1, 2.327, 2.581 Å for Dy2 in complex 3, 2.319, 2.578 Å for Dy1 and 2.318, 2.596 Å for Dy2 in complex 4, respectively. Notably, the average bond length of Dy–O in complex 1 is a little longer than in complexes 2–4 but the Dy–N is shorter.

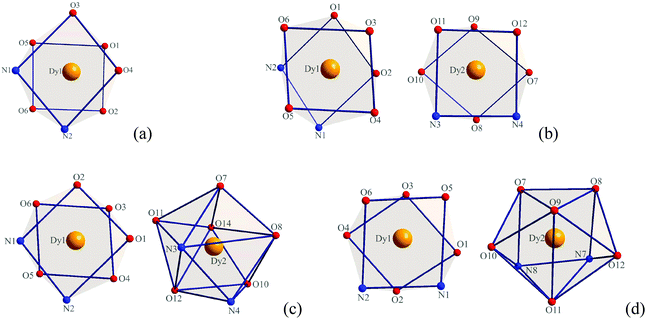Fig. 1 Local coordination geometry of the Dy(III) ions in complexes 1 (a), 2 (b), 3 (c) and 4 (d).

Table 2 δ (°) and ^aφ (°) values for complexes 1, 2 and an ideal square antiprism

Faces	Dy1 (1)		Dy1 (2)		Dy2 (2)		SAP
a δ 1 and δ2 are the planarity of the squares, δ3 and δ4 represent the triangular faces. A[BC]D is the dihedral angle between the ABC and BCD plane. A–B–C–D is the dihedral angle between the ABCD and ABCD where AB is the center of the AB edge.^14
δ 1	N1[N2O3]O4	26.0	N2[O1N1]O2	22.6	O10[O9O8]O7	23.1	0.0
δ 2	O5[O1O6]O2	4.9	O6[O5O3]O4	19.8	O11[O12N3]N4	2.1	0.0
δ 3	N1[O6N2]O2	53.4	N2[O5N1]O4	56.6	O10[O8N3]N4	46.8	52.4
δ 4	O5[O3O1]O4	59.7	O6[O1O3]O2	58.6	O11[O9O12]O7	45.4	52.4
φ 1	N2–O1–N1–O5	26.0	N1–O3–N2–O6	28.5	O8–O12–O10–O11	18.7	24.5
φ 2	O3–O6–O4–O2	34.5	O1–O5–O2–O4	29.1	O9–N3–O7–N4	16.4	24.5

---

Table 3 δ (°) and ^aφ (°) values for complex 3 and an ideal square antiprism and dodecahedron

Faces	Dy1 (3)		Dy2 (3)		SAP	DD
a δ 1 and δ2 are the planarity of the squares, δ3 and δ4 represent the triangular faces. A[BC]D is the dihedral angle between the ABC and BCD plane. A–B–C–D is the dihedral angle between the ABCD and ABCD where AB is the center of the AB edge.^14
δ 1	N1[N2O2]O1	12.1	N4[O8N3]O7	17.5	0.0	29.5
δ 2	O6[O5O3]O4	19.5	O11[O12N3]N4	33.1	0.0	29.5
δ 3	N1[O5N2]O4	54.6	O7[O8O14]O10	30.0	52.4	29.5
δ 4	O6[O3O2]O1	49.8	O11[O12O14]O10	35.7	52.4	29.5
φ 1	N2–O3–N1–O6	24.1	N3–O14–N4–O10	0.6	24.5	0.0
φ 2	O2–O5–O1–O4	21.0	O12–O8–O11–O7	5.9	24.5	0.0

---

Table 4 δ (°) and ^aφ (°) values for complex 4 and ideal square antiprismatic and trigonal prismatic

Faces	Dy1 (4)		Dy2 (4)		SAP	TP
a δ 1 and δ2 are the planarity of the squares, δ3 and δ4 represent the triangular faces. A[BC]D is the dihedral angle between the ABC and BCD plane. A–B–C–D is the dihedral angle between the ABCD and ABCD where AB is the center of the AB edge.^14
δ 1	O4[O3O2]O1	14.2	O7[O8N8]N7	19.0	0.0	0.0
δ 2	O6[O5N2]N1	17.2	O12[O9O11]O10	32.3	0.0	21.8
δ 3	O4[O2N2]N1	54.6	O10[O11N8]N7	51.5	52.4	48.2
δ 4	O6[O3O5]O1	58.7	O7[O9O8]O12	53.4	52.4	48.2
φ 1	O2–O5–O4–O6	30.7	O10–O7–O11–O8	22.1	24.5	14.1
φ 2	O3–N2–O1–N1	26.0	O12–N7–O9–N8	21.0	24.5	14.1

---

Magnetic properties

The magnetic behavior of complexes 1–4 were measured in an applied magnetic field of 100 Oe over the temperature range 300–1.8 K.²² As shown in Fig. 2, the observed χ_mT values at 300 K are 14.12, 14.11, 14.09, and 14.18 cm³ K mol⁻¹ for 1, 2, 3 and 4, respectively, in agreement with the expected value for an isolated Dy(III) ion, where g = 4/3 for the ⁶H_15/2 ground state of the Dy(III) ion (C = 14.18 cm³ K mol⁻¹). Upon reducing the temperature, the χ_mT value for the complexes 1–4 decreases gradually over the temperature range of 300–100 K and more rapidly below 100 K. This thermal behavior is mostly attributed to crystal-field effects, specifically thermal depopulation of the Ln(III) ion Stark sublevels of the ⁶H_15/2 state.¹⁵ Notably, the magnetic moment is still far from the theoretical value (g_J × J = 4/3 × 15/2 = 10 μ_B), but does reach 5.4 μ_B (1), 4.7 μ_B (2), 5.0 μ_B (3) and 5.1 μ_B (4) at 1.8 K, which results from crystal field effects on the Dy(III) ion that eliminate the degeneracy of the ⁶H_15/2 ground state.^10b The non-superimposition of the isofield lines in the M versus H/T plots reveals the existence of low-lying excited states and/or significant magnetic anisotropy, as expected for Dy(III) ions in complexes 1–4 (Fig. 2, inset).^9a

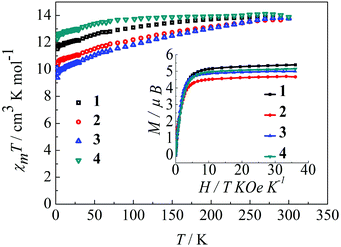Fig. 2 Temperature dependence of χ_mT at 100 Oe for complexes 1–4 in the range 1.8–300 K. Inset: M vs. H/T data for complexes 1–4 at 1.8 K.

In order to investigate the spin dynamics, alternating-current (ac) magnetic susceptibility studies for complexes 1–4 were conducted. Under zero dc field, the out-of-phase (χ′′) signal in the ac susceptibility demonstrates a clear frequency dependence at temperatures below 20 K, but no obvious peaks were observed, indicating the preliminary slow relaxation behaviour for complexes 1–4 (Fig. S11 and S12 in the ESI†). This indicates the onset of pure quantum tunneling of magnetization effects, as often seen in other lanthanide SMMs.^8b,16 To suppress the QTM effect, ac susceptibility studies were carried out under an optimized dc field of 2000 Oe. The χ′′ values also show maxima at 5 K (10 Hz)–12.5 K (1000 Hz) for complex 1 and 7.5 K (10 Hz)–15.5 K (1000 Hz) for complex 2 (Fig. 3). It is worth highlighting that a single relaxation mode in the temperature dependence of the ac susceptibility for complexes 1 and 2 is in accordance with the structure of complex 1 and the same coordination geometries of the Dy1(III) and Dy2(III) ions in complex 2.

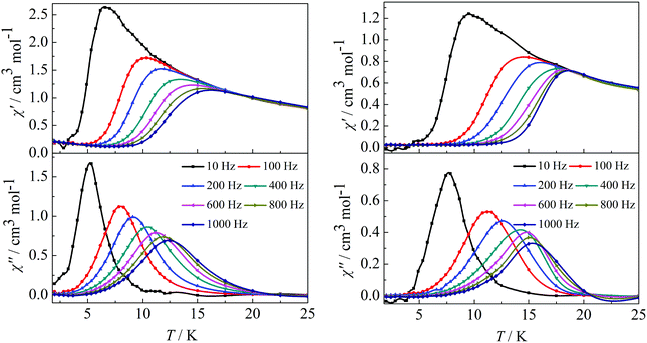Fig. 3 Temperature dependence of the in-phase (χ′) and out-of-phase (χ′′) ac susceptibility of complexes 1 (left) and 2 (right) under 2000 Oe in the frequency range 10–1000 Hz.

Furthermore, ac susceptibility curves for complex 3 show a clear frequency dependence with two obvious peaks between 10 and 1000 Hz under a dc field of 2000 Oe. Interestingly, these data highlight the presence of not one but two thermally activated relaxation modes (Fig. 4, left). To understand the nature of these two thermally activated relaxation modes, the characteristic time of the two relaxation modes was extracted and added to an Arrhenius law plot. According to the Arrhenius law, τ = τ₀exp(E_a/k_BT), and two effective energy barriers were extracted, with U_eff = 32.1 K (τ₀ = 4.2 × 10⁻⁶ s) and U_eff = 50.6 K (τ₀ = 5.4 × 10⁻⁶ s) (Fig. 4, left, inset). Both thermally activated relaxation modes are ascribed to the Orbach process because of the two similar τ₀ values.^6c The effective relaxation barriers primarily originate from SMM anisotropy.¹⁷ Unfortunately, for complex 4, both peaks remain overlapping at higher frequencies under a dc field of 2000 Oe (Fig. 4, right). This was not so obvious as those reported for other β-diketone dysprosium complexes^10c,18 or other Dy₂ SMMs^17,19 which contained two crystallographically inequivalent Dy(III) ions. This is attributed to the following factors. Complex 3 with two obviously different coordination environments of the central Dy(III) ions with D_4d and D_2d symmetry exhibited two distinct slow relaxation regimes. However, for complex 4, the coordination environments of D_4d and C_2v symmetry can convert to each other through a different viewing angle.^4d Thus, the two thermally activated relaxation modes appear with overlapping peaks at higher frequencies.

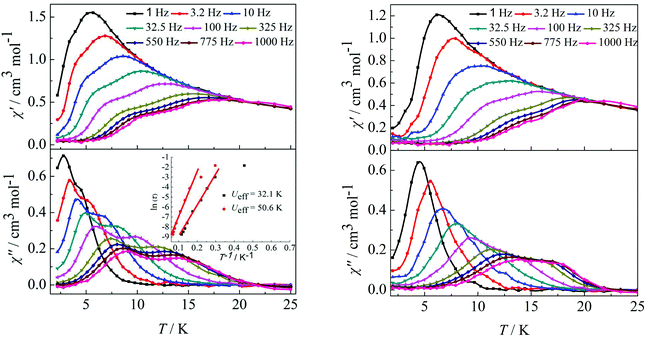Fig. 4 Temperature dependence of the in-phase (χ′) and out-of-phase (χ′′) ac susceptibility of complexes 3 (left) and 4 (right) under 2000 Oe in the frequency range 1–1000 Hz.

Peaks of the out-of-phase (χ′′) signals from the frequency dependence plots were observed between 2 and 12 K under zero dc field for complexes 1, 2 and 4 (Fig. 5 and 6). The anisotropic energy barriers U_eff can be obtained from the frequency-dependent out-of-phase (χ′′) peak maxima on the basis of the Arrhenius law τ = τ₀exp(E_a/k_BT) as U_eff = 16.5 K, τ₀ = 4.0 × 10⁻⁵ s; U_eff = 32.2 K, τ₀ = 4.5 × 10⁻⁵ s and U_eff = 27.3 K, τ₀ = 5.2 × 10⁻⁵ s for complexes 1, 2 and 4, respectively. Obviously, the anisotropy barrier of complex 1 is smaller than that of complex 2, which is ascribed to the large aromatic SAP ligand field of 1,10-phenanthroline around the Dy(III) ion in complex 2. This enables the lowest doubly degenerate sublevels to be essentially separated from the rest of the substates, resulting in a strong uniaxial magnetic anisotropy and a higher anisotropy barrier.^11b The anisotropy barrier of complex 4 is smaller than that of complex 3, which is maybe due to the degree of deviation from the ideal coordination symmetry. The coordination symmetries of the Dy(III) ions in complex 4 are more distorted than those of complex 3 leading to the difference in the anisotropy barriers, as can be seen in Tables 3 and 4.

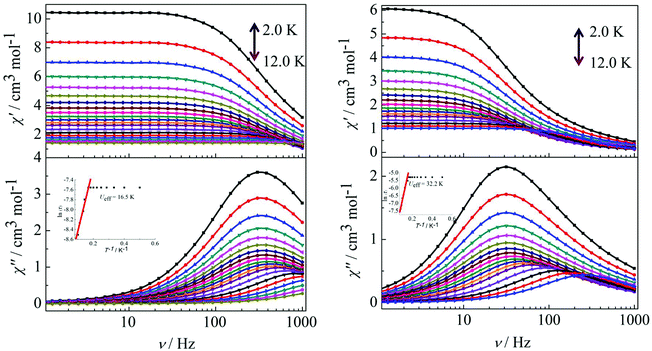Fig. 5 Frequency dependence of the in-phase (χ′) and out-of-phase (χ′′) ac susceptibility for complexes 1 (left) and 2 (right) under 0 Oe in the temperature range 2.0–12 K.

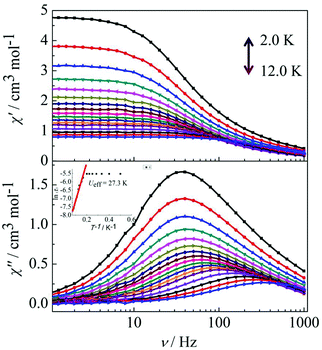Fig. 6 Frequency dependence of the in-phase (χ′) and out-of-phase (χ′′) ac susceptibility for complex 4 in the temperature range 2.0–12 K under 0 Oe.

For complex 3, the out-of-phase (χ′′) signals from the frequency dependence plots demonstrated two thermally activated relaxation modes in accordance with the temperature dependence of the out-of-phase (χ′′) ac susceptibility under a dc field of 2000 Oe (Fig. 7, left). For complex 4, it is worth highlighting that a single relaxation mode in the frequency dependence plots is observed under zero dc field (Fig. 6), and this is further certified by the extrapolation to zero at high frequencies of χ′ (i.e., the whole magnetization is blocked at high frequency).¹⁸ The crystallographically inequivalent Dy(DBM)₃(dppz) unit acts as a single supramolecular entity thanks to the weak, but efficient, magnetic coupling between the two Dy(III) ions. Upon application of a dc field of 2000 Oe to minimize the possibility of a quantum relaxation pathway, multiple thermally activated relaxation modes are discovered (Fig. 7, right). The applied dc field compensates, at least partially, for the weak antiferromagnetic (AF) interaction between the Dy(III) ions, and more than one thermal relaxation mode is detected. In other words, the two crystallographically inequivalent Dy(III) ions can be magnetically “decoupled” by application of a dc field; therefore they must be coupled weakly and antiferromagnetically in the absence of an applied dc field.

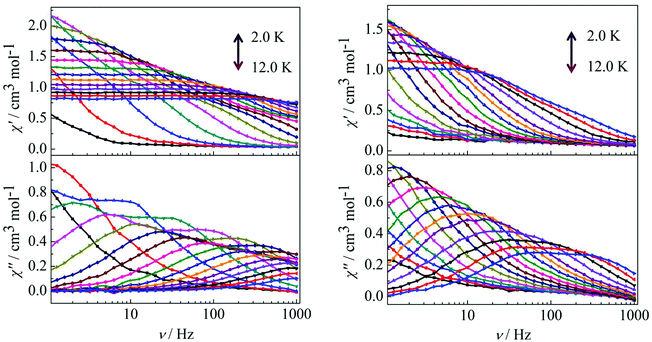Fig. 7 Frequency dependence of the in-phase (χ′) and out-of-phase (χ′′) ac susceptibility for complex 3 (left) and 4 (right) in the temperature range 2.0–12 K under 2000 Oe.

On the basis of a Cole–Cole plot, the complexes 1, 2 and 4 can be fitted to the generalized Debye model in which τ₀ is still larger than expected for a thermally activated relaxation mechanism under zero dc field (Fig. 8). This may be partially explained by the large values of the modified Debye fit, where α values are in a range of 0.09–0.21 between 12 and 2 K that increase significantly as the temperature decreases (Table S3 in the ESI†). It verifies a single relaxation mode with a narrow distribution of relaxation times.

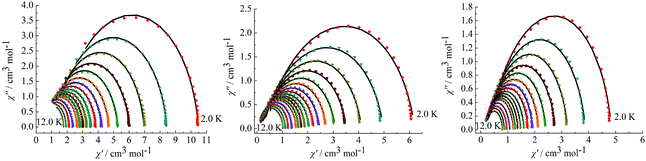Fig. 8 Cole–Cole plots measured at 2.0–12.0 K under 0 Oe for complexes 1 (left), 2 (middle) and 4 (right).

To further observe the relaxation modes, Cole–Cole plots of complexes 3 and 4 were measured under a dc field of 2000 Oe. As a result, two separate semicircles are clearly observed in the Cole–Cole plots between 3.5–5.5 K for complex 3 (Fig. 9, left) and 4.0–12 K for complex 4 (Fig. 9, right), which could be well fitted using the sum of two modified Debye models (Table S3†).²⁰ For complex 3, the parameters α₁ and α₂ are used to estimate slight deviations of the two thermally activated relaxation modes from the corresponding pure Debye modes. In the temperature range 3.5–5.5 K, α₁ values are between 0.11–0.19 and α₂ values are 0.17–0.25, indicating that both thermally activated relaxation processes have a narrow distribution of relaxation times. For complex 4, in the temperature range of 4.0–12 K, Cole–Cole plots are asymmetric at low temperature and have a relatively wide semicircle at high temperature and α values are between 0.14–0.32, further indicating the presence of multiple relaxation modes in accordance with the temperature and frequency dependence of the in-phase (χ′) and out-of-phase (χ′′) ac susceptibilities.

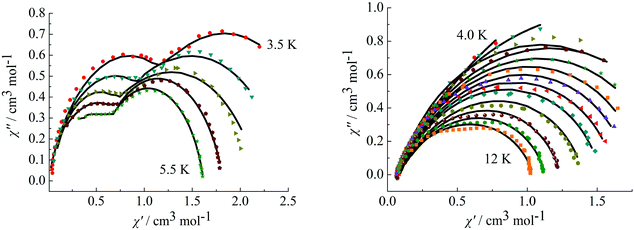Fig. 9 Cole–Cole plots measured at 3.5–5.5 K for complex 3 (left) under 2000 Oe and at 4.0–12 K for complex 4 (right).

Magnetization hysteresis is another important characteristic in the magnetic bistability of SMMs. The M versus H plots of complexes 1–4 all display wide butterfly-shaped hysteresis loops at 1.8 K under a sweep rate of 50 Oe s⁻¹ (Fig. 10, left). Upon decreasing the sweep rate from 400 to 50 Oe s⁻¹, the hysteresis loops for complexes 1–4 become only slightly narrower (Fig. S13–S16 in the ESI†), suggesting that the loops come from the systematic error of the SQUID. When the temperature increases from 1.8 K to 5 K at a sweep rate of 50 Oe s⁻¹, the changes of loop openings are obvious for complexes 1–4 (Fig. 10, right, Fig. S17–S19 in the ESI†). Notably among complexes 1–4, a clear butterfly shape with the widest opening is observed for the hysteresis loop of complex 2 at 1.8 K and a sweep rate of 50 Oe s⁻¹ (Fig. 10, left). Upon raising the temperature, the openings for complex 2 in the hysteresis become narrow and then close above 4 K which is higher than those for previously reported β-diketone dysprosium complexes (Fig. 10, right).^8,11,12 The higher blocking temperature of complex 2 is primarily attributed to the weak magnetic interaction between Dy(III) ions and higher coordination symmetry SAP Dy(III) ions compared to complexes 1, 3 and 4.²¹ Nevertheless, it can be difficult to compare the magnetic hysteresis phenomenon of different SMMs because they are so strongly dependent on the sweep rates and temperature.²²

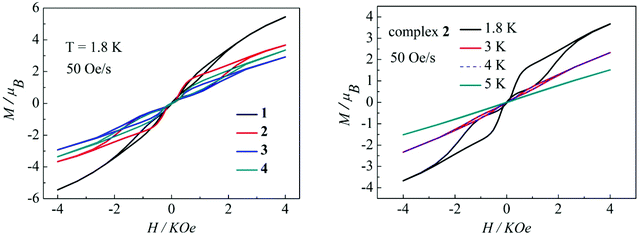Fig. 10 Hysteresis loops for complexes 1–4 at 1.8 K (left); hysteresis loops for complex 2 with a sweep rate of 50 Oe s⁻¹ at 1.8, 3, 4 and 5K (right).

Conclusions

Isolation of a series of four DBM dysprosium lanthanide complexes 1–4 verifies that the DBM and azacyclo-auxiliary ligands are able to co-stabilize the Dy(III) ion by forming mononuclear Dy(III) complexes with an eight-coordinated coordination symmetry. The coordination symmetry around the Dy(III) ions dominates the magnetism of the complexes 1–4. The difference in the two coordination symmetries around the Dy(III) ion dominates the two relaxation modes in complexes 3 and 4. The auxiliary ligands enhance the magnetism of complexes 1–4 by tuning the coordination symmetry and the ligand field around the Dy(III) ions. This approach provides a facile way to afford SMMs of lanthanide complexes with potential applications.

Conflict interest

The authors declare no competing financial interest.

Acknowledgements

This work is financially supported by the National Natural Science Foundation of China (no. 21471051 and 51402092).

References

1. (a) T. Glaser, Chem. Commun., 2011, 47, 116–130; (b) K. Katoh, H. Isshiki, T. Komeda and M. Yamashita, Coord. Chem. Rev., 2011, 255, 2124–2148.
2. A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, J. Am. Chem. Soc., 1991, 113, 5873–5874.
3. (a) D. N. Woodruff, R. E. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148; (b) E. Coronado and P. Day, Chem. Rev., 2004, 104, 5419–5448; (c) R. Bagai and G. Christou, Chem. Soc. Rev., 2009, 38, 1011–1026; (d) G. E. Kostakis, A. M. Ako and A. K. Powell, Chem. Soc. Rev., 2010, 39, 2238–2271; (e) R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328–2341; (f) C.-M. Liu, D.-Q. Zhang, X. Hao and D.-B. Zhu, Cryst. Growth Des., 2012, 12, 2948–2954.
4. (a) A. Cornia, M. Mannini, P. Sainctavit and R. Sessoli, Chem. Soc. Rev., 2011, 40, 3076–3091; (b) M. Atanasov, P. Comba, S. Hausberg and B. Martin, Coord. Chem. Rev., 2009, 253, 2306–2314; (c) F. Habib and M. Murugesu, Chem. Soc. Rev., 2013, 42, 3278–3288; (d) L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092–3104; (e) P. Zhang, Y.-N. Guo and J. Tang, Coord. Chem. Rev., 2013, 257, 1728–1763; (f) W.-B. Sun, B. Yan, Y.-Q. Zhang, B.-W. Wang, Z.-M. Wang, J.-H. Jia and S. Gao, Inorg. Chem. Front., 2014, 1, 503–509; (g) M. Ren, S.-S. Bao, B.-W. Wang, R. A. S. Ferreira, L.-M. Zheng and L. D. Carlos, Inorg. Chem. Front., 2015, 2, 558–566.
5. N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
6. (a) N. Ishikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650–3651; (b) J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733; (c) S. D. Jiang, B. W. Wang, H. L. Sun, Z. M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733; (d) B. Hussain, D. Savard, T. J. Burchell, W. Wernsdorfer and M. Murugesu, Chem. Commun., 2009, 1100–1102; (e) D. T. Thielemann, M. Klinger, T. J. Wolf, Y. Lan, W. Wernsdorfer, M. Busse, P. W. Roesky, A. N. Unterreiner, A. K. Powell, P. C. Junk and G. B. Deacon, Inorg. Chem., 2011, 50, 11990–12000; (f) F. Habib, P.-H. Lin, J. Long, I. Korobkov, W. Wernsdorfer and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 8830–8833; (g) S. Y. Lin, L. Zhao, Y. N. Guo, P. Zhang, Y. Guo and J. Tang, Inorg. Chem., 2012, 51, 10522–10528; (h) L. Zhao, J. Wu, H. Ke and J. Tang, CrystEngComm, 2013, 15, 5301–5306; (i) P. Hu, X. Wang, Y. Ma, Q. Wang, L. Li and D. Liao, Dalton Trans., 2014, 43, 2234–2243.
7. (a) G.-J. Chen, C.-Y. Gao, J.-L. Tian, J. Tang, W. Gu, X. Liu, S.-P. Yan, D.-Z. Liao and P. Cheng, Dalton Trans., 2011, 40, 5579–5583; (b) D. P. Li, X. P. Zhang, T. W. Wang, B. B. Ma, C. H. Li, Y. Z. Li and X. Z. You, Chem. Commun., 2011, 47, 6867–6869; (c) F. Habib, G. Brunet, V. Vieru, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 13242–13245.
8. (a) Y. Dong, P. Yan, X. Zou, T. Liu and G. Li, J. Mater. Chem. C, 2015, 3, 4407–4415; (b) Y. Bi, Y. N. Guo, L. Zhao, Y. Guo, S. Y. Lin, S. D. Jiang, J. Tang, B. W. Wang and S. Gao, Chem. – Eur. J., 2011, 17, 12476–12481.
9. (a) G. Abbas, Y. Lan, G. E. Kostakis, W. Wernsdorfer, C. E. Anson and A. K. Powell, Inorg. Chem., 2010, 49, 8067–8072; (b) J. Li, H. Li, P. Yan, P. Chen, G. Hou and G. Li, Inorg. Chem., 2012, 51, 5050–5057; (c) P. P. Lima, M. M. Nolasco, F. A. A. Paz, R. A. S. Ferreira, R. L. Longo, O. L. Malta and L. D. Carlos, Chem. Mater., 2013, 25, 586–598; (d) V. Divya and M. L. P. Reddy, J. Mater. Chem. C, 2013, 1, 160–170; (e) J. Shi, Y. Hou, W. Chu, X. Shi, H. Gu, B. Wang and Z. Sun, Inorg. Chem., 2013, 52, 5013–5022.
10. (a) N. F. Chilton, S. K. Langley, B. Moubaraki, A. Soncini, S. R. Batten and K. S. Murray, Chem. Sci., 2013, 4, 1719–1730; (b) Y. L. Wang, Y. Ma, X. Yang, J. Tang, P. Cheng, Q. L. Wang, L. C. Li and D. Z. Liao, Inorg. Chem., 2013, 52, 7380–7386; (c) C. M. Liu, D. Q. Zhang and D. B. Zhu, Inorg. Chem., 2013, 52, 8933–8940.
11. (a) S. D. Jiang, B. W. Wang, G. Su, Z. M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448–7451; (b) G. J. Chen, Y. N. Guo, J. L. Tian, J. Tang, W. Gu, X. Liu, S. P. Yan, P. Cheng and D. Z. Liao, Chem. – Eur. J., 2012, 18, 2484–2487.
12. J. Zhu, C. Wang, F. Luan, T. Liu, P. Yan and G. Li, Inorg. Chem., 2014, 53, 8895–8901.
13. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122.
14. E. L. Muetterties and L. J. Guggenberger, J. Am. Chem. Soc., 1974, 96, 1748–1756.
15. (a) M. L. Kahn, J.-P. Sutter, S. Golhen, P. Guionneau, L. Ouahab, O. Kahn and D. Chasseau, J. Am. Chem. Soc., 2000, 122, 3413–3421; (b) M. L. Kahn, R. Ballou, P. Porcher, O. Kahn and J.-P. Sutter, Chem. – Eur. J., 2002, 8, 525–531.
16. (a) A. Mishra, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2004, 126, 15648–15649; (b) S. Koizumi, M. Nihei, T. Shiga, M. Nakano, H. Nojiri, R. Bircher, O. Waldmann, S. T. Ochsenbein, H. U. Güdel, F. Fernandez-Alonso and H. Oshio, Chem. – Eur. J., 2007, 13, 8445–8453.
17. P. H. Lin, W. B. Sun, M. F. Yu, G. M. Li, P. F. Yan and M. Murugesu, Chem. Commun., 2011, 47, 10993–10995.
18. E. M. Fatila, M. Rouzieres, M. C. Jennings, A. J. Lough, R. Clerac and K. E. Preuss, J. Am. Chem. Soc., 2013, 135, 9596–9599.
19. (a) P.-F. Yan, P.-H. Lin, F. Habib, T. Aharen, M. Murugesu, Z.-P. Deng, G.-M. Li and W.-B. Sun, Inorg. Chem., 2011, 50, 7059–7065; (b) S. Das, A. Dey, S. Biswas, E. Colacio and V. Chandrasekhar, Inorg. Chem., 2014, 53, 3417–3426.
20. Y.-N. Guo, G.-F. Xu, P. Gamez, L. Zhao, S.-Y. Lin, R. Deng, J. Tang and H.-J. Zhang, J. Am. Chem. Soc., 2010, 132, 8538–8539.
21. J. J. Le Roy, L. Ungur, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2014, 136, 8003–8010.
22. W. Wernsdorfer, Classical and Quantum Magnetization Reversal Studied in Nanometer-Sized Particles and Clusters, in Advances in Chemical Physics, John Wiley & Sons, Inc., 2007, pp. 99–190.

---

Footnote

† Electronic supplementary information (ESI) available: FT-IR spectra, UV spectra, additional magnetic measurements, powder X-ray diffraction, TG-DSC curves, selected bond lengths and angles for complexes 1–4. CCDC 1062450–1062453. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qi00079c

---