Tailoring polyester-based diblock copolymers for boron-enhanced drug delivery: synthesis, kinetics, and nanoparticle characterization

Abstract

Here, we present the synthesis of diblock copolymers of poly(ethylene glycol) methyl ether-b-poly(ε-caprolactone) (mPEG-b-PCL) with prop-2-ynyl (propargyl) substituents on ε-caprolactone (ε-CL) units. The copolymerization of ε-CL with its propargylated derivative initiated by mPEG, followed by a thiol–yne click reaction with 1-thioglycerol, results in copolymers featuring vicinal diols capable of reversibly binding boronic acid derivatives. Detailed kinetic experiments were conducted to monitor the homo- and copolymerization of ε-CL with 7-(prop-2-ynyl)oxepan-2-one. By analyzing the kinetic data, we calculated the copolymerization parameters and mapped the composition profile of the resulting copolymers. The resulting gradient copolymers exhibited a lightly tapered composition profile, with an increase in ε-CL consumption at higher conversions where the more reactive 7-(prop-2-ynyl)oxepan-2-one is almost depleted. These findings were further validated through quantum chemical calculations, providing insights into the precise structure and composition of the copolymers. Characterization of the self-assembled nanoparticles was performed using static and dynamic light scattering, and their morphology was visualized via conventional and cryogenic transmission electron microscopy, confirming the formation of small, homogeneous spherical micelles. To demonstrate their potential in drug delivery, we combined a model drug consisting of a phenylboronic acid-conjugated metallacarborane cluster with diblock copolymer, utilizing reversible bonding between diols and phenylboronic acid and investigated the impact of drug loading on nanoparticle properties. Our comprehensive study underscores the importance of precise synthesis and structural prediction in the development of biodegradable diblock copolymers, offering valuable insights into their synthesis, kinetic behavior, and nanoscale assembly for advanced drug delivery applications.

---

Introduction

Amphiphilic block copolymers are versatile materials comprising two or more chemically distinct and typically immiscible covalently bonded blocks. By changing these blocks or their order, length, or incompatibility, the material properties can be easily tuned for specific applications. Such a convenient adjustability has prompted their use in diverse fields including tissue engineering, cell encapsulation, gene therapy and drug delivery.^1,2 Many drug polymeric delivery systems (DDSs) have been produced with poly(ε-caprolactone) (PCL) and its copolymers due to their relative affordability, high permeability to numerous drugs, excellent biocompatibility, and ability to be fully excreted from the body once bioresorbed.^3–5 Well-defined PCLs with narrow molar mass distributions are formed by ε-CL ring-opening polymerization (ROP) routinely catalyzed by FDA-approved tin(II) ethylhexanoate (stannous octoate, SnOct2),^6–9 using an mPEG macroinitiator in order to obtain block copolymers. In this regard, mPEG-b-PCL-based nanoDDSs with a high encapsulation efficiency (EE) have been prepared for various active compounds (177–1269 g mol⁻¹, X log P3 −9.9 to 7.5)^10,11 including poorly soluble sulforaphane and paclitaxel. The loading content of the latter increases with the length of the hydrophobic PCL block.¹²

Considerable research efforts have been made to modify synthetic polyesters to tackle their main limitations, namely inherent hydrophobicity and lack of chemical functionalities between the backbone ester groups.¹³ The solution is the modification of the polyester backbone with adequate functional groups that can be attached via polymerization of pre-functionalized monomers,^14–17 post-polymerization modifications^18–20 or the combination of both methods.^21–25 Combined synthetic pathways are based on functionalized monomers that are suitable for subsequent click reactions, such as thiol–ene or thiol–yne click reactions.^26–29 One of the appropriate monomers for the thiol–yne click reaction is propargyl substituted ε-caprolactone (PgCL). This monomer is typically produced as an isomeric mixture of 3- and 7-(prop-2-ynyl)oxepan-2-ones (3- and 7-isomers) containing 30% of the 3-isomer and it has been widely used in biomedical applications of the respective (co)polymers.^29–36

In cancer therapy, conventional low-molecular therapeutics exhibit unfavorable pharmacokinetics, suboptimal biodistribution, short blood half-life and prominent off-target, resulting in severe side effects. In comparison, nanoparticle formulations of the desired size (over 40 kDa to exceed the renal clearance threshold) show reduced kidney excretion and therefore prolonged circulation half-life. The half-life can be further improved by coating the nanoparticles with stealth polymers. Notably, poly(ethylene glycol) coatings are extensively used to prevent aggregation and opsonization with plasma proteins.³⁷ Several types of boron-containing compounds are frequently considered for cancer treatment, such as boronic acids and boron clusters.³⁸ Boronic acids (BAs) are inherently electron-deficient organoboron compounds due to a vacant p-orbital on the boron atom. In aqueous media, hydroxyl groups act as Lewis bases interconverting the sp²-hybridized form of BAs to a tetrahedral sp³ hydroxyboronate anion in a pH-dependent equilibrium. Although both forms bind to 1,2- and 1,3-diols, boronate esters formed by the latter are more hydrolytically stable.³⁹ Despite being highly reactive, BAs show remarkable stability and a very low toxicology profile.⁴⁰ Owing to these properties, BAs are employed as stimuli-responsive groups, as targeting ligands, and as therapeutics. In BA-containing materials for drug delivery, not only pH but also reactive oxygen species (ROS) and diols such as sugars and adenosine triphosphate (ATP) can be used as release triggers.^41–43

Boron clusters are polyhedral boron hydrides whose high boron content makes them suitable for boron neutron capture therapy (BNCT).³⁸ Upon irradiation with thermal neutrons, boron-10 atoms yield recoiling lithium-7 nuclei and alpha particles which destroy biologically active molecules, such as DNA, RNA, and proteins. The short path of these particles (approximately one cell in diameter – 10–14 μm) and the weak hydrogen and nitrogen capture cross-section limit damage to normal tissue.⁴⁴ Nevertheless, delivering boronated compounds to a tumor while avoiding significant uptake in normal tissues and adsorption to plasma proteins remains a challenge.⁴⁵ A promising strategy for overcoming these drawbacks is integrating boron clusters with polymeric delivery systems.³⁸

Thus, we prepared several diblock copolymers mPEG-b-P(ε-CL-co-PgCL) bearing propargyl pendant groups. The subsequent modification of reactive triple bonds via a thiol–yne click reaction with 1-thioglycerol yielded copolymers bearing vicinal diols, which can reversibly bind to boronic acid derivatives. Additionally, we studied the kinetic profile of ε-CL/PgCL copolymerization and characterized the self-assembled nanoparticles by static and dynamic light scattering. The formation of small, homogeneous spherical micelles was visualized using conventional (negatively stained samples) and cryogenic transmission electron microscopy. Finally, we encapsulated a newly synthesized model drug, COSAN-pyridinium-3-boronic acid conjugate, into spherical micelles and investigated the effect of drug loading on these particles.

Results and discussion

Synthesis and characterization of mPEG-b-P(ε-CL-co-PgCL) copolymers

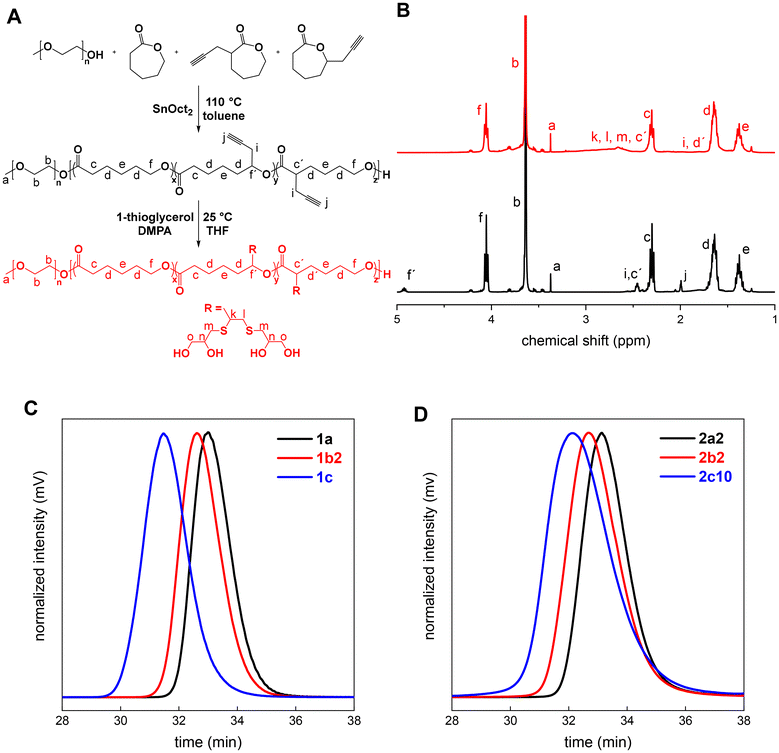
The synthesis of mPEG-b-P(ε-CL-co-PgCL) was performed in one pot with a reaction mixture of twice azeotropically distilled mPEG as a macroinitiator and ε-CL/PgCL as comonomers. PgCL was used as the original mixture of both isomers (30% of 3-(prop-2-ynyl)oxepan-2-one) with a molar ratio of ε-CL/PgCL = 3/1. Three polymerization feeds, with increasing ratio between the mPEG and ε-CL/PgCL units, were prepared (Table 1).

Table 1 Synthesis of mPEG-b-P(ε-CL-co-PgCL) in toluene catalyzed by SnOct₂ at 110 °C^a

Entry	n mPEG (mmol)	PgCL (eq.)	t (h)	Conv.^b (%)	N ε-CL	N PgCL	DS^d (%)	M n ^e (kg mol^−1)	Đ	M n ^NMR ^f (kg mol^−1)
a ε-CL/PgCL = 3/1, mPEG/SnOct2 = 1/0.5, Mn(mPEG) = 5 kg mol^−1, and Vtoluene = 3 ml. b Total monomer conversion determined by ^1H NMR. c Number of repeating units determined by ^1H NMR. d Degree of substitution determined by ^1H NMR. e Apparent number-average molar masses (Mn) and dispersities (Đ) determined by SEC-ELS with PS calibration in THF at 25 °C. f Determined by ^1H NMR.
1a	0.2	11	3	89	33	6	15	12.0	1.19	9.6
1b2	0.2	26	8	91	65	11	15	15.1	1.21	14.1
1c	0.1	71	14	94	202	34	15	30.3	1.27	32.9

---

All three copolymerization experiments showed the controlled polymerization behavior with the dispersity values increasing from 1.20 to 1.30 with prolongation of the polymerization time (Table 1). The total monomer conversion was constantly around 90% for different polymerization times, which was accompanied by the same degree of substitution (DS) for all copolymers (15%). This further indicates the well-controlled polymerization process, even at longer polymerization times (entries 1b2 and 1c, Table 1), which enabled the subsequent modification of the synthesized diblock copolymers via a thiol–yne click reaction.

Thiol–yne click functionalization of mPEG-b-P(ε-CL-co-PgCL)

To obtain the final products containing vicinal diols, UV-initiated thiol–yne click reactions between mPEG-b-P(ε-CL-co-PgCL) diblock copolymers and an excess amount of 1-thioglycerol were studied. At the beginning, we performed the preliminary screening to map the effect of the reaction time and irradiation intensity on the molar mass, its distribution and the DS of the resulting polymers. Minimal degradation and the highest functionalization were observed after 65 minutes at 9 mW cm⁻², which were taken as standard conditions (Table 2).

Table 2 Thiol–yne click reaction of mPEG-b-P(ε-CL-co-PgCL) in THF at 25 °C^a

Entry	n PgCL (mmol)	DS^b (%)	M n ^c (kg mol^−1)	Đ	M n ^NMR ^d (kg mol^−1)
a m mPEG-b-P(ε-CL-co-PgCL) = 0.4 g, VTHF = 4 ml, PgCL/α-TG/DMPA = 1/15/0.5, I = 9 mW cm^−2, and t = 65 min. b Degree of substitution determined by ^1H NMR. c Apparent number-average molar masses (Mn) and dispersities (Đ) determined by SEC-ELS with PS calibration in THF at 25 °C. d Determined by ^1H NMR.
2a2	0.25	16	9.9	1.35	8.6
2b2	0.31	15	12.4	1.42	13.6
2c10	0.41	15	14.5	1.70	—

---

The adopted reaction conditions resulted in negligible degradation within the modification of diblock copolymers 1a and 1b2 (Table 1). Only a slight decrease of molar mass accompanied by mild broadening of its distribution was observed (Table 2), as shown in Fig. S1(A and B).† The only exception was sample 2c10, containing the longest hydrophobic block, that showed twice lower molar mass with the increase of dispersity from 1.27 to 1.70 after UV exposure (C, Fig. S1†). This behavior is in line with the previously published data, describing that longer PCL chains are more inclinable to undergo UV degradation.⁴⁶ However, all diblock copolymers modified with 1-thioglycerol (Table 2) exhibited the same degree of substitution as the starting copolymers (Table 1). Moreover, no double bonds were detected in the ¹H NMR spectra (B, Fig. 1). This indicates that each alkyne functional group was reacted with two thiol species, generating a dithioether. These findings are in line with previous observations, upon monitoring the concentration of functional groups by IR spectroscopy.⁴⁷

Fig. 1 Reaction scheme (A), comparison of the ¹H NMR spectra of alkyne- and diol-containing polymers (B), SEC-ELS chromatograms representing the synthesis of mPEG-b-P(ε-CL-co-PgCL) copolymers in toluene catalyzed by SnOct₂ at 110 °C (C) and modification of these copolymers via a thiol–yne click reaction in THF at 25 °C (D).

Kinetics and modeling of the copolymerization of ε-CL and 7-(prop-2-ynyl)oxepan-2-one

Furthermore, we thoroughly separated both PgCl isomers (3/7-(prop-2-ynyl)oxepan-2-ones) and performed (co)polymerization kinetic experiments with unsubstituted ε-CL to reveal the mutual reactivity of these species. Having in mind that the synthesized PgCl contains only 30% of the 3-isomer,²⁹ we mainly focused on the copolymerization of ε-CL with the 7-isomer, as the content of the 3-isomer is further decreased upon addition of ε-CL (3 eq. of ε-CL towards PgCL in our experiments) and does not have a vast impact on the resulting copolymer structure. Despite the FDA-approval of tin(II) ethylhexanoate,⁸ we decided to study the (co)polymerization kinetics via a metal-free reaction pathway, using the organocatalyst TBD under milder reaction conditions (30 °C), as ROP catalyzed by Sn(Oct)₂ at 110 °C is highly energetically demanding.

Linear dependency of ln([M₀]/[M_t]) (Fig. 2) on time showed that the propagation reaction of ε-CL and 7-isomer copolymerization is first order with respect to the monomer concentration, confirming the controlled character of copolymerization (Fig. 2). Living/controlled copolymerization behavior was further suggested by increasing molar mass with reaction time, showing narrow SEC-ELS traces (right part of Fig. S2†) with low dispersities, which were below 1.20 (Table S1†). Apparent molar masses (SEC-ELS with PS calibration) of the synthesized copolymer displayed linear dependencies when plotted with conversion (left part of Fig. S2†), which is also a crucial factor of living/controlled copolymerization.⁴⁸

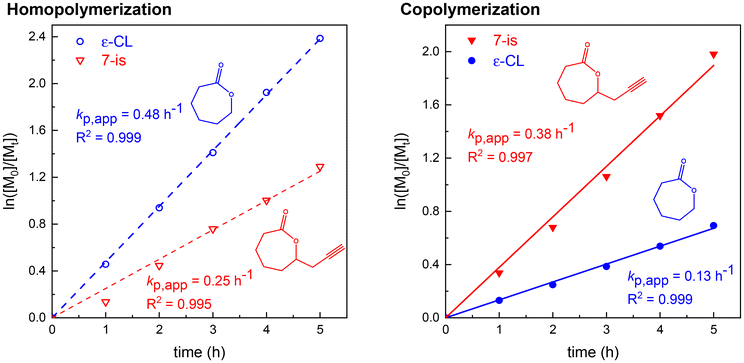Fig. 2 Kinetic plots of the homopolymerization of ε-CL and 7-(prop-2-ynyl)oxepan-2-one (left) and their mutual copolymerization (right) in toluene catalyzed by BnOH/TBD at 30 °C.

Data from kinetic experiments were also utilized in the calculations of the copolymerization parameters of ε-CL and 7-(prop-2-ynyl)oxepan-2-one. The reactivity ratio of both comonomers was identified by ¹H NMR analysis of the reaction mixtures that provided the total monomer conversion and the evolution of monomer feed composition within the copolymerization reaction. This set of experimental data was processed with the Integrated Ideal Model (A, Fig. 3). The Integrated Ideal Model was developed by Frey et al.⁴⁹ and it is derived from Wall's non-terminal (“ideal”) model,⁵⁰ describing the ideal copolymerization (r1·r2 = 1). The calculated copolymerization parameters of the ε-CL and 7-isomer couple obtained from the Integrated Ideal Model (r_ε-CL = 0.36; r_7-is = 2.79) confirmed the higher reactivity of the 7-isomer (A, Fig. 3).

Fig. 3 The Integrated Ideal Model describing the copolymerization of ε-CL and 7-(prop-2-ynyl)oxepan-2-one in toluene catalyzed by BnOH/TBD at 30 °C (A) and the simulated composition profile of the copolymer obtained from a 1 : 1 monomer mixture of ε-CL and 7-(prop-2-ynyl)oxepan-2-one in toluene catalyzed by BnOH/TBD at 30 °C (B).

The same data set (total conversion vs. monomer feed composition) was also evaluated with the more complex terminal model originally proposed by Mayo and Lewis.⁵¹ The differential Mayo–Lewis equation was combined with the Skeist relation⁵² and converted to the integrated model by Meyer and Lowry.⁵³ The Meyer–Lowry model (Fig. S3†) provided similar copolymerization parameters (r_ε-CL = 0.28; r_7-is = 2.05) to the Integrated Ideal Model (r_ε-CL = 0.36; r_7-is = 2.79, Fig. 3A) without a significant change in the fit quality. Overall, the Integrated Ideal Model can sufficiently describe the experimental data, which clearly indicates the ideal copolymerization of ε-CL with the 7-isomer. The similar copolymerization behavior has been already studied for different monomer systems.^49,54,55

Copolymerization parameters obtained from the Integrated Ideal Model⁴⁹ enabled the calculation and further precise display of structural composition along the polymer chain by applying the Skeist model (Table S2† and Fig. 3B).⁵² The resulting gradient copolymer showed a lightly tapered composition profile with an increase of the ε-CL consumption at higher conversions where the more reactive 7-isomer is almost enervated (B, Fig. 3). Moreover, our kinetic experiments were further supported by quantum chemical calculations.

Quantum chemical validation of the kinetics and copolymer structure

To support our experimental findings, we conducted quantum chemical calculations. These calculations offered detailed insights into the electronic structure and reactivity of the adopted comonomers, validating the kinetic and compositional data obtained from our experiments. The integration of computational results enhanced our understanding of the copolymer structure and stability.

Initial step of the ε-CL ROP. By analogy with our previous paper,⁵⁵ the studied system consisted of the polymerized monomer (ε-CL), the initiator (BnOH), and TBD acting as a catalyst dissolved in toluene. In this three-compound system, there are possible three bimolecular complexes and one trimolecular complex, of which the BnOH–TBD bimolecular complex has the lowest Gibbs free energy. Thus, the energy of this most stable complex was taken as the ground state of the system. Based on the results of previous DFT studies of six-membered and larger cyclic lactones^56,57 as well as experimental data,^56,58 we suppose for the calculation of the ROP reaction route the “donor–acceptor” mechanism B, rather than an alternate “amide” mechanism A.⁵⁹

The calculation of the energy profiles (Table S3a†) of the initial step of the ε-CL ROP started with the conformational analysis of the initial structure I1 and the first transition structure TS12 (see Scheme 1). From all obtained conformers, the one showing the lowest Gibbs free energy of TS12 was selected for a detailed study of the ROP mechanism (Scheme 1). The free energy of the starting structure I1 under vacuum is 2.5 kcal mol⁻¹ above the ground state, which agrees very well with the value of 2.8 kcal mol⁻¹ found by Nifant'ev et al.⁵⁹ for an analogical complex of ε-CL with methanol and TBD. In toluene, this value increases to 4.6 kcal mol⁻¹. This value is only slightly lower than the free energies of the structure I1 of the 3-isomer and 7-isomer found in our previous study.⁵⁵ The free energy of the first transition state TS12 of ε-CL was found to be 21.5 kcal mol⁻¹ under vacuum and 22.3 kcal mol⁻¹ in toluene. Both these values lie between the corresponding energies of the TS12 state of the 3-isomer and 7-isomer. This finding indicates that initiation of the ε-CL as well as 7-isomer reaction will be easier than initiation of the 3-isomer one, which is sterically disfavored by the propargyl group bound next to the reactive carbonyl group. Transformation of the structure I2 into I3 proceeds with a small energy barrier of ca. 2 kcal mol⁻¹ and negligible reaction energy. Then, the structure I3 relaxes to its conformers I3r and I3r2. The free energy of the last transition state TS34 is comparable to that of the first transition state TS12. In toluene solution, the last transition state TS34 is the highest one in energy on the whole reaction path. Thus, similarly to the 7-isomer,⁵⁵ ε-CL may undergo several forward and reverse reactions between the initial state I1 and the intermediate state I3r2 before crossing the TS34 transition state. However, the energy difference between the first transition state TS12 and the highest transition state on the whole reaction path is only ca. 0.3 kcal mol⁻¹ for ε-CL (in toluene), while it is 1.1 kcal mol⁻¹ for the 7-isomer. Thus, we expect that the reverse reaction and its impact on the polymerization rate are much less significant for ε-CL than for the 7-isomer which is in agreement with the homopolymerization kinetic study (left, Fig. 2). Note that for ε-CL under vacuum, TS12 is the highest transition state. The free energy of the I4 state is 4.2 kcal mol⁻¹ under vacuum and 7.5 kcal mol⁻¹ in toluene, respectively, i.e. it is much lower than that of the TS34 state. The exothermic reaction from the I4 state to the I5 state consists of straightening of the opened ε-CL ring after cleavage of the weak NH–O hydrogen bond. The free energy of the final state I5 is −1.5 kcal mol⁻¹ under vacuum and 1.2 kcal mol⁻¹ in toluene, respectively, with respect to the ground state. Thus, the entire reaction from I1 to I5 is exothermic with a reaction energy of −3 to −4 kcal mol⁻¹. It should be pointed out that in a solution, the hydrogen bond cleaved in the reaction I4 → I5 can be replaced by a hydrogen bond to surrounding molecules, which further decreases the reaction energy and disfavors the reverse reaction I5 → I1. The complete set of the thermodynamic data (Table S4a†) and optimized Cartesian coordinates of all intermediates and transition states (Table S5†) are shown in the ESI.†

Scheme 1 Mechanism of the ε-CL ROP catalyzed by BnOH/TBD (a similar scheme is also assumed for the ROP of 3- and 7-isomers; conformers I3r and I3r2 of the structure I3 are omitted for clarity).

Subsequent step of the ε-CL ROP within homopolymerization and within copolymerization with the 3-or 7-isomer. Calculations of the energy profiles of the next step of the homopolymerization of ε-CL and its copolymerization with the 3- or 7-isomer were performed in the same way but restricted to toluene solution. The obtained results are presented in Table S3b† and compared with our previous data calculated for the polymerization of the 3- and 7-isomers.⁵⁵ It was found that the free energy of the first transition state TS12 is the highest one (rate limiting) on the whole reaction path for all combinations of the types of the added isomer units (ε-CL, 3-isomer, and 7-isomer) and the chain ends except for addition of the 3-isomer unit to the chain ending with the 7-isomer unit, for which the transition state TS23 is the highest one.

The energy barrier of the subsequent step of the ε-CL homopolymerization reaction (24.9 kcal mol⁻¹) is considerably smaller than that of both other compounds (27.7 and 26.0 kcal mol⁻¹), which agrees with the experimental finding that ε-CL homopolymerization is the fastest one (Fig. 4). It should be noted that although the reverse reaction is possible in the initial step of ε-CL homopolymerization, its effect on the rate of homopolymerization is less significant than for the 7-isomer (vide supra).

Fig. 4 Kinetic plot of the homopolymerization of ε-CL and 3- and 7-(prop-2-ynyl)oxepan-2-ones in toluene catalyzed by BnOH/TBD at 30 °C.

Regarding the copolymerization of ε-CL with the 7-isomer, the energy barrier of addition of a 7-isomer unit is lower than that of addition of a ε-CL unit for both the ε-CL chain end (24.2 vs. 24.9 kcal mol⁻¹) and 7-isomer chain end (26.0 vs. 26.3 kcal mol⁻¹), which explains the observed greater reactivity of the 7-isomer in this copolymerization despite less reactivity of this compound during homopolymerization (Fig. 2). The same effect was previously observed in the copolymerization of the 3-isomer with the 7-isomer.⁵⁵ On the other hand, in the copolymerization of ε-CL with the 3-isomer, the reactivity of the 3-isomer is expected to be lower than the reactivity of ε-CL, similarly to homopolymerization. The complete set of the thermodynamic data (Table S4b†) and the optimized Cartesian coordinates of all intermediates and transition states (Table S6†) are shown in the ESI.†

To compare the obtained theoretical results with the observed reaction rates of ε-CL and the 7-isomer during homopolymerization (left, Fig. 2), we will describe the entire observed ROP reaction simply as a 1^st order reaction with a single activation energy determined according to the Eyring–Polanyi equation

where k is the rate constant, ΔG^‡ is the Gibbs energy of activation, k_B is the Boltzmann constant, T is the temperature, h is the Planck constant, and κ is the transmission coefficient, which is often taken as equal to one. The activation energy values determined in this way are given in Table 3 together with the Gibbs energies of the highest energy transition state (see the bold values in Table S3†) in the initiation and subsequent steps of the ROP reaction.

Table 3 Experimental rate constants k, corresponding Gibbs energies of activation ΔG^‡_exp obtained from eqn (E1)† with the transmission coefficient κ taken as one and temperature T = 303 K, and the Gibbs energies of the highest energy transition state (see the bold values in Table S3†) in the initiation (ΔG^‡_ini) and subsequent (ΔG^‡_next) steps of the ROP reaction calculated by the PCM-B3LYP/6-311G(d) method. Note that there are two values of ΔG^‡_next for subsequent steps of the copolymerization corresponding to the growth of the chain ending with ε-CL of the 7-isomer unit, respectively

(a) Homopolymerization
	k (h^−1)	ΔG^‡exp (kcal mol^−1)	ΔG^‡ini (kcal mol^−1)	ΔG^‡next (kcal mol^−1)
Toluene
ε-CL	0.48	23.12	22.60	24.87
7-Isomer	0.25	23.51	22.70	25.96

---

(b) Copolymerization
	k (h^−1)	ΔG^‡exp (kcal mol^−1)	ΔG^‡ini (kcal mol^−1)	ΔG^‡next (end = ε-CL) (kcal mol^−1)	ΔG^‡next (end = 7-is) (kcal mol^−1)
Toluene
ε-CL	0.13	23.91	22.60	24.87	26.30
7-Isomer	0.38	23.26	22.70	24.16	25.96

---

The experimental values of the Gibbs energies of activation ΔG^‡_exp lie between the theoretical values for the initial step ΔG^‡_ini and for the subsequent steps ΔG^‡_next. Since the weight of the subsequent steps in the polymerization is probably greater than the initial one, theoretical values can be considered slightly overestimated. Nevertheless, for absolute values of activation energies, such differences between the DFT and experimental results are fully acceptable.

To compare the rate constants of both compounds ε-CL and the 7-isomer, we assume the same value of the transmission coefficient κ and the same temperature T. Then, eqn (1) can be rewritten as

We see that the experimental value of the ratio of rate constants k_CL/k_7-is is about 1.9, lying between the theoretical values for the initial step 1.2 and for the subsequent steps 6.1, determined from the DFT-calculated activation energies (Table 3) using eqn (2).

The experimental (right, Fig. 2) and theoretical (Table S3†) results obtained for copolymerization of ε-CL and the 7-isomer can be compared in the same way. The experimental activation energies ΔG^‡_exp lie again between the theoretical values for the initial and subsequent steps. The experimental value of the ratio k_CL/k_7-is is about 0.34. While the theoretical value of this ratio for the initial step is essentially the same as for the homopolymerization (i.e., 1.2), the more important values calculated for the subsequent steps are 0.57 and 0.31, depending on the type of chain end. Since both values are significantly less than one, we conclude that the quantum chemical calculations support the experimentally observed reverse reactivity of ε-CL and the 7-isomer during their homo- and copolymerization.

Nanoparticle self-assembly and characterization

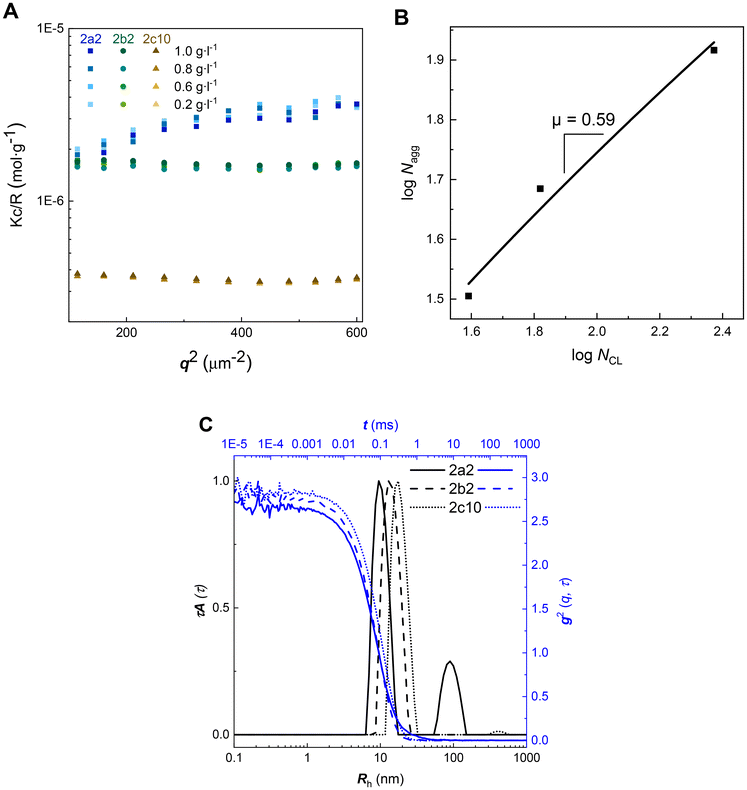
Amphiphilic diblock copolymers self-assemble into micellar aggregates of different morphologies, which are primarily dictated by the ratio between the solvophilic and solvophobic domains and by its effect on chain packing within the aggregate.⁶⁰ It has been established that the preparation method affects the size, its distribution and the stability of poly(ethylene glycol)-b-poly(ε-caprolactone) nanoparticles.⁶¹ Thus, the previously published protocol allowing the formation of well-defined and stable nanoparticles, based on injecting of PEG-b-PCL solutions in a 90% THF/water mixture into an excess amount of water and dialysis to water, was adopted.⁶¹

Light scattering (LS) is a powerful technique for analyzing nanoparticles in solution.⁶² Static light scattering (SLS), utilizing the angle-independent scattering data enabled the determination of the molecular weight of nanoparticles (Fig. 5A and Table 4), however, it did not provide information on the radius of gyration, as the size of nanoparticles is below the limit of λ/20 (λ = 660 nm as described in the Methods section in the ESI†). To assess how many polymer chains comprise one nanoparticle, we determined the aggregation number N_agg by dividing the molar mass of a nanoparticle by the molar mass of an unimer.

Fig. 5 Angle-independent inverse molecular weight of spherical micelles (A), logarithm of the aggregation number N_agg as a function of the logarithm of the number of PCL units N_CL (B) and autocorrelation functions at 90° (blue) and the corresponding apparent size distributions (black) (C).

Table 4 Characterization of nanoparticles based on the light scattering data

Entry	M W ^a (10^5 g mol^−1)	N agg ^a (−)	R H ^b (nm)	ρ (g cm^−3)
a Determined by SLS. b Determined by DLS. c ρ = 3Mw/(4πNARh^3).
2a2	3.0	32	10	0.12
2b2	6.3	41	14	0.08
2c10	27.5	81	18	0.19
Nanoparticles with the encapsulated model drug CosBA
P2a2	2.3	24	10	0.08
P2b2	12.8	83	17	0.11
P2c10	66.2	196	21	0.28

---

The scaling of the mean aggregation number was predicted for diblock copolymers A–B (A represents corona) that form micelles with thin dense coronas (N_B ≫ N_A) and for star-like micelles with extended coronas (N_B ≪ N_A).^63,64 Fitting a plot of log N_agg as a function of the logarithm of the number of PCL units (N_CL) (B, Fig. 5) yielded the scaling relation N_agg ≈ N_CL^μ where μ = 0.59. Our experimental scaling exponent was lower than those determined theoretically for either micellar type (μ = 1.0 for micelles with thin coronas and μ = 0.8 for micelles with extended coronas).⁶³ The discrepancy between our experiments and theory could be explained by the fact that only sample 2c10 (Table 2) fits to the theoretical condition N_B ≫ N_A. Moreover, our hydrophobic (B) block does not consist of one type of monomer unit, which is in contrast with the theoretical data.⁶³

The apparent size distributions of nanoparticles 2a2, 2b2, and 2c10 calculated from the dynamic light scattering (DLS) data measured at a finite scattering angle 90° were unimodal and very narrow (C, Fig. 5). The only exception was sample 2a2; however, the second distribution is minor, as it is intensity weighted (C, Fig. 5). Their hydrodynamic radii were rather small (in agreement with the angle-independent scattering observed in SLS), increasing slightly with the length of the hydrophobic block (Table 4). The average nanoparticle density was determined according to the following relationship: ρ = 3M_w/(4πN_AR_h³), where M_w stands for the molar mass of the nanoparticles determined by SLS, R_h stands for the corresponding hydrodynamic radius of the nanoparticles, and N_A is the Avogadro number. The average densities of the nanoparticles were relatively low. Small hydrodynamic radii accompanied by low aggregation numbers indicate the formation of “fluffy” solvent-swollen nanoparticles. It can be concluded that 2a2, 2b2, and 2c10 formed small spherical micelles.

In light scattering, particle size and shape are determined indirectly. Thus, we visualized the prepared nanoparticles for direct and unambiguous size and shape determination via transmission electron microscopy (TEM). We performed TEM using negative staining with uranyl acetate to improve the TEM contrast⁶⁵ and we also performed cryo-TEM. Both of these techniques depicted small, well-dispersed, and homogeneous spherical micelles of sample 2b2 (Fig. 6) with a micellar core of about 7 nm in diameter (as observed in cryo-TEM), shrinked to approximately 4 nm when the sample was dried (classical TEM). The value obtained from cryo-TEM is in a good agreement with the hydrodynamic radius determined by DLS (R_H = 14 nm, Table 4), as it corresponds to the whole core–shell nanoparticle, while the PEG hydrophilic corona cannot be visualized by TEM techniques, as soft materials with low atomic numbers do not deflect electron beam sufficiently and exhibit poor scattering contrast.^66,67

Fig. 6 Sample 2b2 visualized by TEM with negative uranyl acetate staining (left) and cryo-TEM (right, the inset shows the histogram of micelle size distribution).

Encapsulation of the model drug

As the results of the self-assembly investigation were promising, we further studied the encapsulation of a novel redox probe, COSAN-pyridinium-3-boronic acid conjugate (CosBA). As highlighted in the Introduction section, both boron clusters and boronic acids are highly relevant for cancer therapy. In the model drug, the high boron content of a boron cluster required for BNCT is combined with pH-responsive binding to 1,2- and 1,3-diols characteristic of boronic acids. Thus, together with the vicinal diol-containing polymeric DDS, significant uptake in normal tissues and adsorption to plasma proteins could be avoided while achieving microenvironment-triggered release.

A solution of polymer 2a2, the redox probe CosBA and pyridine in dry acetonitrile-d₃ was prepared and analyzed using ¹H and DOSY NMR in order to investigate the CosBA binding to the diol-decorated polymer. Pyridine was added as a ligand that facilitates the formation of boronic acid ester.⁶⁸ DOSY signals of the polymer and CosBA were integrated manually for each experiment and fitted with the exponential decay of signal intensities, demonstrating that CosBA is attached to polymer 2a2 (A, Fig. 7).

Fig. 7 DOSY (A and B) and ¹H (C) NMR monitoring of CosBA encapsulation, and a simplified scheme of the interaction between polymer 2a2, CosBA and glycerol (D).

Furthermore, we added glycerol (20 eq. with respect to CosBA) to the solution of the polymer and CosBA. Glycerol has a higher binding affinity towards CosBA in comparison with the diol-decorated polymer,⁴¹ resulting in CosBA release from the polymer, as visualized in Fig. 7B. This process was also monitored by ¹H NMR (C, Fig. 7), showing the disappearance/shift of the characteristic CosBA signal at 4.66 ppm when attached to the polymer (black and red curves, Fig. 7). The same signal was observed again after the addition of glycerol (blue curve, Fig. 7C).

Finally, we studied how the encapsulation of CosBA affects the nanoparticle characteristics. We dissolved 2a2, 2b2, and 2c10 (1 eq.) and CosBA (0.7, 0.5 and 0.4 eq. per diol-modified ε-CL unit respectively) in THF and then proceeded according to the previously used protocol to prepare nanoparticle solutions (Experimental section). The THF/water solutions containing CosBA were intensively yellow. During the dialysis, the dialysate remained colorless while the sample inside the dialysis membrane retained its yellow color. No precipitation occurred when the solvent was gradually changed from THF-rich to deionized water and for at least two weeks after the nanoparticle preparation. These observations visually confirmed the encapsulation of CosBA into polymeric micelles as the small molecules did not diffuse through the porous membrane or precipitate due to its limited solubility.

The SLS and DLS experiments of the loaded nanoparticles are summarized in Table 4. Apparent distributions of hydrodynamic radii at 130° were calculated from the corresponding autocorrelation functions (Fig. S4†).

The dispersity of loaded nanoparticles is higher in comparison with neat ones (C, Fig. 5vs. Fig. S4†) and, interestingly, significantly decreases with nanoparticle size (Fig. S4†). We observed virtually no effect of drug loading on the smallest micelles (P2a2, Table 4); however, the asymmetric shape of the distribution curve indicates the presence of a particle fraction with larger hydrodynamic radii, unresolved by the applied fit (size ratio below 2 is beyond the resolution of DLS).⁶² Conversely, loading with CosBA significantly affects the other samples. Regarding P2b2 and P2c10, CosBA incorporation results in approximately 20% and 100% increase of hydrodynamic radii and the molecular weight with the corresponding aggregation number, respectively. The growth of the micelle does not compensate fully the increase in the number of chains; consequently, the micellar density also increases by approximately 50% (Table 4).

Conclusion

In conclusion, we prepared diblock copolymers mPEG-b-P(ε-CL-co-PgCL) bearing vicinal diols by the copolymerization of ε-CL with PgCL, followed by the transformation of alkyne moieties via a thiol–yne click reaction with 1-thioglycerol. Additionally, we studied the kinetic profile of the copolymerization of ε-CL and 7-(prop-2-ynyl)-oxepan-2-one, showing the higher reactivity of the 7-isomer in this comonomer couple which was further verified by quantum chemical calculations.

The synthesized amphiphilic diblock copolymers mPEG-b-P(ε-CL-co-PgCL) decorated with vicinal diols allowed the preparation of self-assembled nanoparticles in water, which were characterized by static and dynamic light scattering. The formation of small, homogeneous spherical micelles was visualized by using conventional and cryogenic transmission electron microscopy.

Finally, we encapsulated a newly synthesized model drug, COSAN-pyridinium-3-boronic acid conjugate, into spherical micelles and investigated the effect of drug loading on these particles. The interplay between the model drug and our diblock copolymer was observed by DOSY NMR and light scattering methods. Ultimately, these findings will lead to the reproducible preparation of fine-tuned amphiphilic block copolymers capable of binding to boronic acid-based anticancer agents.

Author contributions

All authors wrote the manuscript and approved the final version of the manuscript. All authors contributed equally to this work.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors acknowledge the financial support from the LA CEUS bilateral project of the Czech Science Foundation (grant no. 21-20008 K) and the Slovenian Research Agency (project no. N1-0186). The institutional support RVO: 61389013 is gratefully acknowledged. Computational resources for quantum chemical calculations were provided by the e-INFRA CZ project (ID: 90254), supported by the Ministry of Education, Youth and Sports of the Czech Republic.

References

1. F. Perin, A. Motta and D. Maniglio, Amphiphilic copolymers in biomedical applications: Synthesis routes and property control, Mater. Sci. Eng., C, 2021, 123, 111952.
2. V. Agrahari and V. Agrahari, Advances and applications of block-copolymer-based nanoformulations, Drug Discovery Today, 2018, 23(5), 1139–1151.
3. P. Grossen, D. Witzigmann, S. Sieber and J. Huwyler, PEG-PCL-based nanomedicines: A biodegradable drug delivery system and its application, J. Controlled Release, 2017, 260, 46–60.
4. Y. Ikada and H. Tsuji, Biodegradable polyesters for medical and ecological applications, Macromol. Rapid Commun., 2000, 21(3), 117–132.
5. M. A. Woodruff and D. W. Hutmacher, The return of a forgotten polymer—Polycaprolactone in the 21st century, Prog. Polym. Sci., 2010, 35(10), 1217–1256.
6. A. Kowalski, A. Duda and S. Penczek, Kinetics and mechanism of cyclic esters polymerization initiated with tin(II) octoate, 1. Polymerization of ε-caprolactone, Macromol. Rapid Commun., 1998, 19(11), 567–572.
7. T. Biela, A. Kowalski, J. Libiszowski, A. Duda and S. Penczek, Progress in Polymerization of Cyclic Esters: Mechanisms and Synthetic Applications, Macromol. Symp., 2006, 240(1), 47–55.
8. H. R. Kricheldorf, A. Stricker and D. Langanke, Polylactones, 52. Tin Carboxylates as Initiators of ε-Caprolactone, Macromol. Chem. Phys., 2001, 202(15), 2963–2970.
9. T. Öztürk and G.Ş Demir, One-step synthesis of poly(methyl methacrylate-b-ε-caprolactone) block copolymer by simultaneous ATRP and ROP, J. Chem. Sci., 2024, 136(4), 68.
10. Z. Karami, S. Sadighian, K. Rostamizadeh, M. Parsa and S. Rezaee, Naproxen conjugated mPEG–PCL micelles for dual triggered drug delivery, Mater. Sci. Eng., C, 2016, 61, 665–673.
11. X. Shuai, T. Merdan, A. K. Schaper, F. Xi and T. Kissel, Core-Cross-Linked Polymeric Micelles as Paclitaxel Carriers, Bioconjugate Chem., 2004, 15(3), 441–448.
12. X. J. Loh, The effect of pH on the hydrolytic degradation of poly(ε-caprolactone)-block-poly(ethylene glycol) copolymers, J. Appl. Polym. Sci., 2013, 127(3), 2046–2056.
13. C. K. Williams, Synthesis of functionalized biodegradable polyesters, Chem. Soc. Rev., 2007, 36, 1573–1580.
14. X. Lou, C. Detrembleur and R. Jérôme, Novel Aliphatic Polyesters Based on Functional Cyclic (Di)Esters, Macromol. Rapid Commun., 2003, 24(2), 161–172.
15. J.-P. Latere, P. Lecomte, P. Dubois and R. Jérôme, 2-Oxepane-1,5-dione: A Precursor of a Novel Class of Versatile Semicrystalline Biodegradable (Co)polyesters, Macromolecules, 2002, 35(21), 7857–7859.
16. S. Lenoir, R. Riva, X. Lou, C. Detrembleur, R. Jérôme and P. Lecomte, Ring-Opening Polymerization of α-Chloro-ε-caprolactone and Chemical Modification of Poly(α-chloro-ε-caprolactone) by Atom Transfer Radical Processes, Macromolecules, 2004, 37(11), 4055–4061.
17. M. Liu, N. Vladimirov and J. M. J. Fréchet, A New Approach to Hyperbranched Polymers by Ring-Opening Polymerization of an AB Monomer: 4-(2-Hydroxyethyl)-ε-caprolactone, Macromolecules, 1999, 32(20), 6881–6884.
18. S. Ponsart, J. Coudane and M. Vert, A Novel Route To Poly(ε-caprolactone)-Based Copolymers via Anionic Derivatization, Biomacromolecules, 2000, 1(2), 275–281.
19. B. Nottelet, A. El Ghzaoui, J. Coudane and M. Vert, Novel Amphiphilic Poly(ε-caprolactone)-g-poly(l-lysine) Degradable Copolymers, Biomacromolecules, 2007, 8(8), 2594–2601.
20. B. Nottelet, M. Vert and J. Coudane, Novel Amphiphilic Degradable Poly(ε-caprolactone)-graft-poly(4-vinyl pyridine), Poly(ε-caprolactone)-graft-poly(dimethylaminoethyl methacrylate) and Water-Soluble Derivatives, Macromol. Rapid Commun., 2008, 29(9), 743–750.
21. R. Riva, S. Schmeits, C. Jérôme, R. Jérôme and P. Lecomte, Combination of Ring-Opening Polymerization and “Click Chemistry”: Toward Functionalization and Grafting of Poly(ε-caprolactone), Macromolecules, 2007, 40(4), 796–803.
22. P. Lecomte, R. Riva, C. Jérôme and R. Jérôme, Macromolecular Engineering of Biodegradable Polyesters by Ring-Opening Polymerization and ‘Click’ Chemistry, Macromol. Rapid Commun., 2008, 29(12–13), 982–997.
23. W. H. Binder and R. Sachsenhofer, ‘Click’ Chemistry in Polymer and Materials Science, Macromol. Rapid Commun., 2007, 28(1), 15–54.
24. T. Öztürk and E. Meyvacı, Synthesis and characterization poly(ε-caprolactone-b-ethylene glycol-b-ε-caprolactone) ABA type block copolymers via “Click” chemistry and ring-opening polymerization, J. Macromol. Sci., Part A: Pure Appl. Chem., 2017, 54(9), 575–581.
25. T. Öztürk, A. Kılıçlıoğlu, B. Savaş and B. Hazer, Synthesis and characterization of poly(ε-caprolactone-co-ethylene glycol) star-type amphiphilic copolymers by “click” chemistry and ring-opening polymerization, J. Macromol. Sci., Part A: Pure Appl. Chem., 2018, 55(8), 588–594.
26. S. Buwalda, A. Al Samad, A. El Jundi, A. Bethry, Y. Bakkour, J. Coudane and B. Nottelet, Stabilization of poly(ethylene glycol)-poly(ε-caprolactone) star block copolymer micelles via aromatic groups for improved drug delivery properties, J. Colloid Interface Sci., 2018, 514, 468–478.
27. A. Leroy, A. Al Samad, X. Garric, S. Hunger, D. Noël, J. Coudane and B. Nottelet, Biodegradable networks for soft tissue engineering by thiol–yne photo cross-linking of multifunctional polyesters, RSC Adv., 2014, 4(60), 32017–32023.
28. A. B. Lowe, C. E. Hoyle and C. N. Bowman, Thiol-yne click chemistry: A powerful and versatile methodology for materials synthesis, J. Mater. Chem., 2010, 20(23), 4745–4750.
29. O. Jazkewitsch and H. Ritter, Formation and Characterization of Inclusion Complexes of Alkyne Functionalized Poly(ε-caprolactone) with β-Cyclodextrin. Pseudo-Polyrotaxane-Based Supramolecular Organogels, Macromolecules, 2011, 44(2), 375–382.
30. S. R. Petersen, J. A. Wilson and M. L. Becker, Versatile Ring-Opening Copolymerization and Postprinting Functionalization of Lactone and Poly(propylene fumarate) Block Copolymers: Resorbable Building Blocks for Additive Manufacturing, Macromolecules, 2018, 51(16), 6202–6208.
31. S. Ata, S. Basak, D. Mal and N. K. Singha, Synthesis and self-assembly behavior of POSS tethered amphiphilic polymer based on poly(caprolactone) (PCL) grafted with poly(acrylic acid) (PAA) via ROP, ATRP, and CuAAC reaction, J. Polym. Res., 2017, 24(2), 19.
32. S. Bhattacharya, M. N. Ganivada, H. Dinda, J. Das Sarma and R. Shunmugam, Biodegradable Copolymer for Stimuli-Responsive Sustained Release of Doxorubicin, ACS Omega, 2016, 1(1), 108–117.
33. O. Stöhr, J. Winsberg and H. Ritter, A Poly(vinyl alcohol)-graft-Copolyester: Synthesis of a Novel Graft Copolymer Containing Adamantane Moieties as Guest for Cyclodextrin, Macromol. Chem. Phys., 2013, 214(13), 1445–1451.
34. L. Tan, S. Maji, C. Mattheis, Y. Chen and S. Agarwal, Antimicrobial Hydantoin-grafted Poly(ε-caprolactone) by Ring-opening Polymerization and Click Chemistry, Macromol. Biosci., 2012, 12(12), 1721–1730.
35. O. Jazkewitsch, A. Mondrzyk, R. Staffel and H. Ritter, Cyclodextrin-Modified Polyesters from Lactones and from Bacteria: An Approach to New Drug Carrier Systems, Macromolecules, 2011, 44, 1365–1371.
36. D. Vrbata, S. Kereiche, K. Kalíková and M. Uchman, Stimuli-responsive multifunctional micelles of ABC vs. ACB triblock terpolymers using reversible covalent bonding of phenylboronic acid: controlled synthesis, self-assembly and model drug release, J. Mol. Liq., 2021, 335, 116528.
37. J. S. Suk, Q. Xu, N. Kim, J. Hanes and L. M. Ensign, PEGylation as a strategy for improving nanoparticle-based drug and gene delivery, Adv. Drug Delivery Rev., 2016, 99, 28–51.
38. A. Pitto-Barry, Polymers and boron neutron capture therapy (BNCT): a potent combination, Polym. Chem., 2021, 12(14), 2035–2044.
39. Y. Nakagawa and I. Yukishige, Chapter 1 - Molecular architecture and therapeutic potential of lectin mimics, in Adv. Carbohydr. Chem. Biochem, ed. D. Horton, Academic Press, 2012, vol. 68, pp. 1–58.
40. P. C. Trippier and C. McGuigan, Boronic acids in medicinal chemistry: anticancer, antibacterial and antiviral applications, MedChemComm, 2010, 1(3), 183–198.
41. A. Stubelius, S. Lee and A. Almutairi, The Chemistry of Boronic Acids in Nanomaterials for Drug Delivery, Acc. Chem. Res., 2019, 52(11), 3108–3119.
42. V. Ďorďovič, J. Vojtová, S. Jana and M. Uchman, Charge reversal and swelling in saccharide binding polyzwitterionic phenylboronic acid-modified poly(4-vinylpyridine) nanoparticles, Polym. Chem., 2019, 10(40), 5522–5533.
43. D. Vrbata and M. Uchman, Preparation of lactic acid- and glucose-responsive poly(ε-caprolactone)-b-poly(ethylene oxide) block copolymer micelles using phenylboronic ester as a sensitive block linkage, Nanoscale, 2018, 10(18), 8428–8442.
44. T. D. Malouff, D. S. Seneviratne, D. K. Ebner, W. C. Stross, M. R. Waddle, D. M. Trifiletti and S. Krishnan, Boron Neutron Capture Therapy: A Review of Clinical Applications, Front. Oncol., 2021, 11, 601820.
45. T. M. Goszczyński, K. Fink, K. Kowalski, Z. J. Leśnikowski and J. Boratyński, Interactions of Boron Clusters and their Derivatives with Serum Albumin, Sci. Rep., 2017, 7(1), 9800.
46. C.-C. Yeh, C.-N. Chen, Y.-T. Li, C.-W. Chang, M.-Y. Cheng and H.-I. Chang, The Effect of Polymer Molecular Weight and UV Radiation on Physical Properties and Bioactivities of PCL Films, Cell. Polym., 2011, 30(5), 261–276.
47. B. D. Fairbanks, T. F. Scott, C. J. Kloxin, K. S. Anseth and C. N. Bowman, Thiol−Yne Photopolymerizations: Novel Mechanism, Kinetics, and Step-Growth Formation of Highly Cross-Linked Networks, Macromolecules, 2009, 42(1), 211–217.
48. K. Matyjaszewski and A. H. E. Müller, Macromolecular Nomenclature Note No. 12, Polym. Prepr. (Am. Chem. Soc., Div. Polym. Chem.), 1997, 38, 6–9.
49. J. Blankenburg, E. Kersten, K. Maciol, M. Wagner, S. Zarbakhsh and H. Frey, The poly(propylene oxide-co-ethylene oxide) gradient is controlled by the polymerization method: determination of reactivity ratios by direct comparison of different copolymerization models, Polym. Chem., 2019, 10, 2863–2871.
50. F. T. Wall, The Structure of Vinyl Copolymers, J. Am. Chem. Soc., 1941, 63(7), 1862–1866.
51. F. R. Mayo and F. M. Lewis, Copolymerization. I. A Basis for Comparing the Behavior of Monomers in Copolymerization; The Copolymerization of Styrene and Methyl Methacrylate, J. Am. Chem. Soc., 1944, 66(9), 1594–1601.
52. I. Skeist, Copolymerization: the Composition Distribution Curve, J. Am. Chem. Soc., 1946, 68(9), 1781–1784.
53. V. E. Meyer and G. G. Lowry, Integral and differential binary copolymerization equations, J. Polym. Sci., Part A: Gen. Pap., 1965, 3(8), 2843–2851.
54. E. Grune, J. Bareuther, J. Blankenburg, M. Appold, L. Shaw, A. H. E. Müller, G. Floudas, L. R. Hutchings, M. Gallei and H. Frey, Towards bio-based tapered block copolymers: the behaviour of myrcene in the statistical anionic copolymerisation, Polym. Chem., 2019, 10(10), 1213–1220.
55. R. Mundil, L. Kanizsová, P. Toman, O. Kočková and M. Uchman, Unveiling the reverse reactivity and composition profile of copolymers from synthesized and separated 3-/7-(prop-2-ynyl)oxepan-2-one isomers: implications for precise polymer structure prediction, Polym. Chem., 2024, 15(17), 1695–1703.
56. A. Pascual, H. Sardón, F. Ruipérez, R. Gracia, P. Sudam, A. Veloso and D. Mecerreyes, Experimental and computational studies of ring-opening polymerization of ethylene brassylate macrolactone and copolymerization with ε-caprolactone and TBD-guanidine organic catalyst, J. Polym. Sci., Part A: Polym. Chem., 2015, 53(4), 552–561.
57. L. Simón and J. M. Goodman, The Mechanism of TBD-Catalyzed Ring-Opening Polymerization of Cyclic Esters, J. Org. Chem., 2007, 72(25), 9656–9662.
58. A. Chuma, H. W. Horn, W. C. Swope, R. C. Pratt, L. Zhang, B. G. G. Lohmeijer, C. G. Wade, R. M. Waymouth, J. L. Hedrick and J. E. Rice, The Reaction Mechanism for the Organocatalytic Ring-Opening Polymerization of l-Lactide Using a Guanidine-Based Catalyst: Hydrogen-Bonded or Covalently Bound?, J. Am. Chem. Soc., 2008, 130(21), 6749–6754.
59. I. Nifant'ev, A. Shlyakhtin, V. Bagrov, B. Lozhkin, G. Zakirova, P. Ivchenko and O. Legon'kova, Theoretical and experimental studies of 1,5,7-triazabicyclo[4.4.0]dec-5-ene-catalyzed ring opening/ring closure reaction mechanism for 5-, 6- and 7-membered cyclic esters and carbonates, React. Kinet., Mech. Catal., 2016, 117(2), 447–476.
60. M. Karayianni and S. Pispas, Self-Assembly of Amphiphilic Block Copolymers in Selective Solvents, in Fluorescence Studies of Polymer Containing Systems, ed. K. Procházka, Springer International Publishing, Cham, 2016, pp. 27–63.
61. R. Šachl, M. Uchman, P. Matějíček, K. Procházka, M. Štěpánek and M. Špírková, Preparation and Characterization of Self-Assembled Nanoparticles Formed by Poly(ethylene oxide)-block-poly(ε-caprolactone) Copolymers with Long Poly(ε-caprolactone) Blocks in Aqueous Solutions, Langmuir, 2007, 23(6), 3395–3400.
62. W. Schaertl, Light Scattering from Polymer Solutions and Nanoparticle Dispersions, 2007.
63. A. Halperin and S. Alexander, Polymeric micelles: their relaxation kinetics, Macromolecules, 1989, 22(5), 2403–2412.
64. E. B. Zhulina and O. V. Borisov, Theory of Block Polymer Micelles: Recent Advances and Current Challenges, Macromolecules, 2012, 45(11), 4429–4440.
65. J. R. Harris, C. Roos, R. Djalali, O. Rheingans, M. Maskos and M. Schmidt, Application of the negative staining technique to both aqueous and organic solvent solutions of polymer particles, Micron, 1999, 30(4), 289–298.
66. K. Zhang, J. Yi and D. Chen, Bimodal porous superparticles with the optimized structure prepared by self-limited aggregation of PEG-coated mesoporous nanofibers for purification of protein–dye conjugates, J. Mater. Chem. A, 2013, 1(46), 14649–14657.
67. J. B. Hall, M. A. Dobrovolskaia, A. K. Patri and S. E. McNeil, Characterization of nanoparticles for therapeutics, Nanomedicine, 2007, 2(6), 789–803.
68. A. L. Korich, A. R. Walker, C. Hincke, C. Stevens and P. M. Iovine, Synthesis, characterization, and star polymer assembly of boronic acid end-functionalized polycaprolactone, J. Polym. Sci., Part A: Polym. Chem., 2010, 48(24), 5767–5774.

---

Footnote

† Electronic supplementary information (ESI) available: The complete experimental section includes the description of the methods and (co)polymerization protocols, quantum chemical calculations, and all kinetic data. See DOI: https://doi.org/10.1039/d4py01363h

---