Enhanced thermoelectric performance of a wide-bandgap twisted heterostructure of graphene and boron nitride
Naveen
Kumar
 and
Chandan
Bera
and
Chandan
Bera
 *
*
Institute of Nano Science and Technology, Sector-81, Knowledge City, Sahibzada Ajit Singh Nagar, Punjab Pin - 140306, India. E-mail: chandan@inst.ac.in
First published on 13th March 2024
Abstract
The manipulation of the relative twist angle between consecutive layers in two-dimensional (2D) materials dramatically modulates their electronic characteristics. Twisted bilayer graphene (tblg) and twisted boron nitride (tBN) exhibit Moiré patterns that have the potential to revolutionize various fields, from electronics to quantum materials. Here, the electronic and thermoelectric properties of 21.8° tblg and 21.8° tBN and a 21.8° twisted graphene/boron nitride (Gr/BN) heterostructure were investigated using density functional theory and Boltzmann transport theory. The twisted Gr/BN heterostructure possesses a wide band gap of 1.95 eV, which overcomes the limitations of the absence of a band gap of graphene and boron nitride's extremely wide band gap. A significant increase in thermoelectric power factor was obtained for the heterostructure compared to its parent materials, 21.8° tblg and 21.8° tBN. It has a thermal conductivity of 5.88 W m−1 K−1 at 300 K, which is much lower than those of 21.8° tblg and 21.8° tBN. It is observed that graphene plays an important role in electron transport or power factor enhancement, whereas BN helps in reducing the thermal conductivity in twisted Gr/BN systems. A strong role of boundary scattering in thermal transport compared to electrical transport was observed. A high figure of merit (ZT) of 1.28 for the twisted Gr/BN heterostructure at a ribbon width of L = 10 nm and T = 900 K was obtained. This suggests its suitability as an effective material for thermoelectric applications.
1. Introduction
In recent years, thermoelectric materials have attracted considerable interest owing to their exceptional capability to convert waste heat into electrical energy for energy recovery and waste heat utilization applications. Although the low energy conversion efficiency of thermoelectric effect-based technology has limited its potential, recent discoveries have presented promising avenues to boost its performance.1–3 The efficiency of a thermoelectric device is governed by the thermoelectric figure of merit, ZT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and κ is the total thermal conductivity. The tuning of these parameters separately due to their interdependence is a major problem in enhancing the ZT. The reduced dimensionality can lead to improved thermoelectric performance due to quantum confinement effects. 2D materials exhibit unique electronic properties and tunable band structures, which can be engineered to achieve high thermoelectric efficiency.4–6 Twisting bilayer graphene results in a significant decrease in its thermal conductivity. Reduction of the Brillouin zone and alteration of the high symmetry direction give rise to the emergence of hybrid folded phonons that have a significant effect on thermal transport.7 Some other studies on twisted bilayer graphene have demonstrated that the thermodynamic properties of blg can be modulated through the rotation of atomic planes.8–10 A decrease of 22% in thermal conductivity at room temperature in bilayer graphene by twisting it at 20° was previously reported by us.11 For instance, Ahmed et al.12 and Li et al.13 reported 36% and 33%, respectively, reductions in thermal conductivity for 21.8° tblg compared to its untwisted configuration. Here, we have obtained a similar reduction of 38% in the thermal conductivity of 21.8° tblg considering translational symmetry only. The imposition of rotational symmetry further amplifies this reduction to 48%. Boron nitride serves as an unobtrusive dielectric material for graphene to develop various electronic devices exhibiting the quantum Hall effect, leading to an alteration in the optical and electronic properties of graphene.14–16 Crucially, with the ongoing progress in preparation technology, the technique of dynamically adjusting the interlayer rotation angle in graphene/h-BN heterostructures has been significantly developed.17,18 This development results in a Gr/BN multilayer superlattice as the foremost system extensively explored experimentally.19–21 For instance, an experimental study on twisted graphene/h-BN heterostructures reported Hofstadter's butterfly and fractional quantum effects, suggesting their successful synthesis and the potential to study their physical properties.22 A recent study23 on a 21.8° twisted Gr/BN heterostructure reported an unusual thermal conductivity of 0.095 W m−1 K−1 at 300 K, and also its enlarged Grüneisen parameter (∼4500) does not allow the validation of these results. Moreover, the mechanisms of electron scattering were not taken into consideration, which can alter the electric properties. There is a strong stress distribution in the Gr/BN heterostructure for small twisted angles of up to 3.74°.24 It is observed that with anincrease in the twisted angle, the stress distribution range reduces, and it becomes a normal distribution for a twist angle of ∼5.0°.10,25 Therefore, the stress distribution may have minimal impact for a large twisted angle of 21.8° Here, we employed density functional theory (DFT) and Boltzmann transport theory (BTE) incorporating the relaxation time to investigate the structural, electronic, and thermoelectric properties of 21.8° tblg and 21.8° tBN and the 21.8° twisted Gr/BN heterostructure. An enhancement in the thermoelectric power factor and a reduction in thermal conductivity were obtained for the twisted Gr/BN heterostructure compared to its parent materials. A significant effect of boundary scattering on thermal transport was also observed. Our findings demonstrate that the modulation of thermoelectric properties can be achieved through the creation of a 21.8° twisted heterostructure of graphene and boron nitride.2. Methodology
21.8° twisted bilayer graphene (tblg) was created by using 28 carbon atoms using Vaspkit software.26 Similarly, 21.8° twisted boron nitride was also formed with 28 atoms, having 14 boron atoms and 14 nitrogen atoms. The optimized lattice constants for tblg are a = b = 6.53 Å and for tBN they are a = b = 6.64 Å. As the lattice constants of graphene and BN are similar with a lattice mismatch of <1.7%, it is easy to prepare a heterostructure of these materials. The constructed 21.8° twisted heterostructure using graphene and boron nitride has 28 atoms and an optimized lattice constant of 6.56 Å. A vacuum of 20 Å was used to neglect the interlayer interaction between the periodic images.Electronic structure calculations based on density functional theory were performed using the projector augmented wave framework (PAW)27 as implemented in the Vienna ab initio simulation package (VASP).28 The generalized gradient approximation (GGA) with the Perdew–Burke– Ernzerhof exchange–correlation functional was used.29 The van der Waals interactions were corrected by employing a semi-empirical correction term incorporated within the DFT-D3 method along with Becke–Johnson damping.30 A plane-wave basis set with an energy cutoff of 750 eV was employed to ensure greater convergence of the results under the total energy convergence criteria on the order of 10−8 eV throughout all the DFT-based calculations. A dense k-grid of 10 × 10 × 1 was used for the geometry optimization. The electrical transport properties were calculated using the Boltzmann transport theory under relaxation time approximation (RTA) implemented in BoltzTraP2 software.31 The thermoelectric coefficients, electrical conductivity, Seebeck coefficient, and electronic thermal conductivity were calculated using the following equations:32,33
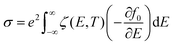 | (1) |
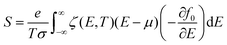 | (2) |
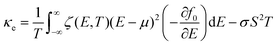 | (3) |
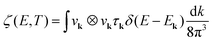 is the transport distribution function, νk is the group velocity of the charge carrier in a particular direction, Ek is the energy of the corresponding electronic state, μ represents the chemical potential, and τk is the total relaxation time for the scattering of electrons. The relaxation time for electron–phonon scattering τe-ph was calculated as2
is the transport distribution function, νk is the group velocity of the charge carrier in a particular direction, Ek is the energy of the corresponding electronic state, μ represents the chemical potential, and τk is the total relaxation time for the scattering of electrons. The relaxation time for electron–phonon scattering τe-ph was calculated as2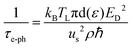 | (4) |
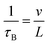 , where v is the velocity of electrons and L is the ribbon width. The total relaxation time was calculated considering both electron–phonon scattering and boundary scattering of electrons.
, where v is the velocity of electrons and L is the ribbon width. The total relaxation time was calculated considering both electron–phonon scattering and boundary scattering of electrons.
| Materials | E D (eV) | u s (m s−1) | ρ (kg m−3) |
|---|---|---|---|
| tblg | 6.85 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835 835 |
3971 |
| tBN | 2.53 | 3455 | 3290 |
| t Gr/BN | 1.98 | 2980 | 3241 |
The phonon dispersion was calculated from the force constants obtained using the finite displacement method and PHONOPY35 under a displacement of 0.01 Å. The rotational sum rules were enforced using the HIPHIVE package.36 A supercell size of 2 × 2 × 1 with 112 atoms was used. The lattice thermal conductivity was determined from Boltzmann transport formalism under relaxation time approximation described as2,37
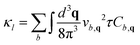 | (5) |
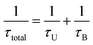 , where τU is the relaxation time for the Umklapp scattering of phonons calculated as
, where τU is the relaxation time for the Umklapp scattering of phonons calculated as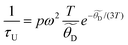 | (6) |
3. Results and discussion
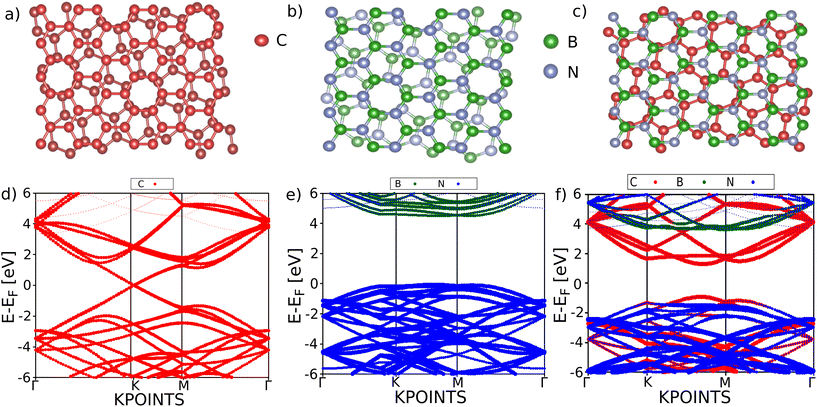
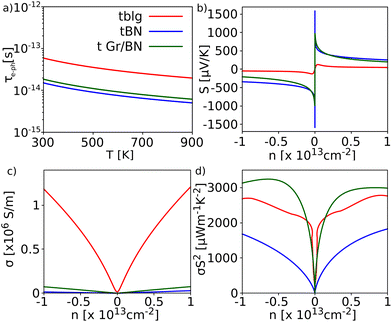
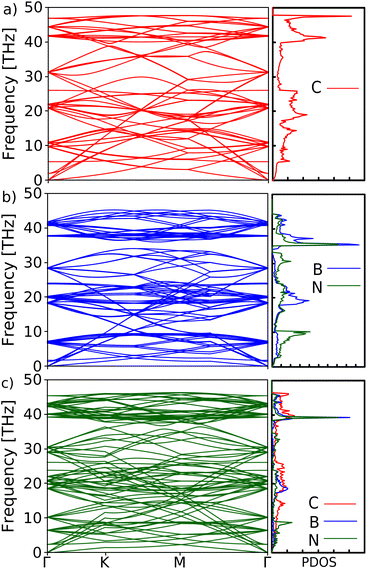
The optimized crystal structures of 21.8° tblg, 21.8° tBN and the twisted Gr/BN heterostructure are shown in Fig. 1(a–c). The top view shows the formation of Moiré patterns in these structures. Fig. 1(d–f) show the electronic band structures with the atomic contribution of these structures. tblg exhibits a metallic nature, consistent with prior findings that reported a zero band gap.42 tBN has a bandgap of 4.40 eV, which suggests that the bandgap is decreased compared to single-crystal boron nitride.43 The conduction band for tBN is mainly contributed by the boron atom, while the valence band is contributed by the nitrogen atom. The 21.8° heterostructure of graphene and boron nitride displays a bandgap of 1.95 eV, effectively addressing the absence of a band gap in tblg and an ultra-wide bandgap in tBN, which are limitations in their individual parent materials. This demonstrates the heterostructure as a semiconductor with a wide bandgap. The conduction bands near the Fermi level are dominated by the C atom, while the valence bands are contributed by both C and N atoms, indicating that C atoms are responsible for the semiconducting bandgap. The semiconducting nature of the material is good for the high thermoelectric performance.44Fig. 2 shows the electron–phonon scattering relaxation times and variations of the Seebeck coefficient, electrical conductivity, and thermoelectric power factor for n-type and p-type carrier concentrations. The relaxation time decreases with an increase in temperature. The relaxation time for tblg is high, followed by the twisted Gr/BN heterostructure and then tBN. tblg has very high electrical conductivity but possesses a low Seebeck coefficient, primarily because of its metallic nature. Conversely, hexagonal tBN demonstrates a favorable Seebeck coefficient, albeit accompanied by its lower electrical conductivity. The twisted Gr/BN heterostructure has lower electrical conductivity than tblg but higher than tBN. Furthermore, its moderate Seebeck coefficient results in a high power factor compared to its parent materials. The n-type case has a slightly higher power factor than the p-type case (Fig. 2d). This indicates that n-type doping is more efficient than p-type doping for these materials. The variation of power factor with the carrier concentration at T = 300 K shows that the tblg/tBN heterostructure has a maximum power factor of 3238 μWm−1 K−2 at a carrier concentration of n = 6.2 × 1012 cm−2. The power factor of tblg and tBN is 2661 μWm−1 K−2 and 1572 μWm−1 K−2, respectively, at the same carrier concentration. This indicates the heterostructure effect boosts the thermoelectric power factor for these twisted materials.Thermal transport is an important parameter in determining the thermoelectric performance of a material. Fig. 3(a–c) show the phonon band structures of tblg, tBN, and the twisted heterostructure. The absence of negative frequency modes confirms the dynamic stability of these materials. There is no phonon gap between the acoustic and optical branches in these materials, indicating a strong optical–acoustic phonon scattering, which can additionally inhibit the lattice thermal conductivity. The localized optical phonons characterized by low frequencies create multiple scattering channels, leading to substantial suppression of phonon transport.45 The obtained phonon dispersion for tblg is in agreement with the previous report.46 The presence of additional scattering channels in twisted bilayer graphene, forbidden in untwisted bilayer graphene by momentum conservation laws, can lead to a reduction in thermal conductivity compared to its bilayer counterpart.47 The projected phonon density of states for tBN shows that the acoustic phonon bands are contributed by both boron and nitrogen. In the case of the tblg/tBN heterostructure, it is notable that boron nitride makes substantial contributions to the acoustic modes, indicating that thermal transport in this system is mainly influenced by it.
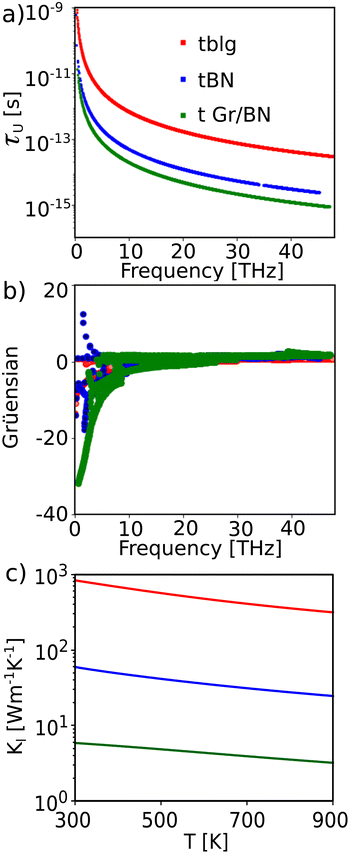
The calculated relaxation times for the Umklapp scattering of phonons, Grüneisen parameter, and lattice thermal conductivity are shown in Fig. 4(a–c). By observing the relaxation time, tblg has the highest relaxation time among the three materials, followed by tBN. In the case of the Grüneisen parameter, boron nitride has a high Grüneisen parameter (7.32) compared to tblg (1.09) related to the anharmonicity of the material. The combination of an intermediate relaxation time and the Grüneisen parameter results in a lower lattice thermal conductivity for tBN when compared to tblg. Conversely, tblg has the highest thermal conductivity due to its high relaxation time and lower Grüneisen parameter. The low relaxation time of the twisted Gr/BN heterostructure indicates a high scattering of phonons. Furthermore, the very high Grüneisen parameter (21.2) results in a much lower thermal conductivity than tblg and tBN. The lattice thermal conductivity shows T−1 dependence on temperature, indicating the dominance of the Umklapp scattering of phonons in these materials. The obtained value of thermal conductivity at T = 300 K for 21.8° tblg is 832 Wm−1 K−1, which is less than 20° tblg and also 48% lower than that of untwisted blg (1400 Wm−1 K−1).11 The high reduction in our case compared to these reports can be understood by analyzing the difference between the calculated and reported phonon dispersions. The enforcement of rotational sum rules in our calculations results in the splitting of acoustic modes that can provide more scattering channels and can reduce thermal conductivity further. An experimental study on 32.2° twisted bilayer graphene shows a thermal conductivity of 1412.8 ± 390 W mK−1 at room temperature.47 In another study, a thermal conductivity range of 1305–657 W mK−1 was observed for approximately 21° tblg, depending on the grain boundary size.48 Therefore, the calculated value is comparable to the experimentally obtained results for similar twisted blg structures. Similarly, the thermal conductivity of tBN is 60 Wm−1 K−1 at room temperature, which is much lower than that of bilayer boron nitride.49 The twisted Gr/BN heterostructure has a thermal conductivity of 5.88 Wm−1 K−1 at T = 300 K. This obtained value is higher than the previously reported theoretical value (0.095 Wm−1 K−1) due to its enlarged erroneous Grüneisen parameter of ∼4500.23 There is a substantial decrease in the thermal conductivity of the twisted heterostructure in comparison with tblg and tBN. The results are analogous to those in the prior study on a BN/silicene heterostructure, wherein the BN layer governs thermal transport while the silicene layer dominates electronic transport due to its weak interlayer non-covalent interaction.50 Here, the electrical transport is dominated by graphene and BN dominates the thermal transport in the Gr/BN heterostructure. Doping or defects in the heterostructure will further reduce the thermal conductivity, which will improve the thermoelectric figure of merit.
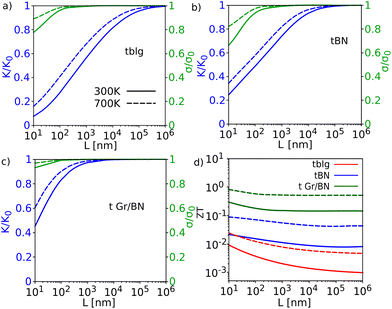
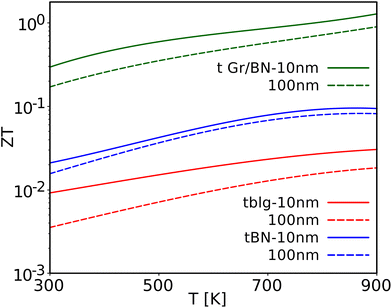
The obtained thermoelectric figure of merit (ZT) for the twisted Gr/BN heterostructure is 0.14 at room temperature, which is 17.5 times and 142 times higher than those of tBN (ZT = 0.008) and tblg (ZT ≃ 0.001) respectively. Although these materials boast a substantial power factor, their ZT values are relatively low for thermoelectric applications due to their high thermal conductivity compared to conventional thermoelectric materials. The thermal conductivities of the graphene monolayer and twisted bilayer are strongly reduced by boundary scattering.11,51,52 Here, the effect of boundary scattering on thermal and electrical transport was explored. Fig. 5(a–c) show the relative contribution of the ribbon width in the electrical conductivity (σ) and thermal conductivity (κ) at T = 300 K and 700 K. It can be seen that the reductions in κ and σ are greater at 300 K compared to at 700 K for all these materials. The reduction in electrical conductivity of tBN is greater than that for tblg and the tblg/tBN heterostructure due to its low electron–phonon scattering relaxation time. A minor effect of boundary scattering on electrical conductivity for the tblg/tBN heterostructure was observed due to the dominance of electron–phonon scattering. Also, the reduction in the thermal conductivity is significant, but less compared to tblg and tBN, by 55% at L = 10 nm and T = 300 K. The ZT value significantly increases with the reduction in boundary size and obtains a high value at a ribbon width of 10–100 nm compared to its sheet value (Fig. 5d). The temperature-dependent figure of merit at L = 10 nm and 100 nm is shown in Fig. 6. The ZT value at 10 nm is higher than that at 100 nm due to the greater reduction in thermal conductivity at 10 nm. The optimized figure of merit for tblg and tBN at a ribbon width of 10 nm and T = 900 K is 0.03 and 0.08, respectively. Furthermore, in the case of the heterostructure, ZT exhibits an increase with values reaching 0.90 and 1.28 at ribbon widths of 100 nm and 10 nm, respectively, at a temperature of 900 K. This emphasizes the significant enhancement in ZT achieved by constructing a 21.8° twisted heterostructure of graphene and boron nitride. This suggests that the twisted Gr/BN heterostructure can be used as a promising material for applications based on the thermoelectric effect.
4. Conclusion
In conclusion, we have theoretically investigated the electronic structural and thermoelectric properties of 21.8° twisted bilayer graphene, 21.8° twisted boron nitride, and a twisted Gr/BN heterostructure using density functional theory and Boltzmann transport theory. A significant increase in the power factor was obtained for the twisted Gr/BN heterostructure compared to tblg and tBN. The comparatively lower thermal conductivity and strong boundary effect result in a high figure of merit of 1.28 for the twisted Gr/BN heterostructure at a ribbon width of L = 10 nm and T = 900 K. The mechanisms of twisting the heterostructures and introducing boundary scattering can be a potent strategy to enhance the thermoelectric performance of materials. The successful synthesis of the Gr/BN heterostructure, along with the theoretical predictions, will stimulate research interest in the electron and phonon transport properties of twisted 2D heterostructures through experimental studies.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
The project was initiated and supervised by C. B. The data curation has been performed by N. K. The manuscript was written, reviewed, and edited by both N. K. and C. B. All authors have read and acknowledged the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
NK acknowledges a PhD fellowship from CSIR, India (grant no. 09/1129(0017)/2019-EMR-I). We also acknowledge the National Supercomputing Mission (NSM) for providing the computing resources of ‘PARAM SMRITI’ at NABI, Mohali, which is implemented by C-DAC and supported by the Ministry of Electronics and Information Technology (MeitY) and the Department of Science and Technology (DST), Government of India.References
- S. Abbey, H. Jang, B. Frimpong, N. Kumar, W. H. Nam, J. H. Park, C. V. Nguyen, H. Shin, J. Y. Song and S.-D. Park, et al. , Energy Environ. Sci., 2023, 16, 125–137 RSC.
- R. Gupta, N. Kumar, P. Kaur and C. Bera, Phys. Chem. Chem. Phys., 2020, 22, 18989–19008 RSC.
- Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69 CrossRef CAS PubMed.
- D. Li, Y. Gong, Y. Chen, J. Lin, Q. Khan, Y. Zhang, Y. Li, H. Zhang and H. Xie, Nano-Micro Lett., 2020, 12, 1–40 CrossRef PubMed.
- K. Nielsch, J. Bachmann, J. Kimling and H. Böttner, Adv. Energy Mater., 2011, 1, 713–731 CrossRef CAS.
- H. Wang, C. Li, P. Fang, Z. Zhang and J. Z. Zhang, Chem. Soc. Rev., 2018, 47, 6101–6127 RSC.
- W. Ren, J. Chen and G. Zhang, Appl. Phys. Lett., 2022, 121, 140501 CrossRef CAS.
- T. Cea and F. Guinea, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2107874118 CrossRef CAS PubMed.
- M. Koshino and Y.-W. Son, Phys. Rev. B, 2019, 100, 075416 CrossRef CAS.
- X. Liu, R. Peng, Z. Sun and J. Liu, Nano Lett., 2022, 22, 7791–7797 CrossRef CAS PubMed.
- N. Kumar, A. Chaudhuri, V. Arya, C. Bakli and C. Bera, J. Appl. Phys., 2023, 134, 044301 CrossRef CAS.
- S. Ahmed, S. Alam and A. Jain, Phys. Rev. B, 2023, 108, 235202 CrossRef CAS.
- C. Li, B. Debnath, X. Tan, S. Su, K. Xu, S. Ge, M. R. Neupane and R. K. Lake, Carbon, 2018, 138, 451–457 CrossRef CAS.
- M. Yankowitz, Q. Ma, P. Jarillo-Herrero and B. J. LeRoy, Nat. Rev. Phys., 2019, 1, 112–125 CrossRef CAS.
- J. Wang, F. Ma and M. Sun, RSC Adv., 2017, 7, 16801–16822 RSC.
- Z.-Y. Ong, G. Zhang and Y.-W. Zhang, 2D Mater., 2021, 8, 035032 CrossRef CAS.
- D. Wang, G. Chen, C. Li, M. Cheng, W. Yang, S. Wu, G. Xie, J. Zhang, J. Zhao and X. Lu, et al. , Phys. Rev. Lett., 2016, 116, 126101 CrossRef PubMed.
- R. Ribeiro-Palau, C. Zhang, K. Watanabe, T. Taniguchi, J. Hone and C. R. Dean, Science, 2018, 361, 690–693 CrossRef CAS.
- D. Kaldre, I. Klose and N. Maulide, Science, 2018, 361, 664–667 CrossRef CAS PubMed.
- J. Jung, A. M. DaSilva, A. H. MacDonald and S. Adam, Nat. Commun., 2015, 6, 6308 CrossRef CAS PubMed.
- M. Yankowitz, J. Jung, E. Laksono, N. Leconte, B. L. Chittari, K. Watanabe, T. Taniguchi, S. Adam, D. Graf and C. R. Dean, Nature, 2018, 557, 404–408 CrossRef CAS PubMed.
- C. R. Dean, L. Wang, P. Maher, C. Forsythe, F. Ghahari, Y. Gao, J. Katoch, M. Ishigami, P. Moon and M. Koshino, et al. , Nature, 2013, 497, 598–602 CrossRef CAS PubMed.
- N. Gupta, S. Rani, P. Kumari, R. Ahuja and S. J. Ray, Carbon, 2023, 215, 118437 CrossRef CAS.
- W. Ren, S. Lu, C. Yu, J. He, Z. Zhang, J. Chen and G. Zhang, Appl. Phys. Rev., 2023, 10, 041404 CAS.
- Y. Cheng, Z. Fan, T. Zhang, M. Nomura, S. Volz, G. Zhu, B. Li and S. Xiong, Mater. Today Phys., 2023, 35, 101093 CrossRef CAS.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- G. K. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- R. Gupta, B. Kaur, J. Carrete and C. Bera, J. Appl. Phys., 2019, 126, 225105 CrossRef.
- N. Kumar and C. Bera, Phys. B, 2021, 619, 413206 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- F. Eriksson, E. Fransson and P. Erhart, Adv. Theory Simul., 2019, 2, 1800184 CrossRef.
- P. Kaur, S. Chakraverty, A. K. Ganguli and C. Bera, Phys. Status Solidi B, 2017, 254, 1700021 CrossRef.
- T. Feng and X. Ruan, Phys. Rev. B, 2018, 97, 045202 CrossRef CAS.
- B. Liao, Nanoscale Energy Transport: Emerging phenomena, methods and applications, IOP Publishing, 2020 Search PubMed.
- L. Lindsay, D. Broido and T. Reinecke, Phys. Rev. Lett., 2013, 111, 025901 CrossRef CAS PubMed.
- T. Feng, L. Lindsay and X. Ruan, Phys. Rev. B, 2017, 96, 161201 CrossRef.
- S. Deng, X. Cai, Y. Zhang and L. Li, Carbon, 2019, 145, 622–628 CrossRef CAS.
- K. Watanabe, T. Taniguchi and H. Kanda, Nat. Mater., 2004, 3, 404–409 CrossRef CAS PubMed.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- K. Pal, Y. Xia, J. He and C. Wolverton, Phys. Rev. Mater., 2019, 3, 085402 CrossRef CAS.
- D. L. Nika, A. I. Cocemasov and A. A. Balandin, Appl. Phys. Lett., 2014, 105, 031904 CrossRef.
- H. Li, H. Ying, X. Chen, D. L. Nika, A. I. Cocemasov, W. Cai, A. A. Balandin and S. Chen, Nanoscale, 2014, 6, 13402–13408 RSC.
- T. B. Limbu, K. R. Hahn, F. Mendoza, S. Sahoo, J. J. Razink, R. S. Katiyar, B. R. Weiner and G. Morell, Carbon, 2017, 117, 367–375 CrossRef CAS.
- C. Wang, J. Guo, L. Dong, A. Aiyiti, X. Xu and B. Li, Sci. Rep., 2016, 6, 25334 CrossRef CAS PubMed.
- Y. Cai, Q.-X. Pei, G. Zhang and Y.-W. Zhang, J. Appl. Phys., 2016, 119, 65102 CrossRef.
- A. Bagri, S.-P. Kim, R. S. Ruoff and V. B. Shenoy, Nano Lett., 2011, 11, 3917–3921 CrossRef CAS PubMed.
- H. Liu, Y. Lin and S. Luo, J. Phys. Chem. C, 2014, 118, 24797–24802 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |