A fluorite-structured HfO2/ZrO2/HfO2 superlattice based self-rectifying ferroelectric tunnel junction synapse†
Dong Hyun
Lee‡
a,
Ji Eun
Kim‡
b,
Yong Hyeon
Cho
a,
Sojin
Kim
c,
Geun Hyeong
Park
a,
Hyojun
Choi
a,
Sun Young
Lee
a,
Taegyu
Kwon
 a,
Da Hyun
Kim
a,
Moonseek
Jeong
a,
Hyun Woo
Jeong
a,
Younghwan
Lee
d,
Seung-Yong
Lee
a,
Da Hyun
Kim
a,
Moonseek
Jeong
a,
Hyun Woo
Jeong
a,
Younghwan
Lee
d,
Seung-Yong
Lee
 *c,
Jung Ho
Yoon
*c,
Jung Ho
Yoon
 *e and
Min Hyuk
Park
*e and
Min Hyuk
Park
 *af
*af
aDepartment of Materials Science and Engineering and Inter-University Semiconductor Research Center, College of Engineering, Seoul National University, Seoul 08826, Republic of Korea. E-mail: minhyuk.park@snu.ac.kr
bElectronic Materials Research Center, Korea Institute of Science and Technology (KIST), Seoul 02792, Republic of Korea
cDivision of Materials Science and Engineering, Hanyang University, Seoul 04763, Republic of Korea. E-mail: syonglee@hanyang.ac.kr
dDepartment of Materials Science and Engineering Chonnam National University, Gwangju 61186, Republic of Korea
eSchool of Advanced Materials Science and Engineering, Sungkyunkwan University, Suwon 16419, Republic of Korea. E-mail: junghoyoon@skku.edu
fInstitute of Engineering Research, College of Engineering, Seoul National University, Gwanak-Ro 1, Gwanak-Gu, Seoul 08826, Republic of Korea
First published on 26th September 2024
Abstract
A self-rectifying ferroelectric tunnel junction that employs a HfO2/ZrO2/HfO2 superlattice (HZH SL) combined with Al2O3 and TiO2 layers is proposed. The 6 nm-thick HZH SL effectively suppresses the formation of non-ferroelectric phases while increasing remnant polarization (Pr). This enlarged Pr modulates the energy barrier configuration, consequently achieving a large on/off ratio of 1273 by altering the conduction mechanism from off-state thermal injection to on-state Fowler–Nordheim tunneling. Moreover, the asymmetric Schottky barriers at the top TiN/TiO2 and bottom HfO2/Pt interfaces enable a self-rectifying property with a rectifying ratio of 1550. Through calculations and simulations it is found that the device demonstrates potential for achieving an integrated array size exceeding 7k while maintaining a 10% read margin, and shows potential for application in artificial synapses for neuromorphic computing with an image recognition accuracy above 92%. Finally, the self-rectifying behavior and device-to-device variation reliability are confirmed in a 9 × 9 crossbar array structure.
New conceptsIn this research, we advance ferroelectric tunnel junctions (FTJs) by integrating a superlattice-structured ferroelectric layer within a TiN/TiO2/Al2O3/HfO2/ZrO2/HfO2/Pt stack, explicitly designed to enhance neuromorphic computing systems, particularly within crossbar array (CBA) architectures. This novel configuration significantly improves the on/off ratio and self-rectifying properties, essential for reducing the reliance on additional selector devices and for increasing the integration density in CBAs. The inclusion of the HfO2/ZrO2/HfO2 superlattice suppressed non-ferroelectric phase formation and enlarged remnant polarization. Consequently, the large polarization switched conduction mechanism from thermal injection at the off state to Fowler–Nordheim tunneling at the on state contributed to increase the on/off ratio. Additionally, the asymmetric Schottky barrier facilitated the self-rectifying properties. The rectifying properties were proved to maintain 10% read margin for more than a 7k array size. This was proved in a 9 × 9 CBA by its excellent cycle-to-cycle variations. This practical proof suggests that the reliability originates from its solid physical model of sub-unit-cell displacement of ions in a ferroelectric layer. These enhancements facilitate achieving more compact and energy-efficient neuromorphic circuits, where rapid and efficient processing is critical. |
Introduction
With exponentially increasing quantities of data to be processed and stored, the energy required for computing is drastically increasing, necessitating novel computing paradigms and new data storage technologies.1 It is predicted that by 2040, the energy required for computing will exceed the total energy production of the world.2 Significant virtues of novel data storage techniques include high operation speed, high power efficiency, high storage density through physical scaling down, and sufficient reliability.1 Emerging data storage techniques based on various physical mechanisms include resistive switching random-access memory (ReRAM), phase-change random-access memory (PcRAM), magnetic random-access memory (MRAM), and ferroelectric random-access memory (FeRAM). These emerging memory devices have also been suggested as hardware suitable for novel energy-efficient computing paradigms such as neuromorphic computing and process-in-memory (PIM).Among these, FeRAM is based on the intrinsic properties of a special class of materials where the centro-symmetry is broken, inducing spontaneous polarization that can modulate the electrical properties of the material itself or nearby materials.3,4 The polarization switching, which governs the program and erase and read processes of FeRAMs, is based on the sub-unit-cell displacement of ions, distinguished from the long-range drift of defects or ions or phase transition. The defect-free physical mechanism of ferroelectricity, based on solid fundamental theory, is attracting increasing interest from both academia and industry. Especially, the discovery of fluorite-structured ferroelectrics such as HfO2 and ZrO2 has revived intensive research on FeRAMs.
There are three different types of FeRAMs based on cell structures: 1 transistor-1 capacitor type FeRAM, a 1-transistor type ferroelectric field-effect transistor (FeFET), and a 1-resistor type ferroelectric tunnel junction (FTJ). Despite their relatively short history of research, FTJs are considered a promising candidate for advanced memory technology in conventional computing paradigms and as core devices for novel computing paradigms such as neuromorphic computing and PIM.5–8 A cell size of 4F2 can be achieved even in planar crossbar array (CBA) structures, and an even lower effective cell size of 4F2/n can theoretically be achieved in n-layer 3D CBA structures.9 Unlike the conductance modulation in ReRAM and PcRAM, the tunneling mechanism, which is in principle free from Joule heating and offers defect-free resistive switching based on reversible sub-unit-cell motion, is considered an inherent advantage of FTJs.
However, the decrease in the film thickness of fluorite-structured ferroelectrics such as HZO is known to induce non-ferroelectric phase formation due to the surface energy effect.10 Worse still, the high concentration of oxygen vacancies, frequently formed by the scavenging effect of electrode materials, further facilitates the formation of a tetragonal phase.11,12 Moreover, increasing the on/off ratio in FTJs is highly challenging because the ratio, governed by an asymmetric potential barrier, tends to be relatively lower compared to the ratio caused by the formation and rupture of direct conducting paths such as vacancies or metallic filaments in ReRAMs or phase changes in PcRAMs.13
Another issue is the integration of devices for neuromorphic computing. Neuromorphic computing relies on matrix-vector multiplication operations for processing vast amounts of data, making the implementation of crossbar arrays (CBAs) essential for practical applications. Thus, in most cases, an external selector device, which has either rectification functionality or a nonlinear current–voltage relationship, is required to prevent the so-called sneak current in the CBA structure. However, there are numerous problems with this approach. For example, the operating voltage and current ranges of the switching device and the selector device must be well matched, but these characteristics are challenging to control as they are strongly influenced by the type of material, switching mechanism, device structure, and more. Additionally, since multiple layers are stacked, there is a high probability of large step differences, which can lead to the formation of leakage paths. It is also difficult to achieve uniform behavior due to the distribution of each device. For the construction of high-performance CBAs, there is a growing demand for the development of FTJs with self-rectifying and nonlinear characteristics, aiming to suppress the sneak currents without additional device integration. Therefore, for the practical applications of FTJs as an advanced memory device in a conventional Von Neumann architecture or platforms for next-generation neuromorphic computing, the development of FTJs with high on/off ratios and strong self-rectifying properties is in urgent demand.14–17
Therefore, in this study, we propose a self-rectifying resistive switching memory device utilising a superlattice-structured ferroelectric layer composed of a TiN/TiO2/Al2O3/HfO2/ZrO2/HfO2/Pt stack. The HfO2/ZrO2/HfO2 superlattice (HZH SL) is a 6 nm-thick ferroelectric layer, which suppresses the interfacial non-ferroelectric phase and increases Pr. This enhanced Pr significantly improves the on/off ratio to 1273, as proven with conduction mechanism analysis. Moreover, the lower Schottky barrier at the TiN/TiO2 interface compared to that at HfO2/Pt contributes to the large rectifying ratio of 1550. With these properties, we have demonstrated that a highly integrated CBA of over 104 size can be realized with the proposed device. For neuromorphic computing, we demonstrated multilevel resistance switching that can achieve Modified National Institute of Standards and Technology (MNIST) image recognition accuracy of over 92%. Finally, the feasibility of achieving self-rectifying properties and device-to-device variation (DTDV) reliability was proven using a 9 × 9 size CBA.
Results and discussion
Fig. 1 illustrates the main strategies suggested in this study to address the general issues of ferroelectric tunnel junctions (FTJs) such as (1) polarization degradation with decreasing film thickness, (2) low on/off ratios which limit the range of conductance available for synaptic operation, and (3) low rectifying ratios that constrain the maximum array size without the co-integration of a selector device, such as a transistor or nonlinear resistor. As depicted in the left panel of Fig. 1, the polycrystalline HfO2/ZrO2/HfO2 superlattice (HZH SL), in place of HZO, is adopted to suppress the formation of a non-ferroelectric tetragonal phase, which is commonly stabilised by high concentrations of oxygen vacancies at the interfacial region or due to surface energy effects.10–12 As shown in the center panel of Fig. 1, the ferroelectric HZH SL is combined with dielectric Al2O3 and TiO2, enhancing the conductance modulation range enabled by an asymmetric potential barrier shape.The optimised stack in this study is TiO2 (17 nm)/Al2O3 (1 nm)/ferroelectric (6 nm) from the top. Depending on the Pr direction, the energy band structure of the oxide layers between the electrodes changes, as shown in Fig. 1. In the calculations, the assumed relative dielectric constants were 30 for both TiO2 and the ferroelectric material, and 9 for Al2O3. Finally, as depicted in the right panel of Fig. 1, the carrier injection barrier is engineered by adopting TiN/TiO2 and Pt/HfO2 interfaces as top and bottom sides, respectively. The Schottky barrier heights of TiN/TiO2 and ferroelectric/Pt were 0.37 eV and 2.65 eV, respectively. These values which were confirmed by the conduction mechanism analysis presented later.
To empirically validate the theoretical result that ferroelectricity-induced Pr is responsible for the resistive switching behaviours in our device, we fabricated three variants of the device incorporating different ferroelectric layers: HfO2, Hf0.5Zr0.5O2 (HZO) solid solution, and HZH SL, as illustrated in Fig. 2(a and b). The HZH SL was deposited through 15 cycles of HfO2, followed by 30 cycles of ZrO2, and another 15 cycles of HfO2, utilising atomic layer deposition (ALD). The formation of the polycrystalline HZH SL was confirmed through an energy-dispersive spectroscopy (EDS) line scan on a cross-sectional scanning transmission electron microscopy (STEM) image, as shown in Fig. 2(c). This image presents the separated HfO2/ZrO2/HfO2 layers as well as the TiO2 and Al2O3 layers. The details of the sample preparation are included in the Methods section.
The crystallographic structure of HfO2, HZO and HZH SL was rigorously assessed through grazing-incidence X-ray diffraction (GIXRD) measurements. The diffraction patterns obtained are depicted in Fig. 2(d), where the arrows indicate the reference peak positions and x(hkl) denotes the (hkl) planes of the x-phase. In the analysis, the sample with HfO2 prominently displayed peaks corresponding to the m-phase at 2θ angles of ∼28.5° and 31.5° referring to m(−111) and m(111) diffraction peaks, respectively. A comparative evaluation of the devices incorporating HZO and HZH SL revealed notable differences in peak positions associated with o(111)/t(101). Specifically, the peaks corresponding to the o(111)/t(101) planes were observed at a lower 2θ angle in the HZH SL device compared to that in the HZO device. This observation, aligned with the lower reference peak position of o(111), suggests that the relative o-phase fraction can be higher in the device with the HZH SL.18–21 A detailed examination of the GIXRD spectra, as illustrated in Fig. 2(e), further supports this finding, indicating a potential increase in the fraction of the ferroelectric o-phase within the HZH SL device.
Moreover, it has been previously reported that an increase in the aspect ratio (AR), calculated using the o(111)/t(101) and o(002) planes, serves as an indicator of a higher relative fraction of the o-phase.18,22 The aspect ratios for the o-phase and t-phase are defined as 2a/(b + c) and c/a, respectively. Through deconvolution of the peak positions shown in Fig. 2(d), the calculated AR values for HZH SL and HZO were determined to be 1.003 and 0.996, respectively. These findings suggest a higher fraction of the o-phase in the HZH SL device, corroborating the hypothesis that the structural composition and doping strategy employed significantly influence the stabilization of the ferroelectric phase.
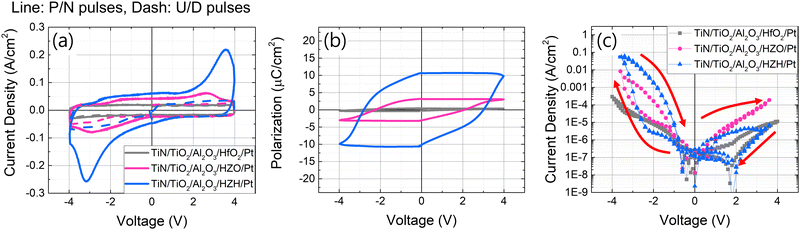
The electrical performance of each device is systematically analyzed and presented in Fig. 3. To investigate ferroelectricity, we applied positive-up negative-down (PUND) and bipolar triangular pulses of ±4 V 1 kHz. The schematic of the pulses is shown in Fig. S1(a) (ESI†). The results measured using PUND pulses are shown in Fig. 3(a and b), while the results for triangular pulses are shown in Fig. S1(b and c) (ESI†). The resultant current in the ferroelectric material due to triangular pulses can be attributed to three primary components: the dielectric response, leakage current, and polarization switching. Given that the pulse frequency remains constant, the current attributed to the dielectric response is also constant. Conversely, the leakage current increases with an increase in voltage. Notably, ferroelectric polarization switching occurs at a specific coercive voltage (Vc), manifesting as a distinct peak in the current profile.
As depicted in Fig. S1(b) (ESI†), all devices exhibited an increase in current with increasing voltage, consistent across both polarities. Because it is difficult to distinguish between the ferroelectric switching and leakage current, we conducted the PUND measurement, which allows the acquisition of nonvolatile polarization switching current by applying pulses in the same direction. Fig. 3(a) shows the current by each PUND pulse, where the current by P and N pulses is shown in the solid line, but the current by U and D pulses is shown in the dashed line. Since the current by U and D pulses does not include the Pr response, subtracting the response by U and D from P and N can give information about the current by ferroelectricity. The device incorporating the HZH SL shows a pronounced current peak at approximately −3V. This observation is further corroborated in Fig. 3(b), where the HZH SL device demonstrates the highest Pr. To confirm the ferroelectricity in the device with the HZH SL, the measurements in random 4 difference cells were conducted as well, which are shown in Fig. S1(d–g) (ESI†). This outcome aligns with the earlier crystallographic analysis, which indicates a higher fraction of the ferroelectric o-phase in the HZH SL device.
Upon further analysis, Fig. 3(c) reveals that the device incorporating the HZH SL, which exhibited the highest Pr, also demonstrated the most significant resistive switching capability. This device achieved an impressive maximum on/off current ratio of 1273 at −2.2 V, alongside a rectifying ratio of 1550. The rectifying ratio is defined as the current ratio between the on-current at a forward bias (in this context, negative voltage) and that at a reverse bias.
Additionally, the correlation between polarization and conductance states is shown in Fig. S2 (ESI†), where the conductance modulation exhibits a hysteresis that corresponds to the hysteresis in the polarization-voltage curve. Fig. S3 (ESI†) further demonstrates multilevel resistance changes depending on applied direct current (DC) voltage. In comparison, the device utilising HZO showed considerably lower on/off and rectifying ratios, approximately 16 and 18, respectively. Meanwhile, the device with HfO2 did not display resistive switching characteristics, with a rectifying ratio of around 10. To verify the results more convincingly, measurements were conducted at 5 different cells for each device, as well as with 5 repeating voltage cycles, which briefly show the DTDV and cycle-to-cycle variation (CTCV). For the best-performing device with HZH, a more rigorous measurement with 50 voltage pulse cycles was conducted. The results are shown in Fig. S4(a–f) (ESI†). For the quantitative evaluation of DTDV and CTCV, the ratio of standard deviation (σ) to mean (μ) current density at −2 V was calculated. The values obtained after positive and negative voltage writing were averaged, and the results are shown in Fig. S4(g) (ESI†). The DTDV of the device with HZH was calculated using measurements from a 9 × 9 crossbar array (CBA). The measured data are shown later. Although all devices demonstrate high resistance to CTCV, the devices with HfO2 and HZO exhibited worse DTDV compared to the device with HZH. This can be attributed to the complex polymorphs of the ferroelectric material, resulting in an inhomogeneous distribution of phases in each device. In the case of the device with HZH, the σ/μ × 100 values are 16.0 and 11.6% for DTDV and CTCV, respectively. These values prove the feasibility of utilising ferroelectric-based memory devices to solve the variability issues in the devices based on the defects.23–26
These findings indicate that the resistive switching behaviour in the proposed device is predominantly influenced by the Pr of the ferroelectric material. However, the presence of rectifying properties, despite being relatively modest, suggests that these characteristics are also affected by the other oxide layers and electrode materials in the device structure. This nuanced interplay highlights that the contributions of other components cannot be overlooked.
To elucidate the contribution of each layer to the device's performance, the current density–voltage (J–V) curves with a DC bias with 0.2 V incremental steps were assessed on the devices with varying layer compositions. Based on the full stack with TiN/TiO2 (17 nm)/Al2O3 (1 nm)/HZH/Pt, the devices without each oxide layer are compared and the measurement results are presented in Fig. 4. First, the device without the HZH SL exhibited no resistive switching characteristics as shown in Fig. 4(a). This observation implies that the operation of the proposed device does not rely on defect-based resistive random-access memory (RRAM) mechanisms, such as filamentary or valency changes within the TiO2 layer.
The DTDV and CTCV in the devices shown in Fig. 4 are also assessed in Fig. S5 (ESI†). The results confirm that the properties observed in Fig. 4 are not limited to single cells within the device structure. The low σ/μ × 100 values in the devices with HZH, similar to those in the device with the full stack, also prove the homogeneous properties of the FTJ with the HZH ferroelectric material, even in different stacking structures.
Excluding that shown in Fig. 4(a), devices including the HZH SL demonstrated resistive switching capabilities. Among these, the one without the TiO2 layer shows the lowest on/off ratio and rectifying ratio of 303 and 57, respectively. Conversely, for the device without Al2O3, the highest on/off ratio of 1804 and rectifying ratio of 2365 were measured. The possible origin of the higher ratio than that of the device with Al2O3 is the increased field (E) drop caused by Pr on the TiO2 layer. E on TiO2 (ETiO2) is proportional to the total capacitance of the device (Ctot) over the capacitance of TiO2(CTiO2). Considering the dielectric constants mentioned in Fig. 1 and the thickness of each layer, ETiO2 can be 1.145 times increased without Al2O3. Since the energy is proportional to E according to the Poisson equation, the energy barrier modulation by the charge of Pr can be larger.
However, this configuration suffered from reliability issues; after the 3rd cycle with ±2.8 V, a formation process was initiated, transitioning the device behaviour to that of a conventional RRAM based on conductive filament formation, as illustrated in Fig. S5(f) (ESI†).27 Note that since we did not set a specific compliance current, the device soon became a permanent broken-down state.
The problem with the device becoming akin to RRAM is that once the filaments are formed, the barrier at the HZH/Pt becomes low, and the rectifying property disappears, as evidenced in Fig. S5(f) (ESI†) following the forming process. Moreover, devices reliant on the movement of defects within the dielectric exhibit inherent stochasticity.28,29 On the other hand, the Al2O3 layer between TiO2 and HZH SL can serve as a protective barrier against oxygen vacancy generation. Consequently, the device maintains high on/off and rectifying ratios, as demonstrated in Fig. 4(d), preserving the primary resistive switching mechanism based on ferroelectric polarization rather than transitioning to defect-based RRAM. This ensures high reliability and consistent rectifying properties, as further evidenced in Fig. S4(f) (ESI†). Additionally, endurance and retention assessments presented in Fig. S6(a) and (b) (ESI†) show that the device successfully maintains an on/off ratio greater than 10 over 106 cycles and sustains extrapolated performance with an on/off ratio of ∼8 for up to 10 years at 80 °C, respectively.
The reliability concerns highlighted in Fig. S5(f) (ESI†) are attributed to the generation of oxygen vacancies during the TiO2 deposition process with oxygen plasma. This has been supported by quantifying oxygen vacancies using the electron energy loss spectrum (EELS) obtained using a STEM. The results from STEM-EELS, along with the process of quantifying the oxygen vacancy concentration, are depicted in Fig. S7 (ESI†). We observed a higher concentration of oxygen vacancies within the HfO2 layer, adjacent to the TiO2 layer, compared to ZrO2, especially when the Al2O3 barrier was absent. The elevated oxygen vacancy levels at the HZH interface with TiO2 suggest that applying a positive voltage to the TiN top electrode can drift the vacancies towards the bottom electrode, potentially forming conductive filaments or even causing a weak tolerance to dielectric breakdown. This hypothesis is further supported by the reset process, where applying a negative voltage retracts the vacancies from the interface with Pt, reversing the resistivity change. Notably, the direction of voltage needed to switch the resistivity in the device based on vacancies is opposite to what would be expected based on ferroelectric polarization switching.
In addition to the reliability assessment, the switching speed and energy consumption of the device were evaluated through the application of DC voltage, as illustrated in Fig. S8 (ESI†). Here, the switching time for the set process is defined as the moment at which the current plateau at the fully off ends and the current begins to increase as the resistance switches to the on state. On the other hand, the reset switching time was defined at the beginning of the current plateau by the resistance state switching to the off state. In the measured switching with the above definition, the required time for the set and reset processes was 5 ms and 1 ms, respectively. The power consumption, defined as the integration over the switching time of the product of the voltage and current, was 187 fJ for the set switching and 49 fJ for the reset switching. As shown in Table S1 (ESI†), compared to previously reported self-rectifying devices, this device not only exhibits superior rectifying and nonlinearity characteristics but also achieves low energy consumption due to its relatively low on-current, small operation voltage, and fast switching speed.
The subsequent step of the investigation delves into the conduction mechanisms specific to the full-stack device configuration comprising TiN/TiO2/Al2O3/HZH/Pt layers. By employing a combination of empirical assessments and theoretical modelling, the contributions of ferroelectric polarization and interfacial effects to the overall conduction pathway can be elucidated. The calculation of E on each layer was conducted based on the permittivities and thicknesses of the dielectrics mentioned in Fig. 1(b), considering charge continuity. Specifically, Elayer = (V × Ctot/Clayer)/tlayer, where the Elayer, Clayer, and tlayer are the E of the inserted layer, capacitance of the inserted layer, and the thickness of the inserted layer, respectively. In addition, for the calculation of E, the absolute value of applied voltage was taken. The results of the conduction mechanism analysis are shown in Fig. 5, with the applied voltage range for fitting indicated at the top of each graph. In the off state under negative forward bias, the conduction mechanism is thermionic emission (TE) through the TiO2 layer, as detailed in Fig. 5(a). TE occurs when carriers overcome the Schottky barrier at the interface between the metal electrode and the dielectric layer via thermal energy, with the barrier being lowered by the image force effect.30 The current density resulting from TE can be expressed using
 | (1) |
Eqn (1) suggests that ln(J/T2) should be linearly proportional to E1/2 at a constant temperature, indicating a region where TE can potentially occur. In the voltage range up to −2.2 V (equivalent to 0.91 (MV cm)−1/2 for |E|1/2), this linear relationship was observed up to 313 K. At a temperature above 313 K, the ln(J/T2) value deviates from the linear relationship. Thus, the fitting was conducted up to −2 V. However, this linear relationship alone does not definitively confirm TE; further verifying that εi, which can be calculated from the slope, should be compatible with εi of the dielectric material. The average εi extracted at various temperatures was 6.75, which corresponds closely to the squared refractive index values of TiO2 (where the refractive index values (n) of TiO2, Al2O3, and HfO2 are approximately 2.61, 1.77, and 1.9, respectively).31–33
Furthermore, the effective barrier height of  can be calculated through the slope in the plot of ln(J/T2) vs. 1/T. Finally, the intercept of the effective barrier height to E1/2 is ϕB at the interface TiN/TiO2, which is 0.37 eV. The plots of the above processes are shown in Fig. S9 (ESI†).
can be calculated through the slope in the plot of ln(J/T2) vs. 1/T. Finally, the intercept of the effective barrier height to E1/2 is ϕB at the interface TiN/TiO2, which is 0.37 eV. The plots of the above processes are shown in Fig. S9 (ESI†).
In the case of the on state in the negative bias, the dominant conduction mechanism confirmed is the Fowler–Nordheim tunneling (FNT). While TE describes the phenomenon where carriers are injected by overcoming the energy barrier with thermal energy, FNT is a quantum mechanical phenomenon, as carriers tunnel through the energy barrier. The difference between FN and direct tunneling (DT) is the thinning of the barrier width to less than the thickness of the thin film, thereby increasing the probability of carrier tunneling. J resulting from FNT can be described using the following equation:
 | (2) |
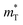 is the tunneling effective mass. From eqn (2), it can be inferred that the conduction following FNT presents a linear relationship when plotting ln(J/E2) as a function of 1/|E|. The linear plot range of voltage was <−1 V as shown in Fig. 5(b). However, observing this linear trend alone is insufficient for definitive confirmation of FNT. Additional verification requires considering the effective electron mass, which can be deduced from the slope of this plot,
is the tunneling effective mass. From eqn (2), it can be inferred that the conduction following FNT presents a linear relationship when plotting ln(J/E2) as a function of 1/|E|. The linear plot range of voltage was <−1 V as shown in Fig. 5(b). However, observing this linear trend alone is insufficient for definitive confirmation of FNT. Additional verification requires considering the effective electron mass, which can be deduced from the slope of this plot,  , ensuring its compatibility with the theoretical expectations for the dielectric material involved. The calculated
, ensuring its compatibility with the theoretical expectations for the dielectric material involved. The calculated  in Fig. 5(b) is 0.08. It is known that the increase of the relative dielectric constant and low ϕB lower the ratio of
in Fig. 5(b) is 0.08. It is known that the increase of the relative dielectric constant and low ϕB lower the ratio of  .34 Considering the results of the study by Hinkle et al., where the ratios of SiO2 and HfO2 are 0.55 and 0.15, respectively, 0.08 seems a reasonable value.34 Therefore, the mechanism by which the polarization charge induced by the ferroelectric switches the resistance in the device is that the positive charge at the interface with Al2O3 induces a high E, sufficient to change the conduction mechanism from TE to FNT.
.34 Considering the results of the study by Hinkle et al., where the ratios of SiO2 and HfO2 are 0.55 and 0.15, respectively, 0.08 seems a reasonable value.34 Therefore, the mechanism by which the polarization charge induced by the ferroelectric switches the resistance in the device is that the positive charge at the interface with Al2O3 induces a high E, sufficient to change the conduction mechanism from TE to FNT.
A schematic of the variation of the energy band structure summarizing the above situation is depicted in Fig. 1(b). According to the Poisson equation, when a positive charge is placed at the interface with Al2O3 (indicated by the blue arrow pointing left for Pr), the energy level at the TiO2/Al2O3 interface decreases, allowing FNT. In contrast, when a negative charge is located at the Al2O3/HZH interface (indicated by the red arrow pointing right for Pr), the energy level at the TiO2/Al2O3 interface increases, preventing FNT and thus establishing TE as the conduction mechanism. Therefore, the HZH ferroelectric layer is essential for realizing resistive switching as proven in Fig. 3, although the conduction mechanism occurs through the TiO2 layer. The resistance switching is driven by the modulation of the energy barrier, with the conduction mechanism changing due to the ferroelectric polarization in the HZH layer.
One of the challenges with two-terminal ferroelectric-based tunnel memories is the low on-current density critical for effective sensing operations.13 Traditionally, reducing the thickness of the film is considered a method to increase J. However, in this device configuration, reducing the TiO2 layer thickness does not serve as a viable solution. The desired increase in J, where the current originates from the FNT through the TiO2 barrier, necessitates a thinner tunneling barrier. This implies that for the same applied voltage, E across TiO2 should be higher. Since the film thickness and capacitance exhibit an inverse relationship, merely reducing the film thickness does not alter E within the TiO2 FNT layer, though it may lower the operational voltage needed to switch the ferroelectric polarization. A potential resolution could involve substituting TiO2 with a material possessing a lower dielectric constant to effectively increase the voltage drop across TiO2.
Finally, regarding the rectifying properties, the current under positive reverse bias is governed by DT through the interface of HZH/Pt. The DT is similar to the FNT, which occurs based on a fully quantum mechanical mechanism. The difference is that DT does not involve a reduction in the barrier thickness when increasing E. J is given as
 | (3) |
Given eqn (3), the plot of ln(J/E2) versus 1/|E| is a logarithmic relation. Fig. 5(c) shows well-fitted logarithmic plots across all temperatures within the voltage range of 0.2 to 2.6 V. Compared to the TE observed at the TiN/TiO2 interface, the DT observed here indicates that among the interface-limited conduction mechanisms, the higher Schottky barrier can suppress carriers from overcoming the barrier, making DT the dominant conduction mechanism. As a result, the rectifying property is realized. The schematic of this asymmetric barrier effect is shown in Fig. 1(c). This result suggests that increasing the HZH thickness can help increase the rectifying ratio.
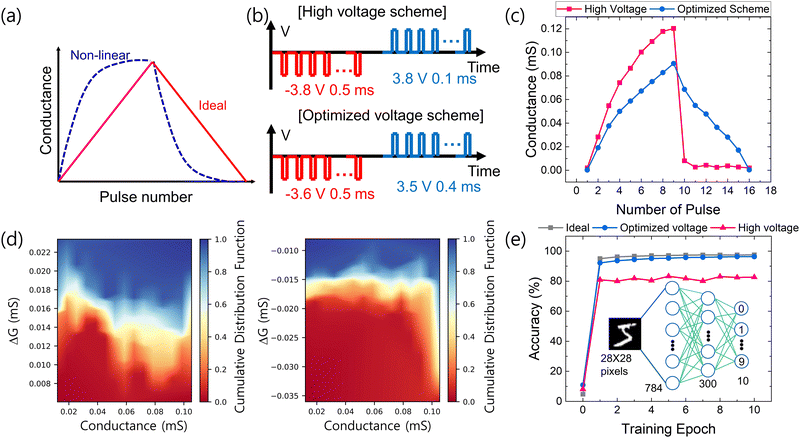
To assess the applicability of our device in neuromorphic computing, we conducted multilevel conductance modulation. Achieving high learning accuracy necessitates two key factors: maintaining excellent linearity during conductance changes and ensuring symmetry between the conductance increase (potentiation) and decrease (depression), as shown in Fig. 6(a). However, conventional FTJs struggle to precisely control domain alignment, resulting in nonlinear potentiation and depression, as well as increased asymmetry. Previous studies have attempted to improve the linearity of conductance modulation by incrementally increasing or decreasing the amplitude of input pulses to address the nonlinearity and asymmetry of conductance modulation, which varies significantly depending on the input pulse train.35–37 These non-identical pulse trains are unrealistic for circuit design and hinder efficient conductance updates, making it a challenging solution. It has been reported that the linearity of conductance modulation can be enhanced by shortening the input pulse duration in ferroelectric-based memory devices.38 Given that the domain wall speed in ferroelectrics is exponentially dependent on both voltage amplitude and duration, optimizing voltage amplitude could potentially improve linearity.39 Therefore, we adopted an alternative approach, exploring optimal switching pulse conditions by finely tuning the amplitude of the input pulse to achieve the most linear and symmetric conductance modulation. The significant impact of pulse amplitude variations on conductance modulation properties is demonstrated in our study. The pulse schemes employed are depicted in Fig. 6(b), featuring high voltage pulses of ±3.8 V (left) and optimized lower voltage pulses of −3.6 to +3.5 V (right). It should be noted that using a voltage lower than −3.6 V could still induce resistance switching, but the modulation ratio was too low to distinguish the 3 bit multilevel. After each pulse, a 1 s delay was implemented before measuring the current at −2 V. The outcomes of these measurements are illustrated in Fig. 6(c).
In the high voltage pulse scheme, while the conductance modulation in the potentiation process seems linear, the device showed ∼33% larger Gmax but abrupt conductance changes during the initial pulses for depression, followed by a small and negligible decrease in conductance changes with subsequent pulses, indicating nonlinear behavior. In the low voltage pulse scheme, the conductance was modulated gradually in both potentiation and depression processes, indicating excellent linearity and symmetry. To evaluate the linearity and symmetry of conductance modulation, we defined a nonlinearity (NL) and symmetry factor as follows:
 | (5) |
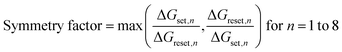 | (6) |
In this equation, i is set or reset, and n represents the number of writing pulses for either potentiation or depression. Gi,n denotes the conductance after the nth writing pulse in the set or reset situation. ΔGset,n and ΔGreset,n indicate the change in conductance caused by the nth set and reset pulses, respectively. A lower NL value suggests improved linearity, with perfect linearity corresponding to a value of 1. The calculated linearity for potentiation and depression was 0.98 and 3.82, respectively, for the high voltage pulse scheme, and 1.17 and 1.29, respectively, for the low voltage scheme, confirming the enhancement in linearity through pulse condition optimization. Additionally, the symmetry factor, ideally at a value of 1, improved from 12.00 to 2.19. Thus, the conductance modulation caused by a low voltage scheme enables gradual domain rotation, resulting in improved linearity and symmetry.
To include both CTCV and DTDV effects of conductance update in the neural network simulation, we conducted 5 repeated cycling tests using the optimized pulse scheme and performed pulse measurements in 5 different cells. The original measured data are shown in Fig. S10 (ESI†). Based on these data, the cumulative distribution function of ΔG for both potentiation (left) and depression (right) is shown in Fig. 6(d). It demonstrates that conductance can be modulated very uniformly, even across repetitive operations. Taking into account the measured results with cycle and device variations, we proceeded with artificial neural network (ANN) simulations using the CrossSim 2.0 platform.40 The network configuration comprised 784 input neurons, 300 hidden neurons, and 10 output neurons. Sigmoid activation functions were applied to the input and hidden neurons, while the output neurons utilised a softmax function. We trained the network for inference using the MNIST dataset and the backpropagation algorithm. As depicted in Fig. 6(e), the maximum inference accuracy of the high voltage scheme was 83.25%, whereas the optimized voltage scheme exhibited a significantly higher accuracy of 96.33%, akin to the ideal numerical case (97.6%). These underscore the substantial potential of the TiN/TiO2/Al2O3/HZH/Pt synapse device for application in neuromorphic computing hardware.
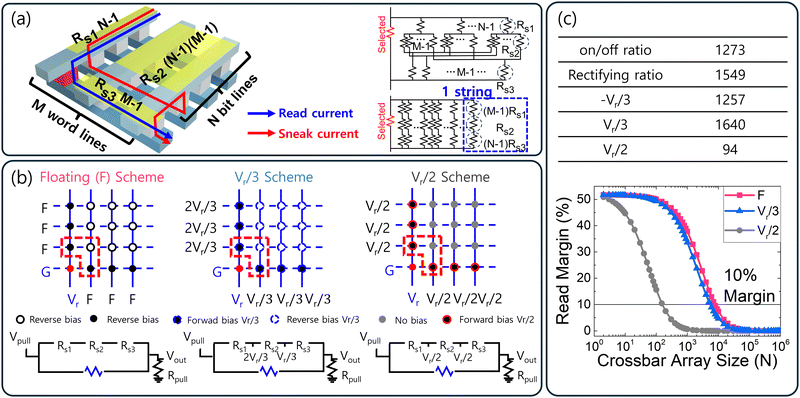
For the application of neuromorphic computing, constructing a crossbar array is crucial. However, the crossbar array, which consists of resistive switching devices, faces a fundamental crosstalk issue during the read process due to the interconnected passive elements through the word and bit lines of the selected cell. Fig. 7(a) presents the schematic N × M CBA structure and its equivalent circuit of the sneak current. The current through the selected cell is shown by the blue arrow, while an example of sneak current through half-selected and unselected cells is indicated by the red arrow. Here, the half-selected cell means cells sharing either the bit or word lines with selected cells. Previous studies have attempted to integrate selector devices to suppress sneak current, but this has been deemed highly challenging due to the complexity of the manufacturing process and the mismatch between the operating ranges of resistive switching and selector devices. Therefore, significant research efforts are underway to develop resistive switching devices with inherent rectifying properties to address this issue, aiming to create 1R arrays capable of autonomously mitigating sneak current. Since the sneak current should pass unselected reverse-biased cells, as shown in Fig. 7(a), the self-rectifying resistive switching device can effectively mitigate the sneak current without the need for selectors, thus solving the crosstalk problem. Additionally, depending on the read scheme, the sneak current path includes neighboring devices subjected to Vr/2 or Vr/3 voltage. Therefore, the intrinsic non-linearity of the device is a critical parameter, as it can effectively reduce the current flowing through these neighboring devices.
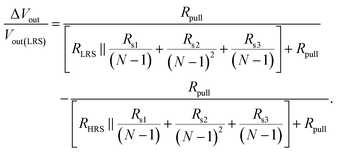
The maximum crossbar array size can be calculated based on the equivalent circuit shown in the right panel of Fig. 7(a). The detailed calculation of the total resistance of the circuit is illustrated in Fig. S10 (ESI†). By conducting this calculation, the evaluation of the rectifying characteristics with the TiN/TiO2/Al2O3/HZH/Pt FTJ in various read schemes can be performed for the 1R array.
Fig. 7(b) illustrates a CBA with induced potential in a read scheme of each F, Vr/3, and Vr/2.41,42 The cells where reverse bias is applied are marked with white dots. The bottom schematic circuits depict resistors composed of red lines and the selected cell (blue) in read processes. In the F scheme, the word and bit line of the unselected cells are left floating, and sneak current mostly affected by the reverse bias current through the unselected cell. In Vr/3, all CBA cells contribute to the sneak current. However, compared to other read schemes, a relatively small voltage (Vr/3) is applied to the cells, which can increase the resistance ratio between selected and half-/unselected cells.41,42 Additionally, since reverse bias is applied to most cells that make up the sneak current, the sneak current can be effectively suppressed through the rectifying characteristics of the device, like in the Vr read scheme. In the Vr/2 scheme, voltage is not applied to cells connected to unselected word and bit lines, so sneak current flows only through the half-selected cells. Here, since reverse bias is not applied to any cells in the sneak path, rectification characteristics cannot prevent the sneak current. Fig. 7(c) shows the parameters for each read scheme and their calculated maximum crossbar array with the read margin of 10%. The parameters are extracted from Fig. 4(d) of the FTJ with the Al2O3 layer between TiO2 and the HZH SL. The rectifying ratio is used for the F scheme, while ±Vr/3 and Vr/2 are for the Vr/3 and Vr/2 schemes, respectively. Here, ±Vr/3 and Vr/2 mean the ratio of the resistance at Vr to resistance at ±Vr/3 and Vr/2 voltage, respectively. To compare the influence of sneak current characteristics in each reading method, we assume a worst-case scenario. This situation assumes that the selected cells are in a high-resistance state, but all other cells are in a low-resistance state, forming the highest leakage current via the sneak current path. On the other hand, the effect of line resistance was not considered. The lower line resistance (RL) compared to the cell resistance in the on state (Ron) can prevent significant voltage decay along the word line. Chen et al. suggested that in a device configuration with an RL/Ron ratio of ∼10−6, the voltage decay on the word line could be less than 10% for a 1k array size.43 In our study, the measured Ron is 733 MΩ at −2.2 V, and the line resistance, calculated based on the TiN electrode with a relatively high resistivity of 300 nΩ m, is 75 Ω, resulting in an RL/Ron ratio of approximately ∼10−7. This value is even lower than those considered in the study reported by Chen et al. Therefore, it is clear that the impact of line resistance in our device would be significantly lower, rendering it negligible when assessing array scalability.
The read margin was defined as ΔVout on the pull-up resistor (Rpull = 0.6 GΩ for 100 μm2 cell size array) in Fig. 7(b) normalized by the pull-up V. Considering the N × N square CBA with Vpull, the read margin can be calculated with44,45
 | (7) |
In the Vr/2 scheme, where no cells were subjected to reverse bias, the intrinsic nonlinearity allows for a maximum crossbar array size of 200 × 200 under a 10% read margin. Moreover, for the F and Vr/3 schemes, the combined effects of rectification and non-linearity allow for maximum array sizes of 7k and 5k, respectively, effectively suppressing sneak current and enabling the large array size. The significant increase in the read margin for the crossbar array is attributed to the excellent intrinsic rectification and non-linearity properties, as well as the high on/off ratio of the TiN/TiO2/Al2O3/HZH/Pt structure, indicating its suitability for 1R crossbar array configurations. Additional proof of the nonlinearity effect on the array scaling in Vr/2 and Vr/3 schemes was conducted by comparing assumed linear device properties, as shown in Fig. S11 (ESI†).
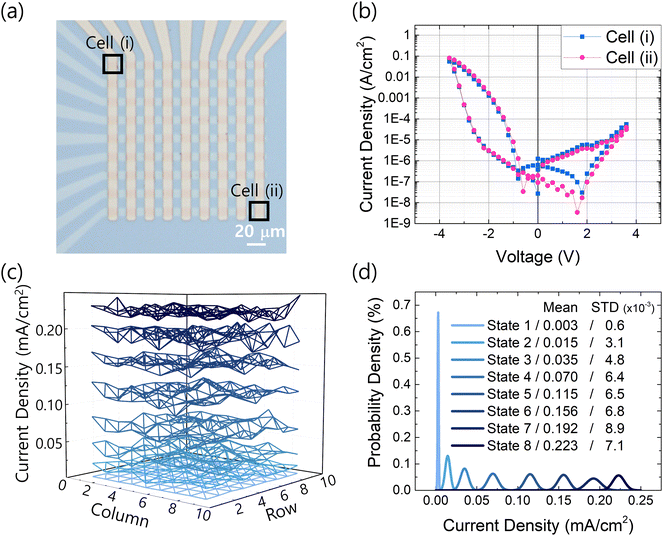
To validate the functional feasibility of our device within an actual CBA configuration, we constructed a 9 × 9 crossbar array with a line size of 10 μm × 10 μm. Fig. 8(a) shows the plan-view images of the fabricated CBA, demonstrating successful fabrication without interline interference. Initially, we examined the possibility of device characteristic deterioration due to line resistance and sneak current to evaluate the characteristics of the fabricated CBA. To access individual memristors in the crossbar array, the column line was biased, while the row line was grounded, and current measurements were conducted on the grounded line. Fig. 8(b) depicts the J–V curves for the cell with the largest line resistance effect (Cell (ii) in Fig. 8(a)) and the cell with the smallest line resistance effect (Cell (i) in Fig. 8(a)) in a 9 × 9 array. The switching characteristics of the two cells exhibit nearly identical behavior, indicating that line resistance does not significantly impact the operation of the fabricated array. Moreover, it indicates that sneak currents are effectively mitigated by the self-rectifying characteristics of FTJ devices, as each cell can switch independently and share the same operating current range.
Additionally, Fig. 8(c) presents the measured data from all 81 devices in the 9 × 9 array, suggesting excellent cell-to-cell uniformity and a multi-bit operation corresponding to 3 bits. The original measurement data for Fig. 8(c) are shown in Fig. S12 (ESI†). The probability density of the 3 bit operation across the 81 cells is summarized in Fig. 8(d), with the inset showing the mean current density and standard deviation (STD) of each state. The consistent performance across cells and the ability to modulate conductance at multiple levels within the array demonstrate the effective implementation of a CBA composed of self-rectifying FTJ, making it suitable for neuromorphic computing applications relying on CBAs.
Methods
Device fabrication
A 10 nm-thick Pt bottom electrode was deposited using an ion beam sputter on a natural SiO2/Si substrate. For the HfO2, ZrO2, and Al2O3 deposition, thermal ALD (iOV-mX1, iSAC RESEARCH) was utilised. The metal–organic precursors used to deposit each oxide were tetrakis(ethyl-methylamino)hafnium, tetrakis(ethyl-methylamino)zirconium, and trimethylaluminum, respectively, and O3 with a concentration of 200 g m−3 was utilised for the reactant. The substrate temperature was ∼270 °C. The growth per cycle of all of the oxides deposited using thermal ALD was similar, ∼0.1 nm per cycle. After deposition of Al2O3 on HZH, HZO, or HfO2, crystallization was conducted using a rapid thermal annealing (RTA) system at 600 °C under a N2 atmosphere for 30 s. TiO2 was deposited on the top of the sample after the RTA process using plasma-enhanced ALD (Atomic-Premium, CN1) with oxygen plasma. The precursor was tetrakis(dimethyl-amido)titanium. The TiN top electrode was deposited using the radio-frequency sputtering system for 50 nm thickness.In the case of CBA, first, the negative photoresistor (PR) was patterned for the bottom electrode on the native SiO2/Si. After the development, the bottom Pt was deposited and then the PR was lifted off. The oxide layers were deposited in the same way as mentioned above, and the top electrode was also patterned with negative PR as the bottom electrode.
Electrical measurements
Electrical property measurements were performed using a semiconductor characterization system (4200A-SCS, Keithley) equipped with ultra-fast current–voltage (I–V) modules (4225-PMU, Keithley) and SMU modules (Keithley). The specific pulses used for measurement are described in the Results and discussion section.Material characterization
GIXRD (Xpert Pro, PANalytical) was conducted with a fixed incidence angle of ω = 0.5° with a Cu Kα X-ray source having a wavelength of 0.15418 nm.The STEM-EDS and STEM-EELS measurements were conducted using a Cs-corrected (probe corrector) JEOL-ARM200CF microscope with a cold-field emission electron gun operated at an acceleration voltage of 200 kV. A Model 965 GIF Quantum ER detector was used for STEM-EELS measurement.
Conclusions
In this work, a self-rectifying FTJ with a high on/off ratio (∼1273) and a rectifying ratio (1550) is demonstrated for synaptic devices for neuromorphic computing based on the three clever engineering strategies of polymorph, tunneling barrier, and injection barrier. By adopting a HZH SL, the formation of a non-ferroelectric interfacial tetragonal phase could be suppressed with enhanced Pr compared to HZO solid solution even with a 6 nm film thickness. A large polarization-affected change in the potential barrier could be induced by the HZH SL combined with the Al2O3 and TiO2 layers. By adopting top TiN/TiO2 and bottom Pt/HfO2 interfaces with Schottky barrier heights of 0.37 and 2.65 eV, a strong self-rectifying nature could be induced. Moreover, the Al2O3 layer contributed to the enhanced switching endurance by preventing oxygen vacancy formation during the sample fabrication process.With these strategies, it could be demonstrated that the self-rectifying FTJ based on the HZH SL is expected to be integrated up to a 7k cell array without a selector device. For neuromorphic computing, multilevel resistance switching that can achieve the MNIST image recognition accuracy of over 92% could be demonstrated. Finally, the feasibility of achieving the self-rectifying properties and sufficiently low DTDV enabling distinguishable 8 weight states was proven in a 9 × 9 size CBA.
Our study advances the performance of ferroelectric tunnel junctions (FTJs) by achieving higher on/off ratios and rectifying properties through material engineering, specifically using a HZH SL and asymmetry electrodes. This approach contrasts with those of previous works, such as using simple bilayer FTJs or stress-induced phase stabilization and charge defects for achieving rectifying properties.44,46–48 The performance of this work is summarized and compared with previous studies in Table 1.
| Device structure | On/off | Rectifying ratio | Nonlinearity | Fabricated array size | Calculated maximum array size | σ/μ × 100 (%) | Ref. |
|---|---|---|---|---|---|---|---|
| a Averaged value of DTDV and CTCV shown in Fig. S3 (ESI). | |||||||
| TiN/HZO (6 nm)/TaN/W | 100 | 1000 | ∼100 | N/A | >4k | N/A | 44 and 46 |
| TiN/Si:HfO2 (4 nm)/SiO2/Si | <10 | ∼60 | 10 | 5 × 5 | N/A | N/A | 47 |
| TiN/HZO (6 nm)/SiO2/Si | 1000 | ∼100 | N/A | N/A | N/A | N/A | 49 |
| TiN/HZO (5.5 nm)/TaO/W | >100 | >1000 | ∼100 | 16 × 16 | N/A | N/A | 50 |
| TiN/Al:HfO2 (∼8 nm)/SiO2/Si | 265 | 1850 | ∼100 | N/A | >1349 | 40.5 | 51 |
| Mo/HZO (10 nm)/HfO2/Si | 268 | ∼100 | ∼90 | N/A | >191 | N/A | 52 |
| Ti/AlOx/AlxScyN (10 nm)/Al | 3173 | ∼100 | 706 | N/A | N/A | N/A | 53 |
| TiN/TiO2/Al2O3/HZH (6 nm)/Pt | 1273 | 1549 | 94 | 8 × 8 | >7k | 13.8a | This work |
Author contributions
D. H. L. and J. E. K. contributed to the methodology, formal analysis, investigation, and writing-original data. Y. H. C. and S. K. contributed to the investigation, resources, and software. G. H. P., T. K., D. H. K., and M. J. contributed to validation, data curation, and writing-review and editing. H. C. and S. Y. L. contributed to resources. H. W. J. contributed to the visualization. Y. L. contributed to the investigation. S. Y. L., J. H. Y., and M. H. P. contributed to the conceptualization and supervision. M. H. P. contributed to the project administration and funding acquisition, as well.Data availability
The data supporting this article have been included in the paper and/or the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation (NRF) and Institute for Information & communications Technology Promotion (IITP) grant funded by the Ministry of Science and Information and Communication Technology of Korea (RS-2024-00399394, RS-2024-00406897).Notes and references
- C. S. Hwang, Adv. Electron. Mater., 2015, 1, 1400056 CrossRef.
- I. R. Committee, International Technology Roadmap For Semiconductors 2.0 2015 Edition, Technical Report, European and Japan and Korean and Taiwan and United States, 2015.
- J. Y. Park, D. H. Lee, G. H. Park, J. Lee, Y. Lee and M. H. Park, Nanotechnology, 2023, 34, 202001 CrossRef PubMed.
- G. H. Park, D. H. Lee, H. Choi, T. Kwon, Y. H. Cho, S. H. Kim and M. H. Park, ACS Appl. Electron. Mater., 2023, 5, 642–663 CrossRef CAS.
- S. Fujii, Y. Kamimuta, T. Ino, Y. Nakasaki, R. Takaishi and M. Saitoh, First demonstration and performance improvement of ferroelectric HfO2-based resistive switch with low operation current and intrinsic diode property, 2016 IEEE Symposium on VLSI Technology, Honolulu, HI, USA, 2016, pp. 1–2.
- S. S. Cheema, N. Shanker, C. H. Hsu, A. Datar, J. Bae, D. Kwon and S. Salahuddin, Adv. Electron. Mater., 2021, 2100499 Search PubMed.
- E. Covi, Q. T. Duong, S. Lancaster, V. Havel, J. Coignus, J. Barbot, O. Richter, P. Klein, E. Chicca and L. Grenouillet, Ferroelectric tunneling junctions for edge computing, 2021 IEEE International Symposium on Circuits and Systems (ISCAS), 2021, Daegu, Korea, pp. 1–5.
- Y. Shimeng, Proc. IEEE, 2018, 106, 260–285 Search PubMed.
- L. Chen, T.-Y. Wang, Y.-W. Dai, M.-Y. Cha, H. Zhu, Q.-Q. Sun, S.-J. Ding, P. Zhou, L. Chua and D. W. Zhang, Nanoscale, 2018, 10, 15826–15833 RSC.
- M. H. Park, Y. H. Lee, H. J. Kim, T. Schenk, W. Lee, K. Do Kim, F. P. Fengler, T. Mikolajick, U. Schroeder and C. S. Hwang, Nanoscale, 2017, 9, 9973–9986 RSC.
- M. Hoffmann, U. Schroeder, T. Schenk, T. Shimizu, H. Funakubo, O. Sakata, D. Pohl, M. Drescher, C. Adelmann and R. Materlik, J. Appl. Phys., 2015, 118, 072006 CrossRef.
- M. H. Park, H. J. Kim, Y. J. Kim, Y. H. Lee, T. Moon, K. D. Kim, S. D. Hyun, F. Fengler, U. Schroeder and C. S. Hwang, ACS Appl. Mater. Interfaces, 2016, 8, 15466–15475 CrossRef CAS PubMed.
- D. H. Lee, G. H. Park, S. H. Kim, J. Y. Park, K. Yang, S. Slesazeck, T. Mikolajick and M. H. Park, InfoMat, 2022, 4, e12380 CrossRef CAS.
- S.-G. Ren, A.-W. Dong, L. Yang, Y.-B. Xue, J.-C. Li, Y.-J. Yu, H.-J. Zhou, W.-B. Zuo, Y. Li, W.-M. Cheng and X.-S. Miao, Adv. Mater., 2024, 36, 2307218 CrossRef CAS PubMed.
- K. Jeon, J. J. Ryu, S. Im, H. K. Seo, T. Eom, H. Ju, M. K. Yang, D. S. Jeong and G. H. Kim, Nat. Commun., 2024, 15, 129 CrossRef CAS PubMed.
- H.-Y. Wang, S. Jou, B.-R. Huang, W.-J. Song and T.-Z. Mao, Appl. Phys. Express, 2016, 9, 045801 CrossRef.
- R. Ni, L. Yang, X. D. Huang, S. G. Ren, T. Q. Wan, Y. Li and X. S. Miao, IEEE Trans. Electron Devices, 2021, 68, 4897–4902 CAS.
- M. H. Park, T. Schenk, C. M. Fancher, E. D. Grimley, C. Zhou, C. Richter, J. M. LeBeau, J. L. Jones, T. Mikolajick and U. Schroeder, J. Mater. Chem. C, 2017, 5, 4677–4690 RSC.
- M. Hyuk Park, H. Joon Kim, Y. Jin Kim, W. Lee, T. Moon and C. Seong Hwang, Appl. Phys. Lett., 2013, 102, 242905 CrossRef.
- U. Schroeder, C. Richter, M. H. Park, T. Schenk, M. Pešić, M. Hoffmann, F. P. G. Fengler, D. Pohl, B. Rellinghaus, C. Zhou, C.-C. Chung, J. L. Jones and T. Mikolajick, Inorg. Chem., 2018, 57, 2752–2765 CrossRef CAS PubMed.
- D. H. Lee, G. H. Park, S. H. Kim, K. Yang, J. Lee, H. Choi, Y. Lee, J. J. Ryu, J. I. Lee, G. H. Kim and M. H. Park, IEEE Electron Device Lett., 2023, 44, 1440–1443 CAS.
- D. H. Lee, G. T. Yu, J. Y. Park, S. H. Kim, K. Yang, G. H. Park, J. J. Ryu, J. I. Lee, G. H. Kim and M. H. Park, Acta Mater., 2022, 222, 117405 CrossRef CAS.
- E. Giacomin, T. Greenberg-Toledo, S. Kvatinsky and P. E. Gaillardon, IEEE Trans. Circuits Syst., 2019, 66, 643–654 Search PubMed.
- P. Bousoulas, S. Stathopoulos, D. Tsialoukis and D. Tsoukalas, IEEE Electron Device Lett., 2016, 37, 874–877 CAS.
- P. Bousoulas, I. Michelakaki, E. Skotadis, M. Tsigkourakos and D. Tsoukalas, IEEE Trans. Electron Devices, 2017, 64, 3151–3158 CAS.
- M. Tsigkourakos, P. Bousoulas, V. Aslanidis, E. Skotadis and D. Tsoukalas, Phys. Status Solidi A, 2017, 214, 1700570 CrossRef.
- J. Lee, K. Yang, J. Y. Kwon, J. E. Kim, D. I. Han, D. H. Lee, J. H. Yoon and M. H. Park, Nano Convergence, 2023, 10, 55 CrossRef CAS PubMed.
- R. Degraeve, A. Fantini, N. Raghavan, L. Goux, S. Clima, B. Govoreanu, A. Belmonte, D. Linten and M. Jurczak, Microelectron. Eng., 2015, 147, 171–175 CrossRef CAS.
- S. Yu, G. Ximeng and H. S. P. Wong, On the stochastic nature of resistive switching in metal oxide RRAM: Physical modeling, monte carlo simulation, and experimental characterization, 2011 International Electron Devices Meeting, 2011, Washington, DC, USA, pp. 17.3.1–17.3.4.
- F.-C. Chiu, Adv. Mater. Sci. Eng., 2014, 578168 Search PubMed.
- J. R. DeVore, J. Opt. Soc. Am., 1951, 41, 416–419 CrossRef CAS.
- M. F. Al-Kuhaili, Opt. Mater., 2004, 27, 383–387 CrossRef CAS.
- I. H. Malitson and M. J. Dodge, J. Opt. Soc. Am., 1972, 62, 1405 Search PubMed.
- C. L. Hinkle, C. Fulton, R. J. Nemanich and G. Lucovsky, Microelectron. Eng., 2004, 72, 257–262 CrossRef CAS.
- S. Majumdar, H. Tan, Q. H. Qin and S. van Dijken, Adv. Electron. Mater., 2019, 5, 1800795 CrossRef.
- Y. Jeong, S. Kim and W. D. Lu, Appl. Phys. Lett., 2015, 107 Search PubMed.
- S. Park, M. Chu, J. Kim, J. Noh, M. Jeon, B. Hun Lee, H. Hwang, B. Lee and B.-G. Lee, Sci. Rep., 2015, 5, 10123 CrossRef CAS PubMed.
- S. Majumdar, Nanoscale, 2021, 13, 11270–11278 RSC.
- D. H. Lee, Y. Lee, K. Yang, J. Y. Park, S. H. Kim, P. R. S. Reddy, M. Materano, H. Mulaosmanovic, T. Mikolajick and J. L. Jones, Appl. Phys. Rev., 2021, 8, 021312 CAS.
- S. J. Plimpton, S. Agarwal, R. Schiek and I. Richter, Crosssim, Sandia National Lab. (SNL-NM), Albuquerque, NM (United States), 2016 Search PubMed.
- J. Y. Seok, S. J. Song, J. H. Yoon, K. J. Yoon, T. H. Park, D. E. Kwon, H. Lim, G. H. Kim, D. S. Jeong and C. S. Hwang, Adv. Funct. Mater., 2014, 24, 5316–5339 CrossRef CAS.
- S. Kim, H.-D. Kim and S.-J. Choi, Solid-State Electron., 2015, 114, 80–86 CrossRef CAS.
- A. Chen, IEEE Trans. Electron Devices, 2013, 60, 1318–1326 Search PubMed.
- Y. Goh, J. Hwang, M. Kim, Y. Lee, M. Jung and S. Jeon, ACS Appl. Mater. Interfaces, 2021, 13, 59422–59430 CrossRef CAS PubMed.
- A. Chen, J. Comput. Electron., 2017, 16, 1186–1200 CrossRef.
- Y. Goh, J. Hwang, M. Kim, M. Jung, S. Lim, S. O. Jung and S. Jeon, High Performance and Self-rectifying Hafnia-based Ferroelectric Tunnel Junction for Neuromorphic Computing and TCAM Applications, 2021 IEEE International Electron Devices Meeting, 2021, San Francisco, CA, USA, pp. 17.2.1–17.2.4.
- R. Berdan, T. Marukame, K. Ota, M. Yamaguchi, M. Saitoh, S. Fujii, J. Deguchi and Y. Nishi, Nat. Electron., 2020, 1–8 Search PubMed.
- B. Max, M. Hoffmann, S. Slesazeck and T. Mikolajick, IEEE J. Electron Devices Soc., 2019, 7, 1175–1181 CAS.
- K. Lee, S. Kim, J.-H. Lee, B.-G. Park and D. Kwon, IEEE Electron Device Lett., 2021, 42, 323–326 CAS.
- S. Lim, Y. Goh, Y. K. Lee, D. H. Ko, J. Hwang, Y. Jeong, H. Shin, S. Jeon and S. O. Jung, IEEE J. Solid-State Circuits, 2023, 58, 1860–1870 Search PubMed.
- E. Lim, D. Ju, J. Lee, Y. Park, M.-H. Kim and S. Kim, ACS Mater. Lett., 2024, 6, 2320–2328 CrossRef CAS.
- J. Kim, Y. Park, J. Lee, E. Lim, J.-K. Lee and S. Kim, Adv. Mater. Technol., 2024, 9, 2400050 CrossRef CAS.
- K.-H. Kim, Z. Han, Y. Zhang, P. Musavigharavi, J. Zheng, D. K. Pradhan, E. A. Stach, R. H. Olsson, III and D. Jariwala, ACS Nano, 2024, 18, 15925–15934 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00519h |
| ‡ These authors have contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |