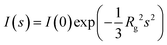Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Perspectives on solution-based small angle X-ray scattering for protein and biological macromolecule structural biology
Ahmed S. A.
Mohammed
 abc,
Dmytro
Soloviov
abc,
Dmytro
Soloviov
 a and
Cy M.
Jeffries
a and
Cy M.
Jeffries
 *a
*a
aEuropean Molecular Biology Laboratory (EMBL), Hamburg Unit, co/DESY, Notkestrasse 85, D-22607 Hamburg, Germany. E-mail: cy.jeffries@embl-hamburg.de
bPhysics Department, Faculty of Science, Fayoum University, 63514 Fayoum, Egypt
cDepartment of Biomedical Physics, Adam Mickiewicz University in Poznań, Uniwersytetu Poznańskiego 2, 61-614 Poznań, Poland
First published on 24th September 2024
Abstract
Small-angle X-ray scattering (SAXS) is used to extract structural information from a wide variety of non-crystalline samples in different fields (e.g., materials science, physics, chemistry, and biology). This review provides an overview of SAXS as applied to structural biology, specifically for proteins and other biomacromolecules in solution with an emphasis on extracting key structural parameters and the interpretation of SAXS data using a diverse array of techniques. These techniques cover aspects of building and assessing models to describe data measured from monodispersed and ideal dilute samples through to more complicated structurally polydisperse systems. Ab initio modelling, rigid body modelling as well as normal-mode analysis, molecular dynamics, mixed component and structural ensemble modelling are discussed. Dealing with polydispersity both physically in terms of component separation as well as approaching the analysis and modelling of data of mixtures and evolving systems are described, including methods for data decomposition such as single value decomposition/principle component analysis and evolving factor analysis. This review aims to highlight that solution SAXS, with the cohort of developments in data analysis and modelling, is well positioned to build upon the traditional ‘single particle view’ foundation of structural biology to take the field into new areas for interpreting the structures of proteins and biomacromolecules as population-states and dynamic structural systems.
Introduction
In a typical SAXS experiment for structural biology, measurements are performed on dilute biomacromolecules in solution (0.1–10 mg mL−1) and from a corresponding matched solvent, or buffer. The sample and the matched buffer are illuminated by a parallel-collimated monochromatic X-ray beam, and the intensities of the elastically scattered X-rays are recorded by a 2D detector at low angles (usually less than 5°). Assuming isotropic scattering, and after a series of appropriate corrections and calibrations have been applied1–4 the azimuthal averaging of the resulting 2D scattering patterns generates a reduced 1D scattering profile of the sample and the matched buffer.5,6 The 1D-scattering profiles record the intensity of the scattered X-rays, I, versus the momentum transfer, s (or q) where s = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ, 2θ is the scattering angle and λ the X-ray wavelength. After all corrections and intensity calibrations have been applied and the matched buffer scattering contributions have been subtracted from the sample scattering, the resulting reduced and subtracted I(s) vs. s profile yields structural information about the population of macromolecules within the sample. As long as there is an excess X-ray scattering contrast present between the sample macromolecules and the buffer, several parameters may be determined. These parameters include the radius of gyration, Rg, the particle volume, V, molecular weight and, of most interest, the particle form factor, P(s), that relates to the square of the time- and rotationally-averaged scattering amplitudes which manifest as scattering intensities and, ultimately, the distribution of time-correlated and preserved real-space scattering pair distances, p(r), internal to the particles i.e., the particle structure. The scattering pattern may also yield insights into the structural polydispersity of the macromolecular population and may also be used to assess the scattering structure factor, S(s), or correlated distances of closest approach between macromolecules within the sample (interparticle interactions). Fundamentally, the magnitude of I(s) is dependent on the number-density, n, and V2 of the particles in the illuminated volume, as well as P(s) and S(s) and, importantly, the square of the contrast, Δρ2, i.e., the squared difference between the average scattering length density of the solute and supporting solvent that relates to the excess electron density distribution of the particles in the sample. This excess is typically very small for biomolecules in solution (e.g., the average electron density of an aqueous solvent is ∼0.335 e Å−3 compared to a protein at ∼0.43 e Å−3) necessitating the optimization of scattering instruments with low inherent background and the avoidance of electron-dense supporting solvents that would otherwise limit Δρ to 0 (contrast matching). In summary, the magnitude of the normalized, calibrated and reduced I(s) measured from a population of tumbling macromolecules in solution can be described by the summed contribution of each-and-every individual particle in the sample population, taking into account any influences caused by interparticle interactions and polydispersity. Polydisperse systems, where the particles are structurally heterogeneous and sample a wide distribution of states, such as modular proteins connected by flexible linkers, intrinsically disordered proteins, oligomeric mixtures or evolving states through time, need to be described in terms of the volume-fraction weighted particle contributions to I(s). For samples occupying a very narrowly distributed structural state where the particles are effectively identical and not influenced by interparticle interactions i.e., samples which are pure, monodisperse and structurally homogeneous in the dilute regime,6 the SAXS intensities will be proportional to the form factor of a single particle oriented over all orientations, weighted by the squared product of the contrast and volume (ΔρV)2 and concentration (N):
θ/λ, 2θ is the scattering angle and λ the X-ray wavelength. After all corrections and intensity calibrations have been applied and the matched buffer scattering contributions have been subtracted from the sample scattering, the resulting reduced and subtracted I(s) vs. s profile yields structural information about the population of macromolecules within the sample. As long as there is an excess X-ray scattering contrast present between the sample macromolecules and the buffer, several parameters may be determined. These parameters include the radius of gyration, Rg, the particle volume, V, molecular weight and, of most interest, the particle form factor, P(s), that relates to the square of the time- and rotationally-averaged scattering amplitudes which manifest as scattering intensities and, ultimately, the distribution of time-correlated and preserved real-space scattering pair distances, p(r), internal to the particles i.e., the particle structure. The scattering pattern may also yield insights into the structural polydispersity of the macromolecular population and may also be used to assess the scattering structure factor, S(s), or correlated distances of closest approach between macromolecules within the sample (interparticle interactions). Fundamentally, the magnitude of I(s) is dependent on the number-density, n, and V2 of the particles in the illuminated volume, as well as P(s) and S(s) and, importantly, the square of the contrast, Δρ2, i.e., the squared difference between the average scattering length density of the solute and supporting solvent that relates to the excess electron density distribution of the particles in the sample. This excess is typically very small for biomolecules in solution (e.g., the average electron density of an aqueous solvent is ∼0.335 e Å−3 compared to a protein at ∼0.43 e Å−3) necessitating the optimization of scattering instruments with low inherent background and the avoidance of electron-dense supporting solvents that would otherwise limit Δρ to 0 (contrast matching). In summary, the magnitude of the normalized, calibrated and reduced I(s) measured from a population of tumbling macromolecules in solution can be described by the summed contribution of each-and-every individual particle in the sample population, taking into account any influences caused by interparticle interactions and polydispersity. Polydisperse systems, where the particles are structurally heterogeneous and sample a wide distribution of states, such as modular proteins connected by flexible linkers, intrinsically disordered proteins, oligomeric mixtures or evolving states through time, need to be described in terms of the volume-fraction weighted particle contributions to I(s). For samples occupying a very narrowly distributed structural state where the particles are effectively identical and not influenced by interparticle interactions i.e., samples which are pure, monodisperse and structurally homogeneous in the dilute regime,6 the SAXS intensities will be proportional to the form factor of a single particle oriented over all orientations, weighted by the squared product of the contrast and volume (ΔρV)2 and concentration (N):| I(s) = N(ΔρV)2P(s) |
Structural parameters 1: radius of gyration
The radius of gyration, Rg, is one of the most important structural parameters that is obtained from a SAXS measurement. The Rg is the root-mean-square distance of all scattering centers (electrons for SAXS) calculated from the center of the excess scattering contrast (which often coincides with the center of mass). Consequently, the Rg is sensitive to the overall size and shape of a particle, and thus the particle mass distribution. After background subtraction, the Rg maybe determined very accurately (within ±0.1 nm). Andre Guinier in 1930s demonstrated a dependency between the scattering intensities measured at the very lowest of scattering angles and the Rg:where the I(0), or the forward scattering intensity at zero angle, is proportionate to the concentration and V2, and hence molecular mass, of the particles. The Guinier approximation describes a linear dependence of ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I(s) versus s2 at the very lowest of scattering angles where the linear dependence typically holds for smax < 1/Rg, which is a reasonable estimate for the upper limit of the approximation. The slope of the linear fit relates to the Rg2, where the linear dependence should, in principle, be stable between 0 < sRg < 1 for monodispersed, ideal samples. However, and often, smax < 1/Rg often contains too few data points for reliable linear fitting, that may become especially acute when estimating the Rg of long-extended rod-like particles. For globular biological macromolecules, the upper limit maybe extended to a more practical smax < 1.3/Rg that increases the number of data points for Rg and I(0) estimation. Intrinsically disordered protein samples – that are structurally heterogeneous – provide more of a conundrum with respect to the choice of smaxRg, where the underestimation of Rg maybe encountered at smaxRg 1.3, necessitating a decrease in the upper smaxRg limit to 1.1, or the application of a modified approach called extended Guinier analysis.7 In effect the Rg of an intrinsically disordered system needs to be viewed as an average over all particles in the sample over time. Irrespective, systematic deviations from linearity in the Guinier region may be a sign that the sample is not ideal, for example, an increase in the estimated Rg and I(0) as s2 limits to zero could be a sign of attractive interparticle effects, i.e., sample aggregation, or conversely a systematic decrease in Rg and I(0) as s2 limits to zero in the Guinier region may indicate repulsive interparticle effects within the sample population.8 Modified Guinier analyses may also be employed across different sRg ranges, e.g., for determining the Rg of cross section of thin rods, or the Rg of thickness for flat objects. Most modern softwares (e.g., ATSAS,9 SASSIE-web,10,11 SASVIEW (https://www.sasview.org), BioXTAS RAW,12 and SASTBX13) have inbuilt Rg modules making the estimation of Rg from Guinier effortless, and many large-scale facilities and laboratory SAXS instruments are equipped with “on the fly” Rg evaluators, that become very useful in a high-throughput or time resolved context for assessing concentration-series and other sample environment dependencies on the Rg.
I(s) versus s2 at the very lowest of scattering angles where the linear dependence typically holds for smax < 1/Rg, which is a reasonable estimate for the upper limit of the approximation. The slope of the linear fit relates to the Rg2, where the linear dependence should, in principle, be stable between 0 < sRg < 1 for monodispersed, ideal samples. However, and often, smax < 1/Rg often contains too few data points for reliable linear fitting, that may become especially acute when estimating the Rg of long-extended rod-like particles. For globular biological macromolecules, the upper limit maybe extended to a more practical smax < 1.3/Rg that increases the number of data points for Rg and I(0) estimation. Intrinsically disordered protein samples – that are structurally heterogeneous – provide more of a conundrum with respect to the choice of smaxRg, where the underestimation of Rg maybe encountered at smaxRg 1.3, necessitating a decrease in the upper smaxRg limit to 1.1, or the application of a modified approach called extended Guinier analysis.7 In effect the Rg of an intrinsically disordered system needs to be viewed as an average over all particles in the sample over time. Irrespective, systematic deviations from linearity in the Guinier region may be a sign that the sample is not ideal, for example, an increase in the estimated Rg and I(0) as s2 limits to zero could be a sign of attractive interparticle effects, i.e., sample aggregation, or conversely a systematic decrease in Rg and I(0) as s2 limits to zero in the Guinier region may indicate repulsive interparticle effects within the sample population.8 Modified Guinier analyses may also be employed across different sRg ranges, e.g., for determining the Rg of cross section of thin rods, or the Rg of thickness for flat objects. Most modern softwares (e.g., ATSAS,9 SASSIE-web,10,11 SASVIEW (https://www.sasview.org), BioXTAS RAW,12 and SASTBX13) have inbuilt Rg modules making the estimation of Rg from Guinier effortless, and many large-scale facilities and laboratory SAXS instruments are equipped with “on the fly” Rg evaluators, that become very useful in a high-throughput or time resolved context for assessing concentration-series and other sample environment dependencies on the Rg.
Structural parameters 2: p(r)
Through the use of regularized indirect inverse Fourier transformation of the background-subtracted sample scattering intensities, the distance distribution function representing the frequency of real space of scattering pair distances, r, can be calculated. The overall particle shape that includes the estimation of the maximum particle dimension, Dmax, is encoded graphically as a histogram of p(r) vs. r.14,15 From the p(r), the forward scattering intensity I(0) and the radius of gyration Rg can be estimated where:and
The procedures of evaluating p(r), identifying a reliable solution, and estimating the Dmax are implemented in the GNOM program of ATSAS package.16 In addition, several other methods are available including the generalized indirect Fourier transformation (GIFT).15,17 Through a further development of GIFT,18 structure factor effects on the scattering caused by repulsive interparticle interference can be identified and separated from the form factor. Several programs such as BayesApp,19 ScÅtter20 and BioXTAS RAW12 can also be utilized for determining the p(r). Recently, using an artificial neural network (NN) method,21 it is possible to reliably assess the p(r) and Dmax directly from experimental data of monodisperse solutions of intrinsically disordered proteins, folded proteins, and nucleic acids. There are numerous ways in which to present the final p(r) plot, for example, unscaled such that the integral relates directly to the I(0) of the measurement (from which the molecular mass may be determined – see below) or scaled such that the integral of p(r) = 1 (a standard frequency plot), or as a ‘single particle p(r)’ following the method of Orthaber3 in cases of pure monodisperse and ideal samples and where the sample concentration, partial specific volume and contrast are known.
Fundamental plots
A simple transformation of the reduced and background subtracted scattering profile generates a Kratky plot (I(s)s2vs. s) that can be further transformed into a dimensionless variant if the Rg and I(0) have been determined ((sRg)2I(s)/I(0) vs. sRg22,23). Kratky plots afford both a visual/qualitative assessment of the compactness of a macromolecule, as well as the quantification of the scattering invariant Q – the area underneath, or integral of the plot – that relates to the reciprocal of the Porod volume, Vp.24,25 SAXS data from compact spherical particles generate a bell-shaped curve with a prominent peak maximum that occurs on a dimensionless Kratky plot at (sRg)2I(s)/I(0) = 1.1 and sRg = √3, while at the other extreme, highly-extended and stiff rod-shaped particles generate an almost linear relationship. In-between these ‘geometric body’ extremes, other simple shape-classifications exist that cluster within regions of ‘dimensionless Kratky space’ that can be identified automatically depending on the relationship between dimensionless Kratky plots calculated at different (sRg)max. For example, intrinsically disordered macromolecules, or thin disc-shaped particles have a tendency to maintain a plateau at higher angles where (sRg)2I(s)/I(0) limits toward 2 as sRg increases. Although the overall and generalized approximation of geometric shape and size can be classified from SAXS data using machine learning methods,26 it is important to note that when attempting to extract more structurally detailed shape-topologies, SAXS data are often highly ambiguous, i.e., often more than one shape can yield identical distributions of scattering pair distances. This effect, often caused by the spherical averaging of the scattering amplitudes arising from randomly-tumbling dilute particles in solution, necessitates careful data analysis and interpretation as aided by the program AMBIMETER27 that calculates the number of shape topologies for a given SAXS profile and provides an assessment of the level of ambiguity of the SAXS data at different (sRg)max.In SAXS experiments, the fundamental nature of the decay in the scattering intensity can be described through the Porod–Debye region.28Fig. 1a presents two SAXS data sets and corresponding fundamental plots distinguishing between two protein cases: urate oxidase (deposited in the small angle biological data bank, SASBDB, as SASDPH7)29 and Histatin 5 (SASDHF8).30 When the SAXS data are displayed on a log-linear scale (Fig. 1a) urate oxidase displays a smooth but strong monotonic decrease in the scattering intensities with oscillatory ‘bumps’ at higher values of s, suggesting the presence of globular and tightly packed particles. In contrast, the SAXS profile of Histatin 5, displays shallow decrease in intensity to high angles suggesting that the protein maybe intrinsically disordered or highly flexible. The p(r) profiles presented in Fig. 1c, show a classic ‘bell shaped’ profile for urate oxidase, suggesting a level of centrosymmetric mass distribution, while Histatin 5 yields an asymmetric p(r) with an elongated tail at higher values of r (3–6 nm) indicating the presence of extended structural states in the Histatin 5 population. The correspondingly dimensionless Kratky plot (Fig. 1d) demonstrates well defined peak-maximum that occurs at √3, 1.1 for the globular and compact urate oxidase sample, while Histatin 5 generates a plateau in the plot at higher values of sRg that is characteristic of intrinsically disordered systems. Conversely, based on Porod–Debye plots (Fig. 1e and f), a plateau for urate oxidase occurs as s increases which is not the case for Histatin 5 (i.e., the transformation of the scattering data as s4I(s) vs. s4 or s4I(s) vs. s for compact systems display curves that asymptotically approach a constant value).
The existence of the Porod–Debye plateau provides supporting evidence for the assumption that compact scattering particles exhibit a more defined surface and sharper-boundary conditions between the particle and solvent. Using a combination of dimensionless Kratky plots and Porod plot evaluations can yield insights into the state(s) of the macromolecular samples prior to any modelling and can in and of themselves yield an understanding of the global/structural changes observed within a sample population. For example, SAXS case studies of ATP dependent DNA repair complex, Mre11-Rad50 complex,31 yield Kratky plots with distinct plateaus whether in the presence (bound state) or absence (apo state) of ATP suggesting that the system has distinct conformational states. On the other hand, Porod–Debye inspections uncovered scenarios in which the presence of ATP led to more-compact states in the sample population while the absence of the ATP led to more flexible state(s).28 Therefore, following the Porod–Debye region, it is possible to qualitatively assess potential compactness, macromolecular flexibility, alterations shape and assembly. When conducting comparative SAXS measurements under different sample conditions, the application of this law enables differentiation between discrete conformational changes/localized flexibility etc. that are pertinent to many biomolecular recognition and interaction events. Porod–Debye criteria enhance the analytical capabilities for studying macromolecules with varying degrees of flexibility, aiding more robust and ‘model-free/unbiased’ analyses, thereby improving overall confidence in SAXS data analysis and interpretation.
Structural parameters 3: molecular mass
Whereas the Rg is sensitive to the size and shape of particles, it is not possible to determine the molecular mass from this parameter. The molecular mass (MM) estimation is a key parameter that guides data analysis and subsequent modelling in terms of evaluating stoichiometry of the sample components (monomers, dimers or oligomeric mixtures, etc.). Several approaches can be used to assess the molecular mass (MM) of biomacromolecules. Concentration-dependent MM determination evaluates the molecular mass from calibrated scattering intensities, (e.g., on an absolute scale, cm−1 relative to the scattering from water3 or glassy carbon32) using the I(0) and sample concentration, taking into account calculated X-ray scattering contrasts and partial specific volume of the sample particles.3 The advantage of concentration-dependent methods are that they can be applied to the MM estimation of almost any type of dilute particle system as long as the scattering intensities have been calibrated correctly. Alternatively, several concentration-independent methods are available to determine the MM. These methods determine the protein volume by utilizing empirically-corrected values of the scattering invariant, Q (the integral of I(s)s2vs. s) or employing the volume of correlation (Vc) that is based on another invariant related to the chord-length distribution (i.e., the invariant obtained from the integral of I(s)s vs. s). Based on a corrected Q from a modified Kratky plot, the molecular weight of a protein can be determined using SAXSMoW.33,34 Based on the definition of the volume of correlation (Vc) by Rambo and Tainer,35 the concentration-independent MM can be determined for both proteins and RNA, e.g., as implemented in ScÅtter software36 and a more recent addition to the available methods ‘Size&Shape’ is based on a classification-based framework.26 A consensus Bayesian inference approach37 takes the outputs from the different individual methods, including Porod-volume calculations (MMQp)38 and combines the pooled MM results to assess the maximum likelihood MM along with a MM range and credibility interval.9 Once again, there are several in-built software modules that are used for MM determination found across SAXS data analysis software packages as well as SAXS data pipelines at synchrotron facilities (e.g., ATSAS,9 SASSIE-web10,11 SASVIEW (https://www.sasview.org), BioXTAS RAW,12 SASTBX,13 SAXSutilties239 and SCÅTTER36). Finally, with the increasing popularity of ‘big data’ trends in structural biology, that includes enormous repositories of well-curated experimental results, models as well predictive artificial-intelligence based protein structures, there are huge opportunities to capitalize on the application of machine-learning methods to explore ‘protein structure space’ in terms of SAXS and to extract MM and other structural parameter information directly from experimental data.40,41Structural modeling of SAXS data from pure monodispersed samples: ab initio modelling
Modeling tools such as DAMMIN,42 DAMMIF,43 and GASBOR,44 are established methods for ab initio shape restoration. DAMMIN and DAMMIF implement simulated annealing (SA) protocol to restore a low-resolution shape of the macromolecule from the SAXS data using dummy atoms set on a grid (assigned to a ‘macromolecule phase or ‘solvent’ phase), while GASBOR uses a set of dummy amino acid residues (DR) for building protein models. The quality of the fit to the experimental data of each corresponding model is evaluated using the reduced χ2 metric and the correlation-map (CorMap) P-value in addition to normalized residual plots, which in combination help quantify systematic deviations (i.e., quality of the fit) between the experimental data and the modelled scattering intensity.45 Reconstructing the 3D shape from the 1D SAXS data cannot provide a unique solution (i.e., different individual models are always obtained) if appropriate penalties are not applied during the SA procedure, for example maintaining DAM or DR volume connectivity. Even then modelling routines are run several times to help overcome the inherent ambiguity of the SAS data.27 Therefore, further routines are used to calculate the spatial variance across an individual-model cohort, including the normalized spatial discrepancy,46 iterative closest point47 (point cloud in real space, ICP), and normalized cross correlation48 (amplitudes in reciprocal space), that generally follows individual model spatial alignment, bead-occupancy, volume averaging, and filtering to obtain an average spatial representation of the sample particle. Moreover, spatially-related but distinct clusters of possible shape solutions can also be evaluated. Another ab initio DAM approach, MONSA42 reconstructs particle shapes from objects consisting of one or more scattering length density region which becomes useful when developing models of, for example, protein/RNA complexes.A more recent method to shape restoration capitalizes on the iterative restoration of the 3D electron density distribution using a phase extension approach – DENSS.49 Among the procedures of many existing modelling algorithms, e.g., DAMMIN, the scattering length density is assumed to be homogeneous inside the envelope of the particles.42,50,51 However, at shorter distances of less than 10 Å, this uniformity assumption may break down due to the complications of short-range internal scattering length density fluctuations and hydration-layer inhomogeneities/dynamics. Calculating the DENSS electron density maps from the solution scattering data could resolve these complications. The potential of this approach was validated by many biological macromolecule systems such as the endophilin-CoA complex,49 and has potentially exciting implications for modelling wide-angle scattering data (WAXS).
Atomistic model fitting to SAXS data
When high-resolution atomic structures available, one can validate the fit of their computed scattering intensities to the scattering data. This validation can be done using a rapid calculation algorithm implemented in the program CRYSOL.52 It employs a multipole expansion of the scattering amplitudes in a series of spherical harmonics to calculate the scattering intensity from the model (where the hydration shell surrounding the protein is taken into account and the contribution of the excluded solvent is subtracted) and compares it to the data. The goodness of fit is assessed using the reduced χ2 test. Another method for computing a SAXS profile is foXS53 which is based on the Debye formula. It provides a rapid and accurate calculation for the SAXS profile of a given molecular structure where it explicitly computes the scattering intensity from all the interatomic (scattering-pair) distances and models the first solvation layer. For a better fit between the computed scattering and the experimental data, foXS optimizes the hydration layer density, the excluded volume of the protein, and any required background-scattering adjustments.Additional methods for computing the SAXS profiles include Pepsi-SAXS54 that calculates the SAXS profiles from atomistic models based the multipole expansion platform where the multipole expansion order is adjusted to the size of the model and the resolution of the collected data. Another successful program, WAXSiS55 calculates SAXS/WAXS curves based on explicit-solvent molecular dynamics (MD) simulations. This method addresses the challenges posed by scattering contributions from the hydration layer and effects accounting to the thermal fluctuations, resulting in reliable and accurate predictions of structural models into the wide-angle regime. A recent comparative analysis of the performance of all four atomistic model fitting programs using consensus SAXS from well characterized proteins has been recently published, highlighting the importance of an MD approach when asking very specific questions relating to solvation dynamics and ion binding.56 Another noteworthy method worth mentioning is WilltFit.57 Using the known chemical composition of the sample and molecular constraints, the WilltFit platform allows for simultaneous fitting of SAXS and SANS data to a variety of analytical and semi-analytical biomolecular models. This approach also incorporates the effects of instrument resolution, that is especially pertinent for SANS. Furthermore, in an ongoing effort to enhance the modeling accuracy and avoid overfitting experimental data, a method known as SWAXS (small and wide-angle X-ray scattering) was developed.58 Scattering profiles and electron density maps in both the SAXS and WAXS regime can be calculated from atomic models and fitted the experimental data with high accuracy. The DENSS 1.7.0 software package (https://github.com/tdgrant1/denss) includes this relatively new SWAXS approach.
Rigid body modelling
There are several rigid-body modelling routines that are available to optimize the spatial position of macromolecular domains, subunits and assembly components. The template atomistic models used for rigid body modelling may be derived from X-ray crystallography, NMR, cryo-EM or predictive algorithms. SASREF, for example, takes the pre-calculated scattering amplitudes of the input rigid body models (e.g., calculated by CRYSOL for SAXS; CRYSON for SANS), and then performs a target-function minimization using simulated annealing to translate and rotate the components with respect to each other, all the while using the fit to the data to guide the model trajectory, without generating unreasonable spatial discrepancies (for example, rigid-body interpenetration or stearic clashes).59 SASREF allows for parallel modelling against multiple SAS datasets that is particularly useful for SAXS and SANS with contrast variation type experiments. However, the SASREF approach requires that the composition of the final model must be completely described by the initial individual rigid body components. This condition may not be satisfied in all cases, for example where linkers connecting protein domains, or additional C- or N-terminal extensions on a protein are unaccounted for in the atomic coordinate files of the input structure(s). For SAXS, the programs BUNCH and CORAL60 maybe used to overcome this limitation, where both the spatial positioning of the rigid bodies and any ‘missing protein portions’ such as linkers are determined by describing the missing sections as dummy residues. Consequently, BUNCH and CORAL are particularly useful in determining the solution state of multi-modular proteins, or protein/RNA or protein/DNA assemblies with regions of unknown structure. All three approaches, SASREF, BUNCH and CORAL also allow for the use of symmetry as well as options to include additional constraints obtained from other biophysical characterizations, such as, inter-residue contacts derived from NMR, inter-subunit distances from FRET, and orientational constraints defining subunit–subunit interfaces obtained from mass spectrometry cross linking, or hydrogen/deuterium exchange experiments.Modeling of complexes from their individual components remains quite challenging, again and in part due to the inherent ambiguity of SAS data. The foXS-Dock method61 of molecular docking has been developed to help improve the errors in orienting the components of protein complexes together in more likely/feasible orientations. In this method, five stages are involved to produce a near-native complex structure from two given component structures: (1) global search by rigid docking, (2) coarse SAXS filtering by radius of gyration, (3) SAXS scoring by profile fitting, (4) clustering, and (5) conformational refinements. The foXS-Dock approach is a hybrid one that simultaneously satisfies physicochemical and structural constraints and aims to improve the accuracy of the spatial sampling by reducing the number of potential models that fit the SAXS data. An alternative approach for complex docking includes pyDockSAXS,62 that provides a pipeline for modelling protein–protein complexes to SAXS data, generating a series of structural models ranked using a function that combines an energy-based scoring term with the χ value of the model fit to the data using CRYSOL.
Normal mode analysis and molecular dynamics
In case of poor fit between the SAXS data and a high-resolution model, normal mode analysis (NMA) can simulate protein-domain movements so that small conformational changes can be modeled. Based on NMA, SREFLEX63 samples small motions based on classical mechanic harmonic oscillations in the high-resolution model, using rigid-body domain partitioning. Due to the possible conformations of the flexible parts in a macromolecule, the SREFLEX method forms ranked conformationally altered structures, and yields information relating to the global movement of protein domains relative to their initial position in the starting structure in order to satisfy a fit to the SAXS data.Understanding the protein–function relationships requires knowledge about the relevant functional conformations. Molecular dynamic (MD) simulations can be combined with SAXS to model protein structures and ensembles as well as dynamics associated with protein function.64,65 Coarse-grained MD simulations are utilized to generate a structural ensemble and then used to refine sub-ensembles against the experimental data.66,67 In recent developments, SAXS information can be incorporated into a Markov state model-based adaptive sampling strategy68 that can predict near-native structures of proteins and complexes without overfitting during the structure determination and refinements. In this approach, the integration of unbiased MD simulations and low-resolution data of great advantage that could lead to the accurate assessment of conformational ensembles of proteins with reduced computational costs. The corresponding studies of this approach were successfully involved in protein-folding examples such as HP35 double norleucine mutant domain, protein G, and α3D; and protein association examples such as the association of E. coli molybdopterin synthase subunits MoaD and MoaE,68 demonstrating that SAXS-guided adaptive sampling is an efficient approach that is able to predict the near-native structure ensembles and the transition pathways of conformational changes of proteins from simulations.
To assist interpreting SAXS data from biomolecular complexes (where flexible ensemble of states is present in solution), a Bayesian-based method has been developed10 to fit ensembles of model structures to the experimental SAXS data while minimizing the risk of overfitting. Furthermore, an iterative Bayesian ensemble estimator from SAS (BEES) program11 was introduced in the form of two versions that are in line with the users workflows, where the low-resolution profiles (SAXS/SANS) are used to re-weight population of states from molecular dynamic trajectories. The SASSIE-web server is the main version of BEES that provides a convenient graphical user interface with access to the computational resources needed to analyze large combinations of states.
AlphaFold
AlphaFold (AF) is an artificial intelligence (AI) system developed by DeepMind that has had a significant impact on protein structural biology by providing predicted protein structures for hundreds of millions of protein sequences.69,70 In effect, for the first time in history, the reliable predictive atomic coordinates calculated for (static) protein structures, RNA, DNA, associated complexes are now available that opens vast opportunities for structural/phylogeny-based research and an understanding of molecular evolution. Small-angle scattering is uniquely positioned to capitalize on the predictive capabilities of AF by providing additional data to augment the often mis-conceived ‘single particle view’ of structural biology. Solution-based SAXS and SANS – by the very nature of the measurements – always probe macromolecular populations spanning structural states sampling anywhere between narrow-to-wide distributions under diverse sample conditions; from pure homogeneous and ideal non-interacting particles through to oligomers, complexes/assemblies, transient complexes, modular/flexible proteins, intrinsically disordered proteins, etc. Consequently, small-angle scattering has enormous potential to add significantly to the ‘biology’ aspect of structural biology by utilizing the static structures that AF produces as initial templates and enriching them toward more realistic protein models that capture the physical-chemistry/biological states of proteins under certain and/or changing environmental conditions.The Ultra Scan SOlution MOdeler AlphaFold (US-SOMO-AF) database and its subsequent extension41 considers a number of calculated solution-based parameters based on AlphaFold protein models including diffusion and sedimentation coefficients, circular-dichroism spectra and predicted SAXS-based p(r) profiles so that researchers can quickly assess the results of their experiments to the predicted structures. Following on, due to the many challenges regarding the prediction of unstructured regions and the arrangements of the flexible linkers connecting structured domains, SAXS and AlphaFold have been combined to evaluate the solutions states of modular proteins71 utilizing SAXS data deposited to the small-angle scattering biological data bank. A Monte Carlo method was developed that generates a pool of ensemble structures based on an initial AlphaFold template in which the backbone dihedral angles in potentially flexible regions are adjusted. These structures can then be optimized by fitting the computed pair distance distribution functions and intensity profiles to experimental data in SASBDB, using a fast ensemble modeling method, demonstrating the complementarity between the solution SAXS and AF prediction for structural modeling.72
Dealing with structural polydispersity 1: oligomeric mixtures
Biological molecules are often present as mixtures of individual components, which is a matter that complicates SAXS data analysis. One of the most important applications of SAXS is the analysis of mixtures such as oligomeric equilibria. A mixture of non-interacting particles in solution comprises of a number of components, each with a certain volume fraction. The corresponding scattering intensity of the mixture can be expressed as the volume-fraction weighted sum of the scattering contributions of each component in the sample.5,73 If the scattering profiles of the components are available (e.g., calculated from atomistic model templates; or the component experimental SAXS profiles themselves), the program OLIGOMER73 employs a non-negative or unconstrained least-squares method to determine the necessary weighting of the individual component scattering functions, i.e., their volume fraction, and provides the corresponding fit to the data for the mixture. While OLIGOMER draws on CRYSOL when using atomistic models to represent the components of a mixture, a similar approach is used in foXS using the Debye formula to calculate the individual component scattering profiles and generates a multi-state function that during the fitting procedure outputs the appropriate individual component model-weightings and fits to the data.74In addition to fitting already-known model components of mixtures to SAXS data, more sophisticated modelling routines have been developed for both the ab initio dummy-residue modelling or rigid-body modelling of component systems. This includes the modelling of equilibrium mixtures of self-associating components or the formation of complexes. GASBORMX75 is an ab initio routine based on GASBOR and develops symmetric dummy residue models of self-associated protein oligomers in equilibrium with free monomer components (e.g., monomer–dimer; monomer–trimer, etc.), using multiple sets of SAXS data as input (e.g., concentration series data). Similarly, SASREFMX75 builds rigid-body atomistic representations of disassociated/associated oligomers or complexes, while foXS-Dock74 can be used to build the quaternary structures of the components from equilibrium mixtures of partially formed/dissociated complexes.
For a variety of cellular signaling and regulatory functions, transient interactions between biomolecules are critically essential and vital. In spite of that, determining the structure of the transient biomolecular complexes is a particularly difficult task that requires mathematically robust approaches. The primary challenge with the transient biomolecular complexes is that multiple species (i.e., complex and isolated components) co-exist in the sample where the relative populations are governed by thermodynamic laws. In this regard, it is difficult to isolate the complexes from the individual partners. With a developed robust chemometric approach, which was named complex objective structural analysis of multi-component systems (COSMiCS), a decomposition of titration SAXS data into species-specific details from such complexes was enabled76 where the power of the approach was validated with unique insights into the biomolecular assemblies. COSMiCS solves for the degeneracy of chemometric methods. It has the capacity to decompose large SAXS datasets where the data are introduced in different representations emphasizing molecular changes at different time and structural resolution ranges. This novel chemometric inspired strategy is very powerful and applicable to any macromolecular mixtures probed by SAXS. Through the decomposition strategy of COSMiCS, multi-component systems could be disassembled as well as structural and thermodynamic/kinetic information could be provided.77 The flexible and open-source nature of COSMiCS allows users to seamlessly customize the tool for a diverse range of systems and effortlessly integrate various biophysical and spectroscopic measurements. In this regard, COSMiCS holds a significant potential in addressing biological questions that often surpass the capabilities of conventional structural biology techniques. It offers valuable insights into various aspects such as encounter complexes, amyloidogenic soluble oligomers, kinetics of structural changes using time-resolved (TR) SAXS, capsid assembly mechanisms, and more.
Dealing with structural polydispersity 2: the case of structurally heterogeneous or intrinsically disordered macromolecules
Solution-based SAXS is one of the strongest structural biology techniques available to assess and model macromolecular flexibility.78 SAXS data from intrinsically disordered proteins (IDPs), or modular-domain proteins interspersed with flexible linkers, or long stretches of flexible loops, requires an ensemble modelling approach in order to interpret the SAXS data in terms of a distribution of heterogeneous structural states. This can be done via the ensemble optimization method (EOM).79,80 In the case of IDPs, EOM generates an initial pool of dummy-atom random chain ensembles based on the amino acid sequence, or for modular proteins, the program combines the atomic coordinates of individual structured domains with dummy-atom linkers, to generate an a pool of structures that sample multiple conformations. The model scattering intensities of each member of the initial ensembles are calculated, in addition to the model Rg and Dmax. Then using a using a genetic algorithm, volume-fraction weighted sub-ensembles are selected that best fit the experimental SAXS data. EOM outputs selected ensemble representative models, but more importantly compares the selected ensemble Rg and Dmax distributions with the Rg and Dmax of the initial random pool of structures. This comparison provides a quantitative insight as to whether the refined ensemble describing the SAXS data maintains a random conformation, or whether the structural states of the ensemble tend toward more compact or more extended states in solution compared to the initial random pool.Addressing the flexible modular proteins can also be facilitated using multi-FoXS.74 This approach accounts for conformational and positional heterogeneity of the protein under investigation where a population weighted ensemble is generated from a single input structure, based on a fitting of the available SAXS profile of the protein. With multi-FoXS, the modeling is performed in two steps: (1) the input structure is sampled based on the space of the dihedral angles, (2) SAXS profiles are computed for each generated conformation and fitted with the SAXS data where the fit is supported by a scoring function and enumeration procedure to rank and identify the most favorable multi-state models.
The native state ensembles of flexible modular proteins can moreover be analyzed using Bayesian interface methods.81–83 In this regard, the inherent flexibility of intrinsically disordered proteins (IDPs) or proteins with intrinsically disordered regions (IDRs) can be addressed by using the ensemble-averaged SAXS data to modify a probabilistic generative model of protein structure. For example, Bayesian ensemble SAXS (BE-SAXS)81 allows for the SAXS data itself to effectively guide, or restrict the search space to a set of finite, plausible atomistic model states commensurate with the SAXS data, without compromising ensemble size or conformational sampling. This BE-SAXS approach utilizes a multi-step expectation maximization algorithm, employing alternating rounds of Markov-chain Monte Carlo simulation and empirical Bayes optimization. Based on the SAXS data from the highly flexible antitoxin PaaA2 protein, the method produces a conformational ensemble highly consistent with the corresponding original set of atomistic structures. By embracing methods such as Monte Carlo simulations and coarse-grained modeling in combination with SAXS, significant progress has been made in facilitating a comprehensive understanding of the structural heterogineity of proteins. For example, the analysis of Histatin 5, a saliva protein that belongs to the family of intrinsically disordered proteins (IDPs) has demonstrated the suitability of these approaches,84 as has the use of coarse-grained simulations and Bayesian-based Monte Carlo procedures for the analysis of modular proteins connected by flexible linkers, such as HcK tyronsine kinase.83
A minimal ensemble search (MES) method has also been developed85 to describe ensemble-state data in terms of a limited set of structural states. This approach uses molecular dynamics (BILBOMD) simulations to generate ensembles and calculates the corresponding SAXS curves that are compared to the experimental SAXS data. Using a genetic algorithm the search for the minimal ensemble that fits the experimental data is determined, comprising of 2–5 most probable representative structures within the thermodynamic range of the ensemble. The performance of MES approach was validated by successfully identifying different levels of conformational changes in four different experimental systems (chimeric scaffoldin (S4), extracellular adherence protein (Eap), mammalian polynucleotide kinase (mPNK), Flavin reductase domain protein (FRDP)).
Among the efforts of dealing with structural polydispersity of intrinsically disordered proteins (IDPs), the development of a method incorporating SAXS data on-the-fly into molecular dynamic (MD) simulations has been developed with the aim to correct for force-filed inaccuracies of intrinsically disordered proteins (IDPs).86 This method upholds the principle of maximum entropy and employs a minimal bias in the conformational sampling to achieve better alignment with the ensemble-state SAXS data. The accuracy of this method was validated by testing suitable models for the RS peptide. An extensive review of methods (combining NMR with SAXS) that effectively tackles the challenge associated with characterizing the disordered structures of proteins and their complexes in the context of their biological functions are presented in ref. 87.
Dealing with structural polydispersity 3: principle component analysis
Principle component analysis (PCA) is a multivariate analysis technique.88 The main idea of PCA is reducing the dimensionality of dataset in which the number interrelated variables is very large, while retaining as much as possible the variation present in the dataset. The reductions lead to a new set of variables (principle components) which are uncorrelated and ordered such that the first few retain most of the variations in all of the original variables. This technique is used in many applications. For instance, in structural biology, processes involving highly dynamic large macromolecular complexes are challenging to interpret due to the presence of their heterogeneity with multiple species or conformations co-existing in equilibrium. These systems can be analyzed by PCA-based approaches (e.g., multivariate curve resolution using alternate least squares MCR-ALS). MCR-ALS allowed the study of transient biomolecular complexes89 and interrogating the effects on the wide-angle scattering regime of folding processes.90Time resolved (TR) measurements also benefit from PCA analyses. One of the most highly complex macromolecular examples that can be mentioned is the structural analysis of multicomponent amyloid systems91 where the evolving states of developing mixtures are analyzed in terms of collecting multiple TR-SAXS measurements spanning minutes to hours. In studies monitoring the fibrillation of insulin or the E46K mutant of α-synuclein,91 an approach based on PCA was developed and, without physically isolating the co-existing species, the data series could be decomposed to the individual components and their relative populations evaluated using COSMiCS and subsequently modelled. Another important aspect of structural biology is understanding the dynamic processes of macromolecules in the very-short time regime over millisecond to sub-millisecond time scales. This may be achieved using coupled a stop-and-flow instrument92 or by combining micro-beam SAXS (where the beam size is reduced to the micrometer range) with continuous-flow turbulent mixer microfluidic devices. For example, this latter experimental set up was applied to unravel the folding kinetics of cytochrome c93 spanning 100–1200 μs, probed with a 100 μs time resolution. Using singular value decomposition (SVD) to analyze the data showed the compaction and subsequent transition to the native state being a highly cooperative process.
Dealing with structural polydispersity 4: the physical separation of sample components using SEC-SAXS and AF4-SAXS
SAXS measurements sometimes necessitate the isolation of an ideal and monodispersed sample. However, this may be a non-trivial exercise in that samples maybe be influenced by time-dependent aggregation or oligomerization that go on to complicate data analysis. As the magnitude of the scattering intensities is dependent on the volume-squared of the particles within a sample, even trace levels of non-specific aggregation may ruin the interpretation of a SAXS profile. The physical separation of the components of a mixture prior to SAXS is an obvious a means to analyze the individual sample components, and although ultra centrifugation94 and ion-exchange chromatography95 have been used in the past to achieve this, it is size exclusion chromatography (SEC) that has become very popular to remove trace aggregates and resolve oligomeric species. The initial implementation of SEC-SAXS was pioneered at the APS beamline BIOCAT in 2004 and later at the photon factory BL10C in 2008.96,97 By 2008 the SWING beamline at SOLEIL made SEC-SAXS accessible to users as a regular method of data acquisition98 and over the past 10 years the coupling of SEC to SAXS beam lines, and even laboratory instruments99,100 has become routine. When SEC-SAXS also includes additional detection systems such as UV spectroscopy, refractive index, multi-angle laser light scattering and dynamic light scattering devices, the eluting species molecular mass can be independently validated and the hydrodynamic radius assessed.96,101,102More recently, asymmetric-flow field-flow fractionation (AF4) has been coupled to SAXS beam lines103,104 Although AF4-SAXS has been previously used in a laboratory setting to investigate strongly-scattering samples,105 the coupling with high-flux synchrotron beam lines is particularly useful for interrogating low contrast samples often encountered in biological macromolecules and materials. AF4 is a size-separation technique based on the lateral diffusion of particles along a semi-permeable membrane surface in a tangential cross-flow, and has significant potential for the separation of mixtures of more-challenging samples that may not be compatible with SEC such as biologics, pharmaceutical formulations, and drug-delivery nanoparticles106 that may irreversibly-interact with SEC-based separation matrices (such as SiO2 or dextran). For example, AF4-SAXS has proven effective in separating the fractions present within lipid–mRNA nanoparticle preparations107 in addition to monoclonal antibodies104 that – when combined with UV-spectroscopy, refractive index and static/dynamic light scattering – yields information about the concentration, absolute size distribution and structure of the separated components. As a result, AF4-SAXS holds significant relevance in pharmaceutical development from both a quality and safety standpoint108 such as the quality assurance processes underpinning the manufacturing and storage of mRNA vaccines and other types of therapeutic formulations.
Dealing with structural polydispersity 5: EFA for the analysis of SEC-SAXS data
Although both SEC-SAXS and AF4 are applied as techniques to physically separate individual components of mixtures, sometimes full separation is not achieved, and the elution trace may still yield poorly-separated or overlapping peaks. In such cases, decomposition procedures using evolving factor analysis (EFA) which is based on the singular value decomposition can be utilized to assess the number of components and further restore the corresponding scattering profiles of each individual component.109–111 For facilitating the SEC-SAXS data analysis and reconstruction of protein scattering from the peaks regions of SEC-SAXS frames, tools such as the data evaluation likelihood (DELA) have been developed101 based on the singular value decomposition and Guinier optimized linear combination (LC) where the number of components is not known a priori.For SEC-SAXS measurements, several hundred to several thousand individual SAXS data frames are generated spanning the SEC-elution profile. In programs such as CHROMIXS112 or SCÅTTER,36 the data frames can be represented as a ‘SAXS chromatogram’ of the intensity, or partial integrated intensity of the scattering versus frame number/time. In straightforward cases, where the background solvent scattering has been subtracted, the Rg and molecular weight estimate correlations through the sample component elution peaks maybe assessed, and if these parameters are stable (e.g., Rg ± 0.1 nm), the peak data may be interpreted in terms of isolated individual components. However, as mentioned above, in some cases the peaks maybe partially overlapping due to incomplete separation of the components in the sample generating significant drift in the Rg and/or molecular weight correlations through the SEC elution profiles, necessitating evolving factor analysis (EFA) of the data.
The EFA approach for SEC-SAXS deconvolution takes the multiple SAXS curves measured through the SEC peak for each measured sample, and describes these curves as a dataset matrix. If the singular value decomposition is implemented on this data matrix, one can get a representation including the singular eigen values in descending order and the corresponding significant eigen vectors. The number of the significant eigen vectors refer to the number of the individual components in the measured sample (i.e., sample mixture). Based on the singular value decomposition, EFA can perform forward and backward EFAs to determine the concentration windows during the system evolution where each component existing outside the concentration windows has a concentration zero. The information obtained from the forward and backward concentration window provides insights into a sequential disappearance of different sample components. The concentration window can be visualized by depicting the eigen values from the forward and backward EFAs versus the time frames. From the information about the concentration windows of the underlying components, a rotation matrix can be obtained and consequently the significant eigen vectors can be transformed into the concentration matrix. Given the data matrix and the concentration matrix, the scattering profiles of the components can be obtained.
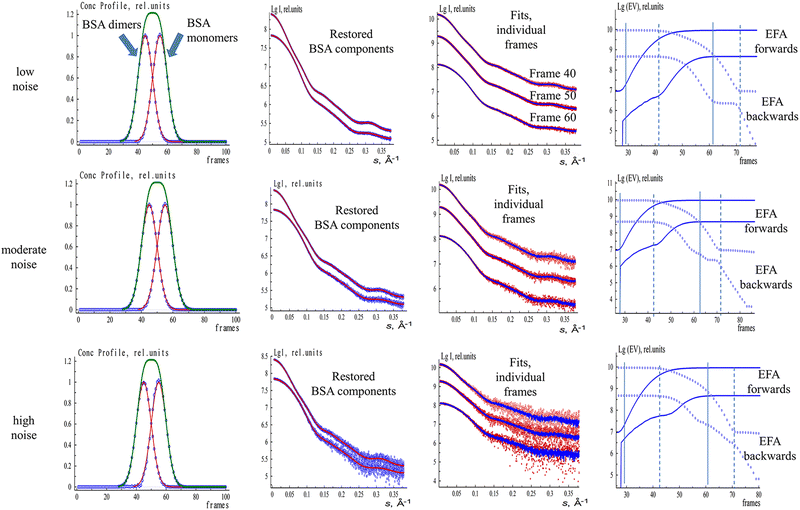
EFAMIX decomposition was tested on simulated SEC-SAXS data from bovine serum albumin (BSA) mixtures of two-components, three-components, and four-components; on ion exchange coupled SAXS (IEC-SAXS); and on experimental SEC-SAXS data.111 These systems could be deconvoluted at different degrees of peak overlap, different concentration ratios, and different signal-to-noise levels. Fig. 2 demonstrates the utilization of the EFAMIX deconvolution technique on synthetic SEC-SAXS data of a monomer–dimer BSA mixture with symmetric concentration profiles of each component within the system. For such a system, elution peaks (similar to those obtained by the SEC columns) with dimer and monomer species could be generated. Different noise levels (low, moderate, and high) depending on the number of photon counts were added to the generated SEC-SAXS data of the BSA two-component system and analyzed via the EFAMIX decomposition strategy. As shown in Fig. 2, at these noise levels, EFAMIX could restore symmetric concentration profiles (modeled by Gaussian functions) where the system has equal fractions of the components and decompose the generated SEC-SAXS data into the scattering profiles of the individual components in the system (monomer and dimer BSA). Both these decomposed profiles and computed profiles from monomeric and dimeric BSA model structures (PDB ID: 4F5S) showed excellent agreement demonstrating the capability of EFAMIX decomposition and analysis for two-component mixtures with symmetric concentration profiles. The accuracy of the results was also reasonable for two-component systems with different peak overlaps in the elution profile (where simple Gaussian functions are used to model these elution profiles) and different noise levels. In cases with asymmetric elution profiles (where exponential and Gaussian hybrid EGH functions are used to model these elution profiles113), EFAMIX results showed some systematic deviations. In addition, simulated SEC-SAXS data of model proteins with significantly different shapes (e.g., a mixture of elongated dimer and tetramer of fibrinogen) were found to moderately influence the EFAMIX deconvolution results where the components could feasibly be restored at all noise levels (low, moderate, high). EFAMIX decomposition results for two-component systems with different concentration ratios (where one of the components is minor and the other one is major) could be reasonably obtained until a concentration ratio limit 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 of monomer–dimer mixtures. For cases with increasing number of components (e.g., 3-component and 4-component systems), EFAMIX could resolve the 3-component system successfully at different noise levels. As for the 4-componet system, the decomposition of the four components is possible only at a relatively low noise level while only the largest components are restored at high noise level which means the noise level has a threshold for the 4-component system (i.e., the noise threshold decreases with increasing the number of components).
10 of monomer–dimer mixtures. For cases with increasing number of components (e.g., 3-component and 4-component systems), EFAMIX could resolve the 3-component system successfully at different noise levels. As for the 4-componet system, the decomposition of the four components is possible only at a relatively low noise level while only the largest components are restored at high noise level which means the noise level has a threshold for the 4-component system (i.e., the noise threshold decreases with increasing the number of components).
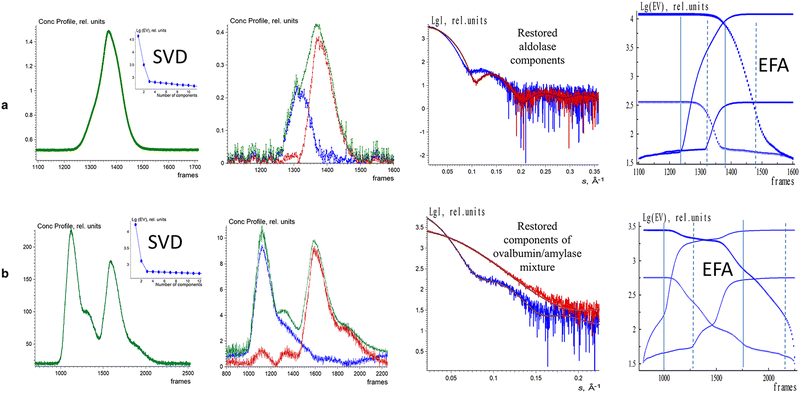
The EFAMIX method was also applied on number of experimental SEC-SAXS data sets with one, and two component systems. Fig. 3 illustrates the EFAMIX decomposition of several SEC-SAXS datasets utilizing the inline SEC setup.102,114 These datasets encompass a range of protein samples, including for instance, class II pyruvate adolase and a combination of ovalbumin with beta-amylase. In the case study of class II pyruvate adolase, the elusion profile is skewed which indicates the possibility of two components in the mixture. As for the SAXS data from the ovalbumin with beta-amylase mixture the elusion profiles showed two partially overlapping peaks as well as a visible shoulder after the first peak.111 In both cases, the singular value decomposition revealed the presence of two significant components and EFAMIX was able to successfully restore the two components in the system and fit them neatly with the available crystallographic models.
Dealing with structural polydispersity 7: REGALS, US-SOMO and BioXTAS RAW
The REGALS (regularized alternating least squares) method is a very useful approach for the analysis of SEC-SAXS and other types of SAXS data that provides robust deconvolutions based on parametrization and regularization.115 Here the idea is that a reliable and model-free separation is provided for an evolving system without the need for priori knowledge about a physicochemical model, how the system evolves or the scattering contributions of the components in the system. A reliable separation of sample and buffer scattering contributions can be achieved by applying smoothness regularization combined with alternating least squares (ALS). The idea of regularized ALS is readily implemented in the REGALS software, and demonstrates its flexible applicability to a wide variety of SAXS data from evolving mixtures where two types of restraints are applied: compact support and smoothness. In addition, in-line ion-exchange chromatography combined with SAXS (IEC-SAXS) data from large subunits of Bacillus subtilis ribonucleotide reductase (BsRNR) were successfully analyzed using the method where the background scattering data from the ever-increasing salt concentration of the ion-exchange eluant change gradually over time.116 Also, the method was successfully applied to other evolving systems such as equilibrium titration of phenylalanine hydroxylase (pheH) with phenylalanine (L-phe), time-resolved mixing of MsbA NBD with ATP, and time-resolved temperature jump of cisproline isomerase (cypA).115At synchrotron beam lines, SEC, IEC and AF4 measurements typically flow the column or AF4 eluates through a capillary past an intense X-ray beam. The consequence of such a setup are that, and especially at high-flux synchrotron sources, there may be significant radiation damage effects to the mobile phase (buffer and sample) that can have unforeseen consequences including sample aggregation, buffer-baseline drift and capillary fouling. Additional complications may also arise from the inevitable interaction between the eluting species and the chosen separation matrix, that may then go on and ‘skew’ elution profiles and yield non-ideal peak separation. Alleviating and analyzing the data comprehensively (primary data treatment, decomposition of unresolved components, and comparison with high resolution models) with the problems mentioned here can be performed thanks to developed tools named ultraScan solution modeler high-performance liquid chromatography SAXS (US-SOMO HPLC SAXS) where simple linear baseline corrections and Gaussian decomposition tools have been developed117 and then extended to include non-symmetrical modified Gaussian functions for the accurate decomposition of SEC-SAXS data.118 This includes corrections for capillary fouling and the extraction of individual component scattering contributions from heavily convoluted/poorly separated peaks of polydisperse samples.118
Additional valuable methods alleviating and analyzing the data comprehensively are made available through the graphical-user-interface-based free open-source program called BioXTAS RAW12 which provides features including calibrating, masking, integrating, and analyzing the SAXS data. This program is developed using the Python and C++ programming languages, ensuring compatibility with all major operating systems. Among the various functionalities, it encompasses the capability to deconvolve SAXS data through methods such as singular value decomposition and evolving factor analysis, as well as regularized alternating least squares (REGALS).
Dealing with polydispersity 8: modelling intermediates in evolving systems
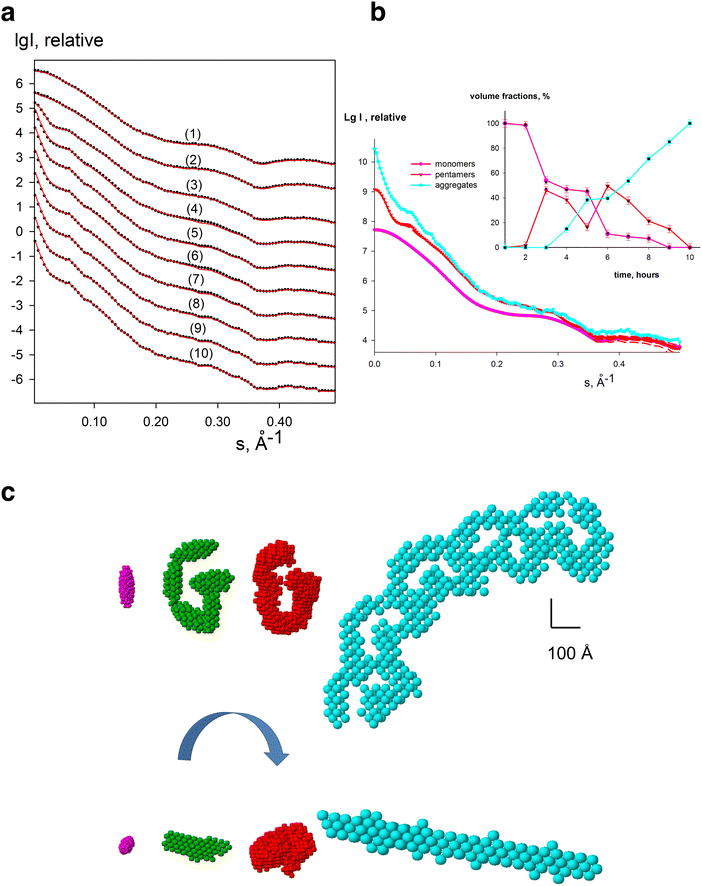
A key advantage of solution-sample based SAXS data is that all information about an evolving system are embedded in the measured scattering intensities, from the initial, intermediate(s) and final states. However, directly retrieving the shape of an intermediate state is very difficult do from a single scattering curve. Therefore, to gain structural models of potential intermediates in an evolving system, multiple scattering curves are measured and then SVD and evolving factor analysis is implemented to retrieve the shape of the unknown intermediate (generated as an ab initio bead model). Treating the SAXS curves from such systems is implemented in DAMMIX119 which has been shown to successfully generate models of intermediate states, and their corresponding volume fractions from both simulated (Fig. 4) and experimental data of evolving systems, for example, the nucleation-dependent process of insulin amyloid fibrillation, and the assembly states of lumazine synthase.119 In the nucleation process of insulin amyloid fibrillation, SAXS data was collected where the initial (insulin monomer) and final states (mature fibril) are known, while the intermediate state is unknown. The SVD revealed the presence of three significant components where the unknown intermediate state could be reconstructed as elongated structure of several insulin monomer blobs120 indicating that the oligomeric nucleus is the primary elongating unit of insulin amyloids fibrils. In the lumazine synthase system, two states t1 capsids (diameter 160 Å) and t3 capsids (diameter 3000 Å) are known, but a combined study including SAXS and cryo-EM showed that the system has additionally dissociated capsids.121 With DAMMIX, the scattering and shape of the intermediate state of these dissociated fragments could be restored as well as the volume fractions of the components where the retrieved shape agreed well with the previously reported results.Conclusion
SAXS is a highly adaptable biophysical/structural technique that affords valuable insights into macromolecular structures and structural-responses across a broad spectrum of conditions that will only to continue to develop and integrate with the multi-variate discipline that is modern structural biology. The ever-improving approaches for modelling biomacromolecules in solution using SAXS data, in combination with data processing and deconvolution methods are yielding more realistic insights into bio-macromolecular populations and how population dynamics are fundamental to molecular biological processes. At is core, solution-based SAXS for structural biology generates fundamental parameters that cannot be overstated in their importance – Rg, p(r), Dmax, scattering invariants and scaling parameters – that in and of themselves yield significant model-independent shape information. Ab initio modelling techniques spanning dummy-atom bead, dummy residue and electron density modelling add to this fundamental base to obtain 3D shapes from 1D scattering profiles, while atomistic modelling – rigid-body, NMA, MD and ensemble approaches – yields insights into aspects of structural heterogeneity that other techniques struggle to capture. Following on, modern approaches to data processing and analysis have made otherwise intractable interpretation(s) of SAXS data accessible such as singular value decomposition and evolving factor analysis. These approaches play a very powerful role for the analysis of mixtures and evolving systems where they are used to determine the corresponding scattering profiles of individual components and intermediates. Many software programs have been developed to implement such decomposition approaches, that are directly relevant for the analysis of more complicated structural-biology systems found throughout biology. The strength of SAXS is the ability to evaluate macromolecular populations and evolving population states under static or changing conditions, in numerous sample environments that can yield insights into structural heterogeneity, dynamics and structural responses. The disadvantage of solution-based SAXS is the inherent ambiguity of the data caused by the time- and rotationally-averaged scattering amplitudes arising from randomly tumbling particles in solution. Yet, SAXS – with ongoing advances in instrumentation, data analysis and modelling as outlined here – acts as a bridge between structural biology disciplines for the interpretation of macromolecular structure(s) by readily incorporating experimental observations from X-ray crystallography,122,123 NMR,124,125 cryo-electron microscopy,126 FRET127 and mass spectrometry,128,129 as well as from predictive techniques such as AlphaFold. Indeed, structural biology as a discipline is undergoing a significant transformation due to AlphaFold, and this breakthrough is revolutionizing the field with profound impact. SAXS – in combination with the myriad of techniques now on offer to the 21st century structural biologist when applied to the interrogation of protein structures, will only go on to emphasize a corresponding synergistic relationship between what is predicted and what is present, thereby significantly improving the modern view of structural biology as integrated structural systems and not merely as structures in and of themselves.130Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review. This study was carried out using publicly available data from the small angle scattering biological databank (SASBDB) at https://www.sasbdb.org with accession numbers SASDPH7 and SASDHF8.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the support, help and guidance from Dr Dmitri Svergun (EMBL Hamburg and bioSAXS). This work was supported by a Deutsche Forschungsgemeinschaft grant (grant no. SV 9/11-1) awarded to A. S. A. M.References
- B. R. Pauw, A. J. Smith, T. Snow, N. J. Terrill and A. F. Thünemann, The modular small-angle X-ray scattering data correction sequence, J. Appl. Crystallogr., 2017, 50, 1800–1811 CrossRef CAS PubMed.
- A. J. Allen, F. Zhang, R. Joseph Kline, W. F. Guthrie and J. Ilavsky, NIST Standard Reference Material 3600: Absolute Intensity Calibration Standard for Small-Angle X-ray Scattering, J. Appl. Crystallogr., 2017, 50, 462–474 CrossRef CAS PubMed.
- D. Orthaber, A. Bergmann and O. Glatter, SAXS experiments on absolute scale with Kratky systems using water as a secondary standard, J. Appl. Crystallogr., 2000, 33, 218–225 CrossRef CAS.
- W. R. Krigbaum and F. R. Kügler, Molecular conformation of egg-white lysozyme and bovine alpha-lactalbumin in solution, Biochemistry, 1970, 9(5), 1216–1223 CrossRef CAS PubMed.
- L. A. Feigin and D. I. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, ISBN 0-306-42629-3, New York/London: Plenum Press, 1987 Search PubMed.
- D. I. Svergun, M. H. J. Koch, P. A. Timmins and R. P. May, Small Angle X-Ray and Neutron Scattering from Solutions of Biological Macromolecules, OUP Oxford, 2013, vol. 19 Search PubMed.
- W. Zheng and R. B. Best, An Extended Guinier Analysis for Intrinsically Disordered Proteins, J. Mol. Biol., 2018, 430, 2540–2553 CrossRef CAS PubMed.
- D. A. Jacques and J. Trewhella, Small-angle scattering for structural biology – Expanding the frontier while avoiding the pitfalls, Protein Sci., 2010, 19, 642–657 CrossRef CAS PubMed.
- K. Manalastas-Cantos, P. V. Konarev, N. R. Hajizadeh, A. G. Kikhney, M. V. Petoukhov, D. S. Molodenskiy, A. Panjkovich, H. D. T. Mertens, A. Gruzinov, C. Borges, C. M. Jeffries, D. I. Svergun and D. Franke, ATSAS 3.0: expanded functionality and new tools for small-angle scattering data analysis, J. Appl. Crystallogr., 2021, 54, 343–355 CrossRef CAS PubMed.
- J. E. Curtis, S. Raghunandan, H. Nanda and S. Krueger, SASSIE: a program to study intrinsically disordered biological molecules and macromolecular ensembles using experimental scattering restraints, Comput. Phys. Commun., 2012, 183, 382–389 CrossRef CAS.
- S. Bowerman, J. E. Curtis, J. Clayton, E. H. Brookes and J. Wereszczynski, BEES: Bayesian Ensemble Estimation from SAS, Biophys. J., 2019, 117, 399–407 CrossRef CAS PubMed.
- J. B. Hopkins, R. E. Gillilan and S. Skou, BioXTAS RAW: improvements to a free open-source program for small-angle X-ray scattering data reduction and analysis, J. Appl. Crystallogr., 2017, 50, 1545–1553 CrossRef CAS PubMed.
- H. Liu, A. Hexemer and P. H. Zwart, The Small Angle Scattering ToolBox (SASTBX): an open-source software for biomolecular small-angle scattering, J. Appl. Crystallogr., 2012, 45, 587–593 CrossRef CAS.
- D. I. Svergun, Determination of the regularization parameter in indirect-transform methods using perceptual criteria, J. Appl. Crystallogr., 1992, 25, 495–503 CrossRef CAS.
- O. Glatter, A new method for the evaluation of small-angle scattering data, J. Appl. Crystallogr., 1977, 10, 415–421 CrossRef.
- M. V. Petoukhov, P. V. Konarev, G. Kikhney and I. Dmitri, ATSAS 2.1 – Supported Small-Angle Scattering Data Analysis, J. Appl. Crystallogr., 2007, 40, s223–s228 CrossRef CAS.
- O. Glatter, Evaluation of small-angle scattering data from lamellar and cylindrical particles by the indirect transformation method, J. Appl. Crystallogr., 1980, 13, 577–584 CrossRef.
- A. Bergmann, G. Fritz and O. Glatter, Solving the generalized indirect Fourier transformation (GIFT) by Boltzmann simplex simulated annealing (BSSA), J. Appl. Crystallogr., 2000, 33, 1212–1216 CrossRef CAS.
- S. Hansen, BayesApp: a web site for indirect transformation of small-angle scattering data, J. Appl. Crystallogr., 2012, 45, 566–567 CrossRef CAS.
- S. Förster, L. Apostol and W. Bras, Scatter: software for the analysis of nano-and mesoscale small-angle scattering, J. Appl. Crystallogr., 2010, 43, 639–646 CrossRef.
- D. S. Molodenskiy, D. I. Svergun and A. G. Kikhney, Artificial neural networks for solution scattering data analysis, Structure, 2022, 30, 900–908.e2 CrossRef CAS PubMed.
- D. Durand, C. Vivès, D. Cannella, J. Pérez, E. Pebay-Peyroula, P. Vachette and F. Fieschi, NADPH oxidase activator p67phox behaves in solution as a multidomain protein with semi-flexible linkers, J. Struct. Biol., 2010, 169, 45–53 CrossRef CAS PubMed.
- S. Doniach, Changes in biomolecular conformation seen by small angle X-ray scattering, Chem. Rev., 2001, 101, 1763–1778 CrossRef CAS PubMed.
- L. A. Feigin and D. I. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, ISBN 0-306-42629-3, New York/London: Plenum Press, 1987 Search PubMed.
- O. Glatter and O. Kratky, Small-angle X-ray scattering, Academic Press Inc., 1982, pp. 1–515 Search PubMed.
- D. Franke, C. M. Jeffries and D. I. Svergun, Machine Learning Methods for X-Ray Scattering Data Analysis from Biomacromolecular Solutions, Biophys. J., 2018, 114, 2485–2492 CrossRef CAS PubMed.
- M. V. Petoukhov and D. I. Svergun, Ambiguity assessment of small-angle scattering curves from monodisperse systems, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 1051–1058 CrossRef CAS PubMed.
- R. P. Rambo and J. A. Tainer, Characterizing flexible and intrinsically unstructured biological macromolecules by SAS using the Porod–Debye law, Biopolymers, 2011, 95, 559–571 CrossRef CAS PubMed.
- J. Trewhella, P. Vachette, J. Bierma, C. Blanchet, E. Brookes, S. Chakravarthy, L. Chatzimagas, T. E. Cleveland, N. Cowieson, B. Crossett, A. P. Duff, D. Franke, F. Gabel, R. E. Gillilan, M. Graewert, A. Grishaev, J. M. Guss, M. Hammel, J. Hopkins, Q. Huang, J. S. Hub, G. L. Hura, T. C. Irving, C. M. Jeffries, C. Jeong, N. Kirby, S. Krueger, A. Martel, T. Matsui, N. Li, J. Pérez, L. Porcar, T. Prangé, I. Rajkovic, M. Rocco, D. J. Rosenberg, T. M. Ryan, S. Seifert, H. Sekiguchi, D. Svergun, S. Teixeira, A. Thureau, T. M. Weiss, A. E. Whitten, K. Wood and X. Zuo, A round-robin approach provides a detailed assessment of biomolecular small-angle scattering data reproducibility and yields consensus curves for benchmarking, Acta Crystallogr., Sect. D: Struct. Biol., 2022, 78, 1315–1336 CrossRef CAS PubMed.
- A. Sagar, C. M. Jeffries, M. V. Petoukhov, D. I. Svergun and P. Bernadó, Comment on the Optimal Parameters to Derive Intrinsically Disordered Protein Conformational Ensembles from Small-Angle X-ray Scattering Data Using the Ensemble Optimization Method, J. Chem. Theory Comput., 2021, 17, 2014–2021 CrossRef CAS PubMed.
- A. Rojowska, K. Lammens, F. U. Seifert, C. Direnberger, H. Feldmann and K. Hopfner, Structure of the Rad50 DNA double-strand break repair protein in complex with DNA, EMBO J., 2014, 33, 2847–2859 CrossRef CAS PubMed.
- F. Zhang, J. Ilavsky, G. G. Long, J. P. G. Quintana, A. J. Allen and P. R. Jemian, Glassy carbon as an absolute intensity calibration standard for small-angle scattering, Metall. Mater. Trans. A, 2010, 41, 1151–1158 CrossRef.
- M. de Oliveira Neto, A. de Freitas Fernandes, V. Piiadov, A. F. Craievich, E. A. de Araújo and I. Polikarpov, SAXSMoW 3.0: new advances in the determination of the molecular weight of proteins in dilute solutions from SAXS intensity data on a relative scale, Protein Sci., 2022, 31, 251–258 CrossRef CAS PubMed.
- H. Fischer, M. De Oliveira Neto, H. B. Napolitano, I. Polikarpov and A. F. Craievich, Determination of the molecular weight of proteins in solution from a single small-angle X-ray scattering measurement on a relative scale, J. Appl. Crystallogr., 2010, 43, 101–109 CrossRef CAS.
- R. P. Rambo and J. A. Tainer, Accurate assessment of mass, models and resolution by small-angle scattering, Nature, 2013, 496, 477–481 CrossRef CAS PubMed.
- R. P. Rambo, ScÅtter – software for the analysis of biological SAXS datasets, 2016, https://bl1231.als.lbl.gov/scatter/ Search PubMed.
- N. R. Hajizadeh, D. Franke, C. M. Jeffries and D. I. Svergun, Consensus Bayesian assessment of protein molecular mass from solution X-ray scattering data, Sci. Rep., 2018, 8, 1–13 CAS.
- G. Porod, Die Röntgenkleinwinkelstreuung von dichtgepackten kolloiden Systemen – I. Teil, Kolloid-Z., 1951, 124, 83–114 CrossRef CAS.
- M. Sztucki, SAXSutilities2: a Graphical User Interface For Processing and Analysis of Small-Angle X-ray Scattering Data, 2021 DOI:10.5281/zenodo.5825707.
- A. G. Kikhney, A. Panjkovich, A. V. Sokolova and D. I. Svergun, DARA: a web server for rapid search of structural neighbours using solution small angle X-ray scattering data, Bioinformatics, 2016, 32, 616–618 CrossRef CAS PubMed.
- E. Brookes and M. Rocco, A database of calculated solution parameters for the AlphaFold predicted protein structures, Sci. Rep., 2022, 12, 1–13 CrossRef PubMed.
- D. I. Svergun, Restoring low resolution structure of biological macromolecules from solution scattering using simulated annealing, Biophys. J., 1999, 76, 2879–2886 CrossRef CAS PubMed.
- D. Franke and D. I. Svergun, DAMMIF, a program for rapid ab-initio shape determination in small-angle scattering, J. Appl. Crystallogr., 2009, 42, 342–346 CrossRef CAS PubMed.
- D. I. Svergun, M. V. Petoukhov and M. H. J. Koch, Determination of domain structure of proteins from x-ray solution scattering, Biophys. J., 2001, 80, 2946–2953 CrossRef CAS PubMed.
- D. Franke, C. M. Jeffries and D. I. Svergun, Correlation Map, a goodness-of-fit test for one-dimensional X-ray scattering spectra, Nat. Methods, 2015, 12, 419–422 CrossRef CAS PubMed.
- M. B. Kozin and D. I. Svergun, Automated matching of high- and low-resolution structural models, J. Appl. Crystallogr., 2001, 34, 33–41 CrossRef CAS.
- P. J. Besl and N. D. McKay, A Method for Registration of 3-D Shapes, IEEE Trans. on Pattern Anal. and Mach. Intell., 1992, 14, 239–256 Search PubMed.
- P. V. Konarev, M. V. Petoukhov and D. I. Svergun, Rapid automated superposition of shapes and macromolecular models using spherical harmonics, J. Appl. Crystallogr., 2016, 49, 953–960 CrossRef CAS PubMed.
- T. D. Grant, Ab initio electron density determination directly from solution scattering data, Nat. Methods, 2018, 15, 191–193 CrossRef CAS PubMed.
- P. Chacón, F. Morán, J. F. Díaz, E. Pantos and J. M. Andreu, Low-resolution structures of proteins in solution retrieved from x-ray scattering with a genetic algorithm, Biophys. J., 1998, 74, 2760–2775 CrossRef PubMed.
- S. J. Henderson, Monte Carlo modeling of small-angle scattering data from non-interacting homogeneous and heterogeneous particles in solution, Biophys. J., 1996, 70, 1618–1627 CrossRef CAS PubMed.
- D. Svergun, C. Barberato and M. H. Koch, CRYSOL – A program to evaluate X-ray solution scattering of biological macromolecules from atomic coordinates, J. Appl. Crystallogr., 1995, 28, 768–773 CrossRef CAS.
- D. Schneidman-Duhovny, M. Hammel and A. Sali, FoXS: a web server for rapid computation and fitting of SAXS profiles, Nucleic Acids Res., 2010, 38, 540–544 CrossRef PubMed.
- S. Grudinin, M. Garkavenko and A. Kazennov, Pepsi-SAXS: an adaptive method for rapid and accurate computation of small-angle X-ray scattering profiles, Acta Crystallogr., Sect. D: Struct. Biol., 2017, 73, 449–464 CrossRef CAS PubMed.
- C. J. Knight and J. S. Hub, WAXSiS: a web server for the calculation of SAXS/WAXS curves based on explicit-solvent molecular dynamics, Nucleic Acids Res., 2015, 43, W225–W230 CrossRef CAS PubMed.
- J. Trewhella, P. Vachette and A. H. Larsen, Benchmarking predictive methods for small-angle X-ray scattering from atomic coordinates of proteins using maximum likelihood consensus data, IUCrJ, 2024, 11, 762–779 CrossRef CAS PubMed.
- M. C. Pedersen, L. Arleth and K. Mortensen, WillItFit: a framework for fitting of constrained models to small-angle scattering data, J. Appl. Crystallogr., 2013, 46, 1894–1898 CrossRef CAS.
- S. R. Chamberlain, S. Moore and T. D. Grant, Fitting high-resolution electron density maps from atomic models to solution scattering data, Biophys. J., 2023, 122, 4567–4581 CrossRef CAS PubMed.
- M. V. Petoukhov and D. I. Svergun, Global rigid body modeling of macromolecular complexes against small-angle scattering data, Biophys. J., 2005, 89, 1237–1250 CrossRef CAS PubMed.
- M. V. Petoukhov, D. Franke, A. V. Shkumatov, G. Tria, A. G. Kikhney, M. Gajda, C. Gorba, H. D. T. Mertens, P. V. Konarev and D. I. Svergun, New developments in the ATSAS program package for small-angle scattering data analysis, J. Appl. Crystallogr., 2012, 45, 342–350 CrossRef CAS PubMed.
- D. Schneidman-Duhovny, M. Hammel and A. Sali, Macromolecular docking restrained by a small angle X-ray scattering profile, J. Struct. Biol., 2011, 173, 461–471 CrossRef CAS PubMed.
- B. Jiménez-García, C. Pons, D. I. Svergun, P. Bernadó and J. Fernández-Recio, PyDockSAXS: protein–protein complex structure by SAXS and computational docking, Nucleic Acids Res., 2015, 43, W356–W361 CrossRef PubMed.
- A. Panjkovich and D. I. Svergun, Deciphering conformational transitions of proteins by small angle X-ray scattering and normal mode analysis, Phys. Chem. Chem. Phys., 2016, 18, 5707–5719 RSC.
- J. S. Hub, Interpreting solution X-ray scattering data using molecular simulations, Curr. Opin. Struct. Biol., 2018, 49, 18–26 CrossRef CAS PubMed.
- J. R. Allison, Using simulation to interpret experimental data in terms of protein conformational ensembles, Curr. Opin. Struct. Biol., 2017, 43, 79–87 CrossRef CAS PubMed.
- Y. Chen, S. L. Campbell and N. V. Dokholyan, Deciphering protein dynamics from NMR data using explicit structure sampling and selection, Biophys. J., 2007, 93, 2300–2306 CrossRef CAS PubMed.
- I. Grubisic, M. N. Shokhirev, M. Orzechowski, O. Miyashita and F. Tama, Biased coarse-grained molecular dynamics simulation approach for flexible fitting of X-ray structure into cryo electron microscopy maps, J. Struct. Biol., 2010, 169, 95–105 CrossRef CAS PubMed.
- C. Zhao and D. Shukla, SAXS-guided Enhanced Unbiased Sampling for Structure Determination of Proteins and Complexes, Sci. Rep., 2018, 8, 1–13 Search PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Highly accurate protein structure prediction with AlphaFold, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- J. Abramson, J. Adler, J. Dunger, R. Evans, T. Green, A. Pritzel, O. Ronneberger, L. Willmore, A. J. Ballard, J. Bambrick, S. W. Bodenstein, D. A. Evans, C. C. Hung, M. O’Neill, D. Reiman, K. Tunyasuvunakool, Z. Wu, A. Žemgulytė, E. Arvaniti, C. Beattie, O. Bertolli, A. Bridgland, A. Cherepanov, M. Congreve, A. I. Cowen-Rivers, A. Cowie, M. Figurnov, F. B. Fuchs, H. Gladman, R. Jain, Y. A. Khan, C. M. R. Low, K. Perlin, A. Potapenko, P. Savy, S. Singh, A. Stecula, A. Thillaisundaram, C. Tong, S. Yakneen, E. D. Zhong, M. Zielinski, A. Žídek, V. Bapst, P. Kohli, M. Jaderberg, D. Hassabis and J. M. Jumper, Accurate structure prediction of biomolecular interactions with AlphaFold 3, Nature, 2024, 630, 493–500 CrossRef CAS PubMed.
- E. Brookes, M. Rocco and J. Trewhella, AlphaFold-predicted protein structures and small- angle X-ray scattering: insights from an extended examination of selected data in the Small-Angle Scattering Biological Data Bank research papers, J. Appl. Crystallogr., 2023, 910–926 CrossRef CAS PubMed.
- V. Receveur-Bréchot, AlphaFold, small-angle X-ray scattering and ensemble modelling: a winning combination for intrinsically disordered proteins, J. Appl. Crystallogr., 2023, 56, 1313–1314 CrossRef PubMed.
- P. V. Konarev, V. V. Volkov, A. V. Sokolova, M. H. J. Koch and D. I. Svergun, PRIMUS: a Windows PC-based system for small-angle scattering data analysis, J. Appl. Crystallogr., 2003, 36, 1277–1282 CrossRef CAS.
- D. Schneidman-Duhovny, M. Hammel, J. A. Tainer and A. Sali, FoXS, FoXSDock and MultiFoXS: single-state and multi-state structural modeling of proteins and their complexes based on SAXS profiles, Nucleic Acids Res., 2016, 44, W424–W429 CrossRef CAS PubMed.
- M. V. Petoukhov, I. M. L. Billas, M. Takacs, M. A. Graewert, D. Moras and D. I. Svergun, Reconstruction of quaternary structure from X-ray scattering by equilibrium mixtures of biological macromolecules, Biochemistry, 2013, 52, 6844–6855 CrossRef CAS PubMed.
- A. Sagar, F. Herranz-Trillo, A. E. Langkilde, B. Vestergaard and P. Bernadó, Structure and thermodynamics of transient protein-protein complexes by chemometric decomposition of SAXS datasets, Structure, 2021, 29, 1074–1090.e4 CrossRef CAS PubMed.
- A. Sagar and P. Bernadó, Disentangling polydisperse biomolecular systems by Chemometrics decomposition of SAS data, Elsevier Inc., 1st edn, 2022, vol. 677 Search PubMed.
- M. Hammel, Validation of macromolecular flexibility in solution by small-angle X-ray scattering (SAXS), Eur. Biophys. J., 2012, 41, 789–799 CrossRef CAS PubMed.
- P. Bernadó, E. Mylonas, M. V. Petoukhov, M. Blackledge and D. I. Svergun, Structural characterization of flexible proteins using small-angle X-ray scattering, J. Am. Chem. Soc., 2007, 129, 5656–5664 CrossRef PubMed.
- G. Tria, H. D. T. Mertens, M. Kachala and D. I. Svergun, Advanced ensemble modelling of flexible macromolecules using X-ray solution scattering, IUCrJ, 2015, 2, 207–217 CrossRef CAS PubMed.
- L. D. Antonov, S. Olsson, W. Boomsma and T. Hamelryck, Bayesian inference of protein ensembles from SAXS data, Phys. Chem. Chem. Phys., 2016, 18, 5832–5838 RSC.
- G. Hummer and J. Köfinger, Bayesian ensemble refinement by replica simulations and reweighting, J. Chem. Phys., 2015, 143, 1–15 CrossRef PubMed.
- S. Yang, L. Blachowicz, L. Makowski and B. Roux, Multidomain assembled states of Hck tyrosine kinase in solution, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15757–15762 CrossRef CAS PubMed.
- C. Cragnell, D. Durand, B. Cabane and M. Skepö, Coarse-grained modeling of the intrinsically disordered protein Histatin 5 in solution: Monte Carlo simulations in combination with SAXS, Proteins: Struct., Funct., Bioinf., 2016, 84, 777–791 CrossRef CAS PubMed.
- M. Pelikan, G. L. Hura and M. Hammel, Structure and flexibility within proteins as identified through small angle X-ray scattering, Gen. Physiol. Biophys., 2009, 28(2), 174–189 CrossRef CAS PubMed.
- M. R. Hermann and J. S. Hub, SAXS-Restrained Ensemble Simulations of Intrinsically Disordered Proteins with Commitment to the Principle of Maximum Entropy, J. Chem. Theory Comput., 2019, 15, 5103–5115 CrossRef CAS PubMed.
- M. Chan-Yao-Chong, D. Durand and T. Ha-Duong, Molecular Dynamics Simulations Combined with Nuclear Magnetic Resonance and/or Small-Angle X-ray Scattering Data for Characterizing Intrinsically Disordered Protein Conformational Ensembles, J. Chem. Inf. Model., 2019, 59, 1743–1758 CrossRef CAS PubMed.
- D. J. Bartholomew, Principal components analysis, Int. Encycl. Educ., 2010, 374–377 Search PubMed.
- T. E. Williamson, B. A. Craig, E. Kondrashkina, C. Bailey-Kellogg and A. M. Friedman, Analysis of self-associating proteins by singular value decomposition of solution scattering data, Biophys. J., 2008, 94, 4906–4923 CrossRef CAS PubMed.
- D. D. L. Minh and L. Makowski, Wide-angle X-ray solution scattering for protein-ligand binding: multivariate curve resolution with bayesian confidence intervals, Biophys. J., 2013, 104, 873–883 CrossRef CAS PubMed.
- F. Herranz-Trillo, M. Groenning, A. van Maarschalkerweerd, R. Tauler, B. Vestergaard and P. Bernadó, Structural Analysis of Multi-component Amyloid Systems by Chemometric SAXS Data Decomposition, Structure, 2017, 25, 5–15 CrossRef CAS PubMed.
- H. Tidow and I. Josts, Chapter Eight – Stopped-flow-time-resolved SAXS for studies of ligand-driven protein dimerization, Methods Enzymol., 2022, 677, 251–262 CAS.
- R. Graceffa, R. P. Nobrega, R. A. Barrea, S. V. Kathuria, S. Chakravarthy, O. Bilsel and T. C. Irving, Sub-millisecond time-resolved SAXS using a continuous-flow mixer and X-ray microbeam, J. Synchrotron Radiat., 2013, 20, 820–825 CrossRef CAS PubMed.
- R. M. G. Hynson, A. P. Duff, N. Kirby, S. Mudie and L. K. Lee, Differential ultracentrifugation coupled to small-angle X-ray scattering on macromolecular complexes, J. Appl. Crystallogr., 2015, 48, 769–775 CrossRef CAS.
- S. Hutin and M. Brennich, B. Maillot and A. Round, Online ion-exchange chromatography for small-angle X-ray scattering, Acta Crystallogr., Sect. D: Struct. Biol., 2016, 72, 1090–1099 CrossRef CAS PubMed.
- E. Mathew, A. Mirza and N. Menhart, Liquid-chromatography-coupled SAXS for accurate sizing of aggregating proteins, J. Synchrotron Radiat., 2004, 11, 314–318 CrossRef CAS PubMed.
- Y. Watanabe and Y. Inoko, Size-exclusion chromatography combined with small-angle X-ray scattering optics, J. Chromatogr. A, 2009, 1216, 7461–7465 CrossRef CAS PubMed.
- G. David and J. Pérez, Combined sampler robot and high-performance liquid chromatography: a fully automated system for biological small-angle X-ray scattering experiments at the Synchrotron SOLEIL SWING beamline, J. Appl. Crystallogr., 2009, 42, 892–900 CrossRef CAS.
- R. Inoue, T. Nakagawa, K. Morishima, N. Sato, A. Okuda, R. Urade, R. Yogo, S. Yanaka, M. Yagi-Utsumi, K. Kato, K. Omoto, K. Ito and M. Sugiyama, Newly developed Laboratory-based Size exclusion chromatography Small-angle X-ray scattering System (La-SSS), Sci. Rep., 2019, 9, 1–12 CrossRef CAS PubMed.
- S. Bucciarelli, S. R. Midtgaard, M. N. Pedersen, S. Skou, L. Arleth and B. Vestergaard, Size-exclusion chromatography small-angle X-ray scattering of water soluble proteins on a laboratory instrument, J. Appl. Crystallogr., 2018, 51, 1623–1632 CrossRef CAS PubMed.
- A. W. Malaby, S. Chakravarthy, T. C. Irving, S. V. Kathuria, O. Bilsel and D. G. Lambright, Methods for analysis of size-exclusion chromatography-small-angle X-ray scattering and reconstruction of protein scattering, J. Appl. Crystallogr., 2015, 48, 1102–1113 CrossRef CAS PubMed.
- M. A. Graewert, D. Franke, C. M. Jeffries, C. E. Blanchet, D. Ruskule, K. Kuhle, A. Flieger, B. Schäfer, B. Tartsch, R. Meijers and D. I. Svergun, Automated pipeline for purification, biophysical and X-ray analysis of biomacromolecular solutions, Sci. Rep., 2015, 5, 1–8 Search PubMed.
- M. A. Graewert, C. Wilhelmy, T. Bacic, J. Schumacher, C. Blanchet, F. Meier, R. Drexel, R. Welz, B. Kolb, K. Bartels, T. Nawroth, T. Klein, D. Svergun, P. Langguth and H. Haas, Quantitative size-resolved characterization of mRNA nanoparticles by in-line coupling of asymmetrical-flow field-flow fractionation with small angle X-ray scattering, Sci. Rep., 2023, 13, 1–13 CrossRef PubMed.
- H. Bolinsson, C. Söderberg, F. Herranz-Trillo, M. Wahlgren and L. Nilsson, Realizing the AF4-UV-SAXS on-line coupling on protein and antibodies using high flux synchrotron radiation at the CoSAXS beamline, MAX IV, Anal. Bioanal. Chem., 2023, 415, 6237–6246 CrossRef CAS PubMed.
- P. Knappe, L. Boehmert, R. Bienert, S. Karmutzki, B. Niemann, A. Lampen and A. F. Thünemann, Processing nanoparticles with A4F-SAXS for toxicological studies: iron oxide in cell-based assays, J. Chromatogr. A, 2011, 1218, 4160–4166 CrossRef CAS PubMed.
- M. J. Mitchell, M. M. Billingsley, R. M. Haley, M. E. Wechsler, N. A. Peppas and R. Langer, Engineering precision nanoparticles for drug delivery, Nat. Rev. Drug Discovery, 2021, 20, 101–124 CrossRef CAS PubMed.
- M. A. Graewert, C. Wilhelmy, T. Bacic, J. Schumacher, C. Blanchet, F. Meier, R. Drexel, R. Welz, B. Kolb, K. Bartels, T. Nawroth, T. Klein, D. Svergun, P. Langguth and H. Haas, Quantitative size-resolved characterization of mRNA nanoparticles by in-line coupling of asymmetrical-flow field-flow fractionation with small angle X-ray scattering, Sci. Rep., 2023, 13, 1–13 CrossRef PubMed.
- J. D. Clogston, V. A. Hackley, A. Prina-Mello, S. Puri, S. Sonzini and P. L. Soo, Sizing up the Next Generation of Nanomedicines, Pharm. Res., 2020, 37, 1–10 CrossRef PubMed.
- H. R. Keller and D. L. Massart, Evolving factor analysis, Chemom. Intell. Lab. Syst., 1991, 12, 209–224 CrossRef.
- J. B. Hopkins, R. E. Gillilan and S. Skou, BioXTAS RAW: improvements to a free open-source program for small-angle X-ray scattering data reduction and analysis, J. Appl. Crystallogr., 2017, 50, 1545–1553 CrossRef CAS PubMed.
- P. V. Konarev, M. A. Graewert, C. M. Jeffries, M. Fukuda, T. A. Cheremnykh, V. V. Volkov and D. I. Svergun, EFAMIX, a tool to decompose inline chromatography SAXS data from partially overlapping components, Protein Sci., 2022, 31, 269–282 CrossRef CAS PubMed.
- A. Panjkovich and D. I. Svergun, CHROMIXS: automatic and interactive analysis of chromatography-coupled small-angle X-ray scattering data, Bioinformatics, 2018, 34, 1944–1946 CrossRef CAS PubMed.
- K. Lan and J. W. Jorgenson, A hybrid of exponential and Gaussian functions as a simple model of asymmetric chromatographic peaks, J. Chromatogr. A, 2001, 915, 1–13 CrossRef CAS PubMed.
- C. E. Blanchet, A. Spilotros, F. Schwemmer, M. A. Graewert, A. Kikhney, C. M. Jeffries, D. Franke, D. Mark, R. Zengerle, F. Cipriani, S. Fiedler, M. Roessle and D. I. Svergun, Versatile sample environments and automation for biological solution X-ray scattering experiments at the P12 beamline (PETRA III, DESY), J. Appl. Crystallogr., 2015, 48, 431–443 CrossRef CAS PubMed.
- S. P. Meisburger, D. Xu and N. Ando, REGALS: a general method to deconvolve X-ray scattering data from evolving mixtures, IUCrJ, 2021, 8, 225–237 CrossRef CAS PubMed.
- M. J. Parker, A. O. Maggiolo, W. C. Thomas, A. Kim, S. P. Meisburger, N. Ando, A. K. Boal and J. A. Stubbe, An endogenous dAMP ligand in Bacillus subtilis class Ib RNR promotes assembly of a noncanonical dimer for regulation by dATP, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4594–E4603 CrossRef CAS PubMed.
- E. Brookes, J. Pérez, B. Cardinali, A. Profumo, P. Vachette and M. Rocco, Fibrinogen species as resolved by HPLC-SAXS data processing within the UltraScan Solution Modeler (US-SOMO) enhanced SAS module, J. Appl. Crystallogr., 2013, 46, 1823–1833 CrossRef CAS PubMed.
- E. Brookes, P. Vachette, M. Rocco and J. Pérez, US-SOMO HPLC-SAXS module: dealing with capillary fouling and extraction of pure component patterns from poorly resolved SEC-SAXS data, J. Appl. Crystallogr., 2016, 49, 1827–1841 CrossRef CAS PubMed.
- P. V. Konarev and D. I. Svergun, Direct shape determination of intermediates in evolving macromolecular solutions from small-angle scattering data, IUCrJ, 2018, 5, 402–409 CrossRef CAS PubMed.
- B. Vestergaard, M. Groenning, M. Roessle, J. S. Kastrup, M. Van De Weert, J. M. Flink, S. Frokjaer, M. Gajhede and D. I. Svergun, A helical structural nucleus is the primary elongating unit of insulin amyloid fibrils, PLoS Biol., 2007, 5, 1089–1097 CrossRef CAS PubMed.
- X. Zhang, P. V. Konarev, M. V. Petoukhov, D. I. Svergun, L. Xing, R. H. Cheng, I. Haase, M. Fischer, A. Bacher, R. Ladenstein and W. Meining, Multiple Assembly States of Lumazine Synthase: A Model Relating Catalytic Function and Molecular Assembly, J. Mol. Biol., 2006, 362, 753–770 CrossRef CAS PubMed.
- S. E. Tsutakawa, G. L. Hura, K. A. Frankel, P. K. Cooper and J. A. Tainer, Structural analysis of flexible proteins in solution by small angle X-ray scattering combined with crystallography, J. Struct. Biol., 2007, 158, 214–223 CrossRef CAS PubMed.
- C. D. Putnam, M. Hammel, G. L. Hura and J. A. Tainer, X-ray solution scattering (SAXS) combined with crystallography and computation: defining accurate macromolecular structures, conformations and assemblies in solution, Q. Rev. Biophys., 2007, 40, 191–285 CrossRef CAS PubMed.
- A. Grishaev, J. Wu, J. Trewhella and A. Bax, Refinement of multidomain protein structures by combination of solution small-angle X-ray scattering and NMR data, J. Am. Chem. Soc., 2005, 127, 16621–16628 CrossRef CAS PubMed.
- P. Rodríguez-Zamora, Conjugation of NMR and SAXS for flexible and multidomain protein structure determination: from sample preparation to model refinement, Prog. Biophys. Mol. Biol., 2020, 150, 140–144 CrossRef PubMed.
- K. Lytje and J. S. Pedersen, Validation of electron-microscopy maps using solution small-angle X-ray scattering, Acta Crystallogr., Sect. D: Struct. Biol., 2024, 80, 493–505 CrossRef CAS PubMed.
- S. Naudi-Fabra, M. Tengo, M. R. Jensen, M. Blackledge and S. Milles, Quantitative Description of Intrinsically Disordered Proteins Using Single-Molecule FRET, NMR, and SAXS, J. Am. Chem. Soc., 2021, 143, 20109–20121 CrossRef CAS PubMed.
- D. P. O’Brien, S. Brier, D. Ladant, D. Durand, A. Chenal and P. Vachette, SEC-SAXS and HDX-MS: a powerful combination. The case of the calcium-binding domain of a bacterial toxin, Biotechnol. Appl. Biochem., 2018, 65, 62–68 CrossRef PubMed.
- E. Karaca and A. M. J. J. Bonvin, On the usefulness of ion-mobility mass spectrometry and SAXS data in scoring docking decoys, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2013, 69, 683–694 CrossRef CAS PubMed.
- M. Beck, R. Covino, I. Hänelt and M. Müller-McNicoll, Understanding the cell: future views of structural biology, Cell, 2024, 187, 545–562 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2024 |