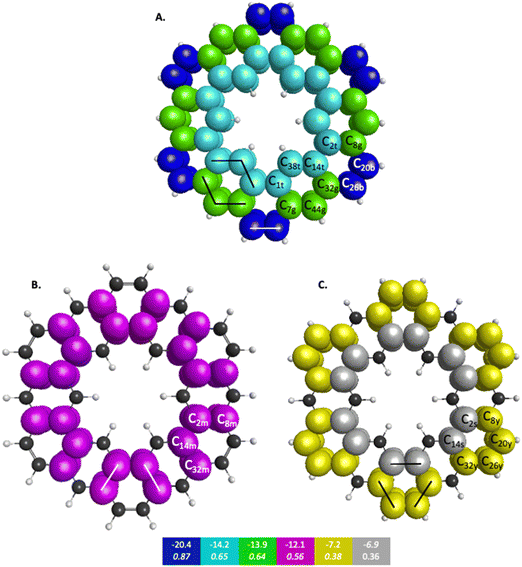Analysis of bonding motifs in unusual molecules II: infinitene

Abstract

The bonding structures of infinitene, the Chemical and Engineering News 2021 Molecule of the Year, is studied by means of oriented quasi-atomic orbitals (QUAOs) to assess the degree of aromaticity within the molecule. It is found that the angularity introduced into infinitene when it takes on the helical shape of the infinity symbol has a profound effect on bond order, delocalization of bonding interactions, and the aromatic character of the system. In kekulene, a planar isomer of infinitene, the bonding analysis shows fluctuations of pocketed delocalization of bonding interactions in π-sextets associated with Clar's rule. Conversely, much smaller fluctuations are observed between the adjacent rings of infinitene. The observations drawn from the quasi-atomic bonding analysis support the idea that there is aromatic character across the entire infinitene molecule, not just localized around individual rings as in kekulene.

---

1. Introduction

Complex polycyclic aromatic hydrocarbons (PAH) represent a set of interesting and often unusual compounds. The discussion of the aromaticity of PAH is often governed by Clar's rule¹ which states that the best resonance structure is the structure with the highest number of disjoint aromatic π-sextets. Aromatic π-sextets are described as benzene-like rings with 6 π-electrons, and the aromatic π-sextets are connected by single C–C bonds. Particular interest has emerged in the study of the aromaticity of novel PAH molecules, including helicenes, those in which the benzene rings are angularly fused together to form helically shaped molecules. The 2021 Chemical & Engineering News molecule of the year² is a special 12-ring Mobius helicene, C₄₈H₂₄, called infinitene (because it has the shape of an infinity sign), that was synthesized by Krzeszewski et al.³

There has been some debate regarding the aromaticity of infinitene. The aromaticity of helicenes can be difficult to deduce due to the angularity of the fused benzene rings that often do not follow conventional aromaticity rules, such as Clar's rule. The nucleus-independent chemical shift (NICS)⁴ indexes have become a popular and powerful computational tool for the characterization of aromaticity. The original Scheleyer index,⁵ NICS(0)_iso = −σ_iso, is calculated by reversing the sign of the isotropic absolute shielding constant of a ghost atom at the center of a ring. In this method, negative NICS indices are indicative of a sustained diatropic current on a ring, inferring aromaticity. Conversely, a positive NICS index denotes antiaromaticity. NICS(1) is calculated 1 Å above the center of the ring to remove perturbations in the structure of the molecule. Krzeszewski and co-authors used NICS calculations³ centered around each of the individual rings of infinitene to attempt to understand the aromatic character of the molecule.⁴ The authors postulate that infinitene is not aromatic as a whole molecule but has localized aromaticity around the individual benzene rings. However, NICS calculations do not always give accurate depictions of aromaticity across entire molecules for systems with curvature through the ring systems.⁶ Orozco-Ic et al. utilized magnetically induced current density and induced magnetic field calculations to study the aromatic character of infinitene. These authors postulate, based on the CAM-B3LYP D3(BJ) functional with the def2-SVP^7–9 basis set and the GIAO approach^10,11 that infinitene is aromatic as a whole molecule and does not only have localized aromaticity around individual rings.^12–15 The effect of the unique angularity of the fused benzene rings in infinitene on aromaticity remains unclear. Comparison of isomers of PAH can aid in determining the effect of the angularity of the benzene rings on aromaticity. In particular. kekulene, a planar isomer of infinitene, can be used as a reference to elucidate the effect of the angularity of the fused rings in benzene on the aromatic character.

The aim of the present study is to analyze the unusual bonding structures of unique chemical bonds in potentially aromatic helicenes as typified by infinitene. In order to analyze the bonding structures of these molecules, the quasi-atomic orbital (QUAO) analysis, developed by Ruedenberg and collaborators,^16–27 is employed. The results are complemented by including popular metrics in the study of aromaticity based on the harmonic-oscillator model of aromaticity (HOMA) structural index,^28,29 and the NICS magnetic index.

The HOMA index is an extensively used structural index that measures the variance of bond lengths from optimal carbon–carbon or carbon–nitrogen bond lengths. The HOMA index was originally parameterized with benzene resulting in a HOMA value of 1 corresponding to maximum aromaticity. HOMA index values lower than 1 indicate lesser aromaticity, due to an increased variance in bond lengths. The HOMA index is computed using the formula defined by Kruszewski and Krygowski,²⁸ and Krygowski:²⁹

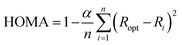where the sum is over the bonds in the ring, n is the number of bonds in the ring, α is a normalization constant, and R_opt is the optimal bond length for maximal aromaticity. If R_i = R_opt for all i then HOMA = 1. More information on the derivation of this metric can be found in the original literature.^28,29

The QUAO analysis is driven by information intrinsic to the chemical system by utilizing the actual molecular wave function, thereby eliminating all bias that is common among other bonding analysis methods. The resulting QUAOs are the ab initio complement to the qualitative concept of hybridized atomic orbitals.¹⁶ This creates a powerful tool for understanding bonding patterns in unique systems, as well as calculating orbital and bonding information, such that the resulting data is presented in a way that is natural to chemists across disciplines. The details of the QUAO analysis are extensively discussed in ref. 16, 17, 20 and 22. The relevant details of the theory are outlined in the preceding paper.

2. Quasi atomic orbital analysis

The QUAO labeling is determined as follows: the first capitalized letter in the label is the atomic symbol of the atom on which the QUAO is centered. If the orbital participates in a bonding interaction, subsequent lowercase atomic symbol(s) represent the QUAOs toward which the QUAO is oriented. The last component of the label indicates the kind of bonding in which the orbital participates; e.g., σ or π.

3. Computational details

The geometries for all molecules discussed in this work were optimized at the RHF/6-31G(d) level of theory, with the bonding analysis performed at the same level of theory. NICS values⁴ were calculated with the ORCA quantum chemistry program package³⁰ using the GIAO method^10,11 at the B3LYP/6-31G(d)//RHF/6-31G(d) level of theory. NICS values were computed at the center of each ring and 1 Å above the center of the rings. Localized quasi-atomic orbitals were obtained employing RHF/6-31G(d) wave functions on the RHF/6-31G(d) optimized geometries. All calculations were done using the GAMESS software,^31–33 and QUAOs were plotted using the MacMolPlt visualization software.³⁴

4. Aromaticity of infinitene

4.1. Reference systems

Benzene and naphthalene, and pentalene are well-known aromatic and antiaromatic systems, respectively. These molecules were chosen as reference systems to display aromatic and antiaromatic bonding characteristics captured by the QUAO bonding analysis.

At the RHF/6-31G(d) level of theory, benzene has carbon–carbon and carbon–hydrogen bond lengths of 1.39 and 1.08 Å, respectively. These bond lengths agree with the experimental observations and multiple theoretical calculations.^35–37 The QUAO bonding analysis yields three σ-type and one unhybridized π-type oriented orbitals per carbon atom center. The σ orbitals in each carbon atom, Ccσ and Chσ, have similar percent s-character, 0.30 and 0.27, respectively, and percent p-character, 0.70 and 0.73, respectively. The fractions characterizing these orbitals are close to the expected sp² hybridization. The occupation number for each orbital type is shown in Table 1. These numbers are consistent with the electronegativity of each atom center. The three unique interactions analyzed using the QUAO bonding analysis are summarized in Table 1. The two σ interactions, Ccσ–Ccσ and Chσ–Hcσ, have a bond order of 0.98 and KBOs of −53.4 and −39.2 kcal mol⁻¹, respectively. The corresponding parameters for the Chσ–Hcσ interactions agree with those reported for other hydrocarbons, including acetylene and naphthalene.²² Similarly, the values reported for Ccσ–Ccσ interactions agree with those computed for systems exhibiting double bonds or intermediate carbon–carbon bond lengths for example, the ones shown for ethene in the ESI,† Table S1 and for naphthalene Table S3.

Table 1 σ and π-bonding interactions in benzene. Orbital occupations, bond occupation totals, bond orders, and KBOs (kcal mol⁻¹) are shown for non-repetitive interactions. Subscripted letters, i, j, k, and l correspond to different atoms. Bond total refers to the total number of electrons in the bonding interaction

Orbital I	Occupation I	Orbital J	Occupation J	Bond total	BO	KBO (kcal mol^−1)
Cicjσ	1.00	Cjciσ	1.00	2.00	0.98	−53.4
Hicjσ	0.86	Cjhiσ	1.14	2.00	0.98	−39.2
Cicjckπ	1.00	Cjciclπ	1.00	2.00	0.66	−14.2

---

The delocalization of the π electrons is captured by a Cccπ orbital bonding with all of its neighboring Cccπ orbitals, yielding six symmetrical C_ic_jc_kπ–C_jc_ic_lπ bonding interactions, where i, j, k, and l indicate carbon atom centers. These bonding interactions showcase the ability of the QUAO analysis to capture multicentered bonding interactions. Although the composite interactions, C_ic_jc_kπ–C_jc_ic_lπ, involve multiple atom centers, each BO and KBO presented are two center indices that correspond to two carbon centers; e.g., i and j. These carbon–carbon π bonds have a BO and KBO of 0.66 and −14.2 kcal mol⁻¹, respectively. This KBO is less negative than the strongly localized π bonding interaction observed in acetylene²² and ethene, shown in Fig. S2 and Tables S1, S2 (ESI†), and is consistent with the delocalized π bonds shown for naphthalene. All of the previously mentioned measurements align with the qualitative predictions one can formulate from chemical intuition associated with the Lewis structures. Moreover, the QUAO analog to the para-related π delocalization originally identified by Bader and co-workers³⁸ and later quantified with the para-delocalization index (PDI) by Poater and co-workers³⁹ is identified in the QUAO bonding analysis. PDI measures the average delocalization in a six-member ring. Indices of non-adjacent atom centers, for example, in the para positions in benzene, are viewed as indicators of delocalization and aromaticity. In benzene, π bonding QUAOs from para-related carbon atoms have a BO and KBO of −0.33 and −0.5 kcal mol⁻¹, respectively.

In addition to benzene, naphthalene and pentalene are suitable representative reference systems in the study of aromaticity, because they share the common feature of fused rings and lack high degrees of angular strain. The symmetry of naphthalene allows the extraction of the bonding characteristics of neighboring rings that possess equal electron density distributions across bridging carbon–carbon bonds between rings. The QUAO bonding analysis of naphthalene was previously presented by West et al.²² The present work reproduces the bonding analysis at the RHF/6-31G(d) level of theory. Table S3 (ESI†) lists all symmetry unique σ and π bonding interactions with their respective bond orders and KBOs. The electron populations for naphthalene are consistent with the ones observed in benzene, shown in Table 1 and are attributed to the different electronegativities of carbon and hydrogen. The percent s- and p-characters of the Ccσ QUAOs in naphthalene are close to the expected sp² hybridization. Similarly, the naphthalene BO and KBO for the Chσ–Hcσ bonding interaction resemble the values observed in benzene. In the carbon–carbon σ bonding space, small variations were observed for KBOs (≤2.1 kcal mol⁻¹).

The π bonding space of naphthalene, illustrated in Fig. 1 and detailed in Table 2, is comprised of four main types of carbon–carbon bonding interactions. Upon fusing a second ring onto benzene, the symmetry of the π bonding QUAOs in each individual ring is decreased since the molecular symmetry is reduced from D_6h to C_2v, though there is still symmetry of the π bonding across the whole molecule. Similarly to benzene, these interactions are all delocalized among multiple carbon centers. The π bonding interactions have BOs between 0.51 and 0.77, and KBOs from −17.7 to −11.0 kcal mol⁻¹. These interactions are similar to the ones (0.66 and −14.2 kcal mol⁻¹) observed in benzene. Three of the four π bonding interactions (blue, green, and magenta in Fig. 1B, C and Table 2), are delocalized across four carbon atom centers.

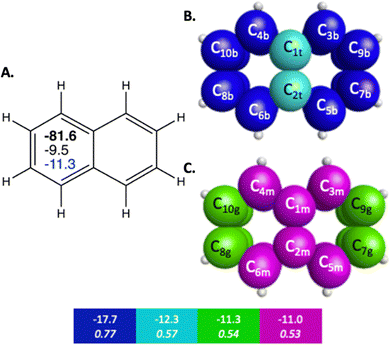Fig. 1 Sets of π-bonding QUAOs for naphthalene that arise from different combinations of the QUAOs shown in Fig. S4 (ESI†). The colored boxes give the KBO (kcal mol⁻¹) with the BO underneath for the corresponding colored π-bonding QUAOs. Each set of QUAOs with a given color share the same bond order and KBO. The atom numbers are generated by GAMESS. (A) The numbers inside the naphthalene structure in bold, black, and blue are the sum of π-bonding QUAOs per ring in kcal mol⁻¹, the NICS(0) and NICS(1), respectively. (B) Blue = b, and teal = t color labeled QUAOs. (C) Magenta = m, and green = g color labeled QUAOs.

Table 2 Detailed π-bonding interactions between QUAOs for naphthalene within each set of colored QUAOs. Bonds between QUAOs of the same color all have the same KBO (kcal mol⁻¹)

QUAO color	Orbital I	Orbital J	KBO (kcal mol^−1)
Blue	C3b	C9b	−17.7
Blue	C5b	C7b	−17.7
Blue	C4b	C10b	−17.7
Blue	C6b	C8b	−17.7
Teal	C1t	C2t	−12.3
Green	C7g	C9g	−11.3
Green	C8g	C10g	−11.3
Magenta	C1m	C3m	−11.0
Magenta	C1m	C4m	−11.0
Magenta	C2m	C5m	−11.0
Magenta	C2m	C6m	−11.0

---

The para-related π delocalization between π bonding QUAOs in naphthalene, C₄c₁c₁₀π–C₆c₂c₈π and C₃c₁c₉π–C₅c₂c₇π in Fig. 1, has a BO and KBO of 0.32 and −0.34 kcal mol⁻¹, respectively. These are even smaller than the ones observed in benzene and are consistent with the associated decrease in magnitude captured by other popular indices in the assessment of aromaticity, such as HOMA, PDI, and NICS.^37,38

Pentalene is a planar polycyclic hydrocarbon composed of two fused cyclopentadiene rings. Pentalene is a useful example of antiaromatic character, because with 8 π electrons, it fits the Hückel 4n π electron antiaromatic rule. The QUAO bonding analysis of pentalene shows noticeable differences in bonding characteristics compared to those observed in benzene and naphthalene, in both the σ and π regions of orbital space. For example, the KBOs of the C–C σ interactions range from −57.0 to −47.5 kcal mol⁻¹. Fluctuations between adjacent C–C bonds have a difference of 2.4 kcal mol⁻¹. Pentalene exhibits a high degree of localization of bonding interaction across its π-bonding region as well. π QUAO bonding pairs are shown in Fig. 2 and detailed in Table 3. The symmetrically unique QUAOs may be seen in Fig. S5 (ESI†). Four of the nine C–C π bonds, the pairs of QUAOs shown in blue and teal in Fig. 2B and Table 3, are comprised of two interacting π-oriented orbitals on neighboring carbon atom centers; these bonds have high bond orders and KBOs that are comparable to the Ccπ–Ccπ bonding characteristics of ethene (see Table S4, ESI†). For example, the bond C₃c₇π–C₇c₃π (blue in Fig. 2B), has a bond order and KBO of 0.93 and −21.4 kcal mol⁻¹, respectively. In contrast, the other π bonding interactions (yellow, green, and magenta in Fig. 2C, D and Table 3), are delocalized across four carbon atom centers and have considerably smaller bond orders and KBOs. The pattern of strongly localized KBOs and small delocalization of KBO in adjacent bonds, indicative of anti-aromaticity, is observed throughout the molecule.

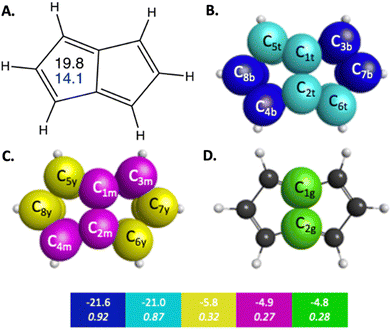Fig. 2 π-Bonding interaction types for pentalene that arise from the symmetry unique QUAOs shown in Fig. S5 (ESI†). The colored boxes give the KBO (kcal mol⁻¹) with the BO underneath for the corresponding colored π-bonding QUAOs. Each set of KBOs with a given color QUAOs have the same bond order. The atom numbers are generated by GAMESS. (A) The numbers inside the pentalene structure in black, and blue correspond to NICS(0) and NICS(1), respectively. (B) Blue = b, and teal = t color labeled QUAOs. (C) Magenta = m, and yellow = y color labeled QUAOs. (D) Green = g color labeled QUAOs.

Table 3 Detailed π-bonding interactions between QUAOs for pentalene within each set of colored QUAOs. Bonds between QUAOs of the same color all have the same KBO (kcal mol⁻¹)

QUAO color	Orbital I	Orbital J	Orbital J
Blue	C3b	C7b	−21.6
Blue	C8b	C4b	−21.6
Teal	C2t	C6t	−21.0
Teal	C1t	C5t	−21.0
Green	C1g	C2g	−4.8
Magenta	C1m	C3m	−4.9
Magenta	C2m	C4m	−4.9
Yellow	C5y	C8y	−5.8
Yellow	C6y	C7y	−5.8

---

The QUAO interactions and the KBOs shown for benzene, naphthalene, and pentalene suggest the QUAO analysis can effectively aid in the characterization of aromatic-like and antiaromatic-like behavior from π-electron delocalization or localization. In general, molecules with aromatic character like benzene and naphthalene have a more homogeneous bonding environment than molecules with antiaromatic character like pentalene, in both bonding regions, σ and π. This behavior in benzene and naphthalene is evident in π bonding interactions delocalized across multiple neighboring carbon atom centers with no or small changes in kinetic bond orders between adjacent carbon–carbon bonds. Also revealed in the QUAO analysis is the para-related π delocalization between π QUAOs in six-carbon atoms rings that exhibit aromatic characteristics. Conversely, the antiaromatic system pentalene, reveals two possible indicators of antiaromaticity. First, the π-bonding space has localized C–C bonds with large KBO and BO, next to delocalized bonding interactions with low KBO and BO. Second, the σ-bonding space also exhibits noticeable changes in the KBO energy between adjacent carbon–carbon bonds. These observations can help elucidate the aromatic character of more complex systems, such as infinitene.

The NICS values can be interpreted as a measure of aromaticity in a system. In general, molecules with greater aromatic characteristics are likely to have a more negative NICS value. The opposite applies to antiaromatic systems; these have a large positive NICS. For example, pentalene has a NICS(0) of 19.8 ppm. Nonaromatic systems, like cyclohexane with a NICS(0) of −2.1, tend to have very small NICS values, indicating no significant ring current effects.⁵ The NICS(0) and NICS(1) computed for benzene and the two polycyclic molecules naphthalene and pentalene are in close agreement with the NICS(0) values computed by Schleyer et al. at the GIAO-SCF/6-31+G(d) and GIAO-SCF/6-31G(d) level of theory.⁵

4.2. Kekulene and infinitene

As described in the Introduction, infinitene is an isomer of kekulene that takes the shape of an infinity symbol. One motivation for applying the QUAO analysis to this molecule, in addition to the fact that it is a fascinating molecule, is that there is disagreement in the literature^3,12–15 regarding the nature and extent of aromatic character in infinitene. Specifically, is the aromaticity global or just localized in particular rings?

The structures for infinitene and kekulene optimized at the RHF/6-31G(d) level of theory are shown in Fig. 3 and 4, respectively. The geometric parameters and optimized geometries are given in Fig. S8 and S9 (ESI†) respectively. One way to understand the three-dimensional arrangement of infinitene is to imagine connecting two chiral[6]helicene molecules at opposite ends as illustrated in Fig. 5. While this is not the actual synthetic route, it is a helpful illustration for a geometrically complex molecule.

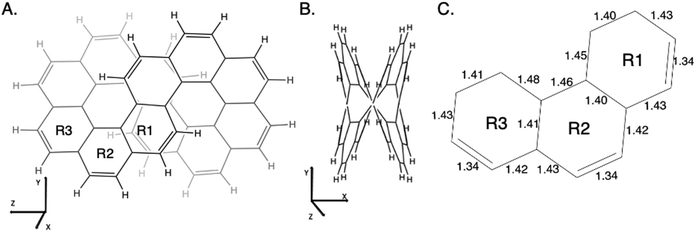Fig. 3 Infinitene rotated to (A) the Y–Z plane and (B) the X–Y plane as given by the MacMolPlot visualization software.³⁴ The coordinate origin is the center of mass. The molecule was optimized at the RHF/6-31G(d) level of theory. R1, R2, and R3 in (A) identify the three unique types of rings in infinitene. (C) The bond lengths of the non-repetitive rings are in angstroms, Å.

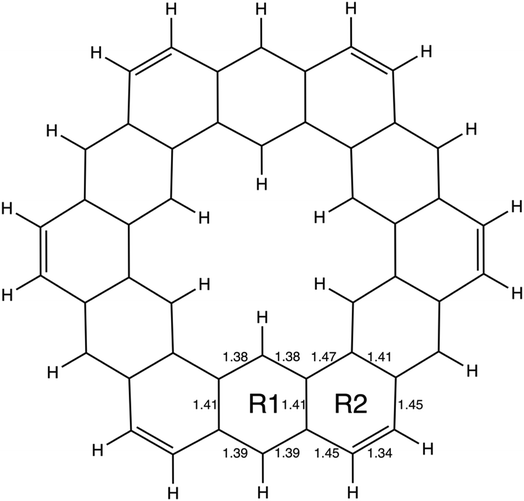Fig. 4 The geometry of kekulene optimized at the RHF/6-31G(d) level of theory. R1 and R2 indicate the two unique types of rings in kekulene. Bond lengths are in angstroms, Å.

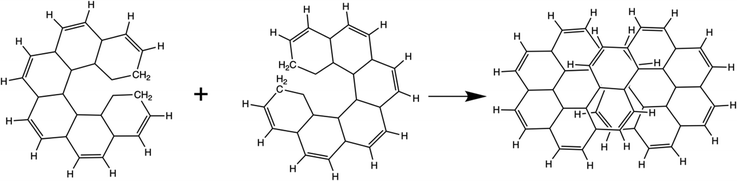Fig. 5 A conceptual representation of the fusing of two chiral[6]helicenes to form the molecule infinitene.

The QUAO occupations (Table 4) for the C–C π- and C–C σ-bonds, and the C–H σ-bonds are the same for kekulene and infinitene, as well as those of the reference molecules benzene, naphthalene and pentalene. The hybridization and partial charges in infinitene and kekulene also mirror those of the reference molecules. Benzene, naphthalene, infinitene, and kekulene each has a partial charge of −0.14 on all C atoms that are bonded to a H, +0.14 for each H atom, and 0.0 for all other C atoms. This is expected given the difference in C vs. H electronegativities. Furthermore, there is no difference in the s- and p-characters of the QUAOs among infinitene, kekulene, and the aromatic reference molecules. Each carbon has one QUAO with 100% p character and three QUAOs with 30% s character and 70% p character corresponding to sp² hybridized orbitals. A full set of all unique QUAO bonding information is given in Tables S8 and S9 (ESI†). The main differences, as discussed in the following paragraphs, between infinitene and kekulene can be found in the magnitude of the BOs and KBOs between these QUAOs in each system. These differences are driven by the differences in the molecular structures caused by the angularity in infinitene.

Table 4 QUAO occupations for infinitene and kekulene compared to benzene, naphthalene and pentalene. Benzene and naphthalene were optimized at the same level of theory as infinitene and kekulene

Molecule	Occupation
	Ccσ	Ccπ	Chσ	Hcσ
Infinitene	1.0	1.0	1.14	0.86
Kekulene	1.0	1.0	1.14	0.86
Benzene	1.0	1.0	1.14	0.86
Naphthalene	1.0	1.0	1.14	0.86
Pentalene	1.0	1.0	1.15	0.85

---

In infinitene each C–H σ-bond has a BO of 0.97 and a KBO of −38.2 kcal mol⁻¹, while the BO and KBO of the C–H σ-bonds in kekulene are in the ranges of 0.97 to 0.98 and −38.9 to −41.7 kcal mol⁻¹, respectively. The corresponding C–H bond distances are consistent with these BOs and KBOs.

The symmetry unique infinitene and kekulene π QUAOs are illustrated in Fig. S8 and S9 in the ESI.† The kekulene and infinitene π-bonding QUAO interactions, including the BOs and KBOs, are illustrated in Fig. 6 and 7, respectively. The π-conjugation of kekulene and infinitene creates a system of π-QUAOs that are bonded with other neighboring π-QUAOs leading to a large number of π–π QUAO interactions. For brevity and clarity, in Fig. 6 and 7 each set of π–π bonding QUAOs that comprises equivalent BOs and KBOs are identified by a given color. Lines are drawn for a symmetric subset of each molecule to explicitly illustrate the QUAO–QUAO bonds within each color set. Tables 5 and 6 detail the bonding interactions of kekulene and infinitene respectively for symmetric subsets of each molecule.

Fig. 6 π-QUAO bonding patterns for kekulene. The colored boxes at the bottom of the figure give the KBO (kcal mol⁻¹) with the BO underneath for each of the six subsets of bonding motifs. All QUAO interactions within a given color share the same bond order and KBO. The lines drawn between QUAOs illustrate which bonds correspond to the given KBO. The atom numbers are generated by GAMESS. (A) Blue = b, teal = t, and green = g color labeled QUAOs. (B) Magenta = m color labeled QUAOs. (C) Yellow = y, and silver = s color labeled QUAOs.

Fig. 7 π-QUAO bonding patterns for infinitene. The colored boxes at the bottom of the figure give the KBO (kcal mol⁻¹) with the BO underneath for each of the four subsets of bonding motifs. All QUAO interactions within a given color share the same bond order and KBO. Lines drawn between QUAOs illustrate which bonds correspond to the given KBO. The atom numbers are generated by GAMESS. (A) Blue = b color labeled QUAOs. (B) Orange = o color labeled QUAOs. (C) Purple = p color labeled QUAOs. (D) Brown = br color labeled QUAOs.

Table 5 π-Bonding interactions between QUAOs for kekulene for a symmetric subset of kekulene. Bonds between QUAOs of the same color all have the same KBO (kcal mol⁻¹)

QUAO color	Orbital I	Orbital J	KBO (kcal mol^−1)
Blue	C20b	C26b	−20.4
Teal	C14t	C38t	−14.2
Teal	C1t	C38t	−14.2
Green	C32g	C44g	−13.9
Green	C7g	C44g	−13.9
Magenta	C2m	C8m	−12.1
Magenta	C14m	C32m	−12.1
Yellow	C8y	C20y	−7.2
Yellow	C26y	C32y	−7.2
Silver	C2s	C14s	−6.9

---

Table 6 π-Bonding interactions between QUAOs for a symmetric subset of infinitene. Bonds between QUAOs of the same color all have the same KBO (kcal mol⁻¹)

QUAO color	Orbital I	Orbital J	KBO (kcal mol^−1)
Blue	C10b	C11b	−18.6
Orange	C9o	C10o	−9.5
Orange	C11o	C12o	−9.5
Orange	C12o	C41o	−9.5
Purple	C9p	C14p	−14.1
Purple	C12p	C13p	−14.1
Purple	C44p	C48p	−14.1
Brown	C13br	C14br	−8.2
Brown	C13br	C44br	−8.2
Brown	C40br	C44br	−8.2

---

Fig. 6 depicts the bonding sets of QUAOs in kekulene, with representative bonds indicated by straight lines. For example, in part A of Fig. 6, there are two equivalent sets of interacting teal QUAOs (denoted ‘t’) on either side of the inner periphery of the molecule. Other sets of equivalent QUAO–QUAO interactions within kekulene consist of pairs of bonds such as those shown in the color yellow (denoted ‘y’ in Fig. 6C), as illustrated by the lines that signify bonding between these particular QUAOs. While there is bonding between C_8y–C_20y and C_26y–C_32y, there is not a bond between C_20y–C_26y within the bonding patterns of the yellow QUAOs. The bond between C₂₀–C₂₆ occurs between the silver QUAOs (C_20s–C_26s) with a different KBO. The point here is that because all connecting QUAO–QUAO interactions depicted by a specific color have the same KBO, these color patterns demonstrate delocalized muti-center bonding, even though each individual KBO corresponds to a 2-center bond.

Similar patterns can be seen in infinitene where the set of brown QUAOs in Fig. 7D (denoted ‘br’) is bonded with each neighboring QUAO so that the bonding completely spans the inner ring as illustrated by the lines that signify bonding between the QUAOs. As with the set of yellow QUAOs on kekulene in Fig. 6C, the set of purple QUAOs on infinitene in Fig. 7C (denoted ‘p’) are pairs of bonds where C_9p–C_14p and C_12p–C_13p are bonded as illustrated by the lines that signify bonding between the QUAOs. The bond between C_13b–C_14b occurs with a different KBO between the brown QUAOs in Fig. 7D. As with kekulene, the lines signifying bonding in Fig. 7 for infinitene demonstrate the bonding pattern within the set of other QUAO colors.

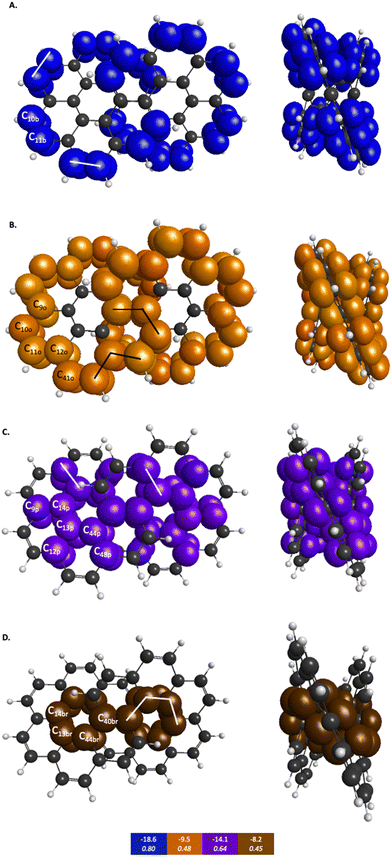
When compared to the aromatic reference systems, benzene and naphthalene, the infinitene KBO values in Fig. 7 of the brown (D), purple (C), and orange (B) QUAO sets exhibit delocalized QUAO bonding interactions and aromatic character around the inner and outer peripheries of infinitene. The set of blue QUAOs in infinitene shown in Fig. 7A are bonding pairs between two neighboring QUAOs with a more negative KBO value (−18.6 kcal mol⁻¹) that exhibit greater localization of bonding interactions than the orange (−9.5 kcal mol⁻¹) and brown (−8.2 kcal mol⁻¹) QUAO–QUAO interactions. When compared to benzene and naphthalene, the KBOs on infinitene suggest there is delocalization of bonding interactions throughout the whole molecule corresponding to aromatic character across the molecule, as exhibited in the brown, purple, and orange QUAO sets, and small areas of more localized bonds around the outer edge of the molecule exhibited in the blue QUAO set.

In kekulene, there are two sets of contiguously bonded π-QUAOs across the inner and outer edges of the R1 rings (see Fig. 4 for the definition of R1) shown in teal and green QUAOs in Fig. 6A. These two sets of QUAO interactions have KBOs of −14.2 and −13.9 kcal mol⁻¹, respectively. When compared to the reference molecules, the bonding analysis suggests that there is strong delocalization of bonding interactions spanning the R1 rings of kekulene. The blue QUAO set in kekulene exhibits strongly localized bonding interactions that are similar to the localization of bonding interactions in pentalene, in which each QUAO is directed solely to the corresponding QUAO bonding partner. The QUAO sets shown in Fig. 6 yellow (C), silver (C), and green (B) have KBO values closer to benzene and naphthalene suggesting that these QUAO sets exhibit more delocalization of bonding interactions and more aromatic character. However, these delocalized bonding interactions are not delocalized across the entire molecule, as opposed to infinitene, but are delocalized only across pockets of the molecule as suggested by Clar's rule.

The multi-centered bonding interactions captured by the bonding analysis further highlight the delocalization of bonding interactions across the entire infinitene molecule and the delocalization within individual rings of kekulene as defined by Clar's rule. Although these two isomers both have bridging bond lengths that are similar to the bridging bond in naphthalene, 1.41 Å, the QUAO bonding analysis characterizes these bonds differently. In infinitene, each QUAO interaction that describes the bridging bonds is directed towards the three neighboring carbon atoms, thereby involving a total of six carbon atoms per bonding interaction. For example, the bonding pair C_12p–C_13p in infinitene shown in purple in Fig. 7C is fully expressed as C₁₂c₁₃c₁₁c₄₁π–C₁₃c₁₂c₁₄c₄₄π. This bond is comparable to the corresponding bond observed in naphthalene, suggesting delocalization between the rings. In kekulene the bridging bond is delocalized along the two neighboring carbon atom centers of R1 in Fig. 4. For example, the C_14m–C_32m bonding QUAOs shown in magenta in Fig. 6B is fully expressed as C₁₄c₃₂c₃₈π–C₃₂c₁₄c₄₄π. This bonding interaction in kekulene exhibits aromatic character that is localized in the individual ring (R1). The multi-centered bonding interactions captured by the bonding analysis highlight the aromatic character and delocalization of bonding interaction exhibited across the full molecule of infinitene. In contrast, kekulene exhibits delocalization of bonding interactions within disjoint sections of the molecule similar to Clar's aromatic π-sextets.

Table 7 contains multiple parameters related to aromatic character in general, and the aromatic character of the symmetrically unique rings in kekulene and infinitene, in particular. The NICS values reported in Table 7 for kekulene and infinitene are in close agreement with those reported previously.^3,40–42 In kekulene, the alternating nature of NICS(0) values, −10.2 and −3.5, on R1 and R2, respectively suggest uneven aromatic strengths across the system. In comparison, the smaller deviation between the NICS(0) values in the rings of infinitene, −7.5, −7.3, and −6.3, suggest similar aromatic characters among the rings. The NICS(0) values reflect the local aromatic character in the individual rings but cannot accurately reflect the aromaticity of the entire systems, given the helical nature of infinitene.⁵ The NICS calculations illustrate that infinitene does not have rings with stronger aromatic character connected by rings of weaker aromatic character as does kekulene. Instead, infinitene has a pattern of moderate aromatic character in neighboring rings.

Table 7 NICS(0), NICS(1), the cumulative sum of KBO from π and σ interactions per ring, HOMA indices, BO, and KBO (kcal mol⁻¹) of para-related π QUAOs

	NICS(0) [ppm]	NICS(1) [ppm]			HOMA index	para-Related π QUAOS
						BO	KBO
a Quantities were computed for six carbon atom rings. b para-Related π QUAOS descriptors for the R2 ring in kekulene are negligible (below 0.001 hartree or 0.06 kcal mol^−1).
Benzene	−9.5	−11.2	−85.2	−320.4	1.00	0.33	−0.50
Naphthalene	−9.5	−11.3	−81.6	−324.5	0.78	0.32	−0.34
Pentalene	19.8	14.1	N/A^a	N/A^a	−0.72	N/A^a	N/A^a
Kekulene R1	−10.2	−12.1	−80.4	−329.4	0.96	0.32	−0.28
Kekulene R2	−3.5	−6.6	−65.9	−322.8	0.42	N/A^b	N/A^b
Infinitene R1	−7.5	−9.8	−73.8	−325.1	0.78	0.25	−0.14
Infinitene R2	−7.3	−10.4	−74.7	−324.7	0.79	0.26	−0.14
Infinitene R3	−6.3	−10.1	−73.9	−323.5	0.75	0.26	−0.13

---

Similar to the NICS results, the rings of kekulene exhibit larger fluctuations of the HOMA index, shown in Table 7, suggesting a lack of delocalization across the entire molecule. In contrast, the HOMA indices computed for the rings of infinitene, shown in Table 7, indicate that the rings have similar aromatic strengths suggesting there is delocalization across the entire molecule. Consistent with the small fluctuations in NICS and HOMA indices observed between the rings of infinitene, the BOs and KBOs of the para-related π bonding QUAOs are constant for all the rings. The magnitudes of BOs and KBOs, shown in Table 7, are smaller than the magnitude of the BOs and KBOs of benzene, naphthalene, and the R1 ring of kekulene. The decrease in the magnitude of BO and KBOs in the rings of infinitene is a consequence of the curvature along the helices, creating a smaller overlap of π QUAOs when compared to the overlap of π QUAOs in the planar reference systems. The R1 ring in kekulene features KBOs and BOs of the para-related π bonding QUAOs comparable to the KBOs and BOs of the para-related π bonding QUAOs of naphthalene. The para-related interactions for the R2 ring in kekulene are negligible. The NICS and HOMA values, as well as the para-related π bonding QUAOs parameters, support the conservation of aromatic character throughout the rings of infinitene.

Table 7 also shows the fluctuations in the total KBO in neighboring rings, R1 and R2 in kekulene. The sum of the six π C–C KBOs per ring provides insight into the strength of the π bonding interactions for each ring in kekulene. Ring R2 has a collective π KBO of −65.9 kcal mol⁻¹, whereas the collective π KBO for ring R1 is −80.4 kcal mol⁻¹. The latter closely resembles the sum of π KBOs in benzene, −85.2 kcal mol⁻¹, while the former is considerably smaller in magnitude. Since a more negative KBO correlates with a stronger bond, a more negative sum of π KBOs in a ring suggests a stronger bonding pattern within that ring, reflecting the aromatic stabilization analogous to benzene.

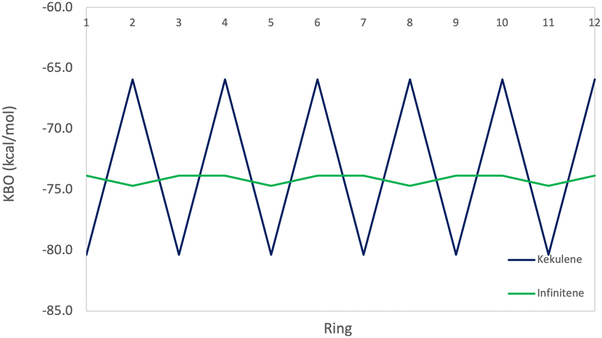
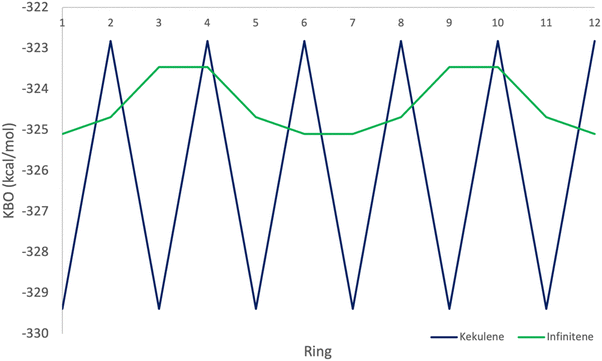
The π KBO variation among the rings in kekulene described in the preceding paragraph is also observed within the σ-bonding space. For example, the collective σ-KBO in ring R1 is −329.4 kcal mol⁻¹, compared to the collective KBO in ring R2 of −322.8 kcal mol⁻¹. Although the fluctuation within the σ-space between the two types of rings is smaller than that in the π space, it reinforces the non-negligible role σ-contributions may play in the characterization of aromaticity as suggested by Shaik and others.⁴² The bonding analysis presented here demonstrates that kekulene follows Clar's rule for PAH. There is a clear localization of stronger bonding interactions in benzene-like rings, with values of total KBO per ring, similar to that of benzene, alternating with rings of weaker bonding interactions. The magnitude of the difference of the cumulative sums of KBOs between R1 and R2 of kekulene is larger than the magnitude of the difference of the cumulative sums of KBOs between the neighboring rings in infinitene in both the π and σ spaces as shown in Fig. 8 and 9.

Fig. 8 Sum of π-bonding KBOs per ring for infinitene and kekulene in kcal mol⁻¹.

Fig. 9 Sum of σ-bonding KBOs per ring for infinitene and kekulene in kcal mol⁻¹.

The nonplanar nature of infinitene blurs the boundaries between well-defined single and double C–C bonds compared to planar kekulene, thereby introducing numerous intermediate C–C bond lengths. The inner sequence of CC bonds in each symmetric half-loop of infinitene, shown in part C of Fig. 3, is characterized by distances in the narrow range of 1.45–1.48 Å. The outer path of carbon atoms in part C of Fig. 3 is characterized by shorter CC bonds in the range 1.34–1.43 Å, mostly alternating between these two extremes. All of the CC bond distances in Fig. 3 and 4 are much shorter than a typical isolated (1.54 Å) single bond, thereby suggesting significant delocalization throughout the system, much more so than in kekulene.

As previously discussed, the infinitene bonding analysis exhibits more delocalization of aromatic QUAO interactions across the molecule than does kekulene. In contrast to the ring-to-ring difference of −14.4 kcal mol⁻¹ in kekulene, the sum of π-bonding KBOs per ring in infinitene has a maximum difference of 0.8 kcal mol⁻¹ between rings. Similar behavior is observed in the σ bonding space in which the maximum variation is 1.2 kcal mol⁻¹. The ring-to-ring differences between kekulene and infinitene in both the π and σ spaces are illustrated in Fig. 8 and 9. There is a clear lack of localized aromatic π-sextets in infinitene compared to kekulene. This suggests the rings in infinitene do not follow Clar's rule. Instead, two observations can be made. First, the rings in infinitene exhibit similar delocalization throughout in their bonding interactions. Second, based on the QUAO analysis (i.e., bond types, bond orders, and kinetic bond orders) the delocalization of bonding interactions extends to adjacent rings. These parameters and NICS values suggest the molecule exhibits clear aromatic character continuously across the whole molecule.

5. Conclusions

The most important conclusion of this work is that the QUAO analysis resolves the question raised in the introduction about the nature of the aromaticity in the molecule infinitene. The evidence is overwhelming that the delocalization in infinitene, in contrast to its isomer kekulene, extends over the entire molecule and is not localized in isolated rings.

The bonding structures of infinitene and kekulene have been analyzed using the quasi-atomic bonding analysis. The QUAO analysis provides insight into the differences in aromaticity between the isomers kekulene and infinitene. The angularity introduced into infinitene when it takes on the helical shape of the infinity symbol has a profound effect on bond order, and the aromatic character of the system. Despite the angularity factor, the molecule infinitene conserves delocalization between the bonding interactions, resembling those observed in naphthalene connected by a somewhat less delocalized bonding interaction. In kekulene, NICS values and the sum of the π bonding QUAOs per ring fluctuate between adjacent rings. These fluctuations are a product of pocketed delocalization of bonding interactions in π-sextets associated with Clar's rule. Conversely, much smaller fluctuations were observed in the sum of the π bonding QUAOs per ring, between the adjacent rings of infinitene. When compared to kekulene, the QUAO bonding analysis of infinitene reveals more delocalization of bonding interactions across the entire molecule.

The aromaticity assessment of infinitene with HOMA and NICS indices produces an acceptable agreement with the general descriptions abstracted from QUAO bonding analysis, more specifically with the para-related π QUAOs and the extracted bonding patterns.

Ultimately, the angularity introduced into the helices of infinitene results in a greater delocalization of bonding interactions among all of the C–C bonds. Unlike kekulene, which exhibits a sequence of rings with pocketed delocalization next to rings with less delocalization, infinitene displays more delocalization of bonding interactions across its rings. The observations drawn from the quasi-atomic bonding analysis support the idea that there is aromatic character across the whole molecule of infinitene not just localized around individual rings as in kekulene.

The insights presented in this work serve to emphasize the power of the quasi-atomic orbital analysis for providing understanding of the widely varying nature of the chemical bond. This is especially satisfying since these insights are drawn entirely from the wave function, with no implicit or explicit bias.

Data availability

All relevant data is available in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by a grant from the Air Force Office of Scientific Research (KF, MSG), AFOSR FA9550-18-1-0321, and a grant from the Department of Energy Computational Chemical Sciences (CCS) effort (DC, TH), from the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biological Sciences, to the Ames National Laboratory. Ames National Laboratory is operated by Iowa State University under contract no. DE-AC02-07CH11338. The authors are also grateful to Professor Klaus Ruedenberg for providing insights into the QUAO analysis.

References

1. E. Clar, The Aromatic Sextet, Wiley, New York, NY, 1972.
2. C. H. Arnaud, Chem. Eng. News, 2021, 45, 99.
3. M. Krzeszewski, H. Ito and K. Itami, Infinitene: A Helically Twisted Figure-Eight [12]Circulene Topoisomer, J. Am. Chem. Soc., 2021, 144, 862–871.
4. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion, Chem. Rev., 2005, 105, 3842–3888.
5. P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. Van Eikema Hommes, Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe, J. Am. Chem. Soc., 1996, 118, 6317–6318.
6. M. Orozco-Ic, J. Barroso, N. D. Charistos, A. Muñoz-Castro and G. Merino, Consequences of Curvature on Induced Magnetic Field: The Case of Helicenes, Chem. – Eur. J., 2020, 26, 326–330.
7. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
8. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297.
9. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
10. F. London, Théorie quantique des courants interatomiques dans les combinaisons aromatiques, J. Phys. Radium, 1937, 8, 397–409.
11. R. Ditchfield, Self-consistent perturbation theory of diamagnetism: I. A gauge-invariant LCAO method for N.M.R. chemical shifts, Mol. Phys., 1974, 27, 789–807.
12. M. Orozco-Ic, R. R. Valiev and D. Sundholm, Non-intersecting ring currents in [12]infinitene, Phys. Chem. Chem. Phys., 2022, 24, 6404–6409.
13. J. Jusélius, D. Sundholm and J. Gauss, Calculation of current densities using gauge-including atomic orbitals, J. Chem. Phys., 2004, 121, 3952–3963.
14. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, The gauge including magnetically induced current method, Phys. Chem. Chem. Phys., 2011, 13, 20500.
15. T. Heine, R. Islas and G. Merino, σ and π contributions to the induced magnetic field: indicators for the mobility of electrons in molecules, J. Comput. Chem., 2007, 28, 302–309.
16. A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A comprehensive analysis of molecule-intrinsic quasi-atomic, bonding, and correlating orbitals. I. Hartree-Fock wave functions, J. Chem. Phys., 2013, 139, 234107.
17. A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A Comprehensive Analysis in Terms of Molecule-Intrinsic, Quasi-Atomic Orbitals. II. Strongly Correlated MCSCF Wave Functions, J. Phys. Chem. A, 2015, 119, 10360–10367.
18. T. Harville and M. S. Gordon, Intramolecular hydrogen bonding analysis, J. Chem. Phys., 2022, 156, 174302.
19. D. Del Angel Cruz, J. L. Galvez Vallejo and M. S. Gordon, Analysis of the bonding in tetrahedrane and phosphorus-substituted tetrahedranes, Phys. Chem. Chem. Phys., 2023, 25, 27276–27292.
20. A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A Comprehensive Analysis in Terms of Molecule-Intrinsic, Quasi-Atomic Orbitals. III. the Covalent Bonding Structure of Urea, J. Phys. Chem. A, 2015, 119, 10368–10375.
21. A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A Comprehensive Analysis in Terms of Molecule-Intrinsic Quasi-Atomic Orbitals. IV. Bond Breaking and Bond Forming along the Dissociative Reaction Path of Dioxetane, J. Phys. Chem. A, 2015, 119, 10376–10389.
22. A. C. West, J. J. Duchimaza-Heredia, M. S. Gordon and K. Ruedenberg, Identification and Characterization of Molecular Bonding Structures by ab initio Quasi-Atomic Orbital Analyses, J. Phys. Chem. A, 2017, 121, 8884–8898.
23. J. D. Heredia, K. Ruedenberg and M. S. Gordon, Quasi-Atomic Bonding Analysis of Xe-Containing Compounds, J. Phys. Chem. A, 2018, 122, 3442.
24. J. J. Duchimaza Heredia, A. D. Sadow and M. S. Gordon, A Quasi-Atomic Analysis of Three-Center Two-Electron Zr–H–Si Interactions, J. Phys. Chem. A, 2018, 122, 9653–9669.
25. G. Schoendorff, M. W. Schmidt, K. Ruedenberg and M. S. Gordon, Quasi-Atomic Bond Analyses in the Sixth Period: II. Bond Analyses of Cerium Oxides, J. Phys. Chem. A, 2019, 123, 5249–5256.
26. E. B. Guidez, M. S. Gordon and K. Ruedenberg, Why is Si₂H₂ Not Linear? An Intrinsic Quasi-Atomic Bonding Analysis, J. Am. Chem. Soc., 2020, 142, 13729–13742.
27. J. L. Galvez Vallejo, J. D. Heredia and M. S. Gordon, Bonding analysis of water clusters using quasi-atomic orbitals, Phys. Chem. Chem. Phys., 2021, 23, 18734–18743.
28. J. Kruszewski and T. M. Krygowski, Definition of aromaticity based on the harmonic oscillator model, J. Chem. Phys., 1972, 13, 3839–3842.
29. T. M. Krygowski, Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of pi-electron systems, J. Chem. Inf. Comput. Sci., 1993, 33, 70–78.
30. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108.
31. J. A. M. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus and M. Dupuis, General Atomic and Molecular Electronic Structure System, J. Comput. Chem., 1993, 14, 1347–1363.
32. M. S. Gordon and M. W. Schmidt, Theory and Applications of Computational Chemistry, Elsevier, 2005, pp. 1167–1189.
33. G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, Recent developments in the general atomic and molecular electronic structure system, J. Chem. Phys., 2020, 152, 154102.
34. B. M. Bode and M. S. Gordon, Macmolplt: A Graphical User Interface for GAMESS, J. Mol. Graphics Modell., 1998, 16, 133–138.
35. B. J. Esselman, M. A. Zdanovskaia, A. N. Owen, J. F. Stanton, R. C. Woods and R. J. McMahon, Precise Equilib. Struct. Benzene, J. Am. Chem. Soc., 2023, 145, 21785–21797.
36. S. Kunishige, T. Katori, M. Baba, M. Nakajima and Y. Endo, Spectroscopic study on deuterated benzenes. I. Microwave spectra and molecular structure in the ground state, J. Chem. Phys., 2015, 143, 244302.
37. I. Heo, J. C. Lee, B. R. Özer and T. Schultz, Mass-Correlated High-Resolution Spectra and the Structure of Benzene, J. Phys. Chem. Lett., 2022, 13, 8278–8283.
38. R. F. W. Bader, A. Streitwieser, A. Neuhaus and K. E. Laidig, Electron Delocalization and the Fermi Hole, J. Am. Chem. Soc., 1996, 118, 4959–4965.
39. J. Poater, X. Fradera and M. Duran, The Delocalization Index as an Electronic Aromaticity Criterion: Application to a Series of Planar Polycyclic Aromatic Hydrocarbons, Chem. – Eur. J., 2003, 9, 400–406.
40. H. Miyoshi, S. Nobusue, A. Shimizu and Y. Tobe, Non-alternant non-benzenoid kekulenes: the birth of a new kekulene family, Chem. Soc. Rev., 2015, 44, 6560–6577.
41. J. Aihara, Nucleus-independent chemical shifts and local aromaticities in large polycyclic aromatic hydrocarbons, Chem. Phys. Lett., 2002, 365, 34–39.
42. S. Shaik, A. Shurki, D. Danovich and P. C. Hiberty, A Different Story of π-Delocalizations The Distortivity of π-Electrons and Its Chemical Manifestations, Chem. Rev., 2001, 101, 1501–1539.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01802h

---