Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A novel approach for estimating the strength of argentophilic and aurophilic interactions using QTAIM parameters†
Sergi
Burguera
 ,
Antonio
Bauzá
,
Antonio
Bauzá
 and
Antonio
Frontera
and
Antonio
Frontera
 *
*
Department of Chemistry, Universitat de les Illes Balears, Crta de Valldemossa km 7.5, 07122 Palma de Mallorca (Baleares), Spain. E-mail: toni.frontera@uib.es
First published on 28th May 2024
Abstract
Metallophilic interactions, specifically argentophilic (Ag⋯Ag) and aurophilic (Au⋯Au) interactions, play a crucial role in stabilizing various molecular and solid-state structures. In this manuscript, we present a convenient method to estimate the strength of argentophilic and aurophilic interactions based on quantum theory of atoms in molecules (QTAIM) parameters evaluated at the bond critical points connecting the metal centres. We employ density functional theory (DFT) calculations and the QTAIM parameters to develop this energy predictor. To validate the reliability and applicability of our method, we test it using a selection of X-ray crystal structures extracted from the cambridge structural database (CSD), where argentophilic and aurophilic interactions are known to be significant in their solid-state arrangements. This method offers a distinct advantage in systems where multiple interactions, beyond metallophilic interactions, contribute to the overall stability of the structure. By employing our approach, researchers can distinctly quantify the strength of argentophilic and aurophilic interactions, facilitating a deeper understanding of their impact on molecular and solid-state properties. This method fills a critical gap in the existing literature, offering a valuable tool to researchers seeking to unravel the intricate interactions in metal-containing compounds.
Introduction
In the realm of supramolecular chemistry, the understanding and rational utilization of non-covalent interactions is fundamental to the development of novel materials and molecular systems.1 Among these non-covalent interactions, argentophilic2 and aurophilic3 interactions have emerged as areas of significant interest due to their unique properties and potential applications.2,3 Several reviews have provided a comprehensive overview of argentophilic and aurophilic interactions, delving into their nature, characteristics, and the pivotal role they play in several fields.2–10Argentophilic interactions are predominantly observed in silver(I) complexes, where the d10 configuration of silver plays a crucial role.4 The relatively large atomic radius of silver facilitates these interactions, which are often compared to hydrogen bonding in terms of their strength. Similarly, aurophilic interactions involve gold atoms and are particularly notable in gold(I) and gold(III) complexes. These interactions are attributed to the relativistic effects on the gold atoms, where the contraction of the 6s orbital and expansion of the 5d orbital lead to distinctive electron configurations conducive to bonding.11–15 Aurophilic interactions are not only intriguing from a theoretical standpoint but also have substantial implications in the design of luminescent materials16–20 and catalysts.21 Both argentophilic and aurophilic interactions contribute to the stability and function of metallo-supramolecular complexes.22 In recent years, these interactions have been harnessed in the creation of porous materials,23 sensors,24 spintronics,25 and in medicinal chemistry, particularly in the development of anticancer and antimicrobial agents.26
In the intricate field of crystal engineering, argentophilic and aurophilic interactions have emerged as pivotal forces, offering novel avenues for the design and synthesis of complex crystal structures.27 These interactions are particularly significant due to their ability to influence and stabilize the geometrical arrangement of atoms within a crystal lattice, a fundamental aspect in tailoring the properties of materials.28 The directional nature of these metallophilic interactions enables the precise arrangement of molecular components, leading to highly ordered and more predictable crystal structures.29,30 This control is crucial in the creation of porous networks, which have applications in gas storage, separation technologies, and catalysis.21,23,24 Additionally, the luminescent properties induced by aurophilic interactions are being exploited in the development of new optoelectronic materials, pushing the boundaries of what is achievable in crystal engineering.31
Argentophilic and aurophilic interactions are distinguished by their unique physical nature, which arises from the specific electronic configurations of silver and gold atoms.11–15 These metallophilic interactions, while being a subset of van der Waals forces, are nuanced and multifaceted in nature. Apart from important relativistic effects, these interactions commonly exhibit electrostatic repulsion that is compensated by dispersion forces.2,3 They are especially relevant due to the involvement of large, polarizable electron clouds in both silver and gold atoms. The larger atomic size and the extensive electron cloud of these heavy atoms enhance the strength of dispersion forces, contributing significantly to the overall stabilization.
This manuscript introduces a convenient methodology for estimating the strength of argentophilic and aurophilic interactions, utilizing the quantum theory of atoms in molecules (QTAIM) and electron density properties at bond critical points between metal centers. Leveraging DFT calculations in conjunction with QTAIM parameters, we have developed an energy predictor model. This model enables the estimation of interaction strengths for Ag(I)⋯Ag(I) and Au(I)⋯Au(I) bonds without necessitating separate calculations for the individual monomers. The practicality of our approach has been validated through analysis of a selection of X-ray crystal structures sourced from the cambridge structural database (CSD), focusing on structures where argentophilic and aurophilic interactions are integral to their solid-state arrangements. The method offers a significant advantage in evaluating the contribution of metallophilic interactions in systems with multiple contributing interactions and in molecular assemblies where the interactions are intramolecular. By applying our technique, researchers can efficiently estimate the strength of argentophilic and aurophilic interactions. This quantification is crucial for understanding and predicting the influence of these interactions on both molecular and solid-state properties, providing a valuable tool for advancements in the field of supramolecular chemistry and material science.
Theoretical methods
The monomers from the studied complexes were firstly optimized at the PBE0-x2c32-D433/x2c-TZVPall34 and PBE0-D4/def2-TZVP levels of theory using a fine grid. The def2-TZVP basis set uses ECPs for Ag and Au atoms.34–36 Relativistic quantum chemistry is essential for properly understanding the chemistry of heavy and super-heavy elements and their compounds, as these effects largely determine their electronic structures, properties, and functions. Relativistic exact decoupling can be achieved using either the x2c (exact two-component) approach or the BSS (Barysz–Sadlej–Snijders) approach. The x2c approach is recommended because it is simpler, avoiding the additional free-particle Foldy–Wouthuysen transformation required by the BSS approach.32b For comparison, we have also used the def2-TZVP basis set, which employs effective core potentials (ECPs). The use of ECPs for heavier atoms is popular for good reasons: it reduces the number of basis functions and, consequently, the computational workload; at the same time, it also accounts for scalar relativistic effects.34–36 The D4 dispersion correction was selected for its ability to provide an accurate, efficient, and particularly robust description of metals.33bThen, for PBE0-x2c-D4/x2c-TZVPall and PBE0-D4/def2-TZVP levels of theory, the homodimers were studied through a first “rough” scan of 0.1 Å of step size on the Ag⋯Ag or Au⋯-Au distance along the main symmetry axis until a minimum was found. The linear ligands were set perpendicular to each other to minimize ancillary interactions. Once the minimum was found, a “refined” scan was performed to better approach the real minimum using 0.0125 Å of step size, moving one Å in each direction from the minimum. The scans were performed as single point calculations at the same level of theory as the monomer optimizations using the Turbomole 7.7 program.37 The minimum geometry was then further analysed by means of Bader's Quantum Theory of Atoms in Molecules38 at the same level of theory. In all cases, a bond critical point (BCP) was found interconnecting the Regium atoms (Ag⋯Ag/Au⋯Au) and its electron density and derivatives of the latter were subtracted and analysed, using the Multiwfn software.39
Results and discussion
X-ray examples
Fig. 1 shows some selected examples of X-ray structures retrieved from the CSD where argentophilic interactions are present and have a structural directing role. For instance, in BIQWEF40 structure (Fig. 1a) the (μ2-ethane-1,2-diamine)-dichloro-di-silver(I) molecules propagate forming 1D polymers via the formation of Ag⋯Ag interactions in combination with H-bonding interactions. 1D infinite assemblies are also observed in HAMMIS41 and LURDIM42 structures, both are diammine-silver(I) salts (counteranions are omitted for clarity) that form either symmetric (HAMMIS) or asymmetric Ag⋯Ag interactions (LURDIM).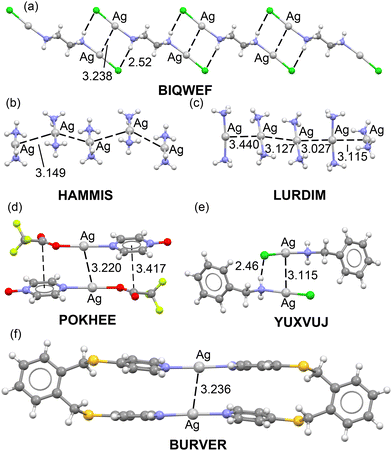 | ||
| Fig. 1 X-ray solid state structures of CSD codes BIQWEF (a), HAMMIS (b), LURDIM (c), POKHEE (d), YUXVUJ (e) and BURVER (f). In HAMMIS, LURDIM and BURVER the counterions are omitted. Distances in Å. | ||
Additional examples comprise discrete dimers formed in (pyrazine N-oxide)-(trifluoroacetato)-silver(I) (POKHEE)43 and benzylamino-chloro-silver(I) (YUXVUJ)44 structures (Fig. 1d and e). In BURVER45 (Fig. 1f), two Ag(I) ions promote the formation of a macrocycle by connecting two μ-4,4′-(1,2-phenylenebis(methylene-sulfanediyl))bispyridine units via Ag–N coordination bonds. The Ag(I) metals are separated 3.236 Å, thus establishing an intramolecular interaction. This distance is similar to the intermolecular distances observed in the rest of X-ray structures supporting its structural-directing role.
The evaluation of the strength of the argentophilic interactions by the traditional supramolecular approach is complicated in all these examples. For instance, in neutral systems like BIQWEF, POKHEE and YUXVUJ additional interactions are established, therefore calculation of the dimerization energies is not useful to extract the contribution of the argentophilic interaction.
In other structures like HAMMIS or LURDIM, the positive charge of the monomer Ag(NH3)2+ anticipates a repulsive interaction due to the dominant coulombic cation⋯cation repulsion in the dimer. Again, difficult to extract the stabilizing contribution from the argentophilic interactions. Finally, in BURVER compound, it is even more complicated, since in addition to the electrostatic repulsion, the contact is intramolecular.
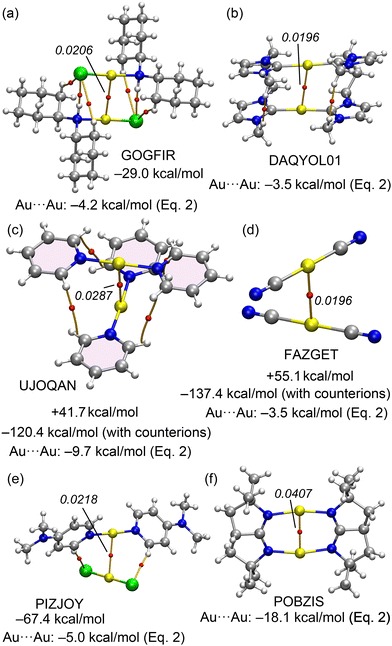
A similar situation is anticipated in Au(I) X-ray structures exhibiting aurophilic interactions. A selection of structures is given in Fig. 2. The GOGFIR46 structure (Fig. 2a) forms self-assembled dimers where the chloro-bis(dicyclohexylamine)-gold(I) monomers establish both Au⋯Au and H-bonding interactions. The PIZJOY47 structure (Fig. 2b) forms 1D infinite assemblies where cationic bis(4-(dimethylamino)pyridine)-gold(I) and anionic dichloro-gold(I) are arranged via the formation of Au⋯Au interactions. The UJOQAN48 structure (Fig. 2c) forms cation⋯cation dimers in the solid state where the monomers are rotated 90°. In FAZGET,49 the dicyano-gold(I) monomers propagate in the solid state forming 1D assemblies (see Fig. 2d). Finally, two additional examples of intramoelcular Au⋯Au interactions are provided in Fig. 2, bottom (DAQYOL0150 and POBZIS51). In one of them (DAQYOL01) the Au⋯Au distance is comparable to those observed in the intermolecular assemblies while in the other one (POBZIS) it is considerably shorter due to the rigidity of the (μ-2,2,5,5-tetramethyl-1,2,3,3a,4,5-hexahydropyrrolo[2,3-b]pyrrole) ligand.
 | ||
| Fig. 2 X-ray solid state structures of CSD codes GOGFIR (a), PIZJOY (b), UJOQAN (c), FAZGET (d), DAQYOL01 (e) and POBZIS (f). The counterions are omitted. | ||
The evaluation of the aurophilic interactions is complicated in these structures, either because of the ancillary interactions or the ionic nature of the monomers. That is, anion⋯anion in FAZGET, cation⋯cation in UJOQAN or anion⋯cation in PIZJOY. In these three cases the dimerization energies would be dominated by strong repulsive (FAZGET and UJOQAN) or strong attractive (PIZJOY) coulombic forces, thus complicating the evaluation of the real strength of the Au⋯Au interaction even in the absence of secondary interactions.
Theoretical study
To effectively evaluate the significance and intensity of metallophilic Ag⋯Ag and Au⋯Au interactions in complex supramolecular systems, particularly those with multiple noncovalent interactions or charged constituents, we propose employing Bader's Quantum Theory of Atoms in Molecules (QTAIM) analysis. This approach is especially advantageous for scenarios where distinguishing individual interaction contributions is otherwise challenging. QTAIM analysis focused on bond critical point properties allows for a more detailed and precise assessment of these intricate bonding scenarios.For hydrogen, halogen, and chalcogen bonds, the use of electronic potential energy density (V) and Lagrangian kinetic energy density (G) has been previously suggested.52–58 These parameters have been explored in molecular crystals, with G recommended for hydrogen bonds and V for halogen and chalcogen bonds.59 However, to our knowledge, the application of these parameters has not been developed or tested for Ag⋯Ag or Au⋯Au interactions.
In this section, we aim to provide a straightforward method for estimating the strength of Ag⋯Ag and Au⋯Au interactions. Utilizing the set of complexes outlined in Scheme 1, we have calculated the dimerization energies, conducted QTAIM analysis, and extracted relevant QTAIM parameters at the BCPs connecting the noble metal atoms.
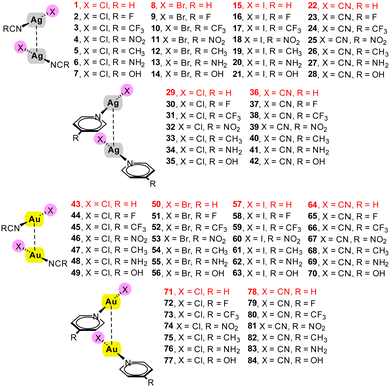 | ||
| Scheme 1 Homodimers 1–84 studied in this work and their numbering. In red those complexes used to validate the equations and not used to construct the regression plots. | ||
Silver complexes
The characteristics and topological parameters for complexes 1–42 are detailed in Table 1. For these complexes, a linear mode of complexation, specific ligands, and a relative orientation of the monomers at a 90° rotation in the dimer were chosen. This configuration was selected to minimize secondary interactions and to reflect ligand arrangements typically observed in solid-state structures. Importantly, the chosen monomers are neutral, thus ensuring that pure coulombic forces (either attractive or repulsive) are not predominant in these systems. Additionally, we utilized scans instead of fully optimized geometries to maintain the complexes in a 'frozen' state, preventing the formation of secondary interactions. This approach allows us to attribute the calculated dimerization energy (the energy of the homodimer minus twice the energy of the monomer) directly to the strength of the metallophilic contact. Fully optimization of the complexes leads to an antiparallel orientation with ligand⋯ligand interactions.| Dimer | E | d | ρ | ∇2ρ | V | G |
|---|---|---|---|---|---|---|
| a Values in parenthesis correspond to PBE0-D4/def2-TZVP level of theory. The repression plots for this level of theory are included in the ESI, Fig. S1. | ||||||
| 1 | –6.06 (–6.16) | 3.038 | 0.0202 | 0.0575 | −0.0155 | 0.0149 |
| 2 | –6.46 (–6.57) | 3.013 | 0.0212 | 0.0607 | −0.0167 | 0.0159 |
| 3 | –6.56 (–6.67) | 3.025 | 0.0208 | 0.0591 | −0.0161 | 0.0155 |
| 4 | –6.49 (–6.58) | 3.013 | 0.0213 | 0.0607 | −0.0167 | 0.0160 |
| 5 | –5.86 (–6.00) | 3.038 | 0.0201 | 0.0576 | −0.0155 | 0.0149 |
| 6 | –5.35 (–5.50) | 3.038 | 0.0200 | 0.0577 | −0.0154 | 0.0149 |
| 7 | –6.03 (–6.16) | 3.025 | 0.0206 | 0.0592 | −0.0161 | 0.0154 |
| 8 | –6.80 (–6.77) | 3.013 | 0.0213 | 0.0605 | −0.0168 | 0.0159 |
| 9 | –7.24 (–7.22) | 2.988 | 0.0223 | 0.0638 | −0.0181 | 0.0170 |
| 10 | –7.35 (–7.34) | 3.000 | 0.0219 | 0.0622 | −0.0174 | 0.0165 |
| 11 | –7.29 (–7.26) | 3.000 | 0.0219 | 0.0621 | −0.0174 | 0.0165 |
| 12 | –6.59 (–6.60) | 3.013 | 0.0212 | 0.0606 | −0.0167 | 0.0159 |
| 13 | –6.07 (–6.08) | 3.025 | 0.0206 | 0.0590 | −0.0161 | 0.0154 |
| 14 | –6.79 (–6.79) | 3.013 | 0.0211 | 0.0605 | −0.0167 | 0.0159 |
| 15 | –8.08 (–7.80) | 3.000 | 0.0219 | 0.0620 | −0.0174 | 0.0165 |
| 16 | –8.56 (–8.28) | 2.975 | 0.0230 | 0.0655 | −0.0188 | 0.0176 |
| 17 | –8.71 (–8.45) | 2.988 | 0.0218 | 0.0622 | −0.0174 | 0.0165 |
| 18 | –8.62 (–8.34) | 2.988 | 0.0226 | 0.0636 | −0.0181 | 0.0170 |
| 19 | –7.88 (–7.65) | 3.000 | 0.0218 | 0.0622 | −0.0174 | 0.0165 |
| 20 | –7.34 (–7.12) | 3.013 | 0.0212 | 0.0605 | −0.0167 | 0.0159 |
| 21 | –8.02 (–7.79) | 3.000 | 0.0218 | 0.0621 | −0.0174 | 0.0164 |
| 22 | –5.40 (–5.48) | 3.075 | 0.0192 | 0.0530 | −0.0141 | 0.0137 |
| 23 | –5.60 (–5.64) | 3.063 | 0.0197 | 0.0544 | −0.0146 | 0.0141 |
| 24 | –5.67 (–5.77) | 3.050 | 0.0202 | 0.0560 | −0.0152 | 0.0146 |
| 25 | –5.54 (–5.62) | 3.050 | 0.0203 | 0.0559 | −0.0152 | 0.0146 |
| 26 | –5.45 (–5.54) | 3.075 | 0.0192 | 0.0531 | −0.0140 | 0.0136 |
| 27 | –5.08 (–5.18) | 3.075 | 0.0191 | 0.0532 | −0.0140 | 0.0136 |
| 28 | –5.57 (–5.66) | 3.063 | 0.0196 | 0.0546 | −0.0145 | 0.0141 |
| 29 | –10.22 (–10.31) | 2.925 | 0.0254 | 0.0739 | −0.0221 | 0.0203 |
| 30 | –10.45 (–10.54) | 2.925 | 0.0254 | 0.0739 | −0.0221 | 0.0203 |
| 31 | –10.53 (–10.65) | 2.925 | 0.0255 | 0.0738 | −0.0221 | 0.0203 |
| 32 | –10.62 (–10.72) | 2.925 | 0.0255 | 0.0738 | −0.0221 | 0.0203 |
| 33 | –9.77 (–9.89) | 2.938 | 0.0248 | 0.0718 | −0.0213 | 0.0196 |
| 34 | –9.31 (–9.44) | 2.925 | 0.0253 | 0.0739 | −0.0220 | 0.0203 |
| 35 | –10.02 (–10.13) | 2.925 | 0.0254 | 0.0739 | −0.0221 | 0.0203 |
| 36 | –9.68 (–9.73) | 2.963 | 0.0241 | 0.0681 | −0.0199 | 0.0185 |
| 37 | –9.60 (–9.67) | 2.963 | 0.0241 | 0.0681 | −0.0199 | 0.0185 |
| 38 | –9.35 (–9.44) | 2.975 | 0.0236 | 0.0662 | −0.0192 | 0.0179 |
| 39 | –9.54 (–9.61) | 2.963 | 0.0242 | 0.0681 | −0.0200 | 0.0185 |
| 40 | –9.29 (–9.37) | 2.963 | 0.0241 | 0.0681 | −0.0199 | 0.0185 |
| 41 | –9.21 (–9.30) | 2.963 | 0.0240 | 0.0682 | −0.0199 | 0.0185 |
| 42 | –9.53 (–9.60) | 2.963 | 0.0240 | 0.0682 | −0.0199 | 0.0185 |
To illustrate our methodology, we showcase the energy profiles for two representative dimers of silver and gold (4 and 83) in Fig. 3. For these profiles, frozen scans (using the optimized geometries of the monomers) were employed to vary the Rg⋯Rg distance and thereby extract the energy profiles. This approach has been consistently applied across dimers 1–84 as reported in our study.
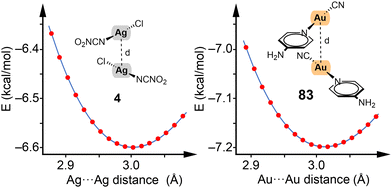 | ||
| Fig. 3 Energy profiles constructed using frozen scans for complexes 4 and 83. Energy in kcal mol−1 and distances in Å. | ||
The minimum energy geometries identified from these profiles were further analysed using QTAIM to obtain parameters at the BCPs connecting the noble metal atoms. The extracted parameters, along with the interaction energies, are compiled in Tables 1 and 2.
Notably, for the argentophilic dimers, we observed energy values ranging from –5 to –9 kcal mol−1 in complexes 1–28, and from –9 to –11 kcal mol−1 in complexes 29–42. This variation suggests that the pyridine ligand either enhances the argentophilic interaction or contributes to the dimerization energy via long-range van der Waals forces. Another interesting observation is that the formation of dimers in those complexes with electron-withdrawing substituents are more favourable compared to those with electron-donating groups. Furthermore, the energy analysis of complexes 1–21 indicates that the interaction strength of argentophilic bonds increases with the atomic weight of the halogen atom involved.
To analyse the effect of relativistic effects, Table 1 also gathers the interaction energies without applying the exact two-component (X2C) method for relativistic corrections in DFT calculations, and using the def2-TZVP basis set. Unexpectedly, the comparison revealed minimal differences between energies with and without relativistic corrections (Table 1), thus suggesting that the PBE0-D4/def2-TZVP level of theory can be also used for studying argentophilic interactions.
To explore the predictive capability of the QTAIM parameters for argentophilic interactions, we evaluated the relevance of density (ρ), potential energy density (V), and Lagrangian kinetic energy density (G), alongside the Laplacian of the electron density (∇2ρ). Regression analyses for Ag⋯Ag dimers, excluding complexes with R = H (1, 8, 15, 22, 29, and 36), which served for method validation, are depicted in Fig. 4. We selected this set to have a representation of each series and minimize the influence of substituents. Notably, ρ (red dots), V (blue dots) and G (pink dots) exhibit good correlations with binding energies, with regression coefficients of 0.970, 0.960 and 0.958 respectively, suggesting their ability in predicting interaction energies, consistent with previous studies on halogen and chalcogen bonds.60
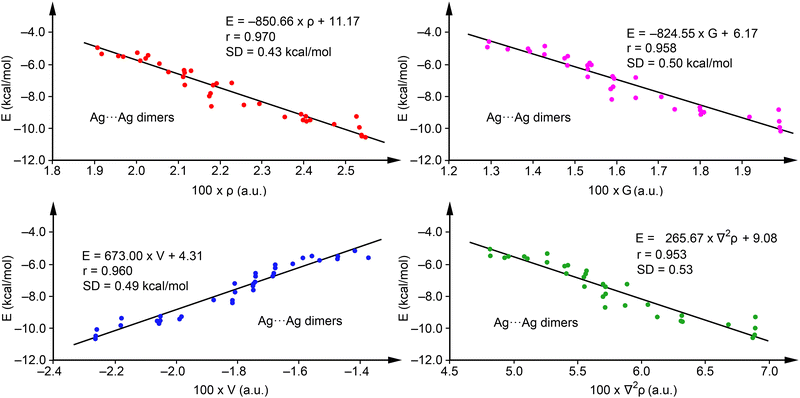 | ||
| Fig. 4 Regression plots for Energy versus ρ (red) and V(r) (blue), G(r) (pink) and ∇2ρ (green) for complexes 1–42. | ||
Furthermore, the correlation using ∇2ρ (r = 0.953, green dots) also demonstrates the predictive utility of QTAIM for argentophilic interactions, with ρ proving most effective due to its highest regression coefficient and minimal standard deviation (SD = 0.43 kcal mol−1). Consequently, we propose eqn (1)
| E(kcal mol−1) = −850.66 × ρ(a.u.) + 11.17, | (1) |
Validation against energies of complexes not initially used in the regression plots (1, 8, 15, 22, 29, and 36), see Table 2, revealed close agreement, with a maximum deviation of 0.61 kcal mol−1 for compound 15 and an SD of 0.31 kcal mol−1, underscoring the accuracy of eqn (1). Furthermore, adding these complexes to the training set had a minimal impact on the equation and the correlation coefficient (r = 0.972 and E = −846.11 × ρ + 11.04), confirming the robustness of the regression model. Although our primary goal was simplicity, further analyses with multivariable models were performed showing the same or even worse correlation coefficient when using combination of two variables (V and G behave the best with r = 0.970, identical to eqn (1)), not justifying the use of more complicated equations. Curiously, worse correlation compared to eqn (1) was observed using three or more variables. More details are given in the ESI,† see Tables S1 and S2.
Gold complexes
A parallel study has been performed for gold complexes. Table 3 gathers the energetic features and topological parameters for complexes 43–84. The main difference with the Ag complexes is that the energies are weaker, ranging from –4.3 to –9.2 kcal mol−1. Previous results have shown that argentophilic interactions are stronger than aurophilic.61 The data of Table 3 also discloses that Au⋯Au dimers with pyridine as ligand are stronger than those with nitrile and that electron withdrawing substituents favour the interaction, as also observed for Ag⋯Ag complexes. A notable distinction between Ag and Au complexes lies in the impact of incorporating relativistic effects on their binding energies. While the differences observed in Ag complexes were minimal, the effect is markedly significant for Au complexes (∼1 kcal mol−1). For instance, the inclusion of relativistic effects alters the binding energy of compound 57 by 1.4 kcal mol−1, accounting for 19% of its total binding energy.| Dimer | E | d | ρ | ∇2ρ | V | G |
|---|---|---|---|---|---|---|
| a Energies in parenthesis were computed using the PBE0-D4/def2-TZVP level of theory. The repression plots for this level of theory are included in the ESI, Fig. S2. | ||||||
| 43 | –5.29 (–4.43) | 3.188 | 0.0217 | 0.0543 | −0.0141 | 0.0138 |
| 44 | –5.73 (–4.83) | 3.150 | 0.0231 | 0.0596 | −0.0154 | 0.0152 |
| 45 | –5.82 (–4.92) | 3.175 | 0.0222 | 0.0561 | −0.0145 | 0.0143 |
| 46 | –5.77 (–4.81) | 3.175 | 0.0222 | 0.0561 | −0.0145 | 0.0143 |
| 47 | –5.05 (–4.25) | 3.175 | 0.0221 | 0.0560 | −0.0145 | 0.0142 |
| 48 | –4.32 (–3.57) | 3.175 | 0.0220 | 0.0560 | −0.0144 | 0.0142 |
| 49 | –5.15 (–4.35) | 3.163 | 0.0225 | 0.0577 | −0.0149 | 0.0147 |
| 50 | –5.96 (–4.92) | 3.150 | 0.0232 | 0.0596 | −0.0154 | 0.0152 |
| 51 | –6.46 (–5.38) | 3.125 | 0.0242 | 0.0633 | −0.0164 | 0.0161 |
| 52 | –6.55 (–5.48) | 3.150 | 0.0232 | 0.0596 | −0.0155 | 0.0152 |
| 53 | –6.50 (–5.38) | 3.163 | 0.0227 | 0.0577 | −0.0150 | 0.0147 |
| 54 | –5.74 (–4.78) | 3.150 | 0.0231 | 0.0595 | −0.0154 | 0.0152 |
| 55 | –5.02 (–4.10) | 3.150 | 0.0230 | 0.0595 | −0.0154 | 0.0151 |
| 56 | –5.87 (–4.89) | 3.138 | 0.0236 | 0.0613 | −0.0159 | 0.0156 |
| 57 | –7.18 (–5.78) | 3.125 | 0.0243 | 0.0633 | −0.0165 | 0.0162 |
| 58 | –7.74 (–6.29) | 3.088 | 0.0260 | 0.0694 | −0.0182 | 0.0178 |
| 59 | –7.81 (–6.40) | 3.113 | 0.0249 | 0.0654 | −0.0171 | 0.0167 |
| 60 | –7.73 (–6.27) | 3.125 | 0.0244 | 0.0633 | −0.0165 | 0.0162 |
| 61 | –7.00 (–5.69) | 3.125 | 0.0243 | 0.0632 | −0.0165 | 0.0162 |
| 62 | –6.28 (–5.01) | 3.125 | 0.0242 | 0.0632 | −0.0165 | 0.0161 |
| 63 | –7.14 (–5.80) | 3.113 | 0.0248 | 0.0652 | −0.0170 | 0.0167 |
| 64 | –5.58 (–4.47) | 3.163 | 0.0229 | 0.0581 | −0.0150 | 0.0148 |
| 65 | –5.82 (–4.70) | 3.150 | 0.0234 | 0.0598 | −0.0155 | 0.0152 |
| 66 | –5.92 (–4.80) | 3.163 | 0.0230 | 0.0581 | −0.0151 | 0.0148 |
| 67 | –5.78 (–4.61) | 3.150 | 0.0235 | 0.0599 | −0.0155 | 0.0152 |
| 68 | –5.60 (–4.55) | 3.163 | 0.0228 | 0.0580 | −0.0150 | 0.0148 |
| 69 | –5.03 (–4.03) | 3.175 | 0.0223 | 0.0562 | −0.0145 | 0.0143 |
| 70 | –5.64 (–4.58) | 3.163 | 0.0228 | 0.0580 | −0.0150 | 0.0148 |
| 71 | –8.44 (–7.53) | 3.063 | 0.0274 | 0.0743 | −0.0196 | 0.0191 |
| 72 | –8.41 (–7.51) | 3.075 | 0.0268 | 0.0720 | −0.0190 | 0.0185 |
| 73 | –9.04 (–8.13) | 3.063 | 0.0274 | 0.0743 | −0.0196 | 0.0191 |
| 74 | –8.90 (–7.97) | 3.075 | 0.0268 | 0.0721 | −0.0190 | 0.0185 |
| 75 | –8.20 (–7.33) | 3.063 | 0.0273 | 0.0743 | −0.0196 | 0.0191 |
| 76 | –7.39 (–6.57) | 3.063 | 0.0273 | 0.0742 | −0.0196 | 0.0191 |
| 77 | –8.19 (–7.32) | 3.063 | 0.0273 | 0.0743 | −0.0196 | 0.0191 |
| 78 | –8.97 (–7.82) | 3.075 | 0.0270 | 0.0722 | −0.0191 | 0.0186 |
| 79 | –9.00 (–7.86) | 3.075 | 0.0270 | 0.0723 | −0.0191 | 0.0186 |
| 80 | –9.18 (–8.05) | 3.075 | 0.0271 | 0.0723 | −0.0191 | 0.0186 |
| 81 | –9.21 (–8.05) | 3.075 | 0.0271 | 0.0723 | −0.0191 | 0.0186 |
| 82 | –8.99 (–7.86) | 3.063 | 0.0276 | 0.0745 | −0.0197 | 0.0192 |
| 83 | –8.28 (–7.20) | 3.075 | 0.0269 | 0.0722 | −0.0190 | 0.0185 |
| 84 | –8.77 (–7.66) | 3.075 | 0.0270 | 0.0722 | −0.0191 | 0.0186 |
Fig. 5 showcases regression plots for Au⋯Au complexes 43–84, plotting energy against the four QTAIM parameters for a comparative analysis with Ag complexes illustrated in Fig. 4. For method validation purposes, complexes with R = H (43, 50, 57, 64, 71, and 78) were omitted from this analysis. It is observed that correlations for electron density (red dots), potential energy density (blue dots), Lagrangian kinetic energy density (pink dots), and the Laplacian of ρ (green dots) in the Au complexes are less robust than those observed in Ag complexes but still maintain acceptable levels of correlation. For the Au⋯Au complexes, the regression coefficients presented in Fig. 5 indicate that the interaction energy has a comparable correlation with all four QTAIM parameters examined, showcasing r values between 0.925 and 0.938, and standard deviation (SD) values spanning 0.51 to 0.56 kcal mol−1. Given the slightly superior correlation coefficient for electron density, we propose the following equation for predicting the strength of aurophilic interactions:
| E(kcal mol−1) = −688.65 × ρ(a.u.) + 10.03 | (2) |
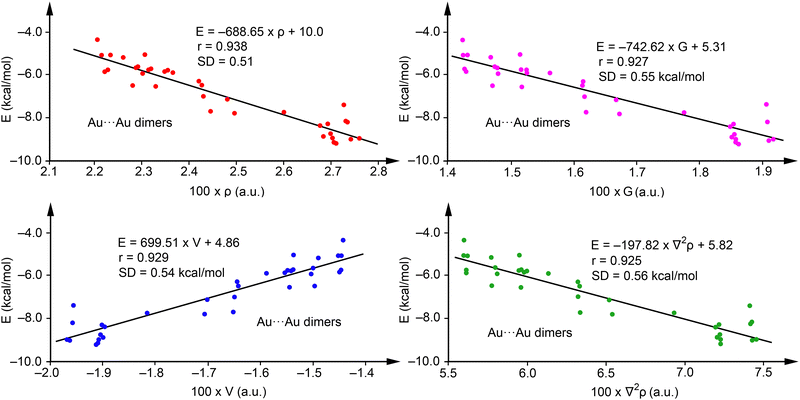 | ||
| Fig. 5 Regression plots for Energy versus ρ (red) and V(r) (blue), G(r) (pink) and ∇2ρ (green) for complexes 43–84. | ||
These findings indicate that employing QTAIM parameters to predict aurophilic interactions, as demonstrated in the regressions of Fig. 5, is plausible. However, such predictions should be approached with more caution than those of Ag. The validation against energies of complexes not initially used in the regression plots (43, 50, 57, 64, 71, and 78) revealed a good agreement, with maximum deviation of 0.47 kcal mol−1 for compound 57 and a SD of 0.35 kcal mol−1, underscoring the applicability of eqn (2) (see Table 4). Similarly to the Ag-complexes, adding these complexes to the training set had a minimal impact on the equation and the correlation coefficient (r = 0.943, E = –681.57 × ρ + 9.84).
Multivariable analysis indicates that incorporating two variables does not enhance the regression coefficient, while including three variables (ρ, V, and G) slightly improves it to r = 0.960. This leads to the formulation of eqn (3)
E(kcal mol−1) = −2533.14 × ρ(a.u.) + 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 737.86 × V(a.u.) + 15 737.86 × V(a.u.) + 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 562.41 × G(a.u.) + 13.56 562.41 × G(a.u.) + 13.56 | (3) |
Physical interpretation of the equations
The electron density represents the distribution of electrons in the space around an atom or molecule, derived from the wavefunction that defines the chemical entity. Consequently, the electron density around a molecule is influenced by the atomic nuclei that constitute the molecule. As two molecules, initially far apart, come closer together, their electronic clouds merge and modify the electronic space around them. Consequently, any bonding interaction between two atoms is exhibited in the electron density distribution [ρ(r)] as a topological saddle conformation around the interatomic zero-flux surface (S). At S, bond critical points (BCPs) appear, where the gradient of density vanishes (∇ρ(r) = 0), and the electron density is a minimum in the direction parallel to the bond and a maximum in the perpendicular plane. Two gradient lines starting at the corresponding nuclei and ending at the BCP form the bond path, which is considered an identifier of the interaction.59We propose that the regression equations in our manuscript, which relate the interaction energies of Ag–Ag and Au–Au bonds to QTAIM parameters, serve as predictors for the strength of metallophilic interactions. The electron density at the BCP is a direct measure of the shared electronic charge between the two metal atoms. Higher ρ values indicate stronger interactions due to greater electron sharing or delocalization, reflecting a more substantial attractive force between the atoms. Additionally, other properties at the BCP, derived from the electron density, such as the Laplacian of the electron density (∇2ρ), the Lagrangian kinetic energy density (G), the potential energy density (V), and the total energy density (H), should also be directly related to the strength of the interaction between the two metal centres. In fact, the kinetic and potential energy densities at the BCP are related to the Laplacian by the local form of the virial theorem: ¼∇2ρ = 2G + V. Moreover, it has been previously demonstrated that G and V are mostly influenced by the Pauli repulsion and the stabilizing effect of the electric field, respectively.52–54
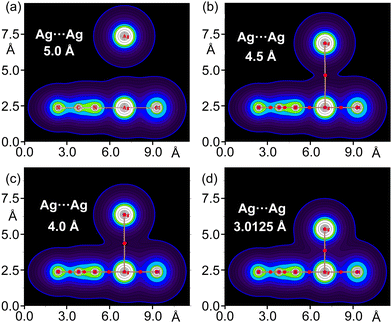
As representative case, Fig. 6 illustrates complex 4 at different distances between the Ag⋯Ag centres. Starting from 5.0 Å and decreasing to the energetic minimum at 3.0125 Å, the electron density is represented, and the progressive merging of the electron clouds of both units gives rise to a bond path and a BCP between the Ag⋯Ag centres. The values of ρ, ∇2ρ, |V|, and G progressively increase as the distance reaches the energy minimum (see Table S3, ESI†). This demonstrates that the electron density at the BCP between the regium metals is proportional to the interaction energies of the two monomers, and consequently, the strength of the metallophilic force.
Application of eqn (1) and (2)
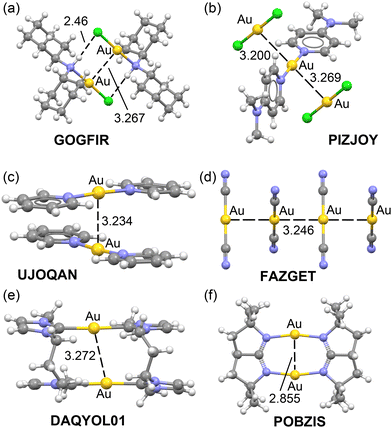
The equations developed in this study were applied to all examples featured in Fig. 1 and 2. For the Ag compounds, we calculated the dimerization energies for BIQWEF, HAMMIS, POKHEE, and YUXVUJ, accompanied by QTAIM analyses as illustrated in Fig. 7. Additionally, for HAMMIS (which also serves as a model for the related LURDIM structure), we calculated the interaction energies, including the counterions. For clarity, the counterions are not depicted in Fig. 7b; however, the complete assembly can be viewed in the ESI,† Fig. S3. In BIQWEF, QTAIM analysis identified three bond critical points (BCPs, small red spheres) and bond paths (solid orange lines) linking the monomers, with two BCPs corresponding to NH⋯Cl hydrogen bonds and one to an argentophilic interaction (Fig. 7a). The substantial dimerization energy (−29.5 kcal mol−1) results from these combined interactions, likely augmented by electrostatic attraction between Cl and Ag atoms. The contribution from the Ag⋯Ag interaction in the dimer is quantified as –1.0 kcal mol−1. QTAIM analysis for HAMMIS reveals only one BCP connecting the two Ag atoms, indicating that the argentophilic interaction is the sole link between the monomers. The binding energy is repulsive at 69.4 kcal mol−1 due to the electrostatic repulsion between the cationic monomers. However, when counterions are included in the calculations, the assembly formation, as shown in Fig. S3 (ESI†), it becomes energetically favorable at –117.9 kcal mol−1. Using the equation developed in this study, the argentophilic contribution is calculated as –3.5 kcal mol−1. For POKHEE (Fig. 7c), QTAIM analysis identifies four BCPs and bond paths linking the neutral monomers, with three BCPs corresponding to anion–π interactions60 and one to an argentophilic interaction. The dimerization energy is –24.8 kcal mol−1, with the Ag⋯Ag interaction contributing –1.1 kcal mol−1, highlighting the dominance of anion–π interactions in this system.62 In YUXVUJ, QTAIM analysis reveals several CH⋯Cl contacts in addition to the argentophilic interaction, resulting in a total of five BCPs and bond paths that connect the monomers.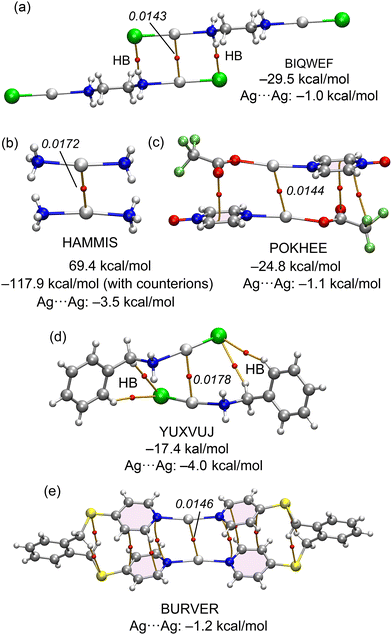 | ||
| Fig. 7 QTAIM analyses of BIQWEF (a), HAMMIS (b), POKHEE (c), YUXVUJ (d) and BURVER (e). The density values are given in italics. Dimerization energies and argentophilic energies are also indicated. | ||
The calculated dimerization energy for YUXVUJ is –17.6 kcal mol−1, with the Ag⋯Ag interactions contributing –4.0 kcal mol−1. For the BURVER dinuclear complex (Fig. 6e), the intramolecular argentophilic interaction is estimated at –1.2 kcal mol−1. Additionally, QTAIM analysis in BURVER reveals two π-stacking interactions, represented by six bond critical points (BCPs) interconnecting the aromatic rings, and four CH⋯S contacts. Each CH⋯S contact is characterized by a BCP and bond path linking the hydrogen and sulfur atoms.
For the Au complexes, we began our analysis with the GOGFIR structure, in which the monomers are neutral. This structure demonstrates a dimerization energy of −29.0 kcal mol−1, attributable primarily to the aurophilic interaction, supplemented by four additional contacts (two CH⋯Cl and two NH⋯Cl). QTAIM analysis has identified corresponding BCPs and bond paths for these interactions. The substantial dimerization energy of −29.0 kcal mol−1 includes an aurophilic contribution of −4.2 kcal mol−1, as calculated from eqn (2). In the case of DAQYOL01 (Fig. 8b), the Au⋯Au contact is intramolecular and thus not amenable to estimation using the supramolecular approach typically employed. Instead, the strength of this Au⋯Au contact, estimated using eqn (2), is −3.5 kcal mol−1. The cation⋯cation and anion⋯anion dimer pairs from the CSD with reference codes UJOQAN and FAZGET were also analysed (see Fig. 8c and d). QTAIM analysis for UJOQAN revealed a BCP connecting the Au atoms, confirming the aurophilic interaction.
Additionally, four BCPs and bond paths interconnecting the aromatic H-atoms of pyridine rings suggest the presence of ancillary van der Waals interactions. In contrast, the FAZGET structure exhibits solely the aurophilic interaction, as denoted by its BCP and bond path (Fig. 8). In both instances, the dimerization energies are repulsive, reflecting the coulombic repulsion between ions of identical charge. However, upon including counterions in the calculations (tetrafluoroborate for UJOQAN and triazolium for FAZGET, see Fig. S3 in ESI† for the computed assemblies), the formation energies turn significantly negative, attributed to the strong attractions between anions and cations. Thus, any of both interactions energies is not useful to underscore the significance of the aurophilic contact strength. Using eqn (2), the contributions from aurophilic interactions are estimated at −9.7 kcal mol−1 for UJOQAN and −3.5 kcal mol−1 for FAZGET, consistent with the findings of Table 3 that evidence that pyridine ligands exhibit stronger interactions than cyanide. The ion pair interaction in PIZJOY has also been investigated. The QTAIM analysis reveals that the anion and cation are linked by three bond critical points (BCPs) and bond paths, involving two CH⋯Cl and one Au⋯Au contacts. The interaction energy is notably substantial, primarily due to the pure Coulombic attraction, measuring at −67.4 kcal mol−1. The aurophilic interaction, as calculated from eqn (2), is −5.0 kcal mol−1. In the case of POBZIS, the intramolecular Au⋯Au interaction is significantly stronger, estimated at −18.1 kcal mol−1. This is largely attributed to the high value of electron density (ρ = 0.0407 a.u.) at the BCP. However, this estimation of the aurophilic interaction should be approached with caution, as this ρ value significantly exceeds the range used to develop eqn (2), potentially affecting the accuracy of this estimation.
Conclusions
Based on the findings of our study, we can draw several key conclusions:1. The interaction energies of argentophilic bonds can be predicted using the charge density (ρ) at the bond critical points (BCPs), as evidenced by strong correlations in our data. We recommend using the equation Eint(kcal mol−1) = −850.66 × ρ(a.u.) + 11.17 for such predictions.
2. Similarly, we observed reliable correlations for aurophilic interactions, indicating that QTAIM parameters are also effective for estimating these interactions. We suggest the equation Eint(kcal mol−1) = −688.65 × ρ(a.u.) + 10.03.
3. Our proposed methodology provides a simple and effective way to calculate Rg⋯Rg interaction energies (Rg = Ag or Au) for both intramolecular and charged system interactions. This method circumvents the complexities of more elaborate modelling techniques.
4. The application of a relativistic Hamiltonian along with all-electron relativistic basis sets shows minimal impact on Ag⋯Ag dimer calculations but significantly affects the results for Au⋯Au complexes, underscoring the importance of considering relativistic effects, particularly for gold-based interactions.
Author contributions
The manuscript was collaboratively developed with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank MICIU/AEI of Spain (PID2020-115637GB-I00, FEDER funds) for financial support, the CTI (UIB) for computational facilities. AF thanks the Alexander von Humboldt Foundation for the J.C. Mutis research award. We thank Rosa M. Gomila for her assistance in the multivariant analysis.Notes and references
- F. Huang and V. Anslyn, Chem. Rev., 2015, 115, 6999–7000 CrossRef CAS PubMed
.
- H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2012, 41, 370–412 RSC
.
- H. Schmidbaur and A. Schier, Angew. Chem. Int. Ed., 2015, 54, 746–784 CrossRef CAS PubMed
.
- S. Sculfort and P. Braunstein, Chem. Soc. Rev., 2011, 40, 2741 RSC
.
- V. W.-W. Yam and E. C.-C. Cheng, Top. Curr. Chem., 2007, 281, 269 CrossRef CAS
.
- M. Bardaji and A. Laguna, J. Chem. Educ., 1999, 76, 201 CrossRef CAS
.
- H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2008, 37, 1931 RSC
.
- S. S. Pathaneni and G. R. Desiraju, J. Chem. Soc., Dalton Trans., 1993, 319 RSC
.
- L. Magnko, M. Schweizer, G. Rauhut, M. Schütz, H. Stoll and H.-J. Werner, Phys. Chem. Chem. Phys., 2002, 4, 1006 RSC
.
- K. M. Anderson, A. E. Goeta and J. W. Steed, Inorg. Chem., 2007, 46, 6444 CrossRef CAS PubMed
.
- P. Pyykkö, Chem. Rev., 1988, 88, 563 CrossRef
.
- P. Pyykkö, Chem. Rev., 1997, 97, 597 CrossRef PubMed
.
- P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412 CrossRef PubMed
.
- P. Pyykkö, Inorg. Chim. Acta, 2005, 358, 4113 CrossRef
.
- P. Pyykkö, Chem. Soc. Rev., 2008, 37, 1967 RSC
.
- N. Mirzadeh, S. H. Privér, A. J. Blake, H. Schmidbaur and S. K. Bhargava, Chem. Rev., 2020, 120, 7551–7591 CrossRef CAS PubMed
.
- M. Pujadas and L. Rodríguez, Coord. Chem. Rev., 2020, 408, 213179 CrossRef CAS
.
- A. Pinto, N. Svahn, J. C. Lima and L. Rodríguez, Dalton Trans., 2017, 46, 11125–11139 RSC
.
- V. W. W. Yam, V. K. M. Au and S. Y. L. Leung, Chem. Rev., 2015, 115, 7589–7728 CrossRef CAS PubMed
.
- J. C. Lima and L. Rodríguez, Chem. Soc. Rev., 2011, 40, 5442–5456 RSC
.
- D. Weber and M. R. Gagné, Top. Curr. Chem., 2015, 357, 167–211 CrossRef CAS PubMed
.
- E. Priola, A. Giordana, R. M. Gomila, E. Zangrando, L. Andreo, R. Rabezzana, L. Operti, E. Diana, G. Mahmoudi and A. Frontera, Dalton Trans., 2022, 51, 5818–5827 RSC
.
-
J. Romanova, M. R. Ranga Prabhath, Y. Sadik and P. D. Jarowski, in Quantum Systems in Physics, Chemistry, and Biology, Progress in Theoretical Chemistry and Physics, ed. A. Tadjer, R. Pavlov, J. Maruani, E. Brändas and G. Delgado-Barrio, Springer, Cham, 2017, Vol. 30 Search PubMed
.
- Q. Zhang, Q. Wang, X.-X. Chen, P. Zhang, C.-F. Ding, Z. Li and Y.-B. Jiang, TrAC, Trends Anal. Chem., 2018, 109, 32–42 CrossRef CAS
.
- S. Komori, K. Tada, N. Taguchi, T. Taniyama and T. Masese, J. Mater. Chem. C, 2023, 11, 11213–11217 RSC
.
- X.-Q. Zhou, P. Wang, V. Ramu, L. Zhang, S. Jiang, X. Li, S. Abyar, P. Papadopoulou, Y. Shao, L. Bretin, M. A. Siegler, F. Buda, A. Kros, J. Fan, X. Peng, W. Sun and S. Bonnet, Nat. Chem., 2023, 15, 980–987 CrossRef CAS PubMed
.
- M. J. Katz, K. Sakai and D. B. Leznoff, Chem. Soc. Rev., 2008, 37, 1884–1895 RSC
.
-
(a) E. Priola, G. Mahmoudi, J. Andreo and A. Frontera, Chem. Commun., 2021, 57, 7268 RSC
; (b) J. Echeverría, CrystEngComm, 2018, 20, 3987 RSC
.
- P. Niermeier, L. Wickemeyer, B. Neumann, H.-G. Stammler, L. Goett-Zink, T. Kottke and N. W. Mitzel, Dalton Trans., 2019, 48, 4109 RSC
.
- J. M. Guevara-Vela, K. Hess, T. Rocha-Rinza, Á. Martín Pendás, M. Flores-Álamo and G. Moreno-Alcántar, Chem. Commun., 2022, 58, 1398 RSC
.
- T. Seki, K. Ida and H. Ito, Mater. Chem. Front., 2018, 2, 1195 RSC
.
-
(a) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
; (b) D. Peng, N. Middendorf, F. Weigend and M. Reiher, J. Chem. Phys., 2013, 138, 184105 CrossRef PubMed
.
-
(a) E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed
; (b) E. Caldeweyher, J.-M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512 RSC
.
-
(a) Y. J. Franzke, R. Treß, T. M. Pazdera and F. Weigend, Phys. Chem. Chem. Phys., 2019, 21, 16658–16664 RSC
; (b) F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC
.
- M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173–194 CrossRef CAS
.
- M. Kaupp, P. V. Schleyer, H. Stoll and H. Preuss, J. Chem. Phys., 1991, 94, 1360–1366 CrossRef CAS
.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kömel, Chem. Phys. Lett., 1989, 162, 164–169 CrossRef
.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed
.
- K. Binnemans, N. R. Brooks, D. Depuydt, L. Van Meervelt, S. Schaltin and J. Fransaer, ChemPlusChem, 2013, 78, 578 CrossRef
.
- Z.-L. You, H.-L. Zhu and W.-S. Liu, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, m1903 CrossRef CAS
.
- D. Sun, N. Zhang, G.-G. Luo, Q.-J. Xu, R.-B. Huang and L.-S. Zheng, Polyhedron, 2010, 29, 1842 CrossRef CAS
.
- R. Puttreddy, J. R. A. Cottam and P. J. Steel, RSC Adv., 2014, 4, 22449 RSC
.
- C. Wolper, M. D. P. Bastardes, I. Dix, D. Kratzert and P. G. Jones, Z. Naturforsch., B: J. Chem. Sci., 2010, 65, 647 CrossRef
.
- H. Xue, F. Jiang, Q. Chen, D. Yuan, J. Pang, G. Lv, X. Wan, L. Liang and M. Hong, Chem. Commun., 2015, 51, 13706 RSC
.
- P. G. Jones and B. Ahrens, New J. Chem., 1998, 22, 1041 RSC
.
- J. C. Y. Lin, S. S. Tang, C. S. Vasam, W. C. You, T. W. Ho, C. H. Huang, B. J. Sun, C. Y. Huang, C. S. Lee, W. S. Hwang, A. H. H. Chang and I. J. B. Lin, Inorg. Chem., 2008, 47, 2543 CrossRef CAS PubMed
.
- R. Corbo, G. F. Ryan, M. A. Haghighatbin, C. F. Hogan, D. J. D. Wilson, M. D. Hulett, P. J. Barnard and J. L. Dutton, Inorg. Chem., 2016, 55, 2830 CrossRef CAS PubMed
.
- W. Dong, Y.-Q. Sun, B. Yu, H.-B. Zhou, H.-B. Song, Z.-Q. Liu, Q.-M. Wang, D.-Z. Liao, Z.-H. Jiang, S.-P. Yan and P. Cheng, New J. Chem., 2004, 28, 1347 RSC
.
- M. Baron, C. Tubaro, A. Biffis, M. Basato, C. Graiff, A. Poater, L. Cavallo, N. Armaroli and G. Accorsi, Inorg. Chem., 2012, 51, 1778 CrossRef CAS PubMed
.
- L. Tong, L. M. Davis, X. Gong, J. Feng, E. S. Beh and R. G. Gordon, Dalton Trans., 2019, 48, 6709 RSC
.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS
.
- I. Mata, I. Alkorta, E. Espinosa and E. Molins, Chem. Phys. Lett., 2011, 507, 185–189 CrossRef CAS
.
- I. Mata, E. Molins, I. Alkorta and E. Espinosa, J. Chem. Phys., 2009, 130, 044104 CrossRef PubMed
.
- M. A. Spackman, Cryst. Growth Des., 2015, 15, 5624–5628 CrossRef CAS
.
- M. L. Kuznetsov, Int. J. Quantum Chem., 2019, 119, e25869 CrossRef
.
- M. A. Spackman, Cryst. Growth Des., 2015, 15, 5624–5628 CrossRef CAS
.
- M. L. Kuznetsov, Int. J. Quantum Chem., 2019, 119, e25869 CrossRef
.
- A. Bauza and A. Frontera, ChemPhysChem, 2020, 21, 26–31 CrossRef CAS PubMed
.
- R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323 CrossRef CAS
.
- L. Ray, M. M. Shaikh and P. Ghosh, Inorg. Chem., 2008, 47, 230–240 CrossRef CAS PubMed
.
- A. Frontera, P. Gamez, M. Mascal, T. J. Mooibroek and J. Reedijk, Angew. Chem., Int. Ed., 2011, 50, 9564–9583 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: X-ray coordinates and correlation plots without relativistic effects and multivariant details. See DOI: https://doi.org/10.1039/d4cp00410h |
| This journal is © the Owner Societies 2024 |