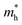Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stability and synthesis across barium tin sulfide material space†
Rachel
Woods-Robinson
 *abcf,
Kristin A.
Persson
*abcf,
Kristin A.
Persson
 bde and
Andriy
Zakutayev
bde and
Andriy
Zakutayev
 *c
*c
aApplied Science and Technology Graduate Group, University of California at Berkeley, Berkeley, CA, 94720 USA
bMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA, 94720 USA
cMaterials Science Center, National Renewable Energy Laboratory, Golden, Colorado, 80401 USA. E-mail: Andriy.Zakutayev@nrel.gov
dMolecular Foundry Division, Lawrence Berkeley National Laboratory, Berkeley, CA, 94720 USA
eDepartment of Materials Science and Engineering, University of California at Berkeley, Berkeley, CA, 94720 USA
fClean Energy Institute, University of Washington, WA, 98105 USA. E-mail: rwoodsr@uw.edu
First published on 10th November 2023
Abstract
Barium tin sulfide (Ba–Sn–S) is a ternary phase space with interesting material candidates for optoelectronic and thermoelectric applications, yet its properties have not been explored in-depth experimentally, and no thin films have been synthesized. This study uses combinatorial sputtering and theoretical calculations to survey the phase space of Ba–Sn–S materials. We experimentally find that at deposition temperatures up to 600 °C, phases of rocksalt-derived BaS structures (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), layered SnS derived structures (Aem2), and heavily distorted rocksalt solid solutions (possibly P121/m) dominate phase space, with amorphous films crystallizing in the middle of the composition space (Sn
m), layered SnS derived structures (Aem2), and heavily distorted rocksalt solid solutions (possibly P121/m) dominate phase space, with amorphous films crystallizing in the middle of the composition space (Sn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ba). Upon annealing with a capping layer, ternary phases of Ba2SnS4 (Pna21) and Ba7Sn5S15 (P63cm) are observed. However the theoretically predicted 0 K thermodynamically stable phase of BaSnS2 (P21/c) does not crystallize. These differences are explained with temperature-dependent computed phase diagrams, which show that BaSnS2 becomes unstable at high temperatures while Ba2SnS4 (Pna21) becomes stabilized. Lastly, we compute electronic and optical absorption properties of selected observed and predicted Ba–Sn–S phases, showing band gaps ranging from 1.67–2.5 eV, electron effective masses from 0.5–1 m0, and hole effective masses from 0.6–1.3 m0. These findings motivate future research into materials within this chemical space for solar energy harvesting and other semiconductor applications.
Ba). Upon annealing with a capping layer, ternary phases of Ba2SnS4 (Pna21) and Ba7Sn5S15 (P63cm) are observed. However the theoretically predicted 0 K thermodynamically stable phase of BaSnS2 (P21/c) does not crystallize. These differences are explained with temperature-dependent computed phase diagrams, which show that BaSnS2 becomes unstable at high temperatures while Ba2SnS4 (Pna21) becomes stabilized. Lastly, we compute electronic and optical absorption properties of selected observed and predicted Ba–Sn–S phases, showing band gaps ranging from 1.67–2.5 eV, electron effective masses from 0.5–1 m0, and hole effective masses from 0.6–1.3 m0. These findings motivate future research into materials within this chemical space for solar energy harvesting and other semiconductor applications.
Introduction
As scientists search for new materials to design our modern world, exploring multinary material phase spaces (consisting of three or more elements) has become a promising avenue to yield a diverse array of stable and metastable phases.1 One such complex ternary material system with promise for solar energy conversion applications is barium tin sulfide (Ba–Sn–S), with many stable competing phases of various structures and compositions, yet these phases and their properties have not been explored in-depth experimentally. Barium, tin, and sulfur are each relatively abundant in the earth's crust2 with moderately abundant reserves as determined by the reserve-to-production ratio,3 so designing materials within this phase space could mitigate material supply chain challenges.‡The binary endpoints of this system are rocksalt BaS (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), a wide band gap insulator with a very low hole effective mass, and SnS, which crystallizes in a variety of experimentally observed p-type semiconductor polymorphs (with band gaps EG > 1 eV) including Pnma, Cmcm, Fm
m), a wide band gap insulator with a very low hole effective mass, and SnS, which crystallizes in a variety of experimentally observed p-type semiconductor polymorphs (with band gaps EG > 1 eV) including Pnma, Cmcm, Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, and Aem2.5 The first Ba–Sn–S compound, a perovskite phase of BaSnS3 (Pnma), was synthesized in 1970 using a high-pressure bulk synthesis method.6 Several more bulk crystalline phases have been grown since, including Ba3Sn2S7 (P21/c),7,8 Ba2SnS4 (Pna21),9,10 BaSnS2 (P21/c),11,12 and BaSn2S3 (P121/m).13 In the 2010s Ba–Sn–S was studied for nonlinear optics applications, yielding compounds with more complicated stoichiometries and structures: Ba6Sn7S20 (C2/c), Ba7Sn5S15 (P63cm), BaSn2S5 (Pccn), Ba8Sn4S15 (Pca21), Ba7Sn3S13 (Pnma), and Ba12Sn4S23 (P21c).14–16 Additional Ba–Sn–S crystal structures have been computationally predicted as thermodynamically stable or metastable – such as Ba7Sn3S13 (Pnma), Ba3SnS5 (I4/mcm), and BaSn3S4 (P1m1) – but to our knowledge these have yet to be synthesized or characterized.17,18
m, and Aem2.5 The first Ba–Sn–S compound, a perovskite phase of BaSnS3 (Pnma), was synthesized in 1970 using a high-pressure bulk synthesis method.6 Several more bulk crystalline phases have been grown since, including Ba3Sn2S7 (P21/c),7,8 Ba2SnS4 (Pna21),9,10 BaSnS2 (P21/c),11,12 and BaSn2S3 (P121/m).13 In the 2010s Ba–Sn–S was studied for nonlinear optics applications, yielding compounds with more complicated stoichiometries and structures: Ba6Sn7S20 (C2/c), Ba7Sn5S15 (P63cm), BaSn2S5 (Pccn), Ba8Sn4S15 (Pca21), Ba7Sn3S13 (Pnma), and Ba12Sn4S23 (P21c).14–16 Additional Ba–Sn–S crystal structures have been computationally predicted as thermodynamically stable or metastable – such as Ba7Sn3S13 (Pnma), Ba3SnS5 (I4/mcm), and BaSn3S4 (P1m1) – but to our knowledge these have yet to be synthesized or characterized.17,18
In addition to the quantity of unique ordered phases, another compelling aspect of the Ba–Sn–S system is the large unit cells of synthesized and predicted thermodynamically stable structures; notably, Ba8Sn4S15 (Pca21) has 216 atoms in its crystal structure, yet is thermodynamically stable (for reference, only 0.1% of compounds on the Materials Project that lie on the convex hull have over 200 atoms). We suspect that these features are due to the diverse bonding preferences of Ba, Sn, and S atoms, which can result in structures with high coordination numbers. These low symmetry structures could lead to interesting polar or scattering properties. Recently, Ba–Sn–S compounds such as BaSnS2 have been predicted as candidates for optoelectronic applications such as photovoltaics and thermoelectrics.19 This BaSnS2 phase space is similar to Cu–Ba–Sn–S, which has been studied as a solar absorber.20 Notably, photovoltaic devices with over 5 percent efficiency have been demonstrated with a Cu2BaSn(S,Se)4 absorber using earth-abundant elements for photovoltaic and photoelectrochemical applications.21,22 However, reports of synthesis and properties of ternary Ba–Sn–S are rare. Moreover, optoelectronic applications usually require thin films with non-stoichiometric compositions, however to our knowledge thin film Ba–Sn–S crystals have not yet been grown nor has off-stoichiometry been explored.
Here, we survey the thin film phase space of Ba–Sn–S using combinatorial sputter synthesis, varying composition and deposition temperature. Cation ratio is varied along approximately the BaxSn1−xS tieline, with binary endpoints of BaS and SnS. We identify a range of disordered and distorted RS-derived and layered phases of Sn-substituted BaS and Ba-substituted SnS, and an amorphous region. To access high-temperature phases, we use a capping layer to anneal as-deposited thin films, and identify Ba7Sn5S15 and Ba2SnS4. Our initial assumption was the that the computationally predicted stable phases near Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn 1
Sn 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 – namely, BaSnS2 (P21/c) and Ba6Sn7S20 (C2/c) – would crystallize, and these phases are referred to for reference throughout the manuscript. However, to our knowledge neither BaSnS2 nor Ba6Sn7S20 was synthesized under any growth condition. A series of computational phase diagrams at various temperatures are analyzed, which support these experimental findings. Lastly, we compute band gaps, effective masses, and optical absorption spectra of compelling Ba–Sn–S compounds to guide future research. We find low electron and hole effective masses (0.5–1 and 0.6–1.3 m0, respectively; subsequently, effective mass is reported as unitless) as well as relatively wide band gaps (1.67–2.5 eV) suggestive of photoelectrochemical applications of these materials.
1 – namely, BaSnS2 (P21/c) and Ba6Sn7S20 (C2/c) – would crystallize, and these phases are referred to for reference throughout the manuscript. However, to our knowledge neither BaSnS2 nor Ba6Sn7S20 was synthesized under any growth condition. A series of computational phase diagrams at various temperatures are analyzed, which support these experimental findings. Lastly, we compute band gaps, effective masses, and optical absorption spectra of compelling Ba–Sn–S compounds to guide future research. We find low electron and hole effective masses (0.5–1 and 0.6–1.3 m0, respectively; subsequently, effective mass is reported as unitless) as well as relatively wide band gaps (1.67–2.5 eV) suggestive of photoelectrochemical applications of these materials.
Methods
Experimental methods
Thin film synthesis was performed with the combinatorial method, using RF sputter deposition with sulfide targets of BaS and SnS and EXG glass substrates, as depicted in Fig. 1(a). Sputter power was kept constant at 40 W for the BaS target and varied between 7 and 40 W for the SnS target to achieve compositional gradients with varying stoichiometries. Powers were varied to target the composition range of Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn = 1
Sn = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
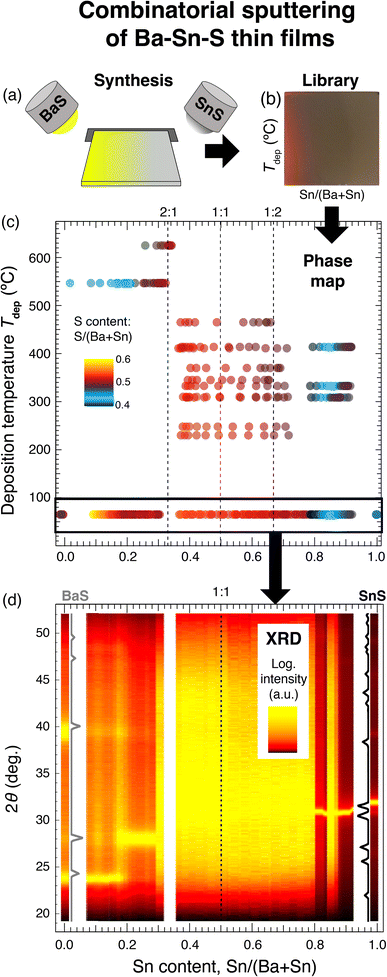
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The substrate heating element temperature was varied between ambient temperature and 600 °C, and deposition temperature Tdep was calibrated as described previously. Each film is measured to be approximately 200–300 nm thick by profilometry, depending on the position within the “combinatorial library”. Fig. 1(b) is a photograph of one of the combinatorial libraries, depicting a semitransparent region on the left (Ba-rich), an opaque region on the right (Sn-rich), and a phase change in the upper left corner (high temperature and Sn-rich).
1. The substrate heating element temperature was varied between ambient temperature and 600 °C, and deposition temperature Tdep was calibrated as described previously. Each film is measured to be approximately 200–300 nm thick by profilometry, depending on the position within the “combinatorial library”. Fig. 1(b) is a photograph of one of the combinatorial libraries, depicting a semitransparent region on the left (Ba-rich), an opaque region on the right (Sn-rich), and a phase change in the upper left corner (high temperature and Sn-rich).
Anneals were performed in an evacuated quartz tube on Ba–Sn–S library rows deposited at ambient temperatures in the composition range of interest, 0.4 < Sn/(Ba + Sn) < 0.6, with anneal temperatures of 400 °C and 500 °C. Anneals with a capping layer of BaS were performed by simply turning off the sputter gun with the SnS target after deposition and growing ∼20 nm of BaS on top of each sample, and then annealing the stack for one hour at 300–600 °C.
After synthesis, the films were measured using mapping style X-ray fluorescence (XRF) on a Fisher XUV-SDD to determine composition and thickness. Structural property mapping was performed with X-ray diffraction (XRD) on a Bruker D8 Discover with a θ–2θ geometry, Cu Kα radiation, and a proportional 2D detector. Measurements were complemented for 11 libraries of interest at beam line 1–5 at the Stanford Synchrotron Radiation Lightsource (SSRL) with Wide Angle X-ray Scattering (WAXS). 2D scattering was collected with a Rayonix 165 CCD Camera at grazing incidence at an incident energy of 12.7 keV. Analysis was conducted using the customized COMBIgor software package.23 The files were automatically harvested using Research Data Infrastructure at NREL,24 and the resulting data is available through High Throughput Experimental Materials Database (HTEM DB).25
Computational methods
Density functional theory (DFT) calculations were performed using the projector augmented wave (PAW) method26,27 as implemented in the Vienna Ab Initio Simulation Package (VASP),28,29 first within the Perdew–Burke–Enzerhof (PBE) Generalized Gradient Approximation (GGA) formulation of the exchange–correlation functional.30 Cutoff, convergence, and correction criteria are described elsewhere.18,31 Thermodynamic stability is assessed using the proxy convex hull construction such that materials in which energy above convex hull (Ehull) is zero are considered thermodynamically stable. Temperature-dependent phase diagrams were assembled with Materials Project data using methodology from Bartel et al.'s machine-learned vibrational energy estimates.32 Materials Project data is from database version v2021.11.10 which uses the GGA(+U) level of theory. Optical absorption spectra were computed with GGA calculations using the independent-particle approximation (IPA), in which frequency-dependent dielectric matrix elements are calculated following the formalism of Gajdoš et al.33 Direct allowed band gaps (EdaG), representing the energy at which band-to-band transitions become significant, were computed from the optical transition matrix elements following the literature approach.34 The screened hybrid functional HSE06 (ref. 35) was used as a scissor shift to correct gaps, direct allowed band gaps, and absorption spectra (with the exception of BaSnS2 and Pnma SnS, in which corrections are from PBE-sol and the absorption coefficients are from the MPContribs dataset from Fabini et al.34). Electron and hole effective masses were computed using the BoltzTraP2 package.36Results
Mapping experimental combinatorial phase space
First, we report composition trends of the 20 thin film Ba–Sn–S sample libraries and resulting 880 data points, as measured with XRF. Fig. 1(c) plots cation composition Sn/(Ba + Sn) on the x-axis, calibrated Tdep on the y-axis, and anion-to-cation ratio S/(Ba + Sn) as the color scale. At ambient temperatures (the lowest Tdep values), films are grown across the full cation phase space. At 200 °C < Tdep < ∼475 °C, cation composition spans the targeted range for BaSnS2 and Sn-rich compositions. At Tdep, values higher than 500 °C, compositions are all Ba-rich; this is because at these high temperatures, Sn is ejected from the growing crystalline film, likely due to its lower vapor pressure than Ba.37 The region of Sn/(Ba + Sn) = 0.5 (i.e. Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn = “1
Sn = “1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1”), the composition at which the thermodynamically stable phase of BaSnS2 would be expected to crystallize, is highlighted with a dashed line.
1”), the composition at which the thermodynamically stable phase of BaSnS2 would be expected to crystallize, is highlighted with a dashed line.
Anion-to-cation ratio S/(Ba + Sn) ranges from 0.4 to 0.6, and analysis of S content yields insights into phase stability. First, we observe trends in the “1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1” region. Stoichiometric crystals of BaSnS2 would have a anion-to-cation ratio of 0.5, but we observe that across all temperatures the “1
1” region. Stoichiometric crystals of BaSnS2 would have a anion-to-cation ratio of 0.5, but we observe that across all temperatures the “1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1” cation region is S-rich with respect to this stoichiometric value. Second, we observe trends in the ambient temperature samples, the boxed region in Fig. 1(c). Some samples are near stoichiometric with S/(Ba + Sn) ≈ 0.5, while others are S-poor. As Sn is incorporated into the samples, S content jumps up around Sn/(Ba + Sn) = 0.1, decreases somewhat between 0.1 < Sn/(Ba + Sn) < 0.3, remains S-rich between 0.35 < Sn/(Ba + Sn) < 0.65, then decreases slightly between 0.65 < Sn/(Ba + Sn) < 0.75. At Sn/(Ba + Sn) = 0.8 samples abruptly become S-poor, and remain S-poor until Sn is the only cation (Sn–S). Lastly, at elevated temperatures it is observed that S content deviates more dramatically from stoichiometric expectations. Both the high temperature Ba-rich regions and Sn-rich regions are S-poor. These trends indicate that sample composition in our films does not perfectly trend along the phase diagram tielines between binary endpoints BaS and SnS.
1” cation region is S-rich with respect to this stoichiometric value. Second, we observe trends in the ambient temperature samples, the boxed region in Fig. 1(c). Some samples are near stoichiometric with S/(Ba + Sn) ≈ 0.5, while others are S-poor. As Sn is incorporated into the samples, S content jumps up around Sn/(Ba + Sn) = 0.1, decreases somewhat between 0.1 < Sn/(Ba + Sn) < 0.3, remains S-rich between 0.35 < Sn/(Ba + Sn) < 0.65, then decreases slightly between 0.65 < Sn/(Ba + Sn) < 0.75. At Sn/(Ba + Sn) = 0.8 samples abruptly become S-poor, and remain S-poor until Sn is the only cation (Sn–S). Lastly, at elevated temperatures it is observed that S content deviates more dramatically from stoichiometric expectations. Both the high temperature Ba-rich regions and Sn-rich regions are S-poor. These trends indicate that sample composition in our films does not perfectly trend along the phase diagram tielines between binary endpoints BaS and SnS.
To assess the structural variety within ambient temperature samples, a corresponding heat map of XRD patterns is plotted in Fig. 1(d). This diagram indicates a wide amorphous region of phase space in the middle of the BaS–SnS compositions. This region spans from approximately 0.28 < Sn/(Ba + Sn) < 0.8, though amorphous samples are also observed at Sn/(Ba + Sn) ≈ 0.85. On the Ba-rich side of this amorphous region, XRD reflections suggest a rocksalt (RS) BaS phase (grey), with a shift to (100) oriented RS at approximately Sn/(Ba + Sn) = 0.18. No significant peak shift is observed, which could indicate that samples in this region are composites of RS BaS and an amorphous SnSy or Ba–Sn–S phase, rather than solid solutions. On the Sn-rich side, experimental XRD patterns correspond to a layered structure of SnS, although it is unclear which phase of SnS has formed (Pnma is plotted in black). As Sn content S/(Ba + Sn) decreases from 1.0 to 0.9, a strong peak shift to lower values of 2θ is observed, likely resulting from either a phase change, change in texturing, or solid solution. This shift is reasonable since Ba cations are larger than Sn cations (ionic radii of Ba2+ and Sn2+ are 135 and 118 pm, respectively). Indeed, a Ba1−xSnxS solid solution should induce an XRD peak shift in the same direction as is observed, however the shift could also be related to the changing S content. In summary, at ambient temperature crystal formation is prohibited in the middle of composition space; therefore, higher temperature growths have been explored.
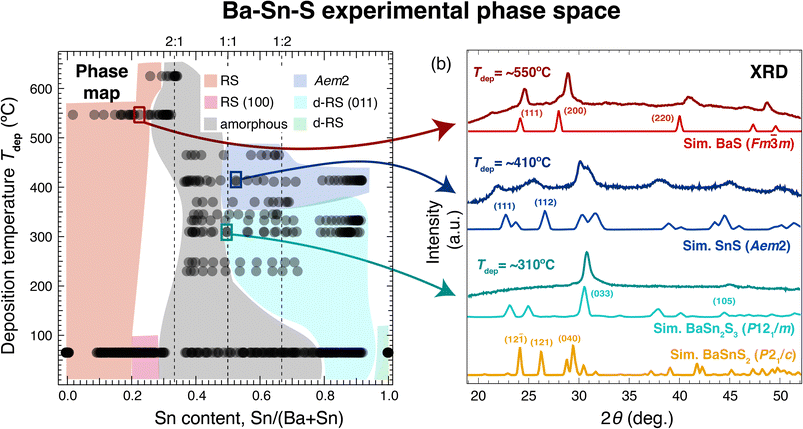
Our combinatorial survey results at elevated deposition temperatures (Tdep) are summarized in Fig. 2, in which crystal structures across this phase space are identified using XRD measurements (b) and approximate regions of the phase space are labeled accordingly (a). The data at ∼60 °C corresponds to the ambient temperature samples shown in Fig. 1. The light red region in the Ba-rich side of the phase map corresponds to RS (derived from Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m BaS), as shown in the first set of diffraction patterns (dark red) in Fig. 2(b). Unidentified peaks or peak splitting may arise from a secondary phase present in some of these films (possibly Ba7Sn5S15; see next section), or slight distortions or disordering in the RS structure. As Sn content is increased in these films, an amorphous region emerges for Tdep > 200 °C for 0.3 ≲ Sn/(Ba + Sn) < 0.5; this is narrower than the amorphous region for ambient temperature samples.
m BaS), as shown in the first set of diffraction patterns (dark red) in Fig. 2(b). Unidentified peaks or peak splitting may arise from a secondary phase present in some of these films (possibly Ba7Sn5S15; see next section), or slight distortions or disordering in the RS structure. As Sn content is increased in these films, an amorphous region emerges for Tdep > 200 °C for 0.3 ≲ Sn/(Ba + Sn) < 0.5; this is narrower than the amorphous region for ambient temperature samples.
In Sn-rich samples, no phases crystallized at Tdep > 500 °C for Sn/(Ba + Sn) ≈ 0.5, however two different phases crystallize in this region at lower temperatures. First, samples in the range 350 °C ≲ Tdep ≲ 465 °C yield XRD patterns represented by the dark blue trace (Tdep = ∼410 °C) in Fig. 2(b). The closest sensible XRD standard we could match to this phase is the Aem2 SnS structure. These reflections are spaced regularly in a manner that resemble superlattice peaks, indicative of a layered structure, though more structural analysis should be performed to confirm this. As Sn increases across the films in this region, the Aem2 peaks shift to higher 2θ values, indicative of a solid solution. For example, the dominant 2θ peak is at ∼30.6 deg. for Sn/(Ba + Sn) = 0.5, and shifts monotonically to ∼31.7 deg. when Sn/(Ba + Sn) = 0.8. Second, in samples in the range 200 °C < Tdep < 350 °C, a single strong peak is present at approximately 2θ = 31 deg. (teal trace, Tdep = ∼310 °C), with only a negligible shift as Sn content increases. Our best guess is that these samples are heavily distorted RS structures. The heavily distorted RS BaSn2S3 (P121/m) is simulated in Fig. 2(b) as a representative ordered standard, and is the closest matching XRD standard we could find for this region. BaSn2S3 (P121/m) has been previously reported in the experimental literature13 and is predicted to be thermodynamically stable at 0 K. However, in our experimental samples only the (033) and (105) peaks are observed, which could be due to strong orientation along the (033) direction. Alternatively, crystals in this region may be better simulated using a disordered model such as special quasirandom structures (SQS), or perhaps correspond to another phase that we have been unable to identify. For comparison, the simulated XRD pattern of BaSnS2 (P21/c) is also plotted in gold at the bottom of Fig. 2(b). Each of the crystal structures represented in this plot (as well as BaSnS2 for comparison) are depicted in Fig. 4(a); each consist of related structures derived from the RS structure.
Annealing with a capping layer
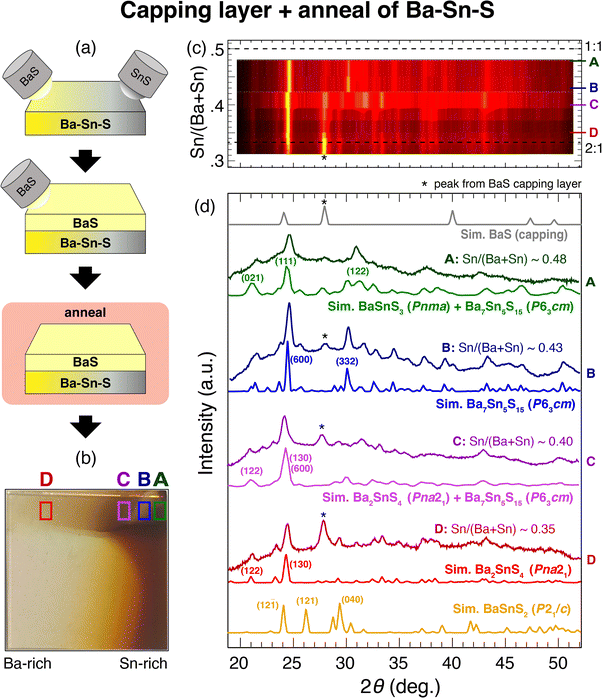
An additional annealing step enables exploration of Ba–Sn–S phase space at a higher temperature than sputtering alone. With 400 °C anneals for one hour, Sn-rich samples crystallize in the layered Aem2 phase again, similarly to as-deposited films at these temperatures, but are still amorphous at Sn/(Ba + Sn) ≈ 0.5. Thickness is reduced in annealed films, indicating either surface evaporation or a phase change to a somewhat denser phase. However, increasing anneal temperature to 500 °C resulted in the evaporation of most of the Sn, and led to Ba-rich phases (possibly Ba8Sn4S15). This observed Sn volatility is likely a result of the low vapor pressure of Sn compared to Ba and S.37 As temperature increases, low vapor pressure should reduce the likelihood of Sn to stick to the film. We did not perform rapid thermal annealing and expect it would also lead to vaporizing Sn, but we encourage follow-up work to explore this and other methods to access phase space.In order to keep Sn incorporated in the lattice while annealing to high temperatures, selected as-depositied Ba–Sn–S thin film libraries have been coated with a capping layer of BaS, as depicted in Fig. 3(a). At 500 °C anneal temperatures with a capping layer, the previously unreachable Ba-rich region in Fig. 2 has been accessed; namely, films crystallize in the region 0.3 < Sn/(Ba + Sn) < 0.5. The opacity of a given sample increases as Sn increases, as shown in Fig. 3(b) going from region “D” to region “A,” with a small semitransparent region emerging at the Sn-rich side of the library (“B”). A heatmap of the XRD reflections for four representative samples in this region is plotted in Fig. 3(c), clearly yielding a crystalline region rather than the amorphous region found in as-deposited samples.
Crystalline regions are identified and compared to standard XRD patterns in Fig. 3(d), and corresponding crystal structures of each standard are depicted in Fig. 4. First, region D (red) corresponds to Ba2SnS4 (Pna21), which has been experimentally synthesized previously and has a Ehull value on the Materials Project of 0.005 eV per atom (the P21/c Ba2SnS4 polymorph is on the thermodynamic hull, but not observed here). The XRF measurement of the Sn/(Ba + Sn) ratio is similar to the expected stoichiometric value, with some tolerance to off-stoichiometry, so this structure identification seems reasonable. We note that Ba2SnS4 lies on more S-rich tieline than BaxSn1−xS (see Fig. 5) such that S/(Ba + Sn) > 1. Region B (blue), which is semitransparent, appears to crystallize as Ba7Sn5S15 (P63cm), an experimental compound similar to Ba8Sn4S15 that is also more S-rich than BaxSn1−xS. Its band gap has been demonstrated experimentally as approximately ∼2.29 eV, which is within the visible regime, and therefore corroborates our observed semitransparency.14 In between B and D, region C appears to be a mixed-phase, likely consisting of Ba2SnS4 (Pna21) and Ba7Sn5S15 (P63cm), and thus a simulated XRD pattern of the two phases is plotted below the measured XRD pattern. Lastly, region A also appears to be a mixed phase of Ba7Sn5S15 (P63cm) and another crystal structure, as it contains peaks not present in B (e.g., at ∼31 deg.). We have plotted a simulated XRD pattern that mixes Ba7Sn5S15 (P63cm) with BaSnS3 (Pnma), which could explain the observed pattern, although it is possible there is another crystal structure here that we have been unable to identify. BaSnS3 is also more absorbing than BaSnS2 and Ba7Sn5S15, with a computed PBE gap of 0.857 eV (compared to 1.996 eV for BaSnS2; see Table 1). For comparison, BaSnS2 (P21/c) is again plotted at the bottom of Fig. 3(d), and it appears that none of the measured data corresponds to this structure. Our hypothesis is that our annealed samples are too S-rich for BaSnS2 to grow; S content would need to be further reduced during growth or post-processing to achieve this predicted thermodynamically stable phase.
| Formula | Sn/(Ba + Sn) | S/(Ba + Sn) | Space group | ID | # of sites | E 0Khull (eV per at.) | E 1000Khull (eV per at.) | E G (eV) | E dG (eV) | Gap method | Grown here? | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a A mixed phase of BaSnS3 with Ba7Sn5S15 may have been synthesized upon anneal; see Fig. 3. b We synthesized a heavily distorted rocksalt; this BaSn2S3 phase has been selected as an ordered representative, but may not have been synthesized. c From Ricci et al. BoltzTraP calculations.41 | |||||||||||||
| BaS | 0 | 1 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
mp-1500 | 2 | 0.000 | 0.000 | 0.42 | 0.80 | 3.08 | 3.25 | HSE | Yes |
| β-Ba2SnS4 | 0.33 | 1.33 | Pna21 | mp-540689 | 56 | 0.005 | 0.000 | 5.88c | 0.93c | 2.31 | 2.31 | PBEsol18,40 | Yes |
| Ba8Sn4S15 | 0.33 | 1.25 | Pca21 | mp-1195594 | 216 | 0.000 | 0.000 | — | — | 2.31 | — | Exp15 | No |
| Ba7Sn5S15 | 0.42 | 1.25 | P63cm | COD-4331670 | 168 | — | — | — | — | 2.29 | — | Exp14 | Yes |
| BaSnS2 | 0.5 | 1 | P21/c | mp-12181 | 16 | 0.000 | 0.040 | 0.96 | 0.90 | 2.50 | 2.55 | HSE | No |
| BaSnS3 | 0.5 | 1.5 | Pnma | mp-1183370 | 20 | 0.016 | 0.035 | 0.75 | 1.25 | 1.67 | 1.92 | HSE | yesa |
| BaSn2S3 | 0.67 | 1 | P121/m | mp-27802 | 36 | 0.000 | 0.091 | 0.54 | 0.64 | 1.88 | 1.88 | HSE | Yesb |
| SnS | 1 | 1 | Pnma | mp-2231 | 8 | 0.000 | 0.147 | 0.20 | 0.53 | 1.30 | 1.59 | HSE | Yes |
| SnS | 1 | 1 | Aem2 | mp-8781 | 4 | 0.046 | 0.000 | 0.19 | 0.19 | 2.07 | 2.07 | HSE | Yes |
The crystal structures observed from annealing are depicted in Fig. 4(b); these consists of more complex structures than in (a) (the three left-most structures with >50 atoms per unit cell). To assess optical properties a few preliminary UV-Vis-NIR measurements were performed, but are not reported here because many of the films decomposed in the presence of oxygen over time, and it was difficult to parse due to absorption from the capping layer. An additional challenge with using an insulating capping layer on these films is that their transport properties cannot be easily measured. It is recommended that follow-up work fabricate contacts with the Ba–Sn–S layer sandwiched between the substrate and the BaS capping layer in order to measure conductivity and mobility. We note that anneals have been performed in a shared space with selenization for CdTe solar cells, and films were exposed to oxygen, so there is a possibility of selenium contamination or oxide formation.
Computed phase diagram
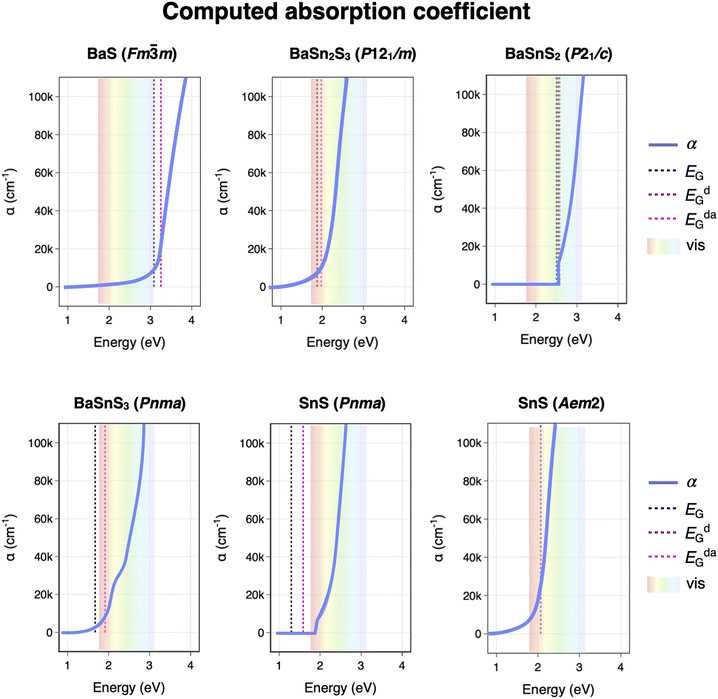
Computed Ba–Sn–S ternary phase diagrams from the Materials Project database are constructed in Fig. 5, with panel (a) depicting the 0 K phase diagram and (b–d) depicting temperature-dependent phase diagrams using the machine-learned SISSO method.32 Green circular markers designate the phase on the convex hull, while shaded diamonds designate “unstable” phases in which formation energies lie above the convex hull. The energy above convex hull (Ehull) at 0 K and 1000 K are both added to Table 1 for guidance. Similar qualitative results are observed with r2SCAN38 and the GGA+U-r2SCAN mixing procedure from Kingsbury et al.,39 as shown in the ESI.† We caution that in the following analysis, thermodynamic temperature should not be compared quantitatively to sputter deposition temperature Tdep; rather, it is a guide to inform qualitative trends in phase stability. | ||
| Fig. 5 Computed ternary phase diagrams for Ba–Sn–S (a) at 0 K and (b–d) as a function of temperature using the high-throughput vibrational energy approximation from Bartel et al., as implemented in the Materials Project.32 Phases of interest are labeled. | ||
Our experimental observations can be contextualized with these calculations. At low temperature, several ternary phases are on the convex hull, including BaSnS2, Ba2SnS4 and Ba2SnS3, as highlighted in (a). We show in the ESI† that increasing the chemical potential of the sulfur reference state does not lead to stabilization of additional S-rich metastable phases. However, as temperature increases using the SISSO descriptor, the phase stability shifts and several of the stable phases at 0 K become metastable. First, the BaSn2S3 (P121/m) phase that we may have observed experimentally appears on the 0 K phase diagram alongside other stable phases, however with the SISSO approximation this phase becomes metastable at elevated temperatures as shown in Fig. 5(b). This could explain the possible observationof this phase or other highly distorted RS phases at lower temperatures in Fig. 2, and its disappearance upon annealing. Similarly, SnS (Pnma) becomes highly metastable at non-zero temperatures (with an Ehull of 0.147 eV at 1000 K) in favor of SnS (Aem2); this corroborates the appearance of the Aem2 phase at deposition temperatures above 300 °C in Fig. 5 (dark blue).
As temperatures increase further in the computed phase diagrams as shown in Fig. 5(c), BaSnS2 is next to leave the convex hull at temperatures greater than ∼600 K. The fact we have not synthesized BaSnS2 could be due to insufficient temperature sampling under appropriate thermodynamic conditions. Below 900 K, Ba2SnS4 (P121/c1) is on the convex hull, though this phase is not observed experimentally. However, at around 900 K the phase that we do observe upon annealing – Ba2SnS4 (Pna21) – overtakes P121/c1 as the most stable polymorph on the hull. Just above 1000 K Ba7Sn5S15, which we observe experimentally upon annealing, becomes destabilized. As temperatures rise, Ba6Sn7S20 leaves the hull next, followed by Ba3Sn2S7, and at temperatures greater than 1400 K only Ba2SnS4 (Pna21) remains on the convex hull. This could explain the predominance of Ba2SnS4 (Pna21) at high annealing temperatures and Ba-rich conditions (see red marker and XRD patterns in Fig. 3). Therefore, since Ba2SnS4 (Pna21) and Ba7Sn5S15 appear at the same temperature under the same anneal, it is likely that the annealing conditions accessed a sweet spot of temperature space corresponding to ∼900–1000 K (∼625–725 °C ) in our calculations: high enough such that the Pna21 phase of Ba2SnS4 was stabilized but low enough such that Ba7Sn5S15 was still accessible.
We show in the ESI† that it is likely the volume-dependent terms lead to temperature instabilities, according to the SISSO framework. We also show in the ESI,† using this approach combined with a Pourbaix methodology, that increased temperature may help stabilize Ba–Sn–S materials in the presence of moisture and air. These plots only account for effects of a machine-learned high-throughput vibrational entropy, rather than first principles computed vibrational entropy, and therefore the trends and temperatures observed should be interpretted as an estimate. In particular, the method used to compute these diagrams has been benchmarked on phases of different composition across a phase diagram, but the authors claim it is not a great descriptor for predicting relative polymorph ordering at a particular composition.32 Additionally, these calculations do not account for configurational entropy or surface-stabilization effects than may come into play in thin film synthesis. However, computed phase diagrams do corroborate some of the phase stability trends of combinatorial experiments, in particular of the annealed samples, and provide insight to a pathway to future stabilization of thin films.
Computed optoelectronic properties
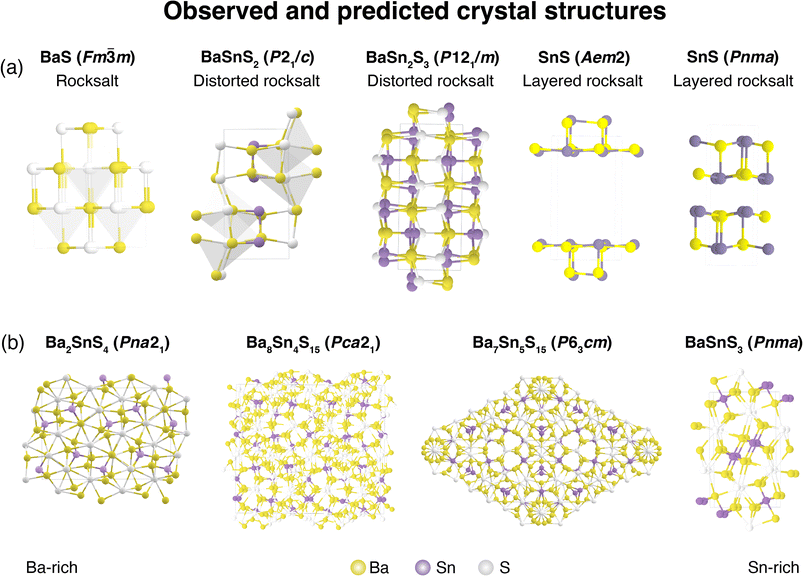
Lastly, we compute optical and electronic properties of representative Ba–Sn–S compounds and summarize properties in Table 1. Compounds are sorted by their fractional Sn cation content, Sn/(Ba + Sn), and their MP identifier (mpid) is reported. Ba7Sn5S15 is not present in the MP database so Ehull values are not reported, but we include the corresponding Crystallography Open Database (COD) identifier.42 Columns E0Khull and E1000Khull denote the energy above convex hull at 0 K and 1000 K as a proxy for stability, as discussed in Fig. 5. Average effective masses and computed band gaps are reported for all compounds except Ba7Sn5S15 and Ba8Sn4S15, since they have unit cells with over 200 atoms (experimental band gaps are included in Table 1 instead14,15).As Sn content increases, both electron effective mass 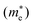 and hole effective mass
and hole effective mass 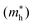 increase between BaS and Ba2SnS4, and then decrease nearly monotonically between Ba2SnS4 and SnS. All computed phases have
increase between BaS and Ba2SnS4, and then decrease nearly monotonically between Ba2SnS4 and SnS. All computed phases have 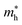 values of approximately 1 or less, notably low for sulfides. Fundamental gap (EG) and direct gap (EdG) are reported in Table 1. EdG decreases from 2.25 eV in BaS to 1.59 eV in SnS (Pnma), but jumps to 2.07 eV in the SnS (Aem2) polymorph. Previous studies have reported BaSnS2 HSE gap of 2.4 eV,43 BaSnS2 experimental gap of 2.4 eV,12 BaSnS3 HSE gap of 2.62 eV;44 each of these are similar to our reported values. To our knowledge, this is the first HSE gap report for BaSn2S3.
values of approximately 1 or less, notably low for sulfides. Fundamental gap (EG) and direct gap (EdG) are reported in Table 1. EdG decreases from 2.25 eV in BaS to 1.59 eV in SnS (Pnma), but jumps to 2.07 eV in the SnS (Aem2) polymorph. Previous studies have reported BaSnS2 HSE gap of 2.4 eV,43 BaSnS2 experimental gap of 2.4 eV,12 BaSnS3 HSE gap of 2.62 eV;44 each of these are similar to our reported values. To our knowledge, this is the first HSE gap report for BaSn2S3.
In Fig. 6, the computed optical absorption spectra is plotted for a representative set of Ba–Sn–S compounds. Rainbow shading corresponds the visible spectrum (“vis.”), and the EG, EdG, and direct allowed gap (EdaG; a proxy for absorption edge, as defined elsewhere34,45) are depicted with dotted lines. Computed absorption coefficient α is plotted as a function of photon energy. As expected, the energy of the absorption edge decreases as Sn concentration increases. It is observed that in BaSnS2 and SnS (Pnma), optical transitions at the direct band gap are weak or forbidden such that the absorption edge is somewhat higher in energy.
Conclusion
In this study, thin films in the Ba–Sn–S phase space have been synthesized using combinatorial sputter deposition, and several of these compounds in the Ba–Sn–S chemical family have been assessed with computational approaches. Experimentally crystallized phases include Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m RS-derived phases in Ba-rich regions, distorted RS (possibly P121/m) and layered (likely Aem2) phases in Sn-rich regions, and amorphous phases throughout. Using a capping layer plus annealing approach, thin films of Ba2SnS4 (Pna21) and Ba7Sn5S15 (P63cm) have been synthesized, as well as possible mixed phases of BaSnS3 (Pnma). Computed temperature-dependent phase diagrams qualitatively support our experimental results, in particular that distorted RS phases such as BaSn2S3 form at lower temperatures and Ba2SnS4 (Pna21) becomes the dominant phase upon annealing. The theoretically-predicted destabilization of BaSnS2 at high temperatures likely explains why BaSnS2 does not form in our experiments, but we expect that reducing S content during growth may enable suitable synthesis condititions to crystallize this phase. The absorption spectra and electronic properties of several experimentally realized phases have been estimated using DFT calculations, resulting in relatively wide (1.67–2.5 eV) band gaps as well as relatively low hole effective masses (0.6–1.3, respectively). This combined experimental and computational study motivates future work on Ba–Sn–S materials to attain single-phase thin films and to evaluate their optical and electronic properties. More generally, by combining experimental and computational methods to investigate emerging materials within a ternary phase space, we hope that this approach can serve as an impetus and a framework for further exploration of new promising multinary material spaces.
m RS-derived phases in Ba-rich regions, distorted RS (possibly P121/m) and layered (likely Aem2) phases in Sn-rich regions, and amorphous phases throughout. Using a capping layer plus annealing approach, thin films of Ba2SnS4 (Pna21) and Ba7Sn5S15 (P63cm) have been synthesized, as well as possible mixed phases of BaSnS3 (Pnma). Computed temperature-dependent phase diagrams qualitatively support our experimental results, in particular that distorted RS phases such as BaSn2S3 form at lower temperatures and Ba2SnS4 (Pna21) becomes the dominant phase upon annealing. The theoretically-predicted destabilization of BaSnS2 at high temperatures likely explains why BaSnS2 does not form in our experiments, but we expect that reducing S content during growth may enable suitable synthesis condititions to crystallize this phase. The absorption spectra and electronic properties of several experimentally realized phases have been estimated using DFT calculations, resulting in relatively wide (1.67–2.5 eV) band gaps as well as relatively low hole effective masses (0.6–1.3, respectively). This combined experimental and computational study motivates future work on Ba–Sn–S materials to attain single-phase thin films and to evaluate their optical and electronic properties. More generally, by combining experimental and computational methods to investigate emerging materials within a ternary phase space, we hope that this approach can serve as an impetus and a framework for further exploration of new promising multinary material spaces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was authored in part at the National Renewable Energy Laboratory (NREL), operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. This material is primarily based upon work performed by the Liquid Sunlight Alliance, a DOE Energy Innovation Hub, supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0021266. This work was also supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC02-05-CH11231 (Materials Project program KC23MP). R. W.-R. acknowledges financial support from the U.C. Berkeley Chancellor's Fellowship, the National Science Foundation (NSF) Graduate Research Fellowship under Grants No. DGE1106400 and DGE175814, and the University of Washington's Clean Energy Institute. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory is supported by DOE's SC, BES under Contract No. DE-AC02-76SF00515. We acknowledge compute resources from National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility. We thank Carolyn Beale for performing ex situ annealing, and Andrea Crovetto for helpful discussion. The views expressed in this article do not necessarily represent the views of the DOE or the U.S. Government.References
- K. Alberi, M. B. Nardelli, A. Zakutayev, L. Mitas, S. Curtarolo, A. Jain, M. Fornari, N. Marzari, I. Takeuchi and M. L. Green, et al. , The 2019 materials by design roadmap, J. Phys. D: Appl. Phys., 2018, 52(1), 013001 CrossRef PubMed.
- J. Rumble, et al., CRC Handbook of Chemistry and Physics, 2017 Search PubMed.
- USGS, Mineral Commodity Summaries, USGS, Reston, VA, USA, vol. 202, p. 2023 Search PubMed.
- European Commission, Study on the Critical Raw Materials for the EU 2023 - Final Report, 2023 Search PubMed.
- O. Madelung, Semiconductors: Data Handbook, Springer Science & Business Media, 2004 Search PubMed.
- S. Yamaoka and B. Okai, Preparations of BaSnS3, SrSnS3 and PbSnS3 at high pressure, Mater. Res. Bull., 1970, 5(10), 789–794 CrossRef CAS.
- J. C. Jumas, M. Ribes and E. Philippo, Radiocrystallographic study on barium dithiostannate BaSn2S7, C. R. Seances Acad. Sci., Ser. C, 1971, 273(20), 1356 CAS.
- R. Greatrex, N. N. Greenwood and M. Ribes, Mossbauer spectra of ternary tin (iv) sulphides in the systems Na2S–SnS2, BaS–SnS2, and PbS–SnS2, J. Chem. Soc., Dalton Trans., 1976, 6, 500–504 RSC.
- K. Susa and H. Steinfink, Ternary sulfide compounds AB2S4: The crystal structures of GePb2S4 and SnBa2S4, J. Solid State Chem., 1971, 3(1), 75–82 CrossRef CAS.
- J.-C. Jumas, E. Philippot, F. Vermot-Gaud-Daniel, M. Ribes and M. Maurin, Etude de la tétracoordination de l’etain dans deux orthothiostannates: Na4SnS4 et Ba2SnS4 (α), J. Solid State Chem., 1975, 14(4), 319–327 CrossRef CAS.
- J. Iglesias and H. Steinfink, A variant of the NaCl structure type: BaSnS2, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29(7), 1480–1483 CrossRef CAS.
- W. D. Gunatilleke, A. F. May, A. R. H. Walker, A. J. Biacchi and G. S. Nolas, Synthesis, crystal structure, and physical properties of BaSnS2, Phys. Status Solidi RRL, 2022, 16(5), 2100624 CrossRef CAS.
- S. Del Bucchia, J. Jumas and M. Maurin, Etude du système SnS–BaS: structure de BaSn2S3, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36(12), 2935–2940 CrossRef.
- Z.-Z. Luo, C.-S. Lin, W.-D. Cheng, H. Zhang, W.-L. Zhang and Z.-Z. He, Syntheses, characterization, and optical properties of ternary Ba-Sn-S system compounds: acentric Ba7Sn5S15, centric BaSn2S5, and centric Ba6Sn7S20, Inorg. Chem., 2013, 52(1), 273–279 CrossRef CAS PubMed.
- Z.-Z. Luo, C.-S. Lin, W.-L. Zhang, H. Zhang, Z.-Z. He and W.-D. Cheng, Ba8Sn4S15: a strong second harmonic generation sulfide with zero-dimensional crystal structure, Chem. Mater., 2014, 26(2), 1093–1099 CrossRef CAS.
- R.-H. Duan, P.-F. Liu, H. Lin, S.-X. Huangfu and L.-M. Wu, Syntheses and characterization of three new sulfides with large band gaps: acentric Ba4Ga4SnS12, centric Ba12Sn4S23 and Ba7Sn3S13, Dalton Trans., 2017, 46(43), 14771–14778 RSC.
- H. Lin, X.-T. Wu and Q.-L. Zhu, Inorganic chalcogenides: From zero-dimensional clusters to three-dimensional frameworks, Adv. Struct. Chem., 2021, 2, 465–530 CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 CrossRef.
- Z. Li, H. Xie, S. Hao, Y. Xia, X. Su, M. G. Kanatzidis, C. Wolverton and X. Tang, Optical phonon dominated heat transport: A first-principles thermal conductivity study of BaSnS2, Phys. Rev. B, 2021, 104(24), 245209 CrossRef CAS.
- Z. Chen, K. Sun, Z. Su, F. Liu, D. Tang, H. Xiao, L. Shi, L. Jiang, X. Hao and Y. Lai, Solution-processed trigonal Cu2BaSnS4 thin-film solar cells, ACS Appl. Energy Mater., 2018, 1(7), 3420–3427 CrossRef CAS.
- D. Shin, T. Zhu, X. Huang, O. Gunawan, V. Blum and D. B. Mitzi, Earth-abundant chalcogenide photovoltaic devices with over 5% efficiency based on a Cu2BaSn(S,Se)4 absorber, Adv. Mater., 2017, 29(24), 1606945 CrossRef PubMed.
- J. Ge, P. Koirala, C. R. Grice, P. J. Roland, Y. Yu, X. Tan, R. J. Ellingson, R. W. Collins and Y. Yan, Oxygenated CdS buffer layers enabling high open-circuit voltages in earth-abundant Cu2BaSnS4 thin-film solar cells, Adv. Energy Mater., 2017, 7(6), 1601803 CrossRef.
- K. R. Talley, S. R. Bauers, C. L. Melamed, M. C. Papac, K. N. Heinselman, I. Khan, D. M. Roberts, V. Jacobson, A. Mis, G. L. Brennecka, J. D. Perkins and A. Zakutayev, COMBIgor: Data Analysis Package for Combinatorial Materials Science, ACS Comb. Sci., 2019, 21(7), 537–547 CrossRef CAS PubMed.
- K. R. Talley, R. White, N. Wunder, M. Eash, M. Schwarting, D. Evenson, J. D. Perkins, W. Tumas, K. Munch, C. Phillips and A. Zakutayev, Research data infrastructure for high-throughput experimental materials science, Patterns, 2021, 2(12), 100373 CrossRef PubMed.
- A. Zakutayev, N. Wunder, M. Schwarting, J. D. Perkins, R. White, K. Munch, W. Tumas and C. Phillips, An open experimental database for exploring inorganic materials, Sci. Data, 2018, 5(1), 1–12 CrossRef PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B, 1994, 50(24), 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59(3), 1758–1775 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B, 1993, 47(1), 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54(16), 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python materials genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- C. J. Bartel, S. L. Millican, A. M. Deml, J. R. Rumptz, W. Tumas, A. W. Weimer, S. Lany, V. Stevanović, C. B. Musgrave and A. M. Holder, Physical descriptor for the gibbs energy of inorganic crystalline solids and temperature-dependent materials chemistry, Nat. Commun., 2018, 9(1), 1–10 CrossRef CAS PubMed.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Linear optical properties in the projector-augmented wave methodology, Phys. Rev. B, 2006, 73(4), 045112 CrossRef.
- D. H. Fabini, M. Koerner and R. Seshadri, Candidate inorganic photovoltaic materials from electronic structure-based optical absorption and charge transport proxies, Chem. Mater., 2019, 31(5), 1561–1574 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened coulomb potential, J. Chem. Phys., 2003, 118(18), 8207–8215 CrossRef CAS.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Boltztrap2, a program for interpolating band structures and calculating semi-classical transport coefficients, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- C. L. Yaws, Handbook of Vapor Pressure: Volume 4: Inorganic Compounds and Elements, Gulf Professional Publishing, vol. 4, 1995 Search PubMed.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and numerically efficient r2SCAN meta-generalized gradient approximation, J. Phys. Chem. Lett., 2020, 11(19), 8208–8215 CrossRef CAS PubMed.
- R. Kingsbury, A. S. Gupta, C. J. Bartel, J. M. Munro, S. Dwaraknath, M. Horton and K. A. Persson, Performance comparison of r2SCAN and SCAN metaGGA density functionals for solid materials via an automated, high-throughput computational workflow, Phys. Rev. Mater., 2022, 6(1), 013801 CrossRef CAS.
- The Materials Project, Materials Data on BaSnS2 by Materials Project, 2020, DOI:10.17188/1188641.
- F. Ricci, W. Chen, U. Aydemir, G. J. Snyder, G.-M. Rignanese, A. Jain and G. Hautier, An ab initio electronic transport database for inorganic materials, Sci. Data, 2017, 4(1), 1–13 Search PubMed.
- S. Gražulis, A. Daškevič, A. Merkys, D. Chateigner, L. Lutterotti, M. Quiros, N. R. Serebryanaya, P. Moeck, R. T. Downs and A. Le Bail, Crystallography open database (COD): an open-access collection of crystal structures and platform for world-wide collaboration, Nucleic Acids Res., 2012, 40(D1), D420–D427 CrossRef PubMed.
- V.-A. Ha, G. Yu, F. Ricci, D. Dahliah, M. J. van Setten, M. Giantomassi, G.-M. Rignanese and G. Hautier, Computationally driven high-throughput identification of cate and Li3Sb as promising candidates for high-mobility p-type transparent conducting materials, Phys. Rev. Mater., 2019, 3(3), 034601 CrossRef.
- Z. Li, H. Xie, Y. Xia, S. Hao, K. Pal, M. G. Kanatzidis, C. Wolverton and X. Tang, Weak-bonding elements lead to high thermoelectric performance in BaSnS3 and SrSnS3: a first-principles study, Chem. Mater., 2022, 34(3), 1289–1301 CrossRef CAS.
- R. Woods-Robinson, Y. Xiong, J. X. Shen, N. Winner, M. K. Horton, M. Asta, A. M. Ganose, G. Hautier and K. A. Persson, Designing transparent conductors using forbidden optical transitions, Matter, 2023, 6(9), 3021–3039 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: S1 – SCAN phase diagrams, S2 – free energy terms from SISSO, S3 – Pourbaix moisture sensitivity, S4 – chemical potential phase diagrams. See DOI: https://doi.org/10.1039/d3ta04431a |
| ‡ Barium ore, barite, has been added to the European Union's critical raw materials list as of 2017.4 |
| This journal is © The Royal Society of Chemistry 2023 |