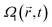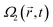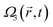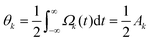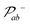Open Access Article
Open Access ArticleTwo-qubit atomic gates: spatio-temporal control of Rydberg interaction
Ignacio R.
Sola
 a,
Vladimir S.
Malinovsky
a,
Vladimir S.
Malinovsky
 b,
Jaewook
Ahn
b,
Jaewook
Ahn
 c,
Seokmin
Shin
c,
Seokmin
Shin
 d and
Bo Y.
Chang
d and
Bo Y.
Chang
 *de
*de
aDepartamento de Quimica Fisica I, Universidad Complutense, 28040 Madrid, Spain
bDEVCOM Army Research Laboratory, 2800 Powder Mill Road, Adelphi, Maryland 20783, USA
cDepartment of Physics, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Republic of Korea
dSchool of Chemistry, Seoul National University, Seoul 08826, Republic of Korea
eResearch Institute of Basic Sciences, Seoul National University, Seoul 08826, Republic of Korea. E-mail: boyoung@snu.ac.kr
First published on 27th January 2023
Abstract
By controlling the temporal and spatial features of light, we propose a novel protocol to prepare two-qubit entangling gates on atoms trapped at close distance, which could potentially speed up the operation of the gate from the sub-micro to the nanosecond scale. The protocol is robust to variations in the pulse areas and the position of the atoms, by virtue of the coherent properties of a dark state, which is used to drive the population through Rydberg states. From the time-domain perspective, the protocol generalizes the one proposed by Jaksch and coworkers [Jaksch et al., Phys. Rev. Lett., 2000, 85, 2208], with three pulses that operate symmetrically in time, but with different pulse areas. From the spatial-domain perspective, it uses structured light. We analyze the map of the gate fidelity, which forms rotated and distorted lattices in the solution space. Finally, we study the effect of an additional qubit to the gate performance and propose generalizations that operate with multi-pulse sequences.
1 Introduction
Due to their excellent optical addressability,1–5 rich many-body physics,6–12 and long decoherence times,13 neutral atoms excited in Rydberg states have been used as vectors for different quantum technologies, including entanglement preparation,14–21 creation of photonic entanglement,22 quantum simulators,23–26 and quantum computation.13,19,27–34A key step involves trapping the atoms at low temperature in magneto-optical traps (MOT). Homogeneous magnetic fields working on the MOT split the degeneracy of the hyperfine ground states of the atoms, allowing to encode and address separately the qubit states by optical fields, through intermediate states or using microwave fields.35–37 Currently, it is possible to create splittings Δ of the order of 10 GHz (ref. 14) that in principle, allow to drive the population from the |0〉 state independently of the |1〉 state in the nanosecond regime.
On the other hand, due to the strong dipole–dipole interaction of Rydberg states,38,39 the energy of a double excitation of Rydberg states |rr〉 is over twice the energy of each atom in a Rydberg state. For weak enough pulses (or close enough atoms) this extra energy is also larger than the Rabi frequency driving the transition, and the |rr〉 state cannot be populated. This defines a maximum distance, called the Rydberg blockade radius, 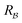 , within which the well-known C-PHASE gate protocol, proposed by Jaksch et al.27, operates. It consists of a three-pulse sequence with a π-pulse acting on the first qubit, followed by a 2π-pulse acting on the second qubit, and a π-pulse again acting on the first qubit. The pulse frequencies are tuned to excite the chosen Rydberg state, |r〉 from the qubit state |0〉 (alternatively, from the |1〉 state) so the other qubit state is decoupled. Then, if the system is initially in the |00〉 state, the first pulse moves the amplitude to i|r0〉, the second does nothing and the third moves the amplitude to −|00〉. If the system starts in |01〉, the first pulse acts as before, driving the amplitude to i|r1〉, the second does nothing and the third induces the transition to −|01〉. When the system is in |10〉 the first pulse does nothing, the second drives the amplitude to −|10〉 and the third does nothing. Finally, the lasers cannot induce any transition from the |11〉 state. In the following, we will refer to this set of operations as the Jaksch protocol (JP).
, within which the well-known C-PHASE gate protocol, proposed by Jaksch et al.27, operates. It consists of a three-pulse sequence with a π-pulse acting on the first qubit, followed by a 2π-pulse acting on the second qubit, and a π-pulse again acting on the first qubit. The pulse frequencies are tuned to excite the chosen Rydberg state, |r〉 from the qubit state |0〉 (alternatively, from the |1〉 state) so the other qubit state is decoupled. Then, if the system is initially in the |00〉 state, the first pulse moves the amplitude to i|r0〉, the second does nothing and the third moves the amplitude to −|00〉. If the system starts in |01〉, the first pulse acts as before, driving the amplitude to i|r1〉, the second does nothing and the third induces the transition to −|01〉. When the system is in |10〉 the first pulse does nothing, the second drives the amplitude to −|10〉 and the third does nothing. Finally, the lasers cannot induce any transition from the |11〉 state. In the following, we will refer to this set of operations as the Jaksch protocol (JP).
There have been several proposals to extend the JP mechanism using more robust adiabatic excitation schemes,40–42 adding alternative processes to the dipole blockade through dark states,43 or addressing multi-qubit gate generalizations.33,34,44,45 Some of these ideas extend well known optical control adiabatic strategies46–49 for dynamics with target states conditioned on the initial state.50–53 One disadvantage of these schemes is the need to work with long pulses, in the microsecond regime. In the JP scheme, this is needed to operate with independent qubits, forcing interatomic distances of the order of ∼5 μm, with Rydberg–Rydberg interactions, 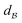 , of a few MHz. The time-scale gap in Δ−1 and
, of a few MHz. The time-scale gap in Δ−1 and 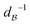 offers an opportunity to speed-up the gates typically by two orders of magnitude, using denser arrays of atoms, therefore boosting the dipole blockade such that
offers an opportunity to speed-up the gates typically by two orders of magnitude, using denser arrays of atoms, therefore boosting the dipole blockade such that 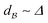 . Although the physics of Rydberg states is rich and several unwanted physical processes may be involved in working in denser media,17,54–60 it is important to estimate if the JP can operate under these conditions or if one can design other robust protocols for the gates with non-independent qubits.
. Although the physics of Rydberg states is rich and several unwanted physical processes may be involved in working in denser media,17,54–60 it is important to estimate if the JP can operate under these conditions or if one can design other robust protocols for the gates with non-independent qubits.
One way to extend the JP to more compact arrangements of atoms is to implement controls not only in time (encoded in the pulse sequence), but also in space (encoded as geometrical parameters) taking into account the strength of the light–matter interaction at the exact qubit locations. In the simplest arrangements, the spatial control might just involve specific focusing of each laser light at different points of the lattice formed by the atoms, not just necessarily at the site that the atom occupies, using various TEM modes of light.61
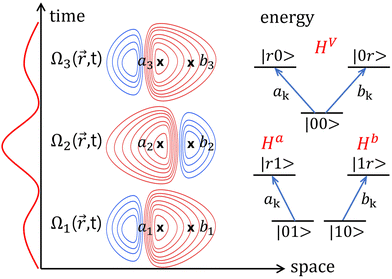
Here we examine the potential advantages of using so-called structured light for the entangling gate implementation. Recent advances in the control of spatial properties of light have been used to create topological electromagnetic effects, as well as almost arbitrary complex geometrical patterns that can be complemented with pulse shaping techniques.5,62,63 For instance, a superposition of TEM00 and TEM01 or TEM10 can be used to create nodes and phase relations between the peak values of the fields at nearby locations. In addition to the space-dependent intensities, such hybrid modes (see the sketch in Fig. 1) may have different phases at different positions of the atoms. The idea is to use a symmetrical protocol where the first pulse and its copy, focusing on the first qubit, are applied before and after a second pulse acts mostly on the second qubit. We prove that a particular relation in the spatial features of the pulses confers special robustness to the gate implementation, giving raise to the Symmetric Orthogonal Protocol or SOP that is proposed in this work. By incorporating the basic features of spatio-temporally controlled pulses as parameters in the Hamiltonian, we design simple models to estimate the fidelities for two- and three-qubit systems, implementing the C-PHASE type gate. The complexity of the system increases with the number of parameters, but what can be seen as a drawback, may be an opportunity to find novel ways to control the system using optimization techniques.
Our study is a first demonstration of quantum control application64–66 to design quantum gates, addressing both the spatial and temporal features of the laser fields. Using simplified models at zero temperature and without noise, we show that the spatio-temporal control of the fields acting locally on each qubit can be used to achieve robust and efficient implementations of fast entangling gates. In fact, this theoretical setup offers many more practical implementations to control gates and prepare entanglement, which will be addressed in the future. The speed of the designed gates justifies some of our assumptions, like neglecting decoherence, dephasing, and most mechanisms that might lead to fidelity losses. However, more detailed studies considering the effect of other states in the system, the presence of Stark shifts, noise in the pulses, and the motion of the atoms, are required to assess the practical implementation of the SOP.
2 Gate performance for non-separated qubits: analysis
The computational basis of a two-qubit in our system is composed of |00〉, |01〉, |10〉 and |11〉 states, and together with the Rydberg ancillary states: |r0〉, |0r〉, |r1〉, |1r〉, form the basis we use to follow the evolution of the system, as we assume that the |rr〉 state cannot be accessed by a strong Rydberg blockade. We assume that the distance between atoms is shorter than the width of the laser beams. As a first approximation to model the local effect of the field on each of the qubits, we define geometrical factors, ak and bk, so the spatially and temporally dependent interaction of the laser k at qubit α (α = a, b) is determined by the Rabi frequencies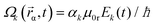 . The geometrical factors can be partially incorporated in the Franck–Condon factor μ0r, so we can assume, without loss of generality, that ak and bk are normalized to unity
. The geometrical factors can be partially incorporated in the Franck–Condon factor μ0r, so we can assume, without loss of generality, that ak and bk are normalized to unity 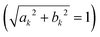 . Using hybrid modes of light (structured light) one can control ak and bk in a wide range of values, including negative factors.
. Using hybrid modes of light (structured light) one can control ak and bk in a wide range of values, including negative factors.
Using a pulse sequence of non-overlapping pulses 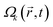 , in resonance between the |0〉 state of the qubit and the chosen Rydberg state |r〉, the Hamiltonian is block-diagonal, HVk ⊕ Hak ⊕ Hbk ⊕ Hd, where
, in resonance between the |0〉 state of the qubit and the chosen Rydberg state |r〉, the Hamiltonian is block-diagonal, HVk ⊕ Hak ⊕ Hbk ⊕ Hd, where 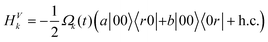 is the Hamiltonian of a 3-level system in V configuration, acting in the subspace of |00〉, |r0〉, |0r〉 states,
is the Hamiltonian of a 3-level system in V configuration, acting in the subspace of |00〉, |r0〉, |0r〉 states, 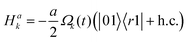 and
and 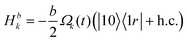 are two-level Hamiltonians acting in the subspace of |01〉, |r1〉 and |10〉, |1r〉, respectively. Finally, Hd = 0 is a zero Hamiltonian acting on the state |11〉, decoupled from any field. The energy diagrams of the subsystems are shown in Fig. 1.
are two-level Hamiltonians acting in the subspace of |01〉, |r1〉 and |10〉, |1r〉, respectively. Finally, Hd = 0 is a zero Hamiltonian acting on the state |11〉, decoupled from any field. The energy diagrams of the subsystems are shown in Fig. 1.
The time-evolution operator of any of these Hamiltonians can be solved analytically through their time-independent dressed states, that have zero non-adiabatic couplings.67–69 For reference, we include here the analytical form of the time-evolution operators at the end of the pulses. For HVk,
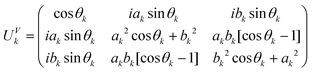 | (1) |
is half the pulse area. Interestingly, HVk supports a dark state, |Φ0k〉 = −bk|r0〉 + ak|0r〉. This is a dressed state of zero energy, which is uncoupled to the ground state, |00〉, that is, |Φ0k〉 cannot decay nor be excited by the field. On the other hand, the time-evolution operator that affects the initial states |01〉 and |10〉, is
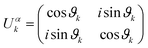 | (2) |
Effect on |00〉
Let us predict the effect of the JP on the partially distinguishable qubits. Excitation from |00〉 with a π-pulse prepares the entangled state |Ψ1〉 = ia1|r0〉 + ib1|0r〉. Because there is population in both qubits and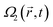 acts on both, the second pulse can induce transitions from |Ψ1〉, breaking the mechanism of the JP. If we want |Ψ1〉 to remain undisturbed, we need |Ψ1〉 to be the dark state of HV2, |Φ02〉, for which a1 = −b2 and b1 = a2. Then, the third pulse can be another copy of the first pulse, transforming |Ψ1〉 back into −|00〉.
acts on both, the second pulse can induce transitions from |Ψ1〉, breaking the mechanism of the JP. If we want |Ψ1〉 to remain undisturbed, we need |Ψ1〉 to be the dark state of HV2, |Φ02〉, for which a1 = −b2 and b1 = a2. Then, the third pulse can be another copy of the first pulse, transforming |Ψ1〉 back into −|00〉.
To generalize the result we define structural vectors, which are normalized two-component vectors formed by the geometrical factors, 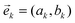 that characterize the spatial properties of the protocol. Success in the gate performance (starting in |00〉) implies that the first diagonal element of the full propagator, UV11 = (UV3UV2UV1)11 = −1. Working out the matrix multiplication we obtain
that characterize the spatial properties of the protocol. Success in the gate performance (starting in |00〉) implies that the first diagonal element of the full propagator, UV11 = (UV3UV2UV1)11 = −1. Working out the matrix multiplication we obtain
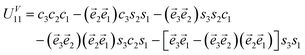 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θk, sk = sin
θk, sk = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θk. This formula is valid in general for a 3-pulse sequence on arrays of N qubits, where
θk. This formula is valid in general for a 3-pulse sequence on arrays of N qubits, where 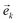 becomes an N-dimensional vector. The condition that |Ψ1〉 = |Φ02〉 (the dark state of HV2) is that
becomes an N-dimensional vector. The condition that |Ψ1〉 = |Φ02〉 (the dark state of HV2) is that 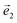 is orthogonal to both
is orthogonal to both 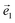 and
and 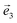 . In symmetric protocols, with
. In symmetric protocols, with 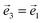 and θ1 = θ3, one obtains the equation that defines the behavior under the SOP,
and θ1 = θ3, one obtains the equation that defines the behavior under the SOP,UV11 = cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 θ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2 − sin2 θ2 − sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 θ1 | (4) |
For 2-qubit systems, the normalization and orthogonality of the structural vectors implies that there is only one free parameter, b ≡ b1 = −a2, that measures the overlap of the field on both qubits and as such, indirectly measures the proximity of the atoms in the trap.
If θ1 = π/2, as in the JP, UV11 = −1 regardless of θ2 and for any value of b. In addition, eqn (4) guarantees remarkable robustness to variations in the pulse areas. Making δθ1′ = π/2 + δ1 = θ3′, and θ2′ = π + δ2, one can easily obtain
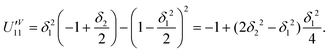 | (5) |
Any error in the pulse areas will only add a quartic error in UV11 (∼δ4).
Effect on |01〉 and |10〉
To evaluate the gate performance when the two-qubit system is initiated in |01〉 or |10〉 we use eqn (2). In a symmetrical sequence, the final state will be (α = a, b)| Uα11 = (Uα3Uα2Uα1)11 = cos(2α1θ1 + α2θ2). | (6) |
In the Jaksch protocol, (θ1 = π/2, θ2 = π), Uα11 = cos([α1 + α2]π) = −1 for independent qubits, as only one component, α1 or α2, exist. But for orthogonal geometrical factors (a1 = b2 ≡ a, b1 = −a2 ≡ b),
Ua11 + Ub11 = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(aπ)cos(bπ) ≈ −2 + b2π2 cos(aπ)cos(bπ) ≈ −2 + b2π2 | (7) |
inducing quadratic deviations in b that lower the fidelity of the gate.
A compromise must be made in the choice of the pulse areas. Because UV11 does not depend on the geometrical factors (nor on A2), the pulse parameters should be adjusted mainly due to their effect on Ua11 and Ub11, which require “rotating” the pulse areas. From eqn (6), for any pulse area in the SOP, we obtain
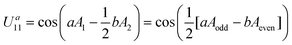 | (8) |
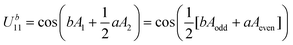 | (9) |
 | (10) |
3 Gate performance for non-separated qubits: numerics
As discussed in the previous section, the orthogonality of the geometrical factors assures that population passage in the V subsystem comprising the |00〉, |r0〉 and |0r〉 states, goes through a dark state. It is so robust that errors in the pulse areas only imply quartic deviations in UV11 regardless of the value of b, that is, of the proximity of the qubits. This is shown in Fig. 2 (solid line), where U11 is computed for the different subsystems as a function of variations in pulse area from the JP, assuming δA = δA1 = δA2/2. On the other hand, Uα11 increases quadratically around the minima (dashed black lines in Fig. 2) and becomes disaligned for |01〉 and |10〉 as b increases. Thus, the desired value of Uα11 = −1 may fall outside of the flat band that characterizes the behavior of UV11 around its minima, disrupting the gate's efficiency.To optimize the gate one needs to change the pulse areas in specific directions. The smallest optimal pulse areas that maximize the fidelity are shown in Fig. 3, for b2 = 0.1. To avoid a distortion in the map of solutions (henceforth fidelity map) we represent the map as a function on the area acting on each qubit, Aodd = A1 + A3 and Aeven = A2, rather than A1 and A2. We obtain a maximum fidelity of 0.96 displaced to larger areas in Aodd and smaller areas in Aeven. The overall pulse area, AT = |Aodd| + |Aeven| = 3.7π, is however smaller than in the JP (4π). On the other hand, the overall robustness of the gate, measured as the area occupied by the maximum in the space of solutions, is practically the same.
 | ||
| Fig. 3 Gate fidelity of the (a) JP and (b) SOP for b2 = 0.1, as a function of the pulse area (in units of π) for the solutions with minimal pulse area. | ||
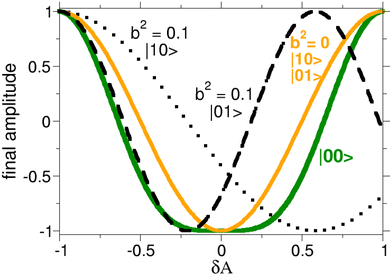
But this is only the minimal pulse area implementation. In the JP, other solutions are possible modulo area 2π in the area of the first and third pulses, A1 and A3, and modulo 4π in A2. Hence, the family of protocols with symmetric pulses (A3 = A1) satisfying Aodd = 2π(1 + 2m) and Aeven = 2π(1 + 2n), where m, n are integers, give perfect fidelity in the absence of noise or perturbations. While in the JP all the different protocols give the same fidelity, this is not the case for the SOP. Exploring solutions for larger pulse areas, better fidelities (F ≥ 0.98) are found, as shown in Fig. 4.
 | ||
| Fig. 4 Fidelity map as a function of the pulse areas (in units of π) for different geometrical factors: (a) b2 = 0, (b) b2 = 0.1, (c) b2 = 0.2, (d) b2 = 0.5. | ||
The fidelity map for the JP is a regular lattice with spacings ΔAodd = ΔAeven = 4π. In the SOP, the lattice is rotated with respect to the JP, with a rotation angle of β = arctan(b/a), in agreement with eqn (10). There are some distortions as b2 increases, regaining a perfect, but different, symmetrical pattern as one reaches b2 = 0.5 (β = π/4). All maps for different b have approximately the same number of maxima, separated by a minimum distance of 4π, so the density of solutions is conserved. However, except for the b = 0 case, not all the fidelities at the maxima reach unity. Typically, larger areas are needed to find better solutions, e.g. Aodd = −6.1π, Aeven = 0.9π for a total area of AT = 7π and a peak fidelity of F = 0.99 for b2 = 0.2. On the other hand, the minimal pulse area at which the first maxima appears decreases with b, and for b2 = 0.5 one observes F = 0.8 using  only, or
only, or 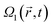 and
and 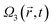 , for a total area of only 2.42π.
, for a total area of only 2.42π.
Instead of plotting how the fidelity map varies as a function of the pulse areas for fixed geometrical factors, we can fix the areas and vary b. This is done in Fig. 5. Only a few possible choices for the pulse areas are shown. The black line shows how the fidelity falls with the JP parameters, A1 = π, A2 = 2π, as b increases. In terms of Aodd and Aeven we classify this protocol with a couple of numbers (Aodd, Aeven) = (2, 2) in units of π. Other implementations of the JP scheme without minimal pulse areas, as (2, 6), decay faster than the (2, 2) because of the larger accumulated pulse area, but surprisingly recover and work perfectly at different values of b. Protocols that do not belong to the JP, such as (8, 6), where Aodd is not of the form Aodd = 2π(1 + 2m), fail at b = 0 but also provide high fidelities at certain values of b.
Although natural multiples of π for the pulse areas usually work relatively well, the ratios between the areas do not need to be natural numbers. The number of solutions is dense. For instance, taking into account the rotation of the optimal pulse areas depending on b, we show how the fidelity changes for the protocol (−6.1, 0.9), which maximizes the fidelity at b2 = 0.2 [see Fig. 4(c)]. More surprisingly, one also finds solutions that do not require the three-pulse strategy, like (14, 0) in which the second pulse does not participate, but nevertheless one achieves high fidelities at low and large b. These protocols are related to approximate solutions of Diophantine equations, where the gate mechanism does not rely on the dark state. They will be explored elsewhere.
The curves in Fig. 5 show that the fidelities decay following a quadratic behavior when the geometrical factors depart from the optimal values, as expected. However, the decay is often slower at larger b (and the effect is even more noticeable if F is plotted against b, instead of b2). Interestingly, the SOP guarantees a slower decay in the presence of the other qubit. We observe this effect by comparing the black line with the black dashed line: in the black dashed line we start in the JP conditions and show what happens when the atoms approach (the qubits are no longer independent) but we do not use structured light. Then 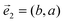 instead of (−b, a). For the solid black line we use the SOP. As long as the displacement of the atoms preserves the orthogonality of the structural vectors, the decay in the fidelity of the SOP is clearly slower.
instead of (−b, a). For the solid black line we use the SOP. As long as the displacement of the atoms preserves the orthogonality of the structural vectors, the decay in the fidelity of the SOP is clearly slower.
4 Three-qubit systems
The protocol proposed in this work implies the use of denser arrays of trapped atoms. It is then important to analyze its robustness in the presence of other qubits not involved in the two-qubit gate. In this section, we check the efficiency of the SOP to prepare the gate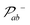 , which is the C-PHASE gate acting on qubits a and b in the presence of qubit c. This gate must operate exactly as with two qubits, regardless of the state of the third qubit, hence the diagonal of the
, which is the C-PHASE gate acting on qubits a and b in the presence of qubit c. This gate must operate exactly as with two qubits, regardless of the state of the third qubit, hence the diagonal of the 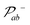 matrix has the signature diagonal {−1, −1, −1, −1, −1, −1, 1, 1} when the basis is ordered as {|000〉, |010〉, |100〉, |001〉, |101〉, |011〉, |110〉, |111〉}. The theoretical treatment follows closely the analysis in section 2, and the main eqn (4) and (6) remain valid by adding a third component, ck, which gives the geometrical factor on qubit c, to the structure vector
matrix has the signature diagonal {−1, −1, −1, −1, −1, −1, 1, 1} when the basis is ordered as {|000〉, |010〉, |100〉, |001〉, |101〉, |011〉, |110〉, |111〉}. The theoretical treatment follows closely the analysis in section 2, and the main eqn (4) and (6) remain valid by adding a third component, ck, which gives the geometrical factor on qubit c, to the structure vector 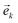 .
.
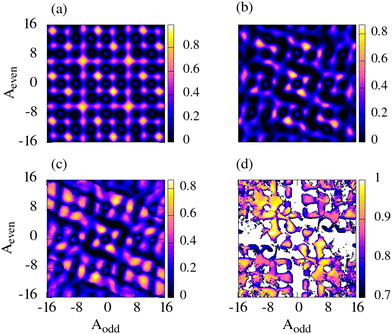
For independent qubits, as in the JP, the result is the same as for two qubits, see Fig. 4(a). However, if the third qubit is close to the other two (ck2 = 0.1 for all pulses), even if the second and first qubits are sufficiently far apart (b2 = 0), the fidelity already decreases, as shown in Fig. 6(a). The lattice of solutions looks the same as in the two-qubit system, but some local maxima can be rather smaller than one, although high fidelity solutions still exist.
On the other hand, if one starts with nearby qubits a and b and implements the SOP, is the presence of qubit c more disrupting? The answer is in Fig. 6(b), where we assumed that ck2 = 0.1 for all pulses, and we applied the SOP to the remaining qubits forcing orthogonality and symmetric conditions.
As in the 2-qubit case, the fidelity map is rotated by approximately the same angle as before, with a slight shift due to ck. But the highest fidelities are now clearly smaller than one (Fmax ∼ 0.85), making the protocol less useful.
What if the ck parameters are optimized? Can one control the position of qubit c (or the spatial profile of the laser located in this qubit) such that the fidelity increases, for fixed values of the other geometrical parameters? Fig. 6(c) shows that the third qubit cannot be used to improve the fidelity of the 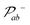 gate. Here we project at every value of (Aodd, Aeven) the best fidelity obtained by optimizing ck, using symmetric pulses [Ω3(t) = Ω1(t)] and forcing orthogonal conditions over the subspace of the first two qubits, as in SOP. The parameters are found using a simplex optimization with linear constraints.70 The optimization does not change the fidelity map drastically, which shows the same angle of rotation, but the picture becomes blurry. By controlling ck (with ck2 ≥ 0.1) the protocols that appear as local maxima become more robust (the peaks become plateaux) and the fidelities at low maxima increase, but the highest fidelities are still F ∼ 0.85.
gate. Here we project at every value of (Aodd, Aeven) the best fidelity obtained by optimizing ck, using symmetric pulses [Ω3(t) = Ω1(t)] and forcing orthogonal conditions over the subspace of the first two qubits, as in SOP. The parameters are found using a simplex optimization with linear constraints.70 The optimization does not change the fidelity map drastically, which shows the same angle of rotation, but the picture becomes blurry. By controlling ck (with ck2 ≥ 0.1) the protocols that appear as local maxima become more robust (the peaks become plateaux) and the fidelities at low maxima increase, but the highest fidelities are still F ∼ 0.85.
Perfect fidelities can be obtained for most pulse areas in the SOP if the geometrical factors of all qubits involved are controlled (forcing a minimal value of αk2 ≥ 0.1 and keeping ck = 0.1 fixed). This is shown in Fig. 6(d), where the minimum fidelity chosen is 0.7 in the map (close to the maximum fidelity in Fig. 6(b)). The patterns of solutions display a regular, non-rotated lattice, similar to that in Fig. 6(a), but with plateaux rather than maxima. They show high fidelities everywhere except for small pulse areas. Even at a minimal pulse area of AT = 4π one can find protocols with F ≥ 0.99. Clearly, there are many protocols that implement efficient and robust 2-qubit gates in systems of 3 not fully distinguishable qubits, but they require finer control. In particular, in optimizing all the geometric parameters we enforce the symmetry (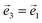 ) but not the orthogonalization, so the working protocols are not necessarily of the SOP type.
) but not the orthogonalization, so the working protocols are not necessarily of the SOP type.
5 Multipulse sequences
The SOP protocol follows a set of rules that can be easily extended to other multipulse sequences, with M number of pulses. We here propose the extended symmetric orthogonal protocol or ESOP, with the following features:(i) In the M-pulse sequence all odd pulses are equal to each other (copies of the same pulse) as well as all even pulses: Ak+2 = Ak, 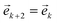 .
.
(ii) Odd and even pulses are orthogonal to each other: 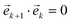 .
.
Under these conditions it can be shown that the number of surviving terms in UV11 [see eqn (1)] is minimal. In particular, for 2-pulse sequences, there is only one term: UV11 = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2
θ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1. For 3 and more pulses, there are always terms involving products of the sines of the areas of even or odd pulses:
θ1. For 3 and more pulses, there are always terms involving products of the sines of the areas of even or odd pulses:
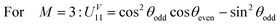 | (11) |
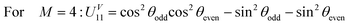 | (12) |
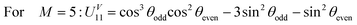 | (13) |
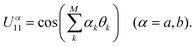 | (14) |
For M = 2 there are no terms depending on sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θodd. In the JP and, to a lesser extent in the SOP with three pulses, this was the main term that forced the pulse areas of the odd pulses to be odd multiples of π, leading to optimal fidelities. The operating mechanism for the gate performance with two pulses is different. Still, it is possible to achieve high fidelities in a smaller set of protocols.
θodd. In the JP and, to a lesser extent in the SOP with three pulses, this was the main term that forced the pulse areas of the odd pulses to be odd multiples of π, leading to optimal fidelities. The operating mechanism for the gate performance with two pulses is different. Still, it is possible to achieve high fidelities in a smaller set of protocols.
Fig. 7(b) shows the same result as in Fig. 4(b), repeated here to facilitate the comparison. Surprisingly, for M = 4 the map is similar to that of M = 2 in spite of UV11 having more terms. The symmetry of the cosine and sine terms on θodd and θeven effectively constrains the possible solutions so the fidelity map is similar to that with M = 2. The same will happen in all sequences with an even number of pulses. Solutions with an odd number of pulses always provide richer fidelity maps, with higher fidelities available with more protocols. Although solutions can be easily generalized to any number of pulses, the highly-constraining nature of the ESOP schemes makes these protocols probably unnecessary, as they do not improve the results of the SOP. This might not be the case, however, when the effects of noise are taken into account. Intensity fluctuations that are proportional to the peak intensity of the lasers will affect more strongly those protocols that use stronger fields, that is, with larger pulse areas. The effect will be dominated by the pulse with a larger area in the sequence, rather than by the sum of all pulse areas. It is possible to find optimal protocols with 5-pulses that distribute the pulse area among all the fields, so that the peak intensities in each field are smaller than in a similar protocol with 3-pulses. Obviously, if the parameters are unconstrained and full optimization is performed to find the solutions, then having more pulses and more parameters will clearly provide more high-fidelity protocols, as will be shown in subsequent studies.
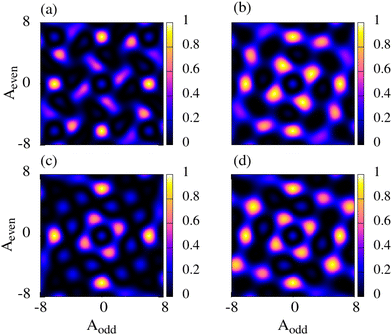 | ||
| Fig. 7 Fidelity map for M-pulse sequence extensions of the SOP with (a) M = 2, (b) M = 3, (c) M = 4, (d) M = 5. We fixed b2 = 0.1 in all cases. | ||
6 Summary and discussion
We have studied the performance of a two-qubit gate in a denser array of trapped atoms under perfect conditions (zero temperature, no external noise) in the regime of strong Rydberg blockade. Extending the well-known Jaksch protocol (JP), we have proposed a novel implementation, called the symmetric orthogonal protocol (SOP), by controlling both the pulse sequence and the spatial properties of the fields, using structured light. The Hamiltonian of the light–atomic system was modeled using geometrical factors, that measure the amplitudes of the fields at the location of the qubits, allowing to obtain analytical formulae for the propagators.From the time-domain perspective, the scheme generalizes the JP with three pulses that operate symmetrically in time, but with different pulse areas. From the spatial-domain perspective, the scheme uses hybrid modes of light. The geometrical factors form orthogonal vectors in the SOP, which allow to decouple the effect of odd and even pulses in the sequence, using a coherent dark state that drives the population through the Rydberg states. The SOP protocol is as robust as the JP to variations in the pulse areas, and more robust to changes in the position of the atoms along certain directions. Implementations with maximal fidelity form a lattice of solutions in the space of the pulse areas, which is rotated with respect to the lattice of solutions in the JP.
We have analyzed the effect of adding a third atom in the proximity of the two-qubit system. The fidelity in the SOP decays more rapidly than in the JP. High-fidelity solutions could not be found by just controlling the position of the third atom, but rather the geometrical factors at the first two-qubits must be optimized for every choice of pulse area. Finally, we have proposed natural generalizations of the SOP to multipulse sequences, showing that sequences with an odd number of pulses form richer lattices with a denser number of solutions than sequences with an even number of pulses.
The SOP shows great promise for possible implementation of fast two-qubit gates. Working in the strong dipole blockade regime 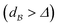 one can in principle accelerate the gate by a factor of 200. However, high fidelities are achieved in the SOP using larger pulse areas than in the JP, typically by a factor of 2 to 10. Hence, gates with comparable or slightly worse fidelity and equal robustness could be in principle prepared in durations of the order 20 to 100 times shorter, moving the scale from the microsecond to the nanosecond regime.
one can in principle accelerate the gate by a factor of 200. However, high fidelities are achieved in the SOP using larger pulse areas than in the JP, typically by a factor of 2 to 10. Hence, gates with comparable or slightly worse fidelity and equal robustness could be in principle prepared in durations of the order 20 to 100 times shorter, moving the scale from the microsecond to the nanosecond regime.
From the physical point of view, the SOP operates as the JP, so one can expect a similar sensitivity to decoherence and noise. However, because the atoms are much closer, the dipole blockade is much larger and the gate time is much shorter, the effect of the thermal motion of the atoms, Rydberg–Rydberg couplings or spontaneous emission, is almost negligible. Only fluctuations in the field intensities (hence pulse areas) as well as in the position of the atoms, leading to changes in the geometrical factors, have some impact on the fidelities. Preliminary estimates of these effects show about 1% reduction of the peak fidelities working at ∼25 μK temperature. However, further comprehensive studies are needed to properly quantify the effect of noise. Equally important will be the assessment of current limitations (time durations, spatial resolution) in using structured light specific to the proposed design. Hybrid modes of light may find many applications in quantum technologies, beyond the present proposal. On the other hand, full optimization of both the pulse areas and the geometrical factors will probably allow refinements in the implementation, the surface of which has only been explored in the present contribution.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Quantum Computing Technology Development Program (NRF-2020M3E4A1079793) and the National Creative Research Initiative Grant (NRF- 2014R1A3A2030423). IRS also thanks the BK21 program (Global Visiting Fellow) for the stay during which this project started and for support from MINECO CTQ2015-65033-P and MINECO PID2021-122796NB-I00. SS acknowledges support from the Center for Electron Transfer funded by the Korea government (MSIT) (NRF-2021R1A5A1030054).References
- Y. Mei, Y. Li, H. Nguyen, P. R. Berman and A. Kuzmich, Phys. Rev. Lett., 2022, 128, 123601 CrossRef CAS PubMed.
- Y. O. Dudin and A. Kuzmich, Science, 2012, 336, 887–889 CrossRef CAS PubMed.
- C. S. Adams, J. D. Pritchard and J. P. Shaffer, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 012002 CrossRef CAS.
- J. D. Pritchard, D. Maxwell, A. Gauguet, K. J. Weatherill, M. P. A. Jones and C. S. Adams, Phys. Rev. Lett., 2010, 105, 193603 CrossRef CAS PubMed.
- Y. Chew, T. Tomita, T. P. Mahesh, S. Sugawa, S. de Léséleuc and K. Ohmori, Nat. Photonics, 2022, 16, 724–729 CrossRef CAS.
- E. Brion, K. Mølmer and M. Saffman, Phys. Rev. Lett., 2007, 99, 260501 CrossRef CAS PubMed.
- T. Pohl, E. Demler and M. D. Lukin, Phys. Rev. Lett., 2010, 104, 043002 CrossRef CAS PubMed.
- M. D. Lukin, M. Fleischhauer, R. Cote, L. M. Duan, D. Jaksch, J. I. Cirac and P. Zoller, Phys. Rev. Lett., 2001, 87, 037901 CrossRef CAS PubMed.
- K. M. Maller, M. T. Lichtman, T. Xia, Y. Sun, M. J. Piotrowicz, A. W. Carr, L. Isenhower and M. Saffman, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 022336 CrossRef.
- Y. Zeng, P. Xu, X. He, Y. Liu, M. Liu, J. Wang, D. J. Papoular, G. V. Shlyapnikov and M. Zhan, Phys. Rev. Lett., 2017, 119, 160502 CrossRef PubMed.
- H. Levine, A. Keesling, A. Omran, H. Bernien, S. Schwartz, A. S. Zibrov, M. Endres, M. Greiner, V. Vuletić and M. D. Lukin, Phys. Rev. Lett., 2018, 121, 123603 CrossRef CAS PubMed.
- E. Urban, T. A. Johnson, T. Henage, L. Isenhower, D. D. Yavuz, T. G. Walker and M. Saffman, Nat. Phys., 2009, 5, 110–114 Search PubMed.
- M. Saffman, T. G. Walker and K. Mølmer, Rev. Mod. Phys., 2010, 82, 2313–2363 CrossRef CAS.
- T. Wilk, A. Gaëtan, C. Evellin, J. Wolters, Y. Miroshnychenko, P. Grangier and A. Browaeys, Phys. Rev. Lett., 2010, 104, 010502 CrossRef CAS PubMed.
- X. L. Zhang, L. Isenhower, A. T. Gill, T. G. Walker and M. Saffman, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 030306 CrossRef.
- T. G. Walker and M. Saffman, Advances in Atomic, Molecular, and Optical Physics, Academic Press, 2012, vol. 61, pp. 81–115 Search PubMed.
- A. Gaëtan, Y. Miroshnychenko, T. Wilk, A. Chotia, M. Viteau, D. Comparat, P. Pillet, A. Browaeys and P. Grangier, Nat. Phys., 2009, 5, 115–118 Search PubMed.
- C. J. Picken, R. Legaie, K. McDonnell and J. D. Pritchard, Quantum Sci. Technol., 2018, 4, 015011 Search PubMed.
- T. M. Graham, Y. Song, J. Scott, C. Poole, L. Phuttitarn, K. Jooya, P. Eichler, X. Jiang, A. Marra, B. Grinkemeyer, M. Kwon, M. Ebert, J. Cherek, M. T. Lichtman, M. Gillette, J. Gilbert, D. Bowman, T. Ballance, C. Campbell, E. D. Dahl, O. Crawford, N. S. Blunt, B. Rogers, T. Noel and M. Saffman, Nature, 2022, 604, 457–462 CrossRef CAS PubMed.
- S. A. Malinovskaya, Opt. Lett., 2017, 42, 314–317 CrossRef CAS PubMed.
- E. Pachniak and S. A. Malinovskaya, Sci. Rep., 2021, 11, 12980 CrossRef CAS PubMed.
- P. Thomas, L. Ruscio, O. Morin and G. Rempe, Nature, 2022, 608, 677–681 CrossRef CAS PubMed.
- H. Weimer, M. Müller, I. Lesanovsky, P. Zoller and H. P. Büchler, Nat. Phys., 2010, 6, 382–388 Search PubMed.
- H. Bernien, S. Schwartz, A. Keesling, H. Levine, A. Omran, H. Pichler, S. Choi, A. S. Zibrov, M. Endres, M. Greiner, V. Vuletić and M. D. Lukin, Nature, 2017, 551, 579–584 CrossRef CAS PubMed.
- A. Keesling, A. Omran, H. Levine, H. Bernien, H. Pichler, S. Choi, R. Samajdar, S. Schwartz, P. Silvi, S. Sachdev, P. Zoller, M. Endres, M. Greiner, V. Vuletić and M. D. Lukin, Nature, 2019, 568, 207–211 CrossRef CAS PubMed.
- H. Kim, Y. Park, K. Kim, H.-S. Sim and J. Ahn, Phys. Rev. Lett., 2018, 120, 180502 CrossRef CAS PubMed.
- D. Jaksch, J. I. Cirac, P. Zoller, S. L. Rolston, R. Côté and M. D. Lukin, Phys. Rev. Lett., 2000, 85, 2208–2211 CrossRef CAS PubMed.
- L. Isenhower, M. Saffman and K. Mølmer, Quantum Inf. Process., 2011, 10, 755 CrossRef CAS.
- V. Parigi, E. Bimbard, J. Stanojevic, A. J. Hilliard, F. Nogrette, R. Tualle-Brouri, A. Ourjoumtsev and P. Grangier, Phys. Rev. Lett., 2012, 109, 233602 CrossRef PubMed.
- K. Mølmer, L. Isenhower and M. Saffman, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 184016 CrossRef.
- M. Müller, I. Lesanovsky, H. Weimer, H. P. Büchler and P. Zoller, Phys. Rev. Lett., 2009, 102, 170502 CrossRef PubMed.
- X.-F. Shi, Phys. Rev. Appl., 2018, 9, 051001 CrossRef CAS.
- M. Khazali and K. Mølmer, Phys. Rev. X, 2020, 10, 021054 CAS.
- J.-L. Wu, Y. Wang, J.-X. Han, Y. Jiang, J. Song, Y. Xia, S.-L. Su and W. Li, Phys. Rev. Appl., 2021, 16, 064031 CrossRef CAS.
- S. Chu, L. Hollberg, J. E. Bjorkholm, A. Cable and A. Ashkin, Phys. Rev. Lett., 1985, 55, 48–51 CrossRef CAS PubMed.
- E. L. Raab, M. Prentiss, A. Cable, S. Chu and D. E. Pritchard, Phys. Rev. Lett., 1987, 59, 2631–2634 CrossRef CAS PubMed.
- K. E. Gibble, S. Kasapi and S. Chu, Opt. Lett., 1992, 17, 526–528 CrossRef CAS PubMed.
- N. Šibalić and C. S. Adams, Rydberg Physics, IOP Publishing, 2018 Search PubMed.
- T. F. Gallagher, Rydberg Atoms, Cambridge University Press, 1994 Search PubMed.
- M. H. Goerz, E. J. Halperin, J. M. Aytac, C. P. Koch and K. B. Whaley, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 032329 CrossRef.
- K. Bergmann, H. Theuer and B. W. Shore, Rev. Mod. Phys., 1998, 70, 1003–1025 CrossRef CAS.
- N. V. Vitanov, T. Halfmann, B. W. Shore and K. Bergmann, Annu. Rev. Phys. Chem., 2001, 52, 763–809 CrossRef CAS PubMed.
- D. Petrosyan, F. Motzoi, M. Saffman and K. Mølmer, Phys. Rev. A, 2017, 96, 042306 CrossRef.
- T. M. Graham, M. Kwon, B. Grinkemeyer, Z. Marra, X. Jiang, M. T. Lichtman, Y. Sun, M. Ebert and M. Saffman, Phys. Rev. Lett., 2019, 123, 230501 CrossRef CAS PubMed.
- H. Levine, A. Keesling, G. Semeghini, A. Omran, T. T. Wang, S. Ebadi, H. Bernien, M. Greiner, V. Vuletić, H. Pichler and M. D. Lukin, Phys. Rev. Lett., 2019, 123, 170503 CrossRef CAS PubMed.
- V. S. Malinovsky, I. R. Sola and J. Vala, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 032301 CrossRef.
- V. S. Malinovsky and I. R. Sola, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 042304 CrossRef.
- V. S. Malinovsky and I. R. Sola, Phys. Rev. Lett., 2004, 93, 190502 CrossRef PubMed.
- V. S. Malinovsky and I. R. Sola, Phys. Rev. Lett., 2006, 96, 050502 CrossRef PubMed.
- J. P. Palao and R. Kosloff, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 68, 062308 CrossRef.
- M. H. Goerz, D. M. Reich and C. P. Koch, New J. Phys., 2014, 16, 055012 CrossRef.
- T. Caneva, T. Calarco and S. Montangero, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 022326 CrossRef.
- M. H. Goerz, T. Calarco and C. P. Koch, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 154011 CrossRef.
- L. S. Theis, F. Motzoi, F. K. Wilhelm and M. Saffman, Phys. Rev. A, 2016, 94, 032306 CrossRef.
- D. Comparat and P. Pillet, J. Opt. Soc. Am. B, 2010, 27, A208–A232 CrossRef CAS.
- D. Tong, S. M. Farooqi, J. Stanojevic, S. Krishnan, Y. P. Zhang, R. Côté, E. E. Eyler and P. L. Gould, Phys. Rev. Lett., 2004, 93, 063001 CrossRef CAS PubMed.
- T. G. Walker and M. Saffman, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 032723 CrossRef.
- T. Pohl and P. R. Berman, Phys. Rev. Lett., 2009, 102, 013004 CrossRef CAS PubMed.
- S. T. Rittenhouse and H. R. Sadeghpour, Phys. Rev. Lett., 2010, 104, 243002 CrossRef PubMed.
- J. P. Shaffer, S. T. Rittenhouse and H. R. Sadeghpour, Nat. Commun., 2018, 9, 1965 CrossRef CAS PubMed.
- M. V. R. K. Murty, Appl. Opt., 1964, 3, 1192–1194 CrossRef.
- A. Forbes, M. de Oliveira and M. R. Dennis, Nat. Photonics, 2021, 15, 253–262 CrossRef CAS.
- H. Rubinsztein-Dunlop, A. Forbes, M. V. Berry, M. R. Dennis, D. L. Andrews, M. Mansuripur, C. Denz, C. Alpmann, P. Banzer, T. Bauer, E. Karimi, L. Marrucci, M. Padgett, M. Ritsch-Marte, N. M. Litchinitser, N. P. Bigelow, C. Rosales-Guzmán, A. Belmonte, J. P. Torres, T. W. Neely, M. Baker, R. Gordon, A. B. Stilgoe, J. Romero, A. G. White, R. Fickler, A. E. Willner, G. Xie, B. McMorran and A. M. Weiner, J. Opt., 2017, 19, 013001 CrossRef.
- S. Rice and M. Zhao, Optical Control of Molecular Dynamics, John Wiley & Sons, Ltd, 2000 Search PubMed.
- M. Shapiro and P. Brummer, Quantum Control of Molecular Processes, John Wiley & Sons, Ltd, 2011 Search PubMed.
- B. Y. Chang, I. R. Sola and S. Shin, Int. J. Quantum Chem., 2016, 116, 608–621 CrossRef CAS.
- B. W. Shore, Manipulating Quantum Structures Using Laser Pulses, Cambridge University Press, 2011 Search PubMed.
- P. R. Berman and V. S. Malinovsky, Principles of Laser Spectroscopy and Quantum Optics, Princeton University Press, 2011 Search PubMed.
- I. R. Sola, B. Y. Chang, S. A. Malinovskaya and V. S. Malinovsky, Advances In Atomic, Molecular, and Optical Physics, Academic Press, 2018, vol. 67, pp. 151–256 Search PubMed.
- J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |