Structural engineering of electrodes for flexible energy storage devices
Yuchu
Sun
 abcd and
Woon Gie
Chong
abcd and
Woon Gie
Chong
 *a
*a
aSchool of Energy and Chemical Engineering, Xiamen University Malaysia, Selangor Darul Ehsan, Malaysia & College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, P. R. China
bInstitute of New Energy & Low Carbon Technology, Sichuan University, Chengdu 610207, Sichuan, P. R. China
cEnergy Resources Centre of Alternative Energy Materials & Devices, Ministry of Education, Chengdu 610065, Sichuan, P. R. China
dCollege of Materials Science and Engineering, Sichuan University, Chengdu 610065, P. R. China
First published on 6th April 2023
Abstract
The emergence of multifunctional wearable electronics over the past decades has triggered the exploration of flexible energy storage devices. As an important component of flexible batteries, novel electrodes with good flexibility, mechanical stability and high energy density are required to adapt to mechanical deformation while powering devices. Electrodes with sophisticated designed structures are key to achieving novel batteries and supercapacitors with extended lifetimes under long-term deformation exposures. Many different novel structures including serpentine, auxetic and biomimetic are explored to construct electrodes thanks to their excellent mechanical deformability in three dimensions. This paper considers the various design strategies established for fabricating flexible electrodes using novel structural modifications. The current state-of-the-art developments of novel structures made of two-dimensional (2D) planar and three-dimensional (3D) cellular, interconnected architectures for flexible energy storage with different functionalities, are discussed. The key tunable geometrical parameters of structures for achieving high performance are critically assessed, and the challenges and limitations of electrodes facing their practical application are revealed, to offer new insights into future prospects of this field.
1. Introduction
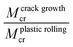
Over the past few decades, there has been a surge of interest in the studies of flexible energy storage with high portability and versatility, which are also light weight, with the expectation to elevate human living standards by integrating electronics into a human body in future electronic markets.1 Keeping pace with the rapid development of the human body conformable electronics – including health monitoring, soft robotics and wearable athletic devices, and flexible and conformable power sources – is considered the driving force to the revolutionary change of the next generation electronic devices.Conventional batteries are generally rigid and bulky which are unfit for flexible device applications. Slurry-casted electrodes suffer delamination during flexing, besides, the mass loading of active materials supported on a metallic current collector can only be improved by increasing the thickness of the electrode which usually leads to high impedance of electrolyte penetration, resulting in degradation of battery performance.2 Due to the aforementioned challenges, it is of great importance to develop a new electrode system with a rational design that satisfies the multifunctional requirements of flexible electronic devices. Significant research work has been directed towards developing functional electrode materials with high flexibility and high conductivity. Extensive studies have shown that electrode structure innovation with novel geometries could positively enhance the mechanical strength of flexible devices. In addition to the stable electrical conduction that facilitates electrochemical reactions, mechanical characteristics such as tensile modulus (E), tensile strain (ε) and energy absorption ability are major contributors to the deformability of flexible energy storage devices.3–5
Two general approaches – intrinsically flexible electrodes and structural flexible electrodes – have demonstrated excellent electrochemical and mechanical properties for flexible electronic applications. To elaborate, intrinsically flexible electrodes are designed to be highly deformable, with their flexibility originating from the molecular interaction between the chemical bond of electrode materials and the incorporated elastomer matrices such as polydimethylsiloxane (PDMS) and ecoflex silicones that form the electrode composites. Despite having high specific capacitance and energy density, intrinsically flexible electrodes fail to demonstrate high rate capability as compared to structural flexible electrodes due to the high content of insulative components.4–8 In contrast, electrodes with novel structural designs are considered as one promising solution with design flexibility and low manufacturing costs. It has been suggested by a series of experimental results, that novel electrodes with modified structures are an effective way to achieve superior mechanical strength and stable electrochemical performances under deformation.9 A variety of novel structures can be easily produced with desired mechanical properties due to the abundant choice of structures and high degree of freedom in geometry customization using 3D printing technologies. To strike a balance between electrical and mechanical durability of electrodes, different planar and three-dimensional structures including serpentine,10,11 biomimetic12–14 and auxetic15,16 structures have been explored as novel electrodes with desired functionalities. Recently, there are have been a few comprehensive review articles reporting the progress on flexible energy devices from the perspective of materials17 and cell configuration design.18 This review is the first attempt to investigate the correlation between the tunable geometrical parameters of novel structures and the corresponding mechanical properties, aiming to bring new insight into the rational electrode design for the fabrication of high-performance energy devices with excellent mechanical flexibility.
Serpentine and wavy structures are found to be highly stretchable among the available structures, while devices requiring high conductivity and electrochemical performance can be achieved by hierarchical, fractal and honeycomb structures. Auxetic structures with negative Poisson's ratio (ν) have demonstrated their superior mechanical properties including advanced impact absorption, enhanced E and stiffness (J). In recent years, one dimensional energy storage devices made from fabric and spring designs are adapted as well due to their exceptional flexibility.19–23 Considering the distinctive features of each structure listed above, it is crucial to investigate current state-of-the-art progress in novel structural designs, which includes selection criteria, geometrical parameters and various applications of these structures in energy storage. In particular, the geometrical parameters employed to create ultra-strong microstructures by tuning the length (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), joining angle (θ) and arc radius (R) of each particular structure are elucidated. For more detailed analysis, several parameters are assembled into dimensionless terms to further clarify the relation between these parameters and their respective mechanical properties. Emerging applications of novel structured electrodes were highlighted with reference to successful examples. Finally, future perspectives of novel structured electrode designs toward practical wearable applications are delineated.
), joining angle (θ) and arc radius (R) of each particular structure are elucidated. For more detailed analysis, several parameters are assembled into dimensionless terms to further clarify the relation between these parameters and their respective mechanical properties. Emerging applications of novel structured electrodes were highlighted with reference to successful examples. Finally, future perspectives of novel structured electrode designs toward practical wearable applications are delineated.
2. Classification of novel structures
Novel structures are classified into three main categories, which are wavy, auxetic and biomimetic structures, as shown in Fig. 1a–f. The classification of these structures is based on their functionalities, with wavy structures generally providing superior stretchability, while auxetic and biomimetic structures demonstrate more diverse distinctive mechanical properties which will be mentioned in Section 3. Wavy structures, as the name suggests, possess numbers of connected curves that account for the superior elastic limit (εk) in the longitudinal direction. Wavy shapes are extensively reported among the novel structures in the fabrication of flexible electrode studies. In comparison, auxetic structures consist of complex geometries which require high precision fabrication methods. However, with a higher level of fabrication complexity, auxetic structures demonstrate superior mechanical properties over serpentine structures with enhanced E and maximum tensile strength.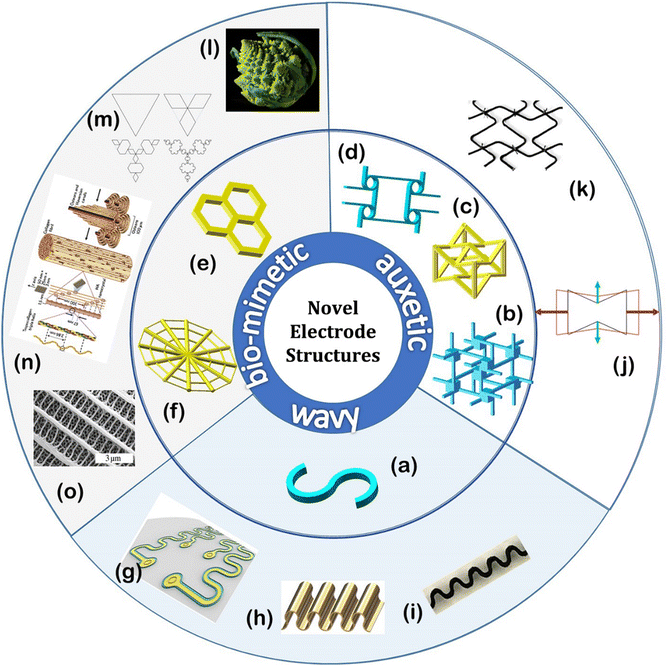 | ||
| Fig. 1 Three general types of novel electrode structure and their corresponding variations. Wavy structure: (a) serpentine structure; auxetic structures: (b) isotropic tetrachiral structure, (c) interlocked re-entrant structure, (d) anisotropic anti-tetrachiral structure. Biomimetic structures: (e) honeycomb structure, (f) spiderweb structure. Outer ring: (g and h) planar wavy structure, (i) linear wavy structure; (j) illustration of deformation of a re-entrant honeycomb structure under tensile strain, (k) photograph of a braided auxetic structure; (l) close-up image of a broccoli – demonstrating a fractal structure, (m) Koch anti-snowflake – fractal geometry, (n) illustration of Osteon in human bones – hierarchical structure, (o) SEM image of Chitin wing – hierarchical structure. Reproduction with permission from ref. 62, Copyright 2019, Elsevier and Reproduction with permission from ref. 24, Copyright 2017, John Wiley & Sons and Reproduction with permission from ref. 30, Copyright 2016, Elsevier and Images courtesy of Jon Sullivan and Images courtesy of Hyacinth and Reproduction with permission from ref. 41, Copyright 2015, the Nature Publishing Group and Images courtesy of Michael Thiel, Karlsruhe Institute of Technology. | ||
Biomimetic design is another emerging method inspired by nature, and has been used to produce various interesting mechanical properties. In particular, spider web, honeycomb, hierarchical and fractal structures have been extensively studied in flexible electronics. A myriad of studies have revealed the excellent mass transport properties of fractal structured electrodes, while ultra-strong honeycomb structures are commonly applied in composites to improve durability. Unlike the previously mentioned categories, biomimetic structures have relatively more diverse geometries to meet the requirements for broad applications.
The greatest challenge to fabricating commercially viable flexible electrodes with novel structures is the difference in deformation behaviour of each structural design. Therefore, the key variables to optimize the electrode fabrication for a corresponding design are systematically highlighted.
2.1 Wavy structures
Two different forms of wavy structure – linear and planar arrangements – are distinguished by their cross-sectional geometries. A planar wavy structure (Fig. 1g and h) is curvy on the plane parallel to the beam, while a linear wavy structure (Fig. 1i) is defined by its radial isometric meandering beams. Serpentine structures are among the most popular wavelike models that have been used to develop stretchable conductors thanks to the distinctive reversible strain (εr), where the skeleton of the structure receives minimum internal stress concentration by dissipating the stress in the longitudinal direction extension.24 The fabrication of serpentine structures is relatively simple compared to other 3D complex structures, allowing scalable production in a low-cost manner. Although serpentines have been widely used as the stretchable configuration of stiff materials, the manipulation of geometrical parameters is still largely empirical. Two important quantities, εr and strain-at-break (ε0) are the key descriptors of the deformability of a serpentine structure. Current studies on the εr of serpentine electrodes have reported varying values in the range 50–100%, on the other hand, a theoretical study on serpentine structures with a specific geometric parameter revealed much higher achievable εr of 140–180%.25 The state-of-the-art metallic serpentine ribbons demonstrated a wide range of ε0 varying from 54–1600%, due to discrepancies between geometric parameters in the construction of these structures. Despite possessing remarkable εr and ε0, wavy structured electrodes commonly exhibit mediocre charge capacity and rate capability due to poor interconnection over the structure and low specific surface area. Hence, wavy structures are superior for applications requiring enhanced mechanical strength, but with a limited rate performance for energy storage.6,7,262.2 Auxetic structures
Auxetic structures have received great attention owing to their extraordinary mechanical responses. Unlike structures with positive v, auxetic structures elongate in the orthogonal direction to the applied tensile stress (σ) as shown in Fig. 1j. v is a measurement of Poisson's effect that describes the expansion or contraction of a material perpendicular to the loading direction. The formula for v is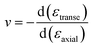 | (1) |
In comparison with conventional structures, the fascinating properties of auxetic structures include enhanced shear modulus (G), fracture toughness, indentation resistance, plane strain fracture resistance and acoustic response. Furthermore, auxetic structures also exhibit a distinctive impact absorption property recognized as a method to create different reinforced composite structures.28,29 A study of braided auxetic structures (Fig. 1k) using carbon rods has revealed the ameliorating effect of the negative v structure with an enhanced ε of 8.7% against the 1.8% of the pristine carbon core under a maximum tensile load of 15.5 kN.30 Taking advantage of these excellent properties, auxetic structures are widely adopted into great numbers of applications including artery opening dilators, pore size adjustable filters, piezoelectric composite polymer matrices, as well as high velocity impact mitigation.31 The high energy absorption ability of auxetic structured electrodes is well suited for energy storage where the side effects of mechanical compression on the device can be successfully prevented.
2.3 Biomimetic structures
Biomimetic designs gain inspiration from the structures and properties in nature, forming structural composites that portray impressive mechanical strength. In particular, bio-inspired honeycomb structures, fractal structures and hierarchical structures have made great contributions in the fields of architecture, electronics and mechanical devices. A honeycomb structure has a hexagonal cell pattern as shown in Fig. 1e, originally discovered in beehives naturally constructed by worker bees. It was considered a structure which could be produced with the lowest material wastage during construction; Marcus Terentius Varro suggested this is because hexagons provide the highest surface/perimeter ratio among all the polygons available for plane tiling.32 Scientists also found that honeycomb structures are able to demonstrate a relatively higher out-of-plane compression and shear strength with a minimal density of building materials.33,34 They are commonly produced in flat or curved planes to fabricate composite materials with an enhanced strength and J value in aerospace utilizations. Finite element analysis (FEA) on aluminium honeycomb structures has demonstrated εr values up to 15%, with E of 271.5 MPa under longitudinal force and 38.5 MPa under vertical force.35 In comparison, the core aluminium material (Aluminium-5052-H39) yields an E value of 68.97 GPa, with εr at 0.04% and ε0 at 10%. These results suggest that the flexibility of a material could be effectively improved by turning the material slab into a honeycomb microstructure. Honeycomb structures made of conductive materials such as metal mesh might be considered as good designs for flexible electrodes to achieve high G and J, enabling deformability and fast electron transport within electrodes. For some mechanical properties, the honeycomb structure yields better results than even isotropic tetrachiral and anisotropic anti-tetrachiral structures.36Fractals are a well-known structure (Fig. 1l) sourced from the mathematical concepts of recursion in the 17th century, referring to functions that are continuous and nowhere differentiable. Fractals were defined as geometries having self-similarity over all scales with infinite iterations. The mathematical concept of fractal structures includes the Koch anti-snowflake, which generates a fractal structure by infinite iterations of self-similar parts at different scales as shown in Fig. 1m. The equation related to fractal dimensions denoted by dim is given by
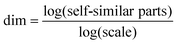 | (2) |
In contrast, another form of biomimetic structure constructed of different substructures on various scales are known as hierarchical structures, which are frequently found in natural materials, for instance, osteons in human bone, wood fibrous, trabecular bone and chitin wings.39,40 The concept is similar to that of fractals, however self-similarity on varied scales is not a necessity for hierarchical structures, the substructures in some cases have different geometries. From the mechanical performance perspective, hierarchical structure are recognised as a promising model for the fabrication of advanced multifunctional materials. One good example of hierarchical structures in nature is found in the architecture of human bones: known as osteons (Fig. 1n) at 200 μm in diameter, they consist of cortical bone with porosity of 6% and lamellae built from fibres 1–10 μm in diameter and 5 μm thick. This intricate architecture of the fibre composite in human bones provides them with a high J value, slow creep behaviour and ability to respond to prevailing stresses.41 Experimental data has shown that human adult bones possess ultrahigh plane strain modulus (Ē) ranges from 7 to 35 GPa owing to the synergistic interaction between cortical bone with E ranges from 9.8 to 15.7 MPa under bending while each lamella unit exhibits superior compressive modulus up to 23 GPa.42,43
The intriguing mechanical properties of hierarchical structures allow the fabrication of electrodes with high J and E. It should be mentioned that multiscale porosity of the structure is effective in improving ion transport efficiency which resembles the electrolyte and nutrient transport in biological systems. More importantly, abundant natural resources such as chitin wings (Fig. 1o) could be used as a template for the conformal deposition of active materials to produce hierarchical structured electrodes.39,40
Another unique biomimetic structure introduced in this review is the spider-web structure which is naturally constructed by thin threads of proteins (Fig. 1f). Despite having a structure made up of silk with a diameter within a few micrometres connected in a web-like pattern, the exceptional strength and elasticity of the web has been proven in view of its ability to catch and entangle prey with ease. This remarkable design reaches an ε of 40%, demonstrating distinctive stretchability. Based on parametric modification, global or local strength optimization of spider webs can be achieved by tuning parameters like the radial thread cross-section diameter (dr), spiral thread cross-section diameter (ds), and understanding their relationship to applied tensile loading. In view of the notable mechanical properties of spider-web structures, they could be a potential candidate for novel electrode structures with the ability to withstand out of plane impact during operation.44,45
3. Tunable parameters
The first challenge to fabricating novel electrode structures is identifying the key geometrical parameters and assembly strategies that determine the mechanical properties, notably J, E, εr and G of the electrodes. A high J and E allow an electrode to endure higher tensile loading before reaching a detrimental state, while an enhanced εr is an important indicator of the stretchability of electrodes. There are currently numerous strategies for production of structural based electrodes, which includes micropatterning,46 mechanical deforming,47 lithography patterning48 and 3D printing techniques.49The preparation of uniform and high-resolution nanoarrays on both rigid and flexible substrates has been realized using nanosphere lithography (NSL). It offers high precision, design flexibility and material flexibility to produce a great range of periodic nanostructures with pore sizes ranging from hundreds of nanometers to several micrometers.50–59 The advantages of this technique are demonstrated in several typical applications related to flexible metallic nanomesh electrodes including RGO/metal grid hybrid film,52 Au nanomesh electrode,53 nanostructured Ni or Cu metallic textiles for Li-ion batteries.54
3D printing is a reliable approach to produce structural based electrodes owing to their ability to model complex geometric structures. In particular, 3D printing allows high precision production of 2D and 3D objects directly from the digital computer-aided design files, rendering the fabrication of novel electrodes with controllable sizes and curvatures. Nevertheless, practical fabrication of 3D electrodes is still in its infancy as the study of the correlation between geometrical variables of complex structures and mechanical properties is still lacking. Therefore, it is essential to establish design strategies for fabricating novel electrodes with a controllable complex architecture. Different strategies including theoretical equations and experimental formulas are critically assessed and the governing parameters of the three major structures are summarized in this section.
3.1 Serpentine structures
Serpentine structures acquire flexibility and stretchability by extending through a meandering shape. In usual practice, serpentine patterned materials are supported on flexible substrates to further enhance the structural strength. A simple serpentine structure is able to sustain ε up to 30%, higher than that of human skin, which is approximately 20%.60 Geometrical parameters that describe the structure are arc radius (R), trace width (ws), height (H), angles θ and α as presented in Fig. 2a and b. Where α is the arc angle of the serpentine structure and θ is defined as the angle between the centres of a circle of two adjacent arcs. It is discovered that stretching behaviours of serpentine structures are affected by any of these parameters. To study the effect of θ on the stretchability of 3D printed serpentine electrodes, tensile tests were conducted on different serpentines of the same R with varying θ as shown in Fig. 2b. The results showed that optimized ε0 of 315% was obtained at θ = 45° among all samples (Fig. 2c).24 In another study, α of the half circles that makes up the ‘horseshoe’ serpentine was investigated to study its correlation to the elastic stretchability (εr). The work discovered that εr of a serpentine structure increases in proportion to α from 90° to 270° (Fig. 2d).61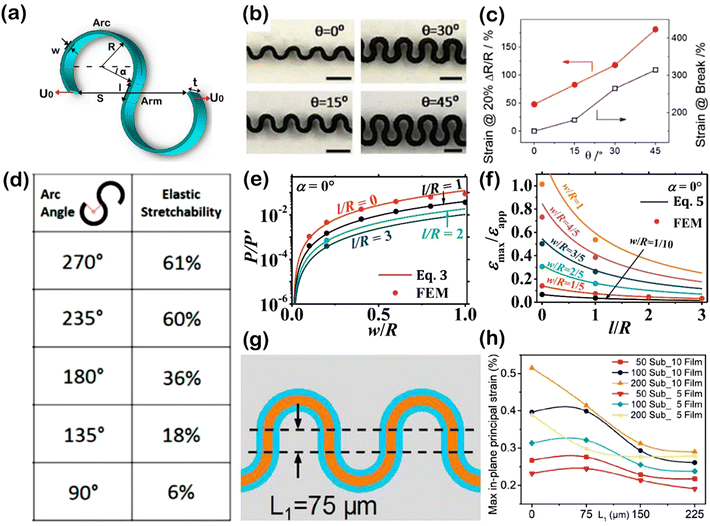 | ||
| Fig. 2 (a) Unit cell of a serpentine structure. (b) Cross-sectional image of 3D printed serpentine electrodes with different joining angles. (c) Resistance change in response to 20% strain (red) and strain-at-break of serpentine electrode (blue) at different angles. (d) Simulated uniaxial elastic stretchability for horseshoe patterns as a function of arc angle. (e) Normalized stiffness as a function of w/R when α = 0° with varying l/R. (f) Normalized stiffness as a function of l/R when α = 0° with varying w/R. (g) Serpentine structure with arm length L1 = 75 μm. (h) FEA results of the maximum in-plane principal strain as a function of length L1. Reproduction with permission from ref. 24, Copyright 2017, John Wiley & Sons and Reproduction with permission from ref. 61, Copyright 2014, Springer Nature Limited and Reproduction with permission from ref. 25, Copyright 2014, Elsevier and Reproduction with permission from ref. 62, Copyright 2019, Elsevier. | ||
Another comprehensive article on J and ε of the “horseshoe” serpentine structure introduced an additional parameter to improve the structure.25 The structure added a linear “arm” section between arcs to construct the modified serpentine structure by manipulating the end-to-end distance (S) and arm length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) of the horseshoe serpentine. J is determined by the ratio of the reaction force of serpentine (P) and straightened ribbons (P′) under the same displacement as given by eqn (3). The term u0 represents tensile displacement under reaction force P. It can be observed that J is dependent on the geometric parameters as shown in Fig. 2e, where S is expressed by the correlation between the R and α as shown in eqn (4). ε is an important indicator of how a structure responds to tensile loading. Similarly, normalized maximum tensile strain is a function of the geometrical variables as given by eqn (5), where εmax and εapp are the maximum tensile strain of the structure and applied tensile strain, respectively.
of the horseshoe serpentine. J is determined by the ratio of the reaction force of serpentine (P) and straightened ribbons (P′) under the same displacement as given by eqn (3). The term u0 represents tensile displacement under reaction force P. It can be observed that J is dependent on the geometric parameters as shown in Fig. 2e, where S is expressed by the correlation between the R and α as shown in eqn (4). ε is an important indicator of how a structure responds to tensile loading. Similarly, normalized maximum tensile strain is a function of the geometrical variables as given by eqn (5), where εmax and εapp are the maximum tensile strain of the structure and applied tensile strain, respectively.
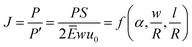
| (3) |
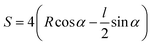
| (4) |
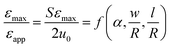
| (5) |
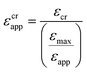
Apart from the stretchability during tensile loading, one can estimate the breaking point at which the structure will rupture using the critical applied tensile strain (εcrapp) function given by eqn (6) where εcr is the intrinsic critical tensile strain of material that makes up the structure. A lower εmax to εapp ratio will lead to enhanced stretchability of the structure.
| (6) |
The model proposed in this work is consistent with finite element modelling (FEM) results, suggesting the effective stiffness increases in proportion to w/R ratios (Fig. 2e) but is inversely proportional to ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /R ratios. On the aspect of normalized maximum tensile strain, the results revealed that for all ratios of w/R, with a larger l/R ratio, yield lower εmax/εapp values as shown in Fig. 2f.25 The effect of the arm length
/R ratios. On the aspect of normalized maximum tensile strain, the results revealed that for all ratios of w/R, with a larger l/R ratio, yield lower εmax/εapp values as shown in Fig. 2f.25 The effect of the arm length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (labelled as L1 in Fig. 2g) between two curvy segments to the maximum strain was further investigated using a serpentine structured electrode supported on a silicone rubber elastomer substrate. FEA results in Fig. 2h reveal the optimal serpentine structure has
(labelled as L1 in Fig. 2g) between two curvy segments to the maximum strain was further investigated using a serpentine structured electrode supported on a silicone rubber elastomer substrate. FEA results in Fig. 2h reveal the optimal serpentine structure has ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 75 μm supported on substrates with thickness ranging from 50 to 100 μm, delivering the highest in-plane maximum principal strain of electrode.62
= 75 μm supported on substrates with thickness ranging from 50 to 100 μm, delivering the highest in-plane maximum principal strain of electrode.62
3.2 Auxetic structures
There are large varieties of auxetic structures including interlocked re-entrant, tetrachiral honeycomb, isotropic tetrahedral, and the well-known re-entrant honeycomb structure. Fig. 3a displays the unit cell of an anti-tetrachiral anisotropic structure where the configuration can be tailored based on the parameters Lx, Ly, r, w, and b, which represents the length along the x or y directions, radius of the node, trace width, and depth of cell, respectively. Four dimensionless parameters were proposed as αx = Lx/r, αy = Ly/r, β = b/r, γ = w/r. These dimensionless quantities allow convenient analysis for the non-dimensional tensile modulus (Ex/Ec) which is defined as the ratio of E along the x direction to the intrinsic tensile modulus of a material being studied. The relation between Ex/Ec and geometry parameters is given by eqn (7) obtained from finite element homogenization and analytical predictions.63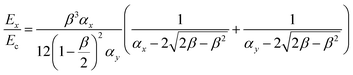 | (7) |
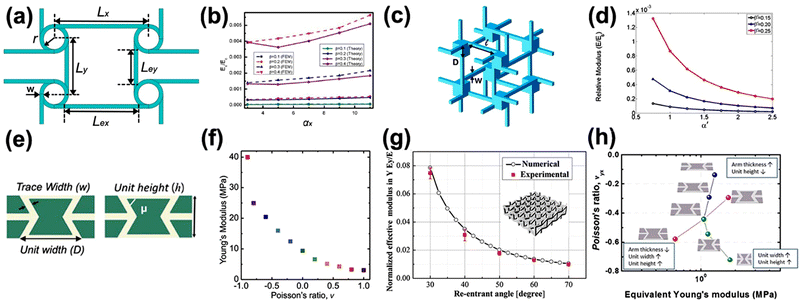 | ||
| Fig. 3 (a) Unit cell of anti-tetrachiral anisotropic honeycomb and the corresponding tunable parameters. (b) Finite element homogenization and analytical predictions of the (Ex/Ec) against αx for anti-tetrachiral anisotropic lattices with different β. (c) Schematic and geometric parameters of 3D isotropic tetrahedral unit cell with cubic nodes, D. (d) E/Es response of isotropic tetrahedral structure against α′ and β′. (e) Unit cell of re-entrant auxetic honeycomb. (f) Young's modulus of honeycomb structure in relation to ν. (g) Young's modulus response to re-entrant angle obtained from experiments (red) and the numerical models (black); inset: schematic of 3D interlocking re-entrant auxetic structure. (h) Influence of geometrical parameters of auxetic structure on the mechanical behavior of the composite. Reproduction with permission from ref. 63, Copyright 2012, Elsevier and Reproduction with permission from ref. 64, Copyright 2017, John Wiley & Sons and Reproduction with permission from ref. 65, Copyright 2017, Seoul National University and Reproduction with permission from ref. 66, Copyright 2018, Elsevier and Reproduction with permission from ref. 67, Copyright 2016, Elsevier. | ||
Isotropic tetrahedral structures are another typical form of auxetics. Being different from anisotropic structures by one additional variable: cubic node width D, was introduced to investigate the E value of the isotropic structure as shown in Fig. 3c.64 Theoretically, E is determined from the ratio of nominal stress (σ) over strain (ε) given by eqn (8). As isotropic structures demonstrate the same behaviour in all directions, the optimization of the structure is easily achieved by investigating the mechanical property in one selected direction. This work proposed a new expression for E with two operational dimensionless parameters: α′ = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /D and β′ = w/D which could be a useful guide to estimate the relative modulus E/Es as given by eqn (9)
/D and β′ = w/D which could be a useful guide to estimate the relative modulus E/Es as given by eqn (9)
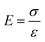 | (8) |
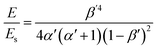 | (9) |
![[E with combining overline]](https://www.rsc.org/images/entities/i_char_0045_0305.gif) c. The E/Es was observed to increase with increasing β′ value and varied inversely with increasing α′ value as shown in Fig. 3d.
c. The E/Es was observed to increase with increasing β′ value and varied inversely with increasing α′ value as shown in Fig. 3d.
Besides chiral structures, the re-entrant honeycomb structure is the most popular structure among the auxetic family. It differs from a conventional honeycomb structure by its negative joining angle, also known as re-entrant angle (μ) between the edges of a cell as shown in Fig. 3e.65 By manipulating μ and the geometric parameters including the unit height (Ha) and unit width (D) that constitute the structure, one could determine the Poisson's ratio in the longitudinal x and transverse y direction, vyx as given by
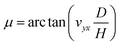 | (10) |
Another study utilized an embedded auxetic structure to investigate the geometric dependence of a re-entrant auxetic structure on the mechanical behaviour of the composite. Fig. 3h shows the influence of trace width wa, unit width D and unit height H on the v and E of the structure. A more negative v was recorded for structures with a higher D and H at the expense of E. These findings shed light on the rational manipulation of geometrical parameters to positively enhance the mechanical properties of auxetic structures.65
3.3 Biomimetic structures
Spiders spin intricate webs that are known for their superior strength and elasticity which enables their function in prey catching and holding. 3D printing is a powerful tool to produce delicate biomimetic structures for flexible electronics applications. A study has identified several parameters to enhance the mechanical strength of 3D printed spider web structures under both localized loading or distributed loading modes.68 The parameters used to define the web structure are the diameter of spiral threads (ds), diameter of radial threads (dr) and number of spiral threads (n) under loading, as illustrated in Fig. 4a. A correlation between n and peak force Fpeak where the structure ruptures, was established to fit experimental and simulation data as shown in Fig. 4b. The onset of the plateau at n = 6 indicates the threshold to achieve the optimal mechanical behaviour of the spider web structure. It worth noting that the web strength does not linearly increase by simply increasing the n under loading and the strength of the radial thread is the limiting factor of the mechanical strength of spider web structures. Unit mass strength was defined as Fpeak/M (M is the total mass of the web), was introduced to facilitate the study of scalable mechanics by controlling the ratio of ds and dr for the structure optimization. For a given ratio, ds/dr, the Fpeak/M is constant. Tensile loading test under point loading and distributed loading, revealed that when ds ≈ dr, the web is at maximum strength under point loading, resembling the small prey catching process. Fig. 4c shows the simulation result of unit mass strength recorded for samples subjected to 4 spiral thread-point loading and homogeneous loading on all spiral threads. Distributed loading is analogous to large prey catching, web design with ds ≪ dr yields better mechanical strength, while the maximum unit mass force for 4-point loading were recorded at ds2/dr2 = 0.76. This work provided two important insights into the facile manipulation of orb sizes and ds/dr to optimize the structure under desired force loading conditions.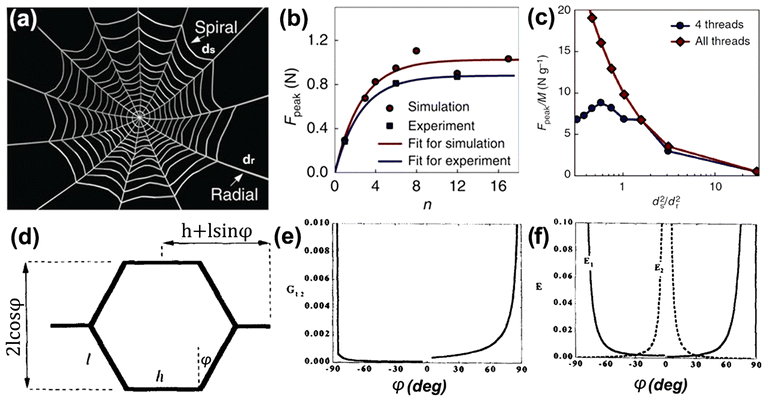 | ||
| Fig. 4 (a) Schematic of spider web consisting of radial threads dr and spiral threads ds. (b) Simulation result of Fpeak/M for the case n = 4 and homogeneously distributed force. (c) Comparison of peak force (Fpeak) obtained from simulation based on function of F-normalized displacement and experiment. (d) Schematic of 2D honeycomb single cell with cell joining angle φ, and different side lengths h and l. (e) Plot of shear modulus (G) vs. φ for flexure model. (f) Plot of Young's modulus (E) vs. φ for flexure model. Reproduction with permission from ref. 68, Copyright 2015, Springer Nature Limited and Reproduction with permission from ref. 69, Copyright,1997, Elsevier. | ||
Honeycomb is another well-known biomimetic structure consisting of hexagonal elemental cells (see Fig. 4d) periodically repeated and connected to each other.69 Honeycomb structures have been applied in a wide range of fields including architectures, biomedicines, mechanical engineering, chemical engineering.70 The exceptional high mechanical strength makes honeycomb structures a potential candidate for stretchable electrodes.71 The mechanical response of a honeycomb structure can be systematically optimized by controlling the wall thickness and unit cell sizes.72 Three different computational intelligence (CI) methods including genetic programming (GP), automatic neural network search (ANS) and support vector regression were used to develop a model for structural optimization. Modelling results from CI revealed that the yield strength and E of the structure increase with wall thickness before reaching the saturation point at 3 mm as opposed to the unit cell size. Although it is relatively more complex to derive a physical model for 3D honeycomb structures, earlier studies have revealed that the 2D model depicted in Fig. 4d provides reliable prediction of an elastic constant of the structure under deformation, including flexure, stretching and hinging which are critical for flexible electrodes design. The study defined the impact contributed by each mode of deformations with a force constant K which relates the displacement of the cell walls of a honeycomb to the applied force. With the lowest K value, the model shows that flexure is the major contributor to the structural deformation. The influence of cellular geometry to E and G of the flexure model was studied by varying the cell angle φ (complementary to the negative joining angle, μ as mentioned in Section 3.1) from −90° to 90°. Through the modification to cell angle φ, G values increase with the magnitude of φ value, while E demonstrated an opposite manner when φ was altered between positive and negative values (Fig. 4e and f). Furthermore, the study concluded that despite having a poorer E and G value, the hexagonal cell usually has a lower density as compared to the re-entrant cell, which is beneficial to fabricating lightweight portable and mobile devices.69 The E value of the structure can be easily improved by tuning the apparent density (ρ*/ρs) of the honeycomb framework, defined as the quotient of density of the cellular solid and the building material.43Table 1 summarizes the general characteristics, fabrication methods, advantages/disadvantages and the application scenarios of the above-discussed structures to provide a guideline for future electrode architectural design.
| Category | Structure | Characteristics | Advantages | Disadvantages | Application scenarios |
|---|---|---|---|---|---|
| Wavy structure | Serpentine | • Optimized ε0 is achieved at θ = 45°. | • Simplicity in manufacturing. | • Low specific surface area. | • Structures require high stretchability in one dimension. |
| • εr increases with the increase of α, given 90° < α < 270°. | • High ε0, εr and εmax. | • Anisotropic ε0, εr, εmax and J. | • High energy density or areal capacity is not the primary objective. | ||
| • J increases with the increase of w/R. | |||||
• εmax/εapp decreases with the decrease of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /R. /R. |
|||||
• εmax is optimal at ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 75 μm given 50 < t < 100 μm. = 75 μm given 50 < t < 100 μm. |
|||||
| Auxetic structures | Anti-tetrachiral anisotropic | • Ex/Ec increases with the increase of αx and αy, given β < 0.3. | • Intermediate specific surface area. | • Intermediate manufacture difficulty. | • Structures require high shear strength and high tensile strength. |
| • Higher in-plane normalized Young's modulus than honeycomb structure. | • Anisotropic tensile modulus. | ||||
| Auxetic structures | Isotropic tetrachiral | • E/Es decreases with the increase of α′. | • High density at high mass loading. | • Complex manufacturing. | • High capability in withstanding multi-directional mechanical loading. |
| • E/Es increases with the increase of β′. | • High specific surface area. | • Well balanced of energy density and mechanical strength. | |||
| • Higher in-plane normalized shear moduli than anti-tetrachiral anisotropic structure. | |||||
| • Isotropic mechanical properties including E/Es. | |||||
| Auxetic structures | Re-entrant honeycomb | • E decreases with the increase of ν. | • High specific surface area. | • Anisotropic mechanical properties. | • Requires incorporation of flexible substrate to relax the tensile loading, |
| • E/Es decreases with the increase of μ | • Simplicity in manufacturing. | • Difficult to generalize into 3D structure. | |||
| • v decreases for v < 0 with a higher D and H on the expense of E. | |||||
| Biomimetic structures | Spiderweb | • Optimal maximum strength under point loading when ds ≈ dr. | • Adaptive to out-of-plane impacts. | • Intermediate manufacture difficulty. | • Ideal for application requiring frequent out-of-plane point loading or distributed loading during usage |
| • ds ≪ dr yields better mechanical strength under distributed loading. | • Could reach ε up to 40%, remarkable stretchability. | • Anisotropic mechanical properties. | •Ideal for structure requires high in-plane ε | ||
| • For 4-point loading, maximum unit mass force is recorded at ds2/dr2 = 0.76. | • Could be optimized for either maximum point load or distributed load. | ||||
| Biomimetic structures | Honeycomb | • Flexure is major contributor to structural deformation at lowest K. | • Lower density than re-entrant structures, preferred by light-weight designs. | • Low mass loading. | • Ideal for application requiring high shear strength and frequent out-of-plane compression |
| • G increases with the increase in magnitude of φ. | • High out-of-plane compression and shear strength with minimal density of materials. | • Low specific surface area. | |||
| • E demonstrated an opposite manner when φ was altered between positive and negative values. | • Enhancement in J by applying honeycomb design. | ||||
| • Improvement in E could be achieved by tuning ρ*/ρs. | |||||
4. Applications
Taking advantage of the design flexibilities of novel structures, researchers have found a broad range of applications in flexible electronic devices including flexible batteries, supercapacitors and strain sensors. Besides microelectronics fabrication, novel structured electrodes have been adopted in heavy duty flow reactors to achieve advanced mass transport characteristics.73 Considering the functionalities required for the above electronics devices, structural engineering of electrodes is a promising strategy to achieve the following features: superior mechanical strength, high electrical conductivity, stable cycling under deformations and distinctive rate capability for high performance energy storage.Two popular electrode designs reported in literature including interdigitated structures and wavy structures with moderate flexibility and conductivity, which have brought new insights into the design of flexible energy storage devices. Despite the high rate capability and power density demonstrated by interdigitated electrodes, their practical applications are limited by weak mechanical strength. Wavy structured electrodes are known for their high tensile strength but their elasticity failed to meet the requirements of high-performance batteries because of their poor rate capabilities due to the lack of interconnects formed within the structures. Hence, it is of great importance to develop structural designs that can provide revolutionary improvement on all the targeted characteristics. The effect of geometrical characteristics of each design on their performance for a device are considered later in the article. It is worth mentioning that not all fundamental aspects of mechanical engineering have been applied in the fabrication of flexible electrodes. Nevertheless, they represent significant technological advances that have common dependence on efficient manufacturing that currently requires improved technology, processes as well as ongoing research. In addition, there is a decent number of works that have demonstrated proof of concept for the geometrical approach, including width of interdigitated fingers, amplitude of the wavy structure and folding angles of the novel structures to achieve high flexibility.
In general, the performance of energy storage devices is classified by their specific storage capacity, rate capability and energy density which are closely related to the electrode/electrolyte interfacial properties and electronic conduction within the electrodes. Therefore, the pore distribution, specific surface area, number of interconnects of the electrodes that form the circuit, are all influential for fast charge/electron transport and ion diffusion in energy storage applications. A cell in planar form can be easily scaled up by stacking the complex architecture electrode to enhance the areal capacitance in supercapacitors. In addition to the aforementioned electrochemical properties, multifunctional electrodes with remarkable mechanical features such as high tensile modulus, energy absorption, stretchability, and their integration in energy storage devices are summarized as follows.
4.1 Applications in supercapacitors
Modern industries require a large amount of electric power in fields including aerospace navigation systems, health monitoring, portable/wearable smart devices, uninterrupted power supply (UPS) and power generating systems in hybrid electric vehicles. It is a great challenge to produce a power supply with light-weight, superior energy density and large power output while offering excellent robustness against mechanical deformations during operation. Supercapacitors are a potential candidate thanks to their high power density which could efficiently bridge the gap between batteries and capacitors. Novel structured supercapacitors with high energy density close to a battery and high power density, are able to provide better mechanical performance to meet the stringent requirements of the above mentioned applications.74 For applications which require high output voltage such as the aerospace industry, supercapacitors are and unequivocal power source which could compensate power intermittency when supplying the high voltage for flight actuation. Improved mechanical strength is a necessity for actuators mounted on wings of the aeroplane, due to the vibrations caused by air turbulence.75,76 It should be mentioned that supercapacitors have been used for start and stop applications in more than 600 thousand hybrid electric vehicles.77 Durability of supercapacitors is one of the focal points of development, aiming to improve the impact absorption property for safer operation. Furthermore, deformable supercapacitors are promising for health care monitoring devices which require small power consumption and rapid charge capability. Supercapacitors are usually integrated into these devices, with self-charging units for energy harvesting and a sensing unit for parameters detection. Considering the involvement of motion during human activities, a power storage system with enhanced flexibility is essential for the applications of advanced wearable electronics.78–81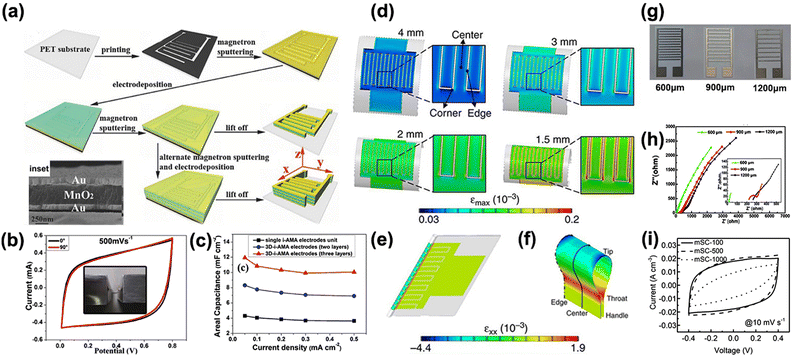 | ||
| Fig. 5 (a) Fabrication process of on-chip pseudo-MSCs with 3D-i-AMA stacked hybrid electrodes. (b) CV curves of the on-chip 3D-i-AMA electrodes pseudo-MSC under normal and bent conditions at a scan rate of 200 mV s−1. Inset: Image of the device under bending. (c) Evolution of the areal capacitance of MSCs with a different number of electrode layers against current density. (d) Finite element method (FEM) based strain profile of Au current collector layer bent at different bending radii ranging from 1.5 to 4 mm, demonstrating nonuniform strain distribution over the corner, edge and center positions. (e) εxx in the Au layer of a folded MSC. (f) Zoomed-in domain of folded Au layer εxx profile at interdigitated finger, with domain dissected into five different zones to highlight the strain distribution patterns. (g) Optical image of paper-based MSC with interdigitated finger distances of 600, 900 and 1200 μm. (h) Nyquist plot corresponding to different interdigitated spacings, with a frequency range from 100 kHz to 0.05 Hz using a perturbation amplitude of 5 mV at the open circuit potential. (i) CV curves of selective wetting induced MSCs at a constant scan rate of 10 mV s−1, with interdigitated spacings of 100, 500 and 1000 μm. Reproduction with permission from ref. 83, Copyright 2016, John Wiley & Sons and Reproduction with permission from ref. 84, Copyright 2018, Springer Nature Limited and Reproduction with permission from ref. 85, Copyright 2016, Royal Society of Chemistry and Reproduction with permission from ref. 86, Copyright 2014, John Wiley & Sons. | ||
The current collector is one of the key components in an energy storage device, providing stable electrical connections between the leads and electrode materials. Mechanical failure in flexible energy storage devices are associated with delamination issues during bending and a large mismatch between the active material layer and current collector owing to their different deformation behaviours. Therefore, the correlation between maximum bending strain εb and bending radius were critically investigated using FEM as shown in Fig. 5d.84 The strain profile of the Au current collector revealed that the distribution of maximum strain (εmax) was concentrated at the corner and edge of the interdigitated fingers regardless of bending radii. The high compression and tension domains along the x-direction of the Au current collector in the folded MSC are indicated with blue and red contours in the strain distribution diagram as shown in Fig. 5e and f. The deformed shape resembled a tennis racket with the tip subjected to compression, the throat domain was under the highest tensile strain while the edge of the tip was the most compressed. In contrast, almost zero strain was recorded at locations away from the folding site due to the absence of bending. Numerical study and analytical modelling results in this work proposed that the elastic deformation of a flexible device is achievable by controlling εmax below the yield strain of the Au layer. The simulation results were verified by the high rate capability of interdigitated single walled carbon nanotube (SWCNT) film supported on a printed chromium/gold (Cr/Au) current collector tested at varying scan rates of 1, 20, 100, 200 and 1000 V s−1. Electrochemical test results of the SWCNT MSC showed a remarkable stability with 96% capacitance retention after 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, confirming the excellent electrical conduction within the interdigitated electrode structures.
000 cycles, confirming the excellent electrical conduction within the interdigitated electrode structures.
To investigate the effect of interdigitated spacing between adjacent fingers on electrochemical performance of the paper based MSCs, interdigitated electrodes with different spacing values of 600, 900 and 1200 μm were fabricated as shown in Fig. 5g.85 Nyquist plots showed that bulk resistance increases with increasing finger spacing value suggesting a large gap impeded the efficient charge transport between the electrodes (Fig. 5h). A similar study looked at the correlation between electrochemical performance of binder-free interdigitated MWCNTs electrodes and finger spacing varying from 100 to 1000 μm: the CV curve of msc-100 exhibited a rectangular shape (Fig. 5i), indicating effective formation of an electrical double layer, while msc-500 and msc-1000 have distorted CV curves owing to the larger equivalent series resistance and slower ion diffusion in the electrolyte, confirming a narrow finger spacing is the key to enhance the capacitance of interdigitated MSC.86
Having achieved superb electronic and ionic conduction between the microscale gaps between interdigitated electrodes, their application in deformable energy storage applications was critically reviewed. Polymer incorporated electrodes are commonly used to provide flexibility to batteries and supercapacitors.87 An interdigitated MSC consisting of titanium carbide (Ti3C2Tx) MXene nanosheets, manganese dioxide nanowires (MnONWs), silver nanowires and fullerene (MXene-AgNW-MnONW-C60) supported on PDMS, was prepared by extrusion-based 3D printing technology.5 Owing to the high flexibility of PDMS, the assembled cell has demonstrated good stretchability up to 50% strain (Fig. 6a). As the development of flexible devices progresses, a high-performance deformable energy storage device should deliver stable capacity when subjected to simulated bending and stretching tests. The MXene-AgNW-MnONW-C60 survived 1000 dynamic stretching cycling tests from 10% to 50% strain, with a competitive capacitance retention of 75%, verifying the outstanding durability of the MSC (Fig. 6b).
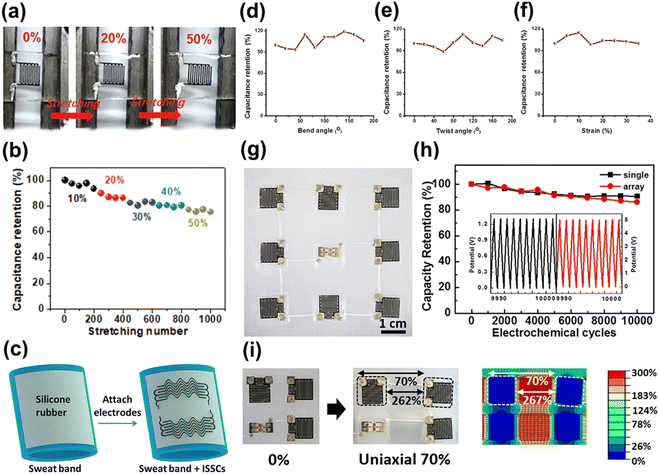 | ||
Fig. 6 (a) Optical image of MXene-AgNW-MnONW-C60 MSC under stretching from 0 to 50%. (b) Capacitance retention of the MXene-AgNW-MnONW-C60 MSC under varying strains. (c) Schematic of the interdigitated solid-state supercapacitor (ISSC) on silicon substrate sweatband. Capacitance retention of the ISSC under three deformation modes of (d) bending, (e) twisting and (f) stretching. (g) Optical image of MWCNT/Mn3O4 MSC array integrated on stretchable substrate under 50% biaxial strain. (h) Capacitance retention of MWCNT/Mn3O4 single MSC and MSC array with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 charge/discharge cycles at a current of 30 μA. (i) Optical image of MSC array stretched from 0% to 70% uniaxial strain and the corresponding FEM profile. Reproduction with permission from ref. 5, Copyright 2020, John Wiley & Sons and Reproduction with permission from ref. 11, Copyright 2019, Elsevier and Reproduction with permission from ref. 88, Copyright 2014, American Chemical Society. 000 charge/discharge cycles at a current of 30 μA. (i) Optical image of MSC array stretched from 0% to 70% uniaxial strain and the corresponding FEM profile. Reproduction with permission from ref. 5, Copyright 2020, John Wiley & Sons and Reproduction with permission from ref. 11, Copyright 2019, Elsevier and Reproduction with permission from ref. 88, Copyright 2014, American Chemical Society. | ||
Fig. 6c shows a hybrid structure consisting of interdigitated electrode and serpentine interconnects prepared from ink composed of CNT, polyaniline and polyurethane printed on a silicone rubber substrate to form an interdigitated solid-state supercapacitor (ISSC). Fig. 6d–f shows the remarkable mechanical stability of ISSC with capacitance retention greater than 90% when subjected to different modes of deformations.11
To enhance the durability of MSC in device level, interdigitated electrodes were arranged in rigid island arrays to compensate the weak structural strength of interdigitated electrodes. A biaxially stretchable array of high performance MSCs on a soft elastomer substrate was fabricated as shown in Fig. 6g.88 The novel design of the MSC array integrated on the modified substrate with implanted PET and liquid metal interconnections, demonstrated a high capacitance retention of over 98.5% after 1000 bending cycles (Fig. 6h). This novel design minimizes the local strain applied to MSC allowing 70% uniaxial strain and with the implanted PET, a maximum principal strain up to 300% was concentrated on the substrate between two adjacent top PET layers as shown in the FEM profile in Fig. 6i, resulting in the negligible degradation of electrochemical performance.
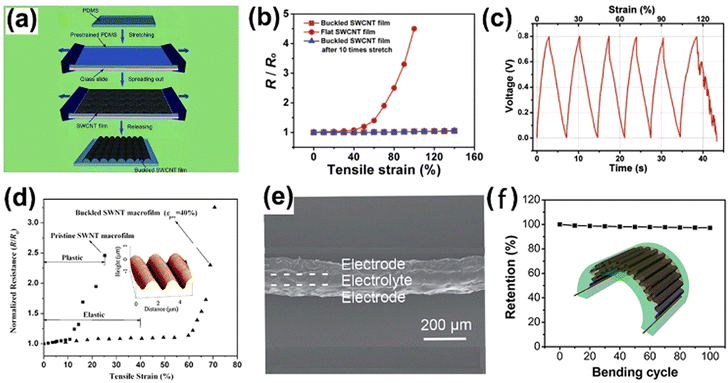 | ||
| Fig. 7 (a) Schematic of buckled SWCNT film assembly on pre-stretched PDMS. (b) Normalized sheet resistance of SWCNT films on PDMS substrate with buckled, flat and buckled after 10 times stretching. (c) GCD curve of a buckled SWCNT film integrated supercapacitor at a constant current of 10 A g−1 with constant strain rate of 3% per second. (d) Resistance change of buckled SWCNT macrofilm and pristine SWCNT macrofilm against varying tensile strain. Inset: AFM image of the buckling profile of the SWCNT macrofilm. (e) Cross-sectional SEM image of the sandwich structure for PANI/graphene electrode, showing excellent interface adherence. (f) Capacitance retention of the Ecoflex encapsulated PANI/graphene supercapacitor under bending. Inset: Schematic of the supercapacitor in bending status. Reproduction with permission from ref. 6, Copyright 2013, John Wiley & Sons and Reproduction with permission from ref. 7, Copyright 2009, John Wiley & Sons and Reproduction with permission from ref. 26, Copyright 2014, Royal Society of Chemistry. | ||
Using a similar fabrication method, a buckled single wall carbon nanotube (SWCNT) electrode was produced by transferring a laminate CNT macro film to a 30% pre-stretched PDMS to form a buckled sinusoidal SWCNT macro film with uniform wavy surface with a wavelength of 2 μm and amplitude of 0.4 μm (Fig. 7d inset).7 Excellent adhesion between the buckled SWCNT macrofilm/PDMS leading to its higher εk and nearly negligible resistance change up to 60% strain as compared to 10% of the pristine SWCNT film (Fig. 7d). A stretchable symmetrical supercapacitor was assembled by sandwiching an electrolyte wetted separator by two sheets of the buckled CNT films. Cycling stability of the supercapacitor was validated from GCD at current density of 1 A g−1 under 30% strain, which demonstrated negligible capacitance degradation from its initial specific capacitance of 52 F g−1 after 1000 GCD cycles.
Conducting polymers are among the promising electrode materials for supercapacitors due to their advantages of chemical diversity, flexibility, tunable geometrical and morphology. A wavy shaped nickel foam was used as the template to prepare a porous graphene using the CVD technique.26 The as-prepared wavy graphene was encapsulated with polyaniline to enhance the tensile strength of the PANI/graphene electrode. Fig. 7e shows that the cross section of the PANI/graphene electrode presented a good adhesion between PANI and graphene layers, suggesting that its structure was robust against mechanical deformation. The Ecoflex encapsulated PANI/graphene supercapacitor survived 100 cycles of 180 degree bending and stretching tests (Fig. 7f) with a marginal capacitance drop of 3%, verifying the superior structural stability of the wavy shaped electrodes.
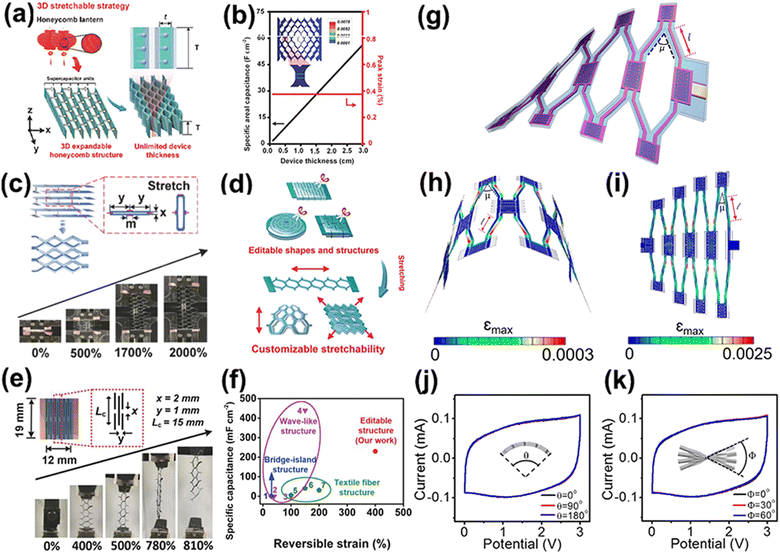 | ||
| Fig. 8 (a) Schematic of 3D expandable honeycomb lantern supercapacitor with unlimited device thickness. (b) Simulation data of electrochemical and mechanical properties of the honeycomb lantern supercapacitor with different device thickness. (c) Digital images of stretchable rectangular-shaped supercapacitors (with geometric parameters of y = 0.7 cm, m = 0.2 cm, x = 194 μm, T = 0.5 cm) under strains between 0 and 2000%. Inset: Deformation pattern of honeycomb lantern structure and enlarged zone of hexagonal unit cell. (d) Schematic of editable honeycomb structured electrode. (e) Digital images of honeycomb-like supercapacitors upon strain. Inset: Geometric parameters of the supercapacitor, Lc = 1.5 cm, x = 0.2 cm, y = 0.1 cm. (f) Areal capacitance versus reversible strain of editable supercapacitor as compared with previous reported stretchable supercapacitors. (g) MSC array consisting of honeycomb unit with islands and beams of interdigitated structure; FEA profile of maximum strain in Au layer for honeycomb interdigitated MSC array under (h) 180° bending and (i) 60° twisting. CV curves of honeycomb interdigitated MSC at different (j) bending angles (k) twisting angles. Reproduction with permission from ref. 89, Copyright 2018, John Wiley & Sons and Reproduction with permission from ref. 90, Copyright 2017, John Wiley & Sons and Reproduction with permission from ref. 91, Copyright 2016, American Chemical Society. | ||
The prototype with geometrical variables of length of supercapacitor unit (y), length of adhesives (m), and thickness of supercapacitor array (x) fixed at: y = 0.7 cm, m = 0.2 cm, x = 197 μm as shown in Fig. 8c, presented an outstanding rupture strain up to 2577%. The electrode delivered a stable electrochemical performance with 95% capacitance retention after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GCD cycles under the cycling tensile strain of 2000%, highlighting the outstanding durability of the novel structure.
000 GCD cycles under the cycling tensile strain of 2000%, highlighting the outstanding durability of the novel structure.
A similar strategy was adopted to fabricate a honeycomb-like stretchable supercapacitor consisting of a composite of mechanically reinforced manganese dioxide nanowires (MNWs) and CNT sandwiched between nanocellulose fibers (NCFs). It is interesting to note that the honeycomb-structures produced in this work do not require complicated preparation steps and they are customizable by scissor-cutting the electrodes into the desired shape (Fig. 8d). An editable honeycomb structured electrode as shown in Fig. 8e, has a dimension of 1.5 cm in length (Lc) and the transverse and axial distance between adjacent cutting lines in the x and y directions was x = 0.2 cm, y = 0.1 cm. The distinctive stretchability of this sample was verified by its remarkable strain-of-rupture reaching 630%. Owing to the non-elasticity of the pristine supercapacitor, it allows only one-time stretching of the supercapacitor, hence polyurethane (PU) threads were inserted affording the supercapacitor reversible strain of up to 400%. Fig. 8f shows that the specific areal, volumetric capacitance and εr of the honeycomb supercapacitor outperformed most stretchable supercapacitors reported in literature, thanks to the inherent mechanical robustness of the mechanically strengthened ultralong MnO2 composite. Tensile tests revealed exceptional flexibility of the honeycomb-like supercapacitors with an elongation up to 500% tensile strain without degradation of electrochemical properties. The honeycomb supercapacitor maintained 98% areal capacitance when subjected to cycling tensile tests to a maximum strain of 400% for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles.90
000 cycles.90
To enhance the notable mechanical property of the honeycomb structures, the arm of the honeycomb unit was replaced by an interdigitated structure to form islands and beams of the MSC array as presented in Fig. 8g.91 FEA profile of maximum strain in Au layer for honeycomb interdigitated MSC array under 180° bending (Fig. 8h) and 60° twisting (Fig. 8i), revealed the local maximum strain concentrated at the joints and outer side of arms for both conditions. The strain on the Au interconnect layer is smaller for bending (0.03%) as compared to twisting (2.5%), more importantly, both values are significantly below the yield strain of Au. The impressive deformability of this stretchable energy storage device relies on the rational placement of the MSC arrays and interconnects in the low-strain regions of the honeycomb structure, minimizing strain on these functional materials during stretching. Fig. 8j and k present overlapping CV curves of the 4 × 4 MSC honeycomb array tested under different twisting and bending conditions, confirming the high reversibility of the electrochemical process and the effective accommodation of large deformation without producing excessive strain in the MSCs and interconnects.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 charge/discharge cycles. The synergistic effects of the highly porous and interconnected network in facilitating mass transport within the conductive networks was proven to be an effective way to enhance the electrochemical performance of the BFE-MSC.38,93Fig. 9b shows the FH fractal structure mimicking the morphology of Fern leaves fabricated by laser scribing, which significantly increases the surface area to volume ratio and reduces the ion transport path leading to its superior electrochemical properties.92
000 charge/discharge cycles. The synergistic effects of the highly porous and interconnected network in facilitating mass transport within the conductive networks was proven to be an effective way to enhance the electrochemical performance of the BFE-MSC.38,93Fig. 9b shows the FH fractal structure mimicking the morphology of Fern leaves fabricated by laser scribing, which significantly increases the surface area to volume ratio and reduces the ion transport path leading to its superior electrochemical properties.92
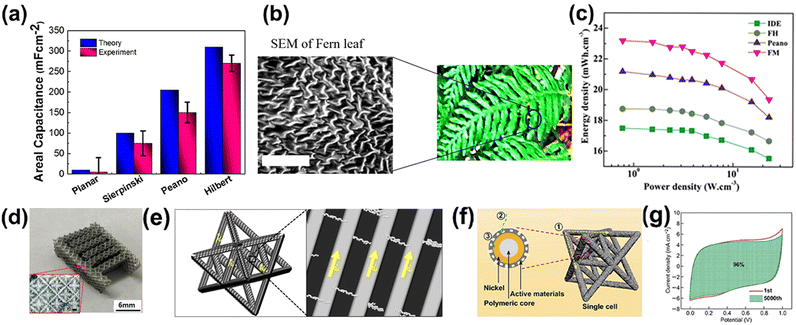 | ||
| Fig. 9 (a) Comparison of areal capacitance between theoretical and experimental calculation results for various BFE and planar MSCs. (b) Schematic of the bioinspired FH electrode structure. (c) Ragone plots of MSCs with different fractal structures. (d) Optical image of 3D hierarchical complex truss interdigitated structure. (e) Schematic of interdigitated electrode (IDE) unit cell composed of interconnected octet structure and the electrochemical mechanism of the electrode in the gel-type electrolyte. (f) Schematic of 3D octet truss electrode, magnified cross section presented with nickel as component of current collector, rGO as active materials and resin as polymeric core. (g) CV curves validate long cycling stability of the 3D octet truss electrode-based supercapacitor. Reproduction with permission from ref. 92, Copyright 2017, Springer Nature Limited and Reproduction with permission from ref. 93, Copyright 2017, John Wiley & Sons and Reproduction with permission from ref. 94, Copyright 2018, American Chemical Society and Reproduction with permission from ref. 95, Copyright 2019 Springer Nature Limited. | ||
Considering the diversity of fractal design, three different fractals Hilbert, Peano and Moore MSCs were compared to conventional interdigitated MSCs in terms of rate performance, power density and cycle life.93 The MSC devices were composed of a thin layer of RuO2 supported on a glass substrate patterned using standard optical lithography. GCD and cycling stability test results were obtained for the three fractal structured electrodes. Among the different electrode designs used in this study, the Moore design demonstrated the best performance with 90% capacitance retention after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles at 1 mA cm−2 current density. The maximum power density of FM MSC ranks the top among all tested structures based on the Ragone plot (Fig. 9c), with the value of 769 mW cm−3, which is about a 32% improvement in the volumetric energy density as compared to interdigitated electrodes when measured at the same power density. This study proposed that the total number of electrical lines of force, due to edging effects in the fractal designs, plays a more important role than the effective surface area in enhancing electrolyte ion absorption leading to an increase in capacitance of fractal electrodes.
000 cycles at 1 mA cm−2 current density. The maximum power density of FM MSC ranks the top among all tested structures based on the Ragone plot (Fig. 9c), with the value of 769 mW cm−3, which is about a 32% improvement in the volumetric energy density as compared to interdigitated electrodes when measured at the same power density. This study proposed that the total number of electrical lines of force, due to edging effects in the fractal designs, plays a more important role than the effective surface area in enhancing electrolyte ion absorption leading to an increase in capacitance of fractal electrodes.
A similar electrode structure for a quasi-solid supercapacitor was fabricated using a stereolithographic (SLA) 3D printing technique.95 An SLA printed polymeric lattice decorated by nickel particles was used as a current collector. The electroactive reduced graphene oxide (rGO) hydrogel was electrodeposited onto the current collector to form a core–shell 3D structure, as shown in Fig. 9f. The 3D electrode delivered an areal capacitance of 293.4 mF cm−2 at 2 mA cm−2 with a capacitance retention of 70.9% when the current density was increased to 40 mA cm−2. In addition, cycling tests revealed the excellent stability of the electrode with a capacitance retention of 96% after 5000 cycles as presented in Fig. 9g. The improved electrochemical performance was attributed to the fast ion diffusion that resulted from the hierarchically porous structure and improved conductivity owing to the better adhesion of the graphene and nickel layer.
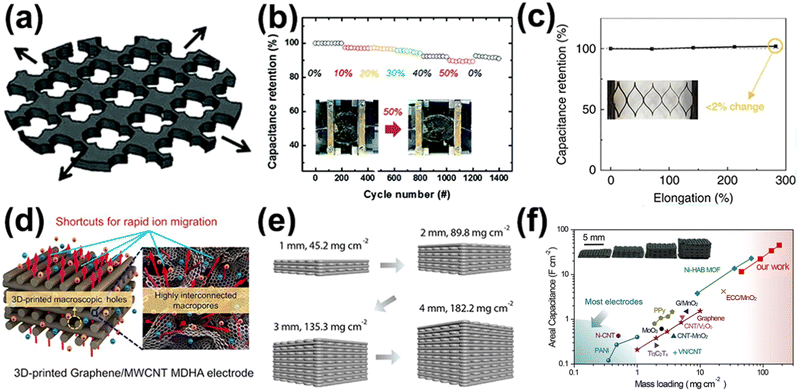 | ||
| Fig. 10 (a) Schematic of 2D auxetic stretchable rGO/CNT electrode. (b) Capacitance retention for the directionalized crystallization produced rGO/CNT supercapacitor, at strains between 0 and 50% tested at constant scan rate of 50 mV s−1. (c) Capacitance retention of kirigami structure based micro-supercapacitor patches as a function of elongation, with scan rate of 200 mV s−1. Inset: optical image of the supercapacitor patches under 282.5% elongation due to post-buckling deformation. (d) Schematic illustrations of ion migration in the 3D-printed graphene/MWCNT hybrid aerogels electrode. (e) Schematic illustration of 3D graphene/MnO2 electrodes with scalable thickness and mass loadings of MnO2. (f) Comparison of areal capacitance and mass loading between the 3D printed symmetrical 3D graphene/MnO2 supercapacitor and other flexible electrodes. Reproduction with permission from ref. 96, Copyright 2017, Royal Society of Chemistry and Reproduction with permission from ref. 98, Copyright 2018, Springer Nature Limited and Reproduction with permission from ref. 99, Copyright 2018, American Chemical Society and Reproduction with permission from ref. 100, Copyright 2018, Elsevier. | ||
Inspired by the natural recovery and expandable properties of paper craft in Japanese culture, origami and kirigami are emerging designs that offer elasticity and flexibility to intrinsically non-elastic electrodes.97 A type of stretchable micro-supercapacitor patch (SMSP) was formed by joining ten deformable units of Kiragami-cut polyimide sheets in series, with each unit mechanically and electrically joined, as presented in Fig. 10c (inset).98 The SMSP survived a horizontal stretching test up to 300% with a marginal change of capacitance, indicating that a high system-level stretchability and high areal coverage of functional components in the MSC could be easily achieved using the compliant kirigami-inspired structure (Fig. 10c).
Woodpile inspired structures are popular in microelectronics fabrication. Such a structure has periodic macropores along the vertical direction within a series of orthogonal woodpile microlattices which are beneficial to facilitate ion-diffusion and electrolyte infiltration. A 3D printed woodpile inspired graphene-based hybrid aerogel electrode was prepared from ink consisting of graphene oxide, Ag nanoparticles, MWCNTs and MoS2 nanosheets (Fig. 10d). The electrode delivered a high areal capacitance of 639.56 mF cm−2 and maintained a moderate capacitance retention of 71.4% when the areal current densities increased from 4 mA cm−2 to 40 mA cm−2.99 The electrode demonstrated a high capacity retention of 90% over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 charge/discharge cycles, suggesting efficient ion transport facilitated by the multidimensional interconnected network formed within the woodpile structure.
000 charge/discharge cycles, suggesting efficient ion transport facilitated by the multidimensional interconnected network formed within the woodpile structure.
A high mass loading of active materials, typically higher than 10 mg cm−2, are crucial for increasing the energy density of supercapacitors. However, increasing electrode thickness usually deteriorates the capacitance of the electrodes due to sluggish ion diffusion. To solve the issue of low mass loading of most supercapacitor electrodes, a woodpile structured pseudocapacitive electrode prepared from graphene, hydroxypropyl methylcellulose and MnO2 ink was developed, using 3D printing.100Fig. 10e shows the straightforward preparation of a 3D printed G/MnO2 aerogel lattice from 1 to 4 mm with extremely high mass loading of 89.8, 135.3, and 182.2 mg cm¬2 obtained on the 2, 3, and 4 mm-thick electrodes, respectively. This novel approach allows facile production of an electrode with ultrahigh mass loading without compromising the high areal, volumetric and gravimetric capacitance. The areal capacitance and mass loading of 3D G/MnO2 topped the list among electrodes with high mass loading of pseudocapacitive materials reported in literature, as shown in Fig. 10f. Remarkably, increasing the electrode thickness effectively enhanced the areal capacitance of the 3D G/MnO2 electrodes linearly, reflecting the superior conductivity and ion diffusion efficiency of the 3D-printed woodpile structure.
4.2 Batteries with novel structures
For practical application of flexible energy storage with high energy density, structural engineering of an electrode is required to create electrodes with large specific surface area and high porosity for efficient charge storage. By mimicking a woodpile structure, a freestanding electrode air cathode for a lithium oxygen battery (LOB) was fabricated by stacking 3D printed graphene mesh made from holey graphene oxide (hGO) without the use of additives or binders.101 The pore size of the air cathode has several effects on performance, such as surface area for interfacial reactions to promote full active-site utilization, efficient gas diffusion, accommodation of discharged products. Fig. 11a shows that the freestanding 3D printed hGO meshes exhibit trimodal porosity in nanoscale pores on the hGO sheets, microscale pores introduced by a lyophilisation process and macroscale pores of the mesh design, synergistically improved the gas diffusion and redox kinetics at the electrode interface leading to its superior areal capacity and cycling stability. The mesh electrode delivered a competitive areal capacity of 13.3 mA h cm−2 among the carbon-based energy storage devices.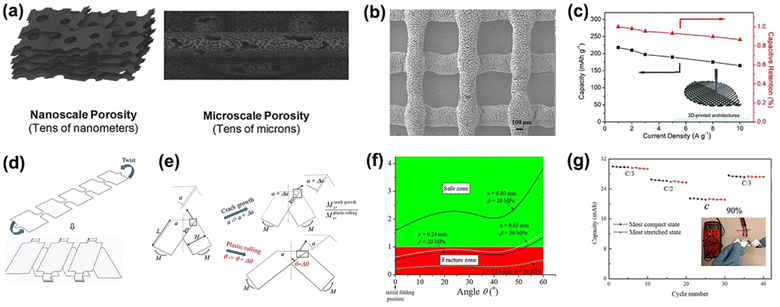 | ||
| Fig. 11 (a) Left: schematic representation of complex 3D architecture with hierarchical porosity prepared from additive-free 3D printable hGO ink. Right: schematic of kirigami cut-N-twist formation applied in a stretchable kirigami lithium-ion battery. (b) SEM image of continuous filaments and hierarchical porous structure forming a 3D-printed cubic lattice framework. (c) Capacity response to current density of 3D printed-NCS/graphene (3DP-NCS/G) aerogels electrode. Illustration of two deformation modes (d) crack growth and (e) plastic rolling of kirigami lithium ion battery. (f) Zone map characterizing “safe zone” and “fracture zone” by ratio of crack growth and plastic rolling moments, as a function of the initial folding angle, for various pre-existing crack size “a” and dissipated energy per unit area of plastic rolling “β”. (g) Rate performance for kirigami lithium ion battery when the charge/discharge rates varied from C/3, C/2, to C, and C/3 again for both compact and stretched states. Inset: optical image of the device stretched up to 90% strain. Reproduction with permission from ref. 101, Copyright 2018, John Wiley & Sons and Reproduction with permission from ref. 102, Copyright 2017, American Chemical Society and Reproduction with permission from ref. 103, Copyright 2018 John Wiley & Sons and Reproduction with permission from ref. 104, Copyright 2015, Springer Nature Limited. | ||
Besides the regular geometries, hierarchical porous structure is a common design approach to enhance battery performance. A novel 3D printed hierarchical porous electrode for sodium ion batteries was prepared from Na3V2(PO4)3 and graphene oxide (NVP-GO) with a macrolevel grid structure.102 The SEM image (Fig. 11b) of the as-prepared electrode shows continuous filaments, with hierarchical porous grids creating an advantage for rapid ion transfer and ion diffusion. GCD measurements showed that the (NVP)-(GO) delivered a high areal capacity of 1.26 mA h cm−2 at 0.2C and retained a stable capacity of 0.65 mA h cm−2 when tested at 20C. The NVP6.8-rGO framework delivered excellent capacity retention of 90.1% after 900 cycles at 1C.
Taking inspiration from the mass transfer characteristics of microchannels formed in leaf veins, a leaf-inspired graphene aerogel composite electrode was fabricated using a 3D printing method.103 The ink was prepared from Ni0.33Co0.66S2 (NCS), graphene and sodium alginate (SA). At a concentration of 50 mg L−1 of solid material, the composite ink showed high elastic modulus and viscosity due to the strong hydrogen bonds formed between SA and graphene.
The interconnected network of the 3D printed-NCS/graphene (3DP-NCS/G) aerogels facilitated efficient electron/ion transport at the electrode and electrolyte interface, contributing to its superior rate capability, with the highest capacity of 217.6 mA h g−1 at 1 A g−1, it retained more than 80% of its capacity when tested at 10 A g−1 (Fig. 11c). More importantly, the areal loading of the electrodes can be easily tuned by adjusting the electrode thickness to 2 mm, the electrode retained exceptional high capacity retention of 78.2% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 charge/discharge cycles.
000 charge/discharge cycles.
Besides having uniaxial bendability, complex multiaxial strains are required for wide applications of flexible batteries. A foldable kirigami-inspired stretchable lithium-ion battery with expandable cut-N-twist kirigami design was developed, as shown in Fig. 11d.104 The novel design consisted of a folded stack of foil which was symmetrically cut at all creases, and then unfolded to a planar state, followed by twisting at the two ends, resembling a twisted telephone cord. Fig. 11e shows two potential modes of deformation: crack growth a and plastic rolling behaviour due to the change of angle θ when concentrated moment M is applied at the end of the strip. To investigate the structural robustness of the novel structure, the durability threshold of the structure was characterized by the ratio of critical moments given by eqn (11).
 | (11) |
Fig. 11f shows the ratio of critical moments can be easily predicted by altering the pre-existing cracks a, and the angle θ of the initial folding position. This study revealed that the fracture due to cutting and folding can be successfully suppressed by plastic rolling of the cut-N-twist kirigami design, enabling the battery superior stretchability up to 90% strain with negligible decline in power density and rate capability under stretched conditions (Fig. 11g).
Given that flexible batteries are designed to be assembled with flexible electronics, it is expected that the battery is able to demonstrate three important features: high bendability, high areal energy density and high bulk volumetric energy density. Fig. 12a shows a flexible LIB fabricated using a novel bioinspired staggered-array structure design to satisfy the requirements as mentioned above. Commercial LIBs (dimensions: 55 mm × 21 mm × 0.4 mm) as the thin sub-cells were bonded together using optical clear adhesives to mimic the microstructure of nacre and bones in the cell assembly.105 Geometrical parameters including length of the cell (L), thickness of sub-cell (hh) and adhesive (hs), the curvilinear coordinate along the central axis of a layer, with the origin O located at the axis centre (x) and distance in the normal direction from the top surface of the staggered array (y), determine the mechanical behavior of the five-layer staggered array in natural and deformed states and were identified using analytical models developed from FEA. The mechanical behaviour was presented by measuring the response of small axial strain (ε) and Δȳ1 against ρ and ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) s, where ρ = L/hh,
s, where ρ = L/hh, ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) s = hs/hh,
s = hs/hh, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = x/L, ȳ = y/hh and Δȳ1 is the normalized deviation of the neutral mechanical plane of the first layer of the staggered array at
= x/L, ȳ = y/hh and Δȳ1 is the normalized deviation of the neutral mechanical plane of the first layer of the staggered array at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0. The response of ε and Δȳ1 was investigated using a staggered array (with R = 4 cm, hh = 20 μm) made from sub-cells and soft adhesives with Young's moduli (Eh = 2.5 GPa, Es = 60 kPa) and Poisson's ratios (υh = 0.34, υs = 0.49). According to the model, ε was found to decrease with a smaller ρ. More notably, the strain distribution among the sub-cells could be easily characterized by Δȳ1. By controlling the ρ ≤ 30 and
= 0. The response of ε and Δȳ1 was investigated using a staggered array (with R = 4 cm, hh = 20 μm) made from sub-cells and soft adhesives with Young's moduli (Eh = 2.5 GPa, Es = 60 kPa) and Poisson's ratios (υh = 0.34, υs = 0.49). According to the model, ε was found to decrease with a smaller ρ. More notably, the strain distribution among the sub-cells could be easily characterized by Δȳ1. By controlling the ρ ≤ 30 and ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) s = 0.1, the interaction among the sub-cells was effectively released at Δȳ1 < 10% leading to a significant reduction in strain, as shown in Fig. 12b and c.
s = 0.1, the interaction among the sub-cells was effectively released at Δȳ1 < 10% leading to a significant reduction in strain, as shown in Fig. 12b and c.
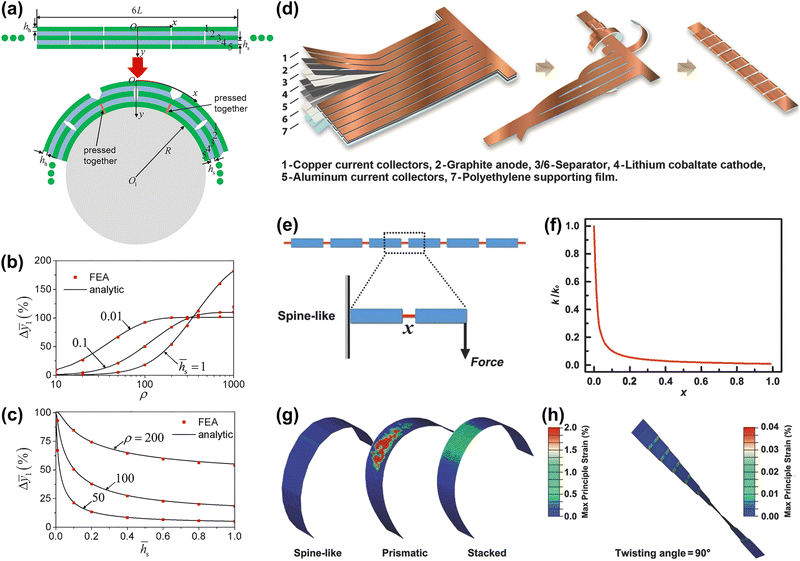 | ||
Fig. 12 (a) Schematic of the staggered structural design, with the deformation mode under bending around a cylinder. (b) Variation of Δȳ1 with ρ under different ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) s. (c) Variation of Δȳ1 with s. (c) Variation of Δȳ1 with ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) s under different ρ. (d) Schematic of spine-like Li-ion battery, structure design and assembly. (e) The length fraction x of the spine-like structure. (f) Variation of k/k0 with x for spine-like Li-ion battery. (g) Principal strain of spine-like, prismatic and stacked structured Li-ion battery under bending deformation. (h) Principal strain of spine-like structured Li-ion battery under 90° twisting angle. Reproduction with permission from ref. 105, Copyright 2022, Elsevier and Reproduction with permission from ref. 106, Copyright 2018, John Wiley & Sons. s under different ρ. (d) Schematic of spine-like Li-ion battery, structure design and assembly. (e) The length fraction x of the spine-like structure. (f) Variation of k/k0 with x for spine-like Li-ion battery. (g) Principal strain of spine-like, prismatic and stacked structured Li-ion battery under bending deformation. (h) Principal strain of spine-like structured Li-ion battery under 90° twisting angle. Reproduction with permission from ref. 105, Copyright 2022, Elsevier and Reproduction with permission from ref. 106, Copyright 2018, John Wiley & Sons. | ||
The electrochemical performance of the optimized LIB with ρ = 26 and hs = 0.125 was tested under static and dynamic bending conditions. The bent battery survived 20 GCD cycles with a capacity decay of 0.111%/cycle, indicating the negligible effect of static bending deformation on the battery. The dynamic bending deformation was performed by flexing the LIB with a bend radius of 35 mm at a frequency of 1.5 times min−1 and the GCD cycles were recorded at different C-rates from 0.5C to 1.5C. The voltage profile of the cell was well maintained at 0.5C during dynamical bending, with a marginal voltage fluctuation below 6 mV, corresponding to a resistance change below 3%. This novel assembly of cells offers a new strategy to produce a flexible battery with bulk volumetric energy density as high as 92.3% of conventional batteries.91
A spine-like design resembles the natural structure of the spine as a flexible and distortable bio-component enabling the facile fabrication of LIB with high flexibility. The spine-like LiCoO2/graphite full battery cell was made from conventionally configured cell stacks cut into strips which were then wound around the backbone, as shown in Fig. 12d.106 The ‘vertebrae’ correspond to thick stacks of electrodes and the ‘soft marrow’ to the unwound part interconnecting all the stacks. The vertebra in the spine corresponds to the energy storage units and the unwound soft marrow part interconnects all energy storage units. Fig. 12e shows the length fraction of the soft interconnect, x, which was varied to investigate the electrochemical performance of the designed battery under stress environments from flat to flexed and torsion. The mechanical analysis was performed by evaluating the effective bending stiffness from the spring constant per unit k/k0 response to length fraction x. Fig. 12f show that the k/k0 decreases exponentially with an increase of x in the spine-like battery design. To further demonstrate the flexibility of the spine-like structure, the strain distributions of spine-like, prismatic and stacked battery wrapped around a human wrist, were further studied using finite element simulations. Fig. 12g shows that the maximum principal strain of a spine-like battery is only 0.08%, which is the lowest compared to the 1.8% and 1.1% for the prismatic and stacked structures, respectively. The robustness of the spine-like structure is evident in Fig. 12h, with torsion up to 90° resulting in maximum strain of 0.04%, indicating the structure is both flexible and twistable.
4.3 Other flexible electrochemical energy devices with novel structures
Tremendous effort has been dedicated to the development of small and lightweight power sources with the rise in demand of portable and smart electronics goods. Apart from the electrochemical energy storage systems, fuel cells and solar cells are promising future small energy sources owing to their high energy density, eco-friendliness and compact design. However, the bulky cell assembly of conventional polymer electrolyte membrane fuel cells (PEMFC) and a variety of technical challenges such as the control of fuel supply at uniform pressure has limited its application in flexible devices.A conical reverse truss origami design was employed in a tubular shaped PEMFC (t-PEMFC) stack as shown in Fig. 13a.107 This strategy allowed the facile manufacturing of clamp-free t-PEMFC composed of unit cells made from stainless-steel mesh, a gas diffusion layer (GDL) and catalyst-coated membrane (CCM) rolled into a conical shape. The number of assembly parts was effectively reduced by stacking the conical cell units using the banded method, enabling the fabrication of flexible PEMFC with lightweight and small volume. A conical reverse truss origami design can be seen as the triangular faces connected by mountain folds and valley folds along the tubular axis as shown in Fig. 13b. The 3D PEMFC is fully compressible in the direction of conical axis by controlling the angle between the adjacent mountain and valley folds. It should be mentioned that the structural properties of the cone are closely related to the number of units on the circumference plane (N) and angle of β1. The number of segments (a single origami cell as shown in Fig. 13c) is one of the factors affecting the compressibility of t-PEMFC. The size of each origami unit and the height of the elements decreases when N increases, where the height of the element is related to the angle of β1.
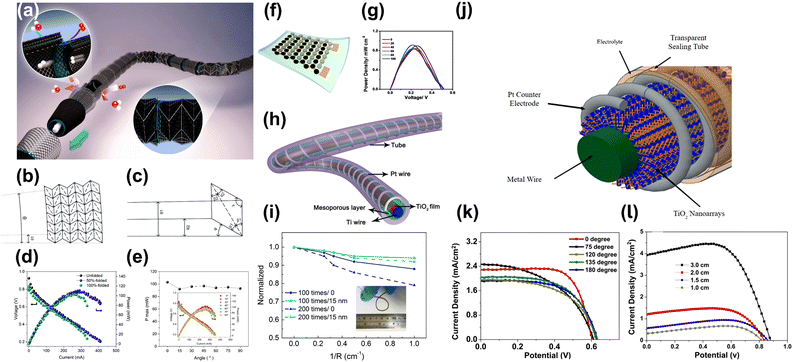 | ||
| Fig. 13 (a) Schematic of the flexible origami tubular PEMFC. Illustration of (b) angle θ corresponding to the overall angle of the origami component and (c) the detailed geometric parameters of a single origami cell. (d) Polarization curves of the kirigami tubular PEMFC under unfolded, 50%-folded and 100%-folded states. (e) Variation of maximum power with bending angle, inset: polarization curve of the kirigami tubular PEMFC at various bending angles. (f) Schematic of the stretchable island-bridge structure, E-BFC. (g) Polarization curve of the island-bridge structure E-BFC under increasing stretching deformation with strain of 50%. (h) Schematic of the FDSSC with TiO2 film coated on anode. (i) Comparison of power conversion efficiency (PCE) of the FDSSC with ALD TiO2 films of different thickness, tested at different bending curvature and bending times. (j) Schematic of the FDSSC with 1D TiO2 nanowire arrays on the anode. Comparison of photovoltaic performances of the FDSSCs tested with (k) varying bending angles and (l) with increasing length. Reproduction with permission from ref. 107, Copyright 2021, American Chemical Society and Reproduction with permission from ref. 108, Copyright 2017, Royal Society of Chemistry and Reproduction with permission from ref. 109, Copyright 2016, Springer Nature Limited and Reproduction with permission from ref. 110, Copyright 2021, Springer Nature Limited. | ||
Fig. 13d. shows the t-PEMFC delivered a maximum power of 109, 112 and 103 mW, for unfolded, 50%-folded and 100%-folded cells, respectively. This result revealed only 4% performance drop caused by folding. The robustness of the cell was evaluated by bending it from 0 to 90°, the maximum power remained almost constant, retaining more than 90% of the unbent cell power (Fig. 13e). The excellent electrochemical performance of the t-PEMFC confirmed the stability of the origami blended structural design and its potential applications requiring mechanical movement.
Another attempt was made to fabricate a stretchable electronic-skin-based biofuel cell (E-BFC) that utilized a Au ‘island-bridge’ configuration that separately connects anode island (CNT-naphthoquinone) and cathode island (CNT-silver oxide) in an interdigitated structure as shown in Fig. 13f.108 The interconnect consists of Au islands arranged in serpentine shaped bridges, which is able to unwind under external stress, reducing stress inhomogeneity across the devices.94
Electrochemical characteristics of the E-BFC under stretching deformation were investigated by exposing the device to 14 mM lactic acid, the power curves of the E-BFC were then recorded every 20 stretching iterations up to 50% strain. Fig. 13g shows negligible change in the power curve after stretching cycles, confirming the mechanical stability of the stretchable E-BFC. The stretchable design in this work offers a solution to alleviate the gradual delamination of active material due to mechanical mismatch between the active layers.
Dye-sensitized solar cells (DSSCs) are an attractive option in renewable energy power generation technologies thanks to their transparency, low cost, and high power conversion efficiencies under cloudy and artificial light conditions. In recent years, novel low-dimensional fiber-shaped DSSCs (FDSSCs) have been widely reported due to their excellent light-harvesting ability and flexibility as compared to the conventional planar DSSCs. Fig. 13h shows a FDSSC fabricated using winding platinum (Pt) wire around a TiO2 coated Ti wire photoanode, prepared from atomic layer deposition (ALD), the electrodes are then immersed in a transparent and flexible plastic tube to form a fiber shaped device.109 Both ends were sealed with wax after filling the tube with electrolyte. The comparison of power conversion efficiency (PCE) of the FDSSC with ALD TiO2 films of different thickness tested at different bending curvature and bending times is presented in Fig. 13i. The FDSSC with ALD TiO2 film retained over 95% of its original performance after the simulated deformation.
Similar work has reported the preparation of one-dimensional (1D) TiO2 nanowire arrays (NWA) decorated with silver plasmonic nanoparticles, as the photoanode for FDSSC as shown in Fig. 13j.110 The mechanical and electrochemical stability of the FDSSC were evaluated by current density–voltage (J–V plot) in response to different bending angles and cell lengths. The J–V plot in Fig. 13k shows a 28% drop in the current density recorded when the FDSSC was bent at 75°, as the bending angle increases up to 180°, the decrease in efficiency is nearly unchanged. The FDSSC demonstrated significant increase in performance when the cell length increased from 1.0 cm to 3.0 cm (Fig. 13l), owing to the larger effective surface area and higher loading of dye on the longer cells. In summary, these novel energy devices have taken the full advantage of the flexibility, wearability and scalability of advanced geometric designs while achieving excellent electrochemical performance.
5. Summary and outlook
Novel energy storage devices with high energy densities and high deformability have been recognized for potential wearable electronic device applications. However, the practical application of flexible energy storage devices is hindered by the complicated fabrication techniques, complex geometries and limited selection of flexible materials. Electrodes with diverse micro and nanostructures have been adopted to resolve these issues with much improved mechanical performance. This review discusses the recent advances in novel electrode designs in energy storage devices with respect to their diverse role in enhancing the robustness and energy density with full functionality. Although remarkable achievements have been made in highly deformable structural designs, strain engineered substrates and finite element models for mechanical failure analysis, there are still many challenges:(1) High-performance flexible energy storage devices should be constructed using all-deformable components including electrodes, separator, electrolyte and cell casing. To date, various electrode designs including biomimetic, wavy and auxetic structures have been developed to enhance the deformability of batteries. Although these electrodes have demonstrated remarkable mechanical and electrochemical performances, the cell assemblies exhibit relatively poor properties on the device level caused by the interface contact and mismatch among the cell components, electrolyte leakage and stripping of electrode active materials triggered by repeated mechanical deformation. Bifunctional electrodes which eliminate the use of a current collector can be one option to reduce the battery components and interface contact issues. However, deformable electrodes are commonly prepared by slurry or deposition methods. Therefore, a well-established design rule to construct an all-in-one structure with high mechanical deformability is in urgent need.
(2) Novel flexible energy storage devices are generally lower in energy density than the conventional ones. The key to a high electrochemical performance energy storage device is closely related to the electrode/electrolyte interfacial properties, electronic conduction within the electrodes and the utilization of electrolyte. Therefore, the pore distribution, specific surface area and number of interconnects of the electrodes that form the circuit, are the determining factors to the fast redox kinetics of electrochemical cells. However, these properties are usually ignored while optimizing the mechanical features such as high tensile modulus, energy absorption, stretchability, and their integration in energy storage devices. In addition, incorporation of non-electroactive materials – elastic binders, elastomer to render flexibility to the electrodes – inevitably deteriorate the electrical conductivity of the device leading to inferior energy density. In this regard, the balance among different critical parameters is necessary to improve the overall performance.
(3) Scalable manufacturing of an electrode with novel structure remains a hurdle for practical applications in flexible energy storage devices. Wet slurry coating and roll-to-roll manufacturing of conventional electrodes has matured such that it is a commonly employed industrial technique. On the contrary, novel structured electrodes require a design rule for high resolution assembly involving manipulating the geometrical parameters to optimize the mechanical behaviour. To date, most of the reported work utilizes additive manufacturing such as lithography patterning, stereolithographic and fused deposition modelling to form different structures with various dimensions using different building materials. As a consequence, mechanical and electrochemical performance among electrodes produced by different techniques is usually incomparable. A standardized assembly method and selection of building materials to produce flexible cell structures on the industrial scale, needs to be further investigated.
(4) Absence of standardized testing conditions due to the vast selection of geometries, scales of materials and electrode fabrication techniques. Most work has demonstrated the mechanical and electrochemical stability of the novel electrodes or on a device level under static bent, strained and stretched conditions. However, it is crucial to investigate the electrochemical and mechanical degradation of each battery component using a quantitative and reliable operando method in order to critically assess the failure mechanism including: internal resistance change, structural degradation and electrode/electrolyte interface changes. To solve these problems, coupling in situ electrochemical impedance spectroscopy and non-destructive imaging techniques, are essential to reveal electrode/electrolyte interface changes and physical fractures with micrometre-level resolution in the electrodes during electrochemical cycles. In addition, detection of temperature changes induced by defects caused by deformation can be a reliable indicator to investigate the stability of flexible energy storage devices.
In summary, electrodes with unique structures have gained tremendous interest for use in flexible energy storage devices. Although great progress has been achieved, research in this regard is still in its infancy. Owing to the lack of intrinsically flexible electrochemically active materials, the development of flexible energy storage devices relies on electrode and cell structure innovations. Thus, numerous efforts are urgently needed to devote to further experimental research, degradation-probing techniques and theoretical simulations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Xiamen University Malaysia Research Fund (Grant No. XMUMRF/2019-C4/IENG/0021) and Fundamental Research Grant Scheme from the Ministry of Higher Education Malaysia (Grant No: FRGS/1/2020/STG05/XMU/02/3).Notes and references
- A. E. Ostfeld, A. M. Gaikwad, Y. Khan and A. C. Arias, Sci. Rep., 2016, 6, 26122 CrossRef CAS PubMed.
- A. M. Gaikwad, B. V. Khau, G. Davies, B. Hertzberg, D. A. Steingart and A. C. Arias, Adv. Energy Mater., 2015, 5, 1401389 CrossRef.
- L. Dong, C. Xu, Y. Li, Z.-H. Huang, F. Kang, Q.-H. Yang and X. Zhao, J. Mater. Chem. A, 2016, 4, 4659–4685 RSC.
- S. Kang, S. Y. Hong, N. Kim, J. Oh, M. Park, K. Y. Chung, S. S. Lee, J. Lee and J. G. Son, ACS Nano, 2020, 14, 3660–3668 CrossRef CAS PubMed.
- X. Li, H. Li, X. Fan, X. Shi and J. Liang, Adv. Energy Mater., 2020, 10, 1903794 CrossRef CAS.
- Z. Niu, H. Dong, B. Zhu, J. Li, H. H. Hng, W. Zhou, X. Chen and S. Xie, Adv. Mater., 2013, 25, 1058–1064 CrossRef CAS PubMed.
- C. Yu, C. Masarapu, J. Rong, B. Wei and H. Jiang, Adv. Mater., 2009, 21, 4793–4797 CrossRef CAS PubMed.
- L. Li, Z. Lou, W. Han, D. Chen, K. Jiang and G. Shen, Adv. Mater. Technol., 2017, 2, 1600282 CrossRef.
- X. Xia, J. Yang, Y. Liu, J. Zhang, J. Shang, B. Liu, S. Li and W. Li, Adv. Sci., 2022, 2204875 Search PubMed.
- H. Lee, G. Lee, J. Yun, K. Keum, S. Y. Hong, C. Song, J. W. Kim, J. H. Lee, S. Y. Oh and D. S. Kim, Chem. Eng. J., 2019, 366, 62–71 CrossRef CAS.
- V. Rajendran, A. V. Mohan, M. Jayaraman and T. Nakagawa, Nano Energy, 2019, 65, 104055 CrossRef CAS.
- W. Tian, Q. Gao, Y. Tan, K. Yang, L. Zhu, C. Yang and H. Zhang, J. Mater. Chem. A, 2015, 3, 5656–5664 RSC.
- C. Huang, L. Kang, N. Zhang, S. Wan, X. Zhou and J. Zhang, ACS Appl. Mater. Interfaces, 2019, 11, 38303–38312 CrossRef CAS PubMed.
- Z. Zhang, W. Yang, Y. Wu, G. Yan, L. Li, Y. Qing and X. Lu, Ind. Eng. Chem. Res., 2021, 60, 11079–11085 CrossRef CAS.
- M. Naguib, S. Allu, S. Simunovic, J. Li, H. Wang and N. J. Dudney, Joule, 2018, 2, 155–167 CrossRef CAS.
- P. Chang, H. Mei, Y. Tan, Y. Zhao, W. Huang and L. Cheng, J. Mater. Chem. A, 2020, 8, 13646–13658 RSC.
- K. Shang, J. Gao, X. Yin, Y. Ding and Z. Wen, Eur. J. Inorg. Chem., 2021, 606–619 CrossRef CAS.
- J. Gao, K. Shang, Y. Ding and Z. Wen, J. Mater. Chem. A, 2021, 9, 8950–8965 RSC.
- S. Wang, N. Liu, J. Su, L. Li, F. Long, Z. Zou, X. Jiang and Y. Gao, ACS Nano, 2017, 11, 2066–2074 CrossRef CAS PubMed.
- Y. Wang, C. Chen, H. Xie, T. Gao, Y. Yao, G. Pastel, X. Han, Y. Li, J. Zhao, K. K. Fu and L. Hu, Adv. Funct. Mater., 2017, 27, 1703140 CrossRef.
- F. Meng, Q. Li and L. Zheng, Energy Storage Mater., 2017, 8, 85–109 CrossRef.
- Y. Zhang, W. Bai, X. Cheng, J. Ren, W. Weng, P. Chen, X. Fang, Z. Zhang and H. Peng, Angew. Chem., Int. Ed., 2014, 53, 14564–14568 CrossRef CAS PubMed.
- Z. Man, X. Zhu, S. Ye, G. Wu and N. Bao, Energy Fuels, 2022, 36, 9866–9881 CrossRef CAS.
- H. Wei, K. Li, W. G. Liu, H. Meng, P. X. Zhang and C. Y. Yan, Adv. Eng. Mater., 2017, 19, 1700341 CrossRef.
- T. Widlund, S. Yang, Y.-Y. Hsu and N. Lu, Int. J. Solids Struct., 2014, 51, 4026–4037 CrossRef CAS.
- Y. Xie, Y. Liu, Y. Zhao, Y. H. Tsang, S. P. Lau, H. Huang and Y. Chai, J. Mater. Chem. A, 2014, 2, 9142–9149 RSC.
- J. J. Zhang, in Applied Petroleum Geomechanics, ed. J. J. Zhang, Gulf Professional Publishing, Cambridge, 2019, pp. 29–83 Search PubMed.
- Y. M. Poplavko, in Electronic Materials, ed. Y. M. Poplavko, Elsevier, 2019, pp. 71–93 Search PubMed.
- S. Hou, T. Li, Z. Jia and L. Wang, Mater. Des., 2018, 160, 1305–1321 CrossRef CAS.
- R. Magalhaes, P. Subramani, T. Lisner, S. Rana, B. Ghiassi, R. Fangueiro, D. V. Oliveira and P. B. Lourenco, Composites, Part A, 2016, 87, 86–97 CrossRef CAS.
- R. R. Madke and R. Chowdhury, Compos. Struct., 2020, 236, 111838 CrossRef.
- M. Mir, M. N. Ali, J. Sami and U. Ansari, Adv. Mater. Sci. Eng., 2014, 2014, 1–17 CrossRef.
- C. Baumgart, T. Halle, C. Weigelt, L. Krüger and C. G. Aneziris, Sci. Technol. Mater., 2018, 30, 35–42 CrossRef.
- D. Asprone, F. Auricchio, C. Menna, S. Morganti, A. Prota and A. Reali, Compos. Struct., 2013, 105, 240–255 CrossRef.
- K. Qiu, Z. Wang and W. Zhang, Aerosp. Sci. Technol., 2016, 58, 258–266 CrossRef.
- D. Mousanezhad, B. Haghpanah, R. Ghosh, A. M. Hamouda, H. Nayeb-Hashemi and A. Vaziri, Theor. Appl. Mech. Lett., 2016, 6, 81–96 CrossRef.
- B. Mandelbrot, Science, 1967, 156, 636–638 CrossRef CAS PubMed.
- S. James and R. Contractor, Sci. Rep., 2018, 8, 17032 CrossRef PubMed.
- S. T. Hyde and G. E. Schröder-Turk, Interface Focus, 2012, 2, 529–538 CrossRef.
- Y. Xu, in Modern Inorganic Synthetic Chemistry, Elsevier, 2nd edn, 2017, ch. 10, pp. 545–574 Search PubMed.
- R. Lakes, Nature Publishing Group, 1993, 361, 511–515 Search PubMed.
- J. R. Caeiro, P. González and D. Guede, Rev. Osteoporosis Metab. Miner., 2013, 5, 99–108 CrossRef.
- P. Fratzl and R. Weinkamer, Prog. Mater. Sci., 2007, 52, 1263–1334 CrossRef CAS.
- F. K. Ko and J. Jovicic, Biomacromolecules, 2004, 5, 780–785 CrossRef CAS PubMed.
- Y. Aoyanagi and K. Okumura, Phys. Rev. Lett., 2010, 104, 038102 CrossRef PubMed.
- H. Park, C. Song, S. W. Jin, H. Lee, K. Keum, Y. H. Lee, G. Lee, Y. R. Jeong and J. S. Ha, Nano Energy, 2021, 83, 105837 CrossRef CAS.
- W. Liu, J. Chen, Z. Chen, K. Liu, G. Zhou, Y. Sun, M. Song, Z. Bao and Y. Cui, Adv. Energy Mater., 2017, 7, 1701076 CrossRef.
- S. Lochmann, J. Grothe, K. Eckhardt, D. Leistenschneider, L. Borchardt and S. Kaskel, Nanoscale, 2018, 10, 10109–10115 RSC.
- D. M. Soares, Z. Ren, S. B. Mujib, S. Mukherjee, C. G. Martins Real, M. Anstine, H. Zanin and G. Singh, Adv. Energy Sustainability Res., 2021, 2, 2000111 CrossRef CAS.
- Z. Liu, T. Zhu, J. Wang, Z. Zheng, Y. Li, J. Li and Y. Lai, Nano-Micro Lett., 2022, 14, 61 CrossRef CAS PubMed.
- C. Xie, J. Chang, J. Shang, L. Wang, Y. Gao, Q. Huang and Z. Zheng, Adv. Funct. Mater., 2022, 32, 2203242 CrossRef CAS.
- T. Qiu, B. Luo, M. Liang, J. Ning, B. Wang, X. Li and L. Zhi, Carbon, 2015, 81, 232–238 CrossRef CAS.
- T. Qiu, B. Luo, F. Ali, E. Jaatinen, L. Wang and H. Wang, ACS Appl. Mater. Interfaces, 2016, 8, 22768–22773 CrossRef CAS PubMed.
- D. Wang, J. Chang, Q. Huang, D. Chen, P. Li, Y.-W. D. Yu and Z. Zheng, Fundamental Res., 2021, 1, 399–407 CrossRef CAS.
- B. Luo, D. Ye and L. Wang, Adv. Sci., 2017, 4, 1700104 CrossRef PubMed.
- P. Zhang, B. Deng, K. Zhu, Q. Zhou, S. Zhang, W. Sun, Z. Zheng and W. Liu, EcoMat, 2022, 4, e12253 CAS.
- T. Qiu, B. Luo, E. M. Akinoglu, J.-H. Yun, I. R. Gentle and L. Wang, Adv. Funct. Mater., 2020, 30, 2002556 CrossRef CAS.
- T. Qiu, E. M. Akinoglu, B. Luo, M. Konarova, J. H. Yun, I. R. Gentle and L. Wang, Adv. Mater., 2022, 34, 2103842 CrossRef CAS PubMed.
- Y. Hu, S. Debnath, H. Hu, B. Luo, X. Zhu, S. Wang, M. Hankel, D. J. Searles and L. Wang, J. Mater. Chem. A, 2019, 7, 15123–15130 RSC.
- M. Ottenio, D. Tran, A. N. Annaidh, M. D. Gilchrist and K. Bruyère, J. Mech. Behav. Biomed. Mater., 2015, 41, 241–250 CrossRef CAS PubMed.
- J. A. Fan, W. Yeo, Y. Su, Y. Hattori, W. Lee, S. Jung, Y. Zhang, Z. Liu, H. Cheng and L. Falgout, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- B. Ji, Z. Xie, W. Hong, C. Jiang, Z. Guo, L. Wang, X. Wang, B. Yang and J. Liu, J. Materiomics, 2020, 6, 330–338 CrossRef.
- Y. J. Chen, F. Scarpa, Y. J. Liu and J. S. Leng, Int. J. Solids Struct., 2013, 50, 996–1004 CrossRef.
- R. Xia, X. Song, L. Sun, W. Wu, C. Li, T. Cheng and G. Qian, Phys. Status Solidi B, 2018, 255, 1700343–1700351 CrossRef.
- Y. Lee, PhD Thesis, Seoul National University Graduate School Publication, 2017.
- T. Li, Y. Chen, X. Hu, Y. Li and L. Wang, Mater. Des., 2018, 142, 247–258 CrossRef.
- X. T. Wang, X. W. Li and L. Ma, Mater. Des., 2016, 99, 467–476 CrossRef.
- Z. Qin, B. G. Compton, J. A. Lewis and M. J. Buehler, Nat. Commun., 2015, 6, 7038 CrossRef PubMed.
- I. G. Masters and K. E. Evans, Compos. Struct., 1996, 35, 403–422 CrossRef.
- Q. Zhang, X. Yang, P. Li, G. Huang, S. Feng, C. Shen, B. Han, X. Zhang, F. Jin, F. Xu and T. J. Lu, Prog. Mater. Sci., 2015, 74, 332–400 CrossRef.
- W. Wu, W. Hu, G. Qian, H. Liao, X. Xu and F. Berto, Mater. Des., 2019, 180, 107950–107962 CrossRef.
- B. Panda, M. Leite, B. B. Biswal, X. Niu and A. Garg, Measurement, 2018, 116, 495–506 CrossRef.
- L. F. Arenas, C. Ponce de León and F. C. Walsh, Electrochem. Commun., 2017, 77, 133–137 CrossRef CAS.
- Handbook of Nanocomposite Supercapacitor Materials I:Characteristics (Springer Series in Materials Science), ed. K. K. Kamal, Springer, Switzerland, 2020 Search PubMed.
- A. Fares, C. Klumpner and M. Rashed, in 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), IEEE,United Kingdom, 2018, 1–524.
- D. P. Dubal, N. R. Chodankar, D. H. Kim and P. Gomez-Romero, Chem. Soc. Rev., 2018, 47, 2065–2129 RSC.
- J. Libich, J. Máca, J. Vondrák, O. Čech and M. Sedlaříková, J. Energy Storage, 2018, 17, 224–227 CrossRef.
- W. Li, X. Xu, C. Liu, M. C. Tekell, J. Ning, J. Guo, J. Zhang and D. Fan, Adv. Funct. Mater., 2017, 27, 1702738 CrossRef.
- Y. Song, H. Chen, X. Chen, H. Wu, H. Guo, X. Cheng, B. Meng and H. Zhang, Nano Energy, 2018, 53, 189–197 CrossRef CAS.
- D. Kim, D. Kim, H. Lee, Y. R. Jeong, S. J. Lee, G. Yang, H. Kim, G. Lee, S. Jeon, G. Zi, J. Kim and J. S. Ha, Adv. Mater., 2016, 28, 748–756 CrossRef CAS PubMed.
- Y. Lu, K. Jiang, D. Chen and G. Shen, Nano Energy, 2019, 58, 624–632 CrossRef CAS.
- S. Li, X. Wang, H. Xing and C. Shen, J. Micromech. Microeng., 2013, 23, 114013 CrossRef.
- H. Hu, Z. Pei, H. Fan and C. Ye, Small, 2016, 12, 3059–3069 CrossRef CAS PubMed.
- J. Pu, X. Wang, R. Xu, S. Xu and K. Komvopoulos, Microsyst. Nanoeng., 2018, 4, 16 CrossRef PubMed.
- W. Liu, C. Lu, H. Li, R. Y. Tay, L. Sun, X. Wang, W. L. Chow, X. Wang, B. K. Tay, Z. Chen, J. Yan, K. Feng, G. Lui, R. Tjandra, L. Rasenthiram, G. Chiu and A. Yu, J. Mater. Chem. A, 2016, 4, 3754–3764 RSC.
- S. K. Kim, H. J. Koo, A. Lee and P. V. Braun, Adv. Mater., 2014, 26, 5108–5112 CrossRef CAS PubMed.
- G. Lee, D. Kim, D. Kim, S. Oh, J. Yun, J. Kim, S.-S. Lee and J. S. Ha, Energy Environ. Sci., 2015, 8, 1764–1774 RSC.
- Y. Lim, J. Yoon, J. Yun, D. Kim, S. Y. Hong, S.-J. Lee, G. Zi and J. S. Ha, ACS Nano, 2014, 8, 11639–11650 CrossRef CAS PubMed.
- Z. Lv, Y. Tang, Z. Zhu, J. Wei, W. Li, H. Xia, Y. Jiang, Z. Liu, Y. Luo, X. Ge, Y. Zhang, R. Wang, W. Zhang, X. J. Loh and X. Chen, Adv. Mater., 2018, 30, 1805468 CrossRef PubMed.
- Z. Lv, Y. Luo, Y. Tang, J. Wei, Z. Zhu, X. Zhou, W. Li, Y. Zeng, W. Zhang, Y. Zhang, D. Qi, S. Pan, X. J. Loh and X. Chen, Adv. Mater., 2018, 30, 1704531 CrossRef PubMed.
- J. Pu, X. Wang, R. Xu and K. Komvopoulos, ACS Nano, 2016, 10, 9306–9315 CrossRef CAS PubMed.
- L. V. Thekkekara and M. Gu, Sci. Rep., 2017, 7, 45585 CrossRef CAS PubMed.
- M. K. Hota, Q. Jiang, Y. Mashraei, K. N. Salama and H. N. Alshareef, Adv. Electron. Mater., 2017, 3, 1700185 CrossRef.
- S. H. Park, M. Kaur, D. Yun and W. S. Kim, Langmuir, 2018, 34, 10897–10904 CrossRef CAS PubMed.
- J. Xue, L. Gao, X. Hu, K. Cao, W. Zhou, W. Wang and Y. Lu, Nano-Micro Lett., 2019, 11, 46 CrossRef CAS PubMed.
- B. S. Kim, K. Lee, S. Kang, S. Lee, J. B. Pyo, I. S. Choi, K. Char, J. H. Park, S. S. Lee, J. Lee and J. G. Son, Nanoscale, 2017, 9, 13272–13280 RSC.
- Z. Song, T. Ma, R. Tang, Q. Cheng, X. Wang, D. Krishnaraju, R. Panat, C. K. Chan, H. Yu and H. Jiang, Nat. Commun., 2014, 5, 3140 CrossRef PubMed.
- R. Xu, A. Zverev, A. Hung, C. Shen, L. Irie, G. Ding, M. Whitmeyer, L. Ren, B. Griffin, J. Melcher, L. Zheng, X. Zang, M. Sanghadasa and L. Lin, Microsyst. Nanoeng., 2018, 4, 36 CrossRef PubMed.
- X. Tang, H. Zhou, Z. Cai, D. Cheng, P. He, P. Xie, D. Zhang and T. Fan, ACS Nano, 2018, 12, 3502–3511 CrossRef CAS PubMed.
- B. Yao, S. Chandrasekaran, J. Zhang, W. Xiao, F. Qian, C. Zhu, E. B. Duoss, C. M. Spadaccini, M. A. Worsley and Y. Li, Joule, 2019, 3, 459–470 CrossRef CAS.
- S. D. Lacey, D. J. Kirsch, Y. Li, J. T. Morgenstern, B. C. Zarket, Y. Yao, J. Dai, L. Q. Garcia, B. Liu, T. Gao, S. Xu, S. R. Raghavan, J. W. Connell, Y. Lin and L. Hu, Adv. Mater., 2018, 30, 1705651 CrossRef PubMed.
- J. Ding, K. Shen, Z. Du, B. Li and S. Yang, ACS Appl. Mater. Interfaces, 2017, 9, 41871–41877 CrossRef CAS PubMed.
- X. Tang, C. Zhu, D. Cheng, H. Zhou, X. Liu, P. Xie, Q. Zhao, D. Zhang and T. Fan, Adv. Funct. Mater., 2018, 28, 1805057 CrossRef.
- Z. Song, X. Wang, C. Lv, Y. An, M. Liang, T. Ma, D. He, Y. J. Zheng, S. Q. Huang, H. Yu and H. Jiang, Sci. Rep., 2015, 5, 10988 CrossRef CAS PubMed.
- S. Li, R. Li, D. An, Y. Wang, X. Xu, R. Xue and Y. Su, Int. J. Solids Struct., 2022, 256 Search PubMed.
- G. Qian, B. Zhu, X. Liao, H. Zhai, A. Srinivasan, N. J. Fritz, Q. Cheng, M. Ning, B. Qie, Y. Li, S. Yuan, J. Zhu, X. Chen and Y. Yang, Adv. Mater., 2018, 30, 1704947 CrossRef PubMed.
- W. Hwang, S. Kim, C. Y. Ahn, Y. H. Cho and Y. E. Sung, ACS Energy Lett., 2021, 6, 3195–3202 CrossRef CAS.
- A. J. Bandodkar, J.-M. You, N.-H. Kim, Y. Gu, R. Kumar, A. M. V. Mohan, J. Kurniawan, S. Imani, T. Nakagawa, B. Parish, M. Parthasarathy, P. P. Mercier, S. Xu and J. Wang, Energy Environ. Sci., 2017, 10, 1581–1589 RSC.
- W. Song, H. Wang, G. Liu, M. Peng and D. Zou, Nano Energy, 2016, 19, 1–7 CrossRef CAS.
- B. D. Choudhury, C. Lin, S. M. A. Z. Shawon, J. Soliz-Martinez, H. Huq and M. J. Uddin, Sci. Rep., 2021, 11, 7552 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |


