Open Access Article
Open Access ArticleMultifunctional sound-absorbing and mechanical metamaterials via a decoupled mechanism design approach†
Zhendong
Li
 ab,
Xinwei
Li
b,
Zhonggang
Wang
*a and
Wei
Zhai
ab,
Xinwei
Li
b,
Zhonggang
Wang
*a and
Wei
Zhai
 *b
*b
aSchool of Traffic & Transportation Engineering, Central South University, Changsha 410075, Hunan, China. E-mail: wangzg@csu.edu.cn
bDepartment of Mechanical Engineering, National University of Singapore, Singapore 117575, Singapore. E-mail: mpezwei@nus.edu.sg
First published on 17th October 2022
Abstract
Multifunctional materials are in high demand for practical engineering applications. Owing to the ubiquitous noise and impact energy hazards in many settings, traditional materials and conventionally designed metamaterials are incapable of preventing these types of hazard simultaneously. Herein, we report a new paradigm, via a decoupled approach, in the design of acousto-mechanical multifunctional metamaterials. We leverage the morphology of a Helmholtz resonator, such that the sound-absorbing and mechanical components are designed independently. For sound absorption, we adopt a coherent coupling design for a favorable resonant response, while for the mechanical response, we adopt customized struts. We then demonstrate our concept via 3D printing. Experimentally measured remarkable broadband absorption in the practical low-frequency range (<1.0 kHz) is achieved. Absorption mechanisms are attributed to viscous and thermal boundary dissipation. Compression tests also reveal that the metamaterials are highly deformation resilient with a recovery of up to 98%, owing to both the lattice structure design and the viscoelastic behavior of the base material. Through this decoupled design, we further demonstrate the potential of our metamaterials in customizable absorption, strength, pseudo-reusability, and impact resistance. The proposed design paradigm broadens the horizon for the design of multifunctional materials, offering an impetus to their exploration for practical applications.
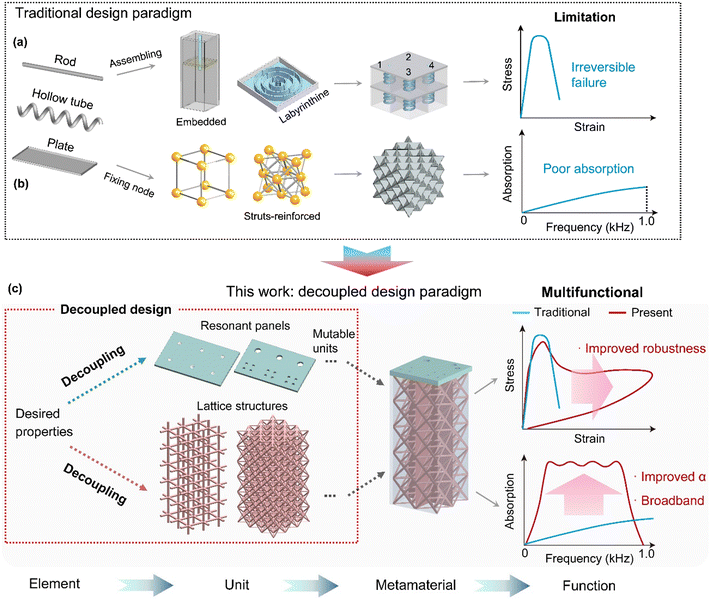
New conceptsTraditional materials, or even modern engineered metamaterials, are incapable of effectively mitigating frequently occurring low-frequency noise and impact energy hazards at the same time. This limitation is primarily due to their mechanism-motivated design principle, where an intrinsic tradeoff between the two exists. A new multifunctional material that can solve this multi-physical problem is highly desirable. Herein, we report a new paradigm in the design of acousto-mechanical metamaterials via decoupling the underlying mechanisms for each function. In particular, we leverage the absorption mechanism of the Helmholtz resonance, which enables independence in the design of structural elements from the sound-absorbing elements. For the sound absorption design, we adopt a coherent coupling design to achieve a favorable localized resonance, while for the mechanical response, we adopt customizable strut features. The metamaterials are 3D printed as a proof of concept. As experimentally demonstrated, the metamaterial is capable of excellent broadband low-frequency (<1.0 kHz) sound absorption, shows high deformation recoverability (up to 98%), and has a physically-tolerable strength for human use (<1 MPa), is pseudo-reusable, and impact resistant. Both the absorption and mechanical responses are fully customizable depending on the requirements. This proposed design approach broadens the horizon in the design of multifunctional metamaterials. |
1. Introduction
Multifunctional materials are highly sought-after in practical engineering design. Materials that are lightweight, tough, have sound-absorbing capabilities, and are safe for human use are in particular demand. Such materials are often used in aerospace, automotive, defence, and construction industries. The characteristics of being lightweight and tough allow materials to contribute to increased fuel-conversion efficiencies and fail-safe designs. In turn, noise attenuation also contributes to safety. For instance, excessive sound, or noise, contributes to thermodynamic instability in machinery/engines, which may lead to their failure; in addition, noise has also been well-established as a serious human-health hazard. One scenario that calls for these aforementioned properties is in the inlet of a jet engine that is often lined with lightweight and strong sound absorbing materials. Therefore, the attenuation of incident sound energy is also of utmost importance for engineering design. Numerous engineering solutions exist for the control of high-frequency (>1.0 kHz) noise.1–5 However, it is really noise in the low-frequency regime that is most difficult to eliminate. Governed by the general rules of linear response,6 commercial sound-absorbing materials, such as foams, fabrics, and panels, are inherently weak in attenuating low-frequency (<1.0 kHz) acoustic waves owing to their long wavelengths and strong penetrating capacities. Through the synthesis of advanced materials, novel foam materials have been proposed as sound absorbers.7–12 Some display decent low-frequency sound absorption.9,12 In recent years, various acoustic metamaterials (AMs) have been proposed as innovative solutions for noise control.13–17 Thus far, AM absorbers have been reported to display low-frequency sound absorption capabilities that far surpass those of traditional materials.18,19 Unlike materials with microstructures determined by their fabrication techniques, most AM absorbers are artificially designed based on specific resonance mechanisms, such as Helmholtz resonance,4,19 non-local,20 and hybrid resonance.21 However, AM absorbers generally suffer from poor mechanical robustness, in particularly poor strength and toughness. As shown in Fig. 1(a), an AM absorber composed of typical resonator units is typically weak and it will experience irreversible failure when the exterior load surpasses the yield strength. They thus lose their sound-absorbing properties this way. Also, they are not designed with the considerations of their mechanical properties in mind from the start. The structures of AM absorbers are typically limited by their resonance mechanisms. Therefore, re-inventing AM absorbers for enhanced mechanical properties without compromising their absorption properties is deemed unfeasible.It is thus intuitive to introduce sound absorption to materials that are already mechanically robust, as opposed to the other way round. One direction we can look into is to leverage the inherent mechanical robustness of lattice structures. Defined as periodic porous structures with elementary features such as struts, shells, plates, or a combination of these, lattice structures display unprecedented mechanical properties that include excellent specific stiffness/strength and unique plateau deformation behaviour that is not found in traditional materials. Intrinsically, lattice structures present high design freedoms for customizable mechanical properties. Notwithstanding, there have been reports on the potential of lattice structures for sound absorption. However, they are mainly limited to the high-frequency range.22–24 The absorption capabilities of these lattices are attributed to their structural porosity, as opposed to a specified acoustic mechanism-guided design. For example, the introduced micro-pores for removing trapped powder in selective laser melting printed lattices opportunely form “flawed resonators”.23,24 In turn, triply periodic minimal surface structures display weak resonance due to the high connectivity of their fluid phases.22 As a result, absorption valleys are commonly observed in these lattices. Moreover, owing to their periodic microscale geometries, they display poor absorption below a frequency of 1.0 kHz (Fig. 1(b)). Even for a lattice with a dedicated design for sound absorption,23 the working frequency range seemingly still focuses on frequencies over 1.0 kHz. A close relative of lattice structures – porous sandwich panels – has been studied as a potential sound absorber.25 However, sandwich panels generally lack customizability for on-demand absorption and mechanical properties.
Interestingly, revisiting the physical mechanism of the Helmholtz resonance, we found that it gives independence to the design of structural elements from the sound-absorbing elements. Specifically, a Helmholtz resonator is composed of a resonant plate with micro-pores and an empty cavity. This “pore-cavity” structure dissipates incident acoustic waves via air frictional flow at the perforations.26 There are two underlying bases for this mechanism: (i) the acoustic energies are mainly dissipated at the pores, and (ii) the empty cavity affects the absorption mainly via its thickness. As mentioned, lattices have unique structural characteristics – such as being ultra-strong or deformation-recoverable – depending on the material selection and design. Thus, theoretically speaking, we can introduce any type of lattice structure in the empty cavity to achieve the desired mechanical property while retaining the sound absorption properties.
Herein, we propose a new paradigm in the design of acousto-mechanical multifunctional metamaterials, based on decoupling of the absorption and mechanical mechanisms. As shown in Fig. 1(c), this approach can overcome the design constraints associated with traditional metamaterials and is also highly customizable for the desired properties. For example, we can modulate the acoustic impedance of resonant plates for frequency-selective absorption and different lattice structures for on-demand mechanical responses, such as high-strength, damage-tolerance, resilience, etc. Thereby, we present a new class of decoupling-enabled porous multifunctional metamaterials (DPMMs). As a proof of concept, these metamaterials are then realized via digital light processing (DLP) 3D printing. As demonstrated experimentally, our DPMM is shown to be capable of excellent broadband low-frequency (<1.0 kHz) sound absorption, having a high deformation recoverability (up to 98%), having a physically-tolerable strength for human uses (<1 MPa), being pseudo-reusable (without apparent absorption loss after cyclic compression), and being impact resistant. Moreover, we further demonstrate the customizable sound-absorbing and mechanical performance of our DPMM for meeting requirements for different applications.
2. Design concept
2.1. Coherent coupling for acoustic absorption
In our decoupled design (Fig. 1(c)), the acoustic and mechanical units are designed independently. First, we focus on sound absorption. The sound absorption characteristics of a Helmholtz resonator are directly related to its acoustic impedance, which is in turn dependent on its geometrical parameters. A proper optimization and design of the resonator is required to achieve good absorptive responses. Before proposing the design, the acoustic impedance is analytically derived here based on the electro-acoustic analogy method.The total impedance of the metamaterial is attained from the calculation of each component. Employing the heterogeneous design, Zs,i represents the surface impedance of the i-th component. This consists of the impedance of the resonant plate (Zm,i) and the cavity (Zc,i), which is calculated as
| Zs,i = Zm,i + Zc,i. | (1) |
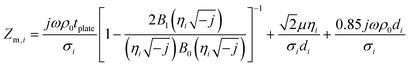 | (2) |
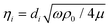 , where ρ0 and μ represent the air density and dynamic viscosity, respectively. B0 and B1 represent the zeroth order and first order Bessel functions, respectively.
, where ρ0 and μ represent the air density and dynamic viscosity, respectively. B0 and B1 represent the zeroth order and first order Bessel functions, respectively.
The impedance of the cavity Zc,i is geometrically determined via the cavity depth. However, in the proposed design, the cavity volume (Vc) is partially occupied by the lattice volume (Vl). Herein, a correction coefficient, λ = Vl/Vc, is introduced to take into account of the influence of the lattice on the effective cavity depth. Hence, the corrected cavity impedance is given by
| Zc,i = −jZ0cot(k(1 − Vl/Vc)D) | (3) |
Thus, the sound absorption coefficient under an incident sound wave is calculated as
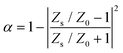 | (4) |
Herein, the surface impedance Zs in this parallel system is calculated as
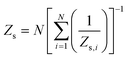 | (5) |
Based on the analytical model, the real parts (acoustic resistance) and imaginary parts (acoustic reactance) of a single and parallel system are schematically compared in Fig. S1(a), ESI.† Apparently, a single circuit can only yield one resonant peak, while the parallel system offers a broad absorption bandwidth. Therefore, a heterogeneous absorber with a parallel connection system is desired for broadband absorption. Herein, we adopt the principle of coherent coupling1,18,20 for the design of our heterogeneous absorber. Using this method, the absorption spectra of each imperfect component (IC) are designed in a weak resonance (Fig. S1(b), ESI†). These components possess different perforation porosity and yield resonant peaks at different frequencies. From a physics point of view, the combination of these weak peaks is synergistic in nature in which a well-damped state is established.
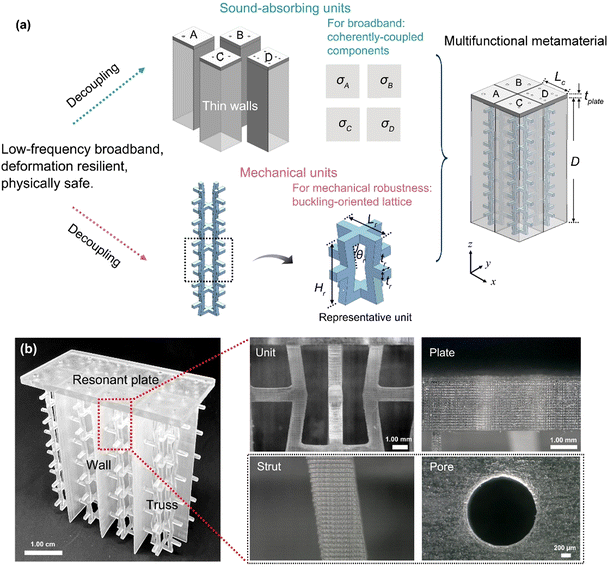
A macroscopic metamaterial unit is shown in Fig. 2(a). Based on the above discussion, the acoustic units are designed with four coherently-coupled weak components. Each component consists of a rigid plate with a different morphology, and they are partitioned by rigid thin walls to impede lateral airflow transfer. The resonant plates possess different perforation ratios, denoted as σA, σB, σC and σD, which are determined by the Zs,i perforation diameter, the number of pores (ni), and the side length (Lc) of each component. As such, the acoustic absorption is associated with the following variables: tplate, di, σi, and D.
2.2. Mechanical robustness
Mechanically efficient lattice structures are necessary to achieve the desired large-strain deformation responses. Since the mechanism of Helmholtz resonance is generally independent of the morphology of the cavity, there are high degrees of freedom to the design in the cavity. It is of note that the structures in the cavity are mutable based on different requirements. Herein, to achieve a stable deformation that bypasses a catastrophic failure, we have adopted re-entrant struts as the mechanical component. There are two main reasons for adopting this configuration. First, it promotes a buckling-dominated deformation when subjected to an axial loading,28,29 which in turn protects the struts from being directly fractured. It is damage-tolerant compared with crystal-inspired lattice structures which display macroscopic shear bands.30,31 Second, the unique auxetic behaviour enables it to shrink inward as opposed to expanding upon compression. In the cavity, re-entrant cells are placed along the x and y directions. The strut geometries are characterized by the cell length Lr, height Hr, angle θr, and strut thickness tr. As mentioned, walls that partition the different resonant cells are necessary. Nonetheless, to eliminate their influence on the mechanical properties of the lattice, these walls are designed to be very thin with a thickness of 300 μm. This very low thickness, compared with the strut thickness, suggests that their contributions to the compressive performance would be negligible.Overall, following the above design steps, a multifunctional metamaterial is constructed. This present decoupling-enabled porous multifunctional metamaterial is thus abbreviated as a DPMM. DPMMs are then fabricated via DLP 3D-printing. An illustration of a cuboid sample with two macroscopic units is shown in Fig. 2(b). The geometric parameters are given in Tables S2 and S3, ESI.† It is worth noting that the correction coefficient, λ, for our re-entrant based DPMM is around 5%. If λ increases owing to an increased number of struts, or an increased strut thicknesses, there might be significant deviations in the sound absorption curves. Also, we limit our concept herein to struts that are sound hard. Our correction model would cease to be accurate if porous, perforated, or ultra-soft struts – those that would have an influence on the effective fluid-flow mechanisms – were introduced into the cavity. Representative microstructural features, including the re-entrant unit, resonant plate, strut, and pore, are observed using a microscope. There are no fractures, burrs, or fault-segmentation observed. The distinct microstructural features of the as-printed micro-perforations are shown in Fig. 2(b). Details of the actual dimensional accuracies are given in Fig. S2 and Table S4, ESI.†
3. Results and discussion
3.1. Absorption performance and mechanism
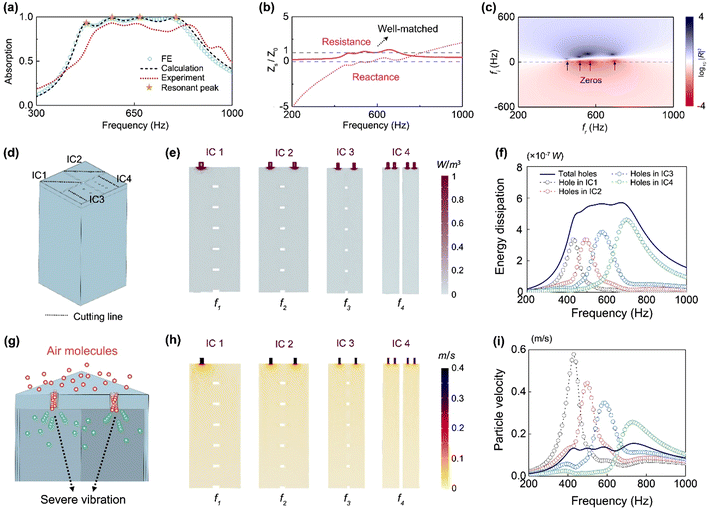
The sound absorption properties and mechanisms of the DPMM are investigated in this section. Fig. 3(a) plots the measured, simulated, and analytically calculated sound absorption coefficient curves. The simulated results are obtained using the Thermoviscous Acoustics Module in the COMSOL Multiphysics package. As shown in Fig. 3(a), the absorption coefficient curve displays a broad effective absorption band from 501 to 883 Hz with α > 0.8, and another sample displays a broadband from 458 to 834 Hz (Fig. S3(b), ESI†). The curves in Fig. 3(a) agree well in terms of the general trend and main working frequency range. Deviations, which are mainly attributed to fabrication defects, are analysed in Fig. S4, ESI.†From eqn (4), an excellent absorption spectrum can be obtained when the structural surface impedance comes in proximity with the impedance of air at the resonant frequencies. Indeed, Fig. 3(b) shows that the real and imaginary parts of the relative impedance Zs/Z0 are close to 1 and 0 over a broad frequency regime. Fig. 3(c) physically illustrates the damping condition via the distribution of log10|R|2 in the complex frequency plane,32 where R denotes the reflection coefficient. In the lossless case, the reflection coefficient contains zeros and poles that are conjugate symmetric. Herein, owing to the coherent coupling design, there are four zeros attained as marked by the black arrows. Apparently, they lie close to the real frequency axis, implying that the energy loss and leakage balance greatly in this system. The superiority of the proposed heterogeneous design is further demonstrated here by comparing it with other patterns (Fig. S5, ESI†). Compared to the present design, the absorption curves in Fig. S5(a) (ESI†) demonstrate that Pattern II yields only one low peak (α < 0.8), and Pattern I and Pattern III produce many absorption valleys with a narrower quasi-perfect (α > 0.9) bandwidth, which is explained by their flawed acoustic resistances (Fig. S5(b), ESI†).
The sound wave attenuation mechanisms are elucidated here. We propose two mechanisms that work synchronously for effective sound absorption: (i) dissipation by friction of the viscous flow of the air molecules, and (ii) thermal boundary layer dissipation. The two mechanisms lead to the obvious thermoviscous effect at the resonance frequency. In the simulations, it is assumed that the system is lossless, and linearization is performed for the Navier–Stokes equation. Eventually, the thermoviscous effect is calculated using the continuity equation, momentum equation and energy conservation equation as given respectively in eqn (S1)–(S3), ESI.† Herein, the four imperfect components (ICs) are cut along the corresponding pores as shown in Fig. 3(d). Then, the acoustic energy-dissipating phenomenon is clearly disclosed by the acoustic features at the resonant frequencies (f1 = 460 Hz, f2 = 520 Hz, f3 = 570 Hz, and f4 = 690 Hz). From the total viscous-thermal energy dissipation density distribution shown in Fig. 3(e), regardless of the IC, the acoustic energy dissipation in the pores is overwhelmingly dominant, while the contributed dissipation in the cavities is negligible. Owing to the high rigidity of the tough polymer (with a Young's modulus of around 1.45 GPa23), the thin walls are treated as solid and sound-hard boundaries, and thus each IC contributes to the sound absorption individually. Fig. 3(f) plots the pores’ contributions in each component. The results coincide with the resonant frequency of a Helmholtz resonator: ωr = (c02Spores/tplateVc)0.5, where Spores denotes the cross-sectional area of the pores. From IC1 to IC4, the increasing Spores and smaller di jointly contribute to the increased resonant frequency observed. Eventually, the overall energy-dissipating curve is high and successive. Also, the resonant frequencies correspond to the dissipation maximum. Similarly, the air velocity is much higher in pores than in cavities (Fig. 3(h)). When air particles are moving vigorously in the air columns in the micro-perforations at the resonant frequencies, the ICs attain the velocity peaks (Fig. 3(h)).
The viscous dissipation is pivotal compared with the thermal dissipation (Fig. S7, ESI†). This can be explained by the difference in their physical mechanisms. Regarding thermal dissipation, this is induced by the breakdown of the adiabatic propagation of sound waves. Energy conversion and loss occur in thermal boundary layers. In turn, viscous dissipation occurs in the pores due to the vibration and friction of air molecules, which is calculated using33
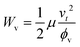 | (6) |
For further understanding of the underlying physics of the outstanding absorptive characteristics, we compare the proposed weak-resonance design recipe with the traditional perfect-resonance strategy. For the latter, the absorption coefficients of the resonant peaks in every component are capable of reaching values above 0.99, owing to the energy leakage and loss being balanced perfectly. Then, these perfect components (PCs) are assembled. A comparison of the absorptive performance is given in Fig. S8(a) and (b), ESI.† In the traditional design, the number of absorption peaks reduces, but for the present design, the four ICs form a higher and wider absorption spectrum. The bandwidth with α = 0.5, 0.9, and 0.95 reflects the huge gap between the two design recipes (Fig. S8(c), ESI†). The pronounced discordant impedance matching state physically explains the vital drawbacks of the traditional design by which the system is heavily over-damped (Fig. S8(d), ESI†). Hence, a flawed response is observed, which is featured as distant zeros far from the real frequency axis. The dotted contour lines in Fig. S8(e) demonstrate the quasi-perfect absorption domains where α > 0.9. In stark contrast to the traditional design, the present design offers a well-matched impedance with the air medium, and the zeros are located close to the real frequency axis, thereby forming a broadband quasi-perfect regime.
Overall, the superb absorptive performance of the DPMM lies with the coherent coupling effect induced by weak resonances. Specifically, the weak components are dexterously tuned via lowering their damping capacities to the target domain (Fig. S9, ESI†). Benefitting from the peculiar heterogeneous arrangement, the dexterously tuned pore size decreases the loss factor, and the system is impelled to balance the energy loss and leakage to the full, thereby attenuating low-frequency noise in a broadband regime.
3.2. Resilience and deformation mechanism
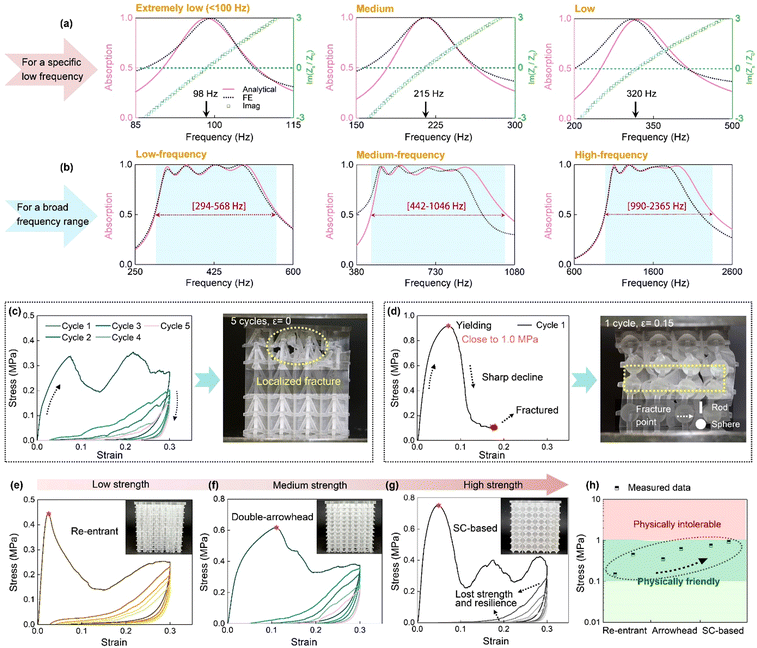
Next, we illustrate the mechanical behaviour of our DPMM. Its resilience to deformation is illustrated through cyclic compression tests. The metamaterial is subjected to an axial quasi-static loading at a strain rate of 0.002 s−1. A relaxation time of 300 s is allowed for full recovery. The experimentally measured cyclic compression stress–strain curves are shown in Fig. 4(a). At this low relative density of 12%, the metamaterial displays a high strength of around 0.16 MPa. The strength also falls within a physically safe value for human protection use34 (<1 MPa). Compression past the 6th cycle reveals that the DPMM converges to a maximum compression strength of around 0.05 MPa. The energy absorption in each cycle is depicted in Fig. S10, ESI.† The energy absorption and specific energy absorption (SEA) upon the first loading cycle are measured to be around 1451 mJ and 185 mJ g−1, respectively. A decline is observed from the 2nd cycle onwards. Nonetheless, the loss of absorbed energy is found to be moderate with successive cycles. A formula is fitted to characterize the decaying phenomenon as: Ea = 1420.73M−1, where Ea denotes the absorbed energy (mJ) and M represents the corresponding cycle. The power law with a coefficient of −1 demonstrates the decaying regularity. The captured experimental deformation modes in the first loop are shown in Fig. 4(b). Interestingly, the expected auxetic behaviour is observed for both the loading and unloading processes. The whole material is being bent inward, with the cross-sectional profile depicted by the yellow dotted lines. The auxetic behaviour becomes more pronounced with continuous loading and then vanishes in the unloading cycle. Upon the completion of each cycle, the metamaterial recovers exactly to its initial shape. Nonetheless, damage associated with the fracture of struts occurs (Fig. S11, ESI†) in the nodal region of the struts, i.e., the high-stress regions. This then results in a reduced number of intact re-entrant struts, which explains the sharp drop in the retained strength during the second cycle. Overall, the metamaterial is resilient enough to recover itsoriginal shape regardless of the damage. | ||
| Fig. 4 Cyclic performance, resilience benchmarking, and mechanisms. (a) Representative cyclic compression stress–strain curve of the DPMM. (b) Digital images of the deformation sequence, including both loading and unloading. (c) Comparison between our metamaterial and previously reported microlattice metamaterials in terms of the recoverability and compressive strength. Referenced data: Al2O3 hollow lattice,35 Ni–P hollow tube,36 Al2O3 nanolattice,37 NiP microlattice,38 nano glass,39 nickel hollow tube,40 Au nanolattice,41 and NiP hierarchical lattice.42 (d) Schematic illustration of the unique buckling behaviour of four selected representative units. | ||
The benchmarking of the resilience of our metamaterials with some previously reported microlattice metamaterials is depicted in Fig. 4(c). Resilience reflects the ability of a material to recover its initial configuration after being subjected to a large applied strain in the plastic or inelastic regime. Generally, the strength and recoverability of metamaterials are mutually exclusive. For quantification, herein, we define the recoverability as the ratio of the recovered strain, εr, to the total applied strain, εt, i.e., εr/εt. For a given strain, the recoverability of a material is close to zero if the material fractures and the recovered strain is marginal. Apart from this re-entrant DPMM, the recovery performance of five other samples, with different lattice structures and densities, are plotted in the same figure. Leveraging the decoupled design, varying properties can be achieved using different lattice designs. Details of these lattices are discussed in the next section. Apparently, four data points are found to display a recoverability of over 80%. Our metamaterials show a marginal degradation over multiple loading cycles compared with previously reported metamaterials. The strength of DPMMs is not the highest among the reported metamaterials, but the overall recoverability–strength performance is exceptional. Other metamaterials with comparable or higher compressive strengths typically have small recoverability values, exhibiting severe failure at low strain values.
To gain a deeper insight into the mechanisms, the characteristic features during deformation are further explored here. We propose that the remarkable resilience lies in two mechanisms: (i) the mechanical units, i.e., the lattice structure, (ii) and the viscoelasticity of the base material. A deformation mode at a compressive strain of 0.1 is presented in Fig. S12(a), ESI.† The localized bending and global buckling are discussed here. Corresponding microscopic characteristics of the representative re-entrant units are illustrated in Fig. 4(d). U1 and U2 are representative units on the left side of the lattice structure as annotated in Fig. S12(a), and they are bent inward to the right side. However, they tilt in the opposite direction. The similar phenomenon is observed for U3 and U4. Moreover, owing to these unique types of buckling behaviour for the individual units, the global auxetic effect is more pronounced (Fig. S12(b), ESI†). Subjected to further axial loading, the strut buckling would then be more prevalent for which interior inter-cell interactions then become significant. Eventually, an obvious cell agglomeration is produced. This agglomeration effect, on the one hand, strengthens the load-bearing ability, but, on the other hand, it causes some damage in high-stress nodes. In the compared reported microlattice metamaterials, most of them exhibit localized fracture of struts. As such, with successive loading, the accumulated strut fracture eventually leads to severe deterioration of the mechanical performance. Nonetheless, a substantial number of localized strut fractures here are suppressed owing to the buckling-dominated behaviour of the auxetic lattice. This ultimately enables our metamaterial to preserve its original morphology in subsequent cycles. Meanwhile, we found that the viscoelasticity of the base material plays an important role in the exceptional recoverability. The viscoelastic effect is experimentally validated by comparing the hysteresis loop of two samples with and without relaxation (Fig. S13, ESI†). Obviously, Sample B without a relaxation time cannot fully recover its original shape, and thus shows reduced recoverability.
4. Further discussion
Herein, we demonstrate the further potential of the metamaterials designed through this decoupled concept. Still applying the Helmholtz resonator-based sound-absorbing units, Fig. 5(a) and (b) demonstrate the capabilities of customizable absorption for different applications and requirements. Fig. 5(a) shows the possibilities for maximum absorption at a specified frequency. A broad selection of frequencies, at 98 Hz, 215 Hz, and 320 Hz is illustrated. In turn, Fig. 5(b) shows the possibilities for a broad absorption spectrum at a diverse selection of frequency bands. In terms of the mechanical performance, we herein introduce two other types of lattice unit: double-arrowhead and simple cubic (SC)-based units. Schematics of the units and the corresponding metamaterial deformation modes are shown in Fig. S14, ESI.† Correspondingly, the cyclic compressive performance and resultant damage to the specimens are exhibited in Fig. 5(c) and (d). For the arrowhead pattern, the strength is well-preserved upon being subjected to cyclic loading; especially for the first cycle, no sharp drop is observed. While for the SC-based pattern, it increases to a high strength of close to 1.0 MPa. After yielding, unsurprisingly, a large decline in the stress occurs and catastrophic fracture occurs. This subsequently leads to clear shear splitting and twisting of the structure (Fig. S14, ESI†). Fractures then take place at the joints between the rods and spheres, which correspond to the regions of the highest stress concentration. Under the desired deformation morphology, if a higher strength is required, the number of lattice units within the cell can be increased. Fig. 5(e) and (f) show the stress–strain curves of the re-entrant, arrow-head, and SC based DPMMs that have twice the number of lattice units per meta-unit. Unsurprisingly, increased strengths are observed for all. Also, the recoverability of the re-entrant and arrowhead DPMM is well-retained, while for the SC-based DPMM it is largely decreased. Basically, the re-entrant and arrowhead units still assist the metamaterial to retain the buckling-dominated mode via strut bending. Nonetheless the SC-based units yield desired localized buckling, and the unbalanced stress distribution leads to eventual fracture in a large area. The geometrical specifications of these structures are given in Section S6, ESI.† Herein, the base material is a tough polymer. Of course, the proposed lattice structures could be made using soft materials to achieve better recovery and auxetic responses. However, this would be at the trade-off of high strength.43,44Considering human use,34 as shown in in Fig. 5(h), we separate the 0.01 to 1 MPa and 1 to 10 MPa regions into physically-friendly and physically-intolerant regions, respectively. Benefiting from the decoupled design, the three kinds of lattice offer a progressive strength range. The experimentally measured yield strengths are depicted by the scattered data points in the physically friendly region. It is of note that the region from 0.01 to 0.1 MPa is easily achieved using soft materials such as polymeric foams. However, these materials would have limited energy absorption capacities in protecting humans from crash hazards.
Fig. 6(a) presents the sound absorption coefficient curves of the DPMM in its pristine and deformation-recovered states after cyclic compression tests. Although strut fractures and damage occur from the compression, the plate layer is, however, unaffected. The ability to fully recover also enables the cavity morphology to be retained. The DPMM is thus able to retain its sound absorption capabilities without distinct changes to the absorption peaks, bandwidth, and trend. Deviations may be attributed to the slight tearing of the cell walls where some lateral sound wave propagation may take place. Generally, the damage after compression has a negligible effect on the sound absorption. Overall, in contrast to traditional sound-absorbing materials, our metamaterial is experimentally verified as being mechanically robust with dynamic functionalities, with sound-absorbing properties retained after multiple mechanical loading cycles. The energy-absorbing protective design also endows the DPMM with an extraordinary force attenuation capacity. We illustrate this via free-fall drop tests, which are schematically illustrated in Fig. S15, ESI.† Herein, we adopted various fragile objects: a beaker, glass light bulb, and goose egg, for illustration. Aftermath images of the drop tests are shown in Fig. 6(b) and Video S1 (ESI†). When the DPMM is used as the protection surface, all of these objects are well protected. No damage is observed. In turn, when there is no DPMM protection, e.g., free-fall tests onto the ground, catastrophic failure occurs with the shattering of these objects.
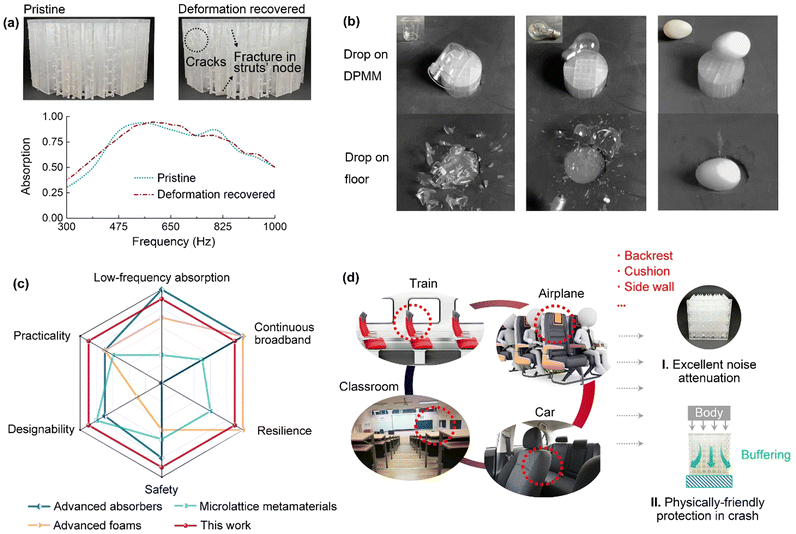 | ||
| Fig. 6 Multifunctionalities and potential applications. (a) Sound absorption curves of the pristine and deformation recovered DPMM. (b) Aftermath images of a beaker, bulb, and goose egg free-fall dropped onto the DPMM (top) and the floor (bottom). (c) Radar chart for the overall appreciation of the DPMM compared with mainstream acoustic and mechanical metamaterials, i.e., advanced absorbers,19,20 microlattice metamaterials,24,30,36 and advanced foams.9,11 (d) Illustration of the potential applications of the DPMM, for use in aerospace, automobile, and construction industries, etc. | ||
Fig. 6(c) shows an overall appreciation of the DPMM via comparing it with mainstream acoustic and mechanical metamaterials. Herein, we base the performance metrics on practical mechanical and acoustic requirements. Specifically, six figures of merit are designated: low-frequency absorption, continuous broadband, resilience, safety, designability, and practicality. The benchmark for these comparisons is detailed in Table S7, ESI.† Low-frequency absorption herein refers to the efficient absorption below 1.0 kHz. Continuous broadband refers to multiple absorption peaks and no abrupt absorption valleys in the spectra. The resilience index means recoverability after a large-strain deformation. Safety is justified by two aspects: the potential risks to human health during the manufacturing process, and the yield strength. Designability refers to the geometric and configurational tunability for the desired properties. Practicality is justified by the low-frequency performance, safety, and reusability after large-strain deformation. Fig. 6(c) indicates that our metamaterials are capable of balancing a high performance in all six criteria. For advanced absorbers, we refer to the elaborately designed sound-absorbing metamaterials.19,20 They are practical in noise control engineering as they can offer excellent low-frequency broadband absorption. However, they display low mechanical robustness. Catastrophic collapse is inevitable upon mechanical loading. Microlattice metamterials24,30,36 have remarkable designability owing to the high design freedom of their geometries. Their acoustic absorption performance is limited, however, and most are not recoverable except for nanolattices. These microlattices possess high strength that far exceeds 1.0 MPa, and hence they are not viable as impact protectors for human use. Advanced foams9,11 refer to foams fabricated with new materials or using advanced processing technologies. We acknowledge that they display a better deformation resilience and sound absorption bandwidth, and that some9,12 even display good absorption at the low frequencies (below 1.0 kHz). However, advanced foams are usually synthesized using hazardous materials. Also, they are ultra-lightweight for which they may pose a hazard to human health if loose fibres are breathed in.45 Next, we list some representative application scenarios of the DPMM in Fig. 6(d). In its pristine state, our metamaterials function as excellent sound absorbers to reduce noise. Under dynamic impact energy, they can absorb crushing energy to protect their inhabitants. Specifically, they could be used as a cushion, backrest, or lining for the walls of an automobile or aircraft. In addition, the concept of DPMM is also materials agonistic – as long as the material is 3D printable. In this way, extended applications and performance, apart from those presented using the tough polymer herein, are made possible. For instance, a DPMM made using a high-strength steel functions as a single-use protection material against high kinetic energy projectiles.
Conclusions
In summary, we present a new paradigm, via decoupling of the functional mechanisms, for the design of simultaneously sound-absorbing and mechanically efficient metamaterials. Leveraging the sound absorption mechanism of a Helmholtz resonator, we independently design the sound-absorbing elements, based on a resonating plate, and the mechanical elements, based on different lattice units. We then present a new class of decoupled porous multifunctional metamaterials (DPMMs) and their performance is validated via 3D printed samples using a tough polymer. Specifically, by modulating the impedance matching of the pores in the resonant plate, a remarkable low-frequency broadband absorption is attained. The high and near-perfect absorption is attributed to the coherent coupling effect, which is produced by the elaborately designed weak resonances. The absorption mechanisms are attributed to the viscous flow and thermal dissipation through the pores. The DPMM with auxetic struts exhibits an excellent deformation-recoverable compressive response. Full recovery from a compressive strain of 30%, at a high strength of around 0.16 MPa, is demonstrated.We have also demonstrated the tremendous potential of our metamaterials, including absorbing sound in a specific low-frequency region, a broadband range, and offering a wide physically-friendly strength range. More significantly, our metamaterial is experimentally verified as being mechanically robust, where its sound absorption properties are retained after multiple cyclic loadings. The demonstrated free-fall tests using fragile objects also indicate that the DPMM displays an extraordinary force attenuation capacity. All in all, the proposed decoupled design enables our metamaterials to be low-frequency broadband sound-absorbing, deformation resilient, impact-resistant, pseudo-reusable, and physically-safe. They can be adopted as protective materials in transportation and construction, where they can eliminate indoor noise and offer protection against potential impact damage.
Methods
Fabrication of the specimens and characterization: specimens were manufactured using a digital light processing (DLP) 3D printer (Asiga, Australia). The base material is a tough resin, PlasClear V2, produced by the same company. The printing parameters are as follows: light intensity, 35 mW cm−2; layer thickness, 100 μm; exposure time, 3 s; and substrate burn-in exposure, 20 s. Printed specimens were rinsed with isopropyl alcohol for 15 mins and then dried using a high-power blowing machine. They were then post-cured using an Asiga Flash UV box for 30 mins. All the specimens in this work were processed using these procedures. Microstructural observations were captured using a KEYENCE VHX-6000 digital microscope.Compression tests: the geometries of the mechanical specimens prepared for compression are illustrated in Section S1, ESI.† Cyclic compression tests were performed using a Shimadzu AG25-TB universal testing machine at a strain rate of 0.002 s−1. The metamaterials were allowed to relax for 300 s before each compression, except for the control group prepared for examining the viscoelastic effect. The specimens were placed in the centre of the platens, and then compressed by the moving rigid plate along the longitudinal direction until each cycle was completed. A digital camera was used for capturing the deformation modes.
Sound absorption tests: the standard impedance tube setup (SKC ZT13) was adopted for sound absorption coefficient measurements. A tube with a 100 mm diameter, with an effective working frequency range of 63 Hz to 1600 Hz, was utilized. The specimens were printed to this tubular dimension so that a snug fit with the impedance tube was ensured.
Finite element analysis: the FE model was constructed in COMSOL Multiphysics using the Thermoviscous Acoustics module with its built-in boundary layer theory. The solid material was set as the hard-boundaries without transverse air transmission. The incident sound wave was transmitted based on the pressure-acoustics module, and a perfectly matched layer (PML) was applied to mimic non-reflecting infinite fields above the model domain.
Author contributions
Z. Li: conceptualization, methodology, investigation, writing – original draft, writing – review and editing. X. Li: methodology, writing – review and editing. W. Zhai: conceptualization, supervision, formal analysis, writing – review and editing. Z. Wang: conceptualization, supervision, formal analysis, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (51875581) and A*STAR under its AME YIRG Grant (Project No. A20E6c0099). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not reflect the views of the A*STAR.Notes and references
- S. Huang, et al., Compact broadband acoustic sink with coherently coupled weak resonances, Sci. Bull., 2020, 65(5), 373–379 CrossRef.
- H. Long, C. Shao, C. Liu, Y. Cheng and X. Liu, Broadband near-perfect absorption of low-frequency sound by subwavelength metasurface, Appl. Phys. Lett., 2019, 115, 103503 CrossRef.
- M. Duan, C. Yu, F. Xin and T. J. Lu, Tunable underwater acoustic metamaterials via quasi-Helmholtz resonance: From low-frequency to ultra-broadband, Appl. Phys. Lett., 2021, 118, 071904 CrossRef CAS.
- M. Yang, S. Chen, C. Fu and P. Sheng, Optimal sound-absorbing structures, Mater. Horiz., 2017, 4, 673–680 RSC.
- F. Ma, C. Wang, Y. Du, Z. Zhu and J. H. Wu, Enhancing of broadband sound absorption through soft matter, Mater. Horiz., 2022, 9, 653–662 RSC.
- H. Y. Mak, et al., Going beyond the Causal Limit in Acoustic Absorption, Phys. Rev. Appl., 2021, 16(4), 044062 CrossRef CAS.
- L. Li, et al., Nanograin–glass dual-phasic, elasto-flexible, fatigue-tolerant, and heat-insulating ceramic sponges at large scales, Mater. Today, 2022, 54, 72–82 CrossRef CAS.
- C. Jia, Z. Xu, D. Luo, H. Xiang and M. Zhu, Flexible Ceramic Fibers: Recent Development in Preparation and Application, Adv. Fiber Mater., 2022, 4, 573–603 CrossRef CAS.
- D. Zong, et al., Bubble Templated Flexible Ceramic Nanofiber Aerogels with Cascaded Resonant Cavities for High-Temperature Noise Absorption, ACS Nano, 2022, 16(9), 13740–13749 CrossRef CAS PubMed.
- D. Zong, et al., Flexible ceramic nanofibrous sponges with hierarchically entangled graphene networks enable noise absorption, Nat. Commun., 2021, 12, 6599 CrossRef CAS PubMed.
- K. Pang, et al., Highly Efficient Cellular Acoustic Absorber of Graphene Ultrathin Drums, Adv. Mater., 2022, 34(14), 2103740 CrossRef CAS.
- C. Jia, et al., Highly compressible and anisotropic lamellar ceramic sponges with superior thermal insulation and acoustic absorption performances, Nat. Commun., 2020, 11, 3732 CrossRef CAS PubMed.
- V. Romero-García, G. Theocharis, O. Richoux and V. Pagneux, Use of complex frequency plane to design broadband and sub-wavelength absorbers, J. Acoust. Soc. Am., 2016, 139, 3395 CrossRef.
- N. Jiménez, V. Romero-García, V. Pagneux and J. P. Groby, Rainbow-trapping absorbers: Broadband, perfect and asymmetric sound absorption by subwavelength panels for transmission problems, Sci. Rep., 2017, 7, 13595 CrossRef.
- N. Jiménez, W. Huang, V. Romero-García, V. Pagneux and J. P. Groby, Ultra-thin metamaterial for perfect and quasi-omnidirectional sound absorption, Appl. Phys. Lett., 2016, 109, 121902 CrossRef.
- S. Qu and P. Sheng, Microwave and Acoustic Absorption Metamaterials, Phys. Rev. Appl., 2022, 17, 047001 CrossRef CAS.
- S. Qu, et al., Underwater metamaterial absorber with impedance-matched composite, Sci. Adv., 2022, 8(20), eabm4206 CrossRef CAS.
- Z. Wang, Z. Guo, Z. Li and K. Zeng, Coupling and scaling effect for low-frequency broadband sound absorption via vertex-based hierarchy, Appl. Phys. Lett., 2021, 119, 171903 CrossRef CAS.
- F. Wu, et al., Low-frequency sound absorption of hybrid absorber based on micro-perforated panel and coiled-up channels, Appl. Phys. Lett., 2019, 114, 151901 CrossRef.
- Z. Zhou, S. Huang, D. Li, J. Zhu and Y. Li, Broadband impedance modulation via non-local acoustic metamaterials, Natl. Sci. Rev., 2021, 9(8), nwab171 CrossRef.
- G. Ma, M. Yang, S. Xiao, Z. Yang and P. Sheng, Acoustic metasurface with hybrid resonances, Nat. Mater., 2014, 13, 873–878 CrossRef CAS.
- W. Yang, J. An, C. K. Chua and K. Zhou, Acoustic absorptions of multifunctional polymeric cellular structures based on triply periodic minimal surfaces fabricated by stereolithography, Virtual Phys. Prototyping, 2020, 15, 242–249 CrossRef.
- X. Li, X. Yu and W. Zhai, Additively Manufactured Deformation-Recoverable and Broadband Sound-Absorbing Microlattice Inspired by the Concept of Traditional Perforated Panels, Adv. Mater., 2021, 33(44), 2104552 CrossRef CAS.
- Z. Li, et al., Additively manufactured dual-functional metamaterials with customisable mechanical and sound-absorbing properties, Virtual Phys. Prototyping, 2022, 17, 864–880 CrossRef.
- Z. Ren, Y. Cheng, M. Chen, X. Yuan and D. Fang, A compact multifunctional metastructure for Low-frequency broadband sound absorption and crash energy dissipation, Mater. Des., 2022, 215, 110462 CrossRef.
- D.-Y. Maa, Potential of microperforated panel absorber, J. Acoust. Soc. Am., 1998, 104, 2861 CrossRef.
- Y. Tang, et al., Hybrid acoustic metamaterial as super absorber for broadband low-frequency sound, Sci. Rep., 2017, 7, 43340 CrossRef PubMed.
- D. Acuna, et al., A three step recipe for designing auxetic materials on demand, Commun. Phys., 2022, 5, 113 CrossRef.
- K. K. Saxena, R. Das and E. P. Calius, Three Decades of Auxetics Research − Materials with Negative Poisson’s Ratio: A Review, Adv. Eng. Mater., 2016, 18(11), 1847–1870 CrossRef CAS.
- X. Li, et al., Microlattice Metamaterials with Simultaneous Superior Acoustic and Mechanical Energy Absorption, Small, 2021, 17(24), 2100336 CrossRef CAS PubMed.
- M. S. Pham, C. Liu, I. Todd and J. Lertthanasarn, Damage-tolerant architected materials inspired by crystal microstructure, Nature, 2019, 565, 305–311 CrossRef CAS PubMed.
- V. Romero-Garciá, et al., Perfect and broadband acoustic absorption by critically coupled sub-wavelength resonators, Sci. Rep., 2016, 6, 19519 CrossRef.
- M. J. Cops, J. G. McDaniel, E. A. Magliula and D. J. Bamford, Analysis of thermal and viscous boundary layers in acoustic absorption by metallic foam, J. Acoust. Soc. Am., 2019, 146, 649 CrossRef CAS.
- E. C. Clough, et al., Elastomeric Microlattice Impact Attenuators, Matter, 2019, 1, 1519–1531 CrossRef.
- L. R. Meza, S. Das and J. R. Greer, Strong, lightweight, and recoverable three-dimensional ceramic nanolattices, Science, 1979, 345(6202), 1322–1326 CrossRef.
- T. A. Schaedler, et al., Ultralight metallic microlattices, Science, 2011, 334(6058), 962–965 CrossRef CAS PubMed.
- L. R. Meza, et al., Resilient 3D hierarchical architected metamaterials, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(37), 11502–11507 CrossRef CAS PubMed.
- A. Torrents, T. A. Schaedler, A. J. Jacobsen, W. B. Carter and L. Valdevit, Characterization of nickel-based microlattice materials with structural hierarchy from the nanometer to the millimeter scale, Acta Mater., 2012, 60(8), 3511–3523 CrossRef CAS.
- R. Liontas and J. R. Greer, 3D nano-architected metallic glass: Size effect suppresses catastrophic failure, Acta Mater., 2017, 133, 393–407 CrossRef CAS.
- L. Salari-Sharif, L. Valdevit and T. A. Schaedler, Energy dissipation mechanisms in hollow metallic microlattices, J. Mater. Res., 2014, 29, 1755–1770 CrossRef CAS.
- L. C. Montemayor and J. R. Greer, Mechanical response of hollow metallic nanolattices: Combining structural and material size effects, J. Appl. Mech., Trans. ASME, 2015, 82(7), 071012 CrossRef.
- X. Zheng, et al., Multiscale metallic metamaterials, Nat. Mater., 2016, 15, 1100–1106 CrossRef CAS PubMed.
- X. Ren, J. Shen, P. Tran, T. D. Ngo and Y. M. Xie, Design and characterisation of a tuneable 3D buckling-induced auxetic metamaterial, Mater. Des., 2018, 139, 336–342 CrossRef.
- X. Zheng, X. Guo and I. Watanabe, A mathematically defined 3D auxetic metamaterial with tunable mechanical and conduction properties, Mater. Des., 2021, 198, 109313 CrossRef CAS.
- J. P. Arenas and M. J. Crocker, Recent trends in porous sound-absorbing materials, Sound Vib., 2010, 44, 12–18 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh00977c |
| This journal is © The Royal Society of Chemistry 2023 |