Metal–organic framework clustering through the lens of transfer learning

Abstract

Metal–organic frameworks (MOFs) are promising materials with various applications, and machine learning (ML) techniques can enable their design and understanding of structure–property relationships. In this paper, we use machine learning (ML) to cluster the MOFs using two different approaches. For the first set of clusters, we decompose the data using the textural properties and cluster the resulting components. We separately cluster the MOF space with respect to their topology. The feature data from each of the clusters were then fed into separate neural networks (NNs) for direct learning on an adsorption task (methane or hydrogen). The resulting NNs were then used in transfer learning (TL) where only the last NN layer was retrained. The results show significant differences in TL performance based on which cluster is chosen for direct learning. We find TL performance depends on the Euclidean distance in the decomposed feature space between the clusters involved in the direct and TL. Similar results were found when TL was performed simultaneously across both types of clusters and adsorption tasks. We note that methane adsorption was a better source task than hydrogen adsorption. Overall, the approach was able to identify MOFs with the most transferable information, leading to valuable insights and a more comprehensive understanding of the MOF landscape. This highlights the method's potential to generate a deeper understanding of complex systems and provides an opportunity for its application in alternative datasets.

---

Design, System, Application

Herein we combine the use of clustering algorithms and transfer learning (TL) to derive new insights into the material landscape of metal–organic frameworks (MOFs). We perform TL of adsorption tasks across clusters in the MOF space; from one set of MOFs to another set of MOFs. We find that the TL performance depends on the distance between the clusters involved. A key insight with design implications for MOFs, is that MOF clusters at or near the center of the feature space are the best TL performers. We also find that different adsorbates are also more apt at TL than others. This suggests that there are gifted MOFs and adsorbates particularly suited to be the basis for TL. These findings will lead to further studies to design MOFs in these feature spaces as well as their use to make predictions in regions of the MOF space with scarce data, which is one of the strengths of TL.

Introduction

Metal–organic frameworks (MOFs) are an exciting material class with great potential in a myriad of applications. They have been researched for different and broad uses such as drug delivery,^1–4 supercapacitors,^5–8 gas storage,^9–11 and separation processes.^12–15 This is because MOFs are both diverse and highly controllable. MOFs are made of inorganic nodes and organic linkers that self-assemble into a network. Generally, MOFs are attractive because their modularity allows researchers to control different material features such as pore size and chemistry, making them ideal for multitudes of tasks and needs.^16–19 The large complexity and scale associated with MOFs have led to the use of computational methods to evaluate them.^20–28

Machine learning (ML) is a growing field that includes different methods to better understand and harness data to make predictions and gather insights. One domain of significant interest is chemical and material research. Regarding MOFs as a materials subset, there are over 100 000 that have been experimentally synthesized and reported in the Cambridge Structural Database and the number is rapidly increasing with time.^29–31 Other databases of note include the 138 000 hypothetical MOFs (hMOFs)^32,33 and those generated by the topologically based crystal constructor (ToBaCCo).^34–36 Grand canonical Monte Carlo (GCMC) are typically used to determine adsorption in porous materials. Briefly, GCMC simulations fix the chemical potential, volume, and temperature thus allowing the number of particles to fluctuate. MC moves like insertions, deletions, and translations are performed in the simulation and the amount adsorbed is determined once the simulation ends at the desired conditions. GCMC simulations have been used with great success to characterize adsorption in MOFs and to produce large amounts of data.^24,37,38 Given the large sets of data, ML has played an important role in understanding MOF performance and the databases themselves. Strong relationships have been found relating MOF performance to their textural properties and their topologies.^{11,28,39–47}

One goal of ML is to acquire and treat large amounts of data to make predictions. Often the amount of quality data available is the largest determinant of success. One solution is a subset of ML applications called transfer learning (TL), which resolves to fix this problem by allowing data from related domains to be used in a new one.^48–53 TL helps ML performance in applications where there is sparse data. Some examples of TL uses are drug efficacy, software defect, and cardiac arrhythmia classification tasks.⁵⁴ The use of TL in this work extends directly from Ma et al.⁵⁵ who analyzed the transfer of gas adsorption tasks in MOFs. In this work, we study TL across domains of the MOF space. We first used clustering to determine the MOF domains.

Clustering is an unsupervised method of data analysis that involves segmenting data into groups with shared similarities based on distances between features, without the need for explicit labeling. Two types of clustering are used in this piece, k-means and agglomerative clustering. K-Means clustering partitions the dataset into k clusters by iteratively assigning data points to their closest centroid. Agglomerative clustering is a hierarchical technique that merges the most similar clusters into larger clusters based on a similarity metric (in our case Euclidean distance). Cluster analysis has recently been used for MOFs with some success. Escobar-Hernandez and coworkers used k-means clustering to evaluate MOF models that deal with thermal stability,⁵⁶ Rosen et al. employed UMAP to determine quantum properties in MOFs,⁵⁷ and Wu et al. used UMAP and k-means to condense MOF features into an accessible representation of the space.⁵⁸

Regarding an accessible representation of the space to use in clustering, we utilize principal component analysis (PCA) to effectively represent and understand the MOF textural space. PCA is a statistical method used to reduce the dimensionality of a dataset while retaining the most important information or patterns present in the data. Here PCA is used to generate a 2D representation of the textural space that will be used to visualize and describe the learning performance.

In this work, we combine clustering with TL to derive new understanding of MOF materials. First, we use a clustering algorithm to divide the MOF textural feature domain into clusters. Then, we use TL on adsorption tasks across the different clusters, finding different efficiencies in the TL performance that depends on the distance between the clusters. Similar trends are also observed when we cluster the space based on the MOF topologies.

Methods

Codes for clustering, TL, and data analysis can be found at: https://github.com/Gregory-Cooper/TL_MOF. The data is also included in the repository. ML techniques were implemented using SciKit-learn⁵⁹ and Pytorch.⁶⁰

Data set

The data set used in this work was originally generated in a previous report and has also been used previously in a transfer learning study. Briefly, over 13 000 MOF structures were computationally generated using the topologically based crystal constructor (ToBaCCo).^34–36 They represent a diverse set of structures from a topology perspective. The textural properties of the structures were also determined using a variety of tools. Lastly, GCMC simulations were performed to determine pure component methane (298 K, 100 bar) and hydrogen (243 K and 77 K, 100 bar) adsorption. In this work, we use the topology of the structures and the textural properties (void fraction, volumetric surface area, gravimetric surface area, limiting pore diameter, largest cavity diameter) for clustering, the same textural properties for training neural networks in direct and transfer learning, and the adsorption of methane and hydrogen as the tasks to be learned. The data set can also be obtained from the relevant publications and github repositories associated with them.^34–36,55

Clustering

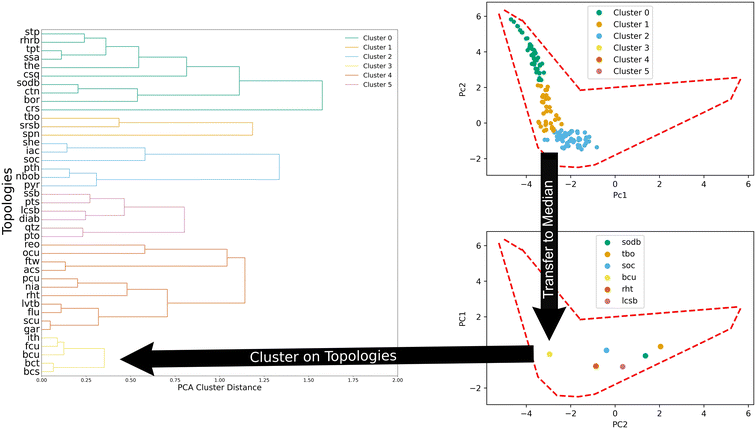
MOFs were clustered in two separate ways.⁶¹ First, a principal component analysis (PCA) was performed on the MOF features used for prediction (volumetric surface area, void fraction, pore limiting diameter, gravimetric surface area, and largest cavity diameter). PCA generated two components that contained 87.7% of the variance and were subsequently used to cluster MOFs. K-Means was used to cluster them using the five base features and we refer to them as generic clusters in this work. The second type of clustering of the MOFs was done using their topologies. The topologies were clustered using the median value of the structures belonging to a given topology in the principal component space as later visually represented in Fig. 4. For example, for 100 MOFs of the same topology, the median PC1 and PC2 components from the set were selected to create a point. All topologies were given a point and these new points were then clustered via agglomerative clustering. Since the clusters had an uneven distribution of MOFs, the amount of data for learning was kept consistent using the same data as that of the smallest cluster. The distribution of structures in the various clusters are summarized in Table 1 below.

Table 1 Number of MOFs contained in each cluster for generic and topology clusters

Generic clusters	0	1	2	3	4	5
Number of MOFs	431	1208	2727	3812	3455	1873

---

Topology clusters	0	1	2	3	4	5
Number of MOFs	4084	1338	1818	561	3288	2417

---

Direct and transfer learning for adsorption tasks

The direct and transfer learning models developed by Ma and coworkers⁵⁵ were used as a starting point in this work. This entailed a three-layer neural network consisting of 5 inputs (MOF features) and one output (adsorption prediction). A batch system was employed where one batch was 128 randomly selected data points; this gave the best performance compared to other batch sizes in terms of time and predictive power. These batches were run until a complete pass was made through the dataset, constituting one epoch of data. Hyperparameter optimization for the hidden layer size, activation function, and learning rate was also performed. Importantly, the optimization was done for the target task (transfer learning), not the source task (direct learning). That is, the chosen model was optimal for the complete process including direct and transfer learning. The optimizer selected was Adam and the loss function was the mean squared error (MSE). The dataset was split into training, validation, and testing, with a ratio of 20 : 4 : 1.

The dataset splits were employed twice in the model, before each learning (direct or transfer) and no data was saved (out of sample) over the entire process. For cases where the transfer cluster was the same as the direct learning cluster, we allowed for some data to be reused in the resulting model. To combat this data leakage into the results, 500 epochs were used for training and only the last epoch was used for analysis. This should remove the overlapping information from the direct learning and make the transfer learning results generalizable.

Results are averaged over 100 trials (100 different data splits and training). This reduced uncertainty in the results and further removed any effects of data leakage between learnings.

Transfer learning across clusters

Transfer learning across clusters (generic and topological) was performed using weight percentage of hydrogen adsorption at 100 bar and 243 K as the task. Transfer learning was done for the two types of clusters separately. For example, if a generic cluster is used for direct learning, then a generic cluster is used to train the transfer learning, never using a topological cluster. For both types of clusters, one cluster was chosen and used in direct learning first. We deem the cluster chosen for direct learning as the base cluster. The resulting model is used as a starting point for transfer learning to the other clusters. The neural network contains two hidden layers of 250 and 125 neurons, respectively. A learning rate of 0.005 was used and PReLu was the activation function. The transfer learning was done with 500 epochs for direct and transfer learning. A generic workflow for transfer learning across clusters can be summarized as follows:

1. Cluster zero is chosen and its data split into test-training.

2. A 3-layer neural network is trained using the training data from cluster zero.

3. Cluster one is selected for transfer learning and its data is split into test-training.

4. The resulting neural net from cluster zero is used for transfer learning with data from cluster one; only the last layer of the neural network is allowed to change its weight with the data from cluster one.

5. Transfer learning into cluster one from cluster zero is analyzed.

Transfer learning across clusters and adsorption tasks

In addition to performing transfer learning of the same adsorption task across clusters, we also investigate transfer learning across clusters and adsorption tasks. The adsorption tasks considered were hydrogen adsorption at 100 bar and 77 K, hydrogen adsorption at 100 bar and 243 K, and methane adsorption at 100 bar and 298. We studied all these tasks in their combinations as source and target task. For example, we used hydrogen adsorption at 100 bar and 77 K as the source adsorption task on cluster 0 and used it for transfer learning of methane adsorption at 100 bar and 298 K on cluster 1. Outside of this change in the source and target tasks, the transfer learning procedure remained the same as when only considering the transfer learning across clusters.

Learning metrics

Some metrics were introduced to understand the learning process besides just predictive performance. These are obtained from the resulting graphs of R²versus epoch as in Fig. 1. The four metrics are:

1. Net R²: measures the final R² value obtained.

2. Worst epoch: measures the change in final versus initial performance. It is calculated by the absolute value of subtracting the initial R² value from the final R² value.

3. Learning: measure of learning efficiency. It is calculated from the integral of the curve until 95% of the final R² is reached.

4. Megabytes: calculated by multiplying the number of epochs by the megabytes per epoch. It is the amount of information needed by the model to transfer learn.

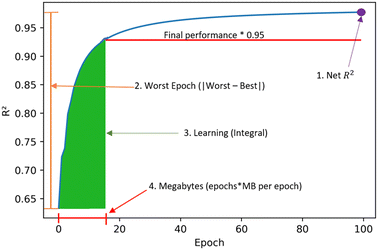Fig. 1 Learning metrics used to quantify transfer learning performance across clusters and tasks. These metrics seek to quantify final performance and learning efficiency.

Results

Generic and topology clusters

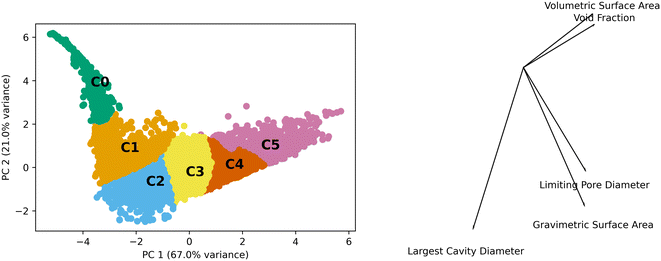
Generic clusters refer to those generated using only the textural features of the MOFs (volumetric surface area, void fraction, pore limiting diameter, gravimetric surface area, and largest cavity diameter) without any concern as to their topology. We performed PCA and the first two components contain approximately 88% of the variance. These two components were used to analyze the k-means generated clusters which used the five features. Fig. 2 shows the data in the principal component (PC) space, the resulting clusters, and a bisect plot to show the direction of the PCA.

Fig. 2 Clustering in principal component space. The left panel shows the top two principal components and how the space was clustered. The right panel shows a bisect plot revealing how the different features are represented in the principal components.

The scales of the components have a range of 12 and 8 units for PC 1 and PC 2, respectively. This is on a standardized scale such that a value of 3 represents 3 standard deviations from the mean. The kurtosis and skew of the set are −0.53 and −0.06 for PC 1 and 7.89 and 2.09 for PC 2, showing the deviations from normal distributions for both PCs. This highlights the heterogeneity of the properties of MOFs in the data set.

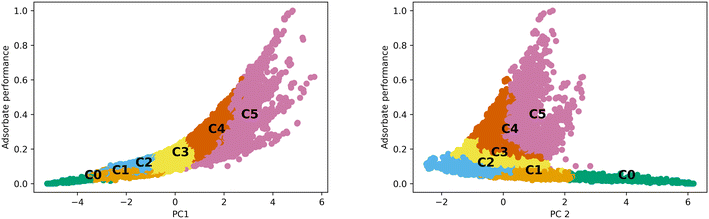
The differences observed in the MOF textural properties, as observed in Fig. 2, drive their performance in various adsorption tasks. Fig. 3 shows how adsorption performance, hydrogen at 100 bar and 243 K, is related to the PCs and how the various clusters occupy the space. Adsorption performance is normalized in the plot. Fig. 3 also shows how performance is expected to behave in the various clusters. For example, cluster 0 does not show performance above 0.2. The performance differences across the clusters are clearly related to the features that make up the clusters. We expect the performance in transfer learning across the clusters will be related to the distance between the clusters as we can clearly see trends in the PC space and in the adsorption space. We expect transfer learning to work well for the uses found in the paper. It has been used previously in the MOF adsorption space in previous works. We found correlation with respect to the whole space between adsorption tasks from 0.97 to 0.99, suggesting transfer learning a valid procedure. Correlation data for the total MOF space and with respect to each generic cluster can be found in the ESI.†

Fig. 3 Standardized adsorption performance for hydrogen at 100 bar and 243 K with respect to each PC. Different clusters clearly occupy different areas of the adsorption space with respect to PC1 and PC2.

We also clustered MOFs according to their topology through agglomeration. Fig. 4 illustrates the process. To cluster them, the median values in the PC space of all the structures of a given topology (top panel, Fig. 4) are used. Then, the distance between the median values of the topologies is used to define new clusters in an agglomerative fashion. We found that six clusters provide a good balance between the total amount of clusters and the number of structures within each cluster.

Fig. 4 Clustering of MOF structures based on their topology. Top right panel shows all structures in one family of MOFs (colored using generic clusters). Bottom right panel shows the median values after transforming one family in the PC space of selected topologies. Left panel shows dendrogram create by agglomerative clustering using the median values distances. Six clusters resulted from this process. Red dashed lines in right panels are to delineate outline of the MOF space.

Another way to understand and describe the topology clusters is by looking at their composition with respect to the generic clusters. The results can be seen in Table 2. This provides insights into the relationships between the topologies and the resulting textural features of MOFs. For example, topology cluster 0 is mostly comprised of MOFs in generic clusters 3, 4, and 5. Similarly, topology cluster 3 is mostly comprised of generic clusters 0, 1, and 2.

Table 2 Percentage of generic clusters in topology clusters

Topology cluster	% generic cluster 0	% generic cluster 1	% generic cluster 2	% generic cluster 3	% generic cluster 4	% generic cluster 5
0	0.1	6.0	6.0	27.6	34.3	26.0
1	0.1	1.1	2.7	13.9	24.5	55.8
2	1.9	10.5	23.5	39.3	24.7	0.0
3	29.6	25.7	42.6	2.1	0.0	0.0
4	6.5	17.5	38.8	31.1	6.1	0.1
5	0.6	1.8	19.4	30.1	45.6	2.6

---

Transfer learning across generic clusters

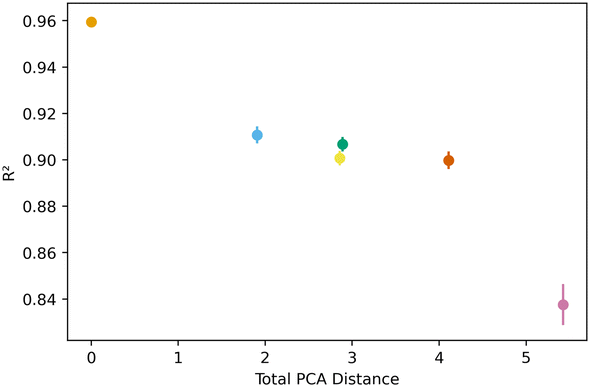
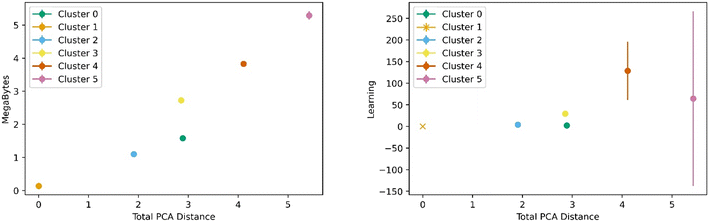
Fig. 5 below shows a representative case of transfer learning across the generic clusters. We used hydrogen adsorption at 100 bar and 243 K as the task to be transferred across clusters. We report the mean R² of the resulting models for 100 trials of learning and the bars are the standard deviation. Fig. 5 shows how the transfer learning performed using cluster 1 as the base for direct learning and transferring to the rest of the clusters. Though performance is high in all clusters, the general trend is that the model performance resulting from transfer learning is inversely correlated with distance in the PC space. We also observe the standard deviation is positively correlated with PCA distance. This trend is observed using all the clusters as bases for transfer learning. The plots for the rest of the clusters are shown in the ESI.†

Fig. 5 Example of how transfer model performs in different clusters, using cluster 1 as the base for direct learning. An increase in the PCA distance between clusters leads to lower performance of the resulting model.

Similar trends were observed for learning metrics beyond the predictive power of the transfer learning model. Fig. 6 below shows the results for learning and megabytes, quantities introduced in the methods section. The panel on the left shows how clusters closer to the base cluster require comparatively fewer MOFs to complete the transfer learning process. The right panel of Fig. 6 shows how variable the model was depending on the distance from the base cluster; closer clusters have smaller standard deviations and average learning values. Similar trends are observed when using all the clusters as the base clusters; the plots can be found in the ESI.†

Fig. 6 Transfer learning performance using direct learning on cluster 1 and transferring to the rest of the clusters. The left panel shows the information needed to achieve a good model increases with increasing PC distance. The right panel shows the average learning and standard deviation increase with PC distance.

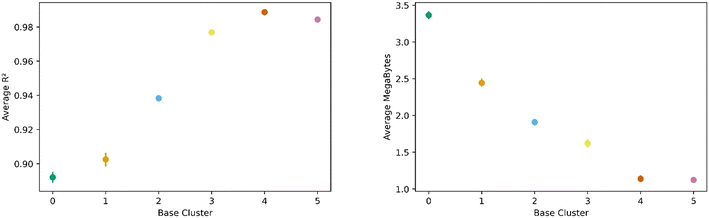
All this analysis implies that there are differences in the transfer learning performance depending on which cluster is chosen for direct learning. Fig. 7 shows our analysis using the average R² and megabytes needed for each base during the transfer learning across all clusters. We find cluster 4 was the best performing base cluster and cluster 0, the worst. An interpretation of this observation is that certain areas of the feature space contain information that better represent the whole feature space and are thus better suited for transfer learning. This interpretation also explains why cluster 0 is the worst performer. When looking back at Fig. 2 and 3, we see cluster 0 is near one of the extremes in the PC space, so it makes sense its data poorly encodes the rest of the feature space. Interestingly, although cluster 3 is nearest to the center of the PC space, cluster 4 was still found to be the top performer.

Fig. 7 Transfer learning performance as a function of base cluster. The left panel shows the average transfer learning performance in terms of R² while the right panel shows the amount of information required for transfer learning. Based on these metrics, we find cluster 4 to be the best while cluster 0 is the worst.

Transfer learning across topological clusters

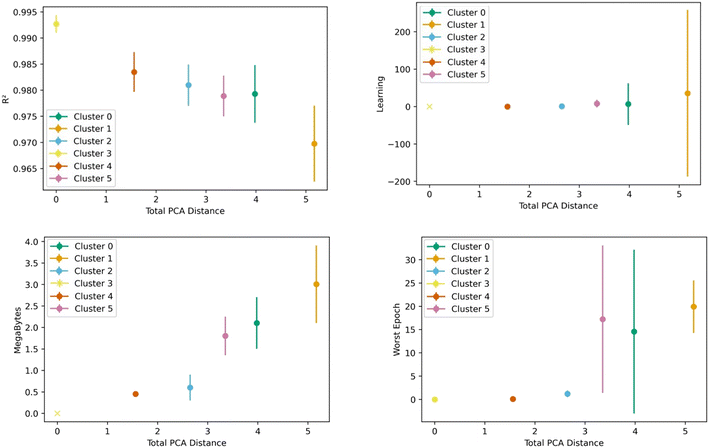
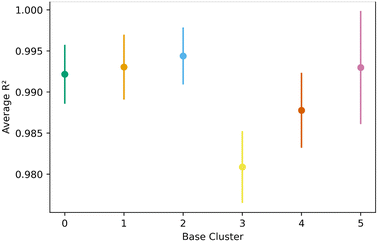
Fig. 8 shows the transfer learning performance using the topological cluster 3 as the base cluster for transfer learning. Overall, the same trends that were observed for the generic clusters are observed for the topological cluster: increasing the distance in the PC space between the base cluster and the ones for transfer learning decreases performance and increases variance.

Fig. 8 Transfer learning performance using direct learning on topological cluster 3 and transferring to the rest of the clusters as a function of PC distance from the base cluster. Panel a show the performance of the model produced from transfer learning. Panel b shows learning, panel c shows amount of information and panel d shows the worst epoch. All the metrics show worsening performance as the PC distance from the base cluster increases.

As done with the generic clusters, different base topological clusters show varying performance. Fig. 9 shows the results. Cluster 2 shows the best performance while cluster 3 shows the worst. The resulting performance can be analyzed using the generic clusters. Table 2 shows the composition of the topological clusters from the generic clusters. Topological cluster 2 performed so well because 98% of its data comes from generic clusters 1–4, which are near the center of the PC space. Conversely, topological cluster 3 only has around 2% of its data from the information-rich area of the generic clusters. Interestingly, when comparing the performance of the generic clusters versus the topological clusters, we see the topological clusters produced better models in the transfer learning. This is because the various topological clusters are comprised of the generic ones, spanning multiple generic clusters in the PC space. This is previously shown in Fig. 4. Given these differences we see that the generic clusters serve to probe relationships in the feature space. The topology clusters, as they contain more general information from the feature space, instead provide insights as to how the families of MOFs relate to each other in the transfer learning environment.

Fig. 9 Transfer learning performance as average R² value as a function of base topological cluster. Overall we find cluster 2 to be the top performer while 3, the worst. The performance of the topological clusters in transfer learning was better than for the generic clusters.

Transfer learning of adsorption tasks across clusters

We also studied transfer learning performance using the generic and topology clusters where we transfer knowledge to a new cluster for a different adsorption task. For instance, we train on cluster 0 for hydrogen adsorption at 243 K and 100 bar and do transfer learning on cluster 1 for methane adsorption at 298 K and 100 bar. Given what we have learned so far when transferring across clusters, any difference that is observed can be attributed to the adsorption tasks on which we train.

First, we perform the transfer learning with hydrogen adsorption at 77 K and 100 bar as the source task and hydrogen adsorption at 243 K and 100 bar as the target task, and vice versa, using the generic clusters. We find similar trends as before, where performance decreases with increasing distance between the clusters. Though, higher variances in general across all metrics are observed. We also find cluster 4 is the top performer while clusters 0 and 1 are the worst. Interestingly, we found a better performance when using hydrogen adsorption at 243 K and 100 bar as the source adsorption task. When looking at the same exercise, but instead using the topology clusters, the general trends with distance in the PC space remain. However, we no longer see a preferential source adsorption task.

The transfer learning exercise using methane adsorption at 298 K and 100 bar and hydrogen adsorption at 243 K and 100 bar as both source and target tasks in the generic clusters revealed interesting trends. We find that hydrogen was a less effective source task, as one cluster could not learn the methane task (negative R²) with remaining clusters showing relatively lower R² values extending from 0.47 to 0.72. This can be seen in the right side of Fig. 10. Methane though, performed well as the source task, with resulting transfer learning models for hydrogen adsorption with R² values ranging from 0.88 to 0.98; figures are in the ESI.† Despite the clear similarities in the features that govern methane and hydrogen adsorption,⁵⁵ our results suggest that the information may not always be transferable when looking at different regions of the feature space.

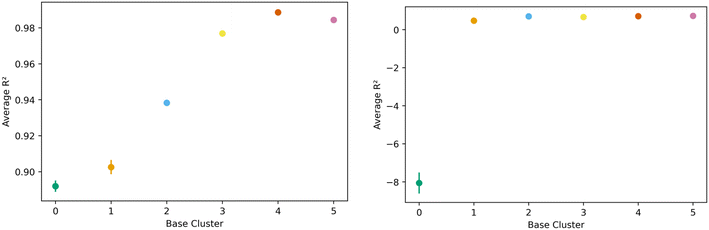Fig. 10 Task transfer learning performance as average R² value as a function of base generic cluster. On the left is transfer from hydrogen at 77 K to hydrogen at 243 K at 100 bar, and mirrors Fig. 7's non-task transfer results. On the right is transfer from hydrogen at 243 K to methane at 298 K. Note the change in scale of the vertical axis.

Digging deeper into this phenomenon, we investigated the results of the transfer clusters. Considering the two cases (transfer to and transfer from methane), it can be observed that the distance becomes a much more important factor in transferring to methane from hydrogen. That is, the further the cluster from the direct learning cluster, the worse the performance. This is emphasized by looking at the predictions from the resulting models using hydrogen as the source in the TL across clusters (Fig. 11). In the ESI,† we also show transfer from hydrogen at different temperatures to see if temperature was a factor in the transfer; we observe similar performance, showing it is not a factor. With this data, we currently cannot place the exact reason for inherent differences in the information transfer between hydrogen and methane; this merits further investigation. Additional graphs and analysis can be found in the ESI.†

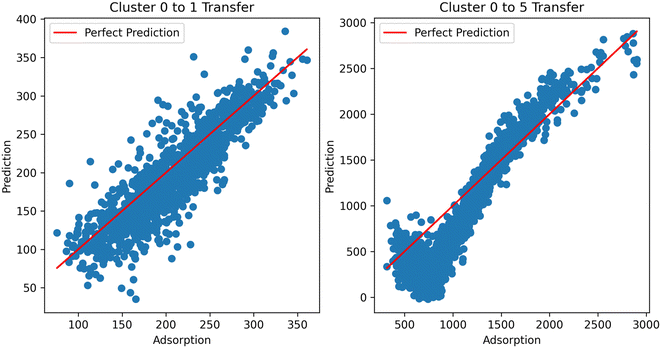Fig. 11 TL performance using hydrogen adsorption as the source and methane as the target task across clusters. TL from cluster 0 to cluster 1 performs well, but not for cluster 5.

Performance in the topology clusters also shows methane is a better source task than hydrogen, but now the performance of both tasks is much better with all clusters being capable of learning (ESI†). The reason is, as seen before, that the topology clusters contain information from across the feature space. This makes them more resistant to the effects seen in the generic clusters.

Conclusion

A topologically diverse set of MOFs were clustered using their features and their topologies and transfer learning was studied using those clusters. The clusters that were determined strictly using the textural properties of the MOFs allowed us to understand transfer learning performance in that feature space while the clustering using the topologies allowed us to understand the relationship between various MOF families. In general, we find that certain clusters are better suited to transfer learning than others. The performance as the base cluster is related to their position in the principal component space. Transfer learning performance was also found to be correlated with the distance between the clusters; the closer the clusters are, the better the performance. Lastly, we find that when performing transfer learning across clusters and adsorption task, performance depends also on the source adsorption task that is used. We find transfer learning performance was better using methane as the source task as opposed to hydrogen. All taken together, our study reveals there are regions of the MOF space and adsorption tasks that are better suited to be the source task in the context of transfer learning. More broadly, this study suggests there are a particular set of MOFs and adsorbates that are well-suited as source of information that can be transferred to other MOFs and other adsorbates. Efforts to understand these relationships could be crucial in future design and discovery of MOFs in new adsorption applications.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Authors gratefully acknowledge NSF CAREER Award CBET-2143346. We also thank the Center for Research Computing at the University of Notre Dame for computational resources.

References

1. P. Horcajada, C. Serre, M. Vallet-Regí, M. Sebban, F. Taulelle and G. Férey, Metal–Organic Frameworks as Efficient Materials for Drug Delivery, Angew. Chem., 2006, 118, 6120–6124.
2. P. Horcajada, C. Serre, G. Maurin, N. A. Ramsahye, F. Balas, M. A. Vallet-Regí, M. Sebban, F. Taulelle and G. R. Férey, Flexible Porous Metal-Organic Frameworks for a Controlled Drug Delivery, J. Am. Chem. Soc., 2008, 130, 6774–6780.
3. J. Della Rocca, D. Liu and W. Lin, Nanoscale Metal–Organic Frameworks for Biomedical Imaging and Drug Delivery, Acc. Chem. Res., 2011, 44, 957–968.
4. C. Orellana-Tavra, S. A. Mercado and D. Fairen-Jimenez, Endocytosis Mechanism of Nano Metal-Organic Frameworks for Drug Delivery, Adv. Healthcare Mater., 2016, 5, 2261–2270.
5. D. Sheberla, J. C. Bachman, J. S. Elias, C.-J. Sun, Y. Shao-Horn and M. Dincă, Conductive MOF electrodes for stable supercapacitors with high areal capacitance, Nat. Mater., 2017, 16(2), 220–224.
6. L. Wang, Y. Han, X. Feng, J. Zhou, P. Qi and B. Wang, Metal–organic frameworks for energy storage: Batteries and supercapacitors, Coord. Chem. Rev., 2016, 307(Part 2), 361–381.
7. D. Sheberla, J. C. Bachman, J. S. Elias, C.-J. Sun, Y. Shao-Horn and M. Dinca, Conductive MOF electrodes for stable supercapacitors with high areal capacitance, Nat. Mater., 2017, 16, 220–224.
8. M. Du, Q. Li, Y. Zhao, C.-S. Liu and H. Pang, A review of electrochemical energy storage behaviors based on pristine metal–organic frameworks and their composites, Coord. Chem. Rev., 2020, 416, 213341.
9. H. Li, K. Wang, Y. Sun, C. T. Lollar, J. Li and H.-C. Zhou, Recent advances in gas storage and separation using metal–organic frameworks, Mater. Today, 2018, 21, 108–121.
10. A. Sturluson, M. T. Huynh, A. R. Kaija, C. Laird, S. Yoon, F. Hou, Z. Feng, C. E. Wilmer, Y. J. Colón, Y. G. Chung, D. W. Siderius and C. M. Simon, The role of molecular modelling and simulation in the discovery and deployment of metal-organic frameworks for gas storage and separation, Mol. Simul., 2019, 45, 1082–1121.
11. Z. Yao, B. Sánchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha, R. Q. Snurr and A. Aspuru-Guzik, Inverse design of nanoporous crystalline reticular materials with deep generative models, Nat. Mach. Intell., 2021, 3, 76–86.
12. Z. Qiao, Q. Xu and J. Jiang, High-throughput computational screening of metal-organic framework membranes for upgrading of natural gas, J. Membr. Sci., 2018, 551, 47–54.
13. R. Lin, B. Villacorta Hernandez, L. Ge and Z. Zhu, Metal organic framework based mixed matrix membranes: an overview on filler/polymer interfaces, J. Mater. Chem. A, 2018, 6, 293–312.
14. R. Anderson and D. A. Gómez-Gualdrón, Deep learning combined with IAST to screen thermodynamically feasible MOFs for adsorption-based separation of multiple binary mixtures, J. Chem. Phys., 2021, 154, 234102.
15. H. Daglar and S. Keskin, Computational Screening of Metal–Organic Frameworks for Membrane-Based CO2/N2/H2O Separations: Best Materials for Flue Gas Separation, J. Phys. Chem. C, 2018, 122, 17347–17357.
16. M. Eddaoudi, D. B. Moler, H. Li, B. Chen, T. M. Reineke, M. O'Keeffe and O. M. Yaghi, Modular chemistry: secondary building units as a basis for the design of highly porous and robust metal-organic carboxylate frameworks, Acc. Chem. Res., 2001, 34, 319–330.
17. J. Kim, B. L. Chen, T. M. Reineke, H. L. Li, M. Eddaoudi, D. B. Moler, M. O'Keeffe and O. M. Yaghi, Assembly of metal-organic frameworks from large organic and inorganic secondary building units: New examples and simplifying principles for complex structures, J. Am. Chem. Soc., 2001, 123, 8239.
18. M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Systematic design of pore size and functionality in isoreticular MOFs and their application in methane storage, Science, 2002, 295, 469.
19. N. L. Rosi, M. Eddaoudi, J. Kim, M. O'Keeffe and O. M. Yaghi, Infinite secondary building units and forbidden catenation in metal-organic frameworks, Angew. Chem., Int. Ed., 2002, 41, 284–287.
20. G. Garberoglio, A. I. Skoulidas and J. K. Johnson, Adsorption of Gases in Metal Organic Materials: Comparison of Simulations and Experiments, J. Phys. Chem. B, 2005, 109, 13094–13103.
21. T. Mueller and G. Ceder, A density functional theory study of hydrogen adsorption in MOF-5, J. Phys. Chem. B, 2005, 109, 17974.
22. Q. Y. Yang and C. L. Zhong, Molecular simulation of adsorption and diffusion of hydrogen in metal-organic frameworks, J. Phys. Chem. B, 2005, 109, 11862–11864.
23. A. Martín-Calvo, E. García-Pérez, J. Manuel Castillo and S. Calero, Molecular simulations for adsorption and separation of natural gas in IRMOF-1 and Cu-BTC metal-organic frameworks, Phys. Chem. Chem. Phys., 2008, 10, 7085–7091.
24. Y. J. Colon and R. Q. Snurr, High-throughput computational screening of metal-organic frameworks, Chem. Soc. Rev., 2014, 43, 5735–5749.
25. C. M. Simon, J. Kim, D. A. Gomez-Gualdron, J. S. Camp, Y. G. Chung, R. L. Martin, R. Mercado, M. W. Deem, D. Gunter, M. Haranczyk, D. S. Sholl, R. Q. Snurr and B. Smit, The materials genome in action: identifying the performance limits for methane storage, Energy Environ. Sci., 2015, 8, 1190–1199.
26. Z. Qiao, C. Peng, J. Zhou and J. Jiang, High-throughput computational screening of 137953 metal–organic frameworks for membrane separation of a CO2/N2/CH4 mixture, J. Mater. Chem. A, 2016, 4, 15904–15912.
27. P. Chen, Z. Tang, Z. Zeng, X. Hu, L. Xiao, Y. Liu, X. Qian, C. Deng, R. Huang, J. Zhang, Y. Bi, R. Lin, Y. Zhou, H. Liao, D. Zhou, C. Wang and W. Lin, Machine-Learning-Guided Morphology Engineering of Nanoscale Metal-Organic Frameworks, Matter, 2020, 2, 1651–1666.
28. K. Mukherjee and Y. J. Colón, Machine learning and descriptor selection for the computational discovery of metal-organic frameworks, Mol. Simul., 2021, 47, 857–877.
29. F. Allen, The Cambridge Structural Database: a quarter of a million crystal structures and rising, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388.
30. D. J. Tranchemontagne, J. L. Mendoza-Cortes, M. O'Keeffe and O. M. Yaghi, Secondary building units, nets and bonding in the chemistry of metal-organic frameworks, Chem. Soc. Rev., 2009, 38, 1257–1283.
31. P. Z. Moghadam, A. Li, X.-W. Liu, R. Bueno-Perez, S.-D. Wang, S. B. Wiggin, P. A. Wood and D. Fairen-Jimenez, Targeted classification of metal–organic frameworks in the Cambridge structural database (CSD), Chem. Sci., 2020, 11(32), 8373–8387.
32. C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Large-scale Screening of hypothetical metal-organic frameworks, Nat. Chem., 2012, 83–89.
33. B. J. Sikora, C. E. Wilmer, M. L. Greenfield and R. Q. Snurr, Thermodynamic analysis of Xe/Kr selectivity in over 137 000 hypothetical metal-organic frameworks, Chem. Sci., 2012, 3, 2217–2223.
34. D. A. Gomez-Gualdron, Y. J. Colon, X. Zhang, T. C. Wang, Y.-S. Chen, J. T. Hupp, T. Yildirim, O. K. Farha, J. Zhang and R. Q. Snurr, Evaluating topologically diverse metal-organic frameworks for cryo-adsorbed hydrogen storage, Energy Environ. Sci., 2016, 9, 3279–3289.
35. Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Topologically Guided, Automated Construction of Metal–Organic Frameworks and Their Evaluation for Energy-Related Applications, Cryst. Growth Des., 2017, 17, 5801–5810.
36. R. Anderson and D. A. Gómez-Gualdrón, Increasing topological diversity during computational “synthesis” of porous crystals: how and why, CrystEngComm, 2019, 21, 1653–1665.
37. R. Q. Snurr, A. T. Bell and D. N. Theodorou, Prediction of adsorption of aromatic-hydrocarbons in silicalite from grand-canonical Monte-Carlo simulations with biased insertions, J. Phys. Chem., 1993, 97, 13742.
38. D. H. Jung, D. Kim, T. B. Lee, S. B. Choi, J. H. Yoon, J. Kim, K. Choi and S. H. Choi, Grand canonical Monte Carlo simulation study on the catenation effect on hydrogen adsorption onto the interpenetrating metal-organic frameworks, J. Phys. Chem. B, 2006, 110, 22987–22990.
39. M. Pardakhti, E. Moharreri, D. Wanik, S. L. Suib and R. Srivastava, Machine Learning Using Combined Structural and Chemical Descriptors for Prediction of Methane Adsorption Performance of Metal Organic Frameworks (MOFs), ACS Comb. Sci., 2017, 19, 640–645.
40. N. S. Bobbitt and R. Q. Snurr, Molecular modelling and machine learning for high-throughput screening of metal-organic frameworks for hydrogen storage, Mol. Simul., 2019, 1–13.
41. B. J. Bucior, N. S. Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, O. K. Farha, N. Bagheri and R. Q. Snurr, Energy-based descriptors to rapidly predict hydrogen storage in metal–organic frameworks, Mol. Syst. Des. Eng., 2019, 4, 162–174.
42. P. Z. Moghadam, S. M. J. Rogge, A. Li, C.-M. Chow, J. Wieme, N. Moharrami, M. Aragones-Anglada, G. Conduit, D. A. Gomez-Gualdron, V. Van Speybroeck and D. Fairen-Jimenez, Structure-Mechanical Stability Relations of Metal-Organic Frameworks via Machine Learning, Matter, 2019, 1, 219–234.
43. T. D. Burns, K. N. Pai, S. G. Subraveti, S. P. Collins, M. Krykunov, A. Rajendran and T. K. Woo, Prediction of MOF Performance in Vacuum Swing Adsorption Systems for Postcombustion CO2 Capture Based on Integrated Molecular Simulations, Process Optimizations, and Machine Learning Models, Environ. Sci. Technol., 2020, 54, 4536–4544.
44. G. S. Fanourgakis, K. Gkagkas, E. Tylianakis and G. Froudakis, A Generic Machine Learning Algorithm for the Prediction of Gas Adsorption in Nanoporous Materials, J. Phys. Chem. C, 2020, 124(13), 7117–7126.
45. I. Tsamardinos, G. S. Fanourgakis, E. Greasidou, E. Klontzas, K. Gkagkas and G. E. Froudakis, An Automated Machine Learning Architecture for the Accelerated Prediction of Metal-Organic Frameworks Performance in Energy and Environmental Applications, Microporous Mesoporous Mater., 2020, 110160.
46. S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun., 2020, 11, 4068.
47. Y. Sun, R. F. DeJaco, Z. Li, D. Tang, S. Glante, D. S. Sholl, C. M. Colina, R. Q. Snurr, M. Thommes, M. Hartmann and J. I. Siepmann, Fingerprinting diverse nanoporous materials for optimal hydrogen storage conditions using meta-learning, Sci. Adv., 2021, 7, eabg3983.
48. S. J. Pan and Q. Yang, A Survey on Transfer Learning, IEEE Trans. Knowl. Data Eng., 2010, 22, 1345–1359.
49. C. Tan, F. Sun, T. Kong, W. Zhang, C. Yang and C. Liu, in Tilte, Springer, 2018.
50. Y. Sun, R. F. DeJaco and J. I. Siepmann, Deep neural network learning of complex binary sorption equilibria from molecular simulation data, Chem. Sci., 2019, 10, 4377–4388.
51. H. Yamada, et al., Predicting Materials Properties with Little Data Using Shotgun Transfer Learning, ACS Cent. Sci., 2019, 5, 1717–1730.
52. F. Zhuang, Z. Qi, K. Duan, D. Xi, Y. Zhu, H. Zhu, H. Xiong and Q. He, A Comprehensive Survey on Transfer Learning, Proc. IEEE, 2021, 109(1), 43–76.
53. F. Zhuang, Z. Qi, K. Duan, D. Xi, Y. Zhu, H. Zhu, H. Xiong and Q. He, A Comprehensive Survey on Transfer Learning, Proc. IEEE, 2021, 109, 43–76.
54. K. Weiss, T. M. Khoshgoftaar and D. Wang, A survey of transfer learning, J. Big Data, 2016, 3, 9.
55. R. Ma, Y. J. Colón and T. Luo, Transfer Learning Study of Gas Adsorption in Metal–Organic Frameworks, ACS Appl. Mater. Interfaces, 2020, 12, 34041–34048.
56. H. U. Escobar-Hernandez, L. M. Pérez, P. Hu, F. A. Soto, M. I. Papadaki, H.-C. Zhou and Q. Wang, Thermal Stability of Metal–Organic Frameworks (MOFs): Concept, Determination, and Model Prediction Using Computational Chemistry and Machine Learning, Ind. Eng. Chem. Res., 2022, 61, 5853–5862.
57. A. S. Rosen, S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein and R. Q. Snurr, Machine learning the quantum-chemical properties of metal–organic frameworks for accelerated materials discovery, Matter, 2021, 4, 1578–1597.
58. X. Wu, Y. Che, L. Chen, E. J. Amigues, R. Wang, J. He, H. Dong and L. Ding, Mapping the Porous and Chemical Structure–Function Relationships of Trace CH3I Capture by Metal–Organic Frameworks using Machine Learning, ACS Appl. Mater. Interfaces, 2022, 14, 47209–47221.
59. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, Scikit-learn: Machine learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830.
60. A. Paszke, et al., PyTorch: An imperative style, high-performance deep learning library, Advances in Neural Information Processing Systems, 2019.
61. D. Xu and Y. Tian, A Comprehensive Survey of Clustering Algorithms, Ann. Data Sci., 2015, 2, 165–193.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3me00016h

---