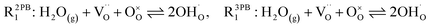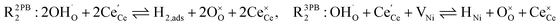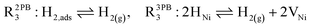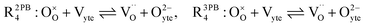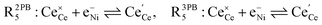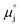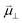DOI:
10.1039/D1TA07351F
(Paper)
J. Mater. Chem. A, 2022,
10, 11121-11130
Non-equilibrium thermodynamics of mixed ionic-electronic conductive electrodes and their interfaces: a Ni/CGO study†
Received
27th August 2021
, Accepted 16th April 2022
First published on 19th April 2022
Abstract
Non-equilibrium thermodynamics describe the current–voltage characteristics of electrochemical devices. For conventional electrode–electrolyte interfaces, the local activation overpotential is used to describe the electrostatic potential step between the two materials as a current is generated. However, the activation overpotential for the metal/mixed ionic-electronic conducting (MIEC) composite electrodes studied in this work originates at the MIEC–gas interface. Moreover, we have studied the effects of non-equilibrium on the electrostatic surface potential and evaluated its influence over electrode kinetics. By investigating two phase (2PB) and three phase boundary (3PB) reactions at the Ni/Ce1−xGdxO2−δ (Ni/CGO) electrode, we have demonstrated that the driving force for coupled ion-electron transfer is held at the CGO–gas interface for both reaction pathways. We also determined that the rate of coupled ion-electron transfer via the 3PB scales with the availability of free sites on the metallic surface, revealing a Sabatier-like relationship with regards to the selection of metallic phases. Finally, we demonstrated how the theory of the electrostatic surface potential can be applied to other systems outside of the well-studied H2/H2O electrode environment. These findings therefore provide an insight into the design of future electrode structures for a range of electrochemical devices.
1. Introduction
The solid oxide cell (SOC) is a highly efficient chemical-to-electrical and electrical-to-chemical energy conversion technology compatible with both existing fuel (i.e. natural gas) and future fuel (i.e. renewably sourced hydrogen) infrastructures. The operation of the cermet electrode i.e. nickel/gadolinium doped ceria (Ni/CGO) under electrical bias has been studied for decades, however a unifying model for hydrogen electrooxidation or water electrolysis has not yet been agreed upon.1–12 We therefore aim to shed light on the water electrolysis reaction, and moreover all solid/gas phase charge transfer reactions, by studying the electrostatic phenomena at the interfaces of the Ni/CGO electrode.
Pristine and doped ceria have relatively large band gaps (5 eV), and as such, mobile electrons are observed as polaronic Ce 4f states found within the “forbidden region” of the band structure, rather than populating the conduction band.13,14 This results in the mixed ionic-electronic conducting (MIEC) properties of Ce1−xGdxO2−δ, where x = 0.1–0.2 (CGO):
| | 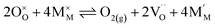 | (1) |
where
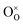
,
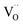
,
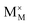
and
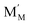
represent an oxide ion at the anion site, a doubly charged oxygen vacancy, a metal ion on the cation site, and a small polaron (localised electron at the cation site) respectively. However, this reaction often occurs
via a fuel intermediate such as CO/CO
2 or H
2/H
2O, where the strength of the intrinsic dipole moment of the adsorbed gas species was understood to determine the performance of the electrode.
15,16 Owing to the relative ease of reduction of CGO under operational conditions, and therefore good electronic conductivity, biasing the electrode modulates the coverage of adsorbates and the concentration of electronic defects. Understanding these phenomena is critical to accurately model and design the electrodes. Therefore, in this study we will analyse and discuss the effects of non-equilibrium operation (under electrical bias) on the electrostatic potential at the interfaces of the Ni/CGO electrode.
The process of establishing the origin of the electrostatic surface potential involves analysis of all steps in the redox reaction and identification of the rate limiting step.17 As an example, we will take the water electrolysis reaction at the fuel electrode, 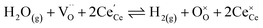 , which can occur via a two phase boundary (2PB) or three phase boundary (3PB) mechanism at the Ni/CGO fuel electrode. The overall reaction equilibrium can be broken down into the following steps depending on the mechanism (Fig. 1):
, which can occur via a two phase boundary (2PB) or three phase boundary (3PB) mechanism at the Ni/CGO fuel electrode. The overall reaction equilibrium can be broken down into the following steps depending on the mechanism (Fig. 1):
where V
yte and O
yte2− refer to the CGO electrolyte species.
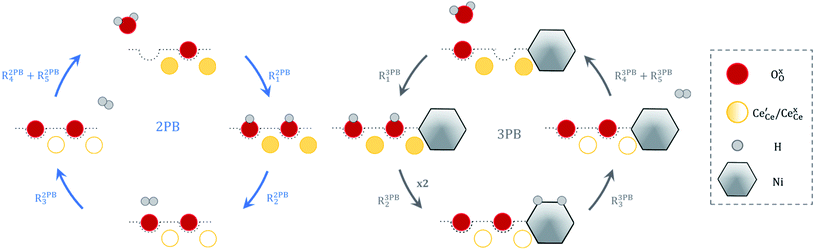 |
| | Fig. 1 Schematic diagram of the water electrolysis reaction via the two-phase boundary (left) and three-phase boundary (right) mechanisms. | |
The water adsorption step R2PB1/R3PB1 is fast close to equilibrium and is only facilitated on the ceria surface and not on the nickel phase.18 At intermediate temperatures and under open circuit voltage (OCV), the coupled ion-electron transfer step (ET) R2PB2/R3PB2 is widely considered to be rate limiting, where the 2PB and 3PB reaction mechanisms display stark thermodynamic and kinetic differences.16,19 Desorption of weakly physisorbed hydrogen gas is given by R2PB3, while under the 3PB reaction mechanism, R3PB3, two adsorbed hydrogen species on the nickel surface combine and desorb. To restore the defect composition of the CGO phase after the hydrogen gas is produced, R2PB4/R3PB4 and R2PB5/R3PB5 are included to illustrate transport of oxygen vacancies from the electrolyte and electrons from the current collector, respectively. In solid oxide cells the electrolyte phase requires low electronic conductivity to avoid short circuiting the cell.
Via the 2PB mechanism, two hydroxyl ions and two surface polarons undergo a coupled electron transfer and proton migration process in a two-electron transfer step, resulting in weakly physisorbed hydrogen gas. Electron transfer may only be facilitated at the 2PB if bulk electronic conductivity in the oxide phase is high. In contrast, the 3PB mechanism involves proton migration to the nickel surface via the one-dimensional 3PB, followed by electron transfer from the oxide phase to the highly conductive nickel phase at the ceria–nickel interface. This mechanism is not dependent on high electronic conductivity in the oxide phase and is therefore most commonly used to model Ni/YSZ electrodes where polaron concentration is low relative to ceria.20
2. Background thermodynamic theory related to solid oxide cells
In order to develop the non-equilibrium models as applied to Ni/CGO interfaces, it is first necessary to briefly consider the thermodynamic treatment of fuel cells, considering both the equilibrium and non-equilibrium cases.
2.1. Electrode thermodynamics
The (electro)chemical potential, μi (eV), of a mobile species in an electrochemical system is expressed as:| | 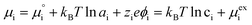 | (2) |
where 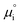 is the standard potential, kBT
is the standard potential, kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ai is the activity potential and eϕi is the electric potential. The activity (ai = γici) is the product of the concentration (ci) and activity coefficient (γi), which is a measure of the non-ideality of the species.18,21 A simplification can be made to express all the non-idealities within the excess chemical potential, μexi, which also includes contributions from the standard and electric potentials. Here, we use the definition of (electro)chemical potential, meaning that if the species of interest is charged, we find the electrochemical potential, and if the species of interest is neutral, we find the chemical potential. If we consider the rate limiting process of an electrode to be a Faradaic reaction whereby n electrons are transferred, then we find the activation overpotential (ηact) as the chemical potential difference of a net reduction reaction:where μ2 and μ1 represent the (electro)chemical potentials for the initial (oxidised) and final (reduced) states, respectively, and the delta symbol represents the difference between the state in equilibrium and non-equilibrium (Δμi = μi − μeqi). The activation overpotential therefore describes the electrostatic potential step at the electrode–electrolyte interface, such that ηact = Δϕcc − Δϕyte, where ϕcc is the electric potential of the metallic current collector and ϕyte is the electric potential of the electrolyte.22,23
ai is the activity potential and eϕi is the electric potential. The activity (ai = γici) is the product of the concentration (ci) and activity coefficient (γi), which is a measure of the non-ideality of the species.18,21 A simplification can be made to express all the non-idealities within the excess chemical potential, μexi, which also includes contributions from the standard and electric potentials. Here, we use the definition of (electro)chemical potential, meaning that if the species of interest is charged, we find the electrochemical potential, and if the species of interest is neutral, we find the chemical potential. If we consider the rate limiting process of an electrode to be a Faradaic reaction whereby n electrons are transferred, then we find the activation overpotential (ηact) as the chemical potential difference of a net reduction reaction:where μ2 and μ1 represent the (electro)chemical potentials for the initial (oxidised) and final (reduced) states, respectively, and the delta symbol represents the difference between the state in equilibrium and non-equilibrium (Δμi = μi − μeqi). The activation overpotential therefore describes the electrostatic potential step at the electrode–electrolyte interface, such that ηact = Δϕcc − Δϕyte, where ϕcc is the electric potential of the metallic current collector and ϕyte is the electric potential of the electrolyte.22,23
2.2. Electrode kinetics
The current density for charge transfer per surface site for the forward and backward reactions is given as:| | 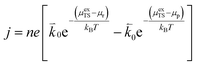 | (4) |
where n is the number of electrons transferred in the reaction, μr and μp represent the electrochemical potential of the reactants and products, respectively, and 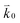 and
and 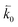 represent the forward and reverse rate constants, respectively. We may assume that the attempt frequency for the forward and backward reactions are equivalent, such that
represent the forward and reverse rate constants, respectively. We may assume that the attempt frequency for the forward and backward reactions are equivalent, such that 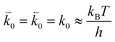 .21 Occupation of the transition state is short lived, therefore we can assume its concentration to be negligible. Thus, we only need to use the excess chemical potential term (μexTS), which is defined following Butler–Volmer kinetics:21,24–26
.21 Occupation of the transition state is short lived, therefore we can assume its concentration to be negligible. Thus, we only need to use the excess chemical potential term (μexTS), which is defined following Butler–Volmer kinetics:21,24–26| | 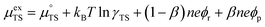 | (5) |
where β is defined as the symmetry factor 0 < β < 1, and is generally assumed to be 0.5.21 While β can be taken to be 0.5, it is retained in the subsequent expressions for generality. The equilibrium potentials under open circuit voltage (OCV) are utilized to formulate the exchange current density, j0, by substituting eqn (5) into eqn (4) (full derivation given in the ESI†):| | 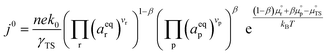 | (6) |
where vi is the stoichiometric coefficient of species i. ai is the activity of species i, and the exponential term 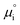 is the standard chemical potential of species i. When an electrical bias is applied, an electrostatic potential step is created at the interface in which the rate-limiting step is located. The current density, j, is introduced as:
is the standard chemical potential of species i. When an electrical bias is applied, an electrostatic potential step is created at the interface in which the rate-limiting step is located. The current density, j, is introduced as:| | 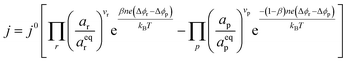 | (7) |
where the exponent (Δϕr − Δϕp) refers to the shift in electrostatic potential across the interface of interest under non-equilibrium conditions. To determine the origin of the activation overpotential at the Ni/CGO electrode, we will evaluate the electrostatic potential at the nickel–CGO and CGO–gas interfaces under non-equilibrium conditions, applying the models derived above.
3. Application to Ni/CGO electrodes
In this section we will apply the theory of non-equilibrium thermodynamics as detailed in Section 2 to the Ni/CGO electrode and elucidate the essence of the activation overpotential for the water electrolysis reaction.
3.1. Electrostatics at the CGO–gas interface
As illustrated in Fig. 2a, under non-equilibrium conditions the electric potential of electrons in the nickel (current collecting, cc) phase (ϕcc) will shift in accordance with the activation overpotential located at the bulk electrolyte contact 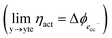 . Using operando X-ray Photoelectron Spectroscopy (XPS), Chueh et al. demonstrated that the shift in electric potential of the ceria phase (ϕCGO) was also equal to the activation overpotential
. Using operando X-ray Photoelectron Spectroscopy (XPS), Chueh et al. demonstrated that the shift in electric potential of the ceria phase (ϕCGO) was also equal to the activation overpotential 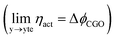 .16 It must be noted that in this study a thin film of dense ceria was used as opposed to a cermet electrode, therefore there was no distribution of the activation overpotential as a function of distance from the bulk electrolyte contact.16 However, charge transfer between ceria and the current collector, and between ceria and the electrolyte, was fast relative to charge transfer with the gas phase. Therefore, throughout the matrix of the Ni/CGO cermet it is rational to assume that the shift in electric potential of the ceria phase will be equal to the shift in the electric potential of the nickel phase (Δϕcc = ΔϕCGO). Consequently, bias of the Ni/CGO electrode does not result in the formation of an electric double layer at the Ni–CGO interface, as demonstrated in Fig. 2a.
.16 It must be noted that in this study a thin film of dense ceria was used as opposed to a cermet electrode, therefore there was no distribution of the activation overpotential as a function of distance from the bulk electrolyte contact.16 However, charge transfer between ceria and the current collector, and between ceria and the electrolyte, was fast relative to charge transfer with the gas phase. Therefore, throughout the matrix of the Ni/CGO cermet it is rational to assume that the shift in electric potential of the ceria phase will be equal to the shift in the electric potential of the nickel phase (Δϕcc = ΔϕCGO). Consequently, bias of the Ni/CGO electrode does not result in the formation of an electric double layer at the Ni–CGO interface, as demonstrated in Fig. 2a.
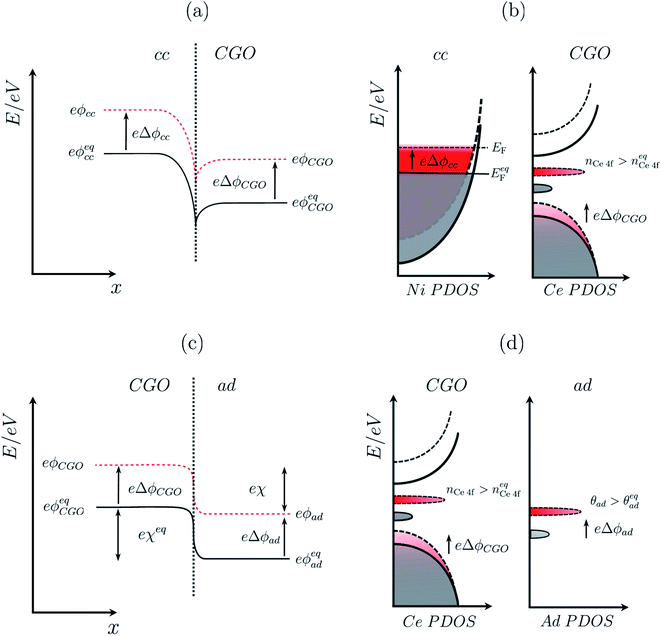 |
| | Fig. 2 (a) Electrochemical equilibrium at a Ni–CGO interface where the electrochemical potential of electrons in the two phases achieve equilibrium by electron density migrating to the CGO phase, resulting in an interfacial voltage in accordance with the Nernst equation (filled line). Under non-equilibrium conditions, the difference in shift between the electrical potential of electrons in Ni and CGO phases shifts with a magnitude proportional to the activation overpotential. (b) Partial density of states for the nickel phase where the Fermi energy at equilibrium (filled line) shifts to a higher value (dashed line) under an applied negative overpotential, and CGO phase where the position of the band centre and integrated area of the Ce 4f state (red) illustrates the shift in the electrical potential and increase in polaron concentration, respectively. (c) Electrochemical equilibrium at a CGO–gas (H2O/H2) interface where the electrochemical potential of electrons in the two phases achieves equilibrium, resulting in gas adsorption and the formation of an electrostatic surface potential in accordance with the Nernst equation (filled line). Under non-equilibrium conditions, the electrical potential of oxygen vacancies in the CGO phases shifts, causing a shift of the electrostatic surface potential with a magnitude explained by eqn (10) (dashed line). (d) Partial density of states of the adsorbate at the CGO surface shows both chemical and electrostatic contribution in non-equilibrium (red) under an applied negative overpotential. An increase in coverage will populate the adsorbate DOS while a change in the electrostatic potential will shift the position of the band centre. The charge density difference schematic illustrates the adsorbate induced electrostatic potential at the ceria (111) termination. | |
The process of charge transfer at the CGO–gas interface comprises the ambipolar exchange of ions and electronic species.27 The result of such a process causes charge separation and an associated electrostatic surface potential χ:17,18
where
ϕCGO is the electrostatic potential experienced by mobile charge carriers in the electrode and
ϕad is the electrostatic potential experienced by the adsorbed species.
18 Under bias, an electrostatic potential shift may be established at the surface (Δ
χ =
χ −
χeq), where an effective double layer is formed between the electrode surface and the adsorbed species (
Fig. 2c and d).
28 We can therefore define the non-equilibrium surface potential shift for a CGO surface in a H
2O/H
2 gas atmosphere in
eqn (8) to be:
18| | 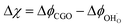 | (9) |
The interaction between polar adsorbed species and the CGO surface was modelled by Williams et al. using first principles calculation at the point of zero charge to accurately predict the coverage and electrostatic surface potential under non-equilibrium conditions.18 It was determined that the shift in electrostatic surface potential at the ceria (111) termination in H2O/H2 gas at 500 °C was a result of a change in coverage of polar adsorbates, such that 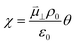 , where
, where 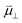 , ε0, ρ0 and θ represent the dipole moment normal to the surface, vacuum permittivity, the density of adsorption sites and the coverage of adsorbates, respectively.
, ε0, ρ0 and θ represent the dipole moment normal to the surface, vacuum permittivity, the density of adsorption sites and the coverage of adsorbates, respectively.
We can derive the η–Δχ relationship by realising that when R2PB2/R3PB2 is rate limiting, the activation overpotential describes the state of non-equilibrium across the CGO–gas interface as:29
| | 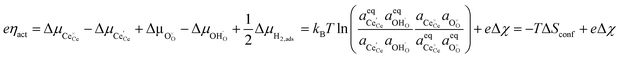 | (10) |
where diatomic hydrogen adsorbed on the ceria surface is in equilibrium with the gas phase
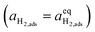
, thus
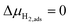
.
Eqn (10) shows that the activation overpotential is a function of configurational entropy (Δ
Sconf) and electrostatic surface potential. If we consider the Ni/CGO cermet electrode illustrated in
Fig. 3a, we are aware that there is no electrostatic potential shift between the CGO and metallic phases (
Fig. 3b). Instead, we observe a shift in electrostatic surface potential which decays exponentially away from the electrolyte contact as the shift in electric potential of the adsorbate equilibrates with the CGO phase approaching the current collector contact, where
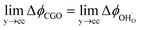
. We note that the potential of the metallic phase is constant throughout the electrode as the electronic resistance is assumed to be close to zero relative to the ionic resistance of the electrolyte phase. This theory contrasts with the Ni/YSZ model (
Fig. 3c), where Faradaic reactions are driven by the difference in the electric potential shift between the current collector and electrolyte phases,
ηact = Δ
ϕcc − Δ
ϕyte.
30
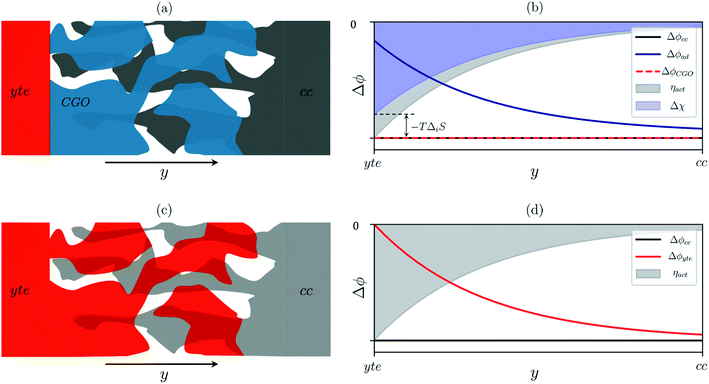 |
| | Fig. 3 (a) Illustration of the porous Ni/CGO cermet electrode comprised of CGO (blue), pore (white) and current collector (grey) phases. (b) Distribution of electrostatic potential shifts as a function of distance from the electrolyte (y), where ΔϕCGO is equal to Δϕcc and out of phase with Δϕad within the active region of the electrode. (c) Illustration of the porous Ni/YSZ cermet electrode comprised of electrolyte (red), pore (white) and metallic (grey) phases. (d) Distribution of electrostatic potential shifts as a function of distance from the electrolyte (y) where Δϕyte is out of phase with Δϕcc within the active region of the electrode.30 | |
3.2. Defect concentration of the CGO phase
At the CGO–gas interface there is a collection of electrostatic phenomena that lead to an interface voltage, such as segregation of mobile defects at the surface, or gas adsorption forming polar adsorbates. The former will result in the formation of a space charge layer at the CGO surface, while the latter will be unscreened and will be highly dependent on the angle and magnitude of the intrinsic dipole moment of the adsorbate.18,31,32 The origin of the space-charge layer is the change in stability of defects at the surface relative to the bulk.19,33 Enrichment of polarons at the ceria surface relative to the bulk has been observed by Haile et al. using X-ray absorption near edge spectroscopy (XANES), where the polaron fraction was found to be between 60–80% of the total cerium sites.34
The defect activities of the CGO surface can be expressed as a function of the activation overpotential:
| | 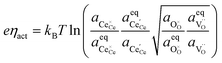 | (11) |
where the (full derivation is given in the ESI).
† The activity of polarons in the Ce 4f state is modulated by the activation overpotential. Using the cation site constraint
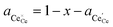
and anion site constraint
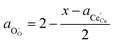
, where
x is the concentration of gadolinium at cation sites, we can model the activity of polarons under bias.
33 Here we assume the dilute solution approximation, as discussed in Section 2.1, such that
γ = 1, and observe a generalised logistic function as the coverage of polarons increases with a negative activation overpotential as shown in
Fig. 4.
35 This highlights that the CGO–gas interface dominates the activation overpotential in the Ni/CGO cermet case.
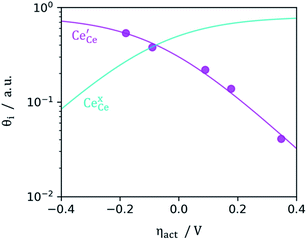 |
| | Fig. 4 Surface cation site coverage at the CGO–gas interface as a function of overpotential. Circles represent  data collected by APXPS on a Sm0.2Ce0.8O1.9–gas interface as a function of overpotential at 500 °C in 1 data collected by APXPS on a Sm0.2Ce0.8O1.9–gas interface as a function of overpotential at 500 °C in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 H2O 4 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar atmospheres (Chueh et al.).16 The fit for Ar atmospheres (Chueh et al.).16 The fit for 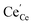 (magenta) and (magenta) and 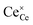 (cyan) are found by solving eqn (11). (cyan) are found by solving eqn (11). | |
3.3. Electrokinetics at the CGO–gas interface via the double phase boundary (2PB)
Section 3.1 illustrated that the activation overpotential of the Ni/CGO cermet electrode was located at the CGO–gas interface. To model the rate of charge transfer between the solid and gas phases, we must consider how the configurational entropy and electrostatic surface potential influence the electrokinetics. Eqn (5) describes the (electro)chemical potential of the transition state, in which the activity coefficient (γTS) describes the surface configuration required for a given reaction to proceed. This is an entropic effect, whereby the probability of a species at the transition state finding a correct configuration to undergo charge transfer is scaled by the availability of free sites.26 In other words, statistical thermodynamics states that a limited availability of free reaction sites would effectively increase the activation energy. This was demonstrated by Bazant et al. for the Li-ion intercalation process where the excess chemical potential of the transition state scaled with the concentration of lithium vacancies at the LiFePO4 electrode surface.26 For the reaction R2PB2, the transition state does not require a free surface site, and therefore activity coefficient of the transition state has no entropic constraint, thus γTS = 1. The activation chemical potential difference for the forward reaction R2PB2 under electrical bias is therefore given as:| | 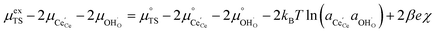 | (12) |
Likewise, the reverse reaction can be expressed as:
| | 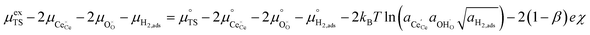 | (13) |
In realising eqn (12) and (13), we rationalise the importance of a large adsorbate dipole moment on the Faradaic reaction rate. The explanation is two-fold; first, a stronger dipole moment will mean that the fraction of the activation overpotential being consumed by the configurational entropy is minimised according to eqn (10). This was first discussed by Fleig, whereby the gradient ∂Δχ/∂η approaches 1 when the intrinsic dipole moment approaches infinity.17 Secondly, since configurational entropy scales logarithmically with respect to adsorbate coverage, a large intrinsic dipole strength is necessary for the thermodynamic driving force to be sustained over a reasonable overpotential range. In other words, a relatively weak dipole moment will result in saturation, or depletion, of adsorbates at the CGO–gas interface, thus limiting the current as the electrostatic potential plateaus.36
By combining eqn (12), (13) and (4) we can derive an expression for current density at the 2PB:37
| | 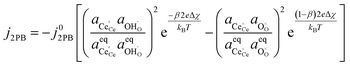 | (14) |
where the exchange current density is derived following
eqn (6):
| | 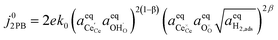 | (15) |
Eqn (15) can be rearranged to express the exchange current density a function of equilibrium electrostatic surface potential at equilibrium (full derivation given in ESI†):18
| | 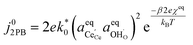 | (16) |
where
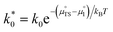
. The pre-exponential terms which are not derived for the conventional Butler–Volmer equation means that the current–voltage characteristics of this electrochemical process will likely be asymmetric under bias. Here we note another argument for designing a system which maximises the dipole moment of the adsorbate, since the exchange current density is highly dependent on the exponentially scaled surface potential, which is linearly proportional to the dipole moment of the adsorbate.
3.4. Electrokinetics at the CGO–gas interface via the triple phase boundary (3PB)
For conventional cermet electrodes like Ni/YSZ, charge transfer with the gas phase is thought to occur exclusively at the triple phase boundary (3PB) due to the limited electronic conductivity of the YSZ phase.1 The relatively high electronic conductivity of CGO under reducing conditions means that charge transfer with the gas phase may occur at the CGO–gas interface, hence the rationale behind Section 3.3. However, charge transfer at the 3PB is still possible and must be considered in the model even though the availability of appropriate 3PB sites is substantially less than that of 2PB sites.38
At the 3PB, the shift in free energy under bias is expressed as:
| | 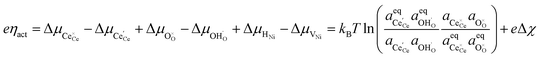 | (17) |
Here we see that the driving force for charge transfer is still expressed in terms of the electrostatic surface potential at the CGO–gas interface even through the reaction occurs at the 3PB, making eqn (10) and (17) equivalent. Note that hydrogen adsorbed on the nickel is in equilibrium with the gas phase 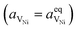 . This makes sense when we recall that there is no double layer at the Ni–CGO interface and that all processes are fast relative to charge transfer, thus the electrostatic potential will likely be spread out across the CGO surface. The transition states for R3PB2 require an unoccupied nickel site at the 3PB, thus we can express the activity coefficient of the transition state as γTS = (aVNi)−1.26 The activation chemical potential defence for the reduction reaction R3PB2 under electrical bias is therefore given as:
. This makes sense when we recall that there is no double layer at the Ni–CGO interface and that all processes are fast relative to charge transfer, thus the electrostatic potential will likely be spread out across the CGO surface. The transition states for R3PB2 require an unoccupied nickel site at the 3PB, thus we can express the activity coefficient of the transition state as γTS = (aVNi)−1.26 The activation chemical potential defence for the reduction reaction R3PB2 under electrical bias is therefore given as:
| | 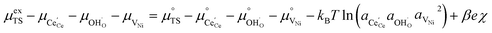 | (18) |
Likewise, the reverse reaction can be expressed as:
| | 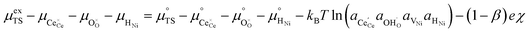 | (19) |
Combining eqn (18) and (19) with (4) we can derive an expression for current density at the 3PB:
| | 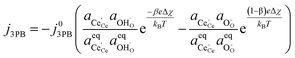 | (20) |
which is similar to the result given by
eqn (14) for the 2PB system. This only differs by the number of electrons transferred and the exchange current density, which is derived following
eqn (6):
| | 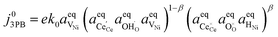 | (21) |
Eqn (21) can be rearranged to include the equilibrium electrostatic surface potential at equilibrium at the 2PB:18
| | 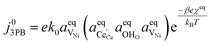 | (22) |
Eqn (21) can be generalised as 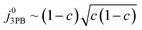 , where
, where 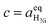 is the concentration of filled sites on the nickel surface. This is equivalent to the derivation for coupled ion–electron transfer given by Bazant et al.26,39
is the concentration of filled sites on the nickel surface. This is equivalent to the derivation for coupled ion–electron transfer given by Bazant et al.26,39
The metallic phase has two main purposes: lowering the electrical resistance of the cermet matrix and catalysing the 3PB reaction.30 The desired catalytic nature of the metallic phase is expressed in eqn (22) whereby the affinity for adsorbed hydrogen and free nickel sites must be balanced, as proposed in the Sabatier principle.40–43 From an entropic perspective, free nickel sites are desired to enhance the probability of a successful “jump” across the 3PB, as expressed by the activity coefficient of the transition state (Fig. 5a–d).26 However, lowering the affinity for adsorbed hydrogen on the nickel surface will increase the free energy of the final state, thus increasing the energy barrier for the R3PB2, as expressed in eqn (5) (Fig. 5e).
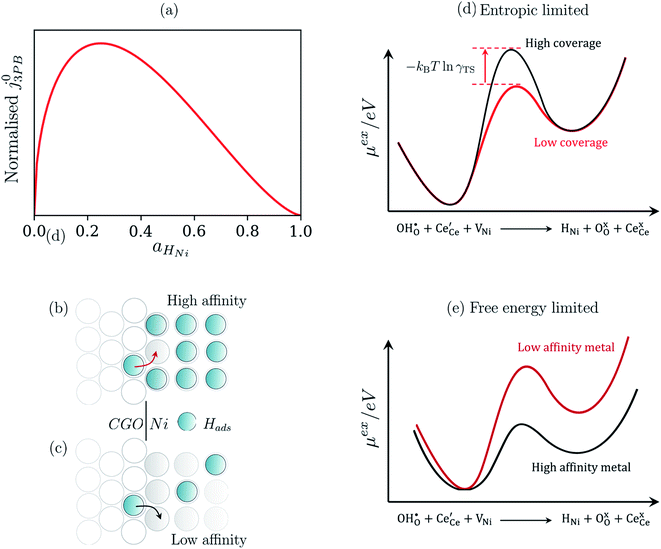 |
| | Fig. 5 (a) Normalised current density as a function of hydrogen coverage on the nickel surface according to eqn (22).26,39 (b and c) Illustrate the entropic constraint caused by filling the nickel surface and blocking viable reaction sites at the 3PB. (d) Schematic diagram of the excess chemical potential landscape exploring reaction R3PB2 using metals with high affinity for hydrogen (black) and low affinity for hydrogen (red), whereby increasing the effective activation barrier by using metals with a higher affinity for hydrogen. (e) Schematic diagram of the excess chemical potential landscape exploring reaction R3PB2 showing the effects of hydrogen affinity on the free energy of the reaction and the size of the energy barrier, where metals with a low affinity for hydrogen (black line) destabilise the final state of the reaction and increase the size of the activation barrier according to eqn (5). | |
Eqn (20) states that the electrostatic surface potential located at the 2PB influences the rate of Faradaic reactions at the 3PB. The origin of this phenomenon is rooted in the dipole–dipole interactions, whereby the coverage of adsorbates at the 3PB will influence the adsorption enthalpy at the 2PB. For example, in water electrolysis mode, electron transfer is driven by the adsorbates seeking to establish thermodynamic equilibrium with the gas phase, resulting in the release of hydrogen, relaxation of the electrostatic surface potential and a spatial region free of adsorbates. If electron transfer occurs via a 2PB mechanism, the adsorbate-free region will be filled as the adsorbates reorganise to maximise configurational entropy and minimise dipole–dipole interactions. The same principle applies to the 3PB mechanism, where a vacant hydroxyl site close to the 3PB will stimulate adsorbate reorganisation across the entire CGO surface, resulting in the relaxation of the electrostatic surface potential at the CGO–gas interface. On calculating which of the mechanistic pathways will dominate the total current density, we can see that the current–voltage relation is identical (eqn (14) and (20)), and only differs due to the exchange current density. However, one must also consider the availability of reaction sites and the energy barrier for the reaction to progress.
3.5. Outlook on other systems
To date we have only applied the theory of the electrostatic surface potential to discuss the interaction between Ni/CGO and H2/H2O. Chueh et al. demonstrated that the electrostatic surface potential at the Sm0.2Ce0.8O1.9–(CO/CO2) interface was invariant under an applied overpotential (Fig. 6a).32 This observation could be a result of the adsorbed carbonate forming a weak intrinsic dipole moment normal to the surface, or that the adsorbate is neutral and therefore has no electric potential.32,44 Nevertheless, the electrode polarisation is significantly increased for the CO/CO2 system compared with the H2/H2O system (Fig. 6b).15,16,45 Analysis of eqn (7) makes it clear that if there is no electrostatic potential driving the charge transfer reaction of the CO/CO2 system, then the respective current density will be severely impeded.36 Given that an exponentially scaled electrostatic driving force is absent for the CO/CO2 system, one may question why the current–voltage relationship in Fig. 6b still exhibits Tafel-like behaviour. This phenomenon is attributed to eqn (11) where the ceria defect concentration is exponentially scaled by the overpotential, such that the pre-exponential factor in eqn (7) is the essence of the observed Tafel-like behaviour.36
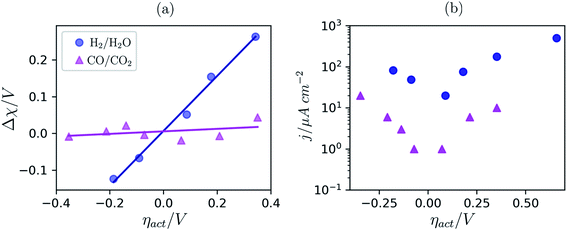 |
| | Fig. 6 (a) Δχ–η and (b) j–η relationship at the Sm0.2Ce0.8O1.9–gas interface in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 H2 4 H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar (blue) and 2 Ar (blue) and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 CO/CO2 (magenta) measured at 500 °C and collected by APXPS.15,16,45 25 CO/CO2 (magenta) measured at 500 °C and collected by APXPS.15,16,45 | |
4. Summary
In this work, the origin and physics of the activation overpotential for a Ni/CGO fuel electrode has been explained. We have analytically demonstrated the effects of non-equilibrium thermodynamics on the concentration of electronic defects and the adsorbate induced electrostatic surface potential. Moreover, we used our understanding of non-equilibrium thermodynamics to formulate analytical expressions for the current-overpotential characteristics of water electrolysis at the Ni/CGO electrode via the 2PB and 3PB mechanism. This rigorous mathematical description allowed the prediction of the origin of the activation overpotential of Ni/CGO electrode and postulates that the shift in electrostatic surface potential was the driving force for current density via both mechanisms. This is a significant consideration for the design and operational conditions of SOC electrodes, as the strength of the intrinsic dipole moment of the adsorbed gas species is shown to have a profound effect on the magnitude of the activation overpotential. The theories put forward in this work are not confined to fuel electrodes and can be extended to other fields where charge transfer occurs at a solid–gas interface, such as nitrogen reduction and in lithium air batteries.
Abbreviations
|
a
j
| Activity of species j (1) |
|
c
j
| Concentration of species j (1) |
| cc | Current collector, electron conducting phase |
|
G
| Gibbs free energy (eV) |
|
H
| Enthalpy (eV) |
|
J
| Current density (A cm−2) |
|
j
0
| Exchange current density (A cm−2) |
|
k
0
| Rate constant (s−1) |
|
k
B
| Boltzmann constant (eV K−1) |
| MIEC | Mixed ionic-electronic conducting phase |
| CGO | Gadolinium doped ceria |
|
R
| Rate of reaction (s−1) |
|
S
| Entropy (kB) |
|
T
| Temperature (K) |
| yte | Electrolyte, ion conducting phase |
Greek symbols
|
β
| Electron transfer symmetry factor (1) |
|
γj | Activity coefficient of species j (1) |
| Δ(·) | Perturbation of quantity j relative to the equilibrium with the gas phase and grounded electrode (1) |
|
ε
0
| Vacuum permittivity (e2 V−1 m−1) |
|
η
| Overpotential (V) |
|
θj | Surface coverage of species j (1) |
|
μj | Electrochemical potential of charged species j, or chemical potential of neutral species j (eV) |
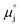
| Standard potential of species j (eV) |
|
μ
exe
| Excess chemical potential of species j (eV) |
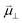
| Dipole moment (D) |
|
ρ
0
| Density of available adsorption sites (m−2) |
|
ϕj | Electric potential of species j (V) |
|
χ
| Electrostatic surface potential (V) |
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
This work was supported by Ceres Power Ltd. IDS and SJS acknowledge the EPSRC for funding through the award of grant EP/R002010/1.
References
- M. C. Doppler, J. Fleig, M. Bram and A. K. Opitz, J. Power Sources, 2018, 380, 46–54 CrossRef CAS.
- K. Yamaji, N. Sakai, M. Ishikawa, H. Yokokawa and M. Dokiya, Ionics, 1997, 3, 67–74 CrossRef.
- S. Primdahl and M. Mogensen, J. Electrochem. Soc., 1997, 144, 3409–3419 CrossRef CAS.
- J. H. Nam and D. H. Jeon, Electrochim. Acta, 2006, 51, 3446–3460 CrossRef CAS.
- H. Yokokawaa and T. Kawadab, Solid State Ionics, 1996, 2738, 1259–1266 Search PubMed.
- N. Sakai, K. Yamaji, T. Horita, H. Kishimoto, Y. P. Xiong and H. Yokokawa, Solid State Ionics, 2004, 175, 387–391 CrossRef CAS.
- M. Brown, S. Primdahl and M. Mogensen, J. Electrochem. Soc., 2000, 147, 475 CrossRef CAS.
- S. P. Jiang and S. P. S. Badwal, J. Electrochem. Soc., 1997, 144, 3777 CrossRef CAS.
- H. Yokokawa, T. Horita, N. Sakai, K. Yamaji, M. E. Brito, Y. P. Xiong and H. Kishimoto, Solid State Ionics, 2004, 174, 205–221 CrossRef CAS.
- A. Bieberle and L. J. Gauckler, Solid State Ionics, 2000, 135, 337–345 CrossRef CAS.
- T. Horita, H. Kishimoto, K. Yamaji, Y. Xiong, N. Sakai, M. E. Brito and H. Yokokawa, Solid State Ionics, 2006, 177, 1941–1948 CrossRef CAS.
- W. G. Bessler, S. Gewies and M. Vogler, Electrochim. Acta, 2007, 53, 1782–1800 CrossRef CAS.
- S. Grieshammer, T. Zacherle and M. Martin, Phys. Chem. Chem. Phys., 2013, 15, 15935–15942 RSC.
- C. Franchini, M. Reticcioli, M. Setvin and U. Diebold, Nat. Rev. Mater., 2021, 6, 560–586 CrossRef CAS.
- Z. A. Feng, M. L. Machala and W. C. Chueh, Phys. Chem. Chem. Phys., 2015, 17, 12273–12281 RSC.
- Z. A. Feng, F. El Gabaly, X. Ye, Z. Shen and W. C. Chueh, Nat. Commun., 2014, 5, 1–9 Search PubMed.
- J. Fleig, Phys. Chem. Chem. Phys., 2005, 7, 2027–2037 RSC.
- N. J. Williams, I. D. Seymour, R. T. Leah, S. Mukerjee, M. Selby and S. J. Skinner, Phys. Chem. Chem. Phys., 2021, 23, 14535–14954 RSC.
- Z. Zhao, M. Uddi, N. Tsvetkov, B. Yildiz and A. F. Ghoniem, J. Phys. Chem. C, 2016, 120, 16271–16289 CrossRef CAS.
- W. G. Bessler, J. Warnatz and D. G. Goodwin, Solid State Ionics, 2007, 177, 3371–3383 CrossRef CAS.
- M. Z. Bazant, Acc. Chem. Res., 2013, 46, 1144–1160 CrossRef CAS PubMed.
- P. Bai and M. Z. Bazant, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- A. Nenning, A. K. Opitz, C. Rameshan, R. Rameshan, R. Blume, M. Hävecker, A. Knop-Gericke, G. Rupprechter, B. Klötzer and J. Fleig, J. Phys. Chem. C, 2016, 120, 1461–1471 CrossRef CAS PubMed.
- M. Z. Bazant, R. Soc. Chem., 2017, 199, 423–463 CAS.
- T. R. Ferguson and M. Z. Bazant, J. Electrochem. Soc., 2012, 159, 1967–1985 CrossRef.
- D. Fraggedakis, M. McEldrew, R. B. Smith, Y. Krishnan, Y. Zhang, P. Bai, W. C. Chueh, Y. Shao-Horn and M. Z. Bazant, Electrochim. Acta, 2021, 367, 137432 CrossRef CAS.
- C. Zhang, Y. Yu, M. E. Grass, C. Dejoie, W. Ding, K. Gaskell, N. Jabeen, Y. P. Hong, A. Shavorskiy, H. Bluhm, W. X. Li, G. S. Jackson, Z. Hussain, Z. Liu and B. W. Eichhorn, J. Am. Chem. Soc., 2013, 135, 11572–11579 CrossRef CAS PubMed.
- C. Zhang, Y. Yu, M. E. Grass, C. Dejoie, W. Ding, K. Gaskell, N. Jabeen, Y. P. Hong, A. Shavorskiy, H. Bluhm, W. Li, G. S. Jackson, Z. Hussain, Z. Liu and B. W. Eichhorn, J. Am. Chem. Soc., 2013, 135, 11572–11579 CrossRef CAS PubMed.
- H. A. Hansen and C. Wolverton, J. Phys. Chem. C, 2014, 118, 27402–27414 CrossRef CAS.
- A. Nenning, C. Bischof, J. Fleig, M. Bram and A. K. Opitz, Energies, 2020, 13, 1–30 CrossRef.
- A. F. Zurhelle, X. Tong, A. Klein, D. S. Mebane and R. A. De Souza, Angew. Chem., 2017, 129, 14708–14712 CrossRef.
- Z. A. Feng, C. Balaji Gopal, X. Ye, Z. Guan, B. Jeong, E. Crumlin and W. C. Chueh, Chem. Mater., 2016, 28, 6233–6242 CrossRef CAS.
- S. Grieshammer and M. Martin, J. Mater. Chem. A, 2017, 5, 9241–9249 RSC.
- W. Yuan, Q. Ma, Y. Liang, C. Sun, K. V. L. V. Narayanachari, M. J. Bedzyk, I. Takeuchi and S. M. Haile, J. Mater. Chem. A, 2020, 8, 9850–9858 RSC.
- Z. Guan, D. Chen and W. C. Chueh, Phys. Chem. Chem. Phys., 2017, 19, 23414–23424 RSC.
- A. Schmid and J. Fleig, J. Electrochem. Soc., 2019, 166, F831–F846 CrossRef CAS.
- W. C. Chueh and S. M. Haile, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 313–341 CrossRef CAS PubMed.
- M. Ouyang, A. Bertei, S. J. Cooper, Y. Wu, P. Boldrin, X. Liu, M. Kishimoto, H. Wang, M. Naylor Marlow, J. Chen, X. Chen, Y. Xia, B. Wu and N. P. Brandon, J. Energy Chem., 2021, 56, 98–112 CrossRef.
- J. Lim, Y. Li, D. H. Alsem, H. So, S. C. Lee, P. Bai, D. A. Cogswell, X. Liu, N. Jin, Y. S. Yu, N. J. Salmon, D. A. Shapiro, M. Z. Bazant, T. Tyliszczak and W. C. Chueh, Science, 2016, 353, 566–571 CrossRef CAS PubMed.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- S. R. Kelly, C. Kirk, K. Chan and J. K. Nørskov, AIChE Annu. Meet., Conf. Proc., 2020, 14581–14591 CAS.
- G. S. Karlberg, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 5158–5161 RSC.
- L. D. Chen, M. Urushihara, K. Chan and J. K. Nørskov, ACS Catal., 2016, 6, 7133–7139 CrossRef CAS.
- E. M. Sala, N. Mazzanti, M. B. Mogensen and C. Chatzichristodoulou, Solid State Ionics, 2022, 375, 115833 CrossRef CAS.
- Z. Albert Feng, Thesis, 2015, 1–141 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Ieuan D.
Seymour
a,
Ieuan D.
Seymour
 a,
Robert T.
Leah
b,
Aayan
Banerjee
a,
Robert T.
Leah
b,
Aayan
Banerjee
 c,
Subhasish
Mukerjee
b and
Stephen J.
Skinner
c,
Subhasish
Mukerjee
b and
Stephen J.
Skinner
 *a
*a
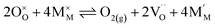
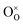 ,
, 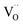 ,
, 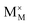 and
and 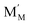 represent an oxide ion at the anion site, a doubly charged oxygen vacancy, a metal ion on the cation site, and a small polaron (localised electron at the cation site) respectively. However, this reaction often occurs via a fuel intermediate such as CO/CO2 or H2/H2O, where the strength of the intrinsic dipole moment of the adsorbed gas species was understood to determine the performance of the electrode.15,16 Owing to the relative ease of reduction of CGO under operational conditions, and therefore good electronic conductivity, biasing the electrode modulates the coverage of adsorbates and the concentration of electronic defects. Understanding these phenomena is critical to accurately model and design the electrodes. Therefore, in this study we will analyse and discuss the effects of non-equilibrium operation (under electrical bias) on the electrostatic potential at the interfaces of the Ni/CGO electrode.
represent an oxide ion at the anion site, a doubly charged oxygen vacancy, a metal ion on the cation site, and a small polaron (localised electron at the cation site) respectively. However, this reaction often occurs via a fuel intermediate such as CO/CO2 or H2/H2O, where the strength of the intrinsic dipole moment of the adsorbed gas species was understood to determine the performance of the electrode.15,16 Owing to the relative ease of reduction of CGO under operational conditions, and therefore good electronic conductivity, biasing the electrode modulates the coverage of adsorbates and the concentration of electronic defects. Understanding these phenomena is critical to accurately model and design the electrodes. Therefore, in this study we will analyse and discuss the effects of non-equilibrium operation (under electrical bias) on the electrostatic potential at the interfaces of the Ni/CGO electrode.
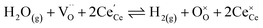 , which can occur via a two phase boundary (2PB) or three phase boundary (3PB) mechanism at the Ni/CGO fuel electrode. The overall reaction equilibrium can be broken down into the following steps depending on the mechanism (Fig. 1):
, which can occur via a two phase boundary (2PB) or three phase boundary (3PB) mechanism at the Ni/CGO fuel electrode. The overall reaction equilibrium can be broken down into the following steps depending on the mechanism (Fig. 1):
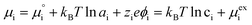
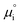 is the standard potential, kBT
is the standard potential, kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ai is the activity potential and eϕi is the electric potential. The activity (ai = γici) is the product of the concentration (ci) and activity coefficient (γi), which is a measure of the non-ideality of the species.18,21 A simplification can be made to express all the non-idealities within the excess chemical potential, μexi, which also includes contributions from the standard and electric potentials. Here, we use the definition of (electro)chemical potential, meaning that if the species of interest is charged, we find the electrochemical potential, and if the species of interest is neutral, we find the chemical potential. If we consider the rate limiting process of an electrode to be a Faradaic reaction whereby n electrons are transferred, then we find the activation overpotential (ηact) as the chemical potential difference of a net reduction reaction:
ai is the activity potential and eϕi is the electric potential. The activity (ai = γici) is the product of the concentration (ci) and activity coefficient (γi), which is a measure of the non-ideality of the species.18,21 A simplification can be made to express all the non-idealities within the excess chemical potential, μexi, which also includes contributions from the standard and electric potentials. Here, we use the definition of (electro)chemical potential, meaning that if the species of interest is charged, we find the electrochemical potential, and if the species of interest is neutral, we find the chemical potential. If we consider the rate limiting process of an electrode to be a Faradaic reaction whereby n electrons are transferred, then we find the activation overpotential (ηact) as the chemical potential difference of a net reduction reaction: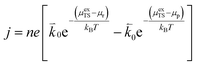
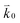 and
and 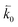 represent the forward and reverse rate constants, respectively. We may assume that the attempt frequency for the forward and backward reactions are equivalent, such that
represent the forward and reverse rate constants, respectively. We may assume that the attempt frequency for the forward and backward reactions are equivalent, such that 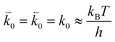 .21 Occupation of the transition state is short lived, therefore we can assume its concentration to be negligible. Thus, we only need to use the excess chemical potential term (μexTS), which is defined following Butler–Volmer kinetics:21,24–26
.21 Occupation of the transition state is short lived, therefore we can assume its concentration to be negligible. Thus, we only need to use the excess chemical potential term (μexTS), which is defined following Butler–Volmer kinetics:21,24–26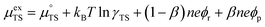
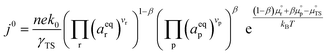
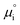 is the standard chemical potential of species i. When an electrical bias is applied, an electrostatic potential step is created at the interface in which the rate-limiting step is located. The current density, j, is introduced as:
is the standard chemical potential of species i. When an electrical bias is applied, an electrostatic potential step is created at the interface in which the rate-limiting step is located. The current density, j, is introduced as: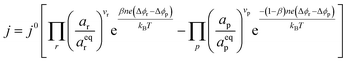
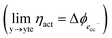 . Using operando X-ray Photoelectron Spectroscopy (XPS), Chueh et al. demonstrated that the shift in electric potential of the ceria phase (ϕCGO) was also equal to the activation overpotential
. Using operando X-ray Photoelectron Spectroscopy (XPS), Chueh et al. demonstrated that the shift in electric potential of the ceria phase (ϕCGO) was also equal to the activation overpotential 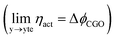 .16 It must be noted that in this study a thin film of dense ceria was used as opposed to a cermet electrode, therefore there was no distribution of the activation overpotential as a function of distance from the bulk electrolyte contact.16 However, charge transfer between ceria and the current collector, and between ceria and the electrolyte, was fast relative to charge transfer with the gas phase. Therefore, throughout the matrix of the Ni/CGO cermet it is rational to assume that the shift in electric potential of the ceria phase will be equal to the shift in the electric potential of the nickel phase (Δϕcc = ΔϕCGO). Consequently, bias of the Ni/CGO electrode does not result in the formation of an electric double layer at the Ni–CGO interface, as demonstrated in Fig. 2a.
.16 It must be noted that in this study a thin film of dense ceria was used as opposed to a cermet electrode, therefore there was no distribution of the activation overpotential as a function of distance from the bulk electrolyte contact.16 However, charge transfer between ceria and the current collector, and between ceria and the electrolyte, was fast relative to charge transfer with the gas phase. Therefore, throughout the matrix of the Ni/CGO cermet it is rational to assume that the shift in electric potential of the ceria phase will be equal to the shift in the electric potential of the nickel phase (Δϕcc = ΔϕCGO). Consequently, bias of the Ni/CGO electrode does not result in the formation of an electric double layer at the Ni–CGO interface, as demonstrated in Fig. 2a.

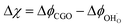
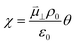 , where
, where 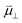 , ε0, ρ0 and θ represent the dipole moment normal to the surface, vacuum permittivity, the density of adsorption sites and the coverage of adsorbates, respectively.
, ε0, ρ0 and θ represent the dipole moment normal to the surface, vacuum permittivity, the density of adsorption sites and the coverage of adsorbates, respectively.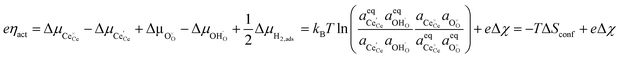
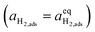 , thus
, thus 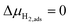 . Eqn (10) shows that the activation overpotential is a function of configurational entropy (ΔSconf) and electrostatic surface potential. If we consider the Ni/CGO cermet electrode illustrated in Fig. 3a, we are aware that there is no electrostatic potential shift between the CGO and metallic phases (Fig. 3b). Instead, we observe a shift in electrostatic surface potential which decays exponentially away from the electrolyte contact as the shift in electric potential of the adsorbate equilibrates with the CGO phase approaching the current collector contact, where
. Eqn (10) shows that the activation overpotential is a function of configurational entropy (ΔSconf) and electrostatic surface potential. If we consider the Ni/CGO cermet electrode illustrated in Fig. 3a, we are aware that there is no electrostatic potential shift between the CGO and metallic phases (Fig. 3b). Instead, we observe a shift in electrostatic surface potential which decays exponentially away from the electrolyte contact as the shift in electric potential of the adsorbate equilibrates with the CGO phase approaching the current collector contact, where 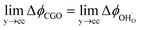 . We note that the potential of the metallic phase is constant throughout the electrode as the electronic resistance is assumed to be close to zero relative to the ionic resistance of the electrolyte phase. This theory contrasts with the Ni/YSZ model (Fig. 3c), where Faradaic reactions are driven by the difference in the electric potential shift between the current collector and electrolyte phases, ηact = Δϕcc − Δϕyte.30
. We note that the potential of the metallic phase is constant throughout the electrode as the electronic resistance is assumed to be close to zero relative to the ionic resistance of the electrolyte phase. This theory contrasts with the Ni/YSZ model (Fig. 3c), where Faradaic reactions are driven by the difference in the electric potential shift between the current collector and electrolyte phases, ηact = Δϕcc − Δϕyte.30

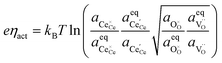
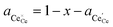 and anion site constraint
and anion site constraint 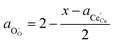 , where x is the concentration of gadolinium at cation sites, we can model the activity of polarons under bias.33 Here we assume the dilute solution approximation, as discussed in Section 2.1, such that γ = 1, and observe a generalised logistic function as the coverage of polarons increases with a negative activation overpotential as shown in Fig. 4.35 This highlights that the CGO–gas interface dominates the activation overpotential in the Ni/CGO cermet case.
, where x is the concentration of gadolinium at cation sites, we can model the activity of polarons under bias.33 Here we assume the dilute solution approximation, as discussed in Section 2.1, such that γ = 1, and observe a generalised logistic function as the coverage of polarons increases with a negative activation overpotential as shown in Fig. 4.35 This highlights that the CGO–gas interface dominates the activation overpotential in the Ni/CGO cermet case.

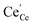 data collected by APXPS on a Sm0.2Ce0.8O1.9–gas interface as a function of overpotential at 500 °C in 1
data collected by APXPS on a Sm0.2Ce0.8O1.9–gas interface as a function of overpotential at 500 °C in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 H2O
4 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2
H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar atmospheres (Chueh et al.).16 The fit for
Ar atmospheres (Chueh et al.).16 The fit for 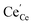 (magenta) and
(magenta) and 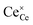 (cyan) are found by solving eqn (11).
(cyan) are found by solving eqn (11).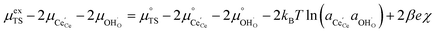
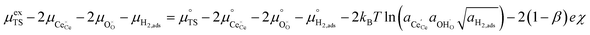
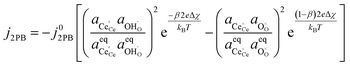
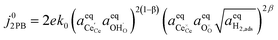
 . The pre-exponential terms which are not derived for the conventional Butler–Volmer equation means that the current–voltage characteristics of this electrochemical process will likely be asymmetric under bias. Here we note another argument for designing a system which maximises the dipole moment of the adsorbate, since the exchange current density is highly dependent on the exponentially scaled surface potential, which is linearly proportional to the dipole moment of the adsorbate.
. The pre-exponential terms which are not derived for the conventional Butler–Volmer equation means that the current–voltage characteristics of this electrochemical process will likely be asymmetric under bias. Here we note another argument for designing a system which maximises the dipole moment of the adsorbate, since the exchange current density is highly dependent on the exponentially scaled surface potential, which is linearly proportional to the dipole moment of the adsorbate.
 . This makes sense when we recall that there is no double layer at the Ni–CGO interface and that all processes are fast relative to charge transfer, thus the electrostatic potential will likely be spread out across the CGO surface. The transition states for R3PB2 require an unoccupied nickel site at the 3PB, thus we can express the activity coefficient of the transition state as γTS = (aVNi)−1.26 The activation chemical potential defence for the reduction reaction R3PB2 under electrical bias is therefore given as:
. This makes sense when we recall that there is no double layer at the Ni–CGO interface and that all processes are fast relative to charge transfer, thus the electrostatic potential will likely be spread out across the CGO surface. The transition states for R3PB2 require an unoccupied nickel site at the 3PB, thus we can express the activity coefficient of the transition state as γTS = (aVNi)−1.26 The activation chemical potential defence for the reduction reaction R3PB2 under electrical bias is therefore given as: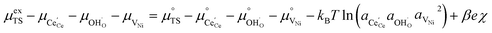
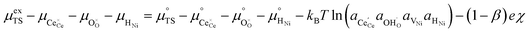
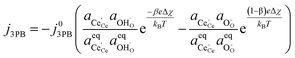
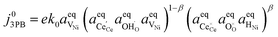
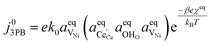
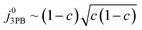 , where
, where 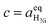 is the concentration of filled sites on the nickel surface. This is equivalent to the derivation for coupled ion–electron transfer given by Bazant et al.26,39
is the concentration of filled sites on the nickel surface. This is equivalent to the derivation for coupled ion–electron transfer given by Bazant et al.26,39

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 H2
4 H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O
H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar (blue) and 2
Ar (blue) and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 CO/CO2 (magenta) measured at 500 °C and collected by APXPS.15,16,45
25 CO/CO2 (magenta) measured at 500 °C and collected by APXPS.15,16,45