Tailoring high-temperature stability and electrical conductivity of high entropy lanthanum manganite for solid oxide fuel cell cathodes†
Yinchun
Shi
 a,
Na
Ni
a,
Na
Ni
 *bc,
Qi
Ding
bc and
Xiaofeng
Zhao
a
*bc,
Qi
Ding
bc and
Xiaofeng
Zhao
a
aSchool of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
bGas Turbine Research Institute, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
cKey Lab of Education Ministry for Power Machinery and Engineering, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China. E-mail: na.ni@sjtu.edu.cn
First published on 20th October 2021
Abstract
High entropy perovskite oxides (HEPOs) have been proposed to serve as improved cathode materials for solid oxide fuel cells (SOFCs); however, the larger compositional design space introduced by HEPOs urges for a better understanding of the correlation among the composition, phase stability and resulting properties of HEPO cathodes. In this work, a series of LaMnO3 based HEPOs (HEALMOs) were designed systematically to investigate the effect of the A site high entropy composition on the structure and thermochemical/electrical properties of HEALMO materials. The results show that the high entropy effect manifests itself on top of the conventional doping effect. First of all, neither the Goldschmidt tolerance factor nor the cation size difference can be used simply to predict the formation ability of single-phase HEALMOs. Meanwhile, HEALMOs may exhibit higher crystallographic symmetry with much higher cation size differences and at Goldschmidt tolerance factor values deviating more largely from 1. Secondly, while high-temperature stability including both resistance to elemental segregation and chemical compatibility with 8YSZ is affected by the A site cation size difference in a similar way to that of conventional perovskite oxides, HEALMOs show much enhanced stability at larger A site cation size differences. Finally, high entropy contributes to the maintenance of electrical conductivity in the high temperature range. The optimum HEALMO with the composition of (La0.2Nd0.2Sm0.2Ca0.2Sr0.2)MnO3 exhibits a combination of excellent high-temperature stability and good electrical conductivity, highlighting its great potential as a promising cathode material for SOFCs.
1 Introduction
An SOFC is a solid-state power generation device that can directly convert chemical energy in hydrocarbon fuels into electricity efficiently and in an environmentally friendly way.1–11 The polarization loss in SOFCs is complex and depends on many factors such as the thickness of the electrolyte, the working temperature, the contact resistance between cell components, the concentration profile at the electrodes and the activation energy barriers of the rate-determining steps on the anode and cathode.2,3,6,10,11 In many cases, the overall polarization loss of a working SOFC with a thin electrolyte is dominated by the polarization loss of the oxygen reduction reaction (ORR) on the cathode, which is partly attributed to the high activation energy and slow kinetics of the ORR compared with that of the hydrogen oxidation reaction on the anode.2,3,6,11 The reaction rate using oxygen gas as an oxidizer on the cathode becomes slower by several orders of magnitude compared with that of fuel oxidation reactions on the anode.3 As a commonly used cathode material for SOFCs, La1−xSrxMnO3−δ (LSM) exhibits high electrical conductivity, excellent electrochemical catalytic activity, appropriate thermal expansion coefficient close to that of 8YSZ, etc.3,5,11–14 However, LSM suffers from various problems.2,5,12,15 It has been extensively reported that LSM is prone to react with 8YSZ at high temperatures, leading to the formation of highly insulating phases such as La2Zr2O7 or SrZrO3.2,5,15–19 These insulating phases at the electrolyte/cathode interface significantly deteriorate the performance of SOFCs. In addition, Sr segregation can also hinder the charge transfer in the ORR and leads to the deactivation of the LSM cathode due to the formation of insulating phases such as SrO and SrCO3.1,7,12,20 Lowering of temperature can alleviate the formation of these phases; however, the reduction in the working temperature in turn leads to the increase of polarization losses.2,11 Thus, a stable and high-performance cathode at high temperatures is especially crucial for the final performance of SOFCs.In recent years, high entropy ceramics (HECs) have attracted great attention and various HECs have been investigated.1,21–28 HECs are multi-principal solid solution ceramics with one or more Wyckoff sites shared by equal or near-equal atomic ratios of elements, in which the large mixed entropy contributes to their formation.6,21–25 It is reported that the mixed entropy of HECs should be larger than 1.5R (0.0124 kJ mol−1 K−1).23,25,26,29 HECs are long-range structurally ordered but compositionally disordered, and the ions with different sizes are highly dispersed, leading to the presence of severe lattice distortion and formation of the stress field.1,23–25 Generally, HECs possess many excellent properties, such as high stability, low thermal conductivity, high strength and hardness, etc.6,22–26,28,30,31 Among HECs, high entropy perovskite oxides (HEPOs) are particularly interesting because of the special and complex structure, giving more possibilities for property tailoring. It is reported that SOFC cathodes can benefit a lot from high entropy tailoring, leading to reduced thermal expansion, improved high-temperature stability, modified electronic transport and catalytic activity because of more redox pairs, reduced cost by substitution of the expensive element, etc.1,32,33 In the infancy stage, research studies focus on the synthesis of single-phase high entropy perovskite oxides.29,34 For example, Jiang et al. and Sarkar et al. successfully synthesized single-phase high entropy perovskite oxides with the B site or both cation sites populated with five different elements in equiatomic amounts, respectively.29,34 Subsequently, several high entropy perovskite oxides have been investigated as cathodes for SOFCs to improve the existing drawbacks of the traditional SOFC cathode, such as Sr segregation, Cr corrosion, etc.1,6,23,33
Although the application of HEPOs for SOFC cathodes has been reported, a systematic study on the correlation among the composition, phase formation ability and resulting properties is still missing, which hinders the rational design of this class of new materials for improved cathode performance. In this work, a series of LaMnO3 based A site solid solution HEPOs (HEALMOs) were designed and synthesized combining several criteria including mixed entropy, Goldschmidt tolerance factor and cation size difference, followed by microstructural characterization and investigation of high-temperature thermal/chemical stability and electrical properties. The focus is to evaluate the typical perovskite phase formation criteria in HEPOs and the interplay between doping and high entropy effects on the resulting properties.
2 Experimental
2.1 Material design
Generally, Mn3+ cations in LaMnO3 (LMO) are prone to change valence to maintain charge neutrality when divalent cations are doped on the La site, leading to the formation of Mn4+.2,7,14,15,35,36 Thus, LSM is almost a pure electronic conductor and its ionic conductivity can be ignored.2,37 The electronic conduction mechanism of LSM depends on the small polaron hopping mechanism, in which electrons hop along the Mn3+–O2−–Mn4+ network during conduction.2,7,15,37 In this work, only La site cations in LMO are substituted with four other metal cations in equiatomic amounts to study the doping and high entropy effect induced by the A site. The idea is that, by not changing the B site element of Mn, the charge imbalance induced by doping on the A site will mostly be compensated by the charge disproportionation of Mn due to its ease of valence change, thus maintaining its nature as an electronic conductor.2 For the design and systematic variation of the HEALMO composition, three criteria considering mixed entropy, Goldschmidt tolerance factor and cation size difference were adopted.1,29,34,38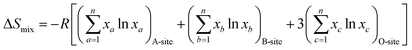 | (1) |
| ΔGmix = ΔHmix − TΔSmix | (2) |
Generally, the most important explanation for the formation of stabilized single-phase solid solution in HECs is the high mixed entropy, and the stability can be enhanced by increasing mixed entropy and lowering the Gibbs free energy.1,23,25 In this work, oxygen deficiency is not taken into account, and the calculated mixed entropies according to the stoichiometric formula are listed in Table 1. As is shown, all ΔSmix values of HEALMOs are 1.61R, meeting the requirement of mixed entropy for HECs.1,29,34
| Nominal composition | Mixed entropy (ΔSmix) | Goldschmidt tolerance factor (t) | A site cation size difference (δA) |
|---|---|---|---|
| HEALMO-1, (La0.2Nd0.2Sm0.2Y0.2Gd0.2)MnO3 | 1.61R | 0.928 | 7.49% |
| HEALMO-2, (La0.2Nd0.2Pr0.2Sr0.2Ba0.2)MnO3 | 1.61R | 0.983 | 8.49% |
| HEALMO-3, (La0.2Nd0.2Sm0.2Ca0.2Sr0.2)MnO3 | 1.61R | 0.959 | 5.30% |
| HEALMO-4, (La0.2Pr0.2Ca0.2Sr0.2Ba0.2)MnO3 | 1.61R | 0.988 | 7.51% |
| HEALMO-5, (La0.2Nd0.2Ca0.2Sr0.2Ba0.2)MnO3 | 1.61R | 0.985 | 8.29% |
| LSM82, (La0.8Sr0.2)MnO3 | 0.50R | 0.975 | 2.33% |
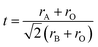 | (3) |
 | (4) |
2.2 Sample preparation
HEALMOs designed using the above criteria were prepared by the sol–gel method. Analytically pure nitrate reagents including La(NO3)3·6H2O, Nd(NO3)3·6H2O, Sm(NO3)3·6H2O, Y(NO3)3·6H2O, Gd(NO3)3, Pr(NO3)3·6H2O, Ca(NO3)2·4H2O, Sr(NO3)2, Ba(NO3)2 and Mn(NO3)2·xH2O were used as precursors. Ethylene diamine tetraacetic acid (EDTA) and citric acid were used as the chelating agents. Each HEALMO was prepared according to the following procedure. First, the specific nitrate aqueous solution was prepared by dissolving related nitrates weighed in stoichiometric ratios in deionized water; meanwhile, the EDTA–NH4OH solution was prepared by dissolving EDTA in ammonia. Subsequently, the nitrate aqueous solution and EDTA–NH4OH solution were mixed. After being stirred for a moment, citric acid was added into the mixed solution and continuously stirred. A homogeneous clear solution can be finally obtained by adjusting the pH to 7 using ammonia. The molar ratio of total metal ions![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EDTA
EDTA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) citric acid in the final solution is 1
citric acid in the final solution is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5. The final solution was continuously stirred at 80 °C in an oil bath until viscous xerogel was formed after gelation. Then, the stirrer was switched off and the xerogel was left for drying at 200 °C for 4 h, yielding fluffy powders. Lastly, these fluffy powders were pulverized using a mortar and pestle, and calcined at different temperatures for 2 h with the heating and cooling rate of 5 °C min−1 until a single-phase structure was obtained, respectively. For comparison, commercial La0.8Sr0.2MnO3 (LSM82) was directly purchased from Sigma-Aldrich.
1.5. The final solution was continuously stirred at 80 °C in an oil bath until viscous xerogel was formed after gelation. Then, the stirrer was switched off and the xerogel was left for drying at 200 °C for 4 h, yielding fluffy powders. Lastly, these fluffy powders were pulverized using a mortar and pestle, and calcined at different temperatures for 2 h with the heating and cooling rate of 5 °C min−1 until a single-phase structure was obtained, respectively. For comparison, commercial La0.8Sr0.2MnO3 (LSM82) was directly purchased from Sigma-Aldrich.
2.3 Characterization
X-ray diffraction (XRD, Rigaku D/max-2550PC) in the scan range of 20–80° at a scan rate of 2° min−1 was carried out to analyze the phase composition of the oxide samples. Additional XRD Rietveld refinement analysis was further conducted for single-phase HEALMOs and LSM82. Microstructure and spatially resolved chemical analysis of specimens was carried out by scanning electron microscopy (SEM, Tescan-Maia3) and transmission electron microscopy (TEM, Talos F200X G2), both combined with energy dispersive spectroscopy (EDS). The accurate cation contents in the single-phase HEALMOs and LSM82 were analysed using inductively coupled plasma atomic emission spectrometry (ICP-AES, iCAP7600). The sample for TEM observation was prepared by directly dispersing the powder onto the TEM copper grid coated with a carbon film.The high-temperature stability of single-phase HEALMOs and LSM82 is investigated from two aspects. On the one hand, the resistance to specific elemental segregation was investigated by comparing the morphologies of the powders screened using 200 mesh sieves before and after annealing at 800, 1000, 1100 and 1200 °C for 100 h in air, respectively. On the other hand, the chemical compatibility with the most commonly used electrolyte material of 8 mol% Y2O3 stabilized zirconia (8YSZ) was evaluated according to the following procedure adopted from the literature.5,8,33,43 Firstly, the screened HEALMO and LSM82 powders using 200 mesh sieves were mixed with 8YSZ powder of 20–30 nm in size in a weight ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 using a mortar and pestle, and stirred for 12 h to obtain an evenly mixed powder, respectively. Secondly, the mixed powder was put into a crucible and annealed at different temperatures for 5 h in air. The phase evolution of the mixed powder before and after annealing was analyzed by XRD.
1 using a mortar and pestle, and stirred for 12 h to obtain an evenly mixed powder, respectively. Secondly, the mixed powder was put into a crucible and annealed at different temperatures for 5 h in air. The phase evolution of the mixed powder before and after annealing was analyzed by XRD.
The electrical conductivity and Seebeck coefficient at 50–1000 °C were measured on rectangle bar samples with the dimension of about 10 mm × 3 mm × 2 mm in an helium atmosphere using a Seebeck coefficient/electrical resistance measuring system (ZEM-3M10). The schematic diagram of the system is given in Fig. S1.† During the measurement, graphite papers were padded on the contact surface between the current electrodes and sample, and platinum paste was applied to the contact points between the thermocouples and the sample for better contact. To prepare the samples, single-phase HEALMO and LSM82 powders screened using 200 mesh sieves were first moulded into pellets at 200 MPa and cold isostatically pressed at 300 MPa followed by sintering in air. The pellet of LSM82 was sintered at 1400 °C for 5 h and that of HEALMOs at 1300–1400 °C for 10 h so that a similar density of 90% was achieved for all samples. In addition, the thermogravimetric (TG) measurement was conducted using a synchronous thermal analyzer (STA 449 F3) between 100 and 900 °C in an argon atmosphere with a heating rate of 10 °C min−1 to investigate oxygen release from the powder samples during heating.
3 Results and discussion
3.1 Phase and microstructure observation
The phase information of the as-synthesized HEALMO powders is shown in Fig. 1 and S2.† It is found that the compositions, HEALMO-1, HEALMO-2 and HEALMO-3 can crystallize as single-phase solid solutions at 1200, 1200 and 1100 °C, respectively, while HEALMO-4 and HEALMO-5 cannot form a single-phase even when calcined at an elevated temperature up to 1400 °C. The phase separation in HEALMO-4 and HEALMO-5 can be further confirmed from the uneven distribution of individual A site elements seen in the SEM micrographs in Fig. S3.†The morphologies and particle sizes of the single-phase HEALMO-1, HEALMO-2, HEALMO-3 and LSM82 powders are shown in Fig. 2 and Table S1.† All single-phase HEALMO powders exhibit a very uniform morphology composed of nearly equiaxed grains with average particle sizes of about 520, 360 and 220 nm, respectively. The average particle size of LSM82 is about 660 nm, which is slightly smaller than the range of 0.7–1.1 μm specified by the manufacturer. The corresponding elemental distribution maps of single-phase HEALMOs are given in Fig. 3. It can be seen that all elements are homogeneously distributed and there exists no segregation, confirming the formation of single-phase HEALMOs. The element contents and corresponding stoichiometric ratios in HEALMO-1, HEALMO-2, HEALMO-3 and LSM82 are further analyzed by ICP, and the results are listed in Table 2. It can be seen that there exists no significant elemental deficiency or excess on both A and B sites of HEALMOs and LSM82 considering measurement errors. In comparison, there exists obvious oxygen deficiency in both HEALMO-1 and HEALMO-2, and oxygen excess in LSM82 to a certain extent, respectively. Clearly, these ratios of HEALMOs are almost in good accordance with the designed equimolar A site solid solution compositions, confirming the successful formation of HEALMOs.
 | ||
| Fig. 2 SEM morphologies of single-phase HEALMO and LSM82 powders: (a) HEALMO-1, (b) HEALMO-2, (c)HEALMO-3 and (d) LSM82. | ||
 | ||
| Fig. 3 Elemental distribution of single-phase HEALMO powders: (a) HEALMO-1, (b) HEALMO-2 and (c) HEALMO-3. | ||
| Composition | La | Nd | Sm | Y | Gd | Pr | Ca | Sr | Ba | Mn | O | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a “I” stands for the expected element content in at%, “II” stands for the actual element content in at%, “III” stands for the standard stoichiometric ratio, and “IV” stands for the actual stoichiometric ratio calculated by forcing that of Mn to be 1. | ||||||||||||
| HEALMO-1 | I | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | — | — | — | — | 20.00 | 60.00 |
| II | 4.64 | 4.60 | 4.92 | 4.35 | 4.63 | — | — | — | — | 22.47 | 54.39 | |
| III | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | — | — | — | — | 1.00 | 3.00 | |
| IV | 0.21 | 0.20 | 0.22 | 0.19 | 0.21 | — | — | — | — | 1.00 | 2.42 | |
| HEALMO-2 | I | 4.00 | 4.00 | — | — | — | 4.00 | — | 4.00 | 4.00 | 20.00 | 60.00 |
| II | 4.83 | 5.07 | — | — | — | 3.88 | — | 4.74 | 4.72 | 24.28 | 52.48 | |
| III | 0.20 | 0.20 | — | — | — | 0.20 | — | 0.20 | 0.20 | 1.00 | 3.00 | |
| IV | 0.20 | 0.21 | — | — | — | 0.16 | — | 0.20 | 0.19 | 1.00 | 2.16 | |
| HEALMO-3 | I | 4.00 | 4.00 | 4.00 | — | — | — | 4.00 | 4.00 | — | 20.00 | 60.00 |
| II | 4.12 | 4.08 | 3.78 | — | — | — | 4.41 | 4.12 | — | 19.86 | 59.64 | |
| III | 0.20 | 0.20 | 0.20 | — | — | — | 0.20 | 0.20 | — | 1.00 | 3.00 | |
| IV | 0.21 | 0.21 | 0.19 | — | — | — | 0.22 | 0.21 | — | 1.00 | 3.00 | |
| LSM82 | I | 16.00 | — | — | — | — | — | — | 4.00 | — | 20.00 | 60.00 |
| II | 15.01 | — | — | — | — | — | — | 3.72 | — | 19.03 | 62.24 | |
| III | 0.80 | — | — | — | — | — | — | 0.20 | — | 1.00 | 3.00 | |
| IV | 0.79 | — | — | — | — | — | — | 0.20 | — | 1.00 | 3.27 | |
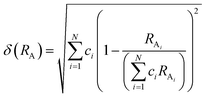
Considering the cation size difference, HEALMO-4 and HEALMO-5 have comparable δA values to HEALMO-1 and HEALMO-2. Thus, there exists no apparent link between the cation size difference and the formation of single-phase high entropy perovskite oxides, which is in agreement with a previous report.34 Meanwhile, having Goldschmidt tolerance factor values closer to 1 (e.g., for HEALMO-4 and HEALMO-5) does not seem to favour the formation of a single-phase either. In contrast, HEALMO-1 with t as small as 0.928 can form a single phase. Therefore, the current results don't support the hypothesis that t ≈ 1 is a necessary criterion for the formation of single-phase high entropy perovskite oxides,27 but confirm that no obvious relationship exists between t and single-phase formation.26 Furthermore, although less frequently used, the basicity–acidity of oxides can be another parameter to evaluate phase stability.38,44 Using the literature data on the relative acidity of relevant oxides,45 the average relative acidity of the A site oxides in HEALMOs is calculated and shown in Table S2.† It can be seen that the average relative acidity of A site oxides in HEALMOs follows the order of HEALMO-1 > HEALMO-3 > HEALMO-5 > HEALMO-2 > HEALMO-4. Since only HEALMO-1, HEALMO-2 and HEALMO-3 exhibit a single-phase structure among HEALMOs, there also exists no obvious relationship between the basicity–acidity and the formation of a single-phase structure.
Two possible factors can be considered to explain why HEALMO-4 and HEALMO-5 cannot form a single phase. First of all, Sarkar et al. and Ma et al. proposed that one criterion in designing high entropy perovskite oxides is that the cations at a specific position, specific oxidation state and specific coordination number need to possess similar ionic radii.26,29 It can be seen from Table S3† that among the divalent 12-coordinated ions, Ba2+ has a significantly larger radius than Ca2+ and Sr2+ in HEALMO-4 and HEALMO-5, which might be the reason for their failure in single-phase formation. However, considering Sr2+ and Ba2+ also co-exist in the single-phase HEALMO-2, this ionic radius criterion fails to explain why HEALMO-2 can form a single phase and therefore does not appear to be a good predictor for the single-phase formation in HEALMOs. Secondly, it has been reported that the valence combination can affect structural stability. The valence electron concentration (VEC) is known to have a determining role in stabilizing FCC and BCC high entropy alloys,46 and it is also indicated that an appropriate VEC just filling the bonding state enables the best phase stability in transition metal borides.47 Further, a higher cation valence difference was shown to lead to the deviation from the perfect high entropy phase with the random distribution of cations and the formation of a partially ordered structure.26,41 Therefore, the largest deviation of the VEC value from the most stable LaMnO3 phase and the highest cation valence differences in HEALMO-4 and HEALMO-5 may explain why they cannot form single phases.
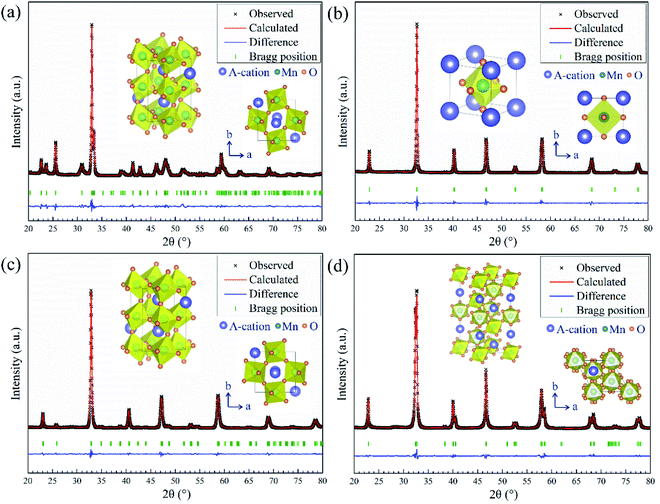
To further investigate the crystal structure, XRD Rietveld refinement was carried out on single-phase HEALMO-1, HEALMO-2, HEALMO-3 and LSM82. The refined patterns as well as the corresponding schematic diagrams of the calculated unit cells are shown in Fig. 1. The crystal structure parameters obtained from the Rietveld results and corresponding unit cells are summarized in Table 3. With a t value closest to 1 (0.983), HEALMO-2 is capable of crystallizing in the cubic perovskite structure with the space group of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Both HEALMO-1 and HEALMO-3 with t values deviating largely from 1 (0.928 and 0.959, respectively) can be identified to have an orthorhombic perovskite structure with the space group of Pnma. LSM82 with a t value of 0.975 is the index in the rhombohedral perovskite structure with the space group of R
m. Both HEALMO-1 and HEALMO-3 with t values deviating largely from 1 (0.928 and 0.959, respectively) can be identified to have an orthorhombic perovskite structure with the space group of Pnma. LSM82 with a t value of 0.975 is the index in the rhombohedral perovskite structure with the space group of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c, which is in agreement with previous reports.1,33 In summary, it can be inferred from the crystallographic information that HEALMO-2 exhibits the highest structural symmetry, followed by LSM82, and then HEALMO-3 and HEALMO-1.
c, which is in agreement with previous reports.1,33 In summary, it can be inferred from the crystallographic information that HEALMO-2 exhibits the highest structural symmetry, followed by LSM82, and then HEALMO-3 and HEALMO-1.
| Composition | Structure | SG | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) |
|---|---|---|---|---|---|---|---|---|
a The space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c belongs to the trigonal crystal class and has a rhombohedral structure. Here “hexagonal” is used to comply with the hexagonal representation of the rhombohedral lattice. c belongs to the trigonal crystal class and has a rhombohedral structure. Here “hexagonal” is used to comply with the hexagonal representation of the rhombohedral lattice.
|
||||||||
| HEALMO-1 | Orthorhombic | Pnma | 5.366 | 5.783 | 7.516 | 90 | 90 | 90 |
| HEALMO-2 | Cubic |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
3.878 | 3.878 | 3.878 | 90 | 90 | 90 |
| HEALMO-3 | Orthorhombic | Pnma | 5.446 | 5.453 | 7.681 | 90 | 90 | 90 |
| LSM82 | Hexagonal (rhombohedral)a |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
5.523 | 5.523 | 13.368 | 90 | 90 | 120 |
| Composition | R wp | R p | χ 2 | Metric distortion (ε) | Bond angle of Mn–O–Mn (°) |
|---|---|---|---|---|---|
| HEALMO-1 | 8.86 | 6.51 | 3.14 | 0.428 | 150.2 |
| HEALMO-2 | 8.60 | 6.47 | 2.77 | 0.340 | 180.0 |
| HEALMO-3 | 7.91 | 5.61 | 2.00 | 0.427 | 162.8 |
| LSM82 | 6.82 | 5.02 | 1.87 | 0.416 | 165.1 |
| Composition | Bond length of Mn–O in MnO6 octahedra (Å) | ||
|---|---|---|---|
| HEALMO-1 | 2.195 | 1.974 | 1.886 |
| HEALMO-2 | 1.939 | 1.939 | 1.939 |
| HEALMO-3 | 1.984 | 1.980 | 1.910 |
| LSM82 | 1.962 | 1.962 | 1.962 |
The correlation between t and the crystal structure, therefore, follows the general trend observed in conventional perovskite oxides, i.e., the crystal symmetry decreases with an increasing deviation of t from 1. When t < 1, which is the case for most of the designed perovskite oxides, the structure transforms from the ideal cubic to rhombohedral and then orthorhombic.29,39 This correlation can also be seen from Fig. 4 where the t values are plotted for a collection of conventional and high entropy perovskites including literature data and the current materials. Fig. 4 also shows the cation size difference associated with different materials. Although the data points in the figure are not inclusive, two indications can be pointed out for further investigation in future studies. Firstly, among all the presented materials with t < 1, the ability to maintain the higher symmetry cubic and rhombohedral structures at the smallest t values is observed with two high entropy materials, which is Sr(Zr0.2Sn0.2Ti0.2Hf0.2Nb0.2)O3 for the cubic structure and La(Mn0.2Fe0.2Co0.2Ni0.2Cu0.2)O3−δ for the rhombohedral structure.33 Secondly, while the correlation between δA values and the structural symmetry is less evident, the largest δA values allowing the formation of higher symmetry cubic and rhombohedral structures when t < 1 are obtained for HEALMO-2 and La(Mn0.2Fe0.2Co0.2Ni0.2Cu0.2)O3−δ, respectively. It is speculated that the high entropy effect may help push the boundary of t and δA to smaller and higher values for maintaining higher symmetry structures.
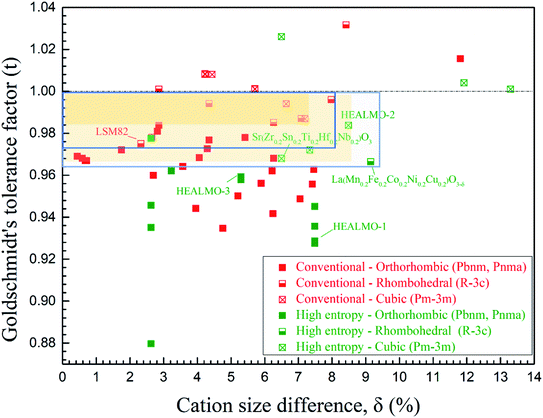 | ||
| Fig. 4 Correlation of the crystal structure with the Goldschmidt tolerance factor and cation size difference. For t < 1, the yellow shaded areas demonstrate the boundaries of the cubic structure for conventional and high entropy materials and the green boxes for the rhombohedral. The space group information specified only includes those available from the literature. The references for the data are given in Table S4.† | ||
To further evaluate the pseudo-cubic symmetry of these samples, the metric distortion (ε) can be calculated according to the following equation:1,29,32,33
 | (5) |
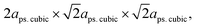 , while that of the rhombohedral (R
, while that of the rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) unit cell is six times larger.32 Thus, the parameters of anorm, bnorm, cnorm and aps. cubic in eqn (5) can be calculated using the following equations:1,29,32,33
c) unit cell is six times larger.32 Thus, the parameters of anorm, bnorm, cnorm and aps. cubic in eqn (5) can be calculated using the following equations:1,29,32,33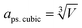 | (6) |
For the unit cells of HEALMO-1, HEALMO-2 and HEALMO-3,
 | (7) |
For the unit cell of LSM82,
 | (8) |
Further, the structural symmetry of the ABO3 perovskite oxide is strongly affected by the tilting and distortion of the BO6 octahedra.1,29,48 The tilting and distortion of BO6 octahedra in perovskite oxides are mainly related to two aspects.1,29 On the one hand, the tilting of BO6 octahedra in perovskite oxides can be directly reflected from the bond angle of B–O–B,29,49 and is enhanced by smaller A site cations.29 On the other hand, the distortion of BO6 octahedra is related to Jahn–Teller distortion and can be reflected from the difference in the bond length of B–O.1,29,48,50 Jahn–Teller distortion can be widely observed in compounds containing Jahn–Teller active cations, such as Cu2+ and Mn3+.29,36,51 For an ideal cubic perovskite structure, the bond angle of B–O–B should be 180° and the bond length of B–O should be equal.1 Once the structural symmetry lowers, the bond angle of B–O–B deviates from 180° and the bond length of B–O becomes unequal. In this work, it can be seen from Fig. 1 and Table 3 that the titling of BO6 octahedra suggested by the deviation of the bond angle from 180° follows the sequence of HEALMO-1 > HEALMO-3 > LSM82 > HEALMO-2, and the distortion of BO6 octahedra suggested by the difference in the bond length of B–O has the ranking of HEALMO-1 > HEALMO-3 > LSM82 = HEALMO-2. These trends can be well explained by the average A site cation size and the content of Jahn–Teller active cation Mn3+, as described above according to the literature.29,51 It should be noted that the determined symmetry is in the resolution of XRD because the subtle indications of alternative symmetry due to the octahedral rotation may not be apparent in XRD due to the low scattering factor of oxygen. Together, the analysis of the crystallographic space group, the metric distortion and the characteristics of the MnO6 octahedra all indicate that HEALMO-2 exhibits the highest structural symmetry, followed by LSM82, HEALMO-3 and HEALMO-1.
3.2 Resistance to elemental segregation
To investigate the resistance to specific elemental segregation, the single-phase HEALMO-1, HEALMO-2, HEALMO-3 and LSM82 were annealed at 800, 1000, 1100 and 1200 °C for 100 h in air, respectively. The morphologies of the annealed powders are given in Fig. 5. It can be seen that the grain sizes of HEALMO-1, HEALMO-2 and HEALMO-3 gradually increase with increasing temperature and the grains remain nearly equiaxed. The surface morphologies of HEALMO-1, HEALMO-3 and LSM82 are quite clean even when annealed at 1200 °C for 100 h; however, many dot-distributed precipitates can be observed on the surface of HEALMO-2 once annealed at 800 °C for 100 h. Thus, HEALMO-1 and HEALMO-3 exhibit good resistance to elemental segregation, which is comparable to that of LSM82 used in the current study. A similar enhancement of Sr segregation resistance has also been reported for a high entropy (La0.2Pr0.2Nd0.2Sm0.2Sr0.2)MnO3−δ cathode.1 The precipitates on the grain surface of HEALMO-2 annealed at 1000 °C for 100 h were further analyzed by TEM, as shown in Fig. 6. These precipitates have a similar size of about 30 nm, and semi-quantitative EDS suggests that they are composed mainly of O and Ba, a small but definite amount of Sr and probably a trace amount of Mn, Nd, La and Pr. In addition, many cracks can be seen in HEALMO-1, which may be due to the large internal stress partially associated with serious Jahn–Teller distortion. | ||
| Fig. 6 (a) TEM micrographs, and (b) elemental distribution of HEALMO-2 annealed at 1000 °C for 100 h in air. The element content of area 1 is listed in the table. | ||
Generally, specific cations with a radius larger than or comparable to La3+, such as Ca2+, Sr2+ and Ba2+, tend to segregate on the surface upon annealing in conventional perovskite oxides.20,52,53 Elastic energy caused by the cation size difference between the host La3+ and dopant Ba2+ is the driving force for the intrinsic segregation of Ba in (La0.8Ba0.2)MnO3 because Ba2+ produces less elastic strain when accommodated at the surface sites.52,53 The easiest segregation observed in HEALMO-2 should be similarly associated with its largest cation size difference as indicated by the highest δA value of 8.49%, which is much larger than those of HEALMO-1 and HEALMO-3, respectively. In comparison, LSM82 exhibits good resistance to elemental segregation because of the lowest elastic energy indicated by the smallest δA value of 2.33%. It is noted that LSM82 has been frequently reported in the literature to exhibit Sr segregation after annealing at 630–800 °C for 1–100 hours.1,53 The discrepancy might be originating from the difference in exact stoichiometry and sample states such as powders, dense pellets, cathode coatings, etc.12 Interestingly, the elemental segregation resistance of HEALMO-1 and HEALMO-3 is also very good despite their much higher δA values of 7.49% and 5.30% compared to that of LSM82. Considering the smaller particle size of HEALMO-1 and HEALMO-3 than that of LSM82, the enhanced stability cannot be explained by the possible surface area factor. It is also reported that a conventional (La0.8Ba0.2)MnO3 material with a δA value of 7.09% already showed segregation of Ba rich particles after annealing at 430 °C for 1 h.52,53 Therefore, it consistently suggests that HEALMOs have higher resistances to elemental segregation at a similar or even higher level of δA compared to conventional perovskite oxides. This enhanced resistance can be attributed to the strong sluggish diffusion effect derived from the stress field in high entropy materials.1,23,25 In summary, minimizing the A site cation size difference is still beneficial as observed for conventional doped perovskite cathode materials52,53 while the sluggish diffusion effect in HEALMOs helps to largely increase the allowable δA for designing segregation free materials.
3.3 Chemical compatibility with 8YSZ
The chemical compatibility with 8YSZ of single-phase HEALMO-1, HEALMO-2, HEALMO-3 and LSM82 is investigated and shown in Fig. 7. In agreement with the literature,15 it is confirmed that LSM82 becomes incompatible with 8YSZ once calcined at 1300 °C, leading to the formation of La2Zr2O7. It is noted that the chemical compatibility with 8YSZ of the LSM82 used in this work may have been improved due to the larger particle size and the smaller surface area of the raw powder. The three HEALMO samples were found to exhibit a different level of chemical compatibility with 8YSZ at high temperatures. The mixed powder containing HEALMO-1 becomes unstable at 1200 °C, where Sm0.2Zr0.8O1.9 emerges, and its content increases gradually with increasing temperature. The mixed powder containing HEALMO-2 is only stable below 1100 °C with diffraction peaks of the new phase indexed to BaSrYZrO5.5 appearing after being calcined at 1100 °C for 5 h. In comparison, the diffraction peaks of the mixed powder consisting of HEALMO-3 and 8YSZ remain intact without any detectable second phase even when calcined at 1400 °C for 5 h in air. Thus, HEALMO-3 exhibits the best chemical compatibility with 8YSZ, followed by LSM82, HEALMO-1 and HEALMO-2. It can be deduced from Fig. 7 and Table 1 that the chemical compatibility with 8YSZ become increasingly better with decreasing A site cation size difference for the HEALMOs investigated in this work, which is similar to the situation for conventional LMO based ones. For instance, it is reported that only rare La2Zr2O7 phases can be detected at the reaction interface annealed below 1400 °C for 100 h for conventional La0.8Ca0.2MnO3 with a δA of 0.59%, indicating the better chemical compatibility with 8YSZ than that of LSM82 used in this work.54 Data from the literature33 can further confirm the observed trend between the chemical stability with 8YSZ and the cation size difference. High entropy La(Mn0.2Fe0.2Co0.2Ni0.2Cu0.2)O3−δ reported by Han et al.33 can be calculated to have a B site cation size difference of 9.15% and was found to be stable with 8YSZ only up to 900 °C. Overall, up to 1000 °C, all the HEALMO materials investigated in our work exhibit much better chemical stability with 8YSZ than this reported high entropy La(Mn0.2Fe0.2Co0.2Ni0.2Cu0.2)O3−δ. Again, it is noted that HEALMO-3 exhibits very good chemical compatibility with 8YSZ although the δA value is about two times that of LSM82, which may also arise from the sluggish diffusion of Mn induced by the high entropy effect.1,23,25 It is reported that the reaction between LSM and YSZ is rather complicated, and is closely associated with the inter-diffusion at the LSM–YSZ interface.16,17 This reaction can be influenced by the compositions of LSM and YSZ, Mn excess in LSM, LSM/YSZ weight ratio, oxygen partial pressure, temperature, interface microstructure, etc.16,17 On the one hand, the prevention of A site cation segregation was found to be beneficial in reducing the reactivity between LSM and YSZ,2 which should be one reason for the best compatibility observed for HEALMO-3 that also shows good resistance to A site elemental segregations. On the other hand, the diffusion of Mn from LSM into YSZ is very significant because of the large solubility of Mn in YSZ.2,17,18,54 Thus, the reaction between LSM82 and YSZ is also considered to be mostly initiated by the diffusion of Mn into YSZ, leading to Mn depletion in LSM82 and the generation of chemically active La2O3, ultimately to the formation of La2Zr2O7 according to the literature.2,15,16,35 Since LSM82 used in this work shows a similar resistance to A site elemental segregation to HEALMO-3, the improvement of HEALMO-3 in the chemical compatibility with 8YSZ appears to also be contributed by a retarded diffusion of Mn. Therefore, it is interesting to note that although high entropy is realized by the multi-component solid solution on the A site, its effect appears to be also active on the B site, presumably because the induced lattice distortion and stress field has an overall effect on both sites. In summary, HEALMO-3 shows much enhanced chemical compatibility with 8YSZ compared to conventional LSM82, and decreasing the cation size difference helps increase the chemical compatibility of HEALMOs with 8YSZ.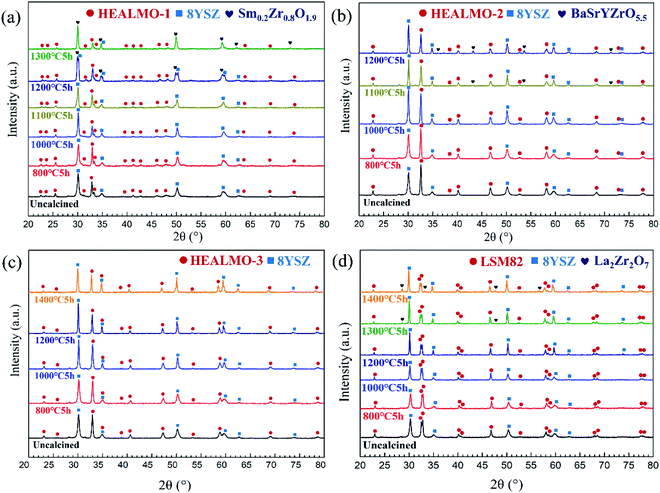 | ||
| Fig. 7 XRD patterns of mixed powders calcined at different temperatures for 5 h in air: (a) HEALMO-1 and 8YSZ, (b) HEALMO-2 and 8YSZ, (c) HEALMO-3 and 8YSZ, and (d) LSM82 and 8YSZ. | ||
3.4 Electrical conductivity
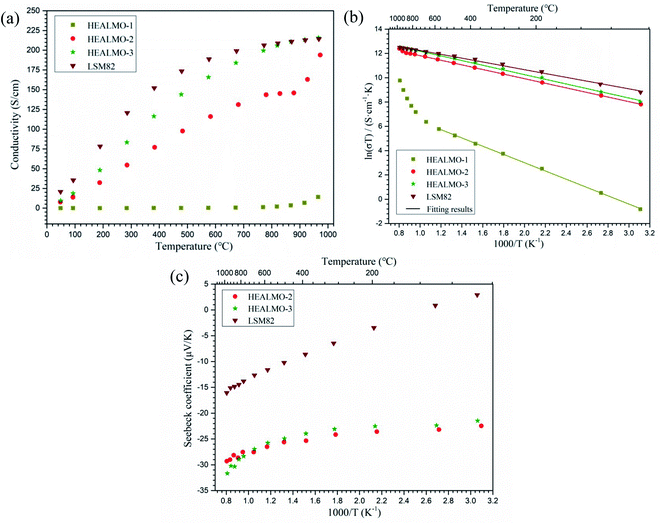
Fig. 8(a) shows the electrical conductivity of HEALMO-1, HEALMO-2, HEALMO-3 and LSM82 in the range of about 50–1000 °C, which was measured from sintered pellets. It is noted that the densities of pellets are all greater than 90% estimated by image analysis based on SEM micrographs shown in Fig. S4,† and that HEALMOs exhibit similar grain sizes of about 2–5 μm, smaller than that of LSM82 (about 10 μm), as shown in Table S1.† Therefore, the obtained conductivity of the HEALMO samples is probably underestimated to a certain extent with respect to LSM82 considering the normally lower electrical conductivity of grain boundaries as well as an increasing conductivity with grain size in LSM82.55,56 As is shown, the electrical conductivity of HEALMO-1, HEALMO-2, HEALMO-3 and LSM82 all increases with increasing temperature. The electrical conductivity of HEALMO-1 is negligible before about 900 °C, and increases slowly with increasing temperature. The electrical conductivity of HEALMO-2 has intermediate values. It increases rapidly with the increase of temperature, becomes stable at around 800 °C and increases rapidly again at about 880 °C. It is noted that the electrical conductivity of HEALMO-1 and HEALMO-2 may have been deteriorated to some extent due to the oxygen-deficiency nonstoichiometry, as the positively charged oxygen vacancy defects are most likely to be compensated by Mn reduction, leading to a reduced amount of Mn4+ required for electronic conduction.2,3,14 The highest electrical conductivity among the three high entropy oxides is achieved in HEALMO-3, and its conductivity is slightly lower than that of LSM82 below about 800 °C; however, it can reach 215.8 S cm−1 at about 970 °C, and is comparable to that of LSM82 in the temperature range of 800–1000 °C, which is considered to be good enough to meet the commercial requirement of electrical conductivity of perovskite cathodes.3,6,9 It is reported that the electrical conductivity of La1−xSrxMnO3+δ is almost independent of δ over the entire nonstoichiometric range.37,57 Thus, the electrical conductivity of LSM82 in this work is considered not to be significantly affected by the oxygen excess.Fig. 8(b) shows the Arrhenius plots according to the Arrhenius law:13,35
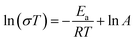 | (9) |
On the one hand, as it is confirmed that the predominant mechanism in LSM82 and HEALMOs is the small polaron hopping mechanism, the higher content of Mn4+ means more hopping sites for electrical conduction and better electrical conductivity. On the other hand, the structure also plays an important role in further influencing the electrical conductivity. Generally, a wide energy band is formed in perovskite oxides containing transition metal cations because of the interaction between the d-orbitals of transition metal and 2p-orbitals of oxygen.49 The degree of overlap and interaction decreases with the lowered structural symmetry and increased magnitude of tilting and distortion of octahedra, leading to the narrowing down of energy bands, localization of electronic states and deterioration of electrical conductivity.39,49 Based on the foregoing considerations, HEALMO-1 exhibits the poorest electrical conductivity and the highest activation energy because of the very low content of Mn4+ due to the absence of divalent cations on the A site and the lowest structural symmetry. In comparison, some of the A site cations in HEALMO-2 and HEALMO-3 are divalent leading to the formation of a high content of Mn4+ and the increased density of hopping sites;37 meanwhile, the structural symmetry is higher in HEALMO-2 and HEALMO-3. Thus, HEALMO-2 and HEALMO-3 exhibit much better electrical conductivity and much lower activation energies compared with HEALMO-1. However, comparing HEALMO-2 and HEALMO-3 that have the same content of divalent cations on the A site, it can be seen that HEALMO-3 with a lower structural symmetry has a higher conductivity. Here the cation size difference should play a more important role. HEALMO-3 has a smaller δA than HEALMO-2, and therefore meaning less lattice distortion and lower intensity of stress field,23 which might be the reason for its better conductivity compared to HEALMO-2. Similar effects of the cation size difference in conventional perovskite oxides have also been reported for Ln0.5Sr0.5CoO3 (Ln = La, Pr, or Nd)60 and inferred for La0.7A0.3MnO3 (A = Sr or Ba).61 Finally, although having a lower divalent cation concentration than those of HEALMO-2 and HEALMO-3, the second-highest structural symmetry and lowest δA value may be the reason for the best conductivity measured in LSM82. In addition, the highest density and largest grain size in LSM82 should have contributed to its high conductivity due to the lower grain boundary resistivity.55,56
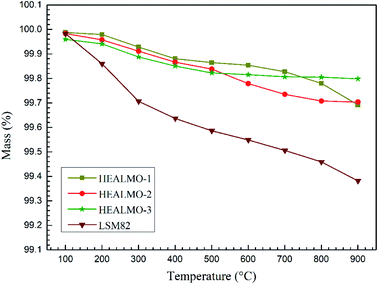
As mentioned earlier, the electrical conductivity of HEALMO-3 is comparable or even better than that of LSM82 in the high temperature range (about 800–1000 °C) due to a much slower increase in the conductivity of LSM82 with temperature compared to that of HEALMO-3. This difference in conductivity change may be correlated with the change of carrier density with temperature, which can be reflected from the Seebeck coefficient results (Fig. 8(c)). In general, the absolute value of the Seebeck coefficient is an indicator of carrier density.24 It is obvious that the variation of absolute values of the Seebeck coefficient is significantly higher than that of HEALMO-3 with increasing temperature, suggesting the larger reduction of the carrier concentration. The decrease of carrier density can originate from the oxygen escape in LSM82 at high temperature and low oxygen partial pressure, which leads to the reduction of Mn4+ to maintain charge neutrality.2,14 To investigate the level of oxygen loss, TG was carried out and the results are shown in Fig. 9. It demonstrates that the weight loss of LSM82 is much more significant than that of HEALMOs during heating at low oxygen partial pressure. The weight loss of LSM82 below 300 °C is probably associated with the release of absorbed water and some gases from air, and that above about 300 °C is believed to be associated with the release of lattice oxygen,7,62,63 confirming that oxygen in LSM82 can much more easily escape than in HEALMOs. The current results therefore indicate further that the high entropy effect enabled by the A site solid solution caused sluggish diffusion of not only the B site element Mn but also oxygen.
4 Conclusions
A series of LMO based HEPOs were designed and synthesized with the help of combined criteria including mixed entropy, Goldschmidt tolerance factor, and cation size difference. Subsequently, microstructural characterization and property investigation were carried out to clarify the correlation among the composition, phase formation ability and resulting properties to guide the design and preparation of HEPO SOFC cathodes. The conclusions are as follows:(1) Neither the Goldschmidt tolerance factor nor the cation size difference can be used simply to predict the formation ability of single-phase LMO based HEPOs. Meanwhile, in comparison with conventional perovskite oxides, HEPOs may exhibit higher crystallographic symmetry with higher cation size differences and at smaller Goldschmidt tolerance factor values (when t < 1).
(2) HEALMO-1 and HEALMO-3 show excellent resistance to specific elemental segregation upon annealing at 1200 °C for 100 h, and the latter exhibits much enhanced chemical compatibility with 8YSZ (up to 1400 °C) compared to LSM82. Both high-temperature stabilities were found to increase with decreasing A site cation size differences in HEALMOs. Furthermore, good stability can be maintained in HEALMOs with much larger δA values (up to 2.2 times) compared to conventional LSM82, thus allowing a more flexible compositional design.
(3) With the same concentration of divalent cations on the A site, the electrical conductivity of HEALMOs is favoured by the smaller cation size difference more than the higher structural symmetry. Compared with LSM82, the less oxygen escape from HEALMO-3 due to the sluggish diffusion effect contributes to the maintenance of electrical conductivity in the high temperature range. Consequently, HEALMO-3 can reach 215.8 S cm−1 at about 970 °C, which is comparable to that of LSM82 in the temperature range of 800–1000 °C.
Overall, the as-synthesized HEALMO-3 possesses good resistance to Sr segregation and excellent chemical compatibility with 8YSZ while maintaining high electrical conductivity. These features highlight the great potential of HEALMO-3 as a promising cathode material for SOFCs. The results also demonstrate that the high entropy effect in HEALMOs effectively increases the tolerance to A site cation size differences within which higher thermochemical stability and good conductivity can be maintained at high temperatures. Similar effects can be expected for B site high entropy solid solution, promising a wider composition engineering space for new perovskite-based SOFC cathode materials.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (No. 52072238) and the China Postdoctoral Science Foundation (No. 2020M671115). The authors would like to acknowledge the valuable discussion with Professor Yanchun Zhou (Science and Technology on Advanced Functional Composite Laboratory, Aerospace Research Institute of Materials & Processing Technology, China).References
- Y. Yang, H. Bao, H. Ni, X. Ou, S. Wang, B. Lin, P. Feng and Y. Ling, J. Power Sources, 2021, 482, 228959 CrossRef CAS.
- S. P. Jiang, J. Mater. Sci., 2008, 43, 6799–6833 CrossRef CAS.
- N. Mahato, A. Banerjee, A. Gupta, S. Omar and K. Balani, Prog. Mater. Sci., 2015, 72, 141–337 CrossRef CAS.
- N. Ni, C. C. Wang, S. P. Jiang and S. J. Skinner, J. Mater. Chem. A, 2019, 7, 9253–9262 RSC.
- S. Harboe, Y. J. Sohn, O. Guillon and N. H. Menzler, J. Eur. Ceram. Soc., 2020, 40, 3608–3617 CrossRef CAS.
- Q. Yang, G. Wang, H. Wu, B. A. Beshiwork, D. Tian, S. Zhu, Y. Yang, X. Lu, Y. Ding, Y. Ling, Y. Chen and B. Lin, J. Alloys Compd., 2021, 872, 159633 CrossRef CAS.
- L. Shen, Z. Du, Y. Zhang, X. Dong and H. Zhao, Appl. Catal., B, 2021, 295, 120264 CrossRef CAS.
- T. Sakai, M. Ogushi, K. Hosoi, A. Inoishi, H. Hagiwara, S. Ida, M. Oishi and T. Ishihara, J. Mater. Chem. A, 2021, 9, 3584–3588 RSC.
- Z. Du, C. Yan, H. Zhao, Y. Zhang, C. Yang, S. Yi, Y. Lu and K. Świerczek, J. Mater. Chem. A, 2017, 5, 25641–25651 RSC.
- A. Leonide, V. Sonn, A. Weber and E. Ivers-Tiffée, J. Electrochem. Soc., 2008, 155, B36–B41 CrossRef CAS.
- E. Ivers-Tiffée, A. Weber and D. Herbstritt, J. Eur. Ceram. Soc., 2001, 21, 1805–1811 CrossRef.
- N. Caillol, M. Pijolat and E. Siebert, Appl. Surf. Sci., 2007, 253, 4641–4648 CrossRef CAS.
- S. Paydar, M. H. Shariat and S. Javadpour, Int. J. Hydrogen Energy, 2016, 41, 23145–23155 CrossRef CAS.
- A. N. Grundy, B. Hallstedt and L. J. Gauckler, Comput. Coupling Phase Diagrams Thermochem., 2004, 28, 191–201 CrossRef CAS.
- N. Q. Minh, J. Am. Ceram. Soc., 1993, 76, 563–588 CrossRef CAS.
- Y. L. Liu, A. Hagen, R. Barfod, M. Chen, H. J. Wang, F. W. Poulsen and P. V. Hendriksen, Solid State Ionics, 2009, 180, 1298–1304 CrossRef CAS.
- M. Chen, Y. L. Liu, A. Hagen, P. V. Hendriksen and F. W. Poulsen, Fuel Cells, 2009, 9, 833–840 CrossRef CAS.
- M. Chen, B. Hallstedt and L. J. Gauckler, Solid State Ionics, 2005, 176, 1457–1464 CrossRef CAS.
- A. Mitterdorfer and L. J. Gauckler, Solid State Ionics, 1998, 111, 185–218 CrossRef CAS.
- H. Kwon, W. Lee and J. W. Han, RSC Adv., 2016, 6, 69782–69789 RSC.
- C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J. P. Maria, Nat. Commun., 2015, 6, 8485 CrossRef.
- C. Oses, C. Toher and S. Curtarolo, Nat. Rev. Mater., 2020, 5, 295–309 CrossRef CAS.
- H. Xiang, Y. Xing, F.-Z. Dai, H. Wang, L. Su, L. Miao, G. Zhang, Y. Wang, X. Qi, L. Yao, H. Wang, B. Zhao, J. Li and Y. Zhou, J. Adv. Ceram., 2021, 10, 385–441 CrossRef CAS.
- Y. Zheng, M. Zou, W. Zhang, D. Yi, J. Lan, C.-W. Nan and Y.-H. Lin, J. Adv. Ceram., 2021, 10, 377–384 CrossRef CAS.
- R.-Z. Zhang and M. J. Reece, J. Mater. Chem. A, 2019, 7, 22148–22162 RSC.
- J. Ma, K. Chen, C. Li, X. Zhang and L. An, Ceram. Int., 2021, 47, 24348–24352 CrossRef CAS.
- Z. Zhao, H. Chen, H. Xiang, F.-Z. Dai, X. Wang, W. Xu, K. Sun, Z. Peng and Y. Zhou, J. Adv. Ceram., 2020, 9, 303–311 CrossRef CAS.
- Z. Zhao, H. Xiang, F.-Z. Dai, Z. Peng and Y. Zhou, J. Mater. Sci. Technol., 2019, 35, 2647–2651 CrossRef.
- A. Sarkar, R. Djenadic, D. Wang, C. Hein, R. Kautenburger, O. Clemens and H. Hahn, J. Eur. Ceram. Soc., 2018, 38, 2318–2327 CrossRef CAS.
- D. Bérardan, S. Franger, A. K. Meena and N. Dragoe, J. Mater. Chem. A, 2016, 4, 9536–9541 RSC.
- H. Chen, H. Xiang, F.-Z. Dai, J. Liu, Y. Lei, J. Zhang and Y. Zhou, J. Mater. Sci. Technol., 2019, 35, 1700–1705 CrossRef.
- J. Dąbrowa, A. Olszewska, A. Falkenstein, C. Schwab, M. Szymczak, M. Zajusz, M. Moździerz, A. Mikuła, K. Zielińska, K. Berent, T. Czeppe, M. Martin and K. Świerczek, J. Mater. Chem. A, 2020, 8, 24455–24468 RSC.
- X. Han, Y. Yang, Y. Fan, H. Ni, Y. Guo, Y. Chen, X. Ou and Y. Ling, Ceram. Int., 2021, 47, 17383–17390 CrossRef CAS.
- S. Jiang, T. Hu, J. Gild, N. Zhou, J. Nie, M. Qin, T. Harrington, K. Vecchio and J. Luo, Scr. Mater., 2018, 142, 116–120 CrossRef CAS.
- G.-J. Li, Z.-R. Sun, H. Zhao, C.-H. Chen and R.-M. Ren, Ceram. Int., 2007, 33, 1503–1507 CrossRef CAS.
- A. N. Grundy, M. Chen, B. Hallstedt and L. J. Gauckler, J. Phase Equilib. Diffus., 2005, 26, 131–151 CrossRef CAS.
- J. A. M. van Roosmalen, J. P. P. Huijsmans and L. Plomp, Solid State Ionics, 1993, 66, 279–284 CrossRef CAS.
- S. Zhou, Y. Pu, Q. Zhang, R. Shi, X. Guo, W. Wang, J. Ji, T. Wei and T. Ouyang, Ceram. Int., 2020, 46, 7430–7437 CrossRef CAS.
- J. Sunarso, S. S. Hashim, N. Zhu and W. Zhou, Prog. Energy Combust. Sci., 2017, 61, 57–77 CrossRef.
- Q. Ji, L. Bi, J. Zhang, H. Cao and X. S. Zhao, Energy Environ. Sci., 2020, 13, 1408–1428 RSC.
- L. Tang, Z. Li, K. Chen, C. Li, X. Zhang and L. An, J. Am. Ceram. Soc., 2021, 104, 1953–1958 CrossRef CAS.
- D. B. Miracle and O. N. Senkov, Acta Mater., 2017, 122, 448–511 CrossRef CAS.
- J. A. M. van Roosmalen and E. H. P. Cordfunke, Solid State Ionics, 1992, 52, 303–312 CrossRef CAS.
- A. Navrotsky, AIP Conf. Proc., 2000, 535, 288–296 CrossRef CAS.
- N. C. Jeong, J. S. Lee, E. L. Tae, Y. J. Lee and K. B. Yoon, Angew. Chem., Int. Ed., 2008, 47, 10128–10132 CrossRef CAS.
- S. Guo, C. Ng, J. Lu and C. T. Liu, J. Appl. Phys., 2011, 109, 213 Search PubMed.
- Y. Zhou, H. Xiang, Z. Feng and Z. Li, J. Mater. Sci. Technol., 2015, 31, 285–294 CrossRef CAS.
- J. A. Alonso, M. J. Martinez-Lope and M. T. Casais, Inorg. Chem., 2000, 39, 917–923 CrossRef CAS.
- S. Dwivedi, Int. J. Hydrogen Energy, 2020, 45, 23988–24013 CrossRef CAS.
- T. Hashimoto, N. Ishizawa, N. Mizutani and M. Kato, J. Mater. Sci., 1988, 23, 1102–1105 CrossRef CAS.
- D. Berardan, A. K. Meena, S. Franger, C. Herrero and N. Dragoe, J. Alloys Compd., 2017, 704, 693–700 CrossRef CAS.
- B. Koo, K. Kim, J. K. Kim, H. Kwon, J. W. Han and W. Jung, Joule, 2018, 2, 1476–1499 CrossRef CAS.
- W. Lee, J. W. Han, Y. Chen, Z. Cai and B. Yildiz, J. Electrochem. Soc., 2013, 135, 7909–7925 CAS.
- H. Taimatsu, K. Wada, H. Kaneko and H. Yamamura, J. Am. Ceram. Soc., 1992, 75, 401–405 CrossRef CAS.
- H. Baaziz, N. K. Maaloul, A. Tozri, H. Rahmouni, S. Mizouri, K. Khirouni and E. Dhahri, Chem. Phys. Lett., 2015, 640, 77–81 CrossRef CAS.
- T. M. Huber, E. Navickas, K. Sasaki, B. Yildiz, H. Hutter, H. Tuller and J. Fleig, J. Electrochem. Soc., 2018, 165, F702–F709 CrossRef CAS.
- J. H. Kuo, H. U. Anderson and D. M. Sparlin, J. Solid State Chem., 1990, 87, 55–63 CrossRef CAS.
- L. Gao, Q. Li, L. Sun, T. Xia, L. Huo, H. Zhao and J.-C. Grenier, J. Mater. Chem. A, 2018, 6, 15221–15229 RSC.
- H.-S. Yoon, S.-W. Choi, D. Lee and B.-H. Kim, J. Power Sources, 2001, 93, 1–7 CrossRef CAS.
- P. V. Vanitha, A. Anthony, P. N. Santhosh and C. N. R. Rao, Chem. Mater., 2000, 12, 1666–1670 CrossRef CAS.
- A. M. George, N. C. Mishra and C. G. Sivan Pillai, J. Mater. Sci. Lett., 1997, 16, 1173–1174 CAS.
- Z. Du, H. Zhao, Y. Shen, L. Wang, M. Fang, K. Świerczek and K. Zheng, J. Mater. Chem. A, 2014, 2, 10290–10299 RSC.
- X. Ding, Z. Gao, D. Ding, X. Zhao, H. Hou, S. Zhang and G. Yuan, Appl. Catal., B, 2019, 243, 546–555 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta07275g |
| This journal is © The Royal Society of Chemistry 2022 |