Solvent-controlled ion-coupled charge transport in microporous metal chalcogenides

Abstract

Interactions between ions and itinerant charges govern electronic processes ranging from the redox chemistry of molecules to the conductivity of organic semiconductors, but remain an open frontier in the study of microporous materials. These interactions may strongly influence the electronic behavior of microporous materials that confine ions and charges to length scales comparable to proton-coupled electron transfer. Yet despite mounting evidence that both solvent and electrolyte influence charge transport through ion–charge interactions in metal–organic frameworks, fundamental microscopic insights are only just beginning to emerge. Here, through electrochemical analysis of two open-framework chalcogenides TMA₂FeGe₄S₁₀ and TMA₂ZnGe₄S₁₀, we outline the key signatures of ion-coupled charge transport in band-type and hopping-type microporous conductors. Pressed-pellet direct-current and impedance techniques reveal that solvent enhances the conductivity of both materials, but for distinct mechanistic reasons. This analysis required the development of a fitting method that provides a novel quantitative metric of concerted ion–charge motion. Taken together, these results provide chemical parameters for a general understanding of electrochemistry in nanoconfined spaces and for designing microporous conductors and electrochemical methods used to evaluate them.

---

Introduction

Semiconductors with permanent microporosity radically diverge from the performance and basic principles of conventional electrochemical materials.^1–3 With pores on the scale of Ångstroms or nanometers, these materials fundamentally challenge notions of electrochemical double layers and charge storage,^4–6 while offering diverse compositional diversity.⁷ Such extreme surface-to-volume ratios, and architectures composed entirely of monolayers wrapped into a wide range of topologies, offer a powerful platform for investigating next-generation electrochemical technologies such as supercapacitors, electrocatalysts, and gas-diffusion electrodes. Metal–organic frameworks, open-framework metal chalcogenides, and microporous metal oxides comprise important classes of materials with opportunities in membranes, energy storage, and catalysis.^8–10 While studies into these systems continue to attract attention of wide-ranging communities, their basic conductivity behavior remains largely unexplored.

The mechanisms of charge transport and redox chemistry of molecular materials become dictated by ion–charge interactions when the distance between ions and charges approach Ångstrom length scales.^11–13 For example, the movement of protons governs charge transfer in molecules^14,15 and biological systems¹⁶ such that the concerted motion of protons and electrons (PCET) is thermodynamically favored over stepwise proton and electron transfer. The redox chemistry of molecules, conductive polymers, and colloidal nanocrystals^17–23 also becomes facilitated by ion pairing with redox-inactive metal ions, such as Sc³⁺ and Ca²⁺.^24–26 Beyond microporous semiconductors, electrodes with high surface-to-volume ratios, such as 2D layered materials, exhibit redox chemistry and delocalized charge transport sensitive to the presence of electrolyte.^27,28 Ion-coupled charge transfer (ICCT) has been recently demonstrated to influence the electron mobility of MOFs as well.^29,30 We propose that ICCT must be considered in materials where external ions, such as electrolytes, exist within Ångstroms of itinerant charges. Conceived classically, the influence of each charge should scale as 1/rε_rε₀, where r denotes the average inter-charge distance, ε_r the operative dielectric constant, and ε₀ the permittivity of vacuum. Therefore, the design of electrochemical capacitors, batteries, and electrocatalysts based on microporous conductors must consider these potentially strong interactions because they all involve the mixed conductivity of both ions and electrons.³¹

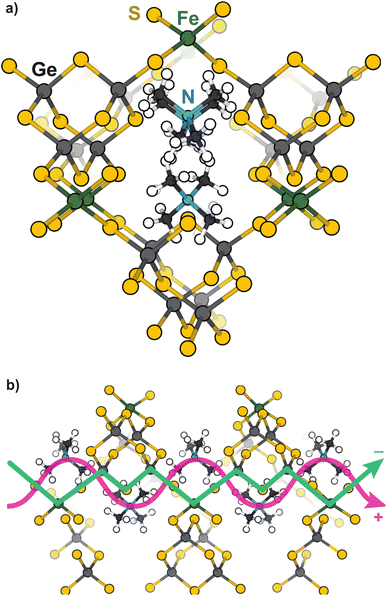
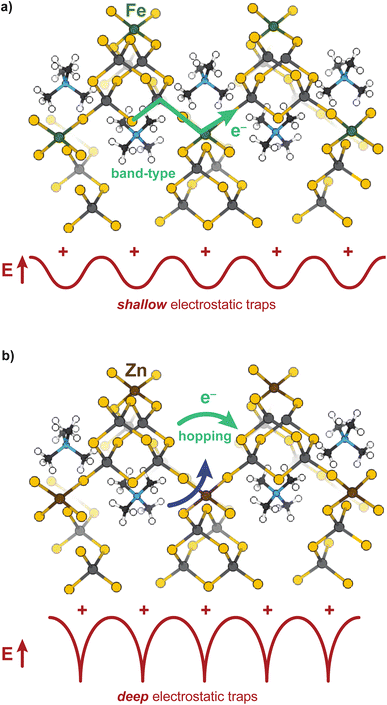
Open-framework metal chalcogenides (OFCs) offer an ideal platform for studying the coupling of ions and electrons in nanoconfined spaces. Like MOFs, these materials afford a wide range of tunable structures through variable cluster sizes, the identity of the cluster elements and linking transition metal, and the identity of the cations that balance the anionic structures.^32–46 Previously, we explored the electronic, magnetic, and conductivity properties of the prototypical family of OFCs, first reported by Yaghi et al.,³² TMA₂MGe₄Q₁₀ (Q: S and Se; M: Fe²⁺, Mn²⁺, Co²⁺, Zn²⁺, and Ni²⁺).⁴⁷Scheme 1a displays a portion of a prototypical microporous metal chalcogenide framework and Scheme 1b highlights the close proximity of the delocalized electron pathway (green) and the direction of cation movement (pink). Importantly, these studies established that whereas the Zn, Mn, Co, and Ni variants exhibit redox hopping-type, mixed conductivity, the Fe analogue exhibits band-type electronic transport. In particular, band structure calculations indicated non-dispersive valence bands localized on sulfur sites, corroborating the assignment of redox hopping between sulfurs as the likely conduction mechanism. In contrast, the partial density of states analysis of the Fe analogue revealed dispersive valence bands delocalized across both the sulfur and Fe atoms. Therefore, the contrast of Fe and Zn materials is convenient for understanding the chemical parameters, such as solvent, that govern ICCT and their impact on the two key forms of charge transport.

Scheme 1 Representations of TMA₂FeGe₄S₁₀ viewed along the (a) [100] and (b) [101] directions. Proposed conduction pathways of delocalized electrons and extra-framework cations are highlighted in green and pink, respectively.

Here, we report solid-state conductivity data showing that this class of materials displays mixed ionic-electronic conductivity controlled by solvent. We hypothesize that solvent untethers the motion of charges from ions by facilitating the motion of ions and by screening strong ion–charge interactions. This effect enhances ambipolar diffusion and thus dramatically improves electronic conductivity. These results, therefore, present guidelines for rationalizing previous observations of conductivity in microporous materials sensitive to environmental conditions and establish design rules for controlling basic charge transport mechanisms.

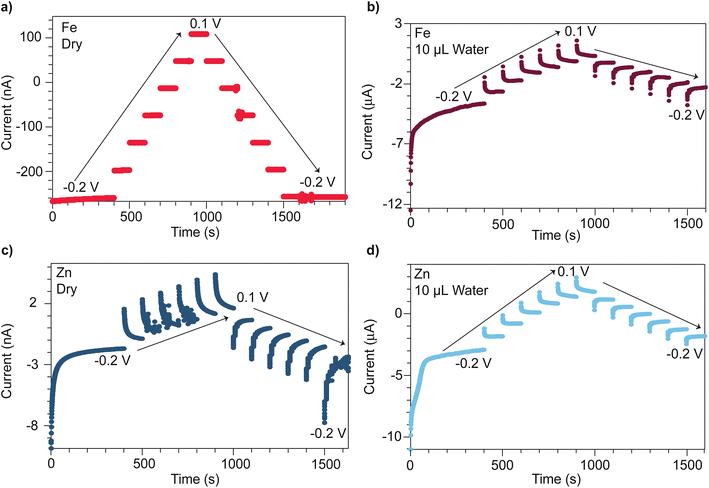
Results and analysis

Microcrystalline powders of open-framework chalcogenides TMA₂MGe₄S₁₀ (M = Zn and Fe) were prepared following modified synthetic procedures previously reported by Yaghi et al.,³² with phase purity verified by powder X-ray diffraction (PXRD) (Fig. S1 and S2†). To compare the distinct mechanisms of mixed conductivity in the Zn and Fe variants, pressed pellets were analyzed by chronoamperometry using stainless steel ion-blocking electrodes while stepping the applied voltages between −0.2 V and +0.1 V. Fig. 1 shows the current transients for both materials when dry and after treatment with deionized water. When dry, the Fe system exhibits steady current transients (Fig. 1a) consistent with the Fe system being a purely electronic band-type conductor. Indeed, when considering the current transient at −0.2 V, an electronic transference number t_e of 0.97 and a minimal ionic contribution of t_i = 0.03 is found. By contrast, the dry Zn analogue (Fig. 1c) displays a non-ohmic current response, indicative of ionic contributions (t_i = 0.15) and, therefore, mixed conductivity. Furthermore, plotting the steady-state current values versus applied voltage reveals a pronounced hysteresis in the Zn system, but no hysteresis in the Fe system (Fig. S5†). Hysteresis in current–voltage (I–V) curves on forward and reverse scans is commonly observed in other classes of mixed conductors, such as conductive organic polymers and perovskites, when analyzed with similar ion-blocking electrodes, and has been attributed to low ion mobilities.^48–51 Indeed, fits of the initial current transient at −0.2 V to the Cottrell relation yields an effective diffusion coefficient of 1.3 × 10⁻²⁰ cm² s⁻¹ for the Zn system (Fig. S3†). This low diffusivity could be explained by poor mobility of bulky TMA⁺ in solid state, with transport limited by nearest neighbor hopping through the lattice. Thus, these current–voltage data corroborate our previous report that the Fe system conducts by pure electronic transport, whereas the Zn system conducts both cations and electrons.⁴⁷ Given that the Fe and Zn systems are isostructural, the substantial difference in conductivity likely arises from the materials possessing distinct transport mechanisms. For the Zn system, redox hopping between clusters necessitates ion movement to maintain charge neutrality,^29,52–56 whereas charge carrier delocalization in the Fe system maintains charge neutrality through motion of both electrons and holes.

Fig. 1 Chronoamperometry traces of TMA₂FeGe₄S₁₀ and TMA₂ZnGe₄S₁₀ pressed-pellets under applied voltages spanning −0.2 V to 0.1 V when dry (a and c), and after treatment with 10 μL of deionized water (b and d), respectively.

Given the proximity of TMA⁺ cations to itinerant electrons in both the Zn and Fe systems, we expected solvent addition to facilitate TMA⁺ movement and screen coulombic interactions between the TMA⁺ and electrons. We therefore varied the solvent size and dielectric strength to explore these effects. The influence of solvent was quantified via chronoamperometry experiments, which were repeated following the treatment of pressed pellets with deionized water. Unlike the dry Fe system, the hydrated Fe system displayed a non-ohmic current response (Fig. 1b). The corresponding ionic transference number increases to 0.77. Fits to the Cottrell relationship for this material yield an effective diffusion coefficient of 2.3 × 10⁻¹⁴ cm² s⁻¹ (Fig. S4†). For the hydrated Zn system, ionic conductivity is enhanced (Fig. 1d), with the Cottrell relationship producing an effective diffusion coefficient of 1.6 × 10⁻¹³ cm² s⁻¹—a ten-million-fold improvement compared to the dry Zn system (Fig. S3†). These diffusion coefficients are comparable to diffusion coefficients found for PF₆ anions in metallocene-modified (Zr₆O₁₆H₁₆)(TBAPy)₂ MOF systems (10⁻¹¹–10⁻¹³ cm² s⁻¹).⁵⁷

The steady-state currents obtained from chronoamperometry across the hydrated Fe and Zn systems were compared as a function of the applied voltage to determine their DC (purely electronic) conductivities. Compared to DC conductivities when dry, the hydrated Fe system increases from 0.11 to 0.93 μS cm⁻¹, whereas the hydrated Zn system increases from 0.0011 to 1.2 μS cm⁻¹. Although the I–V hysteresis of the hydrated Zn system persists, it decreases in magnitude (Fig. S5†). The hydrated Fe system exhibits an I–V curve hysteresis not previously observed for the dry Fe system. The larger hysteresis between steady-state current values observed at −0.2 V on the forward and reverse scan for the Fe system (1.4 μA) versus the Zn system (1.1 μA) reflects the smaller diffusion coefficient determined for the Fe system.

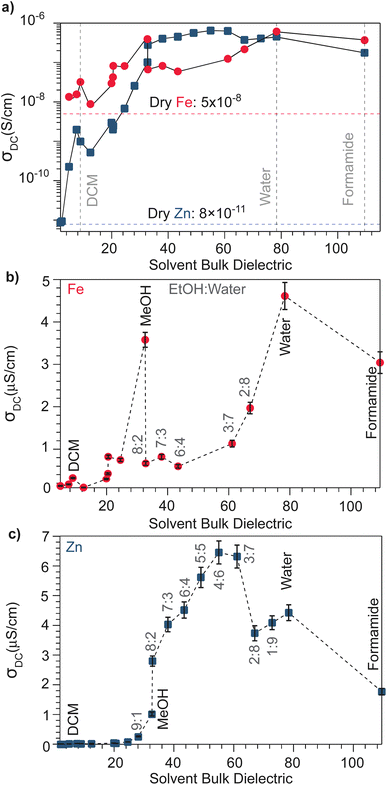
With the observation that water treatment improved the electronic conductivity of both the Fe and Zn systems, we explored the effect of solvents with a wide range of bulk dielectric constants. Fig. 2 summarizes the pressed-pellet DC conductivities after addition of solvent. Values were obtained from linear fits to the plateaued time points of I–V profiles collected at 2 mV s⁻¹ (Fig. S6 and S7†). For a greater range of bulk dielectric values, water/EtOH mixtures were employed in precise ratios.⁵⁸ In general, the DC conductivities of both the Zn and Fe systems dramatically increases with increased solvent dielectric strength. For example, these data indicate a ten-thousand-fold improvement to the electronic conductivity of the Zn system in the presence of formamide compared to the dry pellet. The I–V curves resulting from these solvent-dependent DC conductivities always exhibited non-linearity for the Zn framework, typical of a diffusion-limited process, (Fig. S7†), whereas for the Fe system, the I–V curves appear linear for solvents with low dielectric constants, such as DCM and n-butanol, (Fig. S6†) but non-linear for solvents with high dielectric constants, such as MeOH, acetone, or water (Fig. S6†). Solvent size also correlates with changes to DC conductivity (Fig. S8†). Specifically, smaller solvents generally correspond to higher conductivity values, helping to explain discrepancies in the relationship between dielectric and conductivity. For example, although t-butanol bears a larger bulk dielectric than CH₂Cl₂, the former leads to lower DC conductivities. This discrepancy could be attributed to its larger size (0.55 nm) compared to DCM (0.46 nm),⁵⁹ thereby impeding it from more effectively entering the framework ∼1 nm micropores, to properly solvate TMA⁺. However, conductivity generally improves when employing larger solvents unlikely to fit in the pores. This improvement likely results from solvent interactions with TMA⁺ in the macropores that exist between particles in the pressed pellet. In the case of the Fe system, DC conductivity scales roughly linearly with solvent dielectric strength (Fig. 2b), especially when excluding outliers MeOH and water, likely due to their comparatively smaller size that facilitate improved packing in the micropores. The Zn system, however, shows a strongly non-linear dependence for solvents having a bulk dielectric constant >40 (Fig. 1c). Collectively, these results suggest that for the Fe system, solvent serves to screen the attractions between itinerant electrons and less mobile TMA⁺ cations, in accordance with a semi-classical coulombic interaction. For the Zn system, however, the non-linear relationship could be ascribed to solvent facilitating the ambipolar diffusion of hopping-type transport by improving ion transport, as has been observed for the solvent dependent conductivity of mixed conducting polymers.⁶⁰

Fig. 2 (a) Solvent-dependent DC conductivity values of TMA₂FeGe₄S₁₀ and TMA₂ZnGe₄S₁₀ pressed-pellets obtained from linear fits to I–V curves swept voltammetrically between −0.2 V and 0.2 V at 2 mV s⁻¹. In increasing order of bulk dielectric constants, the solvents included hexanes, toluene, chloroform, DCM, THF, IPA, t-butanol, n-propanol, acetone, ethanol, methanol, (EtOH : water mixtures spanning 9 : 1 to 1 : 9), water, and formamide. Dotted lines correspond to dry-pellet DC conductivity values. Panels (b and c) represent the same data plotted on a linear scale.

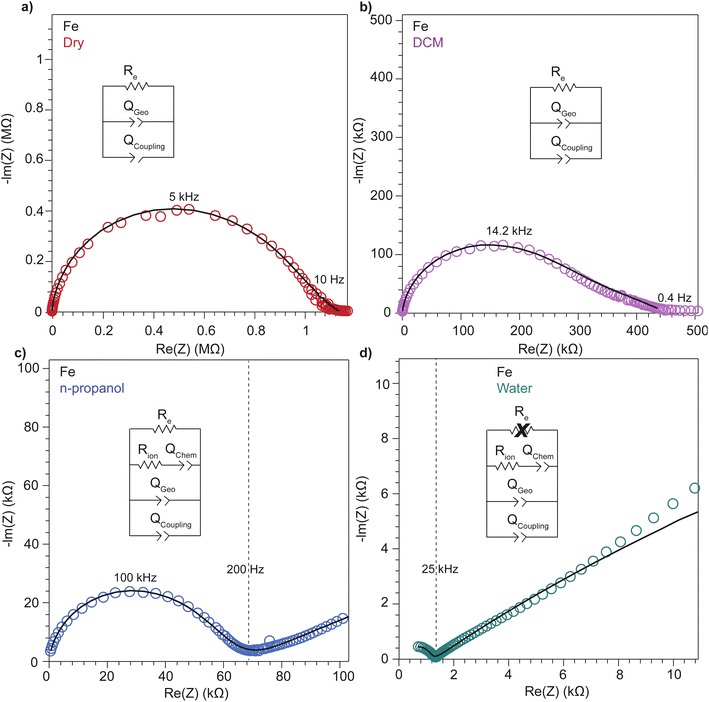
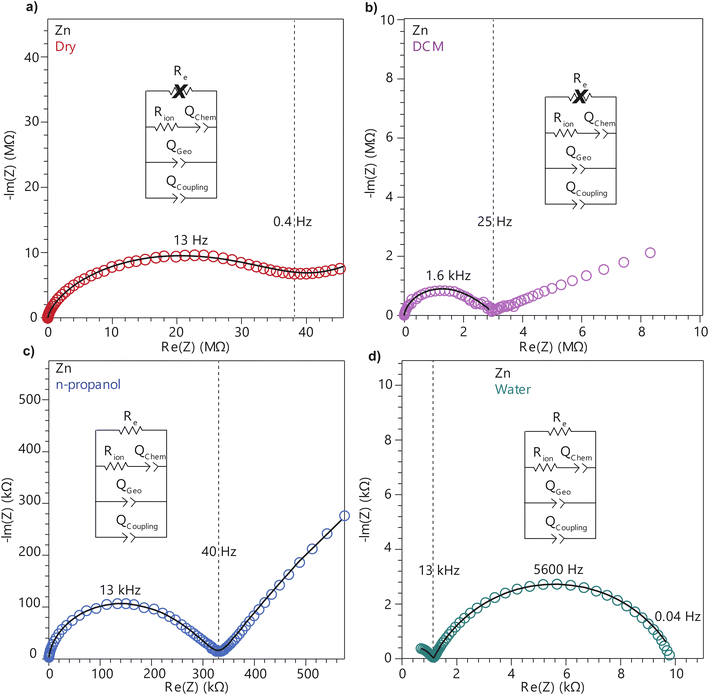
To further deconvolute the charge transport mechanism in the Fe and Zn systems, electrochemical impedance spectroscopy (EIS) was performed on dry and solvent-treated pressed-pellets. Fig. 3 displays Nyquist plots for the Fe system with data fitted to models based on the corresponding equivalent circuit diagrams. The impedance response for the Fe system when dry (Fig. 3a) produces a single semicircle as expected of a pure electronic conductor.⁶¹ The right-most x-intercept (1.13 MΩ) gives the electronic resistance of the system, yielding an electronic conductivity of 0.09 μS cm⁻¹, comparable to DC methods (0.05 μS cm⁻¹) (Fig. 2). Close inspection of the low frequency (right side) of the spectrum reveals a slight distortion of the semicircle that precludes fitting the impedance response to a parallel combination of an electronic resistance and idealized dielectric capacitance. We ascribe this distortion to an additional parallel constant phase element (CPE). Attempts to model this distortion to grain-boundary contributions—commonly modeled as a parallel resistor and capacitor—proved unsuccessful.^61–64 Constant phase elements are defined primarily by their phase, n, with their total impedance (Z) described by 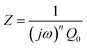. When n = 1, the CPE describes an ideal capacitor, whereas n = 0 corresponds to a pure resistor, and n = 0.5 denotes a semi-infinite diffusion-related process, termed a Warburg element.^65,66 The phase that describes the distortion for the Fe system is 0.37, suggesting ion–electron interactions influence electronic conduction even when dry. This CPE could be attributed to a distribution of contact resistances,⁶⁷ a distribution of conduction pathways through the pellet,^68,69 or a coupling constant between charge transfer pathways.^64,70 While dispersion of contact resistances and conduction pathways are expected to affect the EIS response at high frequencies, the dispersion observed in our systems appears in the low-frequency region (right-side) of the Nyquist plot. This dispersion likely reflects the ionic motion in the impedance response of the bulk material and the inhomogeneous pore resistances.⁷¹ Therefore, we ascribe this circuit element to a CPE we term Q_coupling, which describes the electrostatic coupling between ions and charges. Previous reports theorized that this effect impacts the bulk impedance response of mixed conductors, but it is often neglected in circuit fitting because dielectric responses are typically far larger than any electrostatic coupling.^64,70

Fig. 3 Nyquist plots of TMA₂FeGe₄S₁₀ pressed-pellets when dry (a) and after addition of DCM (b), n-propanol (c), and deionized water (d). Black traces represent fits to the equivalent circuit diagrams shown in the figure. Crossed-out circuit elements denote elements that are too large to adequately fit to the impedance response.

By contrast, the Zn system displays an incomplete semicircle even when dry (Fig. 4a). The x-intercept fit produces a high bulk resistance of 48 MΩ which corresponds to a conductivity of 0.002 μS cm⁻¹. We ascribe this resistance to be predominantly ionic in character. Fits to these data also suggest a significant distortion to the low frequency (right side) of the first semicircle. In contrast to the Fe system, the CPE associated with this distortion has n = 0.45. While the phase for the Fe system is too distorted to definitively define its origin, for the Zn system this n can be ascribed to a a diffusion process. Furthermore, in contrast to the Fe system, a CPE with n = 0.41 controls the impedance response below 0.4 Hz. Microscopically, we attribute this process to a “chemical capacitance” (Q_chem) arising from the hopping of electrons under the influence of TMA⁺ concentration gradients induced by the ion-blocking interfaces.^61,63,72

Fig. 4 Nyquist plots of TMA₂ZnGe₄S₁₀ pressed-pellets when dry (a) and after addition of DCM (b), n-propanol (c), and deionized water (d). Black traces represent fits to the equivalent circuit diagrams shown in the figure. Crossed-out circuit elements denote elements that are too large to adequately fit to the impedance response.

The distorted impedance responses described by Q_coupling observed for the dry Fe and Zn materials suggest distinct manifestations of ICCT. Although typical analysis of mixed conductors treats ions and electrons as separate charges with independent resistances and, hence, parallel resistors, these data suggest a partial convolution of the ionic and electronic rails, which manifests in the CPE we label as Q_coupling.^61,63,72 Furthermore, because Q_coupling for the dry Zn system fits to n = 0.45, these electrochemical process can be physically understood as a diffusion process. In fact, the CPE can be readily exchanged for a Warburg element with little change to the fit (Fig. S10†). This result implies cation–electron ambipolar diffusion. Such Warburg-type responses have been observed for porous electrodes where the movement of ions and electrons are coupled.⁷³ In contrast, the Fe system shows n = 0.37, with this dispersion in the diffusive response potentially due to mean-field attraction from TMA⁺ cations impeding the movement of delocalized electronic carriers.

To better understand the mechanistic role of solvent in a redox hopping-type system, EIS responses were recorded for the Zn system after treatment with solvents spanning a range of bulk dielectric values (DCM, n-propanol, and water; Fig. 4). In general, with increased solvent dielectric strength, the Zn system displayed decreased impedance across all frequencies and a diffusion-related process dominates at low frequencies. As with the dry Zn system, these data were fit best to a circuit with a Q_coupling element attributable to cation-coupled electron transport. With all solvents, the CPE bears an average phase of n = 0.48 equivalent to a Warburg diffusion element, suggesting charge transport proceeds by an ambipolar diffusion mechanism, i.e., by redox hopping compensated by diffusing TMA⁺ cations. Furthermore, the ionic resistances decrease with solvents of greater bulk dielectrics, as observed by the position of the intermediate x intercepts in the Nyquist plots. In addition, the electronic resistances also decrease with solvents of greater bulk dielectrics, as calculated from circuit fits which provide the second low frequency x intercept (Fig. 5). This result implies solvent improves ambipolar diffusion and manifests in decreases in Warburg coefficients for the Q_coupling (Fig. 5) and improved diffusion coefficients. Furthermore, fits for hydrated Zn system included a contact resistance (R_c) to ensure valid interpretation of the impedance results. The R_c found is 150 Ω, in close agreement with the contact resistance found when considering the impedance of the dry Zn system, 106 Ω. This result implies that solvent treatment does not dramatically affect the ohmic contact between the electrode and pellet.

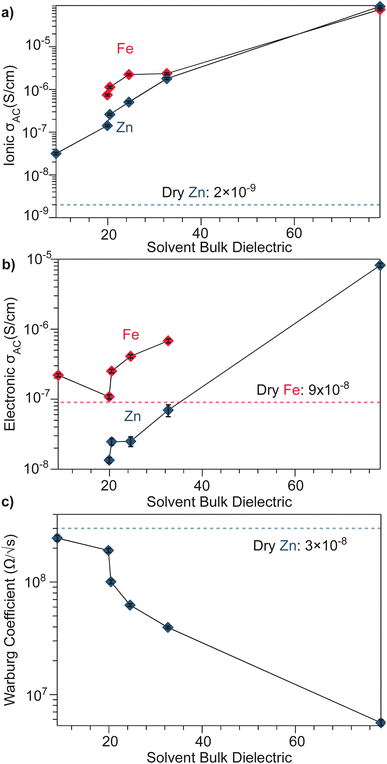Fig. 5 Solvent-dependent parameters fitted from EIS spectra modelled by equivalent circuits shown in Fig. 3 and 4. (a) AC ionic conductivity as a function of solvent bulk dielectric for the Fe and Zn materials. (b) AC electronic conductivity as a function of solvent bulk dielectric for the Fe and Zn materials. (c) High frequency Warburg coefficients derived for TMA₂ZnGe₄S₁₀ from the Q_coupling.

The low-frequency EIS response of the solvent-treated Zn analogues can be modeled by the CPE Q_chem, which corresponds to electron diffusion under the influence of a TMA⁺ gradient. For all solvent treatments, n > 0.5 for Q_chem, with an average phase of 0.56. Like Q_coupling, this phase can be physically understood as a diffusion process and in the context of the mixed conducting literature corresponds to equal charge carrier concentrations of both electrons and ions.⁶¹ This fact provides further evidence for concerted ambipolar motion, where electrons can only conduct with associated ion diffusion.

Based on the hypothesis that electronic conduction improves because of improved ambipolar diffusion promoted by increased ionic conductivity, the Zn system was treated with an aqueous solution of TMABr. After treatment, the electronic resistance further decreased to 8000 Ω (Fig. S12†). This result suggests the increased availability of TMA⁺ leads to greater cation concentration gradients and stronger electric fields to promote electron conduction.⁶² Furthermore, the ionic resistance also decreases from 1300 Ω to 30 Ω, when considering the 150 Ω R_contact. Furthermore, when modeling Q_coupling as a Warburg element, we find a Warburg coefficient of 2.4 × 10⁶ Ω s^−1/2, in comparison to 6.7 × 10⁶ Ω s^−1/2, with just deionized water. This result reflects the increased density of positive point charges that can stabilize hopping electrons leading to improved hopping.

Similarly, to better understand ICCT and the mechanistic role of solvent in a band-type system, the EIS response of the Fe system was recorded after solvent treatment (DCM, n-propanol, and water depicted in Fig. 3). As with the Zn system, increased solvent dielectrics leads to an overall decrease in impedance, but due to a different mechanism. With nonpolar solvents such as DCM, the asymmetry at frequencies below 10 kHz became more pronounced and the low-frequency x-intercept reduced from 1.13 MΩ to 0.45 MΩ. We interpret these changes to mean an increase in charge coupling concomitant with a decrease in DC conductivity. For more polar and higher dielectric materials, such as n-propanol and water, a low frequency impedance “tail” emerges, reminiscent of the chemical diffusion seen in the Zn system (Q_chem). These solvents cause a reduction in the ionic and electronic resistances of the Fe material. Whereas ionic resistance can be found directly from the first x intercepts, the electronic resistances were determined by fitting the spectra to the circuit diagrams shown in Fig. 4. Like the Zn system, fits to the hydrated response included R_contact, producing values of 200 Ω that agree with R_contact of the dry Fe system (114 Ω). Close inspection reveals that the phase of Q_coupling, the process describing coupled electron–cation motion, becomes highly distorted. Across all solvents, we observed an average n value of 0.33, with water treatment leading to the smallest phase of n = 0.15. Furthermore, when utilizing high dielectric solvents, the low frequency CPE Q_chem also exhibits a highly distorted phase that averaged to n = 0.31. These highly distorted CPE values indicate that unlike the ambipolar diffusion of the Zn system, electronic conduction dominates charge transport in the Fe system,⁶¹ but under the influence of cation–electron interactions that become frequency dependent with solvent and cation motion. While solvent screens the interactions between iterant charges, leading to a net decrease in electronic DC resistance and AC resistance, the increase in ionic motion creates non-uniform electric fields and electronic resistances, leading to highly dispersive n values.⁷¹ While electronic resistances were fitted for the Fe system from circuit fits for most solvents, the hydrated system was unable to be fitted to an electronic resistance due to the far lower ionic resistance. This result contrasts with the hydrated Zn system, where improvements to ionic conductivity led directly to a measurable improvement in electronic conductivity, further supporting the claim that the charge transport mechanism for the Zn material proceeds by mixed, hopping-type transport.

Because concerted ion–charge motion improves the thermodynamic driving forces of charge transfer in related systems,²¹ we investigated the impact of solvent on charge transport thermodynamics for the Fe and Zn systems. Temperature-dependent DC conductivity values of the Fe system after treatment with either o-dichlorobenzene or formamide reveals virtually no change in the activation barrier for electron conduction (Fig. S14 and S15†). In contrast, the temperature-dependent EIS response of the Zn system after formamide treatment exhibits a lower activation barrier when fitting both the first and second x intercept resistance (0.25/0.30 eV vs. 0.44/0.37 eV), suggesting increased carrier density for the Zn system (Fig. S13†). Taken together, these results further support the assignment of the Fe system as a band-type conductor: the activation barrier remains unchanged because solvent simply screens the coulombic attraction between electrons and cations, leading to an improvement in the mobility of the electronic charges, but without increasing charge carrier density. For the Zn system, on the other hand, redox hopping becomes more facile with improved ion diffusion, increasing carrier density, and manifesting in a far lower activation barrier then the Fe system.

Discussion

These results provide some of the first evidence that solvent controls both ion and electron transport in a microporous material. To summarize, the overall impedances of both the Zn and Fe materials decrease as the dielectric strength of the solvent increases, causing the purely electronic resistances to decrease as well, yet for different microscopic reasons. Solvent plays two roles mechanistically for both materials: decreasing electronic resistance and improving ion diffusion, yet these results suggest the relative importance of each role to the Fe versus Zn materials depends on the charge transport mechanism. For the band-type Fe material, the dominant role of solvent is to screen resistive cation–electron interactions, while for the hopping-type Zn material, solvent improves ambipolar diffusion (at high frequencies) and generates large electric fields (at low frequencies) leading to improved chemical diffusion of electrons. The “screening” role of solvent for the Fe material is evidenced by the roughly linear dependence of DC conductivity versus dielectric strength, as expected for semi-classical Coulomb interactions. Furthermore, fitting the EIS data to the electron–cation coupling element Q_coupling led to highly distorted phases more consistent with a resistive-based process, rather than classical diffusion expected from a redox hopping process. Lastly, the insensitivity of the charge transport activation barrier to solvent suggests electronic conductivity increases with solvent addition due to improved electron mobility brought about by charge screening, rather than improved ion diffusion aiding in a redox hopping process. In contrast, the Zn system exhibits a decreased activation barrier with solvent addition, which is consistent with a redox hopping process, as solvent decreases the activation barrier for ionic conduction.^60,74,75 The nonlinear dependence of DC conductivity with solvent dielectric also corroborates a hopping-type ICCT in the Zn material, as do the n ∼ 0.5 phase angles for both Q_coupling and Q_chem from EIS fittings. Finally, the nature of the ICCT process in the high frequency regime for the Zn material likely involves concerted cation–electron motion. Scheme 2 summarizes these conclusions. The TMA⁺ provide shallow electrostatic traps in the case of the Fe system, creating increased resistance to the band-type conduction, whereas for Zn, they function as deep traps necessitating concerted motion of both hopping charges and mobile cations.

Scheme 2 Conduction pathways for the band-type Fe (a) versus hopping-type Zn (b) analogues.

Although solvent interactions have been reported to impact the conductivity of diverse classes of inorganic materials, this study provides unprecedented insight the mechanistic role of solvent on charge transport in microporous systems. Because ion diffusion dictates redox hopping mechanisms, as demonstrated in MOFs, metal oxides,⁷⁶ and redox polymers,^52,77 solvent-dependent ion diffusion has been explored. For example, conductivity studies of the MOF Zr(3-hydroxy-2-[7-(4-carboxy-2-hydroxyphenyl)-1,3,6,8-tetraoxo-3,6,7,8-tetrahydro-1H-benzo[lmn][3,8]phenanthrolin-2-yl]benzoate) revealed that diffusion coefficients derived from chronoamperometry decreased with higher dielectric solvents.²⁹ However, the scope of the study was limited to few solvents and focused on just this hopping-type material. However, anecdotal evidence abounds for the solvent- and electrolyte-dependence of charge transport in large-pore MOFs and COFs.^{29,53,57,78–80} We contend that this solvent dependence likely results from the pervasiveness of hopping-type charge transport in MOFs. Furthermore, we expect these effects to be magnified by nanoconfined ions. For example, as the pore sizes of isostructural MOFs decrease, reports have noted that diffusion coefficients of hexafluorophosphate and tetrakis(pentafluorophenyl)borate anions also decrease.³⁰ In the extreme limit (chemical bonding) of ion–charge confinement where ions are close or equal in size to the pore, such interactions could resemble PCET.¹⁴ Elsewhere in the literature, the conductivity of the semiconductor material Pb₃Na_1.5(OH)_0.5(2,3,6,7,10,11-hexakis(butyrylthio)triphenylene) was reported to increase by 10 000-fold upon introduction of water and when measured at high humidity, but without explanation or comparison to other solvent treatments.⁸¹ Similarly, the conductivity of mesoporous NaSbS₂ was shown to increase 1000-fold in humid air as opposed to vacuum, although the exact mechanism remains unknown.^52,74,77,82

These results resemble evidence of ion–electron coupling in organic semiconductors.⁷⁵ While conventional semiconductors such as Si, CdSe, or GaP can be doped through substitution, polymers require doping through redox chemistry that necessitates charge-balancing ions.⁷⁵ The localization of these ions on polymer backbones leads to electronic transport strongly dependent on both solvent and electrolyte identity. Poly(3,4-ethylenedioxythiophene)/poly(4-styrenesulfonate) has been reported to increase in conductivity from 0.8 μS cm⁻¹ in the dry state to 80 μS cm⁻¹ with DMSO, with intermediate conductivities achieved with THF and other solvents of lower dielectric strengths.¹² Morris et al. explicitly attributed the effect to dielectric screening of ion–electron interactions. Similarly, the conductivity of the copolymer poly(3,4-ethylenedioxythiophene)/poly(styrenesulfonate) (PEDOT:PSS) increases from 1 S cm⁻¹ in the dry state to a maximum value of 1000 S cm⁻¹ with DMF.⁸³ Exposure to various solvents with a range of dielectric strengths yielded PEDOT:PSS conductivities that were non-linear with dielectric strength, akin to the data reported here for the Zn system. Portale et al. attributed this enhancement to increased polaron delocalization, evident from the intensified bipolaron optical feature following solvent addition. Lastly, the seminal study on the metallically conductive polymer poly(benzimidazobenzophenanthroline) documented a 200-fold decrease in conductivity when doped with ions, attributed to the formation of coulombic trap states.⁷⁷ In contrast to the results report here, solvent addition induced a 1000-fold diminishment of conductivity, which the authors ascribed to a solvent-induced switch from a band-type to hopping mechanism of charge transport. Evidence for this claim pointed to an increase in the conduction activation barrier from 0.07 eV when dry to 0.63 eV in the presence of MeCN. In the case of the Fe system on the other hand, addition of solvent maintains the activation barrier, suggesting the charge transport mechanism remains band-type.

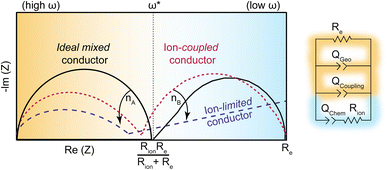
While ion–electron interactions have been well-documented in polymer systems, this report is the first to quantify the coupling strength of ion and electrons with electrochemical impedance analysis. Scheme 3 summarizes the model employed here and the expected ICCT behavior in band-type versus hopping-type systems. For a band-type material, such as the Fe analogue, we expect an impedance response shown in dashed purple, arising from the presence of cations creating a frequency-dependent resistance to the itinerant charges. Hence, we term these materials “ion-limited conductors”. For hopping-type systems, such as the Zn analogue, we expect the impedance response shown in dotted red, which resembles the behavior of an “ideal (non-coupled) mixed conductor”, but with lower impedance across all frequencies and distorted semi-circular features induced by ion–charge concerted motion. The phase of the Q_coupling CPE offers a means to distinguish between concerted hopping-type mechanisms (n ∼ 0.5) versus band-type conduction impeded by ion interactions (n ≪ 0.5). While traditionally reserved for analyzing lower-frequency regions of Nyquist plots, i.e., the diffusion “tail”, such Warburg-like circuit elements have been employed to describe similar distortions present in porous polyamide films impregnated by water and electrolyte.⁸⁴ This analysis, in combination with solvent-dependent activation barriers, provides some of the first evidence of redox-type hopping in microporous materials, although this mechanism is commonly invoked for MOFs, such as Zr(3-hydroxy-2-[7-(4-carboxy-2-hydroxyphenyl)-1,3,6,8-tetraoxo-3,6,7,8-tetrahydro-1H-benzo[lmn][3,8]phenanthrolin-2-yl]benzoate).²⁹ Just as PCET provides lower-energy redox pathways in biological systems,¹⁴ the observation of concerted charge transport in TMA₂ZnGe₄S₁₀ suggests high energy intermediates may be avoided in inorganic systems through ICCT. Mixed conductors feature widely in electrochemical technologies such as fuel cells, batteries, supercapacitors, and electrocatalysts, where ions conduct to balance charges in porous electrodes.³¹ However, achieving both high ionic and electronic conductivity remains an outstanding challenge. For example, while LiFePO₄ possesses large solid state Li⁺ diffusion coefficients (10⁻⁹ cm² s⁻¹) the low electronic conductivity (10⁻⁹ S cm⁻²) necessitates conductive additives.^85,86 In contrast, traditional metal oxide electrodes possess higher electronic conductivities (10⁻⁴–10⁻⁶ S cm⁻²), but are often hindered by poor ionic transport.⁸⁷ These results are therefore critical to the design and analysis of microporous materials for energy storage applications.

Scheme 3 Generalized impedance response for an ideal mixed conductor (black solid trace), an ion-coupled conductor (dotted red trace; TMA₂ZnGe₄S₁₀), and ion-limited conductor (dotted blue trace; TMA₂FeGe₄S₁₀).

Conclusion

In conclusion, experimental comparison of TMA₂FeGe₄S₁₀ and TMA₂ZnGe₄S₁₀ reveals electrochemical signatures of ion-coupled transport and the mechanistic role of solvent in controlling band-type versus redox hopping conductivity in microporous materials. Non-linear responses in direct-current sweep voltammetry and chronoamperometry indicate diffusion-controlled hopping-type transport, whereas linearity supports the assignment of band-type conduction. Electrochemical impedance spectra point to concerted ion–electron hopping when constant phase elements fit to phase values of n ∼ 0.5, whereas band-type electronic conduction appears impeded by ion interactions when n ≪ 0.5. This analysis constitutes a novel method for quantifying ion-coupled conduction. Taken together, these signatures present a microscopic picture of how solvent controls ion-coupled transport in two distinct forms of conduction: whereas solvent improves electronic conductivity by screening ion–charge interactions in band-type systems, it improves ambipolar diffusion in hopping-type systems by accelerating ion transport. Although developed with a model class of materials, these insights and methods unify observations of solvent- and electrolyte-dependent conduction already observed in wide-ranging classes of materials, while providing tools for designing electrochemical systems in general.

Data availability

All supporting data is available free of charge in the ESI.†

Author contributions

J. M. performed data collection and analysis, designed experiments, and prepared the manuscript, P. A. K. assisted in data analysis and manuscript preparation, and C. K. B. oversaw data analysis, experimental design, manuscript preparation, and initial project conception.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This material is based upon work supported by the Department of Energy through the Office of Basic Energy Sciences under grant no. DE-SC0022147. C. K. B. acknowledges the Research Corporation for Science Advancement (Cottrell Award).

References

1. J.-S. M. Lee and A. I. Cooper, Advances in Conjugated Microporous Polymers, Chem. Rev., 2020, 120, 2171–2214.
2. Z. Liu, X. Yuan, S. Zhang, J. Wang, Q. Huang, N. Yu, Y. Zhu, L. Fu, F. Wang, Y. Chen and Y. Wu, Three-dimensional ordered porous electrode materials for electrochemical energy storage, NPG Asia Mater., 2019, 11, 1–21.
3. L. Qu, H. Iguchi, S. Takaishi, F. Habib, C. F. Leong, D. M. D'Alessandro, T. Yoshida, H. Abe, E. Nishibori and M. Yamashita, Porous Molecular Conductor: Electrochemical Fabrication of Through-Space Conduction Pathways among Linear Coordination Polymers, J. Am. Chem. Soc., 2019, 141, 6802–6806.
4. C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, On the molecular origin of supercapacitance in nanoporous carbon electrodes, Nat. Mater., 2012, 11, 306–310.
5. S. Bi, H. Banda, M. Chen, L. Niu, M. Chen, T. Wu, J. Wang, R. Wang, J. Feng, T. Chen, M. Dincă, A. A. Kornyshev and G. Feng, Molecular understanding of charge storage and charging dynamics in supercapacitors with MOF electrodes and ionic liquid electrolytes, Nat. Mater., 2020, 19, 552–558.
6. D. Sheberla, J. C. Bachman, J. S. Elias, C.-J. Sun, Y. Shao-Horn and M. Dincă, Conductive MOF electrodes for stable supercapacitors with high areal capacitance, Nat. Mater., 2017, 16, 220–224.
7. S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun., 2020, 11, 4068.
8. Q. Qian, P. A. Asinger, M. J. Lee, G. Han, K. Mizrahi Rodriguez, S. Lin, F. M. Benedetti, A. X. Wu, W. S. Chi and Z. P. Smith, MOF-Based Membranes for Gas Separations, Chem. Rev., 2020, 120, 8161–8266.
9. H. Li, L. Li, R.-B. Lin, W. Zhou, Z. Zhang, S. Xiang and B. Chen, Porous metal-organic frameworks for gas storage and separation: Status and challenges, EnergyChem, 2019, 1, 100006.
10. B. Silva-Gaspar, R. Martinez-Franco, G. Pirngruber, A. Fécant, U. Diaz and A. Corma, Open-Framework Chalcogenide Materials - from isolated clusters to highly ordered structures - and their photocalytic applications, Coord. Chem. Rev., 2022, 453, 214243.
11. S. Greiner, B. Schwarz, M. Ringenberg, M. Dürr, I. Ivanovic-Burmazovic, M. Fichtner, M. Anjass and C. Streb, Redox-inactive ions control the redox-activity of molecular vanadium oxides, Chem. Sci., 2020, 11, 4450–4455.
12. A. Kumar, D. Lionetti, V. W. Day and J. D. Blakemore, Redox-Inactive Metal Cations Modulate the Reduction Potential of the Uranyl Ion in Macrocyclic Complexes, J. Am. Chem. Soc., 2020, 142, 3032–3041.
13. K. Saito, M. Nakagawa, M. Mandal and H. Ishikita, Role of redox-inactive metals in controlling the redox potential of heterometallic manganese–oxido clusters, Photosynth. Res., 2021, 148, 153–159.
14. S. Hammes-Schiffer, Proton-Coupled Electron Transfer: Moving Together and Charging Forward, J. Am. Chem. Soc., 2015, 137, 8860–8871.
15. R. Feng, X. Zhang, V. Murugesan, A. Hollas, Y. Chen, Y. Shao, E. Walter, N. P. N. Wellala, L. Yan, K. M. Rosso and W. Wang, Reversible ketone hydrogenation and dehydrogenation for aqueous organic redox flow batteries, Science, 2021, 372, 836–840.
16. S. Y. Reece and D. G. Nocera, Proton-Coupled Electron Transfer in Biology: Results from Synergistic Studies in Natural and Model Systems, Annu. Rev. Biochem., 2009, 78, 673–699.
17. C. N. Valdez, A. M. Schimpf, D. R. Gamelin and J. M. Mayer, Proton-Controlled Reduction of ZnO Nanocrystals: Effects of Molecular Reductants, Cations, and Thermodynamic Limitations, J. Am. Chem. Soc., 2016, 138, 1377–1385.
18. A. M. Schimpf, C. E. Gunthardt, J. D. Rinehart, J. M. Mayer and D. R. Gamelin, Controlling carrier densities in photochemically reduced colloidal ZnO nanocrystals: Size dependence and role of the hole quencher, J. Am. Chem. Soc., 2013, 135, 16569–16577.
19. M. N. Braten, D. R. Gamelin and J. M. Mayer, Reaction Dynamics of Proton-Coupled Electron Transfer from Reduced ZnO Nanocrystals, ACS Nano, 2015, 9, 10258–10267.
20. H. Liu, C. K. Brozek, S. Sun, D. B. Lingerfelt, D. R. Gamelin and X. Li, A Hybrid Quantum-Classical Model of Electrostatics in Multiply Charged Quantum Dots, J. Phys. Chem. C, 2017, 121, 26086–26095.
21. K. H. Hartstein, C. K. Brozek, S. O. M. Hinterding and D. R. Gamelin, Copper-Coupled Electron Transfer in Colloidal Plasmonic Copper-Sulfide Nanocrystals Probed by in Situ Spectroelectrochemistry, J. Am. Chem. Soc., 2018, 140, 3434–3442.
22. G. M. Carroll, C. K. Brozek, K. H. Hartstein, E. Y. Tsui and D. R. Gamelin, Potentiometric Measurements of Semiconductor Nanocrystal Redox Potentials, J. Am. Chem. Soc., 2016, 138, 4310–4313.
23. C. K. Brozek, K. H. Hartstein and D. R. Gamelin, Potentiometric Titrations for Measuring the Capacitance of Colloidal Photodoped ZnO Nanocrystals, J. Am. Chem. Soc., 2016, 138, 10605–10610.
24. S. Fukuzumi and K. Ohkubo, Metal ion-coupled and decoupled electron transfer, Coord. Chem. Rev., 2010, 254, 372–385.
25. Y. Morimoto, H. Kotani, J. Park, Y. M. Lee, W. Nam and S. Fukuzumi, Metal ion-coupled electron transfer of a nonheme oxoiron(IV) complex: Remarkable enhancement of electron-transfer rates by Sc³⁺, J. Am. Chem. Soc., 2011, 133, 403–405.
26. E. Y. Tsui and T. Agapie, Reduction potentials of heterometallic manganese-oxido cubane complexes modulated by redox-inactive metals, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10084–10088.
27. J. Yun, V. Natu, I. Echols, R. M. Thakur, H. Cao, Z. Tan, M. Radovic, M. J. Green, M. W. Barsoum and J. L. Lutkenhaus, Anion Identity and Time Scale Affect the Cation Insertion Energy Storage Mechanism in Ti₃C₂T_x MXene Multilayers, ACS Energy Lett., 2022, 7, 1828–1834.
28. O. Mashtalir, M. R. Lukatskaya, A. I. Kolesnikov, E. Raymundo-Piñero, M. Naguib, M. W. Barsoum and Y. Gogotsi, The effect of hydrazine intercalation on the structure and capacitance of 2D titanium carbide (MXene), Nanoscale, 2016, 8, 9128–9133.
29. A. T. Castner, H. Su, E. Svensson Grape, A. K. Inge, B. A. Johnson, M. S. G. Ahlquist and S. Ott, Microscopic Insights into Cation-Coupled Electron Hopping Transport in a Metal–Organic Framework, J. Am. Chem. Soc., 2022, 144, 5910–5920.
30. M. Cai, Q. Loague and A. J. Morris, Design Rules for Efficient Charge Transfer in Metal–Organic Framework Films: The Pore Size Effect, J. Phys. Chem. Lett., 2020, 11, 702–709.
31. M. M. Thackeray, J. O. Thomas and M. S. Whittingham, Science and Applications of Mixed Conductors for Lithium Batteries, MRS Bull., 2000, 25, 39–46.
32. O. M. Yaghi, Z. Sun, D. A. Richardson and T. L. Groy, Directed Transformation of Molecules to Solids: Synthesis of a Microporous Sulfide from Molecular Germanium Sulfide Cages, J. Am. Chem. Soc., 1994, 116, 807–808.
33. K. K. Rangan, S. J. L. Billinge, V. Petkov, J. Heising and M. G. Kanatzidis, Aqueous Mediated Synthesis of Mesostructured Manganese Germanium Sulfide with Hexagonal Order, Chem. Mater., 1999, 11, 2629–2632.
34. S. Bag and M. G. Kanatzidis, Chalcogels: Porous Metal−Chalcogenide Networks from Main-Group Metal Ions. Effect of Surface Polarizability on Selectivity in Gas Separation, J. Am. Chem. Soc., 2010, 132, 14951–14959.
35. S. Bag and M. G. Kanatzidis, Importance of Solution Equilibria in the Directed Assembly of Metal Chalcogenide Mesostructures, J. Am. Chem. Soc., 2008, 130, 8366–8376.
36. S. Haddadpour, M. Melullis, H. Staesche, C. R. Mariappan, B. Roling, R. Clérac and S. Dehnen, Inorganic Frameworks from Selenidotetrelate Anions [T₂Se₆]₄− (T = Ge, Sn): Synthesis, Structures, and Ionic Conductivity of [K₂(H₂O)₃][MnGe₄Se₁₀] and (NMe₄)₂[MSn₄Se₁₀] (M = Mn, Fe), Inorg. Chem., 2009, 48, 1689–1698.
37. K. K. Rangan, P. N. Trikalitis and M. G. Kanatzidis, Light-Emitting Meso-Structured Sulfides with Hexagonal Symmetry: Supramolecular Assembly of [Ge₄S₁₀]^4- Clusters with Trivalent Metal Ions and Cetylpyridinium Surfactant, J. Am. Chem. Soc., 2000, 122, 10230–10231.
38. M. J. MacLachlan, N. Coombs, R. L. Bedard, S. White, L. K. Thompson and G. A. Ozin, Mesostructured Metal Germanium Sulfides, J. Am. Chem. Soc., 1999, 121, 12005–12017.
39. J. Zhang, X. Bu, P. Feng and T. Wu, Metal Chalcogenide Supertetrahedral Clusters: Synthetic Control over Assembly, Dispersibility, and Their Functional Applications, Acc. Chem. Res., 2020, 53, 2261–2272.
40. M. J. MacLachlan, N. Coombs and G. A. Ozin, Non-aqueous supramolecular assembly of mesostructured metal germanium sulphides from (Ge₄S₁₀)⁴⁻ clusters, Nature, 1999, 397, 681–684.
41. K. Tsamourtzi, J.-H. Song, T. Bakas, A. J. Freeman, P. N. Trikalitis and M. G. Kanatzidis, Straightforward Route to the Adamantane Clusters [Sn₄Q₁₀]⁴⁻ (Q = S, Se, Te) and Use in the Assembly of Open-Framework Chalcogenides (Me₄N)₂M[Sn₄Se₁₀] (M = Mn^II, Fe^II, Co^II, Zn^II) Including the First Telluride Member (Me₄N)₂Mn[Ge₄Te₁₀], Inorg. Chem., 2008, 47, 11920–11929.
42. C. L. Bowes, A. J. Lough, A. Malek, G. A. Ozin, S. Petrov and D. Young, Thermally Stable Self-assembling Open-Frameworks: Isostructural Cs⁺ and (CH₃)₄N⁺ Iron Germanium Sulfides, Chem. Ber., 1996, 129, 283–287.
43. P. N. Trikalitis, K. K. Rangan, T. Bakas and M. G. Kanatzidis, Varied pore organization in mesostructured semiconductors based on the [SnSe₄]^4- anion, Nature, 2001, 410, 671–675.
44. M. Duchardt, S. Haddadpour, T. Kaib, P. Bron, B. Roling and S. Dehnen, Different Chemical Environments of [Ge₄Se₁₀]^4– in the Li⁺ Compounds [Li₄(H₂O)₁₆][Ge₄Se₁₀]·4.33H₂O, [{Li₄(thf)₁₂}Ge₄Se₁₀], and [Li₂(H₂O)₈][MnGe₄Se₁₀], and Ionic Conductivity of Underlying “Li₄Ge₄Se₁₀”, Inorg. Chem., 2021, 60, 5224–5231.
45. J. Zhang, P. Feng, X. Bu and T. Wu, Atomically precise metal chalcogenide supertetrahedral clusters: frameworks to molecules, and structure to function, Natl. Sci. Rev., 2022, 9, nwab076.
46. H. Yang, J. Zhang, M. Luo, W. Wang, H. Lin, Y. Li, D. Li, P. Feng and T. Wu, The Largest Supertetrahedral Oxychalcogenide Nanocluster and Its Unique Assembly, J. Am. Chem. Soc., 2018, 140, 11189–11192.
47. J. McKenzie, K. N. Le, D. J. Bardgett, K. A. Collins, T. Ericson, M. K. Wojnar, J. Chouinard, S. Golledge, A. F. Cozzolino, D. C. Johnson, C. H. Hendon and C. K. Brozek, Conductivity in Open-Framework Chalcogenides Tuned via Band Engineering and Redox Chemistry, Chem. Mater., 2022, 34, 1905–1920.
48. S. A. L. Weber, I. M. Hermes, S.-H. Turren-Cruz, C. Gort, V. W. Bergmann, L. Gilson, A. Hagfeldt, M. Graetzel, W. Tress and R. Berger, How the formation of interfacial charge causes hysteresis in perovskite solar cells, Energy Environ. Sci., 2018, 11, 2404–2413.
49. R. Singh and M. Parashar, Origin of Hysteresis in Perovskite Solar Cells, in Soft-Matter Thin Film Solar Cells, AIP Publishing Books, AIP Publishing LLC, 2020, pp. 1–29.
50. T.-Y. Yang, G. Gregori, N. Pellet, M. Grätzel and J. Maier, The Significance of Ion Conduction in a Hybrid Organic–Inorganic Lead-Iodide-Based Perovskite Photosensitizer, Angew. Chem., Int. Ed., 2015, 54, 7905–7910.
51. D. B. A. Rep, A. F. Morpurgo, W. G. Sloof and T. M. Klapwijk, Mobile ionic impurities in organic semiconductors, J. Appl. Phys., 2003, 93, 2082–2090.
52. N. A. Surridge, C. S. Sosnoff, R. Schmehl, J. S. Facci and R. W. Murray, Electron and counterion diffusion constants in mixed-valent polymeric osmium bipyridine films, J. Phys. Chem., 1994, 98, 917–923.
53. S. R. Ahrenholtz, C. C. Epley and A. J. Morris, Solvothermal Preparation of an Electrocatalytic Metalloporphyrin MOF Thin Film and its Redox Hopping Charge-Transfer Mechanism, J. Am. Chem. Soc., 2014, 136, 2464–2472.
54. S. Lin, P. M. Usov and A. J. Morris, The role of redox hopping in metal–organic framework electrocatalysis, Chem. Commun., 2018, 54, 6965–6974.
55. S. Goswami, I. Hod, J. D. Duan, C.-W. Kung, M. Rimoldi, C. D. Malliakas, R. H. Palmer, O. K. Farha and J. T. Hupp, Anisotropic Redox Conductivity within a Metal–Organic Framework Material, J. Am. Chem. Soc., 2019, 141, 17696–17702.
56. E. M. Johnson, S. Ilic and A. J. Morris, Design Strategies for Enhanced Conductivity in Metal–Organic Frameworks, ACS Cent. Sci., 2021, 7, 445–453.
57. P. J. Celis-Salazar, M. Cai, C. A. Cucinell, S. R. Ahrenholtz, C. C. Epley, P. M. Usov and A. J. Morris, Independent Quantification of Electron and Ion Diffusion in Metallocene-Doped Metal–Organic Frameworks Thin Films, J. Am. Chem. Soc., 2019, 141, 11947–11953.
58. G. Akerlof, Dielectric Constants of Some Organic Solvent-Water Mixtures at Various Temperatures, J. Am. Chem. Soc., 1932, 54(11), 4125–4139.
59. Y. Marcus, The properties of solvents, Wiley, Chichester, New York, 1998.
60. J. Imbrogno, K. Maruyama, F. Rivers, J. R. Baltzegar, Z. Zhang, P. W. Meyer, V. Ganesan, S. Aoshima and N. A. Lynd, Relationship between Ionic Conductivity, Glass Transition Temperature, and Dielectric Constant in Poly(vinyl ether) Lithium Electrolytes, ACS Macro Lett., 2021, 10, 1002–1007.
61. J. Jamnik and J. Maier, Treatment of the Impedance of Mixed Conductors Equivalent Circuit Model and Explicit Approximate Solutions, J. Electrochem. Soc., 1999, 146, 4183.
62. P. C. Harikesh, A. Surendran, B. Ghosh, R. A. John, A. Moorthy, N. Yantara, T. Salim, K. Thirumal, W. L. Leong, S. Mhaisalkar and N. Mathews, Cubic NaSbS₂ as an Ionic–Electronic Coupled Semiconductor for Switchable Photovoltaic and Neuromorphic Device Applications, Adv. Mater., 2020, 32, 1906976.
63. W. Lai and S. M. Haile, Impedance Spectroscopy as a Tool for Chemical and Electrochemical Analysis of Mixed Conductors: A Case Study of Ceria, J. Am. Ceram. Soc., 2005, 88, 2979–2997.
64. J. Jamnik, Impedance spectroscopy of mixed conductors with semi-blocking boundaries, Solid State Ionics, 2003, 157, 19–28.
65. S. Holm, T. Holm and Ø. G. Martinsen, Simple circuit equivalents for the constant phase element, PLoS One, 2021, 16, e0248786.
66. A. Lasia, The Origin of the Constant Phase Element, J. Phys. Chem. Lett., 2022, 13, 580–589.
67. C. L. Alexander, B. Tribollet and M. E. Orazem, Contribution of Surface Distributions to Constant-Phase-Element (CPE) Behavior: 1. Influence of Roughness, Electrochim. Acta, 2015, 173, 416–424.
68. C. L. Alexander, B. Tribollet and M. E. Orazem, Contribution of Surface Distributions to Constant-Phase-Element (CPE) Behavior: 2. Capacitance, Electrochim. Acta, 2016, 188, 566–573.
69. B. Hirschorn, M. E. Orazem, B. Tribollet, V. Vivier, I. Frateur and M. Musiani, Constant-Phase-Element Behavior Caused by Resistivity Distributions in Films: II. Applications, J. Electrochem. Soc., 2010, 157, C458.
70. J. Jamnik and J. Maier, Generalised equivalent circuits for mass and charge transport: chemical capacitance and its implications, Phys. Chem. Chem. Phys., 2001, 3, 1668–1678.
71. S. Amand, M. Musiani, M. E. Orazem, N. Pébère, B. Tribollet and V. Vivier, Constant-phase-element behavior caused by inhomogeneous water uptake in anti-corrosion coatings, Electrochim. Acta, 2013, 87, 693–700.
72. J.-S. Lee, J. Jamnik and J. Maier, Generalized equivalent circuits for mixed conductors: silver sulfide as a model system, Monatshefte für Chemie - Chemical Monthly, 2009, 140, 1113–1119.
73. R. de Levie, On porous electrodes in electrolyte solutions: I. Capacitance effects, Electrochim. Acta, 1963, 8, 751–780.
74. J. Y. Kim, J. H. Jung, D. E. Lee and J. Joo, Enhancement of electrical conductivity of poly(3,4-ethylenedioxythiophene)/poly(4-styrenesulfonate) by a change of solvents, Synth. Met., 2002, 126, 311–316.
75. B. D. Paulsen, K. Tybrandt, E. Stavrinidou and J. Rivnay, Organic mixed ionic–electronic conductors, Nat. Mater., 2020, 19, 13–26.
76. V. P. Zhdanov and B. Kasemo, The influence of the electrolyte on the electron diffusion in mesoporous nanocrystalline TiO₂, J. Phys.: Condens. Matter, 2004, 16, 2625–2629.
77. K. Wilbourn and R. W. Murray, The d.c. redox versus electronic conductivity of the ladder polymer poly(benzimidazobenzophenanthroline), J. Phys. Chem., 1988, 92, 3642–3648.
78. P. J. Celis-Salazar, C. C. Epley, S. R. Ahrenholtz, W. A. Maza, P. M. Usov and A. J. Morris, Proton-Coupled Electron Transport in Anthraquinone-Based Zirconium Metal–Organic Frameworks, Inorg. Chem., 2017, 56, 13741–13747.
79. M. G. Campbell, S. F. Liu, T. M. Swager and M. Dincă, Chemiresistive Sensor Arrays from Conductive 2D Metal–Organic Frameworks, J. Am. Chem. Soc., 2015, 137, 13780–13783.
80. Z. Meng, R. M. Stolz and K. A. Mirica, Two-Dimensional Chemiresistive Covalent Organic Framework with High Intrinsic Conductivity, J. Am. Chem. Soc., 2019, 141, 11929–11937.
81. J. Huang, Y. He, M.-S. Yao, J. He, G. Xu, M. Zeller and Z. Xu, A semiconducting gyroidal metal-sulfur framework for chemiresistive sensing, J. Mater. Chem. A, 2017, 5, 16139–16143.
82. R. J. Forster, J. Iqbal, J. Hjelm and T. E. Keyes, Solvent effects on charge transport through solid deposits of [Os(4,4′-diphenyl-2,2′-dipyridyl)₂Cl₂], Analyst, 2004, 129, 1186–1192.
83. J. Dong and G. Portale, Role of the Processing Solvent on the Electrical Conductivity of PEDOT:PSS, Adv. Mater. Interfaces, 2020, 7, 2000641.
84. S. Skale, V. Doleček and M. Slemnik, Substitution of the constant phase element by Warburg impedance for protective coatings, Corros. Sci., 2007, 49, 1045–1055.
85. N. T. M. Balakrishnan, A. Paul, M. A. Krishnan, A. Das, L. R. Raphaez, J.-H. Ahn, M. J. Jabeen Fatima and R. Prasanth, in Metal, Metal-Oxides and Metal Sulfides for Batteries, Fuel Cells, Solar Cells, Photocatalysis and Health Sensors, ed. S. Rajendran, H. Karimi-Maleh, J. Qin and E. Lichtfouse, Springer International Publishing, Cham, 2021, pp. 35–73.
86. K. Striebel, J. Shim, V. Srinivasan and J. Newman, Comparison of LiFePO₄ from Different Sources, J. Electrochem. Soc., 2005, 152, A664.
87. M. Park, X. Zhang, M. Chung, G. B. Less and A. M. Sastry, A review of conduction phenomena in Li-ion batteries, J. Power Sources, 2010, 195, 7904–7929.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc05090k

---